Оценка надежности радиоэлектронного устройства с учетом внезапных отказов путем моделирования на ЭВМ отказов элементов

МГТУ имени Баумана

Кафедра радиоэлектронных средств

Курсовой проект

на тему:

«Оценка надежности радиоэлектронного устройства с учетом внезапных отказов путем моделирования на ЭВМ отказов элементов»

Содержание

Введение

Постановка задачи

Краткое описание метода моделирования на ЭВМ отказов элементов

Решение задачи на ЭВМ

Аналитический расчет показателей надежности

Заключение

Литература

Приложение

Введение

Надежность – это свойство изделия сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции, в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования.

Надежность является комплексным свойством, которое в зависимости от назначения изделия и условий его применения может включать безотказность, долговечность, ремонтопригодность и сохраняемость или определенные сочетания этих свойств.

Для описания различных сторон этого свойства на практике пользуются показателями надежности, представляющими собой количественные характеристики одного или нескольких свойств, определяющих надежность изделия.

Используют единичные и комплексные показатели надежности. Под единичным понимают такой показатель, который характеризует одно из свойств, составляющих надежность изделия. Комплексный показатель характеризует несколько свойств, составляющих надежность изделия.

Для количественного описания различных сторон надежности как свойства обычно используют несколько групп показателей.

Первая группа – показатели безотказности, к которым относятся:

вероятность безотказной работы в течение заданного времени;

вероятность отказа в течение заданного времени ;

интенсивность отказов;

средняя наработка до отказа ( среднее время безотказной работы);

средняя наработка на отказ;

параметр потока отказов;

гамма-процентная наработка до отказа.

Вторая группа – показатели ремонтопригодности, к которым относятся:

вероятность восстановления изделия за заданное время;

среднее время восстановления.

Третья группа – показатели восстановления, к которым относятся:

гамма-процентный ресурс;

средний срок службы;

гамма-процентный срок службы.

Четвертая группа – показатели сохраняемости, к которым относятся:

средний срок сохраняемости;

гамма-процентный срок сохраняемости.

Пятая группа – комплексные показатели надежности, к которым относятся:

коэффициент готовности;

коэффициент технического использования;

коэффициент простоя.

В данном курсовом проекте оценка надежности проводится по показателям безотказности, а именно: по вероятности безотказной работы в течение заданного времени, по среднему времени безотказной работы и гамма-процентной наработки до отказа.

Постановка задачи

Задачей данного курсового проекта является оценка надежности радиоэлектронного устройства (РЭУ) с учетом внезапных отказов путем моделирования на ЭВМ отказов элементов.

В результате решения необходимо определить следующие показатели надежности:

среднее время безотказной работы;

вероятность безотказной работы за время;

гамма-процентную наработку до отказа.

Также необходимо выполнить аналитический расчет тех же показателей надежности и проведя сравнение его результатов с результатами моделирования ,сделать соответствующие выводы.

Для решения данной задачи необходимы следующие исходные данные:

законы распределения времени до отказа каждого из элементов РЭУ;

заданное время безотказной работы РЭУ;

значение гамма.

Исходные данные для решения даны полностью и приведены в таблице 1

Таблица 1

Элемент	Законы распределения времени до отказа	Параметры закона	Приме- чание	T>з>,час	,%
R1R4	Экспоненциальный	=10-5 1/ч		5000	99
DA1	Лог. нормальный	m>x>=4;>x>=0,3	lg
X1X3	Нормальный	m=5000 ч =1000 ч

.

2. Краткое описание метода моделирования на ЭВМ отказов элементов

Областью преимущества моделирования надежности на ЭВМ являются аналитические расчеты , которые необходимы при решении практических задач по обеспечению и оценке показателей надежности РЭУ. Они часто оказываются весьма трудоемкими или ими вообще нельзя пользоваться ..

В результате решения требуемой задачи должны быть получены N реализаций РЭУ и проведена статистическая обработка выходных данных.

В данном случае необходимо смоделировать случайное время до отказа каждого элемента и получить N реализаций РЭУ . Далее необходимо найти минимальное время до отказа для каждой реализации. Затем путем статистической обработки получить среднее время безотказной работы,вероятность безотказной работы за заданное время и гамма-процентную наработку до отказа.

Достоинствами метода является :

отсутствие необходимости испытывать реальные конструкции и технологические процессы, что делает этот метод наиболее дешевым;

получение случайных реализаций первичных параметров;

возможность получения любого числа реализаций РЭУ, что повышает точность оценки надежности.

3. Решение задачи на ЭВМ

Структурная схема алгоритма решения задач на ЭВМ дана в приложении.

Пояснение к алгоритму приведены в таблице 2.

Таблица 2

Номер функц. части.	Пояснение
1	Функция Z1 в которой моделируются случайные значения времени до отказа с учетом экспоненциального закона распределения по формуле
2	Функция Z2 в которой моделируются случайные значения времени до отказа с учетом нормального закона распределения по формуле
3	Функция Z3 в которой моделируются случайные значения времени до отказа с учетом логарифмического нормального закона распределения по формуле
4	Функция min которая реализует поиск элементов в j-той реализации имеющего минимальное значение времени до отказа и присвоение этого значения РЭУ, смоделированному в j-той реализации
5	Ввод количества реалиаций, количества элементов и заданного времени до отказа
6	Ввод кодов законов распределения времени до отказа: (1-экспоненциальный, 2- логарифмический нормальный, 3-нормальный)
7	Ввод данных о каждом элементе РЭУ (код закона распределения, лямбда или МО и СКО)
8	Организация цикла по переменной j, которая является счетчиком количества смоделированных РЭУ
9	Организация цикла по переменной i, которая является счетчиком количества элементов в составе РЭУ
10	Определение среднего времени безотказной работы
11	Определение вероятности безотказной работы за время t>з>
12	Определение гамма-процентной наработки до отказа
13	Вывод результатов моделирования

Описание используемых в программе операторов приведено в таблице 3

Таблица 3

Оператор	Значение оператора
1	Количество реализаций РЭУ
2	Количество элементов в составе РЭУ
3	Минимальное время наработки до отказа в j-той реализации РЭУ
4	МО для нормального закона распределения
5	СКО для нормального закона распределения
6	МО для логарифмического нормального закона распределения
7	СКО для логарифмического нормального закона распределения
8	Лямбда для экспоненциального закона распределения
9	Заданное время наработки до отказа
10	Среднее время безотказной работы
11	Вероятность безотказной работы за время t>з>
12	Количество РЭУ отказавших за время t>з>
13	Гамма процентная наработка до отказа

4. Аналитический расчет показателей надежности

Определение среднего времени безотказной работы РЭУ.

Для группы элементов R1-R2 с учетом экспоненциального закона распределения времени до отказа среднее время безотказной работы определяется по формуле 1:

, (1)

где - суммарная интенсивность отказов, которая определяется по формуле 2:

, (2)

где n – колличество элементов в группе;

- интенсивность отказов элементов с учетом электрического режима и условий эксплуатации, которая определяется по формуле 3:

, (3)

где 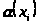- поправочный коэффициент, учитывающий влияние фактора.

В данном случае испытания проводятся в лабораторных условиях и следовательно, все коэффициенты принимаем равными 1.

Тогда (час)

Для группы элементов X1-X3 с учетом нормального закона распределения времени до отказа среднее время безотказной работы равно математическому ожиданию отказа.

Тогда.(час)

Для микросхемы DA1 логарифмический нормальный закон распределения можно заменить на нормальный.Тогда для DA1 среднее время безотказной работы будет также равно математическому ожиданию.

Для перехода кнормальному закону воспользуемся формулами 4 и 5:

(4)

(5)

Для нормального закона распределения

Следовательно, (час) и (час).

Тогда (час).

Так как отказ РЭУ происходит при отказе хотя бы одного элемента, то среднее время безотказной работы всего РЭУ будет равно минимальному из трех Т. В данном случае часов.

Определение вероятности безотказной работы за время t_>з>

Вероятность безотказной работы за время t_>з> определяется по формуле 6:

(6)

Для группы элементов R1-R4 с учетом экспоненциального закона распределения вероятность безотказной работы за время t определяем по формуле 7:

(7)

Тогда

Для группы элементов X1-X2 и DA1 вероятность безотказной работы за время t определяется по формуле 8:

(8)

Тогда и

Следовательно,

Определение гамма-процентной наработки до отказа

Для группы элементов R1-R4 с учетом экспоненциального закона распределения гамма-процентная наработка до отказа определяется по формуле 9:

(9)

Тогда (час)

Для группы элементов X1-X3 и DA1 с учетом нормального закона распределения формулу для гамма-процентной наработки до отказа можно получить из решения уравнения:

Тогда (час) и (час).

Так как отказ РЭУ происходит при отказе хотя бы одного элемента, а гамма-процентная наработка до отказа показывает, когда откажет (100-) процентов РЭУ, то для всего РЭУ необходимо принимать наименьшую. В данном случае час.

Заключение

Подведя итог анализа решения задачи можно сделать вывод, что трудоемкие аналитические расчеты выгоднее заменять моделированием на ЭВМ, что не только облегчает труд инженера, но и дает возможность с достаточно высокой точностью оценивать надежность проектируемых РЭУ, так как существует возможность смоделировать сколь угодно много реализаций РЭУ.

Литература.

Боровиков С.М. Теоретические основы конструирования, технологии и надежности. –Мн.:Дизайн ПРО,1998г-335с.

2.Лабораторный практикум по курсу ТОКТиН для студентов специальности ПиПРЭС. Ч2.Мн: 1997г.