Методи нормування складових інструментальної похибки вимірювань
Методи нормування складових інструментальної похибки вимірювань
Згідно з моделлю (3.3) інструментальної похибки вимірювань і моделями (3.4), (3.5) похибки ЗВТ нормуванню підлягають такі похибки і властивості ЗВТ:
- характеристики основної похибки ЗВТ;
- характеристики чутливості ЗВТ до впливних величин або похибки, викликані впливними величинами і неінформативними параметрами (додаткові похибки);
- динамічні властивості ЗВТ, а отже, опосередковано і динамічні похибки ЗВТ;
- властивості ЗВТ, які визначають похибку взаємодії ЗВТ з ОВ або іншими ЗВТ.
Нормування основної похибки засобів вимірювальної техніки
Основну похибку ЗВТ залежно від прийнятої моделі похибки ЗВТ представляють або з поділом на систематичні і випадкові складові (модель I), або без поділу, коли вказується основна похибка (модель II).
Для встановлення нормованих характеристик основної похибки кожного окремого екземпляра ЗВТ необхідно вибрати таку математичну модель:
 (3.6)
(3.6)
Ця модель записана
для загального випадку
цифрових вимірювальних засобів і
враховує похибку квантування
 як випадкову складову основної похибки.
Очевидно, для переходу до моделі
аналогових вимірювальних засобів
необхідно у формулі (3.6) припустити
як випадкову складову основної похибки.
Очевидно, для переходу до моделі
аналогових вимірювальних засобів
необхідно у формулі (3.6) припустити
 .
.
У моделі основної
похибки
 (3.6) для спрощення аналізу і нормування
випадкової складової
(3.6) для спрощення аналізу і нормування
випадкової складової
 доцільно виділити, якщо це можливо, дві
складові
низькочастотну
доцільно виділити, якщо це можливо, дві
складові
низькочастотну
 і високочастотну
і високочастотну
 .
Тоді остаточно узагальнена модель
основної похибки ЗВТ набирає вигляду:
.
Тоді остаточно узагальнена модель
основної похибки ЗВТ набирає вигляду:

 +
+ +
+ .
(3.7)
.
(3.7)
Такий поділ основної похибки на складові особливо необхідний при аналізі методів зменшення інструментальної похибки ЗВТ.
У моделі (3.6) або (3.7) урахована принципова особливість властивостей основної похибки всієї сукупності ЗВТ даного типу. Зміст цієї особливості такий. Основні похибки окремих екземплярів ЗВТ даного типу відрізняються одна від одної. Тому характеристики моделі похибки o(t) слід розглядати як випадкові величини, що мають свої реалізації для кожного ЗВТ. Виходячи з цього, для кожної із складових основної похибки o(t) слід було б нормувати її статистичні характеристики, наприклад, оцінки математичного сподівання, СКВ та ін. Проте практика показує, що розкид характеристик випадкових складових основної похибки різних екземплярів ЗВТ даного типу значно менший від цих характеристик. Тому розкид характеристик випадкових складових основної похибки o(t) вважається величиною другого порядку малості і не нормується, а розкид характеристик систематичних похибок різних екземплярів ЗВТ даного типу досить великий. Цим пояснюється застосування ймовірнісних характеристик для опису систематичної складової основної похибки ЗВТ даного типу.
Характеристики
систематичної складової основної
похибки ЗВТ вибирають з таких: або
значення систематичної складової
 ,
або значення систематичної складової
,
або значення систематичної складової
 ,
її математичного сподівання
,
її математичного сподівання
 і СКВ
і СКВ
 ,
які дозволяють при розрахунках
характеристик інструментальної складової
похибки вимірювань ураховувати розкид
значень систематичної похибки для
різних екземплярів ЗВТ даного типу.
,
які дозволяють при розрахунках
характеристик інструментальної складової
похибки вимірювань ураховувати розкид
значень систематичної похибки для
різних екземплярів ЗВТ даного типу.
Установлювати
значення математичного сподівання і
СКВ систематичної складової похибки
ЗВТ доцільно тоді, коли можна знехтувати
зміною їх у часі і залежно від зміни
впливних величин або при можливості
одночасного нормування зміни даних
характеристик як функції часу та умов
застосування. Отже, характеристики
 і
і
 відображають властивості всієї сукупності
ЗВТ даного типу.
відображають властивості всієї сукупності
ЗВТ даного типу.
Характеристики
випадкової складової основної похибки
 ЗВТ вибирають з таких: або значення СКВ
ЗВТ вибирають з таких: або значення СКВ
 випадкової складової похибки, або
значення СКВ
випадкової складової похибки, або
значення СКВ
 ,
нормалізованої автокореляційної
функції, або коефіцієнта кореляції
,
нормалізованої автокореляційної
функції, або коефіцієнта кореляції
 ,
чи функції спектральної щільності
потужності
,
чи функції спектральної щільності
потужності
 випадкової складової похибки.
випадкової складової похибки.
При нормуванні систематичної і випадкової складових основної похибки ЗВТ указують границі перелічених характеристик цих похибок.
Зважаючи на прагнення до максимально можливого спрощення системи нормування МХ, рекомендується:
- для ЗВТ з моделлю
I інструментальної похибки нормувати
тільки границі допустимих значень
основної випадкової похибки
 (іноді, коли ЗВТ призначається для
використання у вимірювальних системах,
коефіцієнт кореляції
(іноді, коли ЗВТ призначається для
використання у вимірювальних системах,
коефіцієнт кореляції
 або спектральну щільність потужності
або спектральну щільність потужності
 похибки) і границі допустимих значень
основної систематичної похибки
похибки) і границі допустимих значень
основної систематичної похибки ;
;
- для ЗВТ з моделлю
II нормувати границі допустимих значень
абсолютної основної похибки

Для обох моделей
похибок ЗВТ рекомендується нормувати
границі допустимих значень похибки
гістерезису
 Таке спрощення системи нормування
призводить до деякого завищення
розрахункових значень інструментальної
складової похибки вимірювань, які
визначаються за НМХ ЗВТ, оскільки при
розрахунках будуть ураховуватися
максимально можливі, а не середні для
даного типу ЗВТ характеристики випадкових
похибок. Одночасно указаний підхід до
нормування спрощує процедуру проведення
випробувань і повірки ЗВТ.
Таке спрощення системи нормування
призводить до деякого завищення
розрахункових значень інструментальної
складової похибки вимірювань, які
визначаються за НМХ ЗВТ, оскільки при
розрахунках будуть ураховуватися
максимально можливі, а не середні для
даного типу ЗВТ характеристики випадкових
похибок. Одночасно указаний підхід до
нормування спрощує процедуру проведення
випробувань і повірки ЗВТ.
При необхідності допускається нормувати:
- границю допустимої систематичної складової похибки ЗВТ для заданого інтервалу часу;
- зміну в часі границі допустимої систематичної складової похибки;
- допустимі відхилення
нормованої кореляційної функції
 або функції спектральної щільності
потужності
або функції спектральної щільності
потужності
 випадкової складової похибки ЗВТ від
їх номінальних значень;
випадкової складової похибки ЗВТ від
їх номінальних значень;
- функцію або щільність розподілу ймовірностей систематичної і випадкової складових похибки ЗВТ;
- характеристику основної похибки в інтервалі впливної величини (для моделі II похибки).
Похибка ЗВТ в інтервалі впливної величини це похибка ЗВТ в умовах, коли одна з впливних величин набирає будь-яких значень у її робочій області, а інші впливні величини знаходяться в границях, відповідних до нормальних умов. Ця похибка не є додатковою, оскільки вона обумовлена тільки відмінністю значення впливної величини від нормального значення.
При обчислюванні випадкової основної похибки відповідно до моделі I похибки ЗВТ мається на увазі, що всі її складові незалежні. Тоді дисперсія випадкової складової основної похибки ЗВТ
 ,
,
причому
 (тобто приймається, що випадкова складова
похибки ЗВТ від гістерезису розподілена
за рівномірним законом).
(тобто приймається, що випадкова складова
похибки ЗВТ від гістерезису розподілена
за рівномірним законом).
Нормування додаткових похибок засобів вимірювальної техніки
Як указувалось у § 3.2, додаткові похибки ЗВТ визначаються характеристиками чутливості ЗВТ до впливних величин і неінформативних параметрів вхідних сигналів.
Враховуючи, що впливні величини можуть викликати змінювання не тільки похибки ЗВТ, але й інших МХ ЗВТ, в необхідних випадках доцільно передбачити нормування функцій впливу і на ці МХ ЗВТ. При цьому як нормовані характеристики додаткових похибок ЗВТ можуть бути використані:
а) або функції
впливу
 ,
які являють собою залежності зміни
метрологічних характеристик ЗВТ від
зміни впливної величини
,
які являють собою залежності зміни
метрологічних характеристик ЗВТ від
зміни впливної величини
 або від зміни сукупності впливних
величин;
або від зміни сукупності впливних
величин;
б) або границі зміни значень метрологічних характеристик ЗВТ, викликані зміною впливних величин в установлених границях.
Для ЗВТ функція
впливу може мати або певний вигляд, або
при однаковому вигляді різні значення
параметрів функції. В усіх екземплярах
ЗВТ даного типу функції впливу повинні
бути ідентичними внаслідок однакового
принципу дії цих ЗВТ, а параметри функцій
впливу різних екземплярів ЗВТ даного
типу повинні бути близькими між собою.
Тому як основна характеристика додаткової
похибки береться деяка середня для ЗВТ
даного типу функція впливу і деякі
середні значення її параметрів. Така
функція впливу називається номінальною
функцією впливу, позначимо її
 .
.
Зміна метрологічної характеристики ЗВТ, викликана зміною впливної величини, це різниця (без урахування знака) між значенням метрологічної характеристики, що відповідає деякому заданому значенню впливної величини в границях робочих умов застосування, і значенням даної метрологічної характеристики, яке відповідає нормальному значенню впливної величини.
Для нормування функцій впливу використовують два методи:
1) нормування
номінальної функції впливу
 і допустимих відхилень від неї;
і допустимих відхилень від неї;
2) нормування
граничних функцій впливу - верхньої
 і нижньої
і нижньої
 ,
які обмежують область допустимих значень
функції впливу для будь-якого ЗВТ даного
типу.
,
які обмежують область допустимих значень
функції впливу для будь-якого ЗВТ даного
типу.
Другий метод нормування додаткових похибок застосовується для ЗВТ певного типу, для сукупності яких розкид функції впливу великий, в силу чого встановити номінальну функцію впливу неможливо.
Оскільки функції впливу визначені як залежності зміни МХ ЗВТ від змін впливних величин в робочих умовах застосування ЗВТ, то їх слід нормувати тільки для тих МХ, що нормуються для нормальних (номінальних) умов застосування ЗВТ. Якщо ж деякі МХ нормують для робочих умов застосування ЗВТ, то відповідні функції впливу не нормують. Проте далеко не всі МХ повинні нормуватися для нормальних умов застосування ЗВТ, і ось чому. Майже всі МХ впливають лише на похибку вимірювань, тому можна вважати, що зміна більшості з МХ, яка здійснюється під дією впливних величин, призводить до відповідної зміни похибки вимірювань другого порядку малості, чим можна знехтувати. Тому відповідні МХ слід нормувати для робочих умов застосування ЗВТ, а функції впливу на них не нормувати.
На цей час більш розповсюдженим є нормування не функцій впливу, а характеристик які традиційно визначають додаткові похибки ЗВТ від впливних величин.
Серед таких характеристик найбільш поширеною є границі допустимої (найбільші допустимі зміни) додаткової похибки Yд, що мають місце при зміні впливної величини на деяке встановлене (задане) значення відносно її нормального (номінального) значення ном.
Якщо в реальних умовах експлуатації ЗВТ впливна величина може приймати різні (довільні) значення в межах від нижнього значення нж до верхнього значення в, причому нж< ном< в, то за вказаною вище характеристикою можна визначити лише граничні (найбільш можливі) зміни похибки ЗВТ:
 ;
;
 .
.
При оцінці інструментальної складової похибки вимірювань в реальних умовах експлуатації ЗВТ, що обумовлена дією даної впливної величини , є тільки одна можливість: врахувати найбільш можливу зміну додаткової похибки ЗВТ Yмах, яка дорівнює
або при
при
 ,
,
або при
при
 .
.
Сумарна допустима
інструментальна статична похибка ЗВТ
Yд
в реальних умовах експлуатації ЗВТ може
бути визначена як арифметична сума
границі допустимої основної похибки
Yод
та границь (найбільших) допустимих змін
(значень) додаткових похибок ЗВТ від
усіх впливних величин
 ,
що враховуються:
,
що враховуються:
 .
.
Очевидно, значення похибки Yд практично завжди буде істотно перевищувати значення дійсної похибки ЗВТ в реальних умовах експлуатації, бо вона розраховується за припущенням, що всі похибки (основна і додаткова) мають найбільше допустиме значення при будь-яких умовах експлуатації, але вірогідність виконання такого припущення вкрай мала.
Отже, кількісна характеристика додаткової похибки Yмах ЗВТ, яка традиційно регламентується в технічних описах ЗВТ, не дозволяє оцінювати дійсну інструментальну похибку вимірювань в реальних умовах експлуатації (застосування) ЗВТ з допустимою вірогідністю. Але вона є найбільш простою для практичного використання.
Функції впливу
 і границі допустимих додаткових похибок
ЗВТ нормують, як правило, окремо для
кожної впливної величини. І тільки при
наявності істотної взаємної залежності
декількох функцій впливу різних величин
і границі допустимих додаткових похибок
ЗВТ нормують, як правило, окремо для
кожної впливної величини. І тільки при
наявності істотної взаємної залежності
декількох функцій впливу різних величин
 допускається задання сумісних
(комплексних) функцій впливу
допускається задання сумісних
(комплексних) функцій впливу
 ,
які й використовують при обчисленні
характеристик інструментальної складової
похибки вимірювань.
,
які й використовують при обчисленні
характеристик інструментальної складової
похибки вимірювань.
Критерій істотності для впливних величин установлюється в технічній документації на ЗВТ конкретних типів. При відсутності вказаних критеріїв визначають, що впливна величина істотно впливає на метрологічну характеристику ЗВТ, якщо при зміні цієї впливної величини в границях робочого діапазону дана метрологічна характеристика ЗВТ змінюється більш як на 20% від значення, нормованого для номінальних умов. Функцію однієї впливної величини приймають істотно залежною від іншої впливної величини, при зміні якої в границях робочого діапазону зміна функції перевищує 20% від її номінального значення.
Істотність тієї
чи іншої складової сумарної додаткової
похибки ЗВТ рекомендується визначати
таким чином. Якщо найбільш можливі
значення всіх додаткових похибок ЗВТ
 ,
відповідно до робочих умов застосування
ЗВТ даного типу сумірні, то всі додаткові
похибки визнаються істотними при
виконанні умови
,
відповідно до робочих умов застосування
ЗВТ даного типу сумірні, то всі додаткові
похибки визнаються істотними при
виконанні умови
 ,
,
де
найбільше можливе значення похибки ЗВТ
у робочих умовах застосування.
найбільше можливе значення похибки ЗВТ
у робочих умовах застосування.
Зауважимо, що
додаткові похибки вважаються сумірними,
якщо їх значення відрізняються одне
від одного не більш як на 30%. Якщо серед
додаткових похибок виявляються менші
або несумірні з іншими і їх сума менша
від
 ,
то такі похибки належать до неістотних.
,
то такі похибки належать до неістотних.
Функцію впливу рекомендується не нормувати за умови, що її границі допустимих відхилень від номінальної функції впливу не можуть бути встановлені меншими ніж 20% від номінальної функції впливу. У цьому разі рекомендується нормувати границі допустимої додаткової похибки ЗВТ або допустимої зміни іншої НМХ ЗВТ у всьому робочому діапазоні зміни впливної величини відповідно до робочих умов експлуатації ЗВТ даного типу.
Значення допустимої
додаткової похибки ЗВТ, як правило,
задають у вигляді часткового або кратного
значення допустимої основної похибки.
Наприклад, додаткова похибка ЗВТ, яка
викликана відхиленням його живлення
на
 %
від номінального значення, не повинна
перевищувати 0,5 границі основної похибки
ЗВТ.
%
від номінального значення, не повинна
перевищувати 0,5 границі основної похибки
ЗВТ.
Допустимі значення додаткових похибок, які традиційно застосовуються для розрахунків інструментальної похибки вимірювань, дають завищені результати і тому придатні для одержання тільки досить приблизних оцінок похибки вимірювань. Для одержання більш точних оцінок необхідно враховувати функцію впливу.
Методи нормування додаткових похибок і їх особливості однакові для всіх видів ЗВТ і обох моделей похибки.
Перелік нормованих неінформативних параметрів вхідного і вихідного сигналів ЗВТ, їх номінальні значення і границі допустимих відхилень установлюються в ДСТУ та НТД.
Нормування динамічної похибки засобів вимірювальної техніки
Динамічні похибки ЗВТ нормують опосередковано, шляхом нормування динамічних характеристик (або властивостей) ЗВТ, у зв’язку з тим, що ці похибки залежать не тільки від властивостей ЗВТ, але й від спектральних (частотних) характеристик вхідного сигналу. В існуючих стандартах передбачено нормування таких динамічних характеристик ЗВТ, які дозволяють оцінювати похибки вимірювань під час дії на вході ЗВТ будь-яких змінних сигналів. При цьому головними є вимоги, з одного боку, до детальності опису метрологічних характеристик ЗВТ, а з другого боку до простоти їх нормування, експериментального визначення і контролю (повірки).
Для задання динамічних властивостей ЗВТ рекомендується використовувати їхні повні і частинні динамічні характеристики (див. підп.3.3.4). Повні динамічні характеристики нормуються або для системних ЗВТ, або для вимірювальних перетворювачів реєструвальних приладів, якщо вони призначаються для роботи з вхідними сигналами, в яких змінюються в часі інформативні параметри. Для таких ЗВТ, якщо для них установлені нормальні та робочі умови застосування, додатково нормують дію впливних величин і неінформативних параметрів вхідного сигналу на повні динамічні характеристики (похибки, що при цьому виникають, належать до додаткових). Для показувальних приладів, вимірювальних перетворювачів і реєструвальних приладів, призначених для роботи з постійними або з такими змінними сигналами, для яких динамічною похибкою можна знехтувати, нормують одну або декілька частинних динамічних характеристик, наприклад час реакції ЗВТ.
Динамічні похибки визнаються неістотними, а динамічні характеристики не нормуються, якщо виконується нерівність.
 ,
,
де
найбільше можливе значення динамічної
похибки ЗВТ у робочих умовах застосування.
найбільше можливе значення динамічної
похибки ЗВТ у робочих умовах застосування.
Основним методом нормування динамічних властивостей ЗВТ є задання (вказування) таких повних і частинних характеристик:
1) номінальних характеристик і границь допустимих відхилень від них;
2) границь допустимих значень параметрів вхідного сигналу.
Номінальні динамічні характеристики (повні і частинні) ЗВТ нормують у тих випадках, коли границі допустимих відхилень даної динамічної характеристики не перевищують 20% її номінальної характеристики.
Для ЗВТ, у значній кількості екземплярів яких розкид динамічних характеристик (повних і частинних) великий, і в силу цього для них у НТД установлена необхідність визначення і подальшого використання динамічних характеристик кожного екземпляра ЗВТ, нормують граничну динамічну характеристику (повну або частинну). У таких випадках застосовувати ЗВТ допускається тільки за умови попереднього експериментального визначення динамічної характеристики для даного екземпляра ЗВТ. Граничну динамічну характеристику використовують як критерій придатності ЗВТ і при розрахунках похибок вимірювань.
Динамічні характеристики ЗВТ оцінюють і контролюють при значеннях вхідного сигналу, відповідних усьому діапазону вимірювань (перетворень) або декільком частинам діапазону (піддіапазонам), в яких допускають лінійну апроксимацію динамічних властивостей ЗВТ. Кількість таких динамічних піддіапазонів повинна бути більша чотирьох.
Динамічні характеристики ЗВТ, властивості яких залежать від напряму зміни вхідного сигналу, оцінюють для обох напрямів зміни сигналу. Методики й алгоритми обробки результатів контролю (оцінки) динамічних характеристик повинні встановлюватися в стандартах і технічних умовах на ЗВТ конкретних типів і груп залежно від виду і порядку математичної моделі їх динамічних властивостей, яку називають динамічною моделлю.
Якщо випадкова
складова похибки ЗВТ істотна, то частинні
динамічні характеристики контролюють
за допомогою обробки серії з
 спостережень. Частинну характеристику
приймають такою, що задовольняє вимоги
технічних умов, якщо максимальне значення
із серії n її оцінок не перевищує
допустимого значення.
спостережень. Частинну характеристику
приймають такою, що задовольняє вимоги
технічних умов, якщо максимальне значення
із серії n її оцінок не перевищує
допустимого значення.
Нормування похибки взаємодії
З усіх складових інструментальної похибки вимірювань найменш розроблені методи нормування похибки від взаємодії ЗВТ з ОВ. Згідно з фізичним походженням похибки взаємодії, для її оцінки необхідно нормувати характеристики, що відображають властивості ЗВТ відбирати енергію через свої вхідні або вихідні кола і дозволяють визначити зміну вимірюваної фізичної величини, яка виникає в результаті цього обміну. Для засобів електро - і радіотехнічних вимірювань ця задача вирішується досить просто за допомогою нормування вхідних і вихідних повних опорів ЗВТ, причому ці опори неважко контролювати під час повірки.
У вимірювальних засобах, призначених для вимірювання і перетворення на постійному струмі і в низькочастотному діапазоні вхідних сигналів, вхідний і вихідний (для перетворювачів) опори розглядаються і нормуються як активні. У ЗВТ високочастотного діапазону вхідні і вихідні опори є комплексними і повинні нормуватися як повні. В існуючій НТД вхідний і вихідний повні опори для ЗВТ усіх типів і обох моделей похибок нормуються однаково заданням номінального значення опорів і границь їх допустимих значень або границь їх допустимих змін.
Проте більш часто параметри вхідного повного опору ЗВТ нормуються окремо. Оскільки реактивна складова вхідного повного опору ЗВТ має, як правило, ємнісний характер, то такий опір представляють у вигляді паралельного (іноді послідовного) з‘єднання резистора і конденсатора.
Значно складніше нормувати похибки від взаємодії ЗВТ неелектричних величин з ОВ. У цій галузі вимірювань явища обміну енергією між ЗВТ і ОВ вивчені недостатньо. Але для багатьох ЗВТ неелектричних величин проблема може бути зведена до вже вирішеної, використовуючи теорію електромеханічних аналогій і розрахунку еквівалентних схем перетворювачів неелектричних величин.
Нормування неінформативних параметрів вихідних сигналів засобів вимірювальної техніки
Крім указаних вище метрологічних характеристик, що визначають результат і похибку вимірювань, нормуються неінформативні параметри вихідного сигналу ЗВТ.
Неінформативні параметри вихідних сигналів не належать до метрологічних характеристик ЗВТ. Проте вони визначають можливість нормальної роботи ЗВТ й інших пристроїв, які приєднуються до виходу даного ЗВТ. Наприклад, вихідним сигналом перетворювача напруга-частота або генератора імпульсів є послідовність імпульсів, а її інформативним параметром частота, вимірювана частотоміром. У той самий час похибка частотоміра залежить від амплітуди, тривалості і форми імпульсів, які належать до неінформативних параметрів. Отже, неінформативні параметри повинні задовольняти певні вимоги, тобто підлягають нормуванню. Це нормування здійснюється двома методами: встановленням або номінальних характеристик (наприклад, значень імпедансів) зі вказанням границь допустимих відхилень від них, або граничних значень характеристик (імпедансів), які визначають область їх допустимих значень. Найбільш розповсюдженим з них є задання границь допустимих значень тієї чи іншої характеристики. Ці границі визначають інтервал, в якому значення характеристики кожного екземпляра ЗВТ конкретного типу повинно знаходитися з імовірністю, близькою до одиниці.
Укажемо також, що всі НМХ ЗВТ можуть представлятися у формі іменованого або неіменованого числа, формули або графіка. При цьому задання будь-якої характеристики у вигляді графіка обов‘язково треба супроводжувати одночасним поданням її у вигляді формули або таблиці. Допускається застосування й інших форм подання НМХ за умови, що ці формули дозволяють оцінювати похибки ЗВТ даного типу, а також здійснювати контроль відповідності цих засобів установленим вимогам. У такому випадку форма подання НМХ конкретизується в НТД на даний тип або вид ЗВТ.
Класи точності засобів вимірювальної техніки
Більшість ЗВТ, які знаходяться на теперішній час в експлуатації, мають переважно статичну похибку, тобто динамічна похибка в них не враховується. Нормування статичної похибки цих ЗВТ здійснюється, як правило, встановленням класу точності.
Класом точності називається узагальнена кількісна характеристика ЗВТ, яка визначається гарантованими границями допустимих основної і додаткових похибок, а також іншими характеристиками ЗВТ, що впливають на похибку (точність) вимірювань і значення яких установлюються стандартами на окремі види ЗВТ.
Дійсні значення основної повної похибки окремих екземплярів ЗВТ однакового типу можуть відрізнятися одне від одного як систематичними, так і випадковими складовими, але в цілому для даного типу ЗВТ вони не перевищують границі допустимої основної похибки. Таким чином, установленням і заданням класу точності нормується основна статична похибка ЗВТ, а всі додаткові похибки й інші метрологічні характеристики, що впливають на похибку ЗВТ, указуються окремо.
Відповідність реального значення основної похибки ЗВТ приписаному йому класу точності перевіряється при періодичних повірках. Якщо воно залишається менше від нормованого, то ЗВТ продовжує експлуатуватися, якщо ж реальне значення основної похибки ЗВТ більше від нормованого, то ЗВТ підлягає ремонту та регулюванню.
Основна похибка ЗВТ нормується чотирма різними способами, вибір яких обумовлений співвідношенням адитивної і мультиплікативної складових похибки ЗВТ даного типу.
1. Для ЗВТ, абсолютна похибка яких визначається адитивною складовою і її границі можна вважати практично незмінними для будь-яких значень вимірюваної величини, тобто мультиплікативною складовою похибки можна знехтувати, іноді нормуються границі допустимої абсолютної основної похибки
 ,
,
де a постійна додатна величина, виражена в одиницях вимірюваної величини.
Проте нормування допустимої абсолютної основної похибки ЗВТ використовується рідко, бо для засобів з багатьма межами вимірювань вона різна в кожному піддіапазоні, що створює певні незручності і для вказання всіх границь похибок (треба було б перелічити значення похибок для всіх піддіапазонів), і для практичного застосування. Границі допустимих абсолютних похибок задають для ЗВТ тільки тих фізичних величин, похибки вимірювань яких прийнято виражати в одиницях вимірюваної величини або в поділках шкали, наприклад, для засобів вимірювань довжини, маси, фазового зсуву.
Для більшості ЗВТ з переважною адитивною похибкою нормують границі допустимої основної зведеної похибки ЗВТ, які, згідно з формулою (3.2), визначають за рівністю
 ,
(3.8)
,
(3.8)
деp
стала додатна величина, виражена у
відсотках. Її числове значення вибирається
з ряду:
 ,
де l = 1; 0;
1;
2
і т.д. Значення, які вказані в дужках, не
рекомендуються при створенні нових
ЗВТ. Наведений ряд чисел установлений
відповідно до правила округлення значень
похибок вимірювань (див. § 2.11). При
тому самому показнику степеня l
допускається встановлювати не більш
ніж п’ять різних границь допустимої
основної похибки для ЗВТ конкретного
виду.
,
де l = 1; 0;
1;
2
і т.д. Значення, які вказані в дужках, не
рекомендуються при створенні нових
ЗВТ. Наведений ряд чисел установлений
відповідно до правила округлення значень
похибок вимірювань (див. § 2.11). При
тому самому показнику степеня l
допускається встановлювати не більш
ніж п’ять різних границь допустимої
основної похибки для ЗВТ конкретного
виду.
Слід пам‘ятати, що і при такій формі нормування класу точності ЗВТ характеристикою точності вимірювань залишається відносна похибка. Границі допустимої відносної похибки вимірювань у функції вимірюваної величини визначаються за формулою, одержаною з виразу (3.8) з урахуванням рівності (1.2):
 .
(3.9)
.
(3.9)
З формули (3.9)
виходить, що зменшення розміру вимірюваної
величини
 призводить до збільшення допустимої
відносної похибки вимірювань даним
ЗВТ. Зокрема, при
призводить до збільшення допустимої
відносної похибки вимірювань даним
ЗВТ. Зокрема, при
 допустима відносна похибка
допустима відносна похибка
 дорівнює класу точності ЗВТ лише на
останній (кінцевій) позначці діапазону
вимірювань
дорівнює класу точності ЗВТ лише на
останній (кінцевій) позначці діапазону
вимірювань
 .
При зменшенні
.
При зменшенні
 допустима відносна похибка вимірювань
допустима відносна похибка вимірювань
 зростає і при
зростає і при
 ,
тому при виборі ЗВТ для проведення
вимірювань необхідно враховувати не
тільки їх класи точності, а й співвідношення
,
тому при виборі ЗВТ для проведення
вимірювань необхідно враховувати не
тільки їх класи точності, а й співвідношення
 .
З цієї точки зору рекомендується межу
вимірювань вимірювального приладу
вибирати такою, щоб його покази знаходились
у другій половині і навіть ближче до
верхньої межі вибраного діапазону
вимірювань.
.
З цієї точки зору рекомендується межу
вимірювань вимірювального приладу
вибирати такою, щоб його покази знаходились
у другій половині і навіть ближче до
верхньої межі вибраного діапазону
вимірювань.
Зважаючи на
залежність відносної похибки вимірювань
від значення Х, для ряду ЗВТ обмежують
діапазон вимірювань такими значеннями
вимірюваної величини Х, при яких допустима
відносна похибка вимірювань не перевищує
деякого, заздалегідь заданого значення,
яке дорівнює, наприклад, 4, 10 або 20%. Поза
діапазоном вимірювань, особливо в
початковій частині діапазону показів
для ЗВТ, в яких він починається з нуля,
вимірювання не допустимі, оскільки тут
адитивна похибка може бути порівняна
з вимірюваним значенням
 і навіть перевищувати його.
і навіть перевищувати його.
2. Для ЗВТ, в абсолютній
похибці яких переважає мультиплікативна
складова, границю допустимої основної
похибки виражають у відносній формі,
через те, що у цьому випадку вона
виявляється практично постійною
величиною, не залежною від вимірюваної
величини
 .
Границі допустимої відносної основної
похибки ЗВТ установлюються за формулою:
.
Границі допустимої відносної основної
похибки ЗВТ установлюються за формулою:
 ,
(3.10)
,
(3.10)
де
границя допустимої абсолютної
мультиплікативної похибки ЗВТ;
границя допустимої абсолютної
мультиплікативної похибки ЗВТ;
b додатне безрозмірне число;
 постійна додатна величина,
виражена у відсотках; вона вибирається
з того самого ряду, що й величина p.
постійна додатна величина,
виражена у відсотках; вона вибирається
з того самого ряду, що й величина p.
Таким способом
нормуються похибки масштабних
перетворювачів (подільників напруги,
шунтів, вимірювальних трансформаторів
струму і напруги та ін).
І якщо б співвідношення (3.10) залишалось
справедливим для всього діапазону
можливих значень вимірюваної величини

від 0 до
від 0 до
 ,
то такі вимірювальні перетворювачі
були б найбільш досконалими, тому що
вони мали б широкий робочий діапазон,
зокрема, забезпечували б з тією самою
похибкою вимірювання необмежено малого
значення Х. Проте реально таких
перетворювачів не існує, оскільки поки
що неможливо створити перетворювачі,
в яких повністю вилучена адитивна
похибка в широкому діапазоні значень
вимірюваної величини. Тому для реальних
ЗВТ завжди вказується діапазон вимірювань
ЗВТ, в якому оцінка (3.10) справедлива.
Поза цим діапазоном вплив адитивної
складової похибки ЗВТ зростає настільки,
що нею знехтувати не можна і, як наслідок,
не можна використати допустиму відносну
похибку (3.10) як норму основної похибки
ЗВТ.
,
то такі вимірювальні перетворювачі
були б найбільш досконалими, тому що
вони мали б широкий робочий діапазон,
зокрема, забезпечували б з тією самою
похибкою вимірювання необмежено малого
значення Х. Проте реально таких
перетворювачів не існує, оскільки поки
що неможливо створити перетворювачі,
в яких повністю вилучена адитивна
похибка в широкому діапазоні значень
вимірюваної величини. Тому для реальних
ЗВТ завжди вказується діапазон вимірювань
ЗВТ, в якому оцінка (3.10) справедлива.
Поза цим діапазоном вплив адитивної
складової похибки ЗВТ зростає настільки,
що нею знехтувати не можна і, як наслідок,
не можна використати допустиму відносну
похибку (3.10) як норму основної похибки
ЗВТ.
3. Для ЗВТ, адитивна і мультиплікативна складові абсолютної похибки яких сумірні, тобто жодною з них знехтувати не можна, нормуються або границі допустимої абсолютної основної похибки, або границі допустимої відносної основної похибки. У цьому разі границі допустимої абсолютної основної похибки визначаються виразом.
 .
.
Підставляючи це співвідношення в рівність (2.5), одержимо двочленну формулу для нормування границь допустимої відносної основної похибки, вираженої у відсотках:
 (3.11)
(3.11)
де
адитивна і мультиплікативна складові
відносної основної похибки відповідно.
адитивна і мультиплікативна складові
відносної основної похибки відповідно.
Таким чином, особливість класифікації складових похибки ЗВТ полягає в тому, що при переході від абсолютної похибки до відносної форми її відображення адитивна і мультиплікативна складові похибки міняються місцями: відносне значення абсолютної адитивної похибки є мультиплікативною похибкою, а відносне значення абсолютної мультиплікативної похибки адитивною похибкою.
Вираз (3.11) звичайно
представляють в іншій формі, яку одержують
так. Нехай
 ,
де
,
де

модуль більшої з меж вимірювань. Додамо
до правої частини виразу (3.11) і віднімемо
від неї величину d. Тоді одержимо
модуль більшої з меж вимірювань. Додамо
до правої частини виразу (3.11) і віднімемо
від неї величину d. Тоді одержимо

У цю рівність
уведемо позначення
 і остаточно маємо
і остаточно маємо
 (3.12)
(3.12)
деc, d
постійні додатні величини, виражені у
відсотках; вибираються з того
самого ряду, що й величина p. Співвідношення
між числами c і d установлюються стандартами
на конкретні ЗВТ, причому звичайно

Звернемо увагу на
те, що складові частини формули (3.12)
формально схожі на адитивну і
мультиплікативну складові похибки ЗВТ,
але за своєю суттю вони не є такими,
і тому використовувати ці
терміни до даної формули не можна. Аналіз
двочленної формули (3.12) показує, що
границі допустимої відносної основної
похибки при наявності адитивної і
мультиплікативної складових звужуються
із зростанням вимірюваної величини
 ,
і при
,
і при
 вони набирають мінімального значення,
яке дорівнює
вони набирають мінімального значення,
яке дорівнює
 (рис.3.8).
(рис.3.8).

Рис.1. Графік допустимої відносної похибки ЗВТ при нормуванні за двочленною формулою.
Можливе також
нормування зведеної похибки за двочленною
формулою, якщо в знаменник формули
(3.11) замість
 підставити
підставити
 .
.
4. В окремих випадках границі допустимих абсолютної і відносної основної похибок ЗВТ установлюються за більш складними, спеціальними формулами нормування, а також у вигляді графіка або таблиці.
Обумовлено це тим, що похибки ряду ЗВТ не можуть бути нормовані за описаними вище способами, оскільки мають більш складний вигляд смуги похибок у порівнянні з розглянутими варіантами. Як приклад можна навести цифрові частотоміри, похибка яких залежить від часу вимірювання, параметрів вхідного сигналу і характеристик завад. Нормування похибок подібних ЗВТ здійснюється за формулами, які мають дві і більше складових, причому кількість складових і їх суть можуть бути різними як для окремих типів ЗВТ, так і для різних режимів роботи того самого засобу.
Нормування границь допустимих додаткових похибок ЗВТ здійснюється за однією з чотирьох форм:
- у вигляді постійного значення додаткової похибки від даної впливної величини для всієї робочої області або декількох постійних значень по інтервалах робочої області цієї впливної величини;
- указанням відношення границі допустимої додаткової похибки, яка відповідає заданому інтервалу впливної величини, до цього інтервалу;
- у вигляді залежності границі допустимої додаткової похибки від впливної величини, яку називають граничною функцією впливу;
- у вигляді функціональної залежності границь допустимих відхилень від номінальної функції впливу.
Перші дві форми нормування додаткових похибок не дозволяють визначити їх дійсні значення для будь-якого значення впливних величин і забезпечують можливість їх оцінки тільки "зверху". Це є певним недоліком указаних форм нормування. Цього недоліку можна уникнути, якщо нормування додаткових похибок здійснювати шляхом задання функції впливу (третя і четверта форми). За їх допомогою можуть бути визначені дійсні значення додаткових похибок для будь-яких конкретних значень впливних величин, що відповідають умовам виконання вимірювань. Проте задання функції впливу пов‘язано з великими труднощами, і тому в основному використовуються перші дві форми нормування додаткових похибок.
Нормуванню підлягає також границя допустимої варіації (або похибки, обумовленої гістерезисом) вихідного сигналу ЗВТ, яку задають у вигляді часткового або кратного значення границі основної похибки або в поділках шкали, як і границі допустимої додаткової похибки.
Норми метрологічних характеристик у вигляді границь допустимих основної і додаткових похибок наводяться в технічній документації на ЗВТ. Крім того, умовні позначення класів точності, що відбивають ці норми, наносять на циферблат, щитки, шкали і корпуси ЗВТ. Використовуючи на практиці позначення класів точності, слід пам‘ятати про те, що вони несуть інформацію тільки про границі допустимої основної похибки. Дані про границі допустимих додаткових похибок указують у технічній документації на ЗВТ.
Позначення класу точності дозволяється не наносити на високоточні міри і на ЗВТ, для яких діючими стандартами встановлені особливі зовнішні ознаки, що залежать від класу точності. Правила задання і приклади позначення класів точності наведені в табл.3.2. Пояснимо їх.
Для ЗВТ, границі
допустимої основної похибки яких задають
у формі зведеної або відносної похибок
відповідно до одночленних формул (3.8) і
(3.10), класи точності в документації і на
ЗВТ позначають числами, що дорівнюють
цим границям і виражені у відсотках.
Проте, щоб відносну похибку відрізнити
від зведеної, числове значення, яке
виражає відносну похибку, поміщають у
коло, наприклад 1,5; 0,5 і т.д. Якщо границі
допустимої основної похибки ЗВТ задають
у формі відносної похибки відповідно
до двочленної формули (3.12), то класи
точності для таких ЗВТ позначають
числами c і d, розділяючи їх косою лінією,
наприклад
 При заданні границь допустимої основної
похибки ЗВТ у формі абсолютних похибок
класи точності позначаються в документації
великими літерами латинського алфавіту
або римськими цифрами. Такий самий
спосіб позначення класів точності ЗВТ
застосовується і при відображенні
границь допустимої основної похибки,
якщо вона задається у вигляді графіка,
таблиці або формули. У разі необхідності
до позначення класу точності літерами
латинського алфавіту додається індекс
у вигляді арабської цифри. Більш високим
класам точності (меншим границям
допустимих похибок) відповідають літери,
які знаходяться ближче до початку
алфавіту, і менші числа.
При заданні границь допустимої основної
похибки ЗВТ у формі абсолютних похибок
класи точності позначаються в документації
великими літерами латинського алфавіту
або римськими цифрами. Такий самий
спосіб позначення класів точності ЗВТ
застосовується і при відображенні
границь допустимої основної похибки,
якщо вона задається у вигляді графіка,
таблиці або формули. У разі необхідності
до позначення класу точності літерами
латинського алфавіту додається індекс
у вигляді арабської цифри. Більш високим
класам точності (меншим границям
допустимих похибок) відповідають літери,
які знаходяться ближче до початку
алфавіту, і менші числа.
Таблиця 1.
|
Форми кількісного відображення границь допустимої основної похибки |
Формули границь допустимої основної похибки |
Приклади позначення класів точності: |
|||
|
значення похибки,% |
у документації |
на засобах вимірювальної техніки |
|||
|
Зведена |
|
1,0 |
клас точності 1,0 |
|
|
|
Відносна |
у вигляді одночленної формули
(якщо
|
|
1,5 |
клас точності 1,5 |
1,5 |
|
у вигляді двочленної формули |
|
c = 0,05 d = 0,02 |
клас точності
|
|
Продовження таблиці.
|
в інших формах задання (таблиці, графіки, формули) |
- |
- |
клас точності С1 |
С1 |
|
|
Абсолютна |
|
клас точності D |
D |
П
 означення
класів точності ЗВТ супроводжується
застосуванням додаткових умовних
знаків, Так, наприклад, для вимірювальних
приладів з суттєво нерівномірною шкалою
використовують знак, наприклад 1,5. Для
цих же приладів як додаткова інформація
можуть задаватися границі допустимої
відносної основної похибки для частини
шкали, яка знаходиться у межах, помічених
спеціальними знаками (точками або
трикутниками). В цьому випадку значення
допустимої відносної похибки вказують
у вигляді 1%, але цей знак не є позначенням
класу точності.
означення
класів точності ЗВТ супроводжується
застосуванням додаткових умовних
знаків, Так, наприклад, для вимірювальних
приладів з суттєво нерівномірною шкалою
використовують знак, наприклад 1,5. Для
цих же приладів як додаткова інформація
можуть задаватися границі допустимої
відносної основної похибки для частини
шкали, яка знаходиться у межах, помічених
спеціальними знаками (точками або
трикутниками). В цьому випадку значення
допустимої відносної похибки вказують
у вигляді 1%, але цей знак не є позначенням
класу точності.
Якщо ЗВТ має два і більше піддіапазонів вимірювань тієї самої фізичної величини, то для нього допускається встановлювати декілька класів точності для окремих піддіапазонів вимірювань. Якщо ЗВТ призначений для вимірювань декількох фізичних величин, то клас точності може встановлюватися для кожної з них окремо.
Якщо для ЗВТ однакових типу і класу точності встановлені різні робочі області впливних величин залежно від умов експлуатації, то граничні значення впливних величин також наносяться на ЗВТ.

 1,0
або 1,0
1,0
або 1,0 )
)



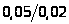
 ;
;
