Исследование электрических цепей
Министерство науки и образования Украины
Харьковский национальный университет радиоэлектроники
Курсовая работа
Пояснительная записка
Тема «Исследование электрических цепей»
по дисциплине
«Основы радиоэлектроники»
Руководитель Выполнил
Ст. гр. xxxxxxxxx
xxxxxxxxxx. xxxxxxxx.
Харьков 2007
РЕФЕРАТ
Курсовая работа: 19 с., 7 рис., 2 табл., 6 источников.
Объект исследования – пассивная линейная цепь второго порядка.
Цель работы – определить отклик пассивной линейной цепи, к входу которой приложен входной сигнал.
Метод исследования – отклик цепи следует определить спектральным и временным методами.
Расчет отклика в пассивной цепи находится двумя способами. Для расчета отклика спектральным способом входной сигнала разлаживается на гармоники, строятся АЧС и ФЧС и, рассчитав комплексный коэффициент передачи, находится выходные спектры, из которых синтезируется выходной сигнал. Для расчета отклика временным методом рассчитываются временные характеристики на периодическую последовательность прямоугольных импульсов.
МЕТОД ПЕРЕМЕННЫХ СОСТОЯНИЯ, ЧЕТЫРЕХПОЛЮСНИКИ, НЕСИНУСОИДАЛЬНОЕ ВОЗДЕЙСТВИЕ, РЯД ФУРЬЕ, КОЭФИЦИЕНТ ПЕРЕДАЧИ, СПЕКТР ОТКЛИКА
СОДЕРЖАНИЕ
Введение
Задание к курсовому проекту
1 Расчет реакции электрической цепи символическим методом
1.1 Разложение заданного сигнала в ряд Фурье
1.2 Нахождение Y-параметров активного четырехполюсника
1.3 Нахождение Y-параметров пассивного четырехполюсника
1.4 Нахождение Y-параметров сложного четырехполюсника
1.5 Расчет коэффициента передачи
1.6 Расчет спектра отклика
2 Расчет электрической цепи методом переменных состояния
ВВЕДЕНИЕ
Курсовая работа по курсу «Основы
радиоэлектроники» один из этапов
самостоятельной работы, который позволяет
определить и исследовать реакцию
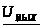 (t)
электрической цепи на несинусоидальное
периодическое напряжение, а также
закрепить знания по символическому
методу и методу переменных состояния
(t)
электрической цепи на несинусоидальное
периодическое напряжение, а также
закрепить знания по символическому
методу и методу переменных состояния
1 РАСЧЕ РЕАКЦИИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ СИМВОЛИЧЕСКИМ МЕТОДОМ
Разложение заданного сигнала в ряд Фурье
Для разложения заданного сигнала, необходимо определить функцию, по которой происходит изменение сигнала, на промежутке равном периоду Т сигнала:
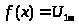 если
если

 если
если

Разложим заданную функцию в ряд Фурье:



Так как заданный сигнал – нечетная
функция, то
 . Таким образом амплитуда комплексного
напряжения для n-той
гармоники описывается выражением:
. Таким образом амплитуда комплексного
напряжения для n-той
гармоники описывается выражением:
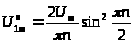
Нахождение Y-параметров активного четырехполюсника
Для активного четырехполюсника уравнения в Y-параметрах будет иметь вид:
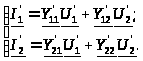
Параметры
 и
и
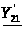 найдем из условия
найдем из условия
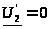 (короткое замыкание на выходе
четырехполюсника)
(короткое замыкание на выходе
четырехполюсника)
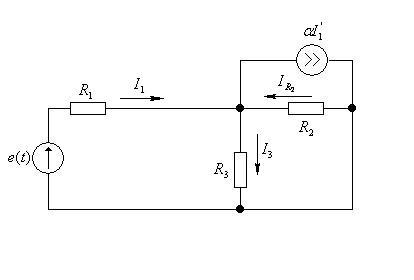
Рисунок 1.1 –Схема расчета параметров активного четырехполюсника при коротком замыкании выхода
В этом случае:
 (1.1)
(1.1)
 ;
;
 ;
(1.3)
;
(1.3)
 ;
;
 ;
;
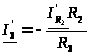 ;
;
 ;
;
 ;
;
 ;
;
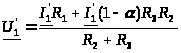 ;
;
 См (1.8)
См (1.8)
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
С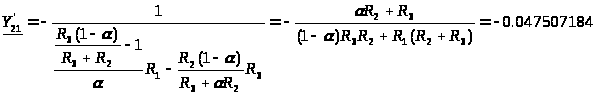 м
м
Параметры
 и
и
 найдем из условия
найдем из условия
 (короткое замыкание на входе
четырехполюсника).
(короткое замыкание на входе
четырехполюсника).
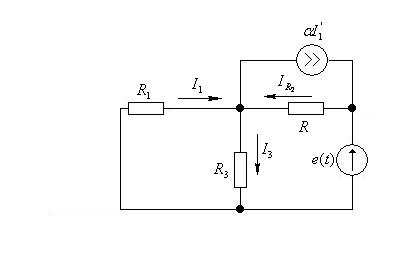
Рисунок 1.2 – Схема расчета параметров активного четырехполюсника при коротком замыкании входа
В этом случае:
 ;
;
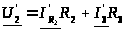 ;
;
 ;
;
 ;
;

 ;
;
 ;
;

 ;
;
 См
См
 ;
;
 См
См
Нахождение Y-параметров пассивного четырехполюсника
Для пассивного четырехполюсника уравнения в Y-параметрах будут иметь вид:

Найдем параметры
 и
и
 при условии
при условии
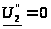 (короткое замыкание выхода четырехполюсника).
(короткое замыкание выхода четырехполюсника).
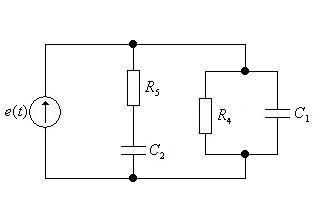
Рисунок 1.4 – Схема расчета параметров пассивного четырехполюсника при коротком замыкании выхода
В этом случае:
 ;
;
 ;
;
 ;
;
 См
См
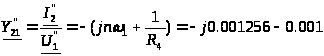 См
См
Найдем параметры
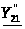 и
и
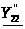 при условии
при условии
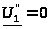 (короткое замыкание выхода четырехполюсника).
(короткое замыкание выхода четырехполюсника).

Рисунок 1.5 – Схема расчета параметров пассивного четырехполюсника при коротком замыкании входа
В этом случае:
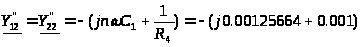 См
См
Нахождение Y-параметров сложного четырехполюсника
Матрица Y-параметров сложного четырехполюсника может быть найдена как сумма матриц Y-параметров активного и пассивного четырехполюсника. Таким образом, получаем:
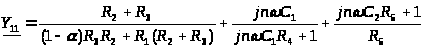 ;
;
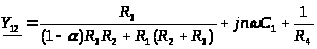 ;
;
 ;
;
 +
+ ;
;
Расчет коэффициента передачи
При параллельном соединении четырехполюсников коэффициент передачи можно определить по формуле:
 ,
,
где
 .
.
Вычисления произведем с помощью программного продукта MathCAD 2000. результаты расчетов представлены в таблице 1.1
Расчет спектра отклика
Гармонические составляющие
выходного напряжения определяются как
 ,
результаты расчетов представим в таблице
1.1.
,
результаты расчетов представим в таблице
1.1.
Таким образом реакция цепи описывается соотношением:

где
 .
.
Временная функция отклика в виде 3-х гармоник имеет вид:
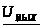 (t)=119.55+95.64sin(1256.64t-0.8657)+13.22sin(3769.91t-1.23)+
(t)=119.55+95.64sin(1256.64t-0.8657)+13.22sin(3769.91t-1.23)+
+4.89sin(6283.18t-1.28)
Данные мгновенных значений
напряжения
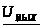 (t)
для интервала времени от 0 до 5 мс
представлены в таблице 1.2.
(t)
для интервала времени от 0 до 5 мс
представлены в таблице 1.2.
Таблица 1.1
-
Гармоники
1
2
3
4
5
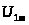 ,
мВ
,
мВ6.366197
0
2.122065
0
1.273239
 ,
,

1256.64
0
3769,91
0
6283.18
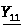 ,
См
,
См0.051618279+j0.00174387
0
0.0519404+j0.0040159302
0
0.0519815+j0.0064352979
 ,
См
,
См-0.00102499-j0.00125664
0
-0.00102499-j0.00376992
0
-0.00102499-j0.0062832
 ,
См
,
См-0.0048507184-j0.001256
0
-0.0048507184-j0.003768
0
-0.048507184-j0.00628
 ,
См
,
См-0.0010287392-j0.00125664
0
-0.0010287392-j0.00376992
0
-0.0010287392-j0.0062832
 ,
Ом
,
Ом387.72553-j487.23141
0
65.73629-j247.82057
0
24.70441-j155,22275

9.73558395-j11.4417114
0
2.08018708-j5.87373582
0
1.09439739-j3.68338887
 ,
мВ
,
мВ61.9786453-j72.8401888
0
4.4142922-j12.4644492
0
1.3934294-j4.6898344
Таблица 1.2
-

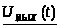 ,
мВ
,
мВ
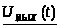 ,
мВ
,
мВ
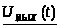 ,
мВ
,
мВ0
29.562
0.00175
200.62
0.0035
80.304
0.00025
67.078
0.002
210.566
0.00375
60.58
0.0005
109.798
0.00225
220.27
0.004
46.081
0.00075
138.707
0.0025
209.537
0.00425
38.48
0.001
158.795
0.00275
172.022
0.0045
28.534
0.00125
178.519
0.003
129.301
0.00475
18.831
0.0015
193.019
0.00325
100.393
0.005
29.563
График зависимости
 (t),
построенный в соответствии с таблицей
1.2, представлен на рис 1.3
(t),
построенный в соответствии с таблицей
1.2, представлен на рис 1.3

Рисунок 1.3 – Результат расчета реакции цепи на воздействие периодического негармонического сигнала
РАСЧЕТ РЕАКЦИИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ МЕТОДОМ ПЕРЕМЕННЫХ СОСТОЯНИЯ
Подлежащая расчету методом переменных состояния схема с выбранными положительными направлениями тока в ветвях приведена на рис.2.1
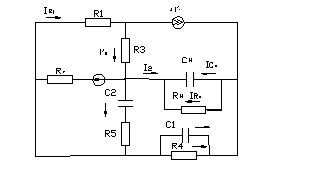
Рисунок 2.1-Схема для расчета реакции цепи на воздействие нескольких периодов входного сигнала методом переменных состояний
Формируем уравнения относительно
переменных состояний
 Запишем уравнения по законам Кирхгофа,
которые содержат токи емкостей:
Запишем уравнения по законам Кирхгофа,
которые содержат токи емкостей:
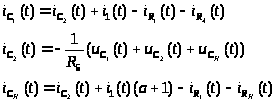
Так как
 то:
то:
 (2.1)
(2.1)
По законам Кирхгофа, определим токи входящие в (2.1):
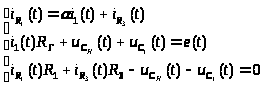 (2.2)
(2.2)
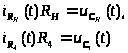
Получаем:

Решая систему (2.2) получаем:
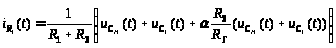
Получаем:
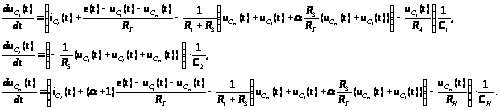
Для решения системы уравнений переменных состояния и нахождения отклика на заданное воздействие воспользуемся программным пакетом MathCAD2000 Professional.

Рисунок 2.2 – Реакция цепи (переходной процесс) на действие двух периодов заданного кусочно-непрерывного сигнала
Выводы
В ходе работы над курсовым
проектом анализировалась схема линейной
цепи. Были рассчитаны реакции
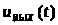 электрической цепи на несинусоидное
периодическое напряжение, при параллельном
соединении активного и пассивного
четырехполюсник, двумя методами: а)-
символичным методом, использую разложение
данного сигнала в ряд Фурье, б)- методом
переменных состояния (для двух периодов
воздействия входного сигнала).
электрической цепи на несинусоидное
периодическое напряжение, при параллельном
соединении активного и пассивного
четырехполюсник, двумя методами: а)-
символичным методом, использую разложение
данного сигнала в ряд Фурье, б)- методом
переменных состояния (для двух периодов
воздействия входного сигнала).
Полученные данные имеют некоторое отличие это связано с применением двух различных методов расчета. В целом полученные расхождения удовлетворяют погрешности расчетов.
СПИСОК ЛИТЕРАТУРЫ
1. Попов В.П.Основы теории цепей: Учеб для вузов. M. : Высш.шк. , 1985.-490с.
2. 3ернов Н.В. ,Карпов В.Г. Теория радиотехнических цепей-М. Энергия , 1972. -715с.
З. Афанасьев В.П. и др. Теория линейных электрических цепей: , Учебное пособие для вузов. -М.: Высш. шк., 1973.-592 с.
4. Белецкий А.Ф. Теория линейных электрических цепей: Учебн. для вузов. -М.: Радио и связь,1986.-544 с.
5. Коваль Ю.О. и др. Основы теории цепей: Учеб для вузов. M. : Харьков:ХНУРЭ; Колегиум , 2004.-436с.
6. Олександров Ю. М., Головенко В. М., Чурилов О. И. Методические указания к курсовой работе по дисциплине “Теория электрических и электронных цепей”. – Х. 2007-24с.