Астигматизм и кривизна изображения. Хроматические аберрации
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра ЭТТ
РЕФЕРАТ
На тему:
«Астигматизм и кривизна изображения. Хроматические аберрации»
МИНСК, 2008
Астигматизм и кривизна изображения
Астигматизм появляется
при значительном смещении точки предмета
с оси и добавляется ко всем остальным
аберрациям. Сместим предмет с оси на
значительное расстояние (рис.1). Астигматизм
состоит в том, что не совпадают точки
фокусов в меридиональной >
 >
и сагиттальной >
>
и сагиттальной >
 >
плоскостях, поэтому лучи бесконечно
узкого пучка не сходятся в одной точке.
Кривизна заключается в том, что
наилучшее изображение получается на
искривленной поверхности, а не на
плоскости.
>
плоскостях, поэтому лучи бесконечно
узкого пучка не сходятся в одной точке.
Кривизна заключается в том, что
наилучшее изображение получается на
искривленной поверхности, а не на
плоскости.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Разложение в ряд волновой аберрации при наличии астигматизма 3 и 5 порядков:
> >
(1)
>
(1)
или >
 >.
>.
Количественно
астигматизм и кривизна характеризуются
продольными астигматическими отрезками
>
 >
и >
>
и >
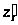 >.
Меридиональная кривизна определяется
отрезком >
>.
Меридиональная кривизна определяется
отрезком >
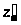 >
– это расстояние от плоскости
параксиального изображения до
меридионального фокуса >
>
– это расстояние от плоскости
параксиального изображения до
меридионального фокуса >
 >.
Сагиттальная кривизна определяется
отрезком >
>.
Сагиттальная кривизна определяется
отрезком >
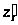 >
– это расстояние от плоскости
параксиального изображения до
сагиттального фокуса >
>
– это расстояние от плоскости
параксиального изображения до
сагиттального фокуса >
 >.
>.
Средняя кривизна определяется полусуммой астигматических отрезков и указывает положение наилучшего изображения для данного пучка:
>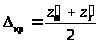 >.
(2)
>.
(2)
Мера астигматизма в продольном измерении определяется разностью астигматических отрезков:
> >.
(3)
>.
(3)
В первом приближении средняя кривизна пропорциональна квадрату расстояния от оси. Зависимость кривизны и астигматизма по полю показывают графики продольных аберраций для внеосевых пучков (рис. 2).
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 2 - Астигматизм 3 порядка (продольные и поперечные аберрации)
Здесь s – относительная предметная координата (на краю поля s = 1 , на оси s = 0):
>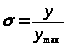 >.
(4)
>.
(4)
Для астигматизма более высоких порядков (5 и выше) графики могут выглядеть, как показано на рис.3:
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 3 - Продольные аберрации при астигматизме 5 порядка.
В зависимости от положения плоскости изображения при астигматизме пятно рассеяния может принимать форму эллипсов, отрезков или круга (рис.4). Горизонтальный отрезок наблюдается, если плоскость изображения совпадает с меридиональным фокусом, а вертикальный – если с сагиттальным. Посередине между ними пятно рассеяния имеет форму круга. В остальных положениях – пятна эллиптической формы.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 4 - Пятна рассеяния астигматического пучка.
Дисторсия
Название происходит от латинского “искажение”.
Если кроме дисторсии других аберраций нет, то точка изображается в виде точки (гомоцентрический пучок остается гомоцентрическим), но эта точка смещена от идеальной (рис.5).
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 5 - Дисторсия.
Разложение в ряд волновой аберрации при наличии дисторсии:
> >
(5)
>
(5)
или >
 >.
>.
При дисторсии величина изображения отличается от идеального:
> >.
(6)
>.
(6)
Абсолютная дисторсия (выражается в тех же единицах, что и величина изображения):
> >,
(7)
>,
(7)
где V – увеличение системы для данной точки поля.
Относительная дисторсия:
> >
.
(8)
>
.
(8)
Дисторсия характерна тем, что ее величина нелинейно зависит от величины предмета, то есть линейное увеличение различно для разных точек поля. Абсолютная дисторсия 3 порядка определяется дифференцированием выражения (8.38) и умножением на квадрат предметной координаты s:
> >
(9)
>
(9)
График относительной дисторсии 3 порядка приведен на рис.6. Для сравнения показан примерный ход кривой дисторсии высшего порядка.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 6 - Дисторсия 3 и высшего порядков.
Наличие дисторсии приводит к искажению прямых линий, не проходящих через ось (рис.7). Если квадратный предмет изображается в виде подушки – это положительная дисторсия. Если изображение квадрата имеет выпуклые стороны (в виде бочки), то это отрицательная дисторсия.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 7 - Дисторсия
Допустимая относительная
дисторсия (то есть дисторсия, которая
при восприятии глазом не вызывает
ощущения, что изображение искажено)
около >
 >.
Исправление дисторсии важно в измерительных
приборах (в частности, в фотограмметрических
системах), так как наличие дисторсии
приводит к нелинейной ошибке измерений.
Например, в фотолитографии допуск на
абсолютную дисторсию не превышает 20
нм.
>.
Исправление дисторсии важно в измерительных
приборах (в частности, в фотограмметрических
системах), так как наличие дисторсии
приводит к нелинейной ошибке измерений.
Например, в фотолитографии допуск на
абсолютную дисторсию не превышает 20
нм.
Хроматические аберрации
Хроматические
аберрации – это проявление зависимости
характеристик оптической системы от
длины волны света (хромо – цвет).
Хроматические аберрации приводят к
тому, что в изображениях неокрашенных
предметов появляется окрашенность.
Хроматические аберрации появляются
из-за того, что оптические системы
изготовлены из оптических стекол с
показателями преломления, зависящими
от длины волны >
 >.
>.
Существуют два основных вида хроматизма:
- хроматизм положения,
- хроматизм увеличения.
Хроматизм положения
Хроматизм положения – это аберрация, при которой изображения одной точки предмета расположены на разном расстоянии от оптической системы для разных длин волн (разные положения плоскости изображения). В этом случае фокусы также расположены на разных расстояниях (рис.).
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 8 - Хроматизм положения.
На рис.9 представлен типичный график зависимости положения изображения от длины волны.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 9 - График зависимости положения изображения от длины волны.
Чем меньше длина волны, тем ближе изображение к оптической системе. Численно хроматизм положения определяется разностью положений плоскости изображения для крайних длин волн (l>1 >и l>2>):
> >.
(10)
>.
(10)
Естественный хроматизм возникает в оптической системе, если все линзы сделаны из одного сорта стекла. В таком случае оптическая система неахроматизована.
Устранение (коррекция) хроматизма может быть произведена двумя способами:
- использование зеркальных систем, где хроматизм в принципе отсутствует (катоптрические системы, например система Кассегрена),
- использование в линзовых (диоптрических) системах нескольких сортов стекла с различными коэффициентами дисперсии n>e>.
Принципы ахроматизации оптических систем
Возьмем две тонких линзы из разных сортов стекла. Если линзы расположены вплотную друг к другу, то получается тонкая система. Задача ахроматизации сводится к тому, чтобы оптическая сила системы линз не зависела от длины волны. Оптическая сила системы из двух тонких линз:
>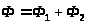 >
(11)
>
(11)
Оптическая сила
каждой линзы >
 >.
Пусть >
>.
Пусть >
 >,
при этом оптическая сила каждой линзы
меняется на величину >
>,
при этом оптическая сила каждой линзы
меняется на величину >
 >.
Зная число Аббе для любого интервала
длин волн >
>.
Зная число Аббе для любого интервала
длин волн >
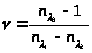 >,
можно получить следующее выражение:
>,
можно получить следующее выражение:
> >.
(12)
>.
(12)
Допустим, что эти линзы изготовлены из разных сортов стекла, тогда условие ахроматизации будет выглядеть так:
> >
(13)
>
(13)
где
>
 >
– оптическая сила системы для основной
длины волны, >
>
– оптическая сила системы для основной
длины волны, >
 >
– оптические силы первой и второй линз
для основной длины волны, >
>
– оптические силы первой и второй линз
для основной длины волны, >
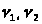 >–
коэффициенты дисперсии стекла первой
и второй линз.
>–
коэффициенты дисперсии стекла первой
и второй линз.
Решив систему линейных уравнений (13), получим уравнения ахроматизации для двух сортов стекла:
> >
(14)
>
(14)
У стекол должны быть
разные коэффициенты дисперсии, причем
коэффициент дисперсии первой линзы
должен быть больше коэффициента дисперсии
второй линзы (n>1>
> n>2>), иначе
может получится так, что система будет
состоять из двух компонентов с близкими
по величине, но противоположными по
знаку оптическими силами. Это приведет
к необходимости увеличения оптической
силы компонентов, и как следствие, к
появлению больших монохроматических
аберраций. Обычно для системы из двух
линз выбирают n>1>
» 60 (крон), n>2>
» 30 (флинт). Тогда >
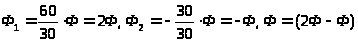 >
(рис.10).
>
(рис.10).
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 10 - Ахроматическая система из двух линз.
В этом
случае график зависимости положения
изображения от длины волны будет
выглядеть, как показано на рис.11. У такой
системы нет хроматизма положения: >
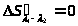 >.
>.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 11 - График хроматизма положения для системы из двух линз.
Разность на краях спектра сводится к нулю, но остается разность положений изображения для центральной l>0> и крайних (l>1>, l>2>) длин волн. Это вторичный хроматизм или вторичный спектр. Его величина определяется следующим образом:
>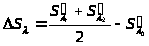 >.
(15)
>.
(15)
Вторичный спектр гораздо меньше первичного хроматизма положения, но тем не менее, он влияет на качество изображения. Для исправления вторичного спектра требуется не меньше трех сортов стекла с различными коэффициентами дисперсии и относительной частной дисперсией (такие системы называются апохроматы). Если при коррекции хроматизма используется еще больше стекол, то такая система называется суперапохроматом.
На рис.12 приведены графики продольного хроматизма первого порядка неахроматизированной и ахроматизированной систем.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 12 - Продольный хроматизм первого порядка.
Если в оптической системе присутствуют монохроматические аберрации третьего и пятого порядка, то графики продольного хроматизма будут выглядеть, как показано на рис.13 и рис.14.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 13 - Продольный хроматизм в присутствии аберраций
третьего порядка
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 14 - Присутствуют аберрации третьего и пятого порядков.
Кривые хроматизма могут быть взаимно наклонены, это так называемый сферохроматизм, то есть хроматизм сферической аберрации (рис.15).
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 15 - Сферохроматизм в присутствии аберраций 3 и 5 порядков
Как видно из рис.8.33, обычно сферохроматизм исправляется для значения r2»0.5.
Хроматизм увеличения
Хроматизм увеличения – это аберрация, при которой увеличение оптической системы зависит от длины волны (рис.16). Вследствие этого вместо изображения точки образуется цветная полоска.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 16 - Хроматизм увеличения.
Численно абсолютный хроматизм увеличения (первичный спектр) определяется как разность величины изображения для крайних длин волн:
> >.
(16)
>.
(16)
Вторичный спектр (вторичный хроматизм увеличения) определяется как разность величины изображения для центральной и крайних длин волн:
> >
(17)
>
(17)
Хроматизм увеличения измеряется в тех же единицах, что и величина изображения: для ближнего типа – в миллиметры, для дальнего типа – в угловой мере.
Относительный хроматизм увеличения:
первичный спектр:
>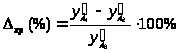 >
(18)
>
(18)
вторичный спектр:
> >
(19)
>
(19)
Если выразить
увеличение для различных длин волн в
виде: >
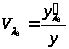 >,
>
>,
>
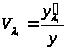 >,
то относительный хроматизм увеличения
можно записать в следующем виде:
>,
то относительный хроматизм увеличения
можно записать в следующем виде:
> >.
(20)
>.
(20)
Хроматизм увеличения принято рассматривать только в одной плоскости установки. Поскольку типы хроматических аберраций не связаны друг с другом, хроматизм увеличения может исправляться независимо от хроматизма положения. В частности, если оптическая система тонкая (рис. 17), а апертурная диафрагма совпадает с ней, то хроматизм положения присутствует, а хроматизма увеличения нет.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010071480000000001000000180300000000000018030000010000006c0000000000000000000000080000001000000000000000000000002f260000790f000020454d4600000100180300001200000002000000000000000000000000000000000500000004000040010000f000000000000000000000000000000000e2040080a90300160000000c000000180000000a000000100000000000000000000000090000001000000087010000a9000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100ccad11001000000030b11100b0ae1100cb4f603230b1110028ae11001000000098af110014b111001c4f603230b1110028ae110020000000e9e12f3128ae110030b1110020000000ffffffff7c0bee0064e22f31ffffffffffff0180ffff01800fff0180ffffffff000000000008000000080000e8ba120001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c006900620072000000000000000000f0ae1100e2882f31e8ad083250b211005cae1100df382731080000000100000098ae110098ae1100307a253108000000c0ae11007c0bee006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410080bb41000000000d000000010000004c00000004000000000000000000000087010000a90000005000000020002d010900000046000000280000001c0000004744494302000000ffffffffffffffff89010000aa000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02a9008701040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000008701a90020c40900040000002d010000040000002d010000030000000000
Рисунок 17 - Хроматизм положения и увеличения тонкой линзы.
Если в системе исправлен первичный хроматизм увеличения, то это ахромат по хроматизму увеличения, если исправлен вторичный хроматизм увеличения, то это апохромат по хроматизму увеличения, если хроматизм увеличения не исправлен, то это неахромат по хроматизму увеличения.
ЛИТЕРАТУРА
Бегунов Б.Н., Заказнов Н.П. и др. Теория оптических систем. – М.: Машиностроение, 2004
Заказнов Н.П. Прикладная оптика. – М.: Машиностроение, 2000
Дубовик А.С. Прикладная оптика. – М.: Недра, 2002
Нагибина И.М. и др. Прикладная физическая оптика. Учебное пособие.- М.: Высшая школа, 2002