Синтез и анализ аналоговых и цифровых регуляторов
Министерство высшего образования российской федерации
Кубанский Государственный технологический Университет
Кафедра Автоматизации производственных процессов
Курсовая работа
По курсу “Теория управления”
Тема курсовой работы: «Анализ и синтез оптимальной одноконтурной САУ при использовании непрерывного и цифрового регуляторов»
Выполнил студент
группы 96-ОА-61
номер зачетной книжки
96-ОА-612
…………………….
Проверил профессор
……………………..
Краснодар 1999
РЕФЕРАТ
Курсовой работа. ___ листов , ___ рисунков, ____таблицы, ____ источника, ____ приложение.
Передаточная функция, переходная функция, регулятор, фиксатор нулевого порядка, оптимальное управление, цифровой -фильтр.
В данном курсовой работе предложено синтезировать и проанализировать работу одноконтурной САУ при использовании непрерывного и цифрового регуляторов, реализующих П-, ПИ- и ПИД- закон регулирования. Оптимизация САУ производится по критерию максимальной динамической точности. В завершении был рассчитан цифровой фильтр, обеспечивающий перевод системы из одного состояния в другое за минимальное число периодов квантования при наличии ограничения на управляющие воздействие.
СОДЕРЖАНИЕ
|
Введение |
|
|
1 Определение параметров оптимальной настройки регуляторов |
|
|
2 Переходные процессы в замкнутой системе при использовании непрерывного регулятора и их анализ |
|
|
3 Определение периода квантования цифрового регулятора и его параметров настройки |
|
|
4 Анализ устойчивости САУ по критерию Джури и построение переходных процессов в цифровых системах |
|
|
5 Расчет цифрового фильтра |
|
|
6 Оптимальное управляющие воздействие и реакция на него приведенной непрерывной части |
|
|
Заключение |
|
|
Список литературы |
|
|
Приложение А |
Введение
Развитие всех областей техники в настоящее врамя характкризуется широкой автоматизацией различных производственных процессов. При этом освобождается труд человека, повышается точность и скорость выполнения операций, что значительно повышает производительность производства.
Автоматизация обеспечивает работу таких обьектов, непосредственое обслуживание человеком невозможно из-за вредности, отдаленности или быстрого протекания процесса.
В настоящее время резко увеличивается производство различного оборудования для автоматизации промышленности, а также внедряются новые типы автоматических устроиств, основанные на последних достижениях науки и техники. Эффективное использование автоматики в народном хозяйстве возможно лишь при условии рационального решения задач на всех этапах ее разработки и освоения. Наиболее ответственным этапом при проектировании систем автоматизации является их синтез, расчет и последующий анализ, которые на сегодняшний день базируются на теории управления. Эта наука позволяет не только найти параметры, при которых система работает устойчиво, различные качественные показатели системы, но также и оптимизировать систему для более рационального использования различных ресурсов.
1ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ НАСТРОЙКИ РЕГУЛЯТОРОВ
Определение оптимальных параметров настройки П, ПИ, ПИД - регуляторов производим по расширенных амплитудно-фазовым характеристикам.
Расширенной амплитудно-фазовой характеристикой звена или системы называют отношение вектора гармонических вынужденных затухающих колебаний на входе к вектору гармонических затухающих колебаний на входе.
Существуют два показателя степени затухания:
- относительная степень затухания;
m - логарифмический декремент затухания, которые связаны между собой следующим далее соотношением:
 ,
(1.1)
,
(1.1)
Из предыдущей формулы (1.1) определяем значение логарифмического декремента затухания m:
 ,
(1.2)
,
(1.2)
Система автоматического управления будет обладать требуемой относительной степенью затухания, если расширенная амплитудно-фазовая характеристика разомкнутой система автоматического управления будет проходить через точку на комплексной плоскости (-1, j0), т.е.
W>p>(m,j)* W>o>(m,j) = -1, (1.3)
или
-W>p>(m,j) = 1/ W>o>(m,j), (1.4)
Для получения расширенной амплитудно-фазовой характеристики необходимо в передаточную функцию подставить:
p = -m + j = (j-m).
Рисунок 1.1 Структура схемы непрерывной САУ
Передаточная функция нашего исходного объекта имеет следующий далее вид:
 ,
(1.5)
,
(1.5)

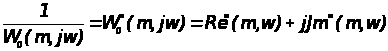 ,
(1.6)
,
(1.6)
Формула (1.6) представляет собой инверсную расширенную амплитудно - фазовой характеристику обьекта.

Так как заданое значение = 0.96, то по формуле (1.2) определим значение m и подставим его в предыдущую формулу расширенной амплитудно-фазовой характеристики, m = 0.512.

Перед тем, как определить оптимальные параметры настройки П, ПИ, ПИД регуляторов найдем частоту среза нашего обьекта.
Частота среза – это такое значение частоты w = w>c>, при котором значение амплитуды на выходе на превышало бы трех процентов от амплитуды при нулевой частоте.
Запишем выражение амплитудно - фазовой характеристики нашего обьекта:
 ,
(1.7)
,
(1.7)
Амплитудно-фазовую характеристику обьекта можно найти из следующей формулы:
 ,
(1.8)
,
(1.8)
где Re(w) – вещественная часть амплитудно-фазовой характеристики;
Jm(w) – мнимая часть амплитудно-фазовой характеристики.
 .
.
При нулевой
частоте значение амплитуды равно 3.1
. Значит необходимо найти такое w = w>с>,
чтобы
 = 0.03*3.1
= 0.093.
= 0.03*3.1
= 0.093.
Таким образом необходимо расчитать уравнение
 ,
(1.9)
,
(1.9)
Решением этого уравнения является то, что мы находим следующие параметры w = 0.417, следовательно и w>c> = 0.417.
Для опреления оптимальных параметров регулятора необходимо решить уравнение (1.6). Приравняв вещественные и мнимые части в уравнении (1.6), можэно получить расчетные формулы для определения параметров регуляторов [4, ст 250]:
П – регулятор:

Пи – регулятор:

Пид – регулятор:


где С>0 > = 1/T>u>;
C>1> = K>p>;
C>2> = T>g>.
Для ПИД – регулятора имеем два уравнения с тремя неизвестными, тогда задаемся отношением:
 ,
,
В этом случае расчет формулы для ПИД – регулятора принимает следующий далее вид:
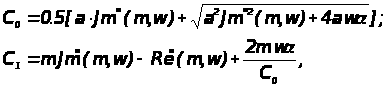
где а = w(m2+1);
 ;
;
 .
.
Расчет оптимальных параметров настройки для П – регулятора представлен следующим образом:
 ,
(1.10)
,
(1.10)
Из второго уравнения системы (1.10) найдем w и подставим это значение в первое уравнение системы. При решении получи, что w = 0.354 и оптимильными параметрами настройки П – регулятора является значение К>р>опт = 1.01.
Рассчитываем оптимальные значения параметров настройки для ПИ – регулятора.
Для каждого значения частота от 0 до частоты среза находи точки С>1>С>0> и С>1>, соответствующие требуемой степени затухания . Оптимальным параметром является является точка на линии, равной степени затухания С>1>С>0> = f(С>1>), лежащия справа от глобального максимума. Эти параметры обеспечивают:
 .
.
Итак, запишем далее следующую систему уравнений для Пи – регулятора:

 ,
(1.11)
,
(1.11)
Таблица 1.2
Данные для расчета оптимальных параметров настроек ПИ – регулятора.
|
w |
C>0> |
C>1> |
C>1>C>0> |
|
0 0.1 0.2 0.3 0.4 0.417 0.5 |
0 0.029 0.073 0.059 -0.09 -0.134 -0.443 |
-0.323 0.117 0.382 0.777 1.228 1.307 1.753 |
0 4.858*10-4 0.028 0.046 -0.11 -0.175 -0.777 |

Рисунок 1.2 – График звисимости С>1>С>0 >= f(C>1>) для Пи – регулятора
Максимальное значение функции С>1>С>0> = 0.048 при С>1> = 0.694. Берем точку правее глобального максимума С>1> = 0.777, С>1>С>0> = 0.0459 . Решив систему уравнений (1.11) получим оптимальные параметры пастройки К>р>опт = 0.777, T>u>опт = 16.928.
Рассчитываем оптимальные параметры настройка для ПИД – регулятора:
 ,
(1.12)
,
(1.12)
Для каждого значения частота от 0 до частоты среза находи точки С>1>С>0> и С>1>, соответствующие требуемой степени колебательности m = 0.512 решив систему (1.12). Данные расчетов представлены в таблице 1.1 по эти данным построим график зависимости С>1>С>0> = f(С>1>).
Таблица 1.1
Данные для расчета оптимальных параметров настроек ПИД – регулятора.
|
w |
C>0> |
C>1> |
C>1>C>0> |
|
0 0.1 0.2 0.3 0.4 0.417 0.5 |
0 0.12 0.2 0.226 0.184 0.172 0.113 |
-0.323 0.097 0.485 0.913 1.447 1.556 2.206 |
0 0.012 0.097 0.207 0.266 0.268 0.25 |

Рисунок 1.3 – График звисимости С>1>С>0 >= f(C>1>)
Нужно взяь точку, лежащую справа от глобального максимума. Максимильное значение С>1>С>0> =0.268 , при С>1> = 1.576. Берем точку С>1>С>0> = 0.2592 при С>1> =1.9456. По этим значениям определим оптимальные параметры регулятора:

Таким образом оптимильные параметры настройки для ПИД – регулятора:

2. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЗАМКНУТЫХ СИСТЕМАХ
Запишем выражение передатичной функции для системы в замкнутом состоянии:
 ,
(2.1)
,
(2.1)
где
 .
.
Тогда выражение (2.1) будут иметь вид:

 , (2.2)
, (2.2)
Найдем передаточную функию для замкнутой системы с П – регулятором, т.е. W>p>(p) = К>p> . К>p> – оптимальное значение, найденное в первом разделе , т. е. К>p> = 1.01.
Предаточная функция замкнутой системы с П – регулятором имеет следующие вид:
 ,
(2.3)
,
(2.3)
Переходная функция замкнутой системы:
 ,
(2.4)
,
(2.4)
Найдем полюса фунгкции (2.4).
Для этого необходимо найти корни следующего уравнения:
p( )
= 0.
)
= 0.
Они равны:
p>1> = 0;
p>2> = - 0.435;
p>3> = - 0.181 – j0.34;
p>4> = - 0.181 + j0.34.
Переходная функция для замкнутой системы с П – регулятором будет иметь следующий вид:
h(t) = 0.757-0.052e-0.424t * cos(0.254t) - 0.3857e-0.181t * sin(0.354t).
Построим переходный процесс функции, изобразим график этого процесса на рисунке 2.1.

Рисунок 2.1 – Переходный процесс в замкнутой системе с П – регулятором.
Запишем передаточную функцию для замкнутой системы с ПИ – регулятором, т.е.:
 .
.
В качестве К>р> и Т>u> берем значения, которые были получены в первом разделе, т.е. берем К>р> = 0.777 и Т>u> = 16.928. Тогда выражение передаточной функции имеет следующие далее вид:
 ,
(2.5)
,
(2.5)
Запишем предаточную функция замкнутой системы с ПИ – регулятором, для этого воспользуемся формулой (2.1):
 ,
(2.6)
,
(2.6)
Переходная функция замкнутой системы имеет следующий вид:
 ,
(2.7)
,
(2.7)
Найдем полюса фунгкции (2.7).
Для этого необходимо найти корни следующего уравнения:
p( )
= 0.
)
= 0.
Они равны:
p>1> = - 0.421;
p>2> = - 0.075;
p>3> = - 0.149 – j0.29;
p>4> = - 0.149 + j0.29;
p>5> = 0.
Переходная функция для замкнутой системы с ПИ – регулятором будет иметь следующий вид:
h(t) = 1- 0.0609e-0.421t – 0.757e-0.148t *cos(0.29t)-0.4870.148t *sin(0.29t)-0.181e-0.075t
Построим переходный процесс функции, изобразим график этого процесса на рисунке 2.2.

Рисунок 2.2 – Переходный процесс в замкнутой системе с ПИ – регулятором.
Запишем передаточную функцию для замкнутой системы с ПИД – регулятором, т.е.:
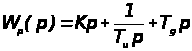 .
.
В качестве К>р> , Т>u> и Т>g> берем значения, которые были получены в первом разделе, т.е. берем К>р> = 1.9456 , Т>u> = 7.506, и Т>g> = 0.976. Тогда выражение передаточной функции имеет следующий далее вид:
 ,
(2.8)
,
(2.8)
Запишем предаточную функция замкнутой системы с ПИД – регулятором, для этого воспользуемся формулой (2.1):
 ,
(2.9)
,
(2.9)
Переходная функция замкнутой системы имеет следующий вид:
 ,
(2.10)
,
(2.10)
Найдем полюса фунгкции (2.10).
Для этого необходимо найти корни следующего уравнения:
p( )
= 0.
)
= 0.
Они равны:
p>1> = 0;
p>2> = -0.405 – j0.116;
p>3> = -0.405 + j0.116;
p>4> = -0.039 – j0.192;
p>5> = -0.039 + j0.192.
Переходная функция для замкнутой системы с ПИД – регулятором будет иметь следующий вид:
h(t) = 1 – 0.2927e-0.404t*cos(0.1157t)- 0.032e-0.404t*sin(0.1157t)- 0.6934e-0.038t*cos(0.1918t)- 0.2055e-0.0388t*sin(0.1918t).
Построим переходный процесс функции, изобразим график этого процесса на рисунке 2.3.

Рисунок 2.3 – Переходный процесс в замкнутой системе с ПИД – регулятором.
3 ОПРЕДЕЛЕНИЕ ПЕРИОДА КВАНТОВАНИЯ ЦИФРОВОГО РЕГУЛЯТОРА И ПЕРЕСЧЕТ ЕГО ВАРАМЕТРОВ
Необходимо выяснить соответствие коэффициентов неопределенногои цифрового регуляторов. Для выбора периода измерений цифрового регулятора строим амплетудно – частотную характеристику замкнутой системы и определяем частоту среза, при которой значение амплетуды на выходе не превышает три проценты от амплитуды при нулевом значении частоты.
Для этого возьмем передаточные функции замкнутой системы (для все типов регуляторов), которые были найдены во втором задании курсовой работы.
Передаточная функция замкнутой системы с П – регулятором:
 ,
(3.1)
,
(3.1)
Передаточная функция замкнутой системы с ПИ– регулятором:
 ,
(3.2)
,
(3.2)
Передаточная функция замкнутой системы с ПИД – регулятором:
 ,
(3.3)
,
(3.3)
Выражение амплетудно – частотной характеристики для системы с П – регулятором будет иметь следующий вид:
 .
(3.4)
.
(3.4)
Выражение амплетудно – частотной характеристики для системы с ПИ – регулятором будет иметь следующий вид:
 .
(3.5)
.
(3.5)
Выражение амплетудно – частотной характеристики для системы с ПИД – регулятором будет иметь следующий вид:
 .
(3.6)
.
(3.6)
Така как частота среза равна трем процентам от нулевого значения, то необходимо решить уравнение следующего вида:
 .
(3.7)
.
(3.7)
При решении уравнений было получено:
-частота среза для системы имеющей в стоем составе П – регулятор w>с> = 2.25;
-частота среза для системы имеющей в стоем составе ПИ – регулятор w>с> = 1.6738;
-частота среза для системы имеющей в стоем составе ПИД – регулятор w>с> = 3.8194.
Частоту измерений принимают как:
 ,
(3.8)
,
(3.8)
где w>c> = 3.8194 (наибольшее значение), при котором период квантования равен T>0> = 0.411.
Так как полученное значение меньше заданного, то произведем пересчет параметров.
В общем виде дискрктную передаточную функцию искоиого элемента можно записать следующим образом:
 .
(3.9)
.
(3.9)
В нашем случае выражение (3.9) примет вид:
 ,
(3.10)
,
(3.10)
г де
де
 ;
;
 ;
;
 .
.
C учетом этих выражений необходимо пересчитать параметры непрерывных регуляторов в параметры цифровых.
Запишем передаточные функции непрерывных регуляторов:
П – регулятор
W>p>(p) = 1.01; (3.11)
ПИ – регулятор
 ;
(3.12)
;
(3.12)
ПИД – регулятор
 .
(3.13)
.
(3.13)
После вычисления коэффициентов q>0>, q>1> и q>2> дискрктные передаточные функции будут иметь вид:
П – регулятор
 ;
(3.14)
;
(3.14)
ПИ – регулятор
 ;
(3.15)
;
(3.15)
ПИД – регулятор
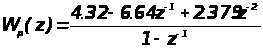 .
(3.17)
.
(3.17)
4 АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО УТРАВЛЕНИЯ ПО КРИТЕРИЮ ДЖУРИ И ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦИФРОВЫХ СИСТЕМАХ

При
анализе цифровых систем управления их
представляют в виде трех элементов:
цифрового фильтра (регулятора), фиксатора
и приведенной непрерывной части.
где y – дискретное значение регулируемой величины;
f – заданное значение регулируемой величины;
e – ошибка управления;
u – управляющее воздействие.
Рисунок 4.1 Структурная схема цифровой системы автоматического управления
Так как в системе имеет мести фиксатор нулевого порядка с передаточной функцией вида:
 ,
(4.1)
,
(4.1)
то с учетом того, что z = e –pT , эту функцию можно записать в следующем далее виде:
 .
(4.2)
.
(4.2)
Сомножитель 1/р относят к линейной части, поэтому передаточная функция приведенной непрерывной части может быть записана в следующем виде:
 .
(4.3)
.
(4.3)
Так как

 ,
,
переходная фнукция ленейной части системы, то z – передаточную функцию линейной части находим по следующему выражению:
 .
(4.4)
.
(4.4)
Найдем выражение для передаточной функции линейной части:
 .
(4.5)
.
(4.5)
Для вычисления h(t) воспользуемся методом неопределенных коэффициентов. Необходимо определить полюса. Для этого необходимо найти корни следйющего уравнения:
( )*р
= 0.
)*р
= 0.
Решив данное уравнение мы получили , что его корни следующего вида:
p>1> = 0;
p>2> = - 0,2;
p>3> = - 0,33;
p>4>= -0,25.
Переходная функция линейной части имеет следующий вид:
h(t) = -21,93e-0.2t –4.03e-0.33t +22.86e-0.25t +3.1 . (4.6)
С учетом формулы (4.4) получаем
 .
.
После раскрытия скобок и приведения подобных мы получаем равенство в следующем виде:
 .
(4.7)
.
(4.7)
Результирующая передаточная функция разомкнутой системы может быть определена как произведение передаточной функции приведенной непрерывной чати и передаточной функции цифрового фильтра:
 .
(4.8)
.
(4.8)
Дискретная передаточная функция замкнутой системы:
 .
(4.9)
.
(4.9)
Определим значение W>3>(z) для каждой из систем:
система с П – регулятором. W>р>(z) = 1.01, W>н.ч.>(z) – определеня по формуле (4.7), тогда:
 ;
(4.10)
;
(4.10)
система с ПИ – регулятором.
 ;
;
W>н.ч.>(z) – определена по формуле (4.7), тогда:
 ;
(4.11)
;
(4.11)
система с ПИД – регулятором.
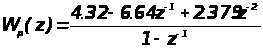 ,
,
W>н.ч.>(z) – определена по формуле (4.7), тогда:
 .
(4.12)
.
(4.12)
После того , как получим выражение дискрктных передаточных функций для всех систем, проанализируем устойчивость этих систем по критерию Джури.
Критерий устойчивости заключается в следующем.
Пусть задан А(z) – характкристический полином:
A(z) = a>0>zn + a>1>n-1 + … + a>n>, a>0> > 0.
Введем понятие обратного полинома, получаемого перестановкой коэффициентов исходного в обратном порядке:
A(z) = a>n>zn + a>n-1>n-1 + … + a>0>.
Разделим A(z) на обратной ему. В итоге получаем частное от деления число q>0> и остаток А>1>(z) – полином n-1 степени.
Домножим полученый результат на z-1 получаем:
A>1>(z) = (a>0>-a>n>q>0>)zn-1 + … + (a>n-1>-a>1>q>0>).
Затем делим остаток A>1>(z) на обратный ему A>10>(z) и определяем новое q>1> и A>2>(z)
 и т.д.
и т.д.
Выполняя деление полиномов A>i>(z) на обратные ему A>i0>(z), получаем последовательность чисел q>i> = {q>0>, q>1>, q>2>,…,q>n-2>}.
Необходимым и достаточным условием устойчивости цифровой системы является неравенства:
А(1)=(a>0>+ a>1>+ a>2>+…+a>n>)>0;
(-1)nА(-1)=(a>0>(-1)n + a>1>(-1)n-1 +…+a>n>)>0;
|q>i>|<1, i=0,1,2,…,n-2.
Используя выше изложенное, определим устойчивость наших систем.
Система с П-регулятором.
Характеристический полином имеет следующий вид:
А(1)= 1 - 2.7544 + 2.5359 - 0.7817=0.003039>0 .
(-1)3A(-1)= -(1 - 2.7544 + 2.5359 - 0.7817) >0.
А(z) = z3-2.7544z2+2.5359z - 0.7817
Обратный полином
 .
.
Разделим A(z) на A>0>(z).
|
|
|
|
-( |
-0.7817=q>0>, |q>0>|<1 |
0,3852z-0,7686z2+0,3888z3
Домножим полученный результат на z-1, тогда:
A>1>(z)= 0,3852-0,7686z+0,3888z2,
A>10>(z)= 0,3888-0,7686z+0,3852z2.
Разделим A>1>(z) на A>10>(z).
|
0,3852-0,7686z+0,3888z2 |
0,3888-0,7686z+0,3852z2 |
|
-(0,3852-0,7614z+0,3816z2) |
0,99065=q>1>, |q>1>|<1 |
-0.00718z+0.00723z2
Домножим полученный результат на z-1, тогда:
A>2>(z)= 0.007238z-0.007187.
В результате расчетов получили, что q>0>, q>1>, q>2> по модулю меньше еденицы, таким образом все три неравенства выполняются. Следовательно цифровая система устойчива.
Система с ПИ-регулятором.
Характеристический полином имеет вид:
Степень полинома n=4. Множество q>i> = {q>0>, q>1>, q>2>}.
А(1)=
 >0.
>0.
(-1)4A(-1)=
 >0.
>0.
 .
.
Обратный полином:
 .
.
Разделим A(z) на A>0>(z).
|
0.78-3.326z+5.3001z2-3.756z3+ z4 |
1-3.7556z+5.3001z2-3.32z3+0.7834z4 |
|
-(0.78-2.943z+4.152z2-2.606z3+0.61z4) |
0,783447=q>0>, |q>0>|<1 |
-0,383z+1.147z2-1.1506z3+0,3861 z4
Домножим полученный результат на z-1, тогда:
A>1>(z)= -0,383+1.147z-1.1506z2 +0,3861 z3,
A>10>(z)= -0,361+1.1506z-1.147z2 +0,383 z3.
Разделим A>1>(z) на A>10>(z).
|
-0,383+1.147z-1.1506z2 +0,3861 z3 |
-0,361+1.1506z-1.147z2 +0,383 z3 |
|
-(-0,383+1.141z-1.138z2 +0,3801 z3) |
-0,992116=q>1>, |q>1>|<1 |
0,006046z-0,01207z2+0,00605z3
Домножим полученный результат на z-1, тогда:
A>2>(z)= 0,006046z-0,01207z2+0,00605z3,
A>20>(z)= 0,00605-0,005474z2-0,006046z3.
Разделим A>2>(z) на A>20>(z).
|
0,006046z-0,01207z2+0,00605z3 |
0,00605-0,005474z2-0,006046z3 |
|
-(0,006046z-0,01207z2+0,00603z3) |
0,99774=q>2>, |q>2>|<1 |
-0,000027278z+0,000027353z2
Домножим полученный результат на z-1, тогда:
A>3>(z) = -0,000027278z+0,000027353z2
В результате расчетов получили, что q>0>, q>1>, q>2> по модулю меньше еденицы, таким образом все три неравенства выполняются. Следовательно цифровая система устойчива.
Система с ПИД-регулятором.
Характеристический полином имеет вид:
Степень полинома n=5. Множество q>i> = {q>0>, q>1>, q>2>, q>3>}.
А(1)= >0.
>0.
(-1)5A(-1)= >0.
>0.
 ,
,
Обратный полином:
 .
.
Разделим A(z) на A>0>(z).
|
|
|
|
|
0,01589163=q>0>, |q>0>|<1 |
0,7347z-3,1644z2+5,102835z3-3,6802818z4+0,999747z5
Домножим полученный результат на z-1, тогда:
A>1>(z)= 0,7347-3,1644z+5,102835z2-3,6802818z3+0,999747z4,
A>10>(z)= 0.99974 -3,680218z+5,1028z2-3,1644z3+0,7347z4.
Разделим A>1>(z) на A>10>(z).
|
0,7347-3,1644z+5,102835z2-3,6802818z3+0,999747z4 |
0,7347-3,1644z+5,102835z2-3,6802818z3+0,999747z4 |
|
-(0,7347-2.704z+3.750z2-2.3256z3+0.53999z4) |
0,734938361=q>1>, |q>1>|<1 |
-0,4596z+1,3255z2-1,3545z3+0,4597z4
Домножим полученный результат на z-1, тогда:
A>2>(z)= -0,4596+1,3255z-1,3545z2+0,4597z3,
A>20>(z)= -0,4597+1,3545z-1,3255z2+0,4596z3.
Разделим A>2>(z) на A>20>(z).
|
-0,4596+1,3255z-1,3545z2+0,4597z3 |
-0,4597+1,3545z-1,3255z2+0,4596z3 |
|
-0,4596-1,3244z+1,3525z2+0,4595z3 |
-0,99986442=q>2>, |q>2>|<1 |
-0,0288981z-0,02926z2+0,91927z3
Домножим полученный результат на z-1, тогда:
A>3>(z)= -0,0288981-0,02926z+0,91927z2,
A>30>(z)= 0,91927-0,02926z-0,02889881z2.
Разделим A>3>(z) на A>30>(z).
|
-0,0288981-0,02926z+0,91927z2 |
0,91927-0,02926z-0,02889881z2 |
|
0,0288981-0,0009198z+0,0.028898z2 |
0,0314359=q>2>, |q>2>|<1 |
-0,0305301z+1.028762z2
Домножим полученный результат на z-1, тогда:
A>4>(z)= -0,0305301+1.028762z.
В результате расчетов получили, что q>0>, q>1>, q>2> по модулю меньше еденицы, таким образом все три неравенства выполняются. Следовательно цифровая система устойчива.
После того, как определили устойчивость системы по критерию Джури, необходимо построить переходный процессы в замкнутых цифровых системах.
Для построения переходных процессов в замкнутых цифровых системах воспользуемся обратным z-преобразованием.
Eсли функция имеет m-полюсов z>k>={z>1>, z>2>,…, z>n>} , то:
 ,
(4.13)
,
(4.13)
где A(z>k>) – числитель функции W>3>(z);
B’(z>k>) – производная знаменателя функции W>3>(z);
Замкнутая система с П – регулятором.
Передаточная функция для цифровой замкнутой системы с П-регулятором имеет вид:

Переходная функция замкнутой системы равна:
 .
.
Для вычисления f[n] найдем полюса функции
 .
.
Полюся функции:
z>1> = 1;
z>2> = 0,8422;
z>3> = 0,954 – j0,313;
z>4>= 0,954 – j0,313.
Производная знаменателя функции:
B’(z) = -11.25z2+10.574z-3.317+4z3.
Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для :
где a = z>1>;
b = z>2>;
c = z>3>;
d = z>4>;

Изобразим переходый процесс на рисунке 4.2

Рисунок 4.2 - Переходный процесс в системе с П – регулятором
Замкнутая система с ПИ – регулятором.
Передаточная функция для цифровой замкнутой системы с ПИ-регулятором имеет вид:
 ;.
;.
Переходная функция замкнутой системы равна:
 .
.
Для вычисления f[n] найдем полюса функции
 .
.
Полюся функции:
z>1> = 1;
z>2> = 0.847;
z>3> = 0.965;
z>4> = 0.973 – j0.0113;
z>5>= 0.973 + j0.0113.
Производная знаменателя функции:
B’(z) = 5z4-19.027z3+27.171 z2-17.253z+4.110
Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для f[n]:
где а = z>1>;
b = z>2>;
c = z>3>;
d = z>4>;
e = z>5>;

Изобразим переходый процесс на рисунке 4.3

Рисунок 4.3 - Переходный процесс в системе с ПИ – регулятором
Замкнутая система с ПИД – регулятором.
Передаточная функция для цифровой замкнутой системы с ПИД-регулятором имеет вид:
 .
.
Переходная функция замкнутой системы равна:
 .
.
Для вычисления f[n] найдем полюса функции
 .
.
Полюся функции:
z>1> = 1;
z>2> = -0,021;
z>3> = 0,84;
z>4> = 0,935-j0,171;
z>5>= 0,935+j0,171;
z>6>=0,98.
Производная знаменателя функции:
B’(z) = 6z5-23.347 z4+34.893 z3-24.39 z2+7.505z-0.660
Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для f[n]:

где а = z>1>;
b = z>2>;
c = z>3>;
d = z>4>;
e = z>5>;
f = z>6>.
Изобразим переходый процесс на рисунке 4.4

Рисунок 4.4 - Переходный процесс в системе с ПИД – регулятором.
5 Расчет цифрового фильтра
Для расчета цифрового фильтра, переводящего линейную часть из начального в конечное состояние за минимальное число периодов квантования и обеспечивающего ограничение на заданное управляющие воздействие, необходимо вычислить минимально возможный период квантования, но чтобы было удовлетворено условие:
|U>m> – q>0>|0,05, (5.1)
где U>m> = 1,0.
Вычисление значения q>0> следует начать с определения значений коэффициентов числителя Z-передаточной функции приведенной непрерывной части для принятого периода дискретности. Пусть Z-передаточная функция приведенной непрерывной части представима в виде:
 . (5.2)
. (5.2)
Тогда Z-передаточная функция оптимального по быстродействию цифрового фильтра W>ф>(z) имеет вид:
 , (5.3)
, (5.3)
где p>i> = b>i>q>0>, i = 1,2,…,m;
q>i> = a>i>q>0>, i = 1,2,…,m;
 .
.
Воспользуясь формулой (4.7) для W>нч>(z) . Находим функции b>i> , а>i> и Т>0>.
Для коэффициентов b>i> имеем:
 ; (5.4)
; (5.4)
 ;(5.5)
;(5.5)
 . (5.6)
. (5.6)
Для коэффициентов а>i> имеем:
 ; (5.7)
; (5.7)
 ; (5.8)
; (5.8)
 . (5.9)
. (5.9)
Найдем выражение для q>0> :

 . (5.10)
. (5.10)
Определим Т>0> при котором выполняется условие (5.1), для этого построим график зависимости и изибразим его на следующем рисунке 5.1.

Рисунок 5.1 – График зависимости |U>m> – q>0>(Т>0>)|
При построении графика видим, что Т>0> = 4,61 , q>0>(Т>0>) = 1,002.
Определим коэффициенты , подставив найденное значение Т>0> в выражение (5.4) и (5.5):
b>1>(Т>0>) = 0,718;
b>2>(Т>0>) = 0,332;
b>3>(Т>0>) = -0,052;
a>1>(Т>0>) = -0,932;
a>2>(Т>0>) = 0,281;
a>3>(Т>0>) = -0,027;
Подставляя найденные значения в выражения (5.2) и (5.3) определим передаточные функции приведенной непрерывной части и цифрового фильтра.
 .
(5.7)
.
(5.7)
 .
(5.8)
.
(5.8)
Находим Z – передаточную функцию для разомкнутой цифровой системы по формуле:
W>p>(z) = W>н.ч.>(z) * W>ф>(z). (5.9)
Определим Z – преобразованную функцию замкнутой системы по каналу задание – управляюшее воздействие по формуле:
 ,
(5.10)
,
(5.10)
Определим Z – преобразованную функцию замкнутой системы по каналу задание – выходной сигнал по формуле:
 ,
(5.10)
,
(5.10)
Пусть
f – функция
определяющая зависимость между q>0>
от Т>0>,
т.е. q>0>=f(Т>0>),
тогда f –1
– обратная ей функция,
т.е. Т>0>=f
–1(q>0>).
Для того, чтобы найти
период квантования необходимо
минимизировать
функцию
Т>0>=f
–1(q>0>)
с учетом условия (5.1).
Так как в явном виде функцию Т>0>=f –1(q>0>) вывести сложно, но из графика видно, что она монотонно убывает, следовательно минимум на отрезке q>0> [3,45; 3,55] будет при q>0>=3,55.
Расчет Т>0> сводится к решению уравнения
 . (5.11)
. (5.11)
Для решения данного уравнения воспользуемся алгоритмом поиска корня уравнения методом дихотомии. После решения уравнения мы получили, что
Т>0> =1,25.
Подставляя значение Т>0> =1,25 в выражения (5.4)-(5.9) найдем коэффициенты Z-передаточной функций приведенной непрерывной части.
Тогда
 .
(5.12)
.
(5.12)
При этом q>0> =3,540075. Согласно формуле (5.3)
 .
(5.13)
.
(5.13)
Найдем Z-передаточную функцию разомкнутой цифровой системы. Она равна W>р>(z)=W>нч>(z)W>ф>(z) и равна
 .
(5.14)
.
(5.14)
Z-передаточная функция замкнутой цифровой системы по каналу задание – управляющие воздействие равна
 (5.15)
(5.15)
и равна
 .
.
Z-передаточная функция замкнутой цифровой системы по каналу задание – выходная величина равна
 (5.16)
(5.16)
и равна
 .
.
Вычислим коэффициенты усиления по указанным каналам. По определению коэффициент усиления есть отношение изменения на выходе к изменению на входе в установившемся режиме, т.е.
 .
(5.17)
.
(5.17)
Так как
 ,
(5.18)
,
(5.18)
то подставляя выражения (5.15) и (5.16) в выражение (5.17) найдем, что ()=1, а ()=0,4. Так как x()=1, а (0>->)=0 и (0>->)=0, то коэффициент усиления по каналу задание – выходная величина равен 1, а по каналу задание – управляющие воздействие равен 0,4.
Построим переходную функцию цифрового фильтра. Она равна
 .
.
Для вычисления f[n] найдем полюса функции
 .
.
Находим
2 полюса 1-го порядка и 1 полюс 2-го порядка.
Полюса
1-го порядка: z=-0,307 и z=-0,045. Полюс
2-го z=1. Для вычисления переходной функции
необходимо вычислить производную
следующей функции
 .
Производная данного выражения равна
.
Производная данного выражения равна
 .
.
Тогда передаточная функция примет вид
 .
.
Изобразим переходный процесс на графике.

Рисунок 5.2 – Переходная функция цифрового фильтра.
Для построения переходных процессов в замкнутой цифровой системе по каналам задание – выходная величина и задание – управляющие воздействие воспользуемся уравнениями в конечных разностях.
Суть метода заключается в следующем. Пусть передаточная функция цифровой системы
 .
.
Этой передаточной функции соответствует уравнение в конечных разностях:
 .
.
Значение искомой выходной величины равно
 . (5.19)
. (5.19)
Согласно формуле (5.19) получим, что переходная функция замкнутой цифровой системе по:
каналу задание – выходная величина
y[k]=0,647726x[k-1] –0,620803x[k-2] –0,037272x[k-3] +0,149369x[k-4] –0,024633x[k-2] –0,001394x[k-2] +1,481007y[k-1] –0,695097y[k-2]+ +0,101098y[k-3];
каналу задание – управляющие воздействие
y[k]=3,540075x[k]
–10,485749x[k-1]
+12,686121x[k-2]
–
–8,004397x[k-3]
+2,770507x[k-4]
–0,497542x[k-5]+0,036182x[k-6]+
+1,481007y[k-1]
–0,695097y[k-2]+
+0,101098y[k-3].
Данные расчетов были сведены в таблицы с учетом того, что x[k]=1.
Таблица 5.1 – Переходная функция замкнутой цифровой системе по каналу задание – выходная величина
-
k
y[k]
0
0
1
0,648
2
0,986
3
1
4
1
6 Оптимальное управляющие воздействие и реакция на него приведенной непрерывной части
Оптимальное управляющие воздействие было найдено в пункте 5 и в координатах времени имеет следующий вид:
(t)=3,54(h(t)-h(t-T>0>)) –1,703(h(t-T>0>)-h(t-2T>0>))+ (6.1)
+0,758(h(t-2T>0>)-h(t-3T>0>))+0,4 h(t-3T>0>),
где
h(t) – функция Хевисайда;
T>0> – период квантования равный 1,25.
Тогда
(t)=3,54(h(t)-h(t-1,25)) –1,703(h(t-1,25)-h(t-2,5))+ (6.2)
+0,758(h(t-2,5)-h(t-3,75))+0,4 h(t-3,75).
И

Рисунок 6.1 – Оптимальное управляющие воздействие.
Для нахождения реакции непрерывной линейной части на данное воздействие воспользуемся изображением Лапласа. Используя свойство линейность данного изображения и теорему запаздывания найдем, что
(t)= 3,54(g(t) - g(t-1,25)) –1,703(g(t-1,25)-g(t-2,5))+ (6.3)
+0,758(g(t-2,5)-h(t-3,75))+0,4 h(t-3,75),
где
g(t)=f(t)h(t),
 –
переходная функция линейной части,
найденная нами в пункте 4.
–
переходная функция линейной части,
найденная нами в пункте 4.
Изобразим реакцию непрерывной линейной части на оптимальное управляющие воздействие.

Рисунок 6.2 – Реакция непрерывной линейной части на оптимальное управляющие воздействие
На этом все построения окончены.
Заключение
В данной курсовой работе был сделан синтез и анализ оптимальной одноконтурной САУ при использовании трех типов регуляторов, реализующих П-, ПИ- и ПИД-закон регулирования. Проведены сравнительный характеристики данных типов регуляторов и был сделан вывод, что ПИД-закон регулирования является наилучшим среди рассмотренных.
Были проведены расчеты по использованию данных регуляторов в цифровых системах. Как показали расчеты, несмотря на то, что цифровые системы – это системы дискретного действия и действуют через определенные промежутки времени, переходные процессы в цифровых системах не сильно отличаются от переходных процессов в непрерывных системах, а конечное состояние выходной величины одинаково. Кроме того развитие микропроцессорной техники и использование теории управления в цифровых системах позволяют создать регуляторы различной сложности и с заранее заданных свойствами. Один из регуляторов, обеспечивающий перевод системы из одного состояния в другое за минимальное число периодов квантования при наличии ограничения на управляющие воздействие, был синтезирован в данной курсовой работе.
Список литературы
Пугачев В.И. Методические указания по курсу: «Теория автоматического управления» для студентов всех форм обучения специальности 21.01 – автоматика и управление в технических системах. Часть I. Краснодарский политехнический институт – Краснодар, 1990. – 157 с.
Пугачев В.И. Методические указания по курсу: «Теория автоматического управления» для студентов всех форм обучения специальности 21.01 – автоматика и управление в технических системах. Часть III. Краснодарский политехнический институт – Краснодар, 1995. – 114 с.
Колосов С. П., Калмыков И. В.,Нефедова В. И. “Элементы автоматики”
издательство “Машиностроение”, Москва, 1970.


 )
)

