Построение информационно-управляющей системы с элементами искусственного интеллекта
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
СУМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра автоматики и промышленной электроники
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовому проекту на тему: “ Построение информационно-управляющей системы с элементами искусственного интеллекта.”
По дисциплине: “Элементы систем автоматического контроля и управления.”
Проектировал:студент группы ПЭЗ-51 Симоненко А.В.
Проверил: Володченко Г.С.
Сумы 2000 г.
СОДЕРЖАНИЕ.
ВВЕДЕНИЕ.
1.СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ КВАЗИСТАЦИОНАРНЫМ ОБЪЕКТОМ.
Построение информационной управляющей системы с элементами самонастройки.
1.2 Построение логарифмических АЧХ и ФЧХ и нескорректированной системы
1.3. Построение желаемых ЛАЧХ и ФЧХ скорректированной квазистационарной системы.
1.4. Построение ЛАЧХ корректирующего звена системы.
2.СИНТЕЗ ИНФОРМАЦИОННО-ПАРАМЕТРИЧЕСКОЙ СИСТЕМЫ ИДЕНТИФИКАЦИИ НЕСТАЦИОНАРНОГО ОБЪЕКТА УПРАВЛЕНИЯ.
2.1. Выбор метода синтеза системы.
2.2. Поиск минимизированного функционала качества.
3.ПОСТРОЕНИЕ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ДИНАМИЧЕСКИМ ОБЪЕКТОМ.
3.1. Синтез адаптивной системы управления нестационарным объектом с элементами искусственного интеллекта.
ЗАКЛЮЧЕНИЕ.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.
ВВЕДЕНИЕ.
При современном уровне развития науки и техники все большее распространение получают информационно-управляющие системы с элементами искусственного интеллекта на производстве, в быту, военной технике, а также там , где присутствие человека невозможно.Их особенностью является наличие в самой системе подсистем анализа и контроля состояния как самой системы управления так и состояния объекта управления с целью своевременного принятия решения и реагирования на внешние воздействия и изменения в самой системе.
Системы автоматического контроля и управления должны обеспечить требуемую точность регулирования и устойчивость работы в широком диапазоне изменения параметров.
Если раньше теория автоматического управления носила в основном линейный и детерминированный характер, решаемость теоретических задач определялась простотой решения, которое стремились получить в виде замкнутой конечной формы, то в настоящее время решающее значение приобретает четкая аналитическая формулировка алгоритма решения задачи и реализация его с помощью ЭВМ.
1.СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ КВАЗИСТАЦИОНАРНЫМ ОБЪЕКТОМ
1.1Построение информационной управляющей системы с элементами самонастройки.
Для нестационарного динамического объекта управления, поведение которого описывается нестационарными дифференциальными уравнениями вида (1.1):



 введем
условие квазистационарности на интервале
введем
условие квазистационарности на интервале
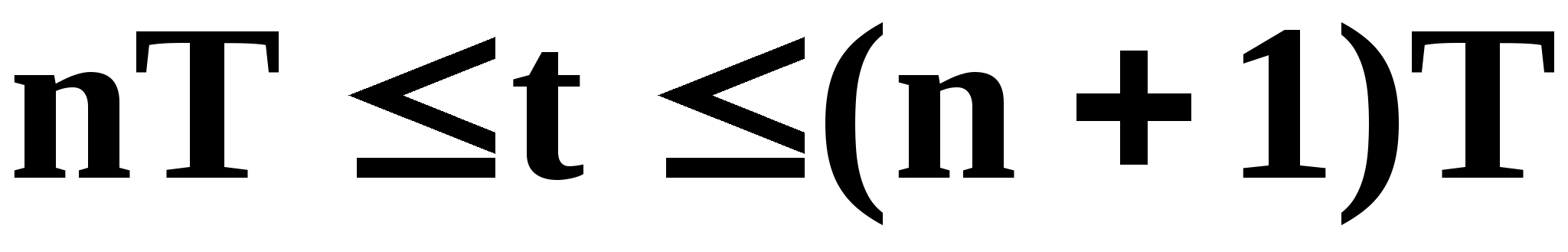 (1.2)
(1.2)
 (1.3)
(1.3)
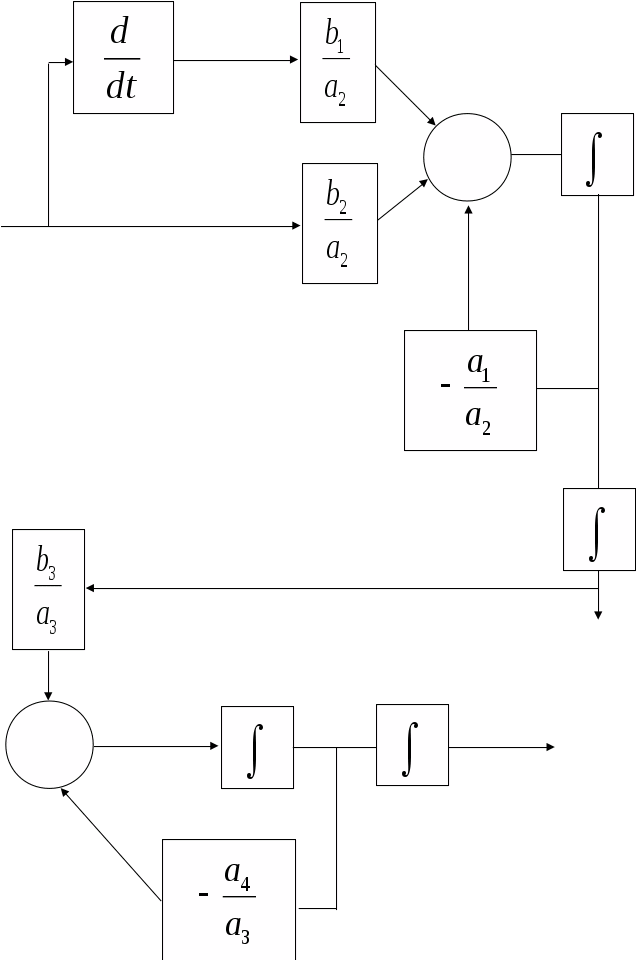
Для решения задачи представим объект управления в пространстве состояний, разрешив систему (1.1) относительно старшей производной:


 (1.4)
(1.4)
Полученная система уравнений описывает структуру объекта управления в пространстве состояний. Соответствующая структурная схема представлена на рисунке 1.
Y1’’(t)
Y1’(t)
U(t)
U(t)
U’(t)
Y1(t)
Y2’’(t)
Y2’(t)
Y2(t)
Рис.1


Представим схему переменных состояний в форме Коши. Для этого введем переобозначение через z.
Пусть (1.5) :
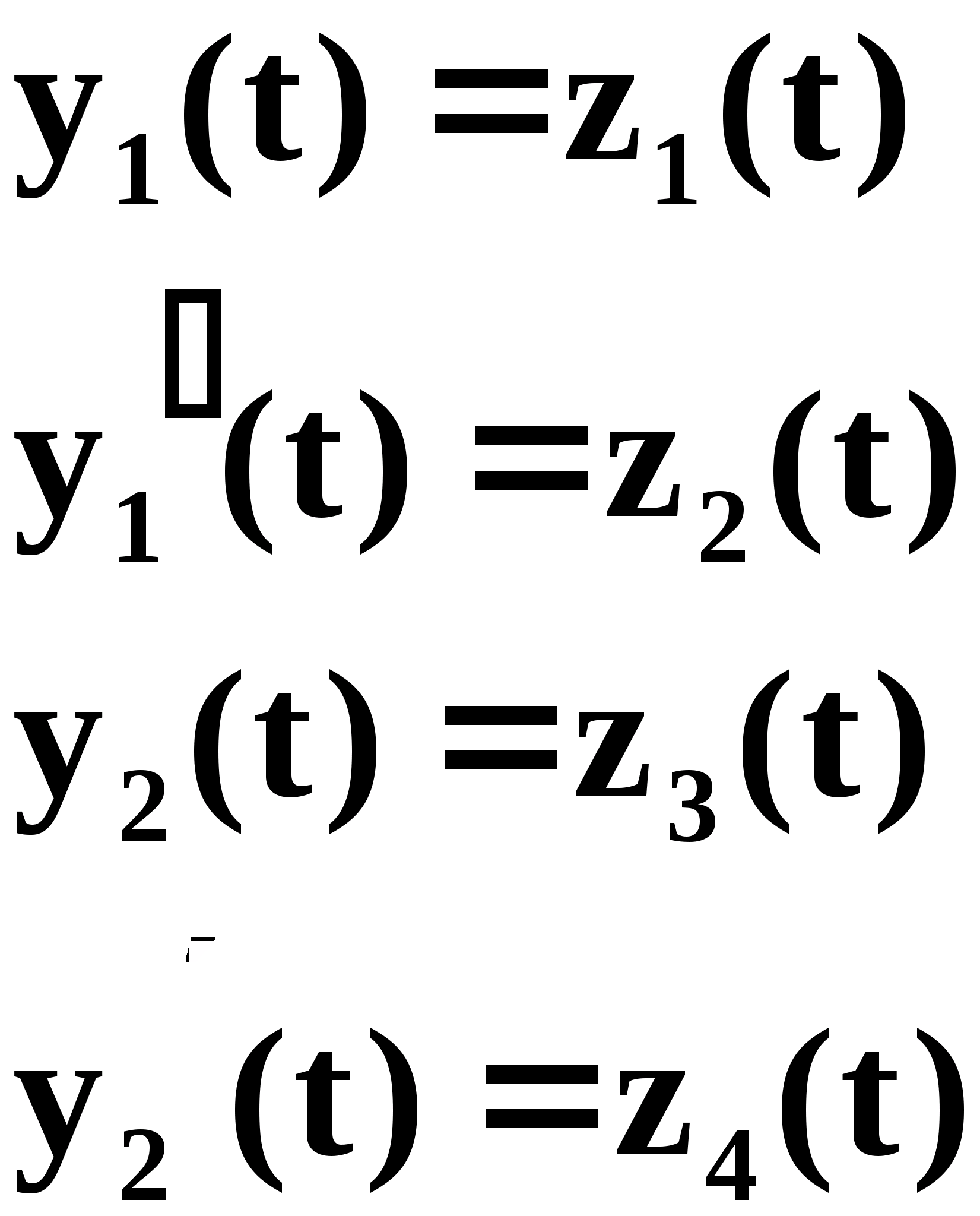

Система (1.5)-математическая модель объекта управления в форме Коши. Представим (1.5) в векторной форме:

 (1.6)
(1.6)
где
 вектор
состояний (1.7)
вектор
состояний (1.7)
 производная
вектора состояний (1.8)
производная
вектора состояний (1.8)
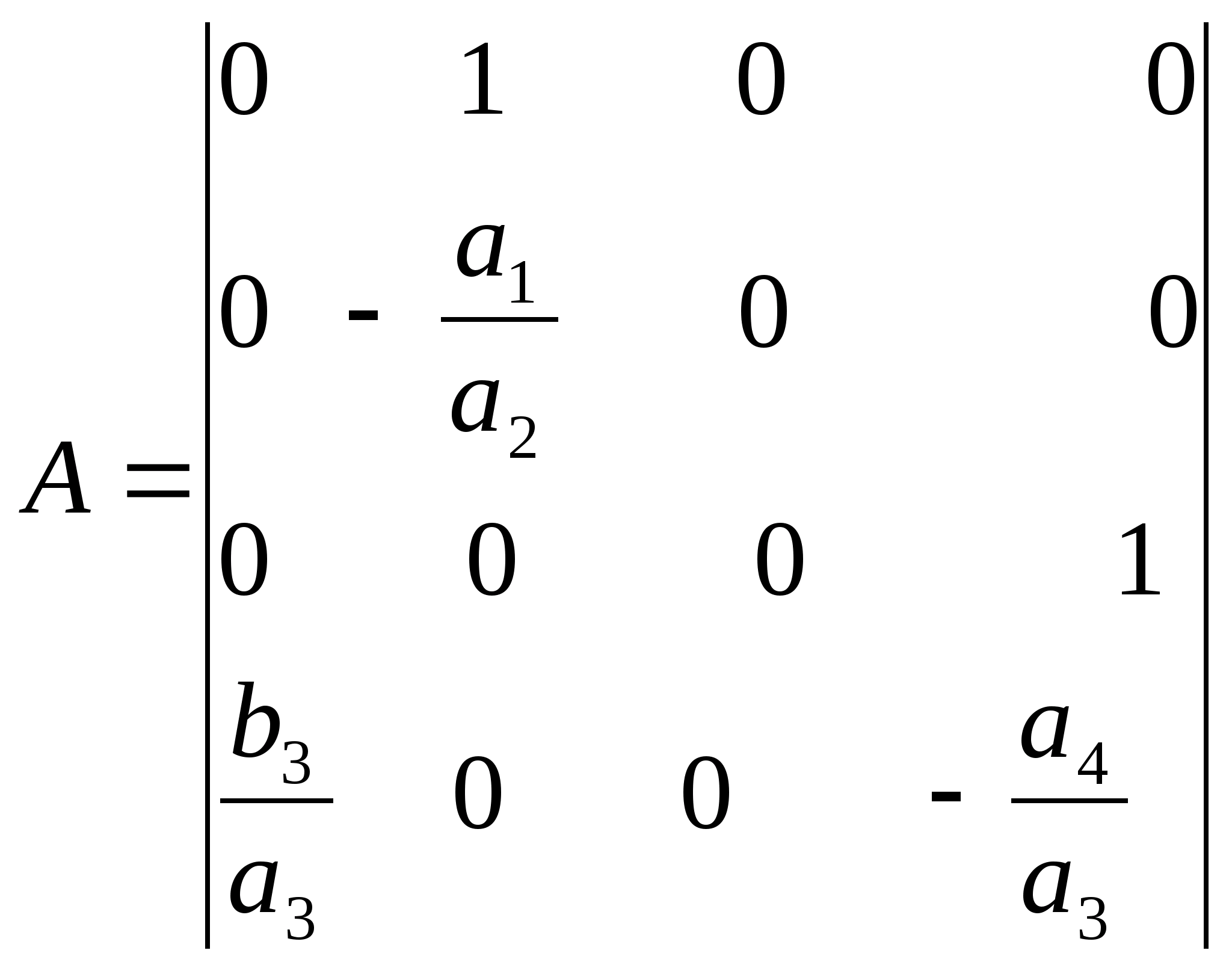 динамическая
матрица о/у (1.9)
динамическая
матрица о/у (1.9)
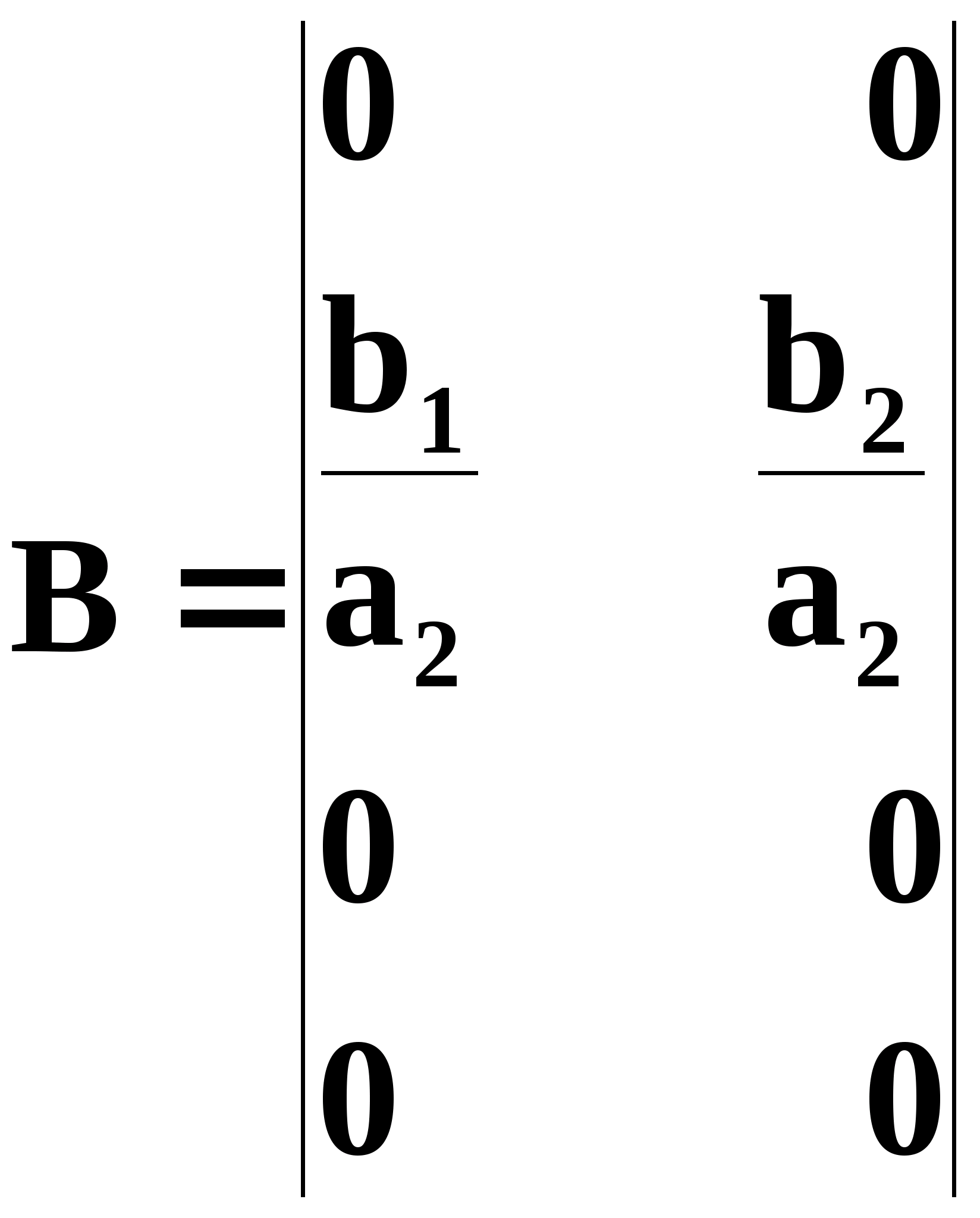 матрица
управления о/у (1.10)
матрица
управления о/у (1.10)
 вектор
управляющих воздействий (1.11)
вектор
управляющих воздействий (1.11)
 матрица
измерений (1.12)
матрица
измерений (1.12)
Определяем переходную матрицу состояний в виде:

Находим передаточные функции звеньев системы управления, для чего представляем систему дифференциальных уравнений (1.1) в операторной форме:
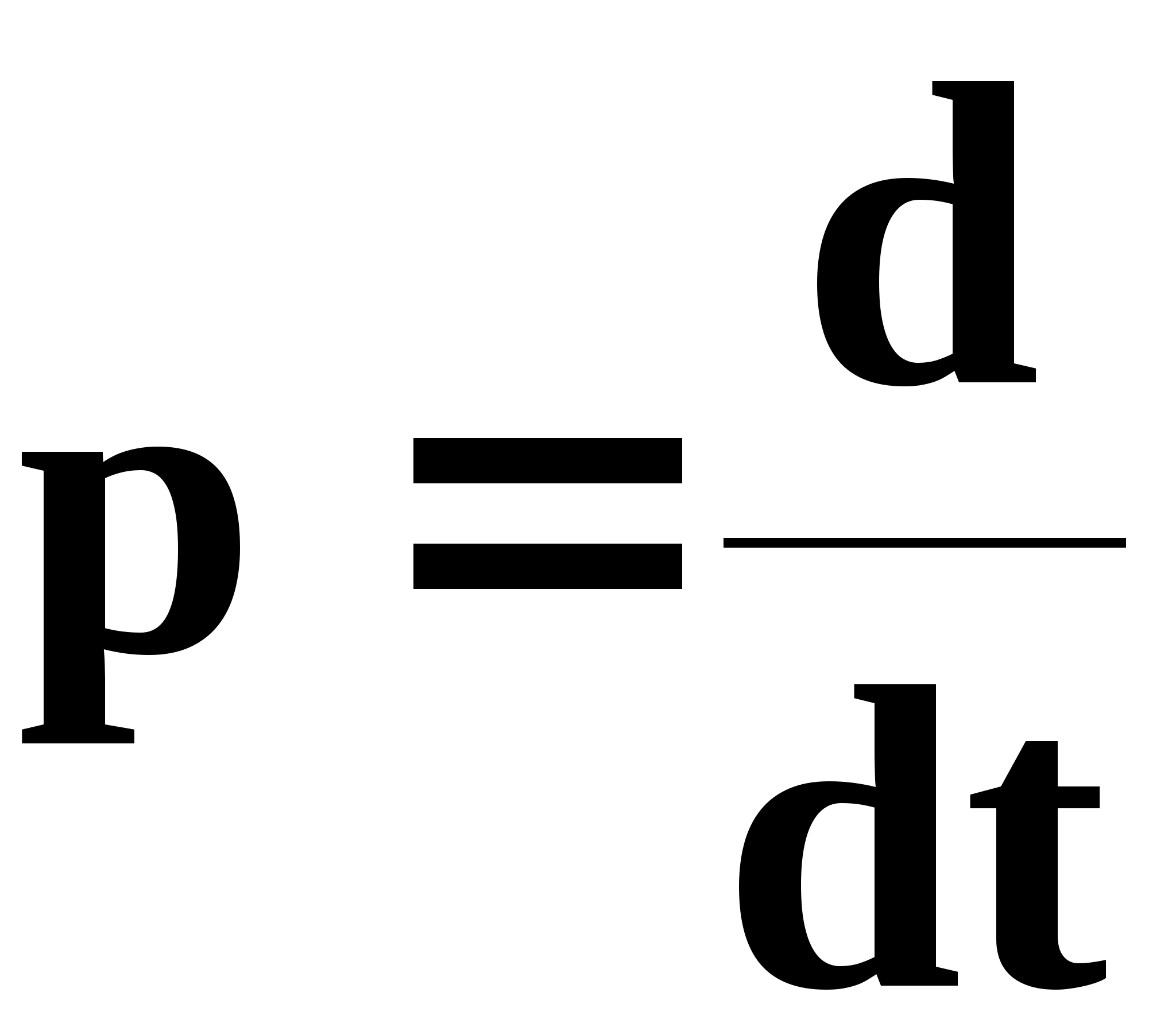 (1.13)
(1.13)


(1.14)
Вынесем общий множитель за скобки
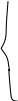
 (1.15)
(1.15)
Передаточная функция первого звена

где

тогда
 (1.16)
(1.16)
Подставляем численные значения> > (см.т/з):
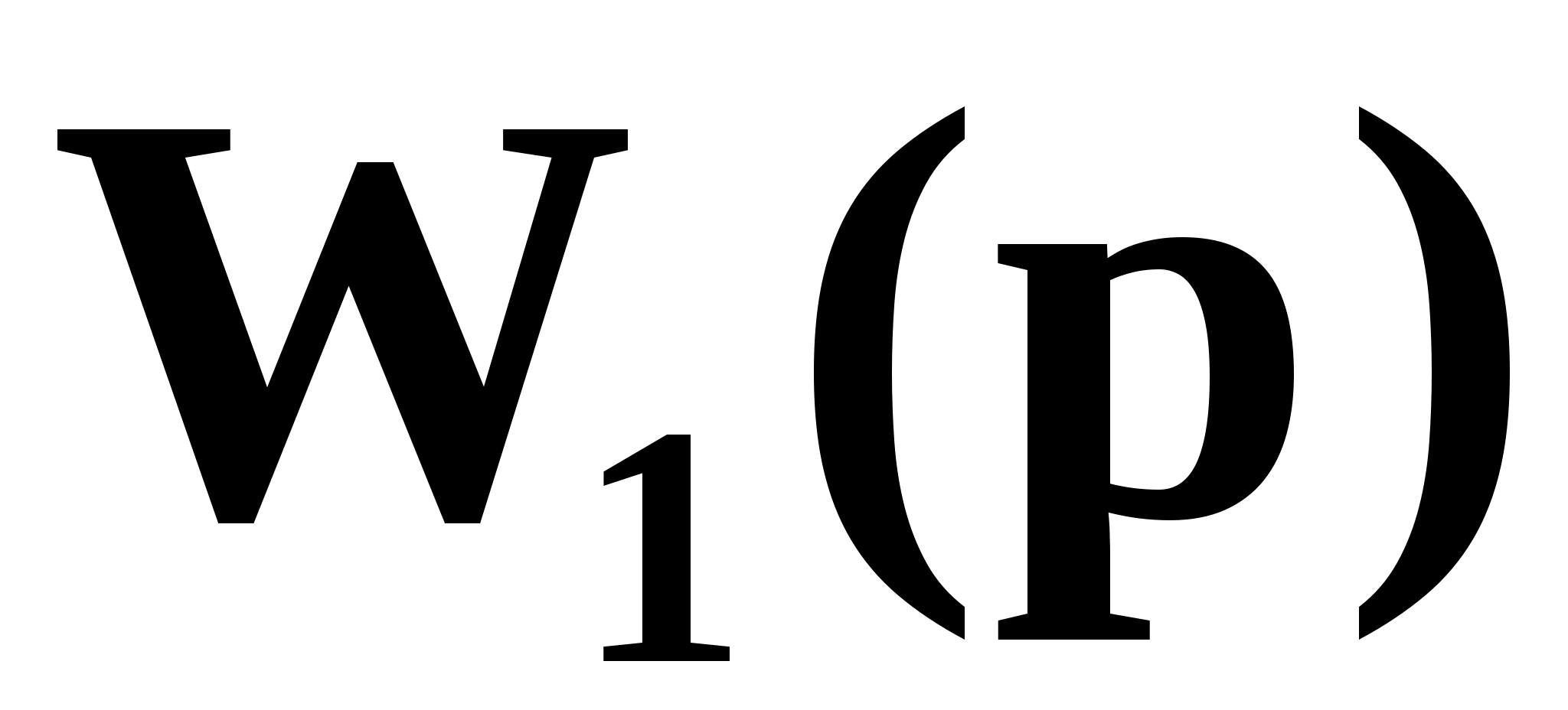

Передаточная функция второго звена:

где

тогда
 (1.17)
(1.17)
Подставляем численные значения:
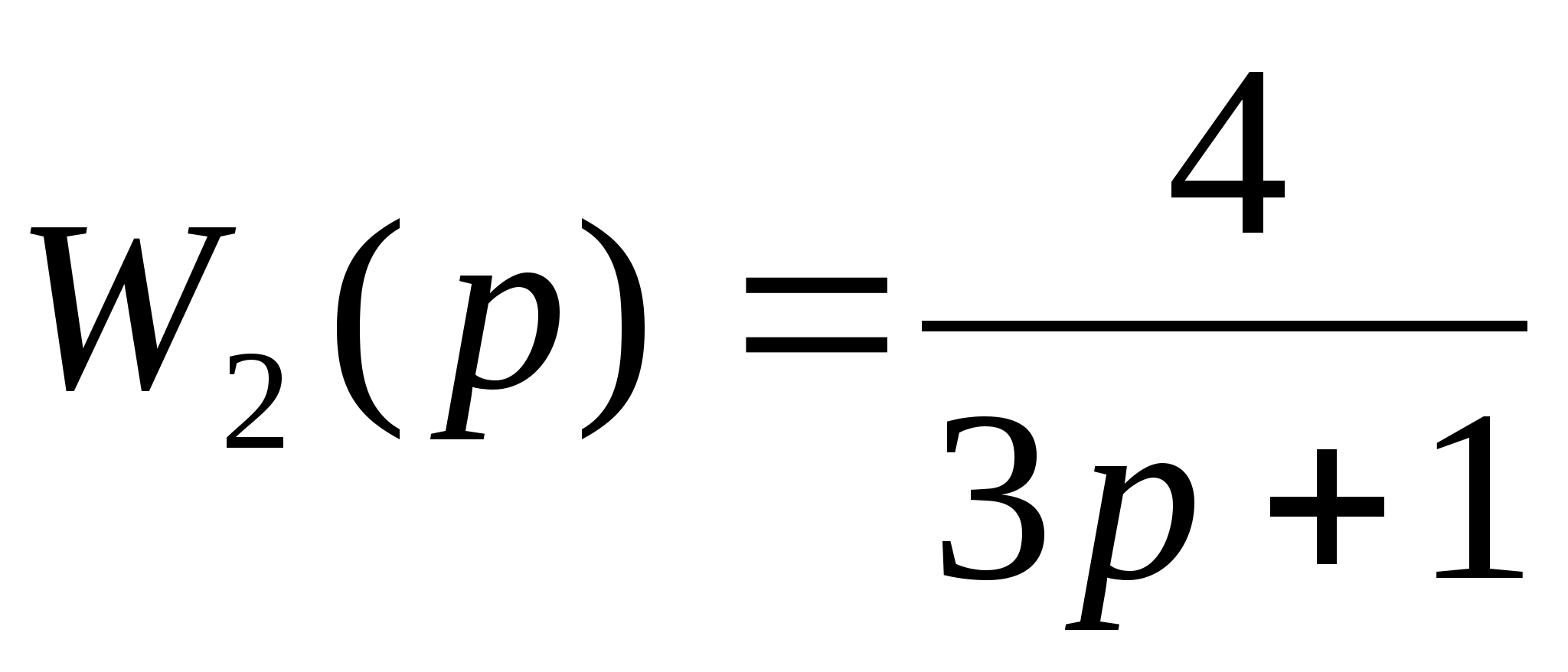
Используя заданный коэффициент ошибки по скорости, находим требуемый коэффициент усиления на низких частотах:
 (1.18)
(1.18)

Для
обеспечения требуемого коэффициента
усиления вводим пропорциональное звено
с коэффициентом усиления
 ,
равным
,
равным

Передаточная функция системы численно равна:
 (1.19)
(1.19)

Построение логарифмических АЧХ и ФЧХ нескорректированной системы.
Заменив
в выражении (1.19)
 , получим комплексную амплитудно-фазочастотную
функцию разомкнутой системы:
, получим комплексную амплитудно-фазочастотную
функцию разомкнутой системы:
 (1.20)
(1.20)
Представим (1.20) в экспоненциальной форме:
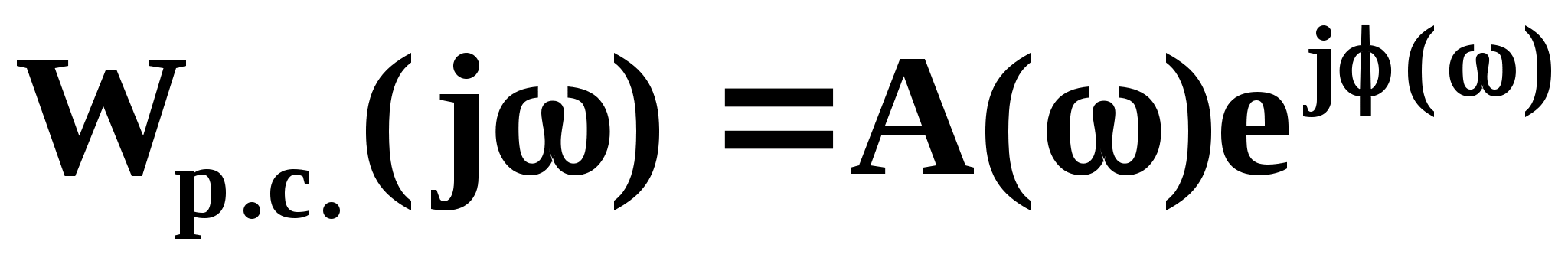 (1.21)
(1.21)
Здесь
 (1.22)
(1.22)
 (1.23)
(1.23)
Логарифмируем выражение (1.22):
 (1.24)
(1.24)
Слагаемые
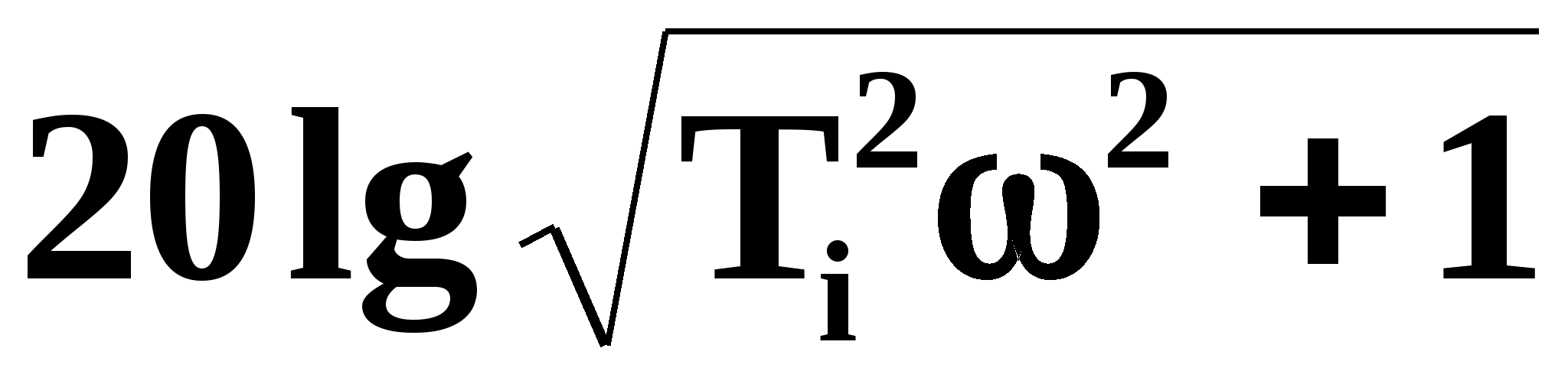 на частотах
на частотах
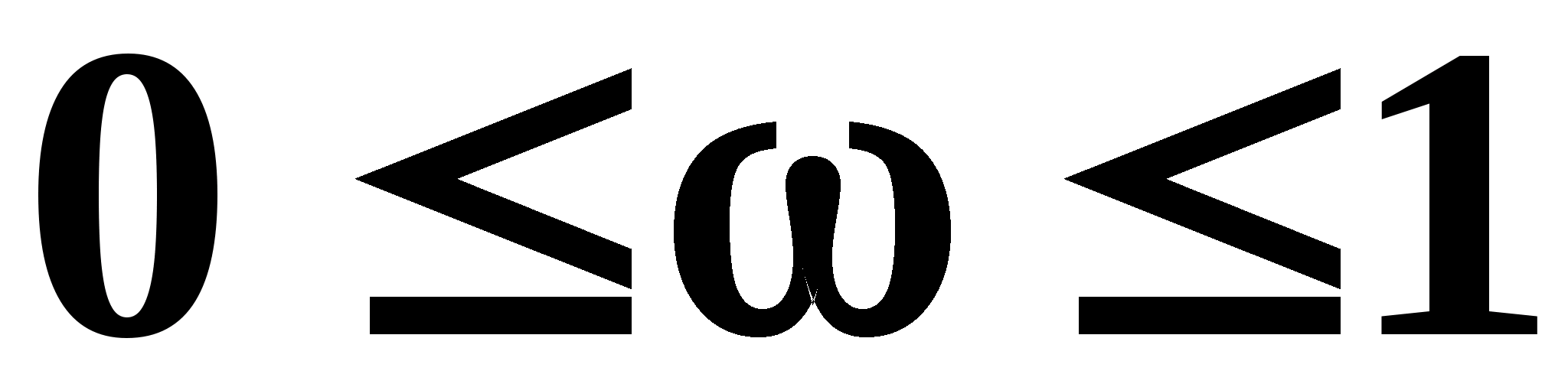 равны нулю,
а на частотах
равны нулю,
а на частотах
 принимают
значения
принимают
значения
 .
.
Соответственно, тогда логарифмическая амплитудно-частотная характеристика определяется выражением:
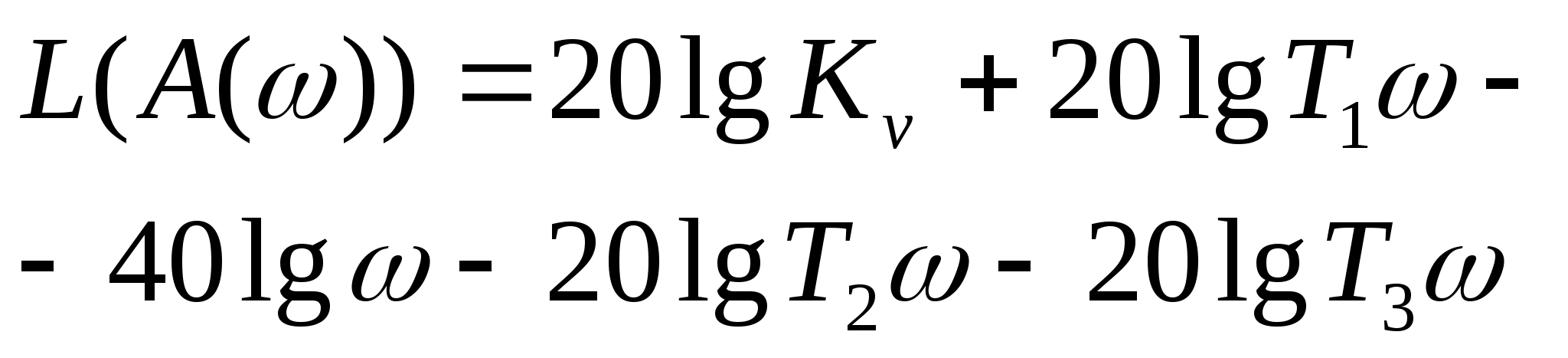 (1.25)
(1.25)
Определим частоты сопряжения:
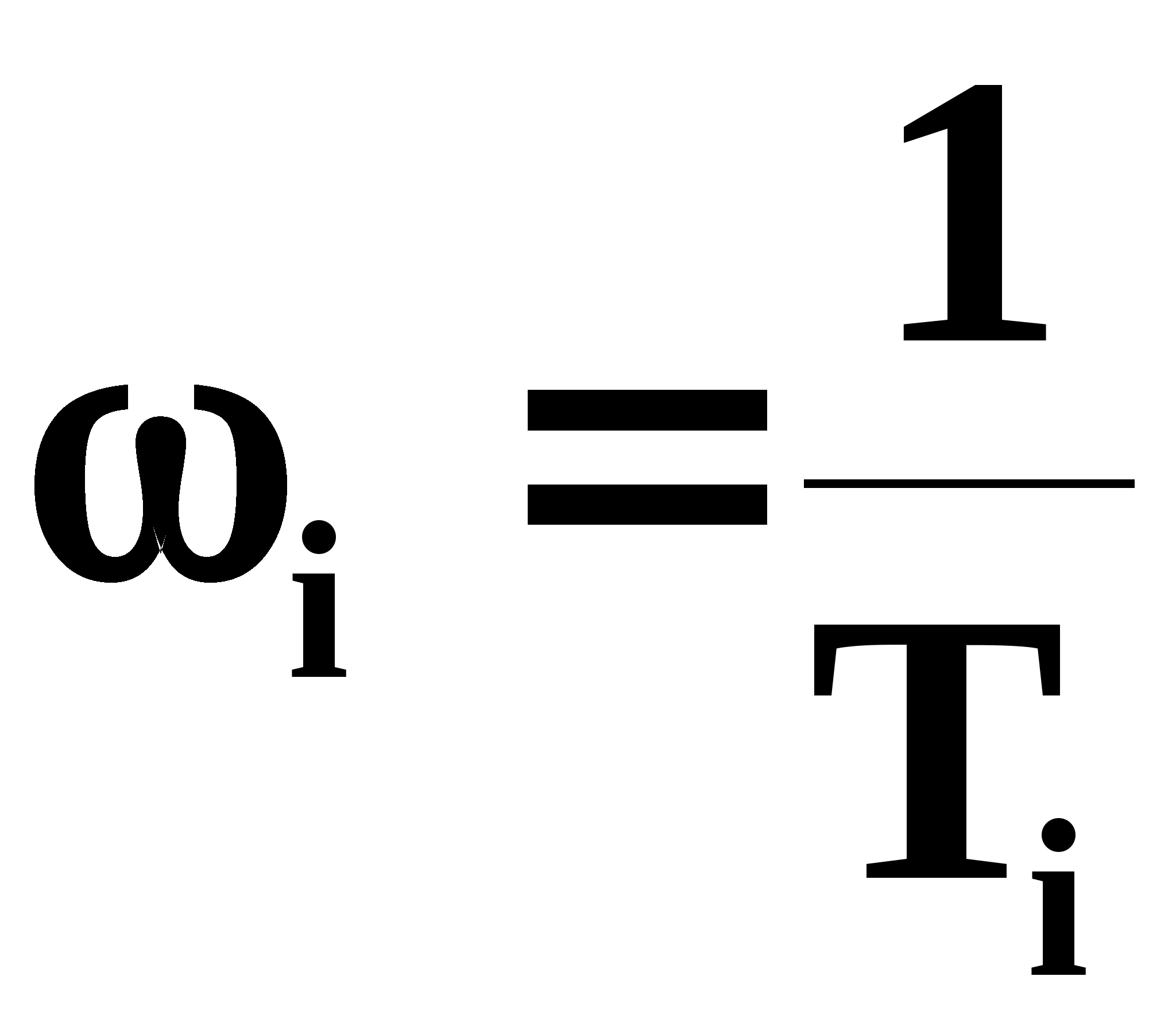 (1.26)
(1.26)


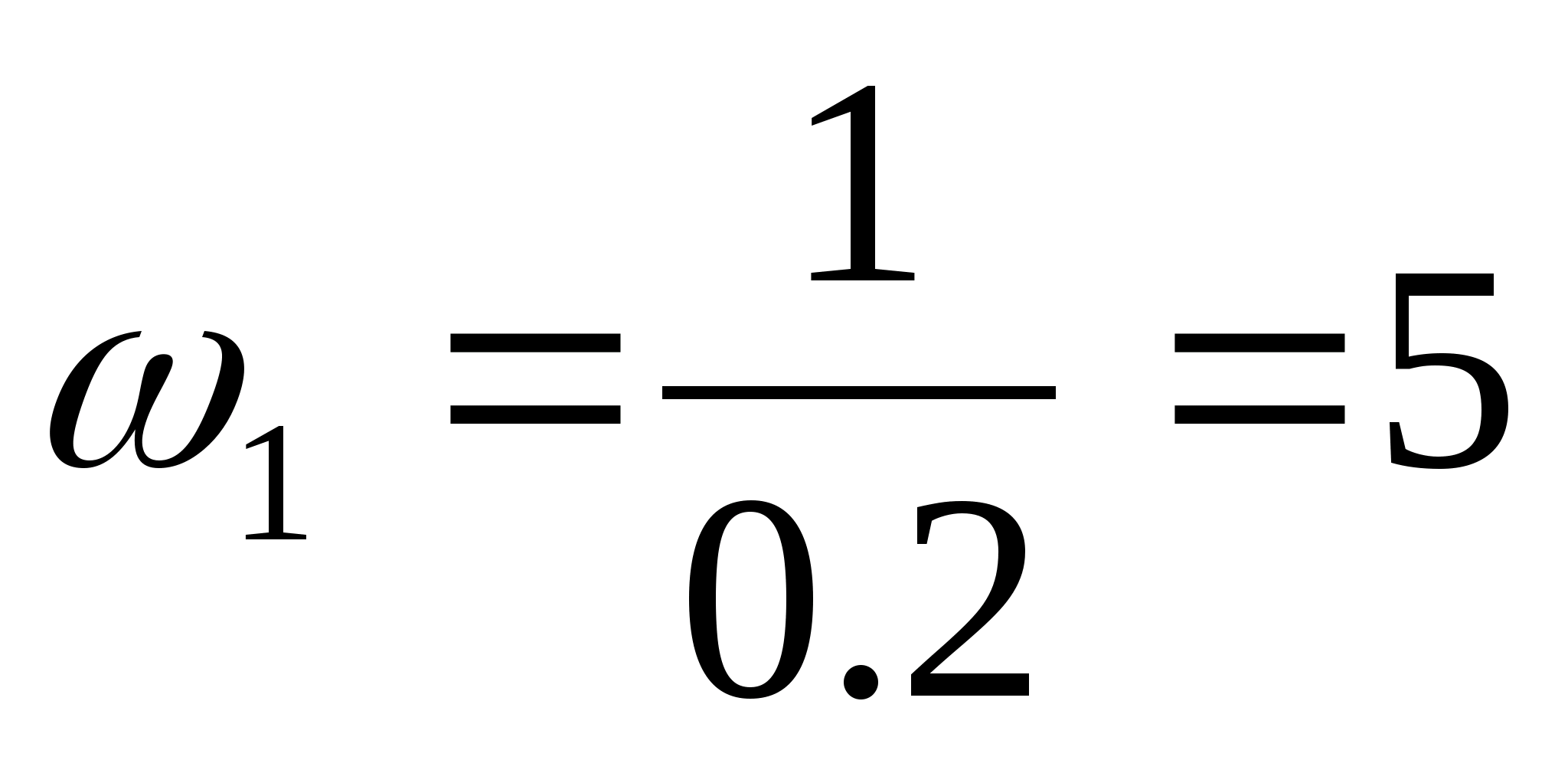
Для построения логарифмических частотных характеристик выбираем следующие масштабы:
-одна декада по оси абсцисс-10 см;
-10 дб по оси ординат-2 см;
-90° по оси ординат-4.5 см.
В этих масштабах откладываем:
-по оси частот-сопрягающие частоты;
-по
оси ординат-значение


Через
точку
 проводим прямую с наклоном -40 дб/дек, до
частоты сопряжения
проводим прямую с наклоном -40 дб/дек, до
частоты сопряжения
на
частоте
 сопрягается следующая прямая с наклоном
-20 дб/дек по отношению к предыдущей
прямой .Эта прямая проводится до частоты
сопряжения
сопрягается следующая прямая с наклоном
-20 дб/дек по отношению к предыдущей
прямой .Эта прямая проводится до частоты
сопряжения

на
частоте
 сопрягается третья прямая с наклоном
-20 дб/дек по отношению ко второй прямой.
сопрягается третья прямая с наклоном
-20 дб/дек по отношению ко второй прямой.
Третья прямая проводится до частоты сопряжения

Полученная таким образом ломаная кривая представляет собой ЛАЧХ разомкнутой нескорректированной квазистационарной системы, первая прямая проходит с наклоном к оси частот-40 дб/дек;вторая-20 дб/дек;третья0 дб/дек;
четвертая-20 дб/дек.
Фазочастотная характеристика нескорректированной разомкнутой системы строится в тех же координатах согласно выражения (1.24) , где
-первое
слагаемое
 -это прямая, проходящая параллельно
оси частот на расстоянии
-это прямая, проходящая параллельно
оси частот на расстоянии
 ;
;
-второе-четвертое
слагаемые-тангенсоиды с точками перегиба
на частотах сопряжения; в области высоких
частот асимптотически приближаются к
 , а при
, а при

Алгебраическая сумма ординат всех четырех характеристик дает фазочастотную характеристику нескорректированной разомкнутой системы..
Для определения запасов устойчивости не скорректированной системы по амплитуде и по фазе необходимо:
-точку
пересечения суммарной ФЧХ с линией
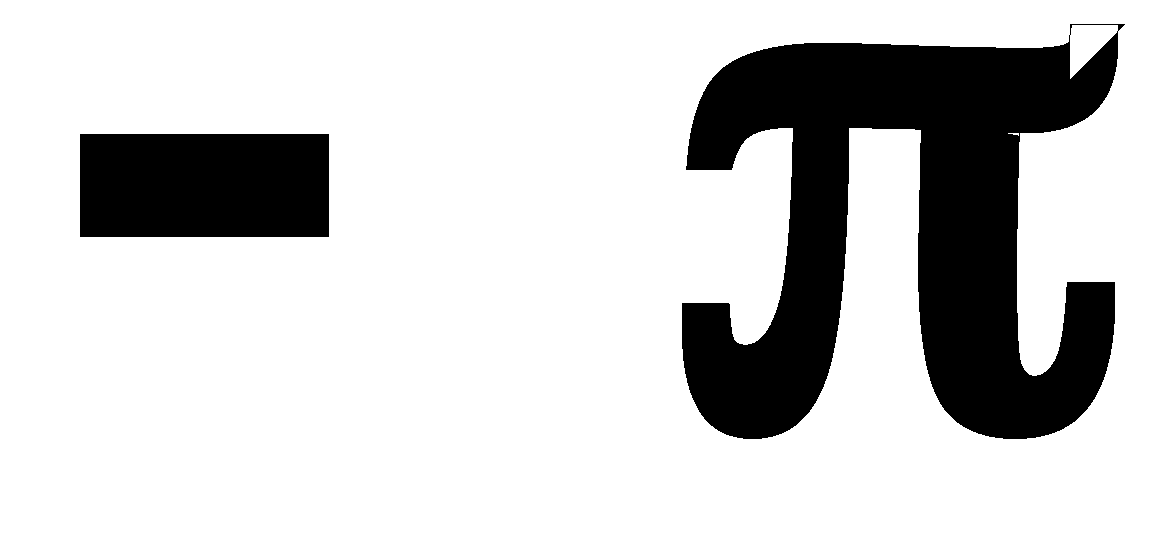 спроектировать на ЛАЧХ, тогда расстояние
проекции этой точки до оси частот будет
величиной запаса устойчивости по
амплитуде в дб. Если же проекция этой
точки окажется выше оси частот, то запаса
устойчивости по амплитуде нет.
спроектировать на ЛАЧХ, тогда расстояние
проекции этой точки до оси частот будет
величиной запаса устойчивости по
амплитуде в дб. Если же проекция этой
точки окажется выше оси частот, то запаса
устойчивости по амплитуде нет.
-проекция
частоты среза на суммарную ФЧХ относительно
линии
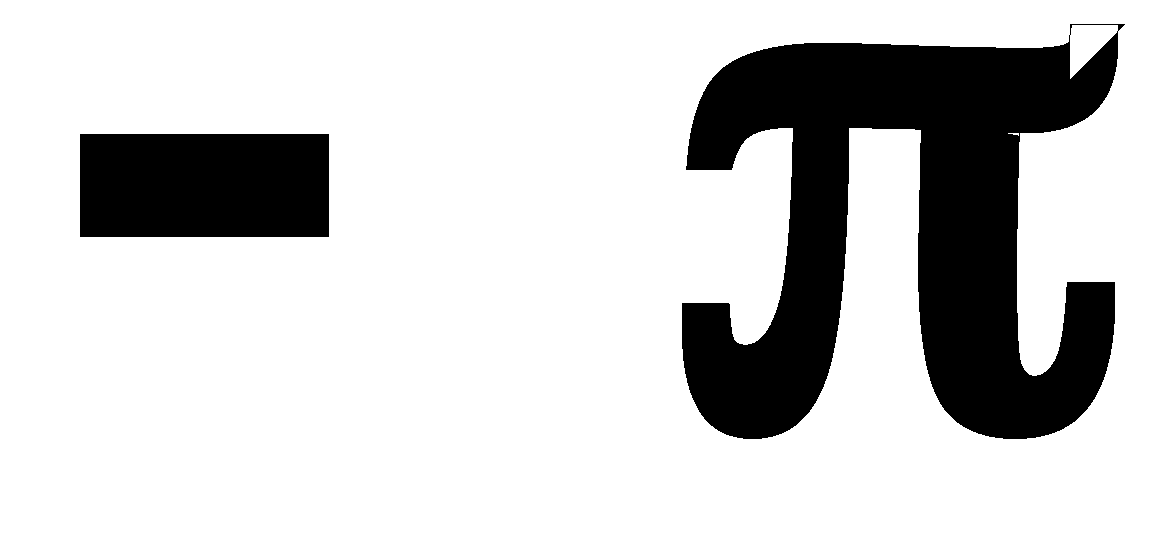 определяет величину запаса устойчивости
по фазе в градусах, если проекция точки
находится выше линии
определяет величину запаса устойчивости
по фазе в градусах, если проекция точки
находится выше линии
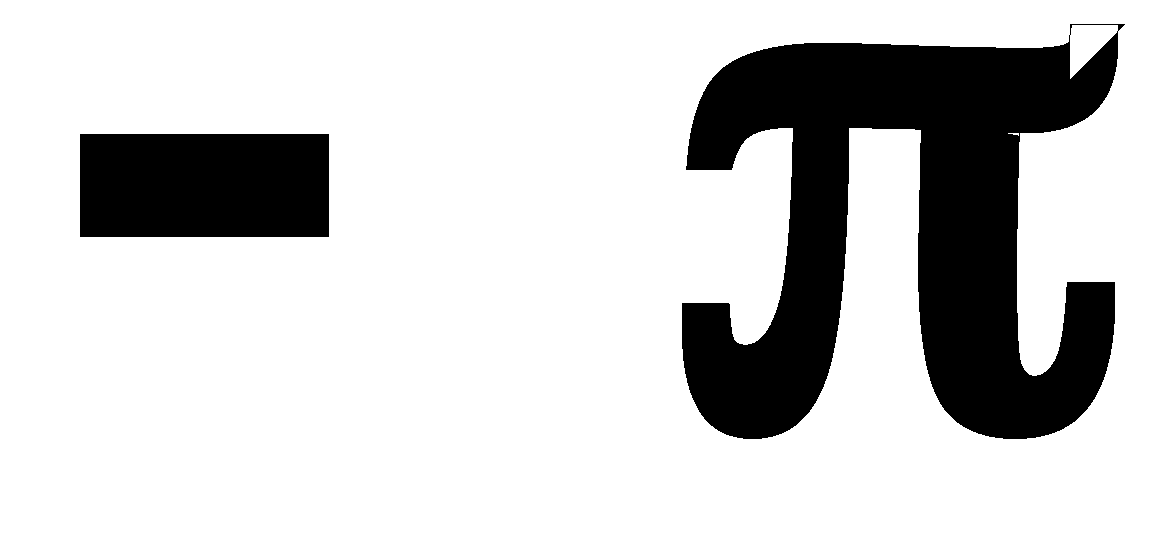 .
.
Произведенные построения показывают, что рассматриваемая система неустойчива как по амплитуде, так и по фазе. С целью достижения заданных показателей качества строим корректирующее звено.
1.3. Построение желаемых ЛАЧХ и ФЧХ скорректированной квазистационарной системы.
1.3.1. Определяется частота среза.
 (1.27)
(1.27)
где
 -время
регулирования квазистационарной
системы, т.е. один из заданных в условии
показателей качества;
-время
регулирования квазистационарной
системы, т.е. один из заданных в условии
показателей качества;
 -коэффициент,
зависящий от величины перерегулирования
-коэффициент,
зависящий от величины перерегулирования
 , определяемый по графику зависимости
[1],
, определяемый по графику зависимости
[1],


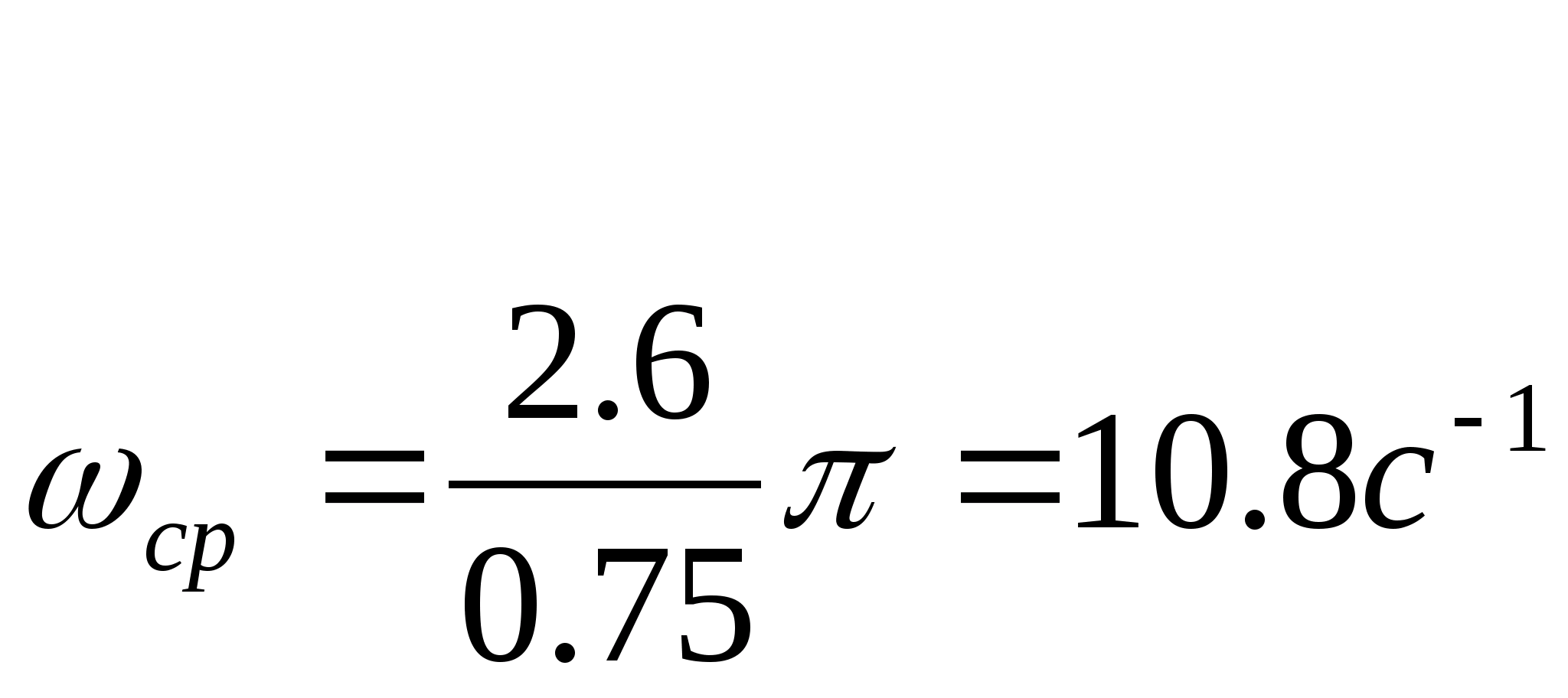
1.3.2.
Через точку
 проводится участок ЛАЧХ на средних
частотах с наклоном –20дб/дек.
проводится участок ЛАЧХ на средних
частотах с наклоном –20дб/дек.
1.3.3.
Определяются сопрягающие частоты

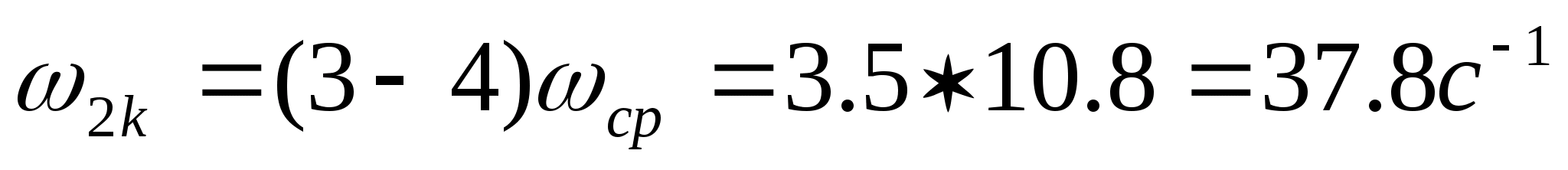 (1.28)
(1.28)
 (1.29)
(1.29)
1.3.4.
По частоте
 графически находится величина амплитуды
в децибелах на низких частотах
графически находится величина амплитуды
в децибелах на низких частотах
 и через точку
и через точку
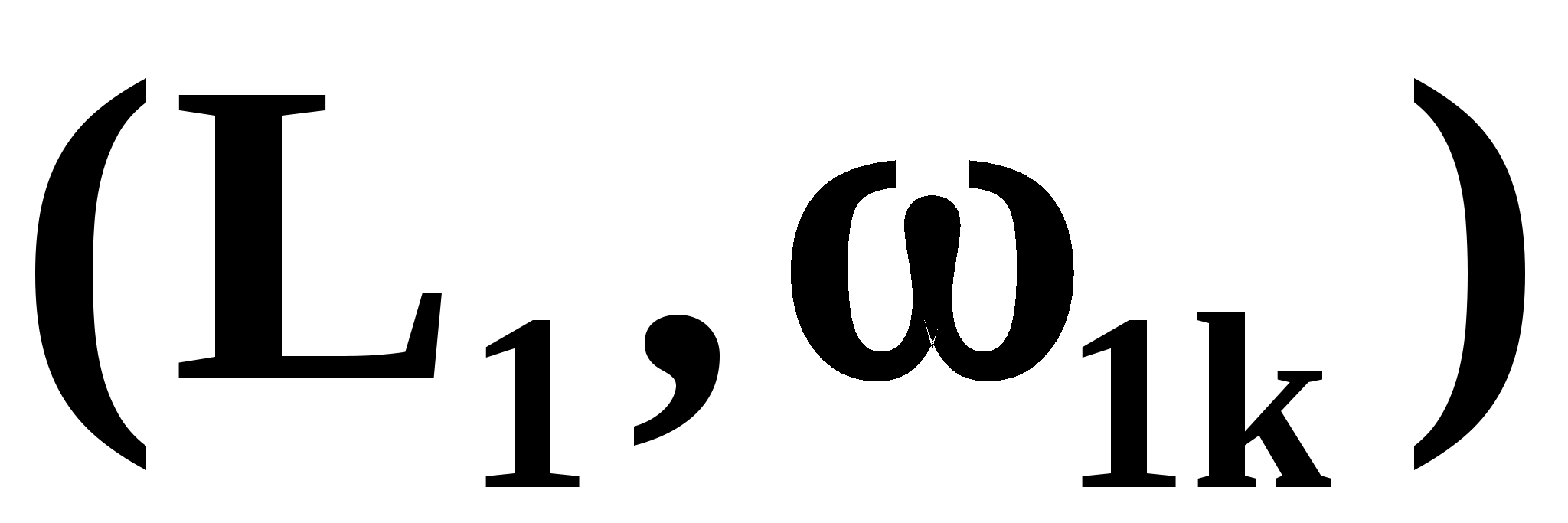 проводится участок ЛАЧХ с наклоном -40
или –60 дб/дек. до ее пересечения на
сопрягающей частоте
проводится участок ЛАЧХ с наклоном -40
или –60 дб/дек. до ее пересечения на
сопрягающей частоте
 с участком ЛАЧХ на низких частотах с
наклоном
с участком ЛАЧХ на низких частотах с
наклоном
 дб/дек.
дб/дек.
1.3.5.
По частоте
 графически определяется величина
амплитуды в децибелах
графически определяется величина
амплитуды в децибелах
 и через точку
и через точку
 проводится
прямая с наклоном –40 или –60 дб/дек,
которая определяет характер желаемой
ЛАЧХ в области высоких частот.
проводится
прямая с наклоном –40 или –60 дб/дек,
которая определяет характер желаемой
ЛАЧХ в области высоких частот.
По виду желаемой ЛАЧХ построена желаемая ФЧХ и определены запасы устойчивости по амплитуде и по фазе.
Произведенные построения показывают, что запасы устойчивости удовлетворяют заданным в техническом задании на проект.
1.4. Построение ЛАЧХ корректирующего звена системы.
Учитывая то, что передаточная функция разомкнутой скорректированной системы определяется выражением

или
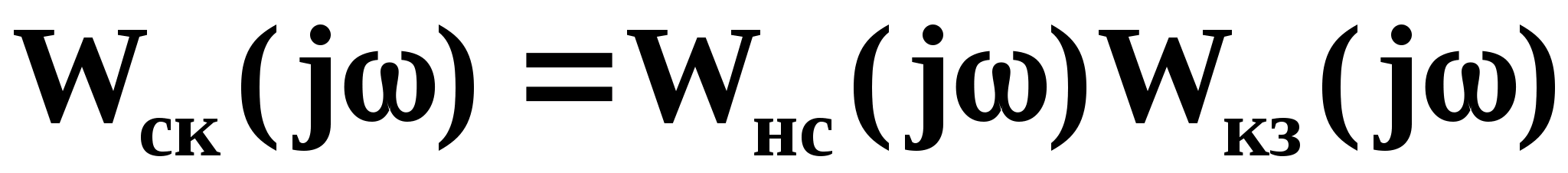
где
 - передаточная амплитудно-фазочастотная
функция корректирующего звена, имеем
- передаточная амплитудно-фазочастотная
функция корректирующего звена, имеем

Логарифмируя, получим
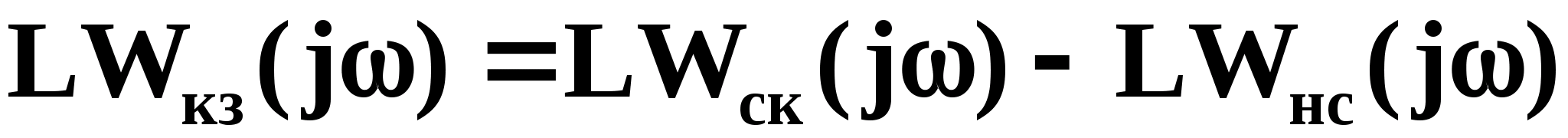 (1.31)
(1.31)
Из выражения (1.31) следует, что ЛАЧХ корректирующего устройства квазистационарной системы равна разности ЛАЧХ скорректированной и нескорректированной ЛАЧХ соответственно.
Таким образом, вычитая ординаты ЛАЧХ нескорректированной системы из ординат желаемой ЛАЧХ на частотах сопряжения, получим ординаты ЛАЧХ корректирующего устройства, к-рая построена на той же схеме путем соединения частот сопряжения прямымыи с наклонами, соответствующими разностям.
Согласно выполненных построений передаточная функция корректирующего устройства :

(1.32)
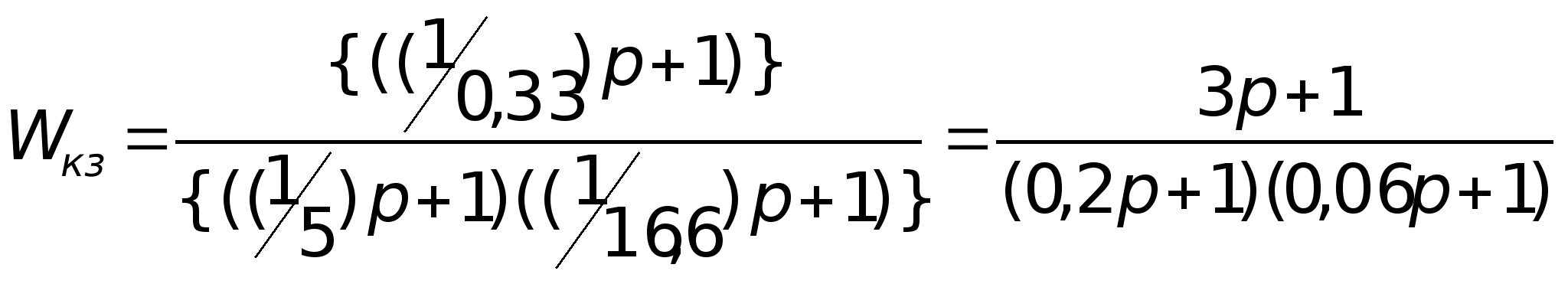
(1.33)
Разомкнутая система управления квазистационарным объектом, состоящая из трех звеньев, представлена на рис.2.
рис.2
2.СИНТЕЗ ИНФОРМАЦИОННО-ПАРАМЕТРИЧЕСКОЙ СИСТЕМЫ ИДЕНТИФИКАЦИИ НЕСТАЦИОНАРНОГО ОБЪЕКТА УПРАВЛЕНИЯ.
2.1. Выбор метода синтеза системы.
При
снятии наложенных ограничений
квазистационарности параметры объекта
управления становятся функциями времени.
Для выработки управляющих воздействий,
близких к оптимальным, необходима
информация о параметрическом состоянии
объекта управления. Для этого необходимо
решение задачи синтеза
информационно-параметрической системы
идентификации, т.е. нахождение ее
структуры и алгоритма функционирования.
Для решения поставленной задачи
выбирается метод подстраиваемой модели
объекта управления с параллельным
включением. А в качестве процесса
функционирования-итерационный процесс
поиска минимизируемого функционала
качества
 ,
т.е. отделение процесса определения
величины и направления изменения
параметра от процесса перестройки
параметра. Такой процесс позволяет
производить оценку параметра при нулевых
начальных условиях на каждом итеративном
шаге, что сводит ошибку оценки параметра
к
,
т.е. отделение процесса определения
величины и направления изменения
параметра от процесса перестройки
параметра. Такой процесс позволяет
производить оценку параметра при нулевых
начальных условиях на каждом итеративном
шаге, что сводит ошибку оценки параметра
к
 и независящей от переходных процессов
системы, вызванных перестройкой
параметров модели.
и независящей от переходных процессов
системы, вызванных перестройкой
параметров модели.
2.2. Поиск минимизированного функционала качества.
В качестве минимизированного функционала целесообразно выбрать интегральный среднеквадратический критерий качества вида:
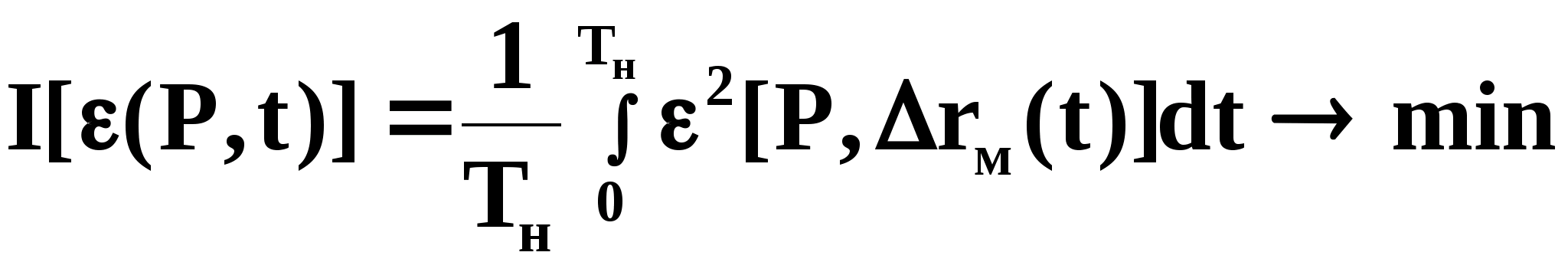
(2.1)
сводящий
к
 рассогласования
рассогласования
 между выходными сигналами объекта и
его модели к параметрам объекта
управления.
между выходными сигналами объекта и
его модели к параметрам объекта
управления.

где
 -изменение
вектора параметров модели, равное
-изменение
вектора параметров модели, равное

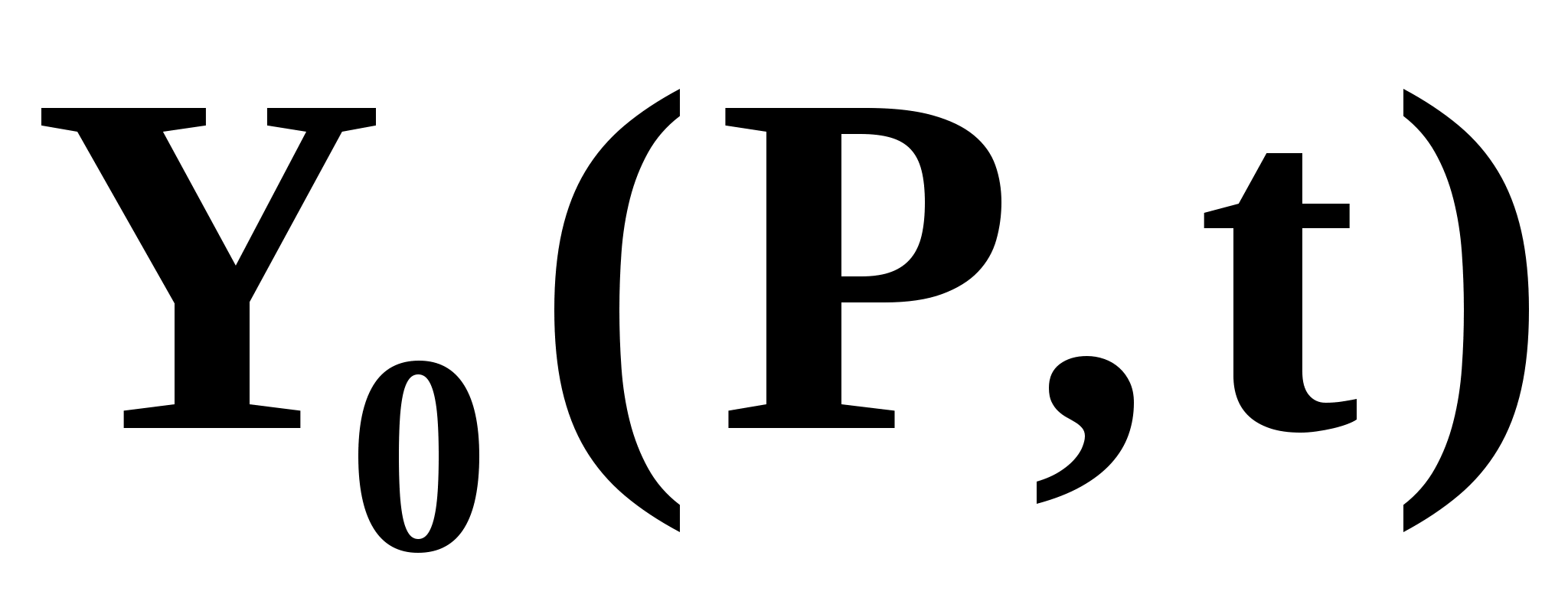 -реакция
объекта управления на управляющее
воздействие
-реакция
объекта управления на управляющее
воздействие

 -реакция
модели объекта управления на управляющее
воздействие
-реакция
модели объекта управления на управляющее
воздействие
 . Тогда
. Тогда
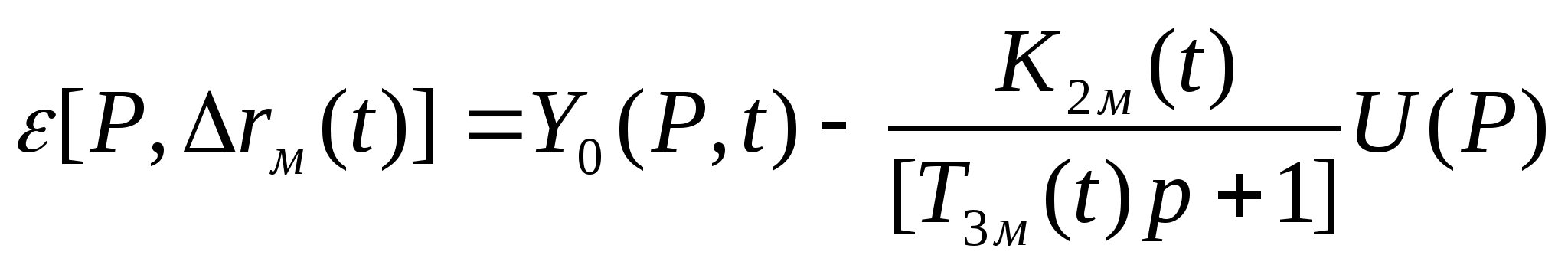
и функционал качества приобретает вид
 (2.2)
(2.2)
Для
нахождения структуры информационно-параметрической
системы идентификации и ее алгоритма
функционирования необходимо осуществить
минимизацию функционала качества (2.2)
по настраиваемым параметрам

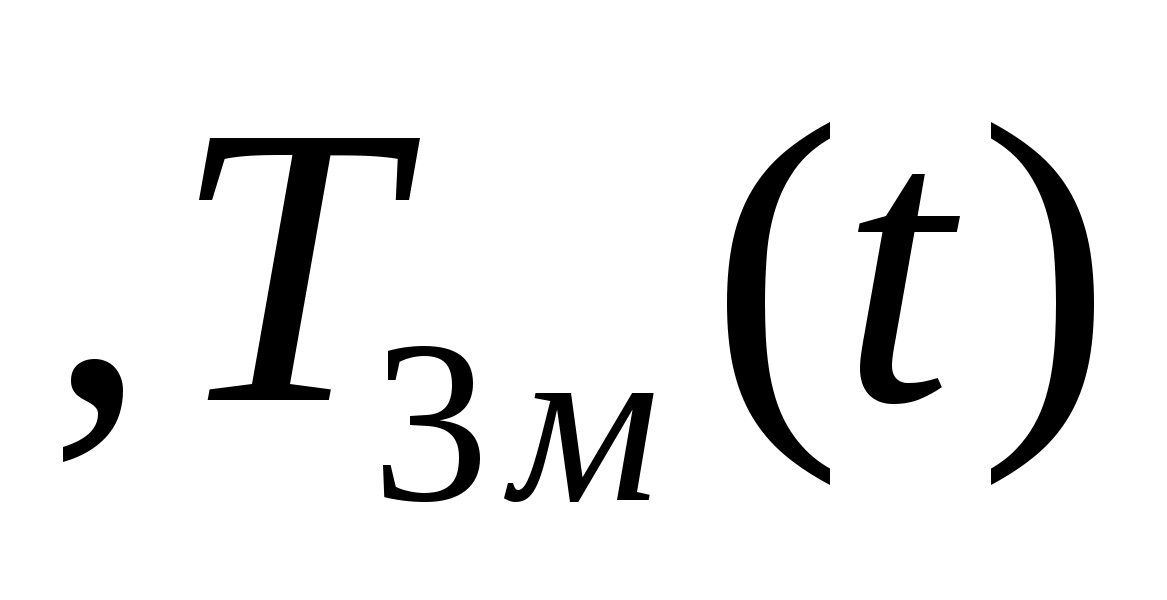 модели объекта управления. Взяв частную
производную от минимизируемого
функционала по настраиваемым параметрам
на интервале времени
модели объекта управления. Взяв частную
производную от минимизируемого
функционала по настраиваемым параметрам
на интервале времени
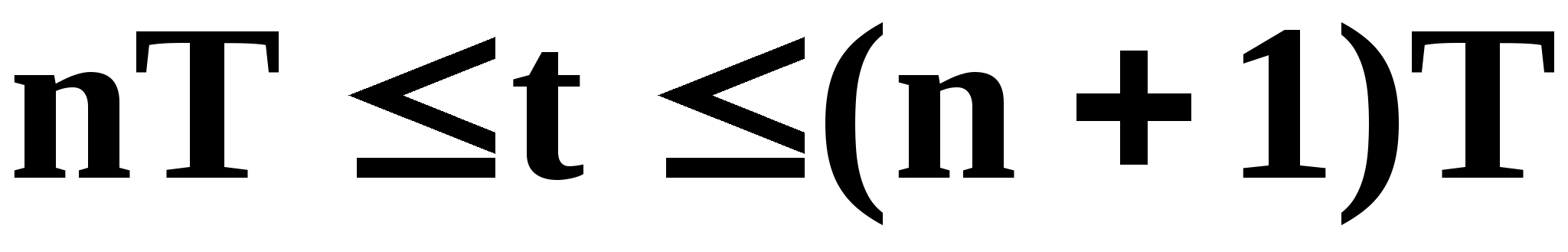 ,
получим
,
получим


(2.3)
где
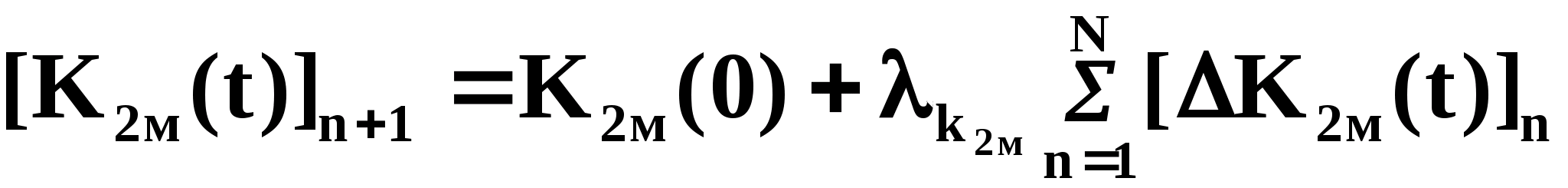

тогда
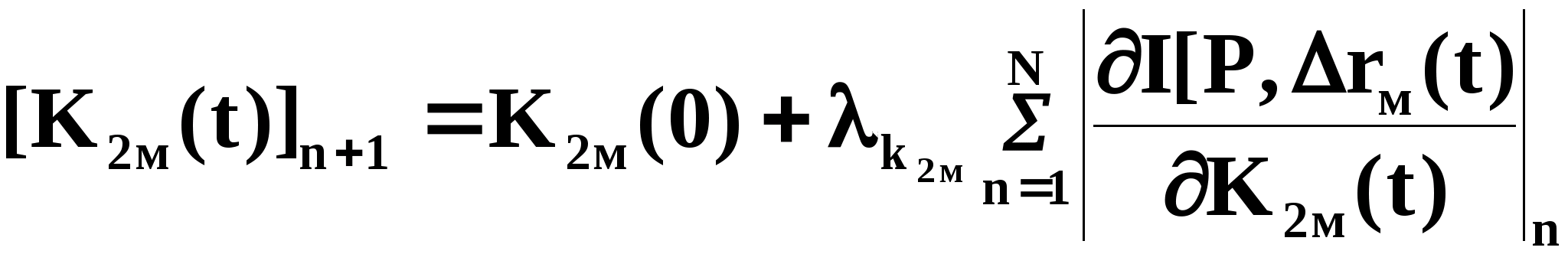
(2.4)
Полученная
система интегро-дифференциальных
уравнений (2.3,2.4) описывает структуру
контура самонастройки
информационно-параметрической системы
идентификации по параметру
 и его алгоритм функционирования.
Поступая аналогично, найдем структуру
и алгоритм функционирования контура
самонастройки информационно-параметрической
системы идентификации по параметрам
и его алгоритм функционирования.
Поступая аналогично, найдем структуру
и алгоритм функционирования контура
самонастройки информационно-параметрической
системы идентификации по параметрам
 .
.

(2.5)

(2.6)
Здесь
 -коэффициенты
передачи контуров самонастройки по
параметрам
-коэффициенты
передачи контуров самонастройки по
параметрам
 соответственно.
соответственно.
Полученная
система интегродифференциальных
уравнений (2.5-2.6) описывают структуру
контуров самонастройки
информационно-параметрической системы
по параметру
 .
.
В целом система интегродифференциальных уравнений (2.3-2.6) описывает структуру информационно-параметрической системы идентификации и ее алгоритм функционирования.
Циклограмма работоспособности информационно-параметрической системы идентификации, поясняющая принцип ее работы, приведена на рис.3
3.ПОСТРОЕНИЕ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ДИНАМИЧЕСКИМ ОБЪЕКТОМ.
Полученная
структура системы управления
квазистационарным объектом (рис.2)
обеспечивает устойчивость и заданные
показатели качества на интервале
квазистационарности
 при условии постоянства параметров
объекта управления на этом интервале
времени. При наличии изменений параметров
объекта управления управляющее
воздействие
при условии постоянства параметров
объекта управления на этом интервале
времени. При наличии изменений параметров
объекта управления управляющее
воздействие
 ,
вырабатываемое регулятором (управляющим
устройством) с жесткой отрицательной
обратной связью, не обеспечивает
устойчивости и заданных показателей
качества квазистационарной системы. В
работу вступает гибкая параметрическая
обратная связь, т. к. управляющему
устройству в этом случае необходима
информация о параметрическом состоянии
нестационарного объекта управления.
,
вырабатываемое регулятором (управляющим
устройством) с жесткой отрицательной
обратной связью, не обеспечивает
устойчивости и заданных показателей
качества квазистационарной системы. В
работу вступает гибкая параметрическая
обратная связь, т. к. управляющему
устройству в этом случае необходима
информация о параметрическом состоянии
нестационарного объекта управления.
Выработанное
управляющим устройством воздействие
с учетом информации о параметрическом
состоянии нестационарного объекта
управления будет сводить к ошибку рассогласования регулируемого
процесса
ошибку рассогласования регулируемого
процесса
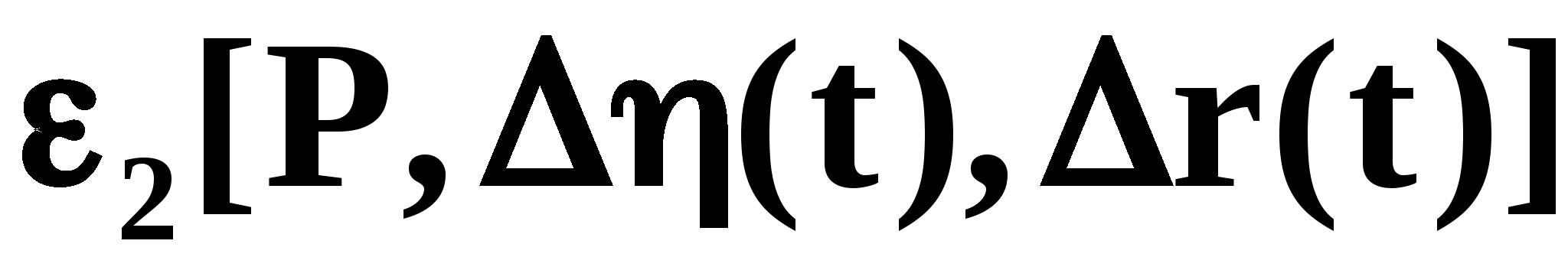 , где
, где
 -изменение
вектора параметров управляющего
устройства.
-изменение
вектора параметров управляющего
устройства.
3.1. Синтез адаптивной системы управления нестационарным объектом с элементами искусственного интеллекта.
Для
оценки качества регулируемого процесса
нестационарного объекта управления
выберем интегральный критерий минимума
среднеквадратической ошибки регулируемого
процесса, зависящего от изменения
параметров объекта управления
 ,
изменения параметров управляющего
устройства
,
изменения параметров управляющего
устройства
 ,
и задающего воздействия
,
и задающего воздействия
 .
.
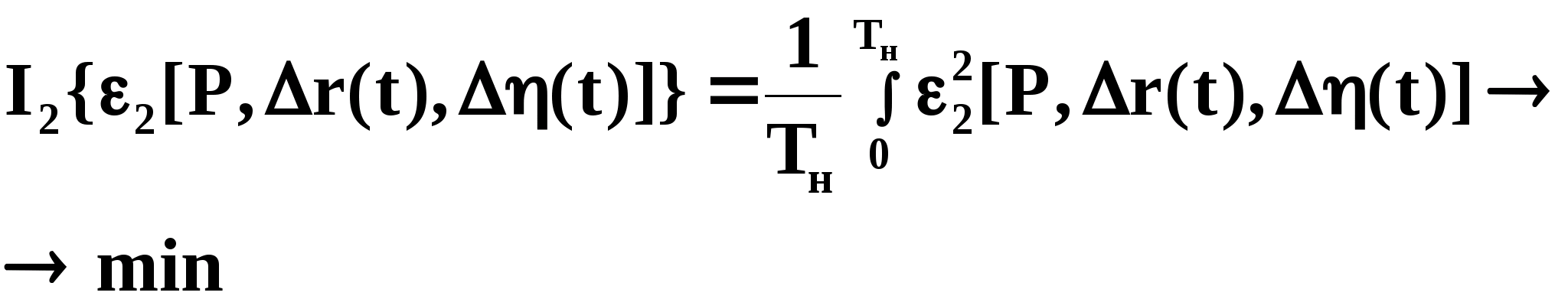 (3.1.1)
(3.1.1)
где
 (3.1.2)
(3.1.2)
 (3.1.3)
(3.1.3)
здесь

Решив
выражение (3.1.2) относительно
 с учетом (3.1.3), получим
с учетом (3.1.3), получим
 (3.1.4)
(3.1.4)
где
 -вектор
настраиваемых параметров регулятора
(управляющего устройства), обеспечивающий
качество регулируемого процесса.
-вектор
настраиваемых параметров регулятора
(управляющего устройства), обеспечивающий
качество регулируемого процесса.
Учитывая
то, что на состояние нестационарного
объекта управления в каждом
 -том
цикле может указать самонастраивающаяся
модель объекта, положим в уравнении
(3.1.4)
-том
цикле может указать самонастраивающаяся
модель объекта, положим в уравнении
(3.1.4)
 (3.1.5)
(3.1.5)
Тогда
выражение сигнала ошибки регулируемого
процесса
 для каждого
для каждого
 -го
цикла будет иметь вид
-го
цикла будет иметь вид
 (3.1.6)
(3.1.6)
Подставляя
значение
 выражения (3.1.6) в (3.1.1) имеем:
выражения (3.1.6) в (3.1.1) имеем:
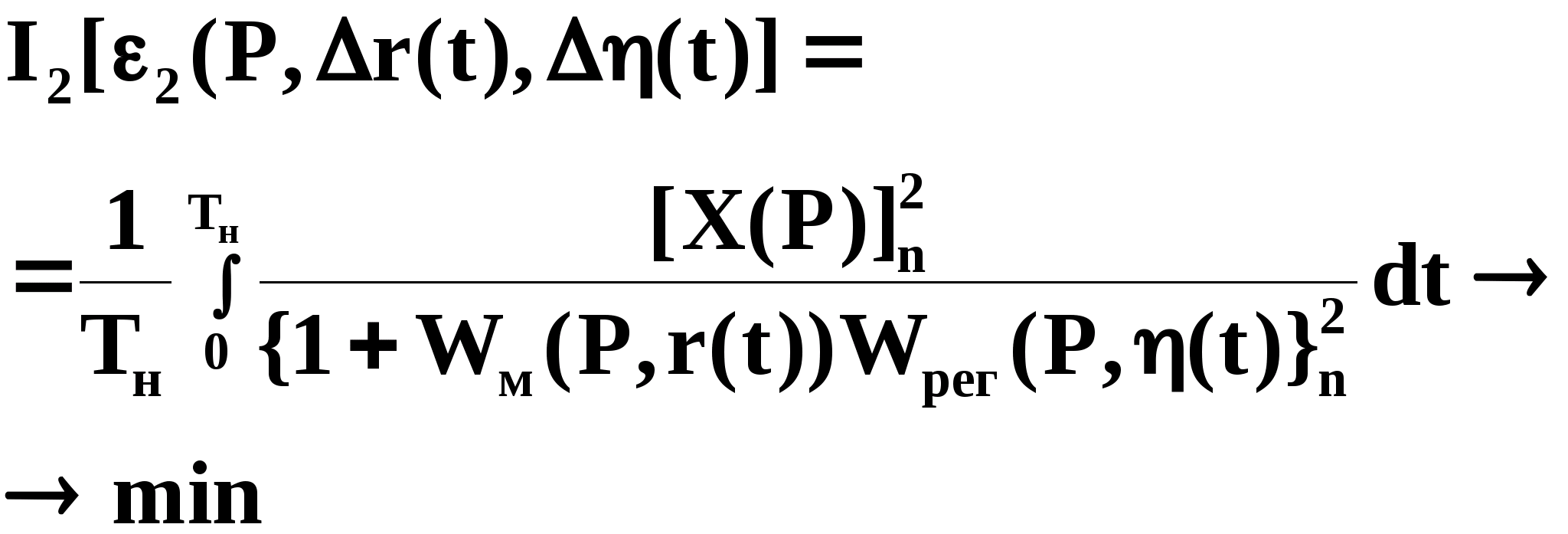
(3.1.7)
Минимизируя функционал качества (3.1.7) по вектору настраиваемых параметров регулятора на интервале
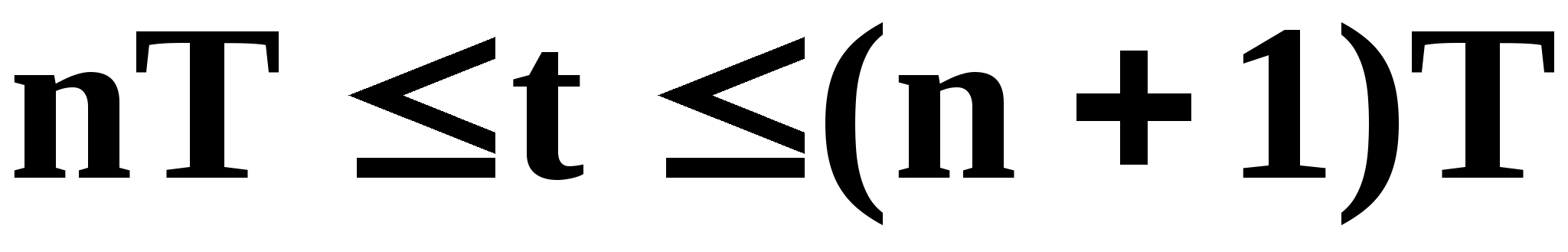 ,получим
,получим
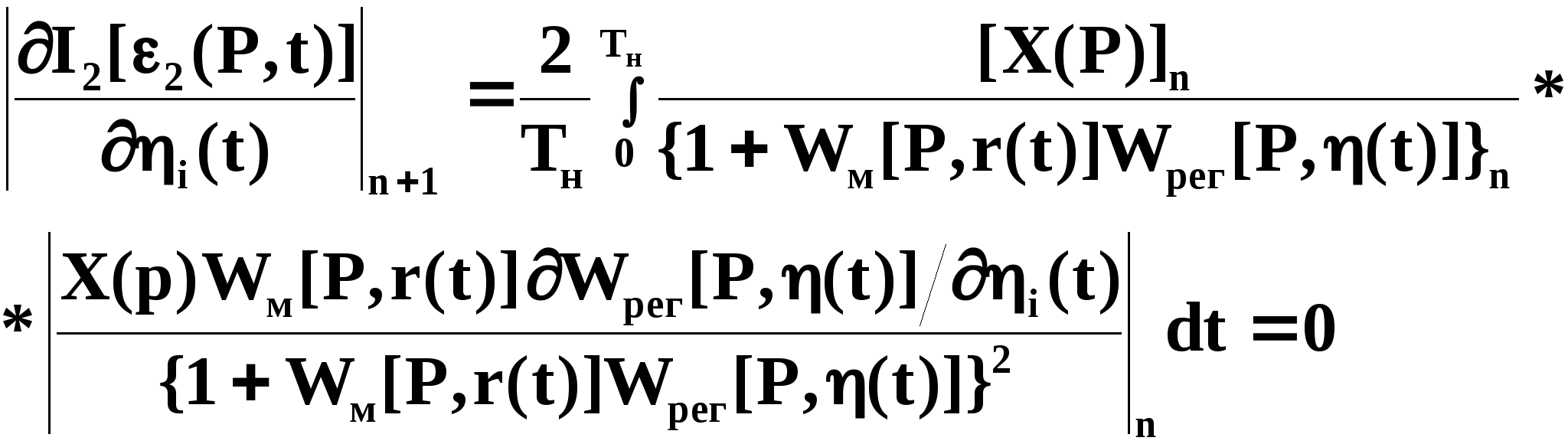
(3.1.8)
где
 (3.1.9)
(3.1.9)
 (3.1.10)
(3.1.10)

(3.1.11)
Полученные выражения (3.1.8-3.1.11) описывают структуру и алгоритм функционирования системы анализа параметрического состояния нестационарного объекта управления в векторно-матричной форме.
Подставляя
значения
 в (3.1.7), получим
в (3.1.7), получим
 (3.1.12)
(3.1.12)
Взяв
частные производные от минимизируемого
функционала качества
 по настраиваемым параметрам регулятора
по настраиваемым параметрам регулятора
 ,
с учетом выражения (3.1.8) получим:
,
с учетом выражения (3.1.8) получим:

(3.1.13)
 (3.1.14)
(3.1.14)
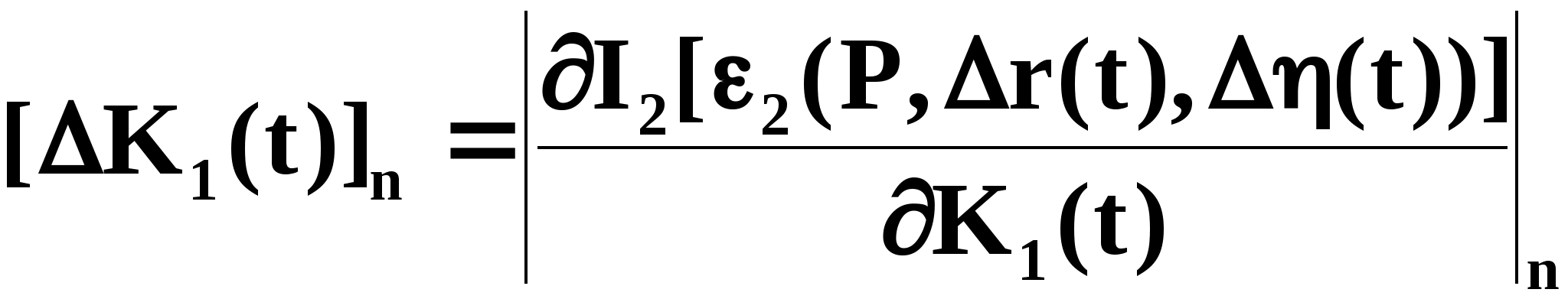
Тогда

(3.1.15)
Полученные
выражения (3.1.13-3.1.15) описывают контур
самонастройки системы анализа
параметрического состояния и принятия
решения по параметру
 .
.
Поступая
аналогично тому, как это было выполнено
по параметру
 ,
найдем структуру и алгоритм функционирования
контура самонастройки анализа
параметрического состояния и принятия
решений по параметрам
,
найдем структуру и алгоритм функционирования
контура самонастройки анализа
параметрического состояния и принятия
решений по параметрам
 :
:
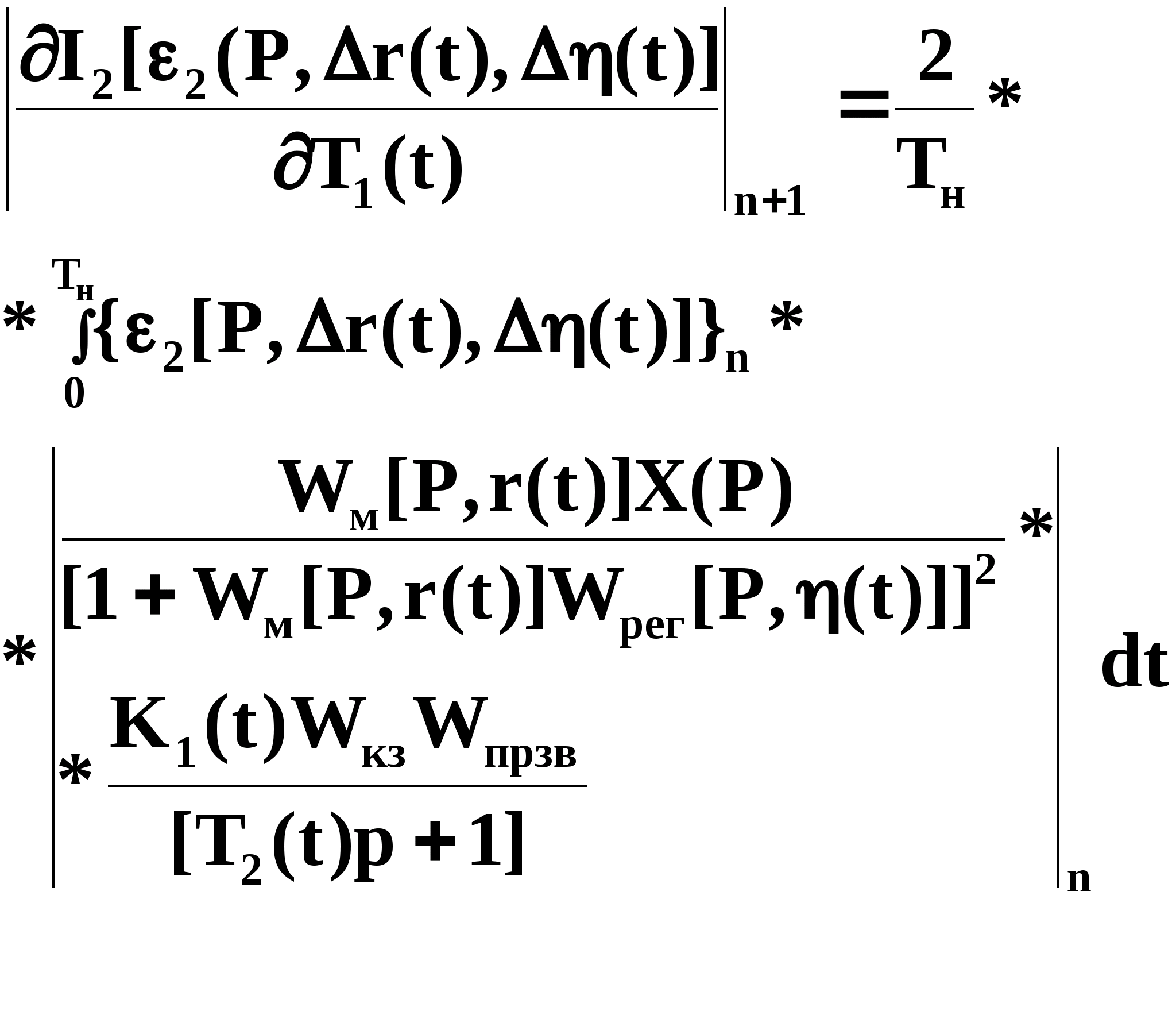 (3.1.16)
(3.1.16)

где
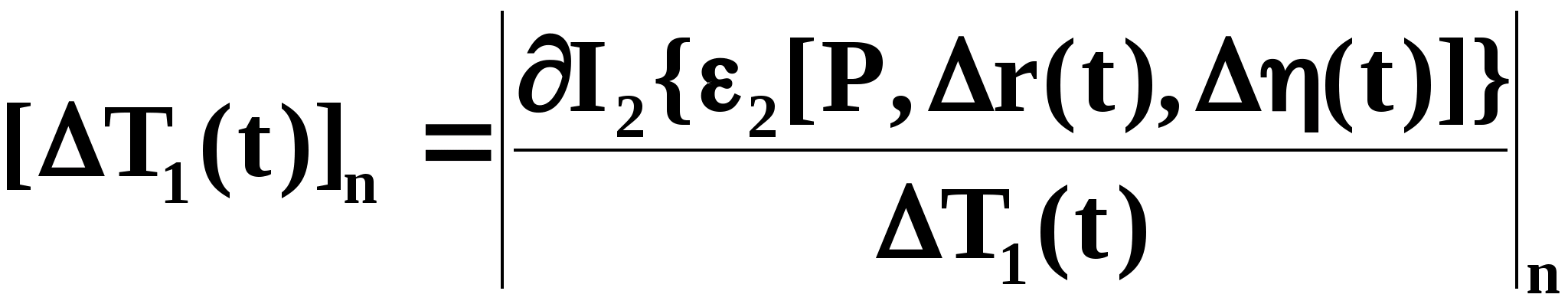 (3.1.17)
(3.1.17)
Тогда

(3.1.18)
Полученная
система уравнений (3.1.16-3.1.18) описывает
структуру и алгоритм функционирования
системы анализа параметрического
состояния и принятия решения по параметру
 .
.
Аналогично

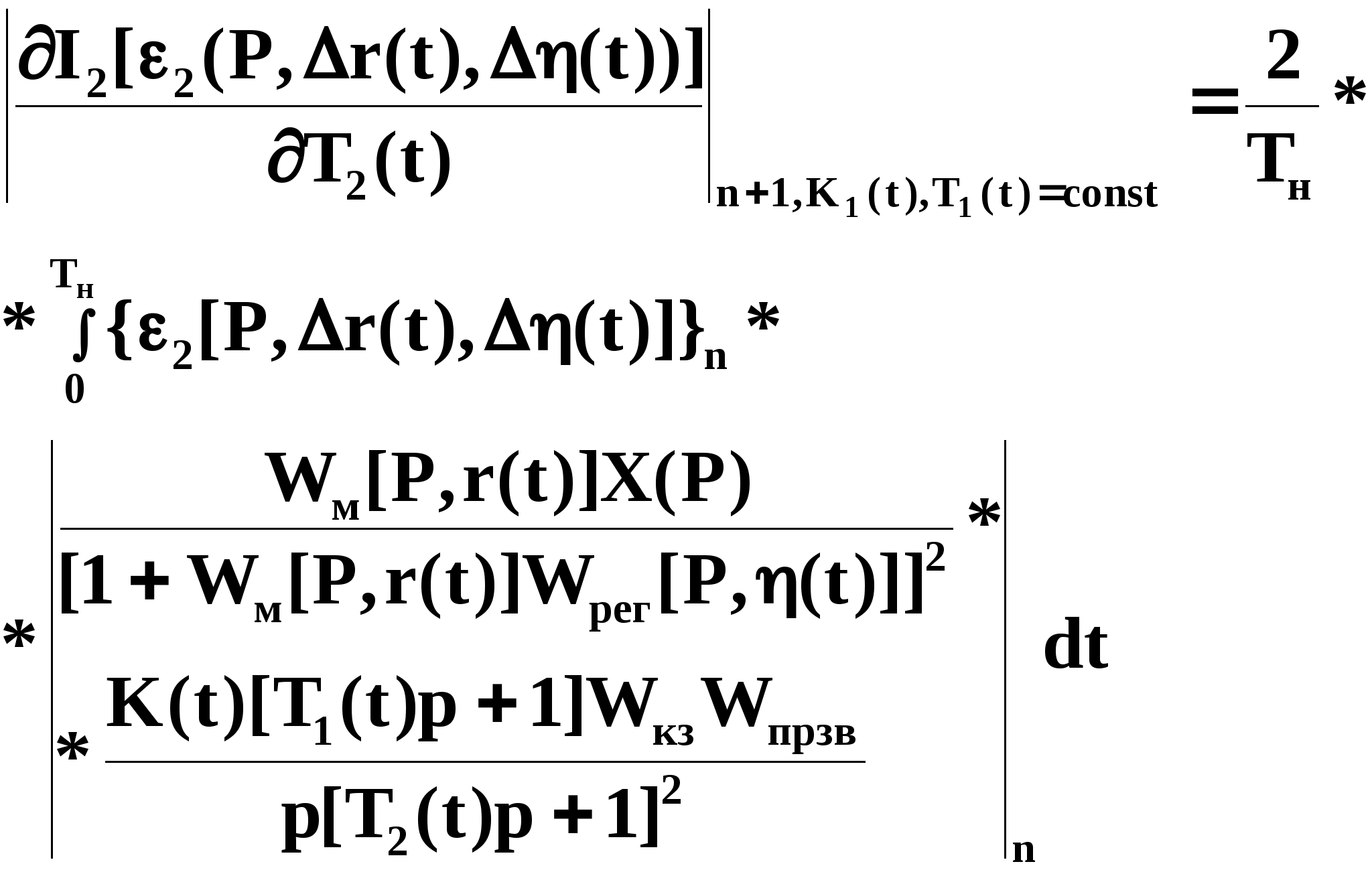
(3.1.19)
 (3.1.20)
(3.1.20)
где
 (3.1.21)
(3.1.21)
Тогда
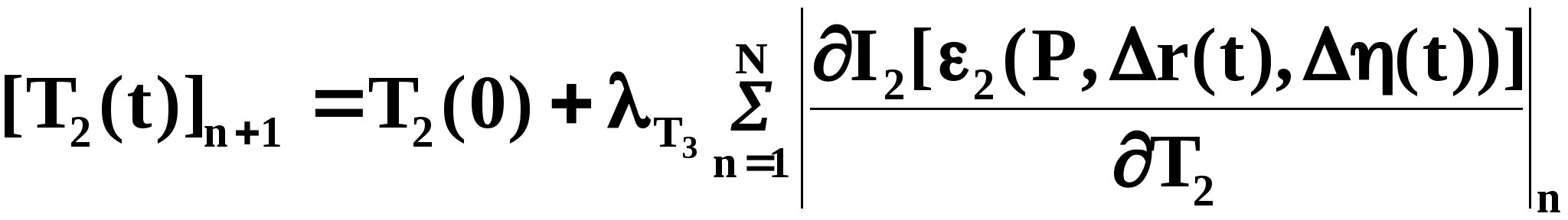
(3.1.22)
Полученная
система интегродифференциальных
уравнений (3.1.8-3.1.22) описывает структуру
и алгоритм функционирования системы
анализа параметрического состояния и
принятия решений по параметрам
 .
.
Пользуясь полученным алгоритмом функционирования, строим адаптивную систему оптимального управления нестационарным объектом управления с элементами искусственного интеллекта.
ЗАКЛЮЧЕНИЕ.
Построенная адаптивная система управления нестационарным объектом полностью соответствует заданной математической модели и удовлетворяет условиям технического задания.
Соответствующие структурные схемы информационно-параметрической системы идентификации и адаптивной системы управления могут быть реализованы с помощью современной элементной базы и использоваться в промышленности, военно-промышленном комплексе и научных исследованиях.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.
1.Г.С.Володченко,А.И.Новгородцев. Методические указания к комплексной курсовой работе.С.:СГУ,1996г.
2. Александров А.Г. Оптимальные и адаптивные системы.М.:Высш.шк.,1989-263 с.
3. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. 3-е изд., испр. М.:Физматгиз, 1975.-768 с.
4. Сборник задач по теории автоматического регулирования и управления / под ред. В.А. Бесекерского. М.:Наука,1978-512 с.
5.Ту Ю. Т. Цифровые и импульсные системы автоматического управления. М.: Машиностроение,1964.-703 с.