Решение матричных игр
Оглавление
Оглавление 1
1. Цель работы 2
программа матрица игра итерационный листинг 2
2. Задание 3
3. Краткие теоретические сведения 4
4.1 Проектирование 14
4.2 Листинг программного кода 14
5. Пример работы программы 22
Выводы 23
Используемая литература 24
Используемые программные средства 24
1. Цель работы
Необходимо разработать программное средство для решения матричных игр.
программа матрица игра итерационный листинг
2. Задание
Задать матрицу игры вручную и случайным образом.
Найти оптимальные стратегии игроков, используя итерационный метод и методом чистых стратегий.
Сделать возможность сохранять матрицу игры и загружать из файла.
3. Краткие теоретические сведения
Постановка общей задачи теории игр
Теория игр – математическая теория конфликтных ситуаций. Экономические соревнования, спортивные встречи, боевые операции – примеры конфликтных ситуаций. Простейшие модели конфликтных ситуаций – это салонные и спортивные игры.
В игре могут сталкиваться интересы двух противников (игра парная или игра двух лиц), интересы n (n > 2) противников (игра множественная или игра n лиц). Существуют игры с бесконечным множеством игроков.
Стратегией игрока называется система правил, однозначно определяющих выбор поведения игрока на каждом ходе в зависимости от ситуации, сложившейся в процессе игры. В зависимости от числа возможных стратегий игры делятся на конечные и бесконечные.
Процесс игры состоит в выборе
каждым игроком i одной
своей стратегии .В
результате сложившейся ситуации s
игрок i получает выигрыш
.В
результате сложившейся ситуации s
игрок i получает выигрыш .
.
Игры, в которых целью каждого участника является получение по возможности большего индивидуального выигрыша, называются бескоалиционными в отличие от коалиционных, в которых действия игроков направлены на максимизацию выигрышей коллективов (коалиции) без дальнейшего разделения выигрыша между участниками.
По определению бескоалиционной игрой называется система
 ,
,
в которой I и
 – множества,
– множества,
 – функции на множестве
– функции на множестве
 принимающие вещественные значения.
принимающие вещественные значения.
Бескоалиционная игра называется
игрой с постоянной суммой, если существует
такое постоянное C,
что
 для всех ситуаций
для всех ситуаций
 .
.
Ситуация s в игре называется приемлемой для игрока i, если этот игрок, изменяя в ситуации s свою стратегию s>i> на какую-либо другую s>i>', не может увеличить своего выигрыша.
Ситуация s, приемлемая для всех игроков, называется ситуацией равновесия.
Процесс нахождения ситуации равновесия в бескоалиционной игре есть процесс решения игры.
Матричные игры
Игра называется парной, если в ней сталкиваются интересы двух противников. Игра называется с нулевой суммой, если один игрок выигрывает столько, сколько второй проигрывает в той же партии.
Каждая фиксированная стратегия, которую может выбрать игрок, называется его чистой стратегией.
Матричной называют парную игру с нулевой суммой при условии, что каждый игрок имеет конечное число чистых стратегий.
Пусть первый игрок имеет m чистых стратегий, а второй – n.
Парная игра с нулевой суммой
задается ' формально системой чисел –
матрицей ,
элементы которой определяют выигрыш
первого игрока (и соответственно проигрыш
второго), если первый игрок выберет i-ю
строку (i-ю стратегию),
а второй игрок j-й
столбец (j-ю стратегию).
Матрица
,
элементы которой определяют выигрыш
первого игрока (и соответственно проигрыш
второго), если первый игрок выберет i-ю
строку (i-ю стратегию),
а второй игрок j-й
столбец (j-ю стратегию).
Матрица
 называется платежной матрицей или
матрицей игры.
называется платежной матрицей или
матрицей игры.
Задача первого игрока – максимизировать свой выигрыш.
Задача второго игрока – максимизировать свой выигрыш – сводится к минимизации проигрыша второго, что эквивалентно задаче минимизации выигрыша первого игрока.
Чистые стратегии
Гарантированный выигрыш первого игрока, применяющего чистую i-ю стратегию,

Число
 называется нижним значением игры, а
соответствующая чистая стратегия i>0>,
при которой достигается
называется нижним значением игры, а
соответствующая чистая стратегия i>0>,
при которой достигается
 называется максиминной стратегией
первого игрока. Аналогично,
называется максиминной стратегией
первого игрока. Аналогично,
 называется верхним значением игры а j>0>
– минимаксной стратегией второго
игрока.
называется верхним значением игры а j>0>
– минимаксной стратегией второго
игрока.
Всегда
 .
Если
.
Если
 то
игра имеет седловую точку в чистых
стратегиях; число
то
игра имеет седловую точку в чистых
стратегиях; число
 называется значением игры (или ценой
игры). Игра имеет седловую точку в
чистых стратегиях тогда и только тогда,
когда существует элемент матрицы
называется значением игры (или ценой
игры). Игра имеет седловую точку в
чистых стратегиях тогда и только тогда,
когда существует элемент матрицы
 ,
минимальный в своей строке и в то же
время максимальный в столбце
,
минимальный в своей строке и в то же
время максимальный в столбце

Любая пара (i>0>, j>0>), обладающая свойством (10.1), называется седловой точкой.
Смешанные стратегии
Если обозначить через x>1>,
x>2>, …, x>m>
вероятности (частоты), с которыми первый
игрок выбирает соответственно первую,
вторую, . . ., m-ю чистую стратегию, так
что через
 ; через y>1>,
y>2>, …, y>n>
вероятности, с которыми второй игрок
выбирает первую, вторую, ,.., n-ю
свою чистую стратегию, причем
; через y>1>,
y>2>, …, y>n>
вероятности, с которыми второй игрок
выбирает первую, вторую, ,.., n-ю
свою чистую стратегию, причем
 ,
то наборы чисел x=(
x>1>, x>2>,
…, x>m>)
и y=(y>1>,
y>2>, …, y>n>)
называются смешанными стратегиями
первого и второго игроков соответственно.
Каждый игрок имеет бесчисленное множество
смешанных стратегий. Множество смешанных
стратегий первого игрока обозначим
через s>1> и
множество смешанных стратегий второго
игрока – через s>2>.
,
то наборы чисел x=(
x>1>, x>2>,
…, x>m>)
и y=(y>1>,
y>2>, …, y>n>)
называются смешанными стратегиями
первого и второго игроков соответственно.
Каждый игрок имеет бесчисленное множество
смешанных стратегий. Множество смешанных
стратегий первого игрока обозначим
через s>1> и
множество смешанных стратегий второго
игрока – через s>2>.
Задача первого игрока состоит
в выборе такой стратеги
 чтобы при отсутствии информации о выборе
другого максимизировать свой выигрыш.
Задача второго игрока состоит в выборе
такой стратегии
чтобы при отсутствии информации о выборе
другого максимизировать свой выигрыш.
Задача второго игрока состоит в выборе
такой стратегии
 ,
чтобы при отсутствии информации о
поведении первого игрока минимизировать
выигрыш первого.
,
чтобы при отсутствии информации о
поведении первого игрока минимизировать
выигрыш первого.
Если первый игрок применяет
стратегию ,
а второй – стратегию
,
а второй – стратегию то средний выигрыш M(x,
y) первого
игрока равен
то средний выигрыш M(x,
y) первого
игрока равен

Выигрыш M(x, y) называют функцией игры.
Например, в задаче с матрицей
первый игрок имеет две чистые
стратегии
 ,
,
 и бесчисленное множество смешанных
стратегий, таких, как
и бесчисленное множество смешанных
стратегий, таких, как
 ,
,

 и т. д.; все они являются элементами
множества
и т. д.; все они являются элементами
множества
 второй игрок имеет четыре чистые
стратегии
второй игрок имеет четыре чистые
стратегии и бесчисленное множество смешанных
стратегий, таких, как
и бесчисленное множество смешанных
стратегий, таких, как


 ,
являющихся элементами множества
,
являющихся элементами множества

Если первый игрок применяет
смешанную стратегию
 ,
а второй применяет стратегию
,
а второй применяет стратегию ,
то средний выигрыш первого игрока,
определяемый функцией игры, окажется
равным
,
то средний выигрыш первого игрока,
определяемый функцией игры, окажется
равным

Если же первый игрок применяет
стратегию ,
а второй — стратегию
,
а второй — стратегию
 ,
то
,
то
 .
Оптимальная стратегия первого игрока
.
Оптимальная стратегия первого игрока
 второго игрока
второго игрока ;
;
 —цена
игры.
—цена
игры.
Седловая точка в смешанных стратегиях
Пара смешанных стратегий (х*, у*) называется седловой точкой функции М(х, у), если

Каждая матричная игра с нулевой суммой имеет решение в смешанных стратегиях, т. е. существуют такие смешанные стратегии х* и y* первого и второго игроков соответственно, что выполняется условие (10.2). Гарантированный выигрыш первого игрока, применяющего смешанную стратегию

Стратегия х*, при которой гарантированный выигрыш первого игрока достигает максимального значения, называется оптимальной стратегией первого игрока:

Гарантированный проигрыш второго игрока

y* – оптимальная стратегия второго игрока, если

Гарантированный выигрыш первого
игрока, применяющего свою оптимальную
стратегию, равен гарантированному
проигрышу второго игроку, применяющего
свою оптимальную стратегию:
 – цена игры.
– цена игры.
Сведение задачи теория игр к задаче линейного программирования
Задача максимизации гарантированного выигрыша первого игрока и задача минимизации гарантированного проигрыша второго игрока сводятся к паре взаимно двойственных задач линейного программирования:
-
Задача первого игрока
Задача второго игрока


Процесс решения задач упрощается,
если перейти к Переменным
 .
Это возможно, если
.
Это возможно, если .
.
Имеем:
-
Задача первого игрока
Задача второго игрока


Оптимальные стратегии игроков
не изменятся, если матрицу игры заменить
на
заменить
на
 .
Цена игры при этом увеличивается на с.
.
Цена игры при этом увеличивается на с.
Методы решения задач теории игр во многом зависят от условий задачи и от матрицы А выигрышей первого игрока.
Если матрица А имеет седловую
точку, то решение игры сводится к
нахождению седловой точки матрицы А.
Оптимальные стратегии игроков
определяются при этом координатами
(i,j)
седловой точки матрицы А, а цена
игры элементом
 в седловой точке.
в седловой точке.
Если задача теории игр не имеет решения в чистых стратегиях, то может быть решена итерационным методом.
Итерационный метод.
Разыгрывается мысленный эксперимент, в котором игроки А и В применяют против друг
друга свои стратегии. Эксперимент состоит из последовательности партий. А выбирает стратегию
Аi, игрок В уже знает об этом и отвечает своей стратегией Вj, наиболее выгодной для него в сложившейся ситуации. Далее, первый игрок выбирает дальнейшие стратегии основываясь на предыдущей игре. Таким образом, на каждом шаге итерационного процесса игрок отвечает на шаг другого той своей стратегией, которая является оптимальной относительно всех предыдущих ходов. Если партии продолжать достаточно долго, то средний выигрыш стремится к цене игры, а частоты – к вероятностям оптимальных стратегий. Главным достоинством этого метода является независимость его сложности от размерности игры.
4. Реализация программного средства
Среда разработки: С++ Builder XE
Язык программирования: C++
4.1 Проектирование
Список модулей с кратким описанием:
Mainform.cpp – это главный модуль в котором, реализованы функции: расчёта в чистых стратегиях, сохранение/загрузка и ввод исходных данных .
Iter. cpp – это вспомогательный модуль в котором реализован итерационный метод решения матричной игры.
4.2 Листинг программного кода
Модуль Mainform.cpp:
//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include "Series.hpp"
#include "Iter.h"
#include "pic.h"
#include "mainform.h"
#include <fstream.h>
#include <iostream>
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
void __fastcall TForm1::RaschetClick(TObject *Sender) // расчёт
{
double MaxMin=0, MinMax=0;
double MinRow[100];
double MaxCol[100];
int i, j, n, m;
double A0[100][100];
n = StrToInt(Edit4->Text);
m = StrToInt(Edit5->Text);
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
//перевод значений из таблицы в массив double матрицы A0:
A0[j][i]=StrToFloat(StringGrid1->Cells[i+1][j+1]);
}
}
//--------------------- расчёт в чистых стратегиях -----------------------------
for (i = 0; i < n; i++) {
MinRow[i]=A0[i][0];
}
for (i = 0; i < m; i++) {
MaxCol[i]=A0[0][i];
}
//очистим стрингриды 2 и 3:
for (register int i = 0; i < StringGrid2->RowCount; i++)
{
StringGrid2->Rows[i]->Clear();
}
for (register int i = 0; i < StringGrid3->RowCount; i++)
{
StringGrid3->Rows[i]->Clear();
}
StringGrid2->Cells[0][0]="Min";
StringGrid3->Cells[0][0]="Max";
// расчёт минимумов и максимумов
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++) {
//поиск минимального значения в строках :
if (A0[i][j] <= MinRow[i]) {
MinRow[i] = A0[i][j];
}
}
//вывод минимумов строк в СтрингГрид2 :
StringGrid2->Cells[0][i+1] = MinRow[i];
}
for (j = 0; j < m; j++) {
for (i = 0; i < n; i++) {
//поиск максимального значения в столбцах :
if (A0[i][j] >= MaxCol[j]){
MaxCol[j] = A0[i][j];
}
}
//вывод максимумов столбцов в СтрингГрид3 :
StringGrid3->Cells[j+1][0] = MaxCol[j];
}
//найдём максимин
MaxMin = MinRow[0];
for (i = 0; i < n; i++) {
if (MinRow[i] >= MaxMin ){MaxMin = MinRow[i];}
}
Edit2->Text=MaxMin;
//найдём минимакс
MinMax = MaxCol[0];
for (i = 0; i < m; i++) {
if (MaxCol[i] <= MinMax ){MinMax = MaxCol[i];}
}
Edit3->Text=MinMax;
if (MinMax == MaxMin) {
ShowMessage("Игра решена в чистых стратегиях");
Edit1->Text = MinMax;
} else {ShowMessage("Игра не решается в чистых стратегиях, попробуете решить её итерационным методом");}
//------------------------------------------------------------------------------
}
//------------------------------------------------------------------------------
void __fastcall TForm1::Button1Click(TObject *Sender)
{
Form2->Show();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::Button2Click(TObject *Sender)
{
int i, j, n, m;
double A0[100][100];
n = StrToInt(Edit4->Text);
m = StrToInt(Edit5->Text);
//очищаем СтрингГрид1:
for (register int i = 0; i < StringGrid1->RowCount; i++){
StringGrid1->Rows[i]->Clear();
}
for (i = 0; i < n; i++) {
StringGrid1->Cells[0][i+1]="A"+String(i+1);
}
for (i = 0; i < m; i++) {
StringGrid1->Cells[i+1][0]="B"+String(i+1);
}
}
//---------------------------------------------------------------------------
void __fastcall TForm1::SaveClick(TObject *Sender)
{
int n,m;
n = StrToInt(Edit4->Text);
m = StrToInt(Edit5->Text);
// сохранение в файл
SaveTextFileDialog1->Execute();
SaveTextFileDialog1->FileName;
ofstream myfile(SaveTextFileDialog1->FileName.t_str());
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
myfile << StrToFloat(StringGrid1->Cells[j+1][i+1]);
myfile << " ";
}
myfile << "\n";
}
myfile.close();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::Button4Click(TObject *Sender)
{
int n,m;
n = StrToInt(Edit4->Text);
m = StrToInt(Edit5->Text);
//Загрузка файла
int a;
if (OpenDialog1->Execute()){
OpenDialog1->FileName;
ifstream loadfile(OpenDialog1->FileName.c_str());
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
loadfile >> a;
StringGrid1->Cells[j+1][i+1] = IntToStr(a);
}
//StringGrid1[i+1][j+1]=ch;
}
loadfile.close();
}
}
//---------------------------------------------------------------------------
void __fastcall TForm1::Button5Click(TObject *Sender)
{
int i, j, n, m;
double A0[100][100];
n = StrToInt(Edit4->Text);
m = StrToInt(Edit5->Text);
//Создаём рандомную матрицу
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++) {
A0[i][j] = RandomRange(1, 10);
}
}
//Матрицу в СтрингГрид1:
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++) {
StringGrid1->Cells[j+1][i+1]=String(A0[i][j]);
}
}
}
5. Пример работы программы
Пример случайно заданной матрицы решённой в чистых стратегиях:

Пример платёжной матрицы не решаемой в чистых стратегиях:
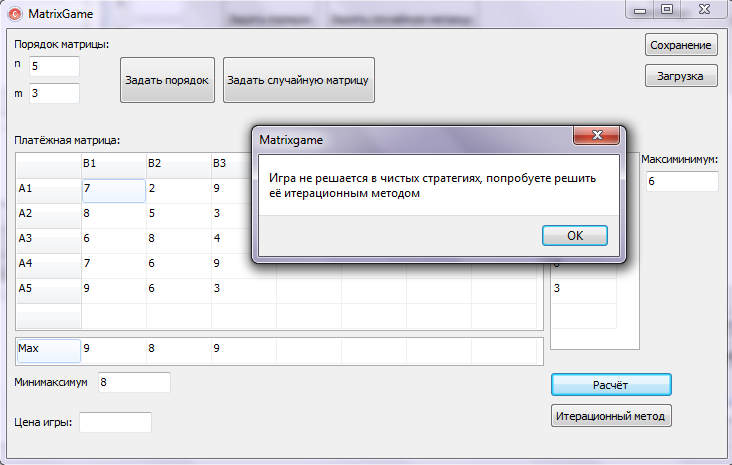
Пример матрицы игры решаемой итерационным методом:

Выводы
В результате проделанной работы было разработано программное средство для решения матричных задач методом чистых стратегий и итерационным методом.
Используемая литература
1)Гейл Д. Теория линейных экономических моделей. М.: Изд–во иностранной литературы, 1968.
2)Петросян Л.А. Зенкевич Н.А. Семина Е.А. Теория игр : Учеб. пособие – М.: ВЫСШ. ШК.; : УНИВЕРСИТЕТ, 1998. – 300 с.
3) Орлов, А.И. Теория принятия решений. Учебное пособие / А.И.Орлов.- М.:
Издательство ≪Март≫, 2004. - 656 с
Используемые программные средства
С++ Builder XE