Многокритериальные задачи. Метод альтернативных решений
1. Постановка задачи
Необходимо разработать программное средство для поиска альтернативных решений для следующей задачи:
многокритериальная задача
входные данные: количество критериев и решений; весовые значения, заданные напрямую, степень важности критериев, интервалы превосходства, цена перехода значения в соседний класс.
выходные данные: матрица согласия; матрица несогласия; ядро бинарного отношения.
программный альтернативный решение многокритериальный
2. Краткие теоретические сведения
Пусть задан набор
числовых функций
,
определенных на множестве возможных
решений X. В зависимости от содержания
задачи выбора эти функции именуют
критериями оптимальности, критериями
эффективности или целевыми функциями.
Указанные выше
числовые функции образуют векторный
критерий
,
который принимает значения в пространстве
m-мерных векторов
.
Это пространство называют критериальным
пространством или пространством оценок,
а всякое значение
именуют векторной оценкой возможного
решения x. Все возможные векторные оценки
образуют множество возможных оценок
(возможных или допустимых векторов)
Как правило, между множествами возможных решений X и соответствующим множеством векторов Y можно установить взаимно однозначное соответствие, т.е. каждому возможному решению поставить в соответствие определенный возможный вектор, и обратно – каждому возможному вектору сопоставить определенное возможное решение. В таких случаях выбор во множестве решений с математической точки зрения равносилен выбору во множестве векторов и все определения и результаты можно формулировать как в терминах решений, так и в терминах векторов, причем при желании всегда можно без труда осуществить переход от одной формы изложения к другой.
Задачу выбора, которая включает множество допустимых решений X и векторный критерий f, обычно называют многокритериальной задачей или задачей многокритериальной оптимизации.
Необходимо отметить, что формирование математической модели принятия решений (т.е. построение множества X и векторного критерия f ) нередко представляет собой сложный процесс, в котором тесно взаимодействуют специалисты двух сторон. А именно, представители конкретной области знаний, к которой относится исследуемая проблема, и специалисты по принятию решений (математики). С одной стороны, следует учесть все важнейшие черты и детали реальной задачи, а с другой, – построенная модель не должна оказаться чрезмерно сложной с тем, чтобы для ее исследования и решения можно было успешно применить разработанный к настоящему времени соответствующий математический аппарат. Именно поэтому этап построения математической модели в значительной степени зависит от опыта, интуиции и искусства исследователей обеих сторон. Его невозможно отождествить с простым формальным применением уже известных, хорошо описанных алгоритмов.
Здесь следует еще добавить, что любая задача выбора (в том числе и многокритериальная) тесно связана с конкретным ЛПР(лицо, принимающее решение). Уже на стадии формирования математической модели при построении множества возможных решений и векторного критерия дело не обходится без советов, рекомендаций и указаний ЛПР, тем более что векторный критерий как раз и служит. Принятие решения при многих критериях для выражения целей ЛПР. При этом ясно, что построить модель в точности соответствующую всем реальным обстоятельствам невозможно. Модель всегда является упрощением действительности. Важно добиться, чтобы она содержала те черты и детали, которые в наибольшей степени влияют на окончательный выбор наилучшего решения.
Рассмотрим два
произвольных возможных решения
и
.
Для них имеет место один и только один
из следующих трех случаев:
1) справедливо
соотношение
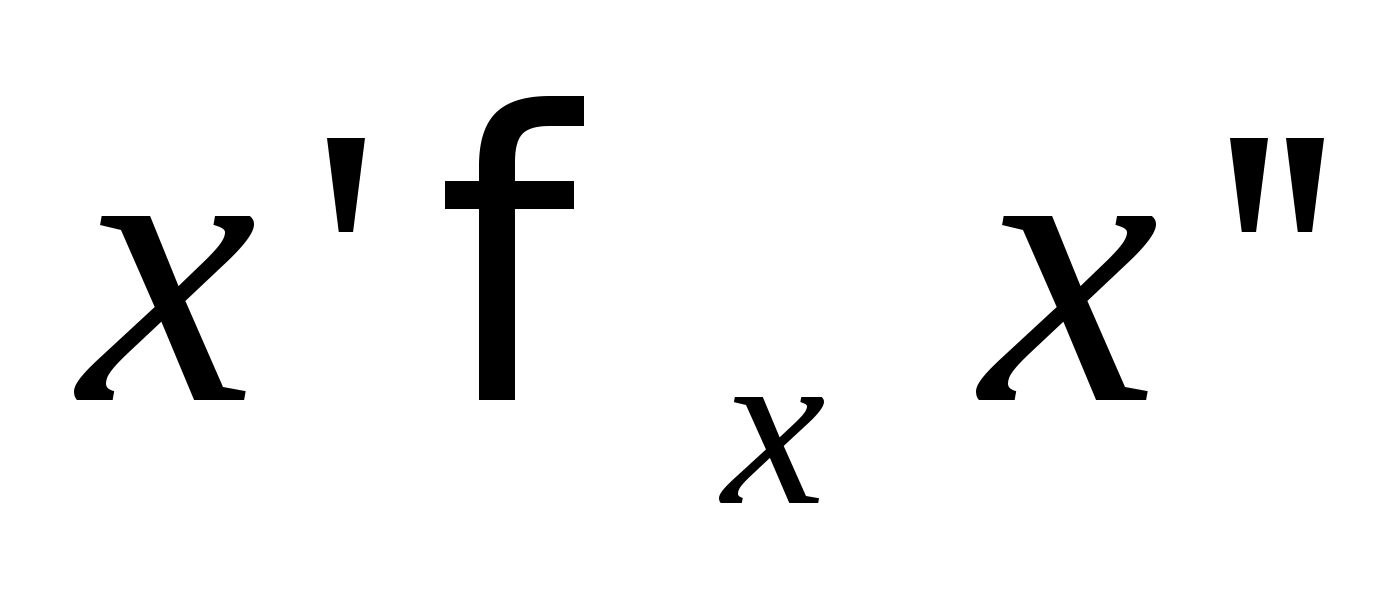(ЛПР первое решение предпочитает
второму),
2) справедливо
соотношение
(ЛПР второе решение предпочитает
первому),
3) не выполняется ни
соотношение
,
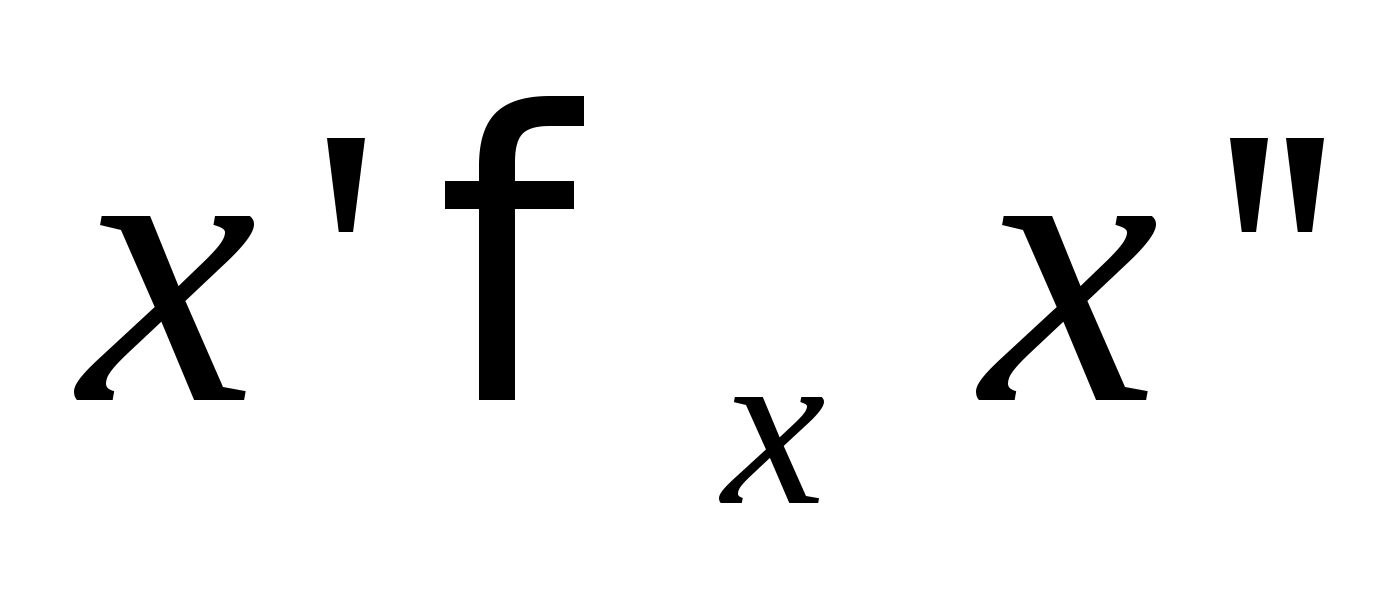ни соотношение
(ЛПР не может отдать предпочтение ни
одному из указанных двух решений).
Заметим, что четвертый
случай, когда оба участвующих здесь
соотношения
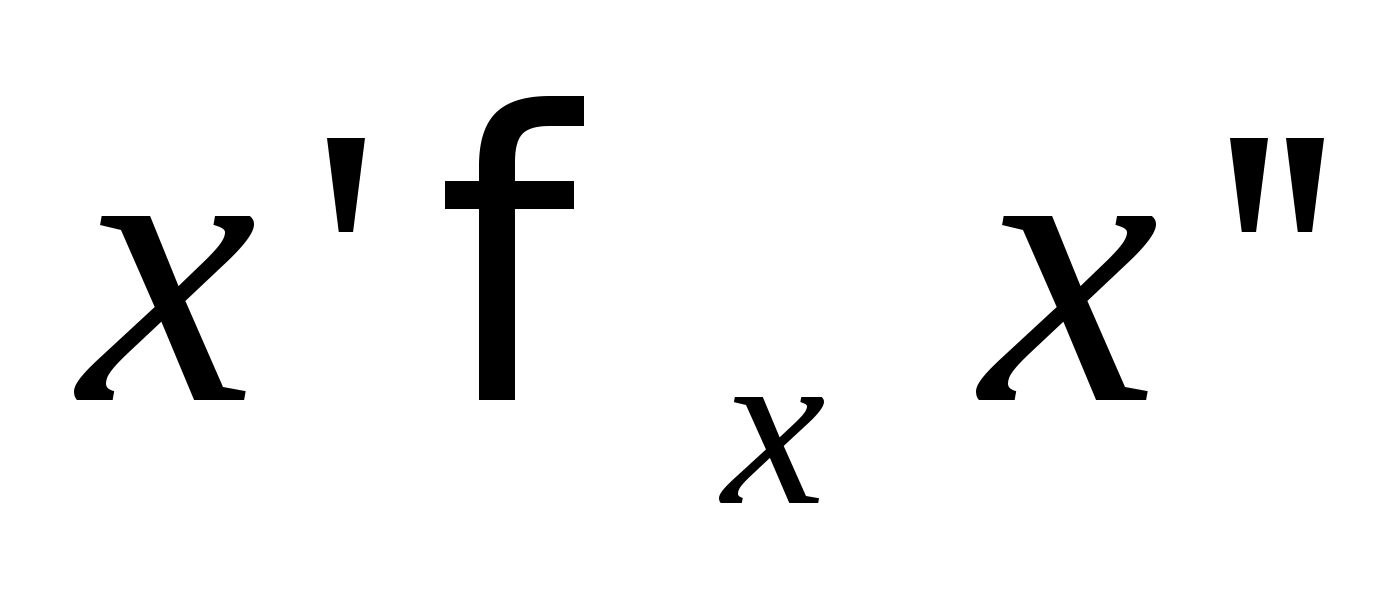и
выполняются, невозможен благодаря
асимметричности отношения предпочтения
В первом из указанных
выше случаев, т.е. при выполнении
соотношения
,
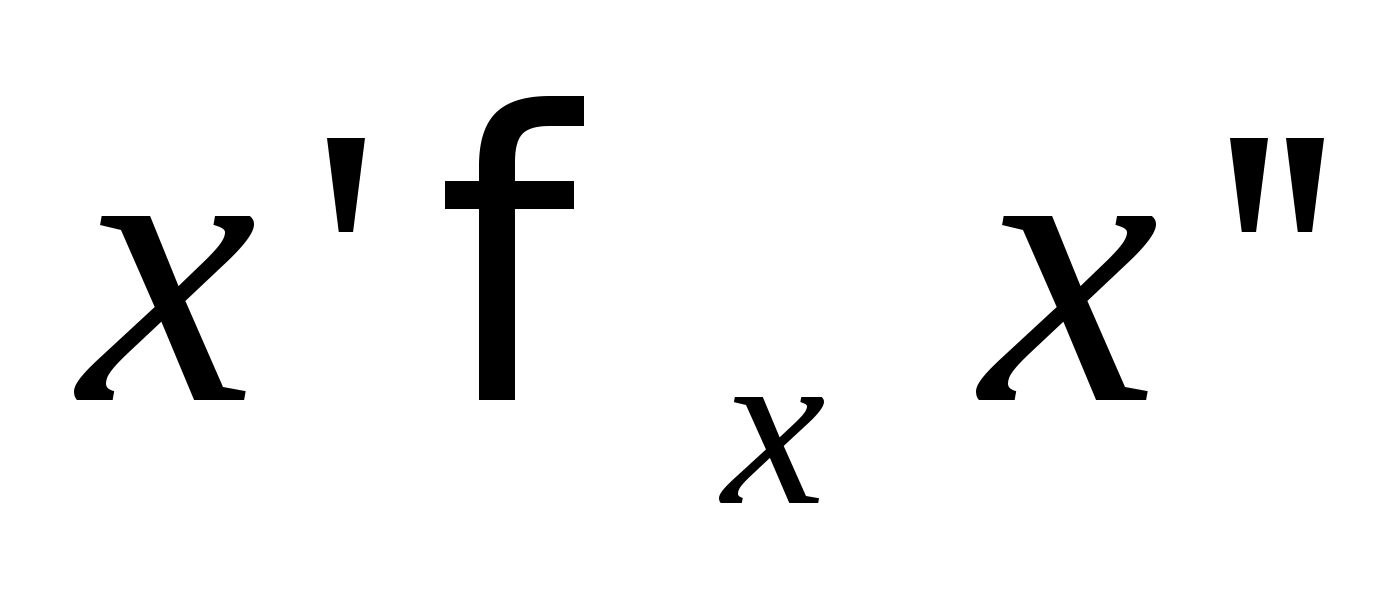говорят, что решение
доминирует решение
.
Если же реализуется
третий случай, то говорят, что решения
и
не
сравнимы по отношению предпочтения.
3. Реализация программного средства
Среда разработки: Visual Studio 2008 Язык программирования: C#
3.1 Проектирование
При проектировании программного средства будем использовать объектно-ориентированный подход. Список классов с кратким описанием:
Program.cs – это главное окно, служит для ввода данных, запуска работы алгоритма поиска парето-оптимальных решений, содержит методы для решения поставленной задачи.
Reader.cs – методы для загрузки данных из файла
Writer.cs – методы для сохранения данных в файл
3.2 Алгоритм поиска альтернативных решений
Шаг 1. Назначение
весов. Назначаются положительные веса
каждого из критериев
Шаг 2. Построение индекса согласия. Для
каждой пары альтернатив j
и k
множество критериев
разбивается на три группы:
,
,
Множество
включает те категории, по которым j-я
альтернатива лучше k-й,
множество
,
состоит из критериев, которым j-я
альтернатива хуже k-й,
а множество
,
состоит из тех критериев, по которым
j-я
и k-я
альтернативы эквивалентны. Индекс
согласия с тем , что альтернатива j
лучше альтернативы k
определяется следующим образом:
,
Где α – параметр, α
Шаг 3. Построение списка несогласия. Для каждой пары j и k индекс несогласия с тем, что альтернатива j лучше альтернативы k определяется по формуле:
Где интервал
превосходства k-й
альтернативы над j-й
по i-му
критерию определяет число последовательных
переходов из класса в класс, которое
необходимо осуществить для того, чтобы
j-й
вариант стал эквивалентен k-му
по i-му
критерию, умноженное на цену одного
деления такого перехода. При этом
требуется, чтобы величины
не превышали единицу
Шаг 4. Построение
решающего правила. На основе чисел
и
,
определяемы ЛПР, на множестве альтернатив
строится следующее бинарное отношение:
j-я
альтернтива признается лучше альтернативы
k,
при условии того, что
.
Сразу можно заметить, что при
указанное бинарное отношение становится
аналогом бинарного отношения Слейтера,
поскольку в этом случае j-я
альтернатива доминирует k-ю
лишь тогда, когда
,
т.е.
для всех
.
При
могут возникнуть другие пары альтернатив,
связанные введенным бинарным отношением.
После того как бинарное отношение построено, представляется множество взаимнонедоминирующих альтернатив, на котором построенное бинарное отношение обладает НМ-свойством. Далее ЛПР выбирает окончательное решение из этого множества. Таким образом данный метод позволяет сократить число анализируемых вариантов, облегчая тем самым выбор ЛПР.
3.3 Листинг программного кода
public partial class Form1 : Form
{
private int countOfVariant;
private int countOfCriterion;
private double p;
private double q;
private double alfa;
private int max = 0;
private double Interval = 0;
private int count1 = 0;
private int count2 = 0;
private int row1;
private int col1;
private static int rows;
private static int cols;
private Double[,] tablesWeight;
private Double[,] tablesCriterionImportance;
private Double[,] tablesIntervalSuperiority;
private Double[,] TableOfAgreementIndex;
private Double[,] TableOfDisagreementIndex;
private String[,] TableofDecisiveRule;
// private Double[,] tablesCriterionImportance;
private double CriterionSumm = 0;
public Form1()
{
InitializeComponent();
}
// получение числа вариантов, числа критериев и параметра альфа
private void GetDate()
{
countOfVariant = (int)numericUpDown1.Value;
countOfCriterion = (int)numericUpDown2.Value;
alfa = Convert.ToDouble(comboBox1.Text);
}
// создание и заполнение таблицы весов из формы
private void createTableOfWeightFromForm()
{
tablesWeight = new double[rows, cols];
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < cols; j++)
{
tablesWeight[i, j] = Convert.ToDouble(dataGridView1.Rows[i].Cells[j].Value);
}
}
}
// создание и заполнение таблицы важности критериев, числа интервалов превосходства
//и стоимость перехода с уровня на уровень из формы
private void createTableOfCriterionImportanceFromForm()
{
tablesCriterionImportance = new double[cols, 3];
for (int i = 0; i < cols; i++)
{
tablesCriterionImportance[i, 0] = Convert.ToDouble(dataGridView5.Rows[i].Cells[0].Value);
CriterionSumm += tablesCriterionImportance[i, 0];
//textBox1.AppendText(CriterionSumm.ToString());
}
}
//создание таблицы интервалов превосходства из формы
private void createTableOfIntervalSuperiorityFromForm()
{
tablesIntervalSuperiority = new double[cols, (max + 1)];
for (int i = 0; i < cols; i++)
{
for (int j = 0; j < (max + 1); j++)
tablesIntervalSuperiority[i, j] = Convert.ToDouble(dataGridView6.Rows[i].Cells[j].Value);
}
}
//создание таблицы весов на форме
private void CreateTableOfWeightOnForm(int row, int col)
{
int _row = row;
int _col = col;
dataGridView1.ColumnCount = _col;
dataGridView1.RowHeadersVisible = false;
dataGridView1.AutoSizeRowsMode = DataGridViewAutoSizeRowsMode.AllCells;
dataGridView1.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells;
dataGridView1.RowCount = _row;
}
// создание таблицы важности критериев на форме
private void CreateTableOfCriterionImportanceOnForm(int row)
{
int _row = row;
int _col = 3;
dataGridView5.ColumnCount = _col;
dataGridView5.RowHeadersVisible = false;
dataGridView5.AutoSizeRowsMode = DataGridViewAutoSizeRowsMode.AllCells;
dataGridView5.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells;
dataGridView5.RowCount = _row;
}
// создание таблицы ядра из формы
private void CreateTableofDecisiveRuleFromForm()
{
TableofDecisiveRule = new string[rows, 1];
for (int i = 0; i < rows; i++)
{
TableofDecisiveRule[i, 0] = dataGridView4.Rows[i].Cells[0].Value.ToString();
}
}
private void button1_Click(object sender, EventArgs e)
{
GetDate();
rows = (int)countOfVariant;
cols = (int)countOfCriterion;
CreateTableOfWeightOnForm(rows, cols);
CreateTableOfCriterionImportanceOnForm(cols);
}
//добавление интервала превосходства
private void IntervalSuperiority(int row)
{
for (int i = 0; i < cols; i++)
{
if (max < Convert.ToDouble(dataGridView5.Rows[i].Cells[1].Value))
{
max = Convert.ToInt16(dataGridView5.Rows[i].Cells[1].Value);
}
}
int _row = row;
int _col = (max + 1);
dataGridView6.ColumnCount = _col;
dataGridView6.RowHeadersVisible = false;
dataGridView6.AutoSizeRowsMode = DataGridViewAutoSizeRowsMode.AllCells;
dataGridView6.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells;
dataGridView6.RowCount = _row;
}
// получение матрицы индексов согласия
private void GetTableOfAgreementIndex(int row, int col)
{
double IPlus = 0;
double IMinus = 0;
double IZero = 0;
int _row = row;
int _col = col;
dataGridView2.ColumnCount = _col;
dataGridView2.RowHeadersVisible = false;
dataGridView2.AutoSizeRowsMode = DataGridViewAutoSizeRowsMode.AllCells;
dataGridView2.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells;
dataGridView2.RowCount = _row;
TableOfAgreementIndex = new double[rows, rows];
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < rows; j++)
{
if (i == j)
{
TableOfAgreementIndex[i, j] = 0;
}
else
{
IPlus = 0;
IMinus = 0;
IZero = 0;
for(int k = 0; k < cols; k++)
{
if (Convert.ToDouble(dataGridView1.Rows[i].Cells[k].Value) > Convert.ToDouble(dataGridView1.Rows[j].Cells[k].Value))
{
IPlus += Convert.ToDouble(dataGridView5.Rows[k].Cells[0].Value);
}
else if (Convert.ToDouble(dataGridView1.Rows[i].Cells[k].Value) == Convert.ToDouble(dataGridView1.Rows[j].Cells[k].Value))
{
IZero += Convert.ToDouble(dataGridView5.Rows[k].Cells[0].Value);
}
else
{
IMinus += Convert.ToDouble(dataGridView5.Rows[k].Cells[0].Value);
}
}
TableOfAgreementIndex[i, j] = (IPlus + alfa * IZero) / (CriterionSumm);
}
dataGridView2.Rows[i].Cells[j].Value = TableOfAgreementIndex[i, j];
}
}
}
получение матрицы индексов несогласия
private void GetTableOfDisagreementIndex(int row, int col)
{
Double[,] count;
int _row = row;
int _col = col;
dataGridView3.ColumnCount = _col;
dataGridView3.RowHeadersVisible = false;
dataGridView3.AutoSizeRowsMode = DataGridViewAutoSizeRowsMode.AllCells;
dataGridView3.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells;
dataGridView3.RowCount = _row;
count = new double[cols, 2];
TableOfDisagreementIndex = new double[rows, rows];
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < rows; j++)
{
if (i == j)
{
TableOfDisagreementIndex[i, j] = 0;
}
else
{
Interval = 0;
for (int k = 0; k < cols; k++)
{
count[k, 0] = 0;
count[k, 1] = 0;
count1 = 0;
count2 = 0;
for (int m = 0; m < (Convert.ToInt32(dataGridView5.Rows[k].Cells[1].Value) + 1); m++)
{
if (Convert.ToDouble(dataGridView1.Rows[i].Cells[k].Value) > Convert.ToDouble(dataGridView6.Rows[k].Cells[m].Value))
{
count1 += 1;
}
else
{
count1 = count1;
}
if (Convert.ToDouble(dataGridView1.Rows[j].Cells[k].Value) > Convert.ToDouble(dataGridView6.Rows[k].Cells[m].Value))
{
count2 += 1;
}
else
{
count2 = count2;
}
/* textBox1.AppendText(" ");
textBox1.AppendText(count1.ToString());
textBox1.AppendText(" ");
textBox1.AppendText(count2.ToString());
//textBox1.AppendText(" ");
//textBox1.AppendText(dataGridView1.Rows[i].Cells[k].Value.ToString());*/
}
count[k, 0] = count1;
count[k, 1] = count2;
if (count[k, 0] < count[k, 1])
{
Interval += (count[k, 1] - count[k, 0]) * (Convert.ToDouble(dataGridView5.Rows[k].Cells[2].Value));
}
else
{
Interval = Interval;
}
TableOfDisagreementIndex[i, j] = Interval/100;
textBox1.AppendText(" ");
textBox1.AppendText(Interval.ToString());
}
}
dataGridView3.Rows[i].Cells[j].Value = TableOfDisagreementIndex[i, j];
}
}
}
получение параметров p и q
private void GetParametrsForDecisiveRule()
{
p = Convert.ToDouble(numericUpDown3.Value);
q = Convert.ToDouble(numericUpDown4.Value);
}
//построение решающего правила
private void GetDecisiveRule(int row,int col)
{
bool flag = false;
int count = 0;
int countOfq = 0;
int countOfp = 0;
int _row = row;
int _col = col;
dataGridView4.ColumnCount = _col;
dataGridView4.RowHeadersVisible = false;
dataGridView4.AutoSizeRowsMode = DataGridViewAutoSizeRowsMode.AllCells;
dataGridView4.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells;
dataGridView4.RowCount = _row;
for (int i = 0; i < rows; i++)
{
count = 0;
countOfq = 0;
countOfp = 0;
for (int j = 0; j < cols; j++)
{
count += 1;
if (i != j)
{
if (Convert.ToInt32(dataGridView3.Rows[i].Cells[j].Value) < q)
{
countOfq += 1;
if (Convert.ToInt32(dataGridView2.Rows[i].Cells[j].Value) < p)
{
countOfp += 1;
}
else
{
if ((count == cols) & (countOfp == 0))
{
flag = true;
}
}
}
else
{
if ((count == cols) & (countOfq == 0))
{
flag = true;
}
}
}
}
dataGridView4.Rows[i].Cells[0].Value = flag;
}
}
private void button2_Click(object sender, EventArgs e)
{
createTableOfCriterionImportanceFromForm();
createTableOfWeightFromForm();
GetTableOfAgreementIndex(rows, rows);
}
private void button3_Click(object sender, EventArgs e)
{
GetTableOfDisagreementIndex(rows, rows);
}
private void закрытьToolStripMenuItem_Click(object sender, EventArgs e)
{
Close();
}
private void button6_Click(object sender, EventArgs e)
{
IntervalSuperiority(cols);
}
private void button5_Click(object sender, EventArgs e)
{
GetDecisiveRule(rows, 1);
CreateTableofDecisiveRuleFromForm();
}
private void button4_Click(object sender, EventArgs e)
{
GetParametrsForDecisiveRule();
}
//загрузка таблицы весов
private void button8_Click(object sender, EventArgs e)
{
string FN;
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
openFileDialog1.InitialDirectory = "G:\temp";
openFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
FN = openFileDialog1.FileName;
Reader My = new Reader(FN);
My.ReadTable(out tablesWeight, out rows, out cols);
alfa = Convert.ToDouble(comboBox1.Text);
CreateTableOfWeightOnForm(rows, cols);
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < cols; j++)
{
dataGridView1.Rows[i].Cells[j].Value = tablesWeight[i, j];
}
}
}
}
// сохранение таблицы весов
private void button7_Click(object sender, EventArgs e)
{
string FN;
saveFileDialog1.InitialDirectory = "G:\temp";
saveFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FN = saveFileDialog1.FileName;
Writer.WriteTable(FN, tablesWeight);
}
}
// загрузка таблицы критериев важности
private void button9_Click(object sender, EventArgs e)
{
string FN;
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
openFileDialog1.InitialDirectory = "G:\temp";
openFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
FN = openFileDialog1.FileName;
Reader My = new Reader(FN);
My.ReadTable(out tablesCriterionImportance, out row1, out col1);
alfa = Convert.ToDouble(comboBox1.Text);
CreateTableOfCriterionImportanceOnForm(row1);
for (int i = 0; i < row1; i++)
{
for (int j = 0; j < col1; j++)
{
dataGridView5.Rows[i].Cells[j].Value = tablesCriterionImportance[i, j];
}
}
}
}
// загрузка таблицы интервалов превосходства
private void button11_Click(object sender, EventArgs e)
{
string FN;
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
openFileDialog1.InitialDirectory = "G:\temp";
openFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
FN = openFileDialog1.FileName;
Reader My = new Reader(FN);
My.ReadTable(out tablesIntervalSuperiority, out row1, out col1);
alfa = Convert.ToDouble(comboBox1.Text);
IntervalSuperiority(row1);
for (int i = 0; i < row1; i++)
{
for (int j = 0; j < col1; j++)
{
dataGridView6.Rows[i].Cells[j].Value = tablesIntervalSuperiority[i, j];
}
}
}
}
//сохранение таблицы критериев важности
private void button10_Click(object sender, EventArgs e)
{
string FN;
saveFileDialog1.InitialDirectory = "G:\temp";
saveFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FN = saveFileDialog1.FileName;
Writer.WriteTable(FN, tablesCriterionImportance);
}
}
// сохранение таблицы интервалов превосходства
private void button12_Click(object sender, EventArgs e)
{
string FN;
saveFileDialog1.InitialDirectory = "G:\temp";
saveFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FN = saveFileDialog1.FileName;
Writer.WriteTable(FN, tablesIntervalSuperiority);
}
}
// сохранение матрицы индексов согласия
private void button13_Click(object sender, EventArgs e)
{
string FN;
saveFileDialog1.InitialDirectory = "G:\temp";
saveFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FN = saveFileDialog1.FileName;
Writer.WriteTable(FN, TableOfAgreementIndex);
}
}
//сохранение матрицы индексов несогласия
private void button14_Click(object sender, EventArgs e)
{
string FN;
saveFileDialog1.InitialDirectory = "G:\temp";
saveFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FN = saveFileDialog1.FileName;
Writer.WriteTable(FN, TableOfDisagreementIndex);
}
}
//сохранение ядра
private void button15_Click(object sender, EventArgs e)
{
string FN;
saveFileDialog1.InitialDirectory = "G:\temp";
saveFileDialog1.Filter = "diag files(*.diag)|*.abs|All files|*.*";
if (saveFileDialog1.ShowDialog() == DialogResult.OK)
{
FN = saveFileDialog1.FileName;
Writer.WriteTableOfRule(FN, TableofDecisiveRule);
}
}
}
class Reader
{
private string fileName;
private string[] inputTxt;
private double[,] matrix;
private int row;
private int col;
private System.Globalization.NumberFormatInfo numberFormat;
public Reader(string Name)
{
fileName = Name;
}
public void ReadTable(out double[,] table, out int rows, out int cols)
{
numberFormat = new System.Globalization.NumberFormatInfo();
numberFormat.CurrencyDecimalSeparator = ".";
string[] output = File.ReadAllLines(fileName);
string[] aloneString = output[0].Split(new char[] { ' ' });
//double[,] temp = new double[output.Length, aloneString.Length];
table = new double[output.Length, aloneString.Length];
rows = output.Length;
cols = aloneString.Length;
for (int i = 0; i < aloneString.Length; i++)
{
table[0, i] = double.Parse(aloneString[i], numberFormat);
}
for (int i = 1; i < output.Length; i++)
{
aloneString = output[i].Split(new char[] { ' ' });
for (int j = 0; j < aloneString.Length; j++)
{
table[i, j] = double.Parse(aloneString[j], numberFormat);
}
}
}
}
class Writer
{
private static string fileName;
private static string[] outputTxt;
private static double[,] matrix;
private static string[,] matrix1;
private static int row;
private static int col;
private static System.Globalization.NumberFormatInfo numberFormat;
public static void WriteTable(string nameFile, double[,] table)
{
Writer.fileName = nameFile;
Writer.matrix = table;
if (Writer.matrix != null)
{
row = matrix.GetLength(0);
col = matrix.GetLength(1);
outputTxt = new string[row];
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
outputTxt[i] += matrix[i, j].ToString();
if(j != (col - 1))
outputTxt[i] += " ";
}
}
File.WriteAllLines(nameFile, outputTxt);
}
}
public static void WriteTableOfRule(string nameFile, string[,] table)
{
Writer.fileName = nameFile;
Writer.matrix1 = table;
if (Writer.matrix1 != null)
{
row = matrix1.GetLength(0);
col = matrix1.GetLength(1);
outputTxt = new string[row];
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
outputTxt[i] += matrix1[i, j];
if (j != (col - 1))
outputTxt[i] += " ";
}
}
File.WriteAllLines(nameFile, outputTxt);
}
}
}
4. Пример работы программы
4.1 Многокритериальная задача
Реализуем пример. Для этого воспользуемся уже заготовленными файлами с входными данными:
Рис
Найдем матрицу согласия:
Рис
Найдем матрицу индексов несогласия:
Рис
Найдем ядро бинарного отношения:
Рис
Выводы
В результате проделанной работы было разработано программное средство для поиска альтернативных вариантов решений для многокритериальных задач.
Данное приложение может использоваться лишь как демонстрационно-обучающее по теме «Многокритериальные задачи. Метод альтернативных решений» дисциплины «Теория принятия решений».
Используемая литература
1. А.В Лотов, И.И. Поспелова Многокритериальные задачи принятия решения Учебное пособие.– М. : МАКС Пресс, 2008. – 197 с.
Используемые программные средства
Microsoft Visual Studio 2008