Расчет информационных характеристик дискретного канала

Содержание

Часть 1. Теория информации

1. Система передачи дискретных сообщений

1.1 Схема дискретного канала, функции блоков, источника и приемника

1.2 Виды информации

2. Канальная матрица (КМИ; КМП; КМО) и их взаимосвязь

2.1 Свойства канальных матриц

3. Информационные характеристики источника сообщений

3.1 Количество информации источника

3.2 Информационные потери

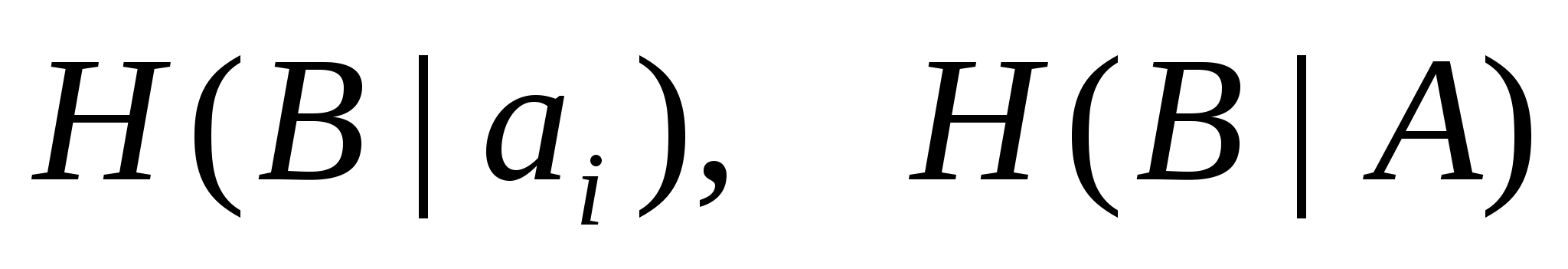
4. Информационные характеристики приемника

4.1 Количество информации приемника

4.2 Информационные потери

5. Скоростные характеристики

5.1 Скорость модуляции 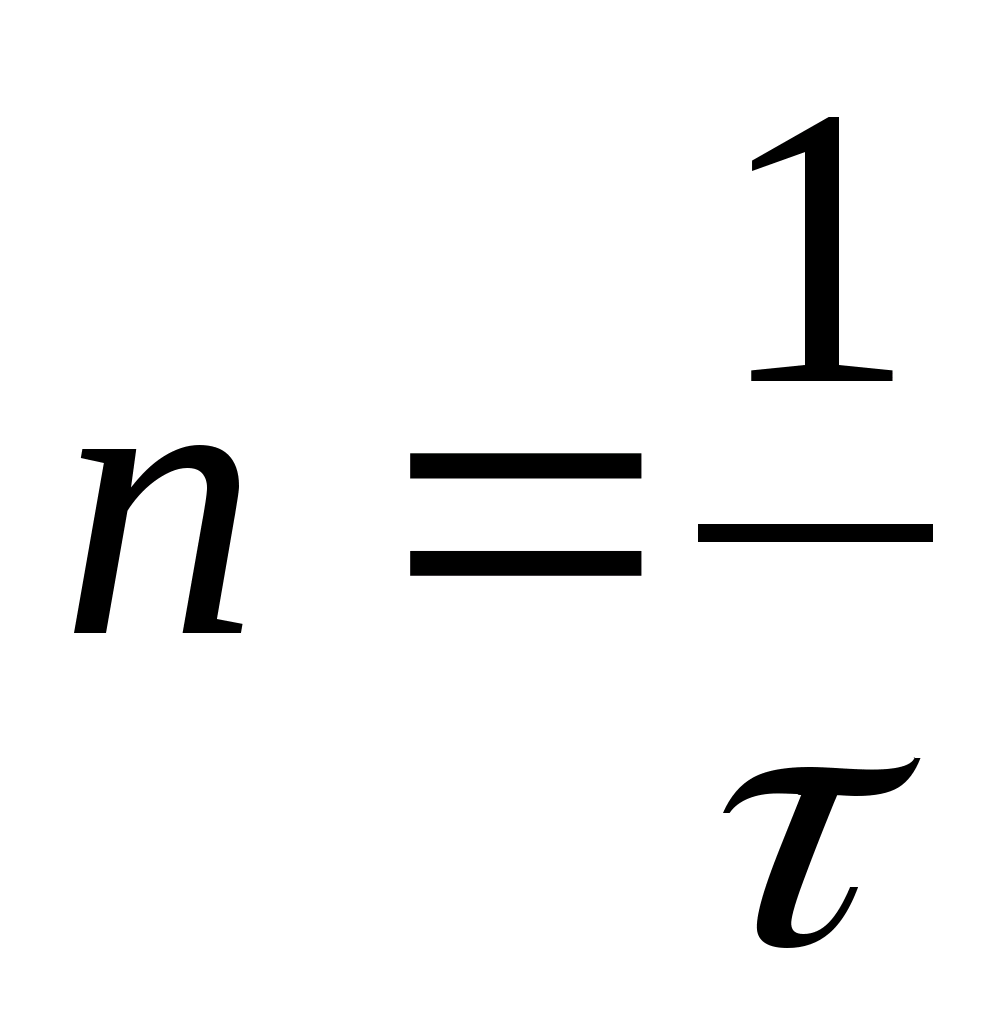симв/сек;

5.2 Производительность источника бод;

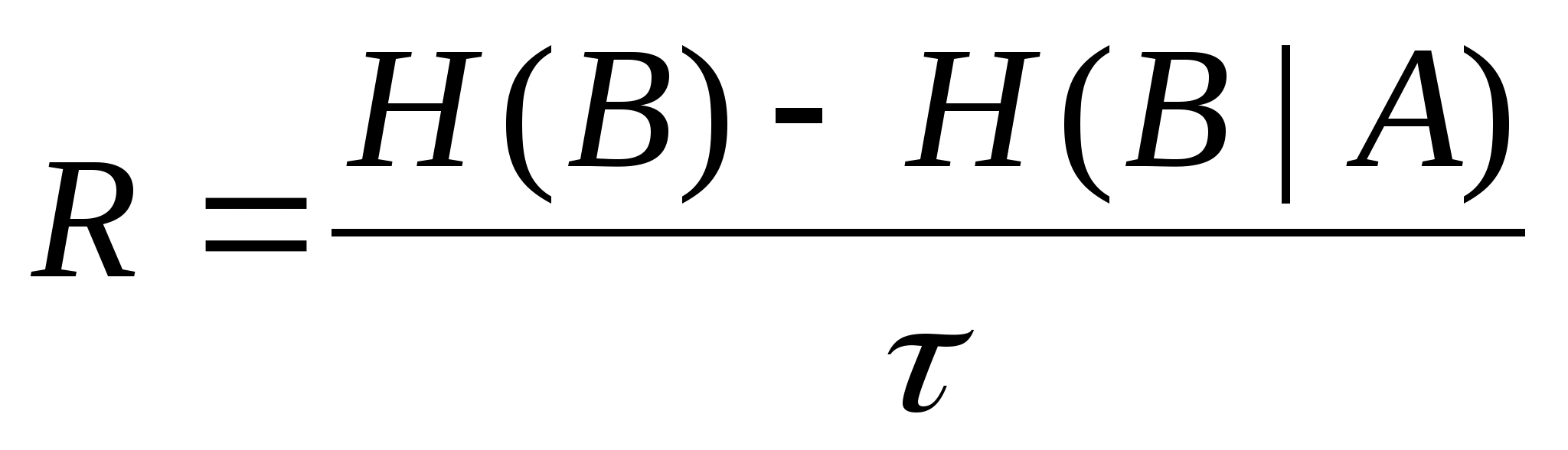5.3 Скорость передачи или бод;

5.4 Емкость канала 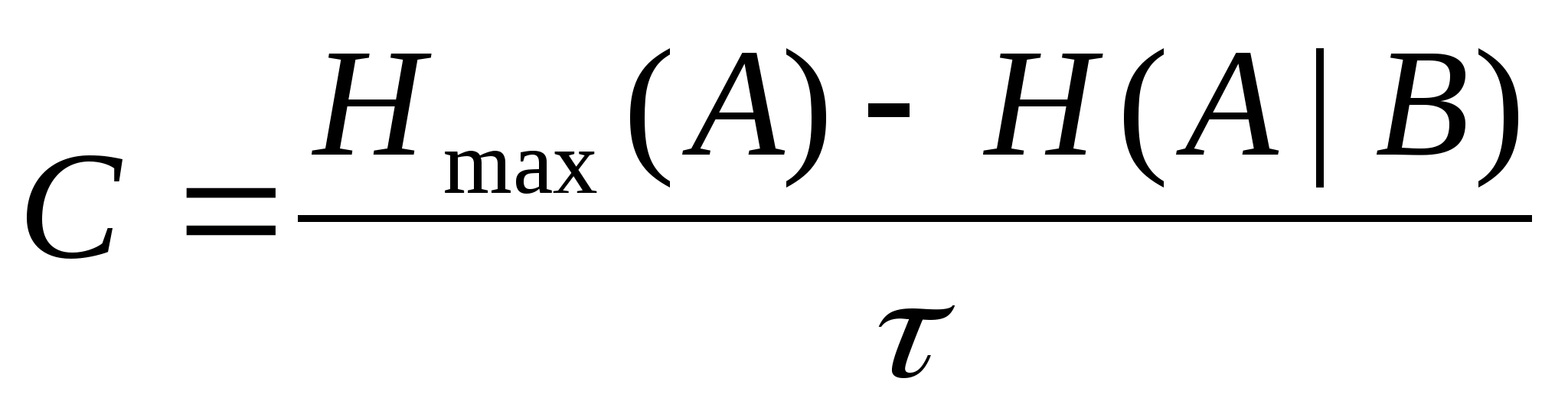или бод;

5.5 Коэффициент эффективности дискретного канала ;

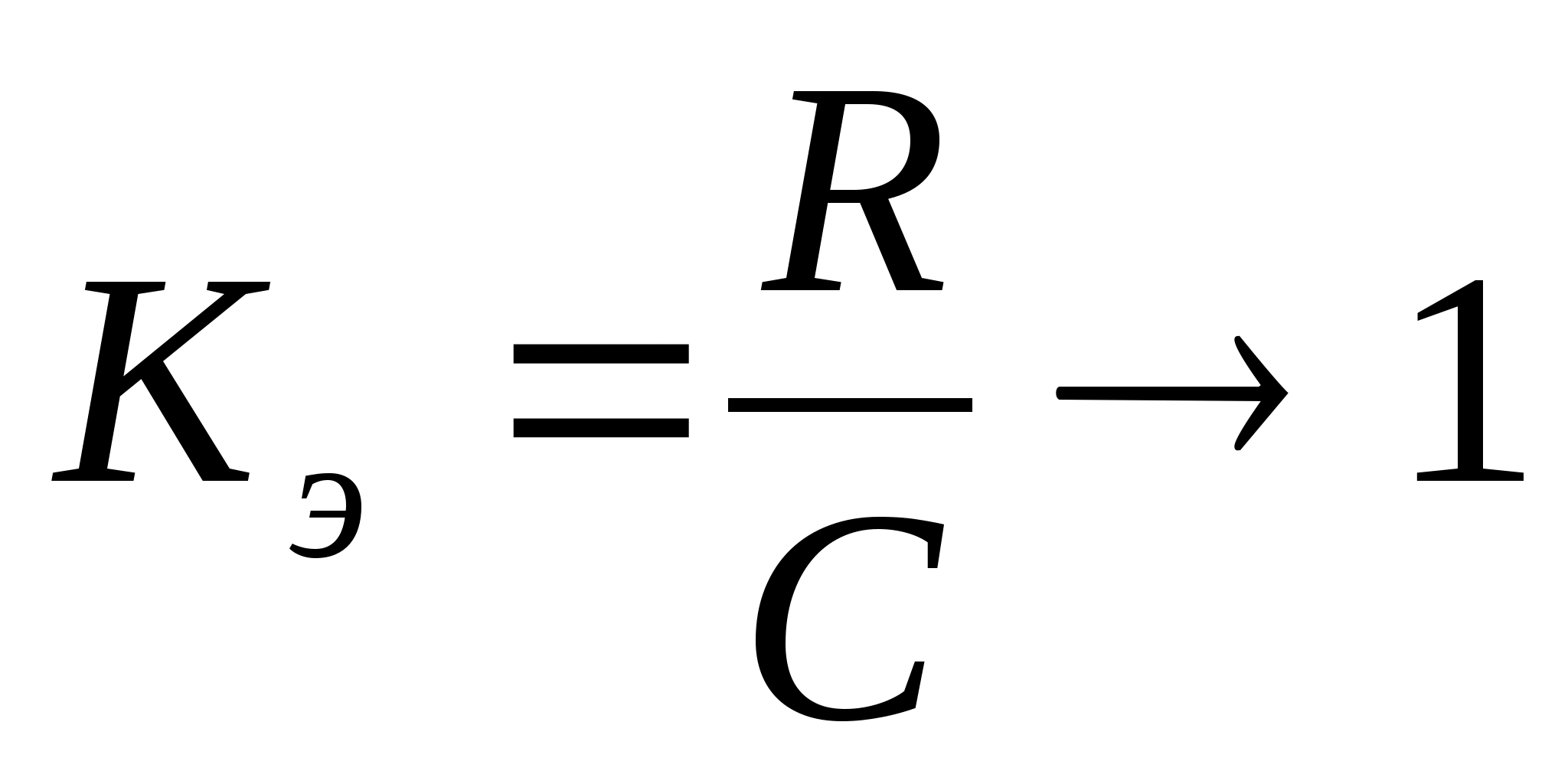5.6 Теоремы Шеннона о критической скорости и кодированию

Часть 2. Теория кодирования

6. Оптимальное кодирование. Идея сжатия

6.1 Равномерный двоичный код (РДК), корневое бинарное дерево РДК, длина кода РДК, сообщение в РДК

6.2 Оптимальный неравномерный код ОНК Шеннона-Фано, алгоритм расчета ОНК, средняя длина, энтропия, коэффициент сжатия, коэффициент эффективности, сообщение в ОНК, критерий Фано, корневое бинарное дерево ОНК Шеннона-Фано

6.3 Оптимальный неравномерный ОНК Хаффмана, алгоритм расчета ОНК, средняя длина, энтропия, коэффициент сжатия, коэффициент эффективности, сообщение в ОНК, КБД

6.4 Эффективность ОНК

7. Помехоустойчивое кодирование. Назначение

7.1 Обнаруживающие коды

7.1.1 Обнаруживающий код четности (ОКЧ)

7.1.2 Обнаруживающий код удвоения (ОКУ)

7.1.3 Обнаруживающий код инверсией (ОКИ)

7.1.4 Обнаруживающий код Стандартный телеграфный код (ОК СТК №3) №3

7.2 Корректирующий систематический код Хэмминга: генерация, диагностика, коррекция, декодирование

7.3 Корректирующий циклический код: генерация, диагностика, коррекция, декодирование

7.4 Корректирующий мажоритарный код: генерация, диагностика, коррекция, декодирование (другие названия – код по голосованию, К-удвоения)

7.5 Эффективность помехоустойчивых кодов

8. Криптографическое кодирование. Назначение

8.1 Основы криптографического кодирования

8.2 Принципы криптографии по Шеннону

8.3 Требования к криптографическим алгоритмам

8.4 Криптографическое правило Кирхгофа

8.5 Абсолютно стойкий ключ по Шеннону

8.6 Жизненный цикл конфиденциальности данных

8.7 Критерии взлома ключа

8.8 Классификация криптографических методов

Часть 1. Теория информации

1. Система передачи дискретных сообщений

Информационные каналы бывают аналоговые (информация в непрерывном виде) и цифровые (дискретные). Широкое развитие получила цифровая техника и дискретные каналы.

1.1 Схема, функции блоков источника и приемника

Информационную систему передачи данных по каналу связи можно представить крупноблочно (Рис1).

Рис1.Крупноблочное представление информационного канала

Источник сообщения (ИС) – вырабатывает сообщения, кодеры источника преобразуют сообщения в кодовые слова, используя методы оптимального, помехоустойчивого и криптографического кодирования. Модулятор преобразует бинарные коды в электрические сигналы.

Линия связи (ЛС) – это физическая среда, в которой распространяются сигналы: кабельные, радио и спутниковые линии.

Приемник сообщения (ПС) – выполняет обратное превращение: демодулятор преобразует электрические сигналы в бинарные коды, декодеры выполняют диагностику и корректирование ошибок, снимают сжатие, помехоустойчивость и криптографическую защиту информации.

Рис.2.Схема системы передачи дискретных сообщений

Функции блоков источника:

    АЦП – алфавитно-цифровой преобразователь (аналоговая информация преобразуется в дискретную);

    Шифратор – устанавливает криптографическую защиту;

    Кодер ОНК (ОНК - оптимальный неравномерный код) - сжимает данные;

    Кодер ПЗК (ПЗК – помехозащищенный код) – устанавливает защиту от помех;

    Модулятор – преобразует цифровую информацию в электрические сигналы;

    Линии связи – телефонные, кабельные, радио, спутниковые.

Функции блоков приемника:

    Демодулятор – преобразует электрические сигналы в двоичный код;

    Декодер ПЗК – определяет наличие ошибки, вычисляет адрес ошибки, корректирует её, снимает помехоустойчивую защиту;

    Декодер ОНК – неравномерный код преобразуется в равномерный двоичный код;

    Дешифратор – снимает криптозащиту;

    ЦАП – цифро-аналоговый преобразователь (дискретную информацию преобразовывает в непрерывную).

1.2 Виды информации

В процессе прохождения по каналу информация многократно меняет свою форму, сохраняя при этом свое содержание:

    Непрерывная информация;

    Дискретная информация;

    Криптокод;

    Оптимальный неравномерный код (двоичный);

    Помехоустойчивый код;

    Электрические сигналы.

Расчёт количества информации символов алфавита

Для начала нам необходимо вычислить v>i>> >– частоту появления каждого символа алфавита. Сумма v>i> будет равна длине сообщения l>s>.

Теперь рассчитываем P(a>i>)– вероятность появления символа нашего алфавита в сообщении.

P(a>i>) = v>i>/l>s>

Сумма таких вероятностей должна быть равна единице.

После этого мы можем найти требуемое количество информации по формуле: I(a>i>) = - log(P(a>i>)) [бит]

Свойства количества информации:

1. Количество информации не отрицательно:

I(a>i>) ≥ 0

2. Чем выше вероятность, тем меньшее количество информации содержит символ.

Рис.3. График к свойству 2

3. Если вероятность символа равна 1, то количество информации этого символа равно 0:

Р(a>i>) = 1 ⇒ I(a>i>) = 0

4. Аддитивность. Количество информации нескольких символов равно сумме количеств информаций каждого:

I(a>1, >a>2, >a>3>) = I(a>1>) + I(a>2>) + I(a>3>)

Энтропия дискретного ансамбля сообщения

Энтропия – среднее количество информации на символ сообщения.

Расчёт энтропии алфавита

Для вычисления энтропии алфавита нам понадобится l>а> - количество символов алфавита.

Максимальная энтропия алфавита будет равна:

H>max>(А)= log l>a >[бит/символ]

Причём нужно отметить, что логарифм мы берём по основанию 2.

Расчёт энтропии сообщения

Для нахождения энтропии сообщения нам требуется вычислить такое значение:

H (A) = -∑(P(a>i>)*logP(a>i>)) [бит/символ]

Расчёт максимальной энтропии

Максимальную энтропию считаем по формуле:

H>max>(А)= log l>s>> >[бит/символ]

Свойства энтропии:

1. Энтропия не отрицательна:

Н(A) ≥ 0

2. Энтропия равна нулю тогда и только тогда, когда вероятность символа равна 1.

Н(A) = 0 ⇔ Р(a>i>) =1

3. Энтропия ограничена:

H (A) ≤ log l>s>> >[бит/символ]

где l>s> – количество символов в сообщении.

4. Максимальная энтропия равна:

H>max>(А ) = log l>s>> >[бит/символ]

Рис.4. График к свойству 4

Расчётная таблица результатов

В данную таблицу мы внесем все наши результаты расчётов и, как результат, построим график количества информации и график энтропии.

S= (У жизни есть чувство юмора)

А= (У,ж,и,з,н,е,с,т,ь,ч,в,о,ю,м,р,а, .)

i

a>i>

v>i>

P(a>i>)

I(a>i>)

H

1

У

2

0,077

3,700

0,285

2

ж

1

0,038

4,700

0,181

3

и

2

0,077

3,700

0,285

4

з

1

0,038

4,700

0,181

5

н

1

0,038

4,700

0,181

6

е

1

0,038

4,700

0,181

7

с

2

0,077

3,700

0,285

8

т

2

0,077

3,700

0,285

9

ь

1

0,038

4,700

0,181

10

ч

1

0,038

4,700

0,181

11

в

2

0,077

3,700

0,285

12

о

2

0,077

3,700

0,285

13

ю

1

0,038

4,700

0,181

14

м

1

0,038

4,700

0,181

15

р

1

0,038

4,700

0,181

16

а

1

0,038

4,700

0,181

17

_

4

0,154

2,700

0,415

Суммы

26

1,000

3,931

H(А)= log l>a>> >= log16 = 4 [бит/символ]

H>max>(A)= log22= 4,4594 [бит/символ]

2. Канальные матрицы (КМИ, КМП, КМО) и их взаимосвязь

Канальная матрица определяет действие помех на дискретном канале.

Канальные матрицы бывают трёх видов: канальная матрица источника, канальная матрица приёмника и канальная матрица объединения.

Канальная матрица источника (КМИ)

Канальная матрица источника состоит из условных вероятностей принимаемых сигналов относительно переданных сигналов , которые отражают действие помех на канал.

Эта матрица отражает статистические характеристики действия помех. Канальная матрица источника является матрицей прямых переходов переданных сигналов в принятые сигналы .

Каждая строка КМИ представляет собой распределение условных вероятностей принятых сигналов относительно переданных сигналов . Все эти условные вероятности p(b>j>/a>i>) и образуют КМИ.

Канальная матрица приемника (КМП)

Дискретный канал полностью задан, если известны безусловные вероятности приема сигналов и задана канальная матрица приемника.

Условные вероятности р(a>i> /b>j>) приёма сигналов относительно переданных сигналов составляют канальную матрицу приемника (КМП) и отражают действие помех на канале.

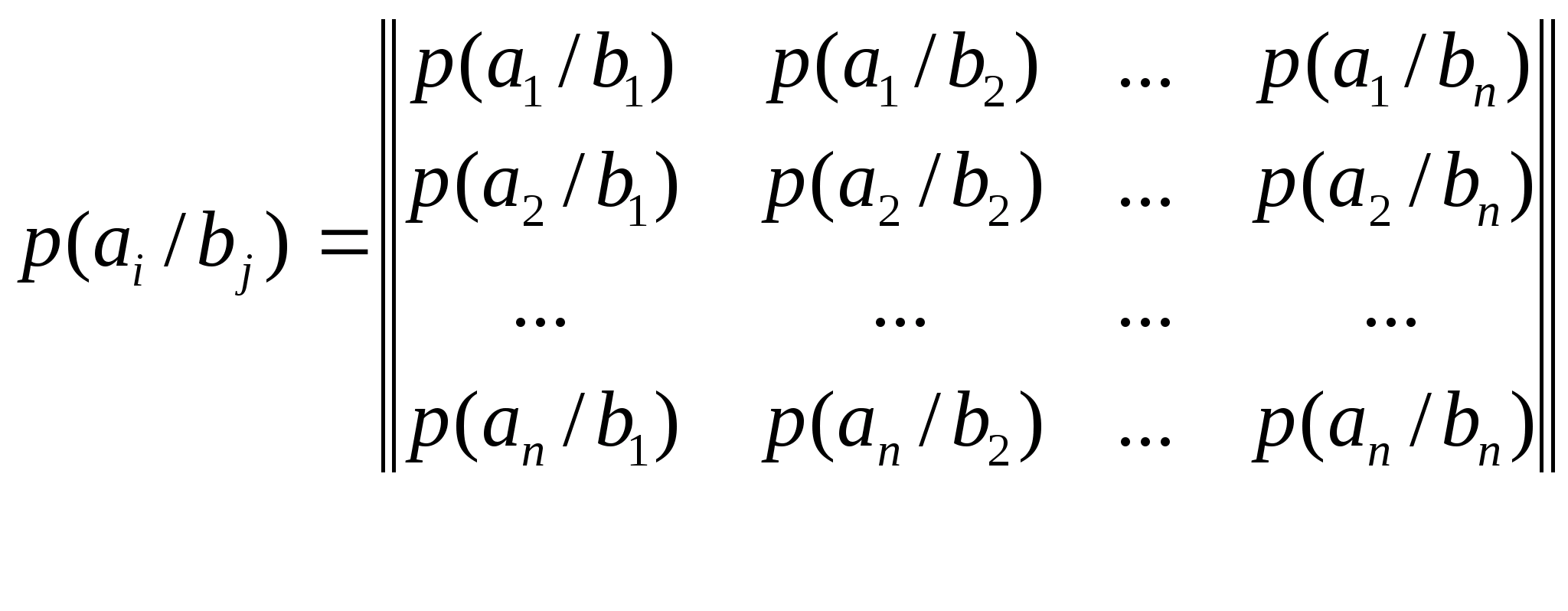
Канальная матрица объединения (КМО)

Дискретный канал полностью задан канальной матрицей объединения (КМО).

КМО состоит из совместных вероятностей появления сигналов и - р(a>i> ,b>j>) и отражает действие помех на канале связи.

Элементами матрицы являются совместные вероятности:

Взаимосвязь канальных матриц

Из КМО в КМИ

p(b>i>/a>j>) =

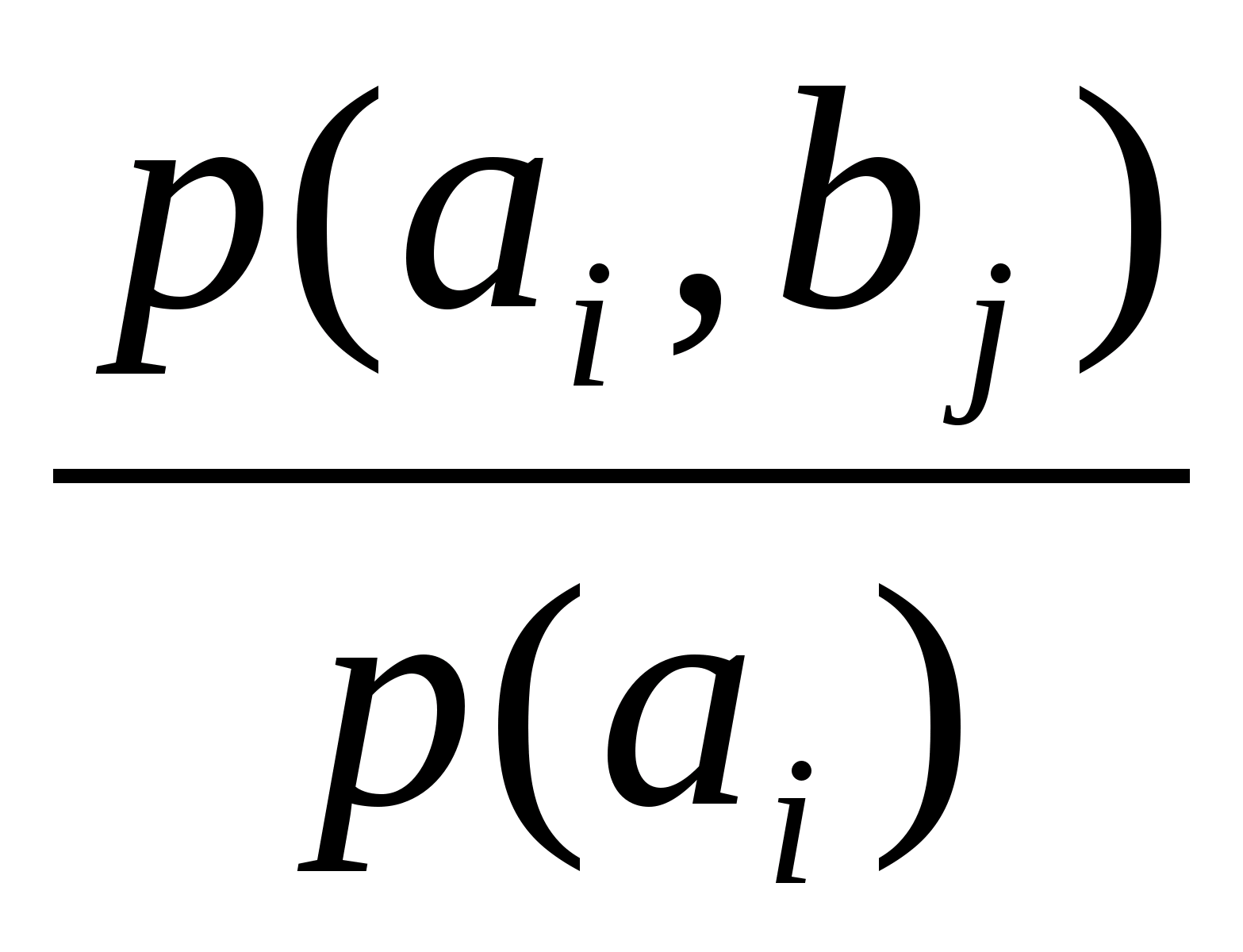
p(a>i>) = p(a>i>,b>j>) (i=1,2…n)

Из КМИ в КМО

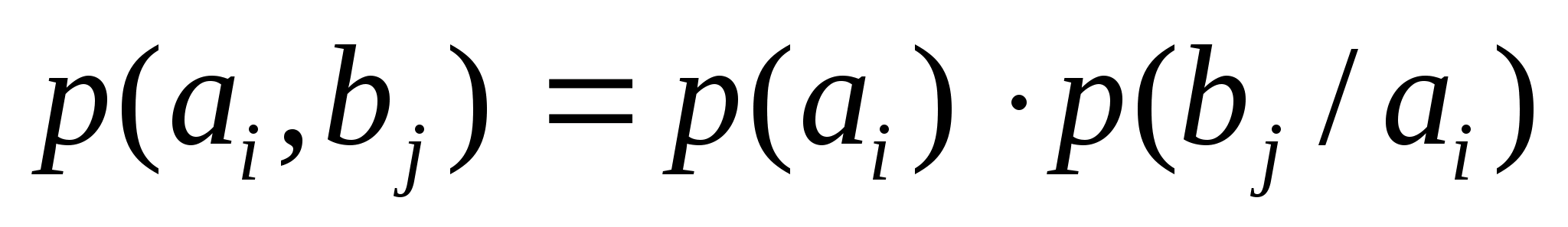
Из КМО в КМП

p(a>i>/b>j>) =

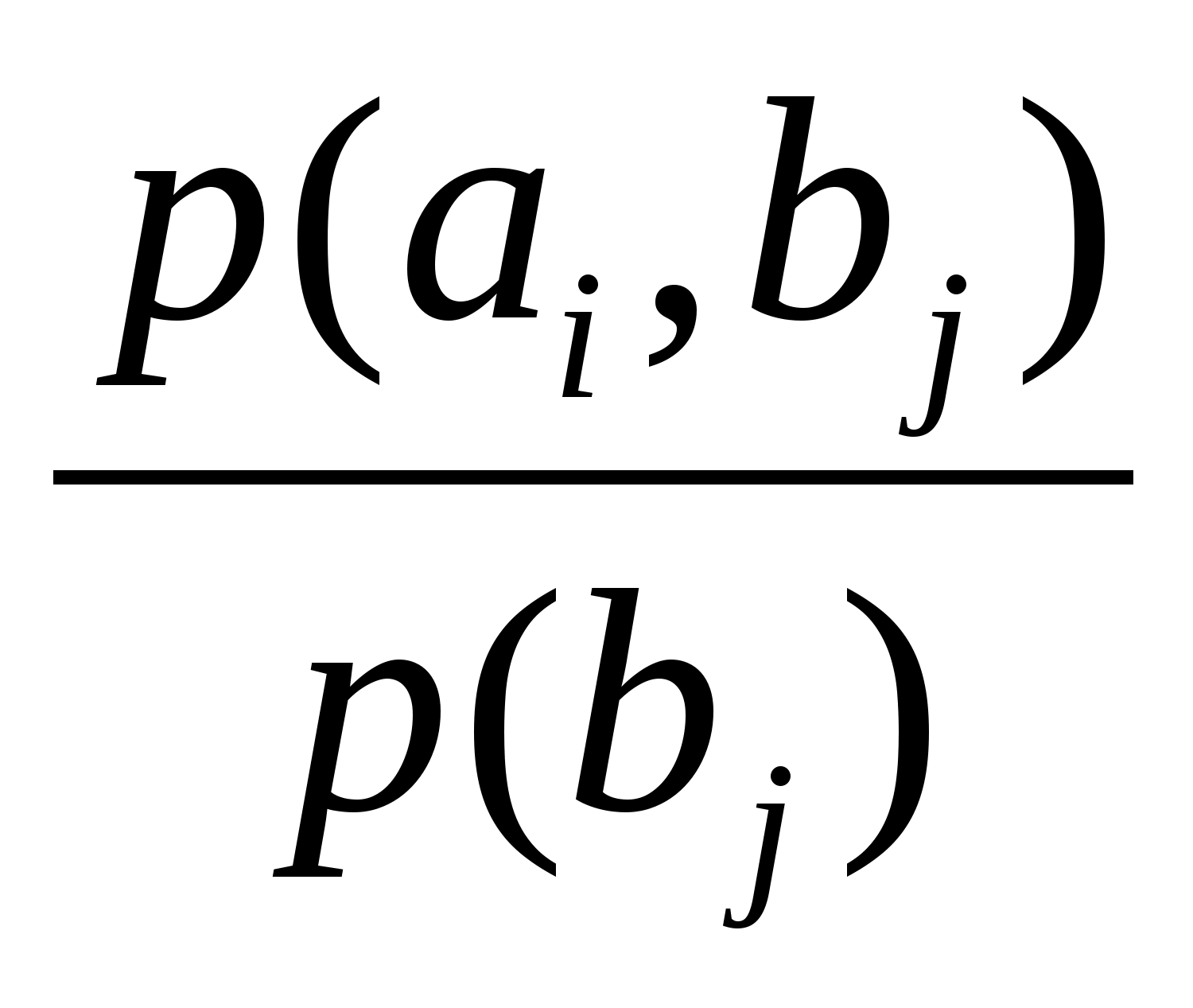
p(b>j>) = p(a>i>,b>j>) (j=1,2…n)

Из КМП в КМО

p(a>i>, b>j>) = p(b>j>) ·p(a>i>/b>j>)

2.1 Свойства канальных матриц

Свойства канальной матрицы источника (КМИ):

    КМИ – квадратная матрица, то есть её размер nxn ;

    Сумма условных вероятностей каждой строки равна 1, то есть образует полную группу:

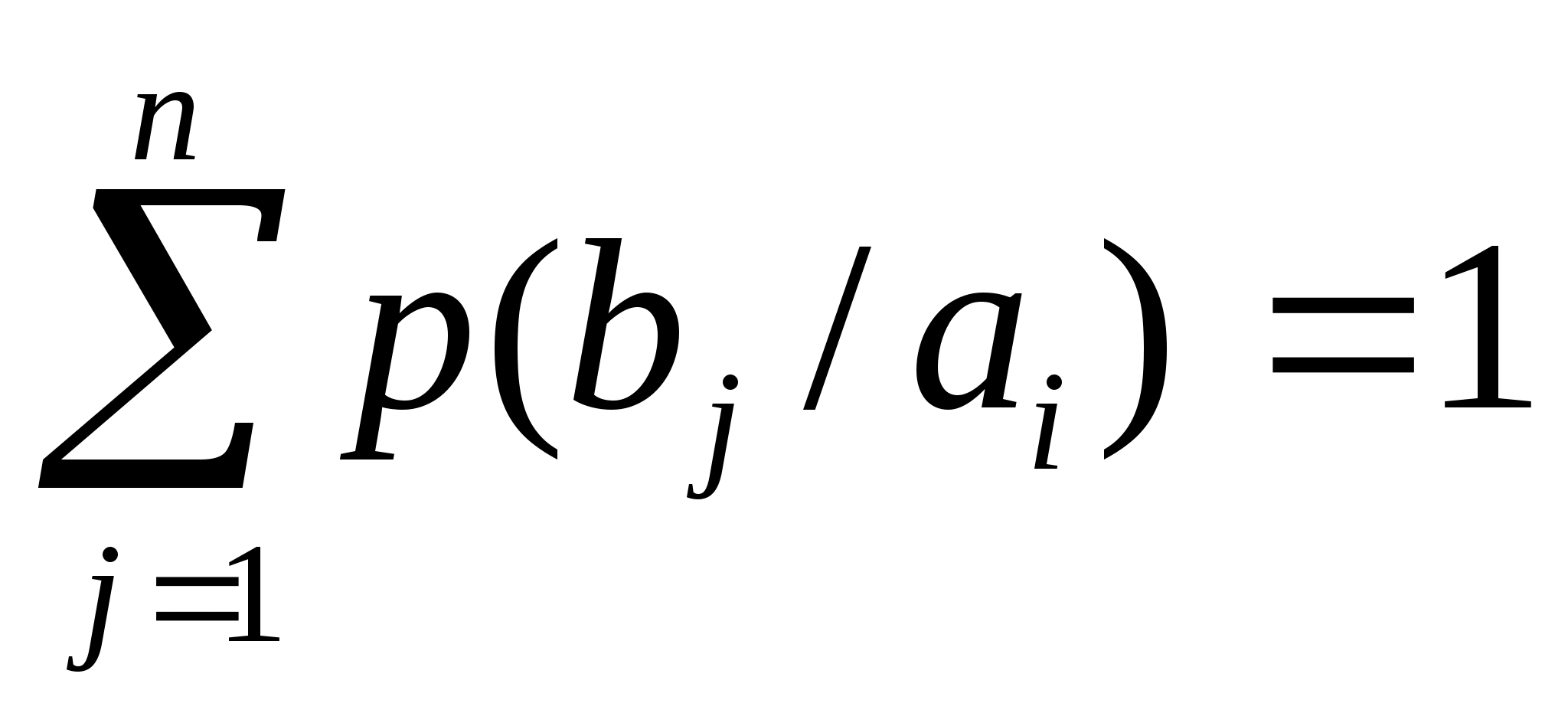(i=1,2…n)

    Условные вероятности главной диагонали КМИ отражают вероятность правильного приема сигналов относительно переданных сигналов ;

    Остальные условные вероятности канальной матрицы (кроме главной диагонали) отражают вероятность ложного приема переданных сигналов;

    Для идеального канала, на котором нет помех, канальная матрица имеет вид:

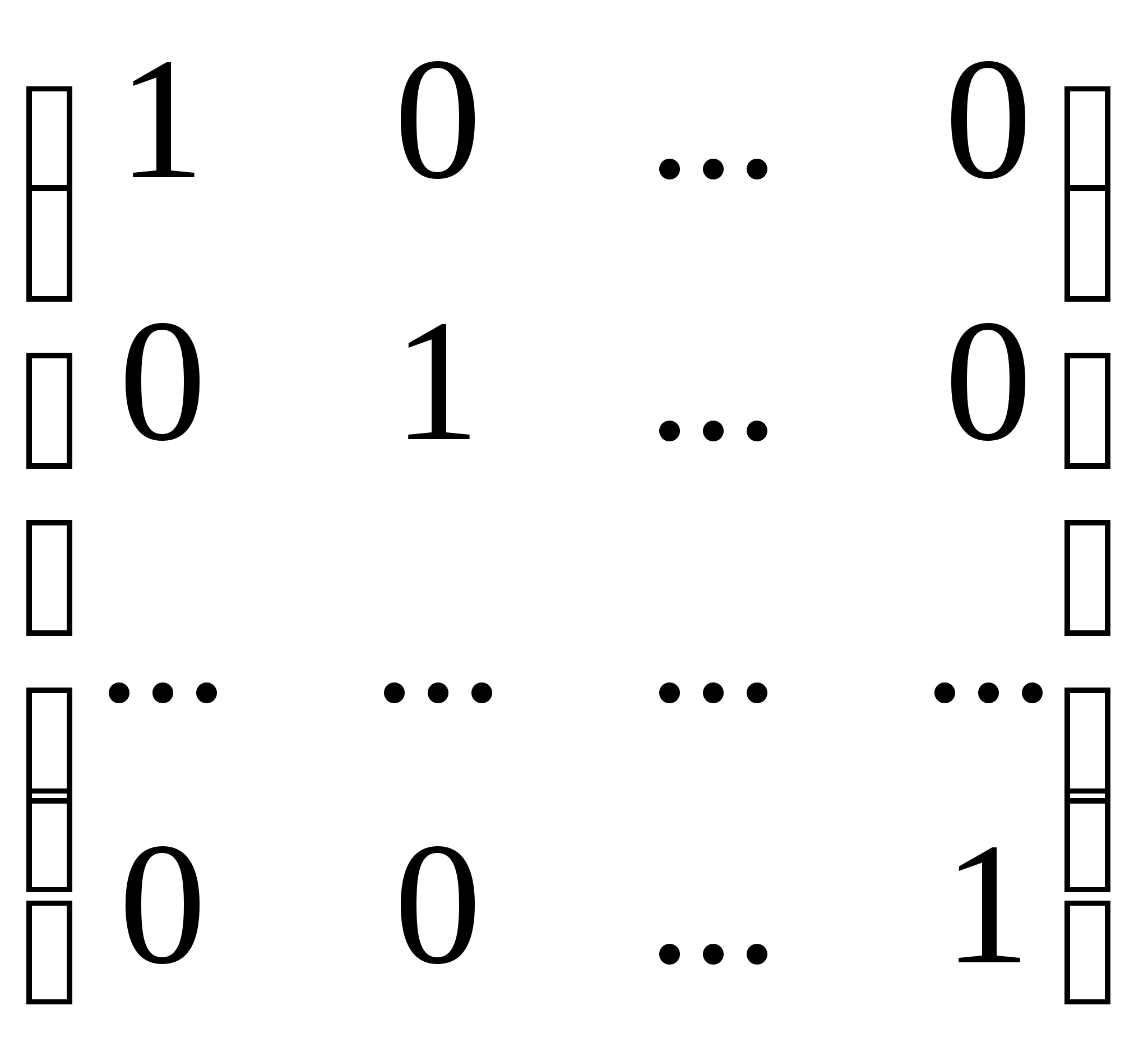
Свойства канальной матрицы приемника (КМП):

    КМП – это квадратная матрица, то есть её размер nxn ;

    Сумма условных вероятностей каждого столбца равна 1, то есть образует полную группу:

(j=1,2…n)

    Условные вероятности главной диагонали КМП отражают вероятность правильного приема сигналов относительно переданных сигналов ;

    Остальные условные вероятности канальной матрицы приемника (кроме главной диагонали) отражают вероятность ложного приема переданных сигналов;

    Для идеального канала, на котором нет помех, КМП имеет вид:

Свойства канальной матрицы объединения (КМО):

    Сумма совместных вероятностей каждой строки равна безусловной вероятности источника:

дискретный матрица приемник кодирование

(i=1,2…n)

Σ p(a>i>) = 1

    Сумма совместных вероятностей каждого столбца равна соответствующей безусловной вероятности приемника:

(j=1,2…n)

    Сумма всех элементов канальной матрицы объединения равна 1.

Σ p(b>j>) = 1

3. Информационные характеристики источника сообщений

Для того, чтобы понять что такое информационные характеристики, нужно вначале дать определение таким терминам, как алфавит сообщения, кортеж упорядоченных уникальных символов и дискретный ансамбль сообщения (ДАС).

Алфавитом сообщения называются символы, которые входят в сообщение. Например:

A={a>1>, a>2>,…,a>n>}

Кортеж упорядоченных уникальных символов – это упорядоченная последовательность символов.

Х={х>1>, х>2>,…, х>n>} – сообщение – кортеж символов

Дискретный ансамбль сообщения (ДАС) – сообщение с вероятностями символов ДАС {Х, p(х>i>) или A, p(a>i>)}

3.1 Количество информации источника сообщений

Количество информации

Количеством информации символа сообщения определяется:

I(a>i>) = - log>2>(p(a>i>)) = - log(p(a>i>)) [бит] (i=1,2…n)

В Шенноновской теории информации количество информации источника определяется вероятностью появления символа.

I(a>i>) = - ln(p(a>i>)) [нат]

I(a>i>) = - lg(p(a>i>)) [дит]

Каждый символ сообщения содержит своё количество информации.

Свойства количества информации источника сообщений

1. Количество информации неотрицательно:

I(a>i>) >= 0

2. Чем выше вероятность, тем меньшее количество информации содержит символ.

3. Если вероятность символа равна 1, то количество информации этого символа равно 0.

р(a>i>) = 1 ⇒ I(a>i>) = 0

4. Аддитивность. Количество информации нескольких символов равно сумме количеств информаций каждого.

I(a>1, >a>2, >a>3>) = I(a>1>) + I(a>2>) + I(a>3>)

Энтропия – среднее количество информации на символ сообщения (средневзвешенное).

[бит/символ]

Свойства энтропии

1. Энтропия неотрицательна: Н(А) ≥ 0

2. Энтропия равна нулю тогда и только тогда, когда вероятность символа равна 1: Н(a>i>) = 0 ⇔ р(a>i>) =1

3. Энтропия ограничена: H (a>i>) ≤ log n> >[бит/символ]

где n – количество символов в сообщении.

4. Максимальная энтропия равна: H>max>(А) = log n> >[бит/символ]

3.2 Информационные потери

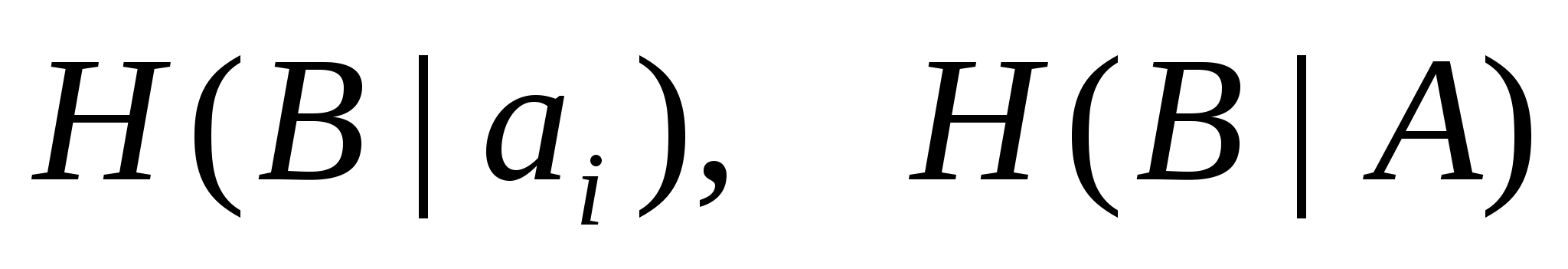
Существует два вида условной энтропии, которые определяют действия помех на дискретном канале – это частная условная энтропия (ЧУЭ) и общая условная энтропия (ОУЭ).

Частная условная энтропия источника (ЧУЭИ) сообщений отображает количество потерь информации при передаче каждого сигнала а>i>> >:

H(В/а>i>) = − 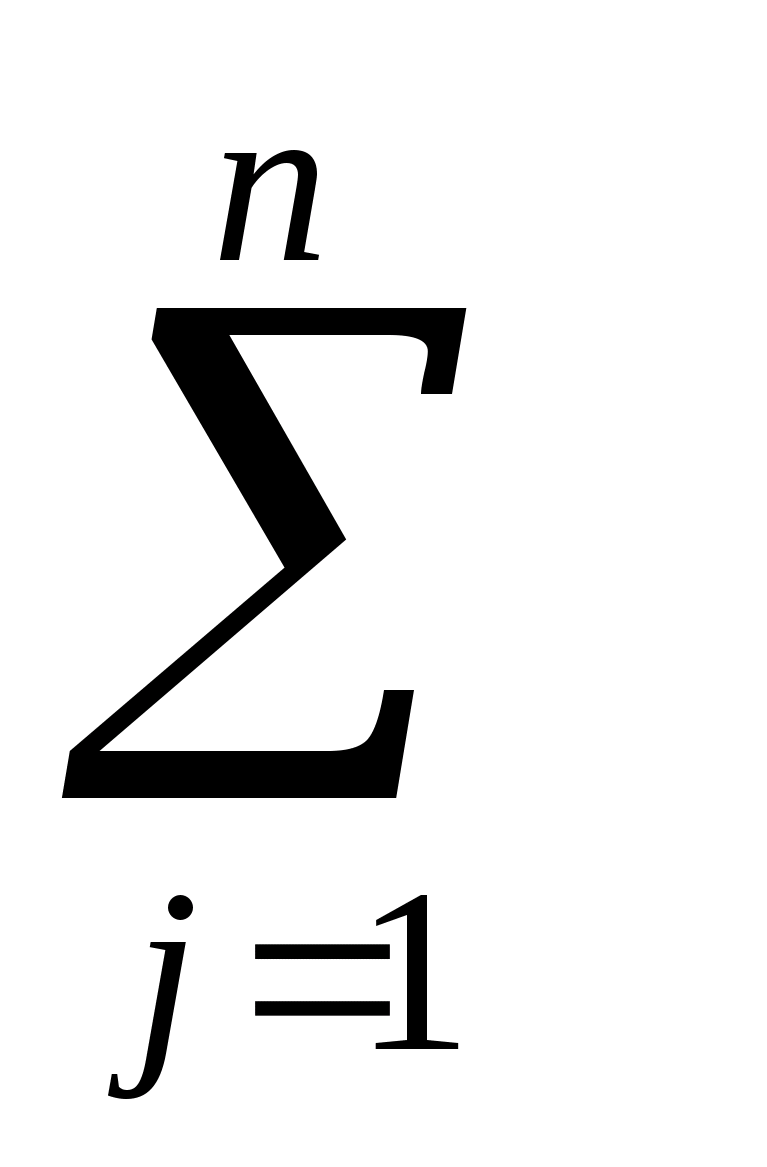p(b>j>/a>i>)log p(b>j>/a>i>) (i = 1,2…n) [бит/символ]

Общая условная энтропия источника (ОУЭИ) определяет средние потери количества информации на принятый сигнал относительно переданных сигналов .

[бит/символ]

4. Информационные характеристики приемника сообщений

4.1 Количество информации приёмника

Количество информации

Количеством информации символа сообщения определяется:

I(b>j>) = - log>2>(p(b>j>)) = - log(p(b>j>)) [бит] (j=1,2…n)

В Шенноновской теории информации количество информации приемника определяется вероятностью появления символа.

I(b>j>) = - ln(p(b>j>)) [нат]

I(b>j>) = - lg(p(b>j>)) [дит]

Каждый символ сообщения содержит своё количество информации.

Свойства количества информации приемника сообщений

1. Количество информации неотрицательно: I(b>j>) ≥ 0

2. Чем выше вероятность, тем меньшее количество информации содержит символ.

3. Если вероятность символа равна 1, то количество информации этого символа равно 0.

р(b>j>) = 1 ⇒ I(b>j>) = 0

4. Аддитивность. Количество информации нескольких символов равно сумме количеств информаций каждого.

I(b>1, >b>2, >b>3>) = I(b>1>) + I(b>2>) + I(b>3>)

Энтропия – среднее количество информации на символ сообщения (средневзвешенное).

[бит/символ]

Свойства энтропии

1. Энтропия неотрицательна:

Н(А) ≥ 0

2. Энтропия равна нулю тогда и только тогда, когда вероятность символа равна 1:

Н(a>i>) = 0 ⇔ р(a>i>) =1

3. Энтропия ограничена

H (B) =< log n> >[бит/символ]

где n – количество символов в сообщении.

4. Максимальная энтропия равна

H>max>(B) = log n> >[бит/символ]

Hmax=1


4.2 Информационные потери

Существует два вида условной энтропии, которые определяют действия помех на дискретном канале – это частная условная энтропия (ЧУЭ) и общая условная энтропия (ОУЭ).

Частная условная энтропия приемника (ЧУЭП) сообщений определяет потери информации каждого принятого сигнала >.>

H(A/ b>j>) = − p(a>i>/b>j>)log p(a>i>> >/ b>j>) (j = 1,2…n) [бит/символ]

Общая условная энтропия приемника (ОУЭП) определяет средние потери информации на символ при приеме ансамбля {B, p()}:

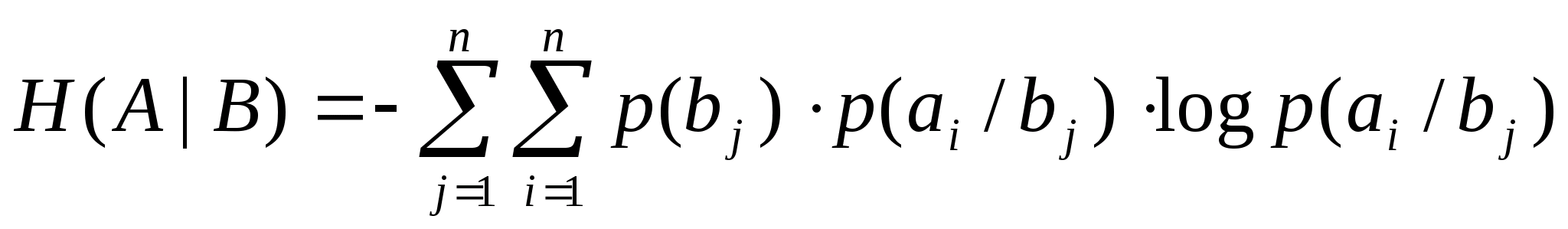[бит/символ]

5. Скоростные характеристики

5.1 Скорость модуляции 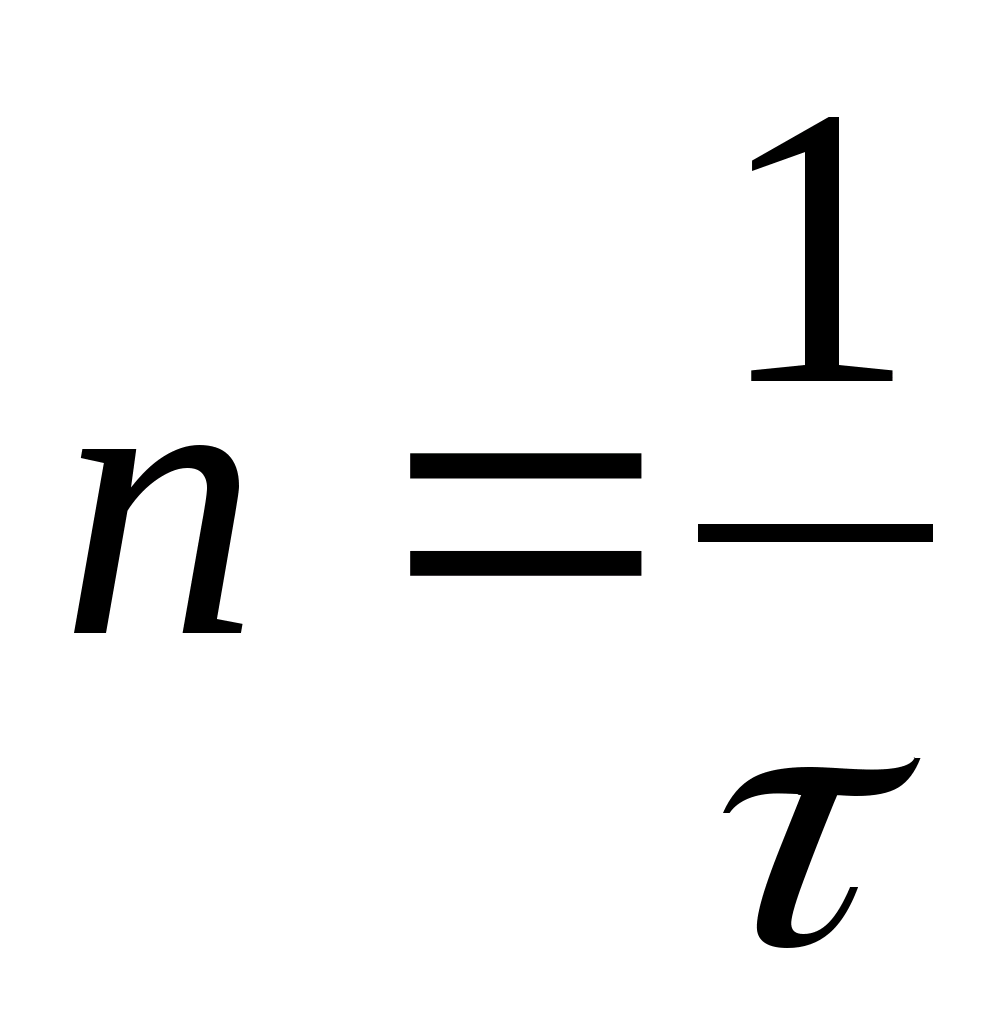[симв/сек]

[симв/сек],

где - длительность передачи одного сигнала

Если длительность передачи сигналов различна, то вычисляется среднее время передачи одного сигнала.

    5.2 Производительность источника бод;

Производительность источника - количество бит, вырабатываемых в единицу времени - 1 секунду.

[бод]

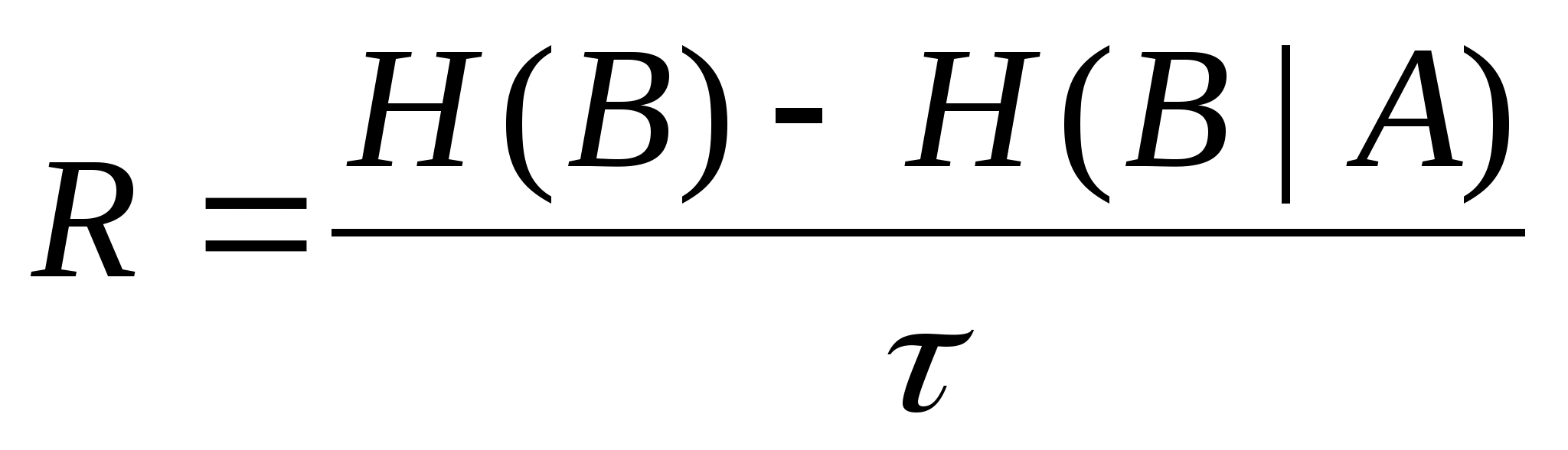5.3 Скорость передачи или бод;

Скорость передачи источника:

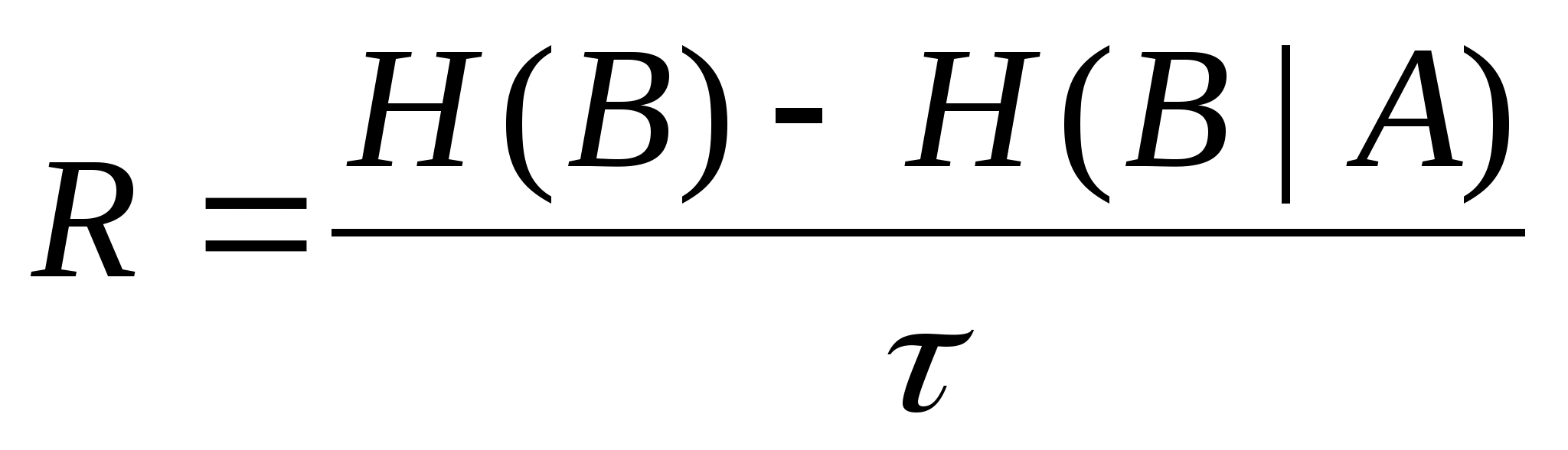[бит/сек], [бод]

Скорость передачи приёмника:

[бит/сек], [бод]

5.4 Емкость канала 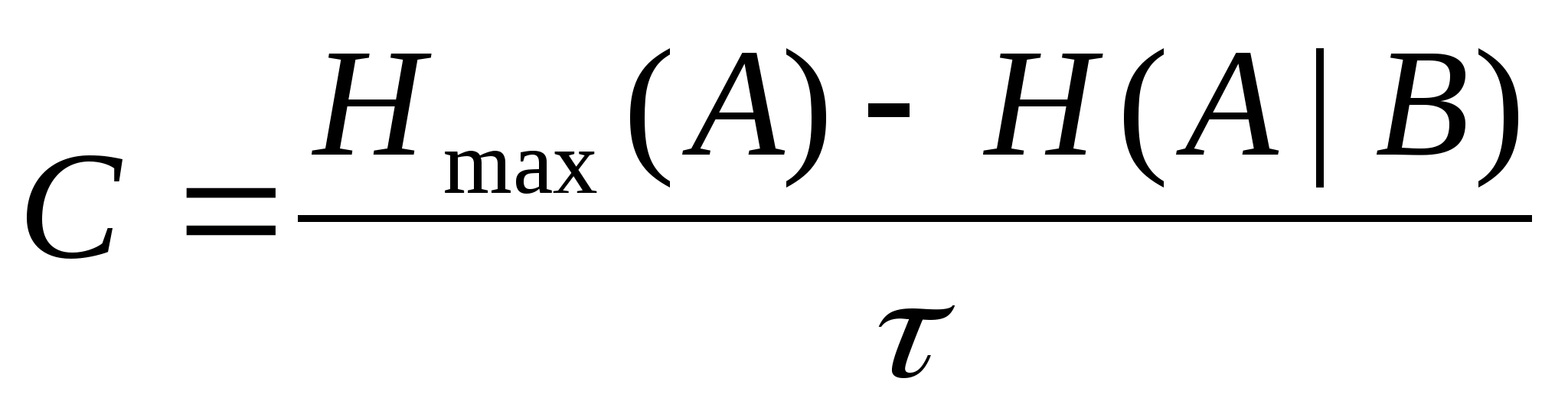или бод;

Емкость канала (пропускная способность канала) - это максимальное

количество бит, передаваемое в единицу времени – секунду.

Пропускная способность – максимальная скорость передачи.

C=maxR

Емкость канала источника:

[бит/сек], [бод]

Емкость канала приёмника:

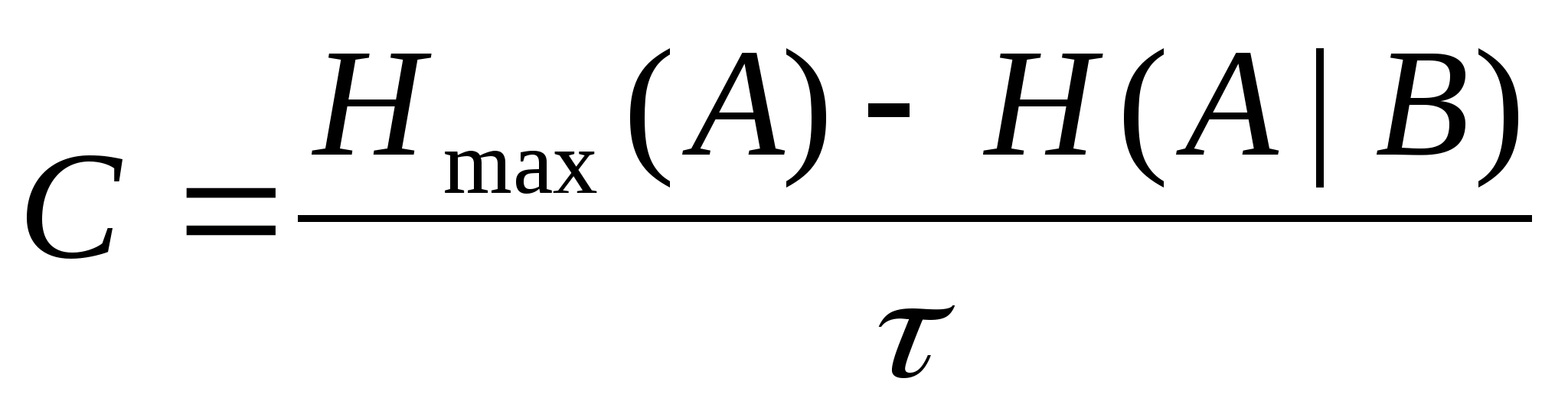[бит/сек], [бод]

5.5 Коэффициент эффективности дискретного канала

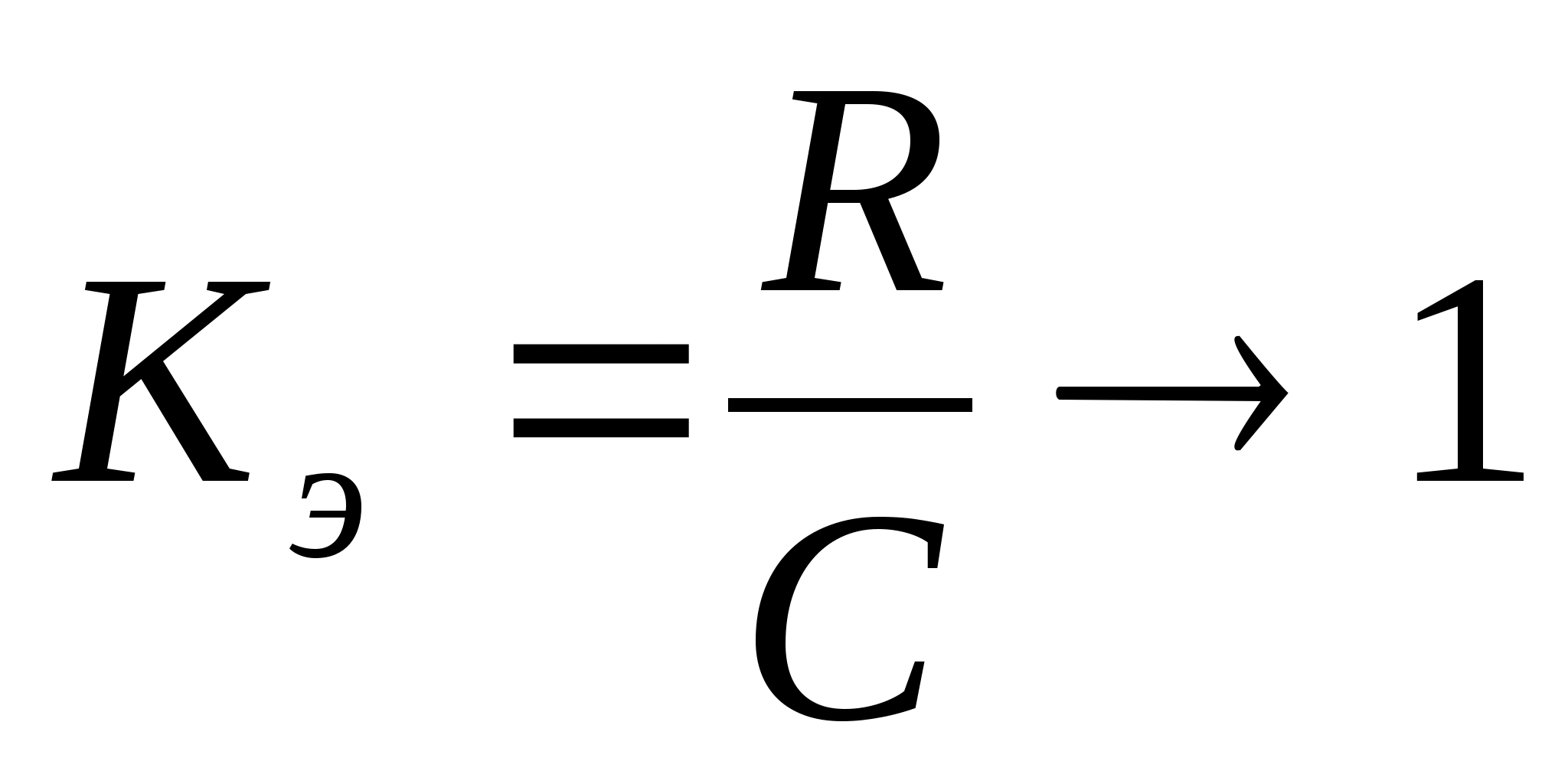
Чем больше коэффициент эффективности дискретного канала стремится к единице, тем эффективнее канал и тем меньше информационные потери на нём.

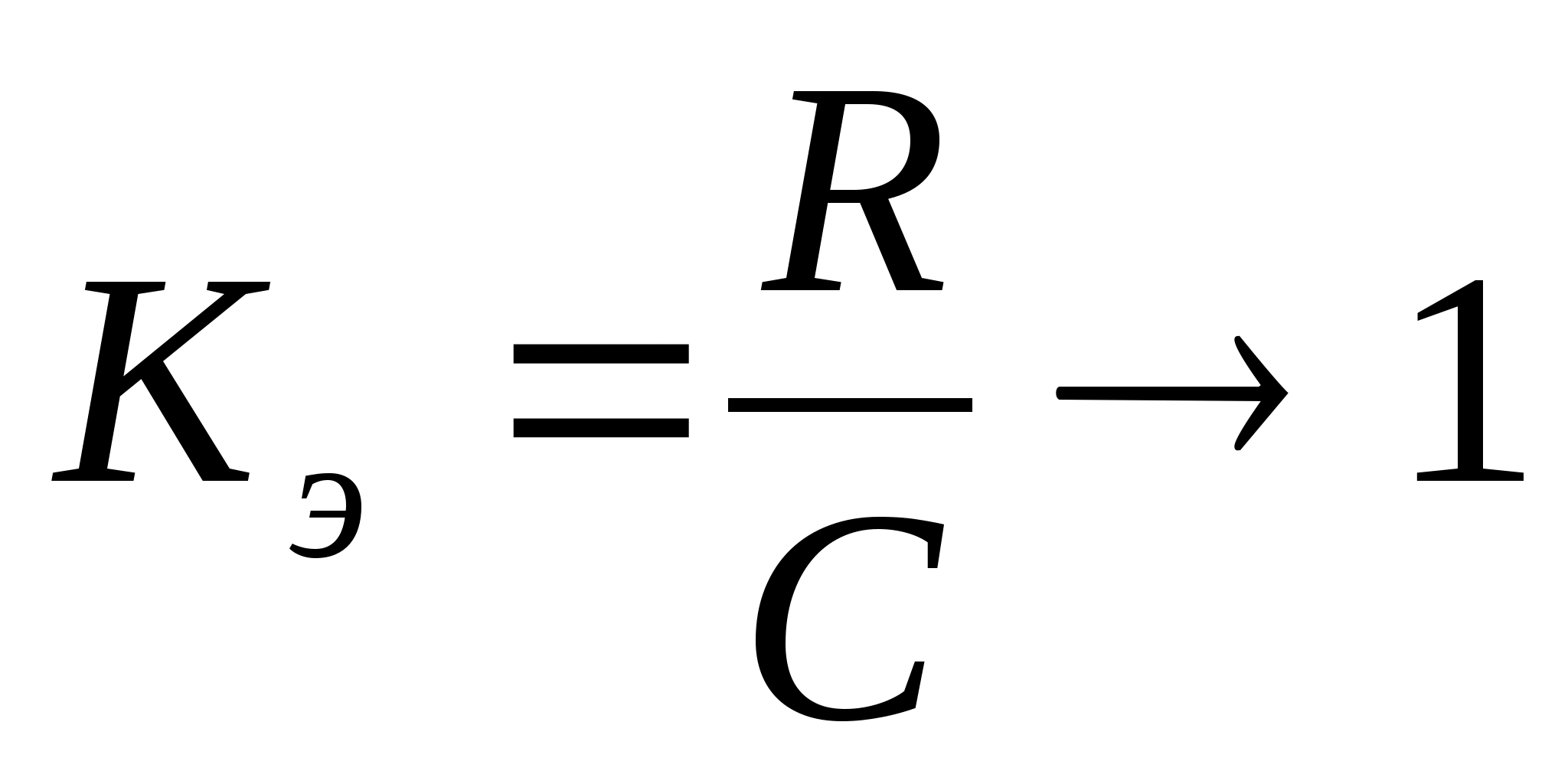
5.6 Теоремы Шеннона о критической скорости и кодировании

    Теорема о критической скорости:

Теорема определяет критическую скорость передачи 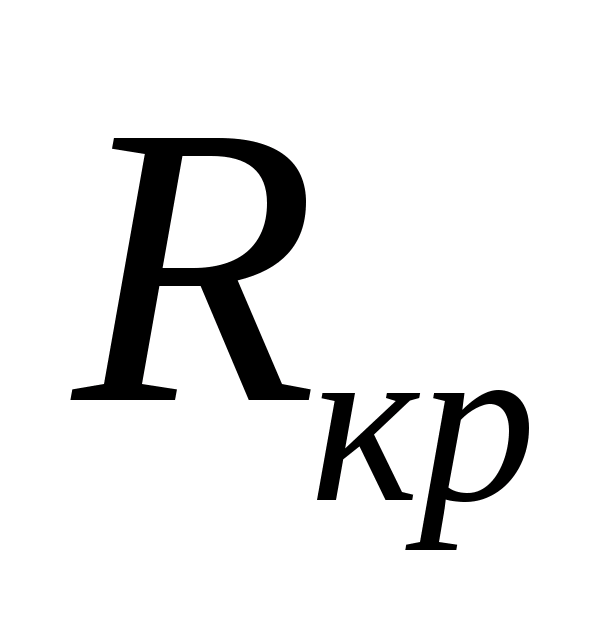, зависящую только от распределения вероятности, при которой существует способ передачи со скоростью R (), при котором возможно восстановление исходного сообщения (), где С – пропускная способность канала, Н(А) – энтропия источника;

    Теорема о кодировании:

Если H’(A) – производительность источника - меньше емкости канала (), то существует способ кодирования и декодирования, при котором вероятность ошибки будет сколь угодно мала 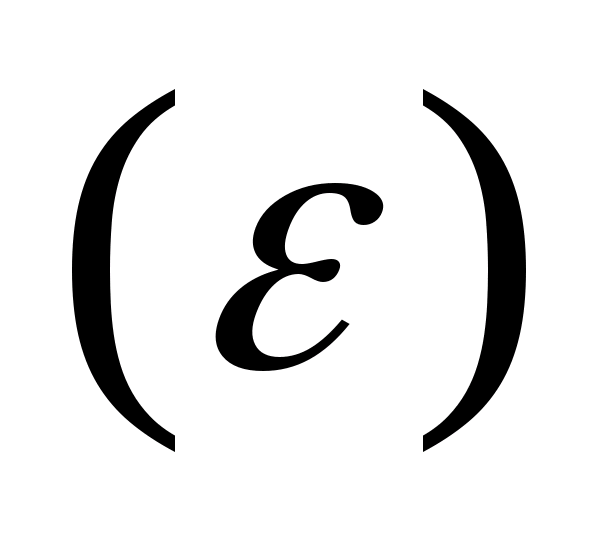и наоборот.

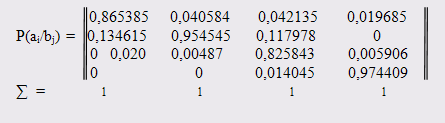
Пример расчёта скоростных характеристик для канальной матрицы источника.

1. Исходные данные

Дана матрица условных вероятностей, которые отражают действие помех дискретного канала связи.

Сумма вероятностей каждой строки равна 1,00.

Время передачи символа τ = 0,0002 сек. Передано 250 символов.

Безусловные вероятности появления символов на выходе:

p(a>1>)=0.25, p(a>2>)=0.35, p(a>3>)=0.15, p(a>4>)=0.25

2. Расчёты

1) Количество информации I(a>i >)каждого символа a>1>, a>2>, a>3> дискретного сообщения :

(i=1,2,3) [ бит]

[бит]

[бит]

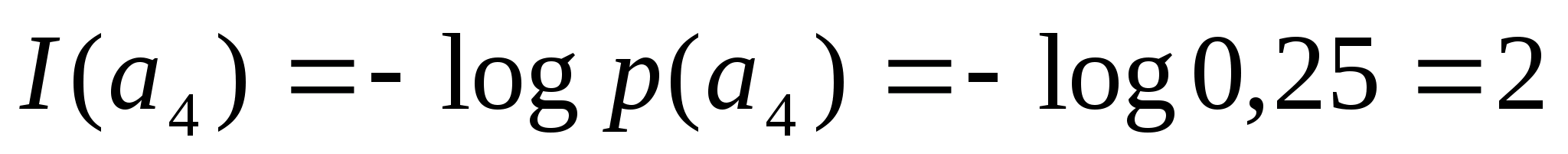[бит]

[бит]

2)Среднее количество информации, переданное одним символом определяет энтропия источника сообщений Н(А):

[бит/символ]

H(A) = -(0,25*(-2) + 0,35*(- 1,51) + 0,15*(- 2,73) + 0,25*(-2) = -(-0,5 - 0,53 – 0,41 – 0,5) = 1,94 [бит/символ]

3)Максимальная энтропия источника сообщений H>max>(A)

H>max>(A)= log N=log 4=2 [бит/символ]

где N-количество символов в алфавите сообщения.

4)Информационные потери при передаче каждого символа a>i >определяет частная условная энтропия H(B/a>i >):

[бит/символ]

H(B/a>1 >)= -(0,9*(-0,15) + 0,05*(-4,32) + 0,03*(-5,05)+0,02*(-5,64) =

-(-0,1368 – 0,2161 – 0,1518 – 0,1129) = 0,6175 [бит/символ]

H(B/a>2 >)= -(0,1*(-3,32) + 0,84*(-0,25) + 0,06*(-4,05)+0) =

-(-0,3321 – 0,2112 – 0,2435 – 0) = 0,787 [бит/символ]

H(B/a>3 >)= -(0 + 0,01*(-6,64) + 0,98*(-0,03)+0,01*(-6,64)) =

-(-0 – 0,0664 – 0,0286 – 0,0664) = 0,1614 [бит/символ]

H(B/a>4 >)= -(0 + 0 + 0,01*(-6,64)+0,99*(-0,0145)) =

-(-0– 0 – 0,0664 – 0,0144) = 0,081 [бит/символ]

5)Средние потери информации при передаче одного символа определяет общая условная энтропия источника Н(B/А):

H(B|A) = 0,25*0,6175 + 0,35*0,787 + 0,15*0,1614 + 0,25*0,081 = 0,1543 + 0,2755 + 0,0242 + 0,02 = 0,4743 [бит/символ]

6)Общие потери информации в канале святи при передаче сообщения, состоящего из 250 символов  I

 I = k H (B / A) = 2500,737476 = 184 [бит]

где k – количество символов в переданном сообщении.

    Среднее количество информации, принятое приемником на один символ, определяется энтропией приемника Н(B)

[бит/символ]

p(b>1>) = 0,9*0,25 + 0,35*0,1 + 0 + 0 = 0,225 + 0,035 = 0,26

p(b>2>) = 0,05*0,25 + 0,84*0,35 + 0,01*0,15 +0 = 0,0125+0,294+0,0015 =0,35

p(b>3>) = 0,03*0,25 + 0,06*0,35 + 0,98*0,15+0,01*0,25 = 0,0075+0,021+ 0,147+0,0025 = 0,178

p(b>4>) = 0,02*0,25 + 0 + 0,01*0,15 + 0,99*0,25 = 0,005 + 0+0,0015+ 0,2475=0,254

H(B) = -(0,26*(-1,94) + 0,35*(-1,7) + 0,178*(-2,49) + 0,254*(-1,97)) = -

-(-0,5 – 0,5234 – 0,4432 – 0,5) = 1,974 [бит/символ]

8) Максимальная энтропия приемника, H>max>(B)

H>max>(B)= log N = log 4 =2 [бит/символ]

9)Среднее количество принятой приемником информации, на один символ с учетом потерь информации, I (A, B)

I (A, B) = H (B) – H (B / A) = -= 1,5 [бит/символ]

10) Скорость модуляции дискретного канала, n

n===500 [бод]

11) Продуктивность дискретного канала сообщений, H’(A)

H’(A)=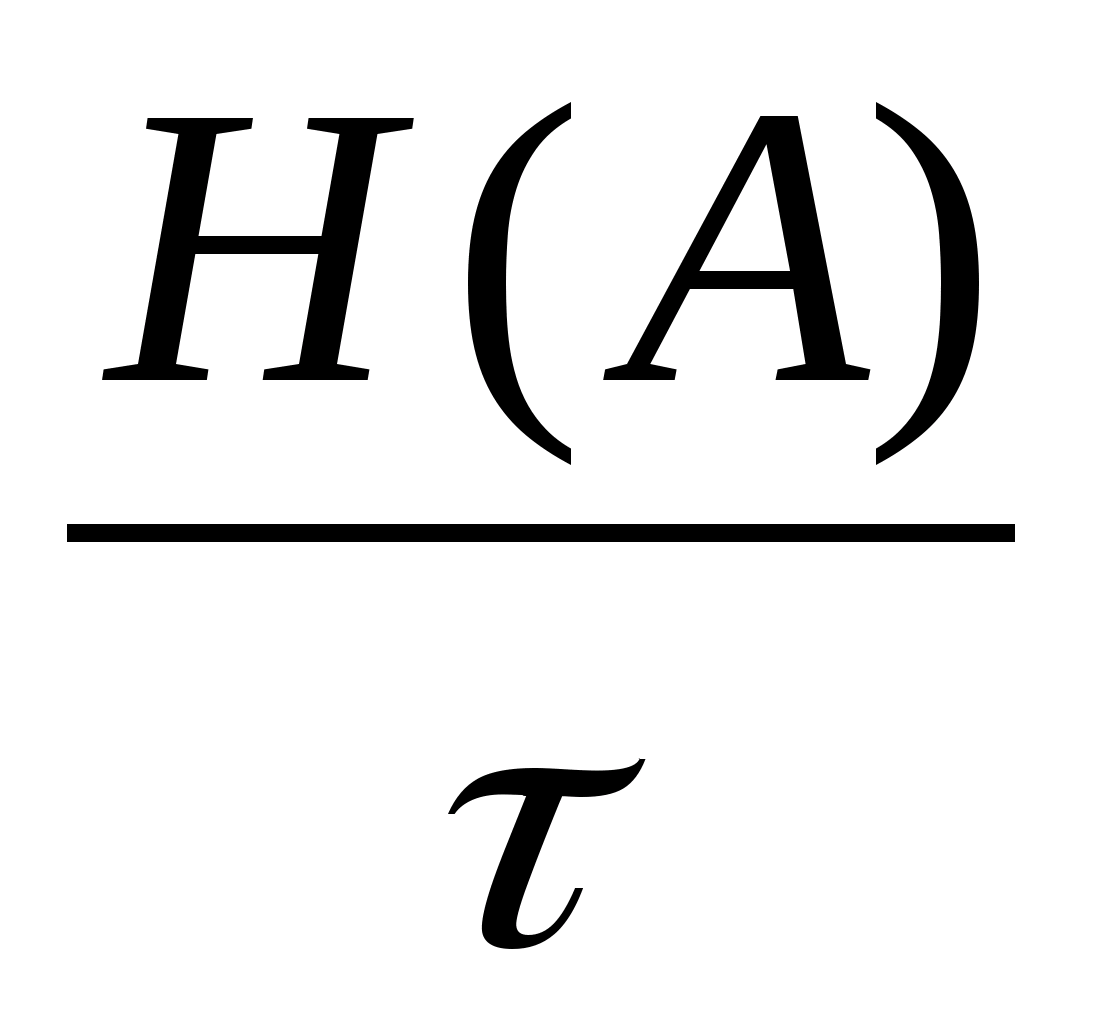 [бод]

H’(A) = = 970,3227 [бод]

12) Скорость передачи информации, R

R =

R= (1,974 - 0,4743)/0,002 = 749,8676 [бод]

13) Пропускная способность (емкость) дискретного канала связи определяется максимальной скоростью передачи: C=max R

С=

C== 762,8716 [бод]

14) Коэффициент эффективности дискретного канала связи K>э>

K>э>===0,9829

15) Критическая скорость передачи R>кр>

R>кр>=== 393,102 [бод]

Оценка надёжности и эффективности дискретного канала связи

    Оценка теоремы Шеннона по скорости

R<R>кр>

749,8676 > 393,102

    Оценка выполнения теоремы по кодированию

H’(A) < C

970,3227 > 762,8716

    Рекомендации по повышению надёжности и эффективности

Из-за невыполнения теоремы о скорости передачи невозможным становится восстановление исходного сообщения. При кодировании и декодировании информации вероятность ошибки может быть сколь угодно велика. Для улучшения эффективности необходимо увеличить емкость канала С.

Теоремы Шеннона не выполняются, а значит, наш канал связи не является эффективным и надежным.

Построение канальной матрицы объединения

Найдем безусловные вероятности появления сигналов на входе приемника по формуле:

Зная КМИ можно построить КМО: р(а>i,>,b>j>)= p(a>i>)p(b>j>/а>i>)

Построение канальной матрицы приемника

Зная КМО мы можем построить КМП, найдя элементы по формуле :

p(a>i> / b>j>)= p(a>i>,b>j>)/p(b>j>)

Часть 2. Теория кодирования

6. Оптимальное кодирование. Идея сжатия

Основной характеристикой дискретного канала связи является скорость передачи данных. При избыточности переданного сообщения скорость передачи уменьшается. Для исключения избыточности сообщения используют математические и программные средства компрессии данных без потери содержания информации, в том числе оптимальное кодирование.

Оптимальное кодирование применяют для того, чтобы:

    сжимать данные (компрессия);

    снижать время передачи данных при той же скорости передачи;

    уменьшить возможные потери и искажения данных;

    архивировать данные, эффективно использовать память.

Основная идея оптимального кодирования лежит в том, что символам сообщения, которые имеют большую вероятность, присваивают короткие бинарные коды, то есть образуются бинарные кодовые слова разной длины – неравномерные коды. Оптимальным неравномерным кодом (ОНК) называется такой код, для которого средняя длина кода есть минимальной.

Такая идея сжатия была применена в азбуке Морзе, где наиболее встречающимся символам соответствовали наиболее короткие коды. Сам алфавит состоял из точек и тире.

6.1 Равномерный двоичный код (РДК), корневое бинарное дерево РДК, длина кода РДК, сообщение в РДК

Составление сообщения

Нам дано сообщение:

Х= "Остановите землю, я сойду"

Длина сообщения L>x>=24 [символа]

Алфавит сообщения

Найдём алфавит нашего сообщения:

A={о,с,т,а,н,в,и,е,з,м,л,ю,я,с,й,д,у,_. }

Длина алфавита L>a>=21 [символ]

Вероятности

На данном этапе вычисления РДК нам требуется вычислить вероят-ности появления каждого символа в алфавите сообщения. Для этого мы воспользуемся формулой:

p>i> = v>i>/ l>s>

где v>i>> >- количество раз, которое символ встречается в сообщении.

Сумма v>i> должна соответствовать длине исходного сообщения.

Таблица данных, РДК

Таким образом, наше сообщение будет выглядеть:

S>РДК>=00001000110010001001001100000100111010000010000101000100101000100101011011000110100010011100001000011000001011111000010001

6.1.6 Длина сообщения

Длина сообщения, записанного в РДК равна:

l>s>>рдк> = l>s>> ·> l>рдк>

где l>рдк >= 5 бит.

Таким образом, длина сообщения:

l>s>>рдк> = 24·5 = 120 бит

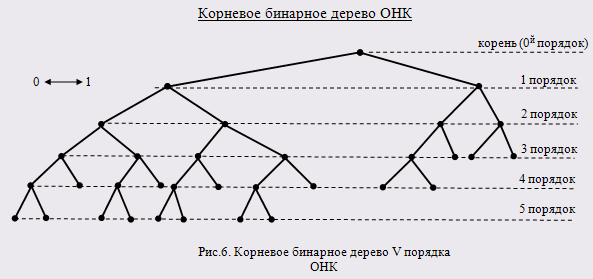
6.2 Оптимальный неравномерный код ОНК Шеннона-Фано, алгоритм расчета ОНК, средняя длина, энтропия, коэффициент сжатия, коэффициент эффективности, сообщение в ОНК, критерий Фано, корневое бинарное дерево ОНК Шеннона-Фано

Расчёт ОНК

Оптимальный неравномерный код (ОНК) мы будем рассчитывать по методу Шеннона-Фано, который ещё называют методом бисекции.

Для вычисления ОНК вся работа разбивается на несколько этапов.

    Предварительный шаг: вероятности появления символа в сообщении ранжируются по убыванию.

    Шаг первый: все вероятности разбиваются на две равновероятные группы. Символам верхней секции назначим 0, символам нижней секции – 1. Первый бит ОНК вычислен.

    Шаг второй: каждую группу делим на две равновероятные подгруппы. Верхним подгруппам присваивается 0, нижним – 1. и т. д.

Деление заканчивается, когда в подгруппе остаётся один символ.

Нахождение ОНК

Критерий Фано однозначного декодирования ОНК: ни одно слово ОНК не является началом другого слова ОНК. Это ещё называется свойством префиксности.

Критерий Фано позволяет однозначно декодировать сжатое сообщение S>ОНК >. Сообщение в ОНК будет выглядеть:

S>ОНК>=111101100101010111111011010110010011000110010011000010000011001010010010011010111100010001100000

      Характеристики ОНК

    Средняя длина ОНК

L>cp.онк>= 4.23 [бит]

    Энтропия ОНК

H(A)= 1,18 [бит/символ]

    Максимальная энтропия

H>max>= log 17= 4,08 [бит/символ]

    Относительная энтропия

    Информационная избыточность

    Абсолютная недогруженость

    Коэффициент сжатия

К>с >= 1- L>cp.онк>/ L>РДК >= 0,15 = 15 %

    Коэффициент эффективности К>э>

К>э>=Н/ L>cp.онк >= 0,27

Эффективность ОНК тем выше, чем больше средняя длина ОНК стремится к энтропии.

6.3 Оптимальный неравномерный ОНК Хаффмана, алгоритм расчета ОНК, средняя длина, энтропия, коэффициент сжатия, коэффициент эффективности, сообщение в ОНК, КБД

      Расчет ОНК Хаффмена

При расчёте оптимального неравномерного кода Хаффмена нам потребуются вероятности появления символов в нашем сообщении. Они у нас уже рассчитаны и выстроены в порядке убывания.

Сам оптимальный неравномерный код Хаффмена мы будем вычислять при помощи алгоритма Хаффмена:

Шаг 1. "Склеиваются" две самых маленьких вероятности.

Шаг 2. В усечённом алфавите снова "склеивают" две самых маленьких вероятности.

Объединение вероятностей заканчивается, когда в усечённом алфавите остаётся лишь одна вероятность.

Критерий Фано

      Полученный ОНК Хаффмена обязан обладать свойством пре-фиксности, то есть ни одно слово ОНК не должно являться началом другого слова. Критерий Фано позволяет однозначно декодировать сжатое сообщение.

Cообщение примет вид:

S=1001101011011111001001010101100011101010011101000100001100010111101111111001100101101000

      Характеристики ОНК

    Средняя длина ОНК

L>cp.онк>= 4.23 [бит]

    Энтропия ОНК

H(A)= 1,18 [бит/символ]

    Максимальная энтропия

H>max>= log 17= 4,08 [бит/символ]

    Относительная энтропия

    Информационная избыточность

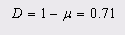
    Абсолютная недогруженость

    Коэффициент сжатия

К>с >= 1- L>cp.онк>/ L>РДК >= 0,15 = 15 %

    Коэффициент эффективности К>э>

К>э>=Н/ L>cp.онк >= 0,27

Эффективность ОНК тем выше, чем больше средняя длина ОНК стремится к энтропии.

6.4 Эффективность ОНК

Однозначно декодировать ОНК можно с помощью критерия Фано, который говорит о свойстве префиксности, которым обладают коды. Благодаря сжатию информации возможно значительно сократить исходный код.

Эффективность ОНК можно определить с помощью коэффициента эффективности, то есть чем ближе К>э> стремится к единице, тем эффективнее оптимальный неравномерный код.

ОНК не обладает избыточностью, так как к нему не прикрепляются контрольные биты.

7. Помехоустойчивое кодирование. Назначение

Назначение помехоустойчивого кодирования состоит в защите данных от действия помех.

Эти коды делятся на две группы:

    Обнаруживающие коды – коды только обнаруживают ошибки, но не указывают их адрес

    Корректирующие коды – обнаруживают наличие ошибки, вычисляют адрес ошибки (позицию), в котором появился ошибочный бит.

7.1 Обнаруживающие коды

Двоичный код становится обнаруживающим за счет добавления дополнительных контрольных бит.

Можно назвать следующие обнаруживающие коды: обнаруживающий код четности (ОКЧ), обнаруживающий код удвоения (ОКУ), обнаруживающий код инверсией (ОКИ), обнаруживающий код стандартный телеграфный код № 3 и другие.

7.1.1 Обнаруживающий код четности (ОКЧ)

Данный двоичный код дополняется одним контрольным битом в конце слова.

n>и >- длина информационной части, количество бит.

n>к >- длина контрольной части.

n> >= n>и >+ n>к >- длина слова.

Пример.

Генерация.

Пусть исходное слово 0101.

Макет ОКЧ - 0101К,

где К – контрольный бит, равно сумме по модулю 2 информационных бит исходника.

К = 0101 = 0

ОКЧ (n; n>и >)

ОКЧ (5; 4) = 01010

Проверим:

S = 0 1010 = 0 - ошибки , то есть ошибки не существует

Количество ошибок

Передано

Принято

Наличие ошибки

Нет ошибок

01010

01010

S = 0, ошибки

1 ошибка

01010

11010

S = 1, ошибка

2 ошибки

01010

11011

S = 0, ошибки

3 ошибки

01010

10011

S = 1, ошибка

4 ошибки

01010

10111

S = 0, ошибки

Недостаток: ОКЧ позволяет определять наличие ошибки при нечетном их количестве и не определяет ошибку при их четном количестве.

Эффективность.

1. Минимальное количество контрольных бит.

2. Просто и удобный алгоритм генерации кода и диагностики (обнаружения ошибок).

7.1.2 Обнаруживающий код удвоения (ОКУ)

Генерация ОКУ.

Пусть исходное сообщение будет 0101.

Макет ОКУ: 0101 К>1> К>2> К>3> К>4>,

где n>и >= 0101 и n>к >= К>1> К>2> К>3> К>4>, то есть n>и >= n>к.>

Контрольные биты равны соответствующим информационным битам.

ОКУ (8; 4) = 01010101

Диагностика.

При диагностике суммируются по модулю 2 информационная и контрольная части ОКУ.

Во всех остальных случаях ошибка существует.

Передано 01010101.

Принято 00010101.

Эффективность ОКУ.

    Обнаруживает любое число ошибок и приблизительно указывает адрес ошибки;

    Простота алгоритма генерации и диагностики;

    Недостаток – избыточность, длина контрольной части 100%.

7.1.3 Обнаруживающий код инверсии (ОКИ)

Генерация ОКИ.

Пусть исходное сообщение будет 0101.

Макет ОКИ: 0101 К>1> К>2> К>3> К>4>,

где n>и >= 0101 и n>к >= К>1> К>2> К>3> К>4>, то есть n>и >= n>к.>

Контрольные биты ОКИ равны инверсии соответствующих бит

информационной части исходника.

ОКУ (8; 4) = 01011010

Диагностика.

При диагностике суммируются по модулю 2 информационная и

контрольная части ОКУ.

Если S = 1 – ошибка не существует. S=0 - 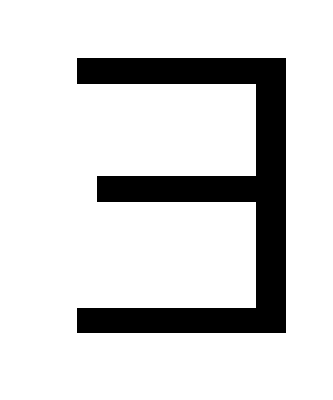ошибка

Передано 01011010.

Принято 10011011.

Эффективность ОКИ.

    Обнаруживает любое число ошибок и приблизительно указывает адрес ошибки.

    Простота алгоритма генерации и диагностики.

    Недостатком является избыточность, длина контрольной части 100%.

7.1.4 Обнаруживающий код Стандартный телеграфный код (ОК СТК №3) №3

Количество единиц в двоичном коде называется весом кода.

Для всех символов, букв, цифр, спецзнаков разработаны двоичные коды весом, равным 3 ( т. е. содержат 3 единицы).

Диагностика.

Если в принятом двоичном слове количество единиц равно 3, то ошибки нет. Во всех остальных случаях ошибка есть.

Символ с ошибкой не корректируется, а удаляется.

7.2 Корректирующий систематический код Хэмминга: генерация, диагностика, коррекция, декодирование

Генерация КСКХ.

Определим количество контрольных бит и их позиции по формуле:

П>i>=2j-1 => k>j> —> П>i>

Отсюда получаем:

для K>1>, j=1, П>i> =21-1=20=1 , K>1> →П>1> ;

для K>2>, j =2, П>i> =22-1=21=2 , K>2> →П>2> ;

для K>3>, j =3, П>i> =23-1=22=4 , K>3> →П>4> ;

для K>4>, j =4, П>i> =24-1=23=8 , K>4> →П>8> ;

Макет КСКХ

n>и> = 7 бит, n>k> = 4 бит, n = 7+4 = 11 бит.

Позиции

П>1>

П>2>

П>3>

П>4>

П>5>

П>6>

П>7>

П>8>

П>9>

П>10>

П>11>

Макет

к>1>

к>2>

1

к>3>

0

0

1

к>4>

1

0

0

Определим правила четности Хемминга.

Вычислим значения контрольных бит. Макет КСКХ обработаем правилами четности, получим уравнения с одной переменной, решив которые, найдем значения к.

ПЧ1 => к>1>10110 = 0. к>1>1= 0 → k>1> = 1

ПЧ2 => к>2>10100 = 0. к>2>0= 0 → k>2> = 0

ПЧ3 => к>3>001 = 0. к>3>1= 0 → k>3> = 1

ПЧ4 => к>4>00 = 0. к>4>1= 0 → k>4> = 1

Позиции

П>1>

П>2>

П>3>

П>4>

П>5>

П>6>

П>7>

П>8>

П>9>

П>10>

П>11>

Макет

к>1>

к>2>

1

к>3>

0

0

1

к>4>

1

0

0

КСКХ

1

0

1

1

0

0

1

1

1

0

0

КСКХ(11;7) = 10110011100

Диагностика.

Передан КСКХ: 10110011100

Принят: 10111011100

Обрабатываем КСКХ правилами четности:

ПЧ1 => 110110 = 1 → АО=1

ПЧ2 => 010100 = 0 → АО=0

ПЧ3 => 1101 = 1 → АО=1

ПЧ4 => 1100 = 0 → АО=0

АО=0101>2>=5>10>

АО =П>5>

Коррекция.

Заключается в инверсии ошибочной позиции П>5>:1→0

КСКХ(11;7) = 10110011100

Декодирование.

Заключается в удалении контрольных бит: 1001100

Эффективность. Контрольные биты размещаются между битами исходника. Код содержит минимальное количество контрольных бит и является плотноупакованным.

7.3 Корректирующий циклический код: генерация, диагностика, коррекция, декодирование

Корректирующий циклический код (КЦК) определяет и корректирует одну ошибку. Широко употребляется в станках с числовым программным управлением (ЧПУ).

Контрольные биты размещаются в конце информационной части кода. Значения контрольных бит вычисляются с помощью порождающего полинома.

Диагностика наличия ошибки и вычисление её адреса также выполняются с помощью порождающего полинома.

Генерация КЦК.

Дано сообщение:

Л = 1001101

n>и> = 7 бит

Построим корректирующий циклический код.

Запишем исходник в форме полинома

К = 1001100 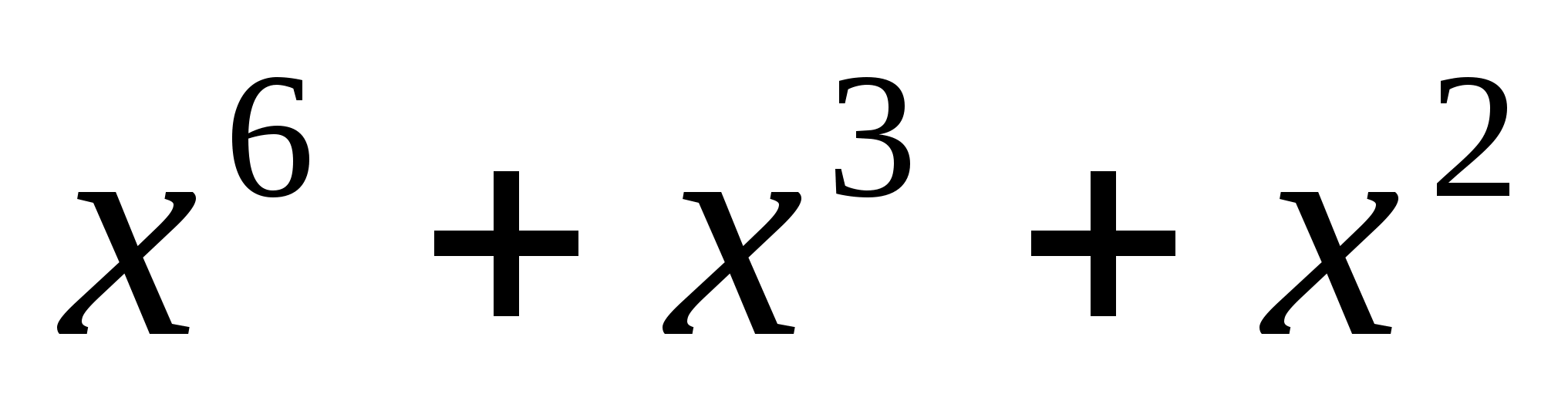=Q(x).

n>и> = 7 бит, n>k> = n>и>+2=9 бит, n = 7+9 = 16 бит.

Макет строится путем сдвига исходника на 9 бит влево

=

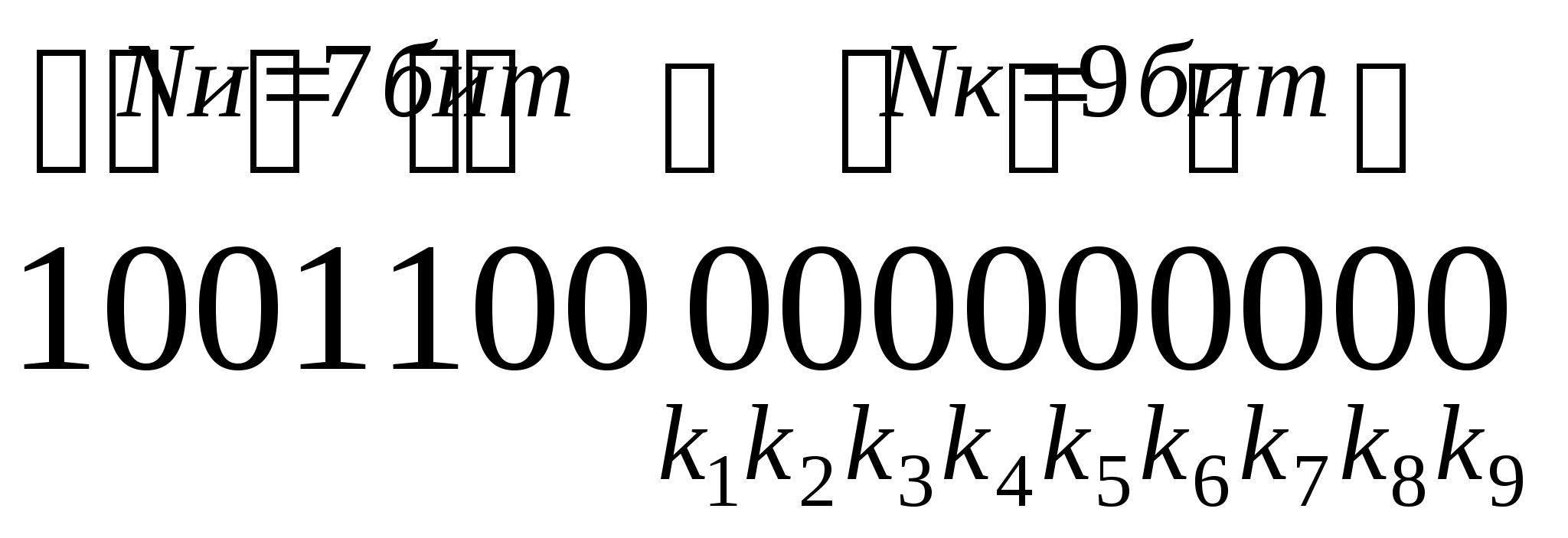
Вычислим значения контрольных бит. Для этого макет поделим на порождающий полином. Порождающим полиномом в нашем случае является:

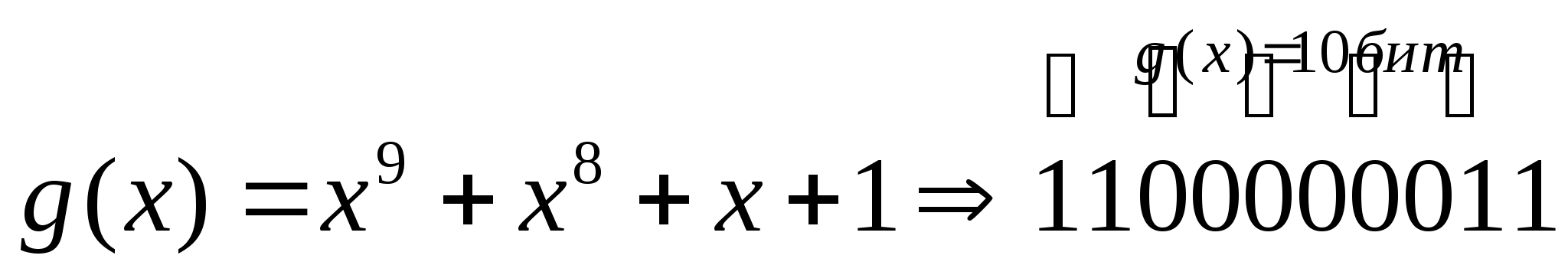
Запишем корректирующий циклический код:

КЦК(16;7)=

Диагностика.

Принятый КЦК делится по модуля 2 на порождающий полином.

Наличие и адрес ошибки определяется по остатку m(x):

- если m(x)=0, то ошибки нет.

- ошибка в информационной части, есть m(x) имеет "обрамление".

Адрес ошибки указывает единица внутри обрамления.

- ошибка в контрольной части, если m(x) содержит одну единицу, а

остальные биты равны нулю. Единица указывает адрес ошибки в

контрольной части.

- КЦК содержит более одной ошибки при другой форме остатка m(x).

1. Ошибка в информационной части

Передано 1001100110011001

Принято 1001110110011001

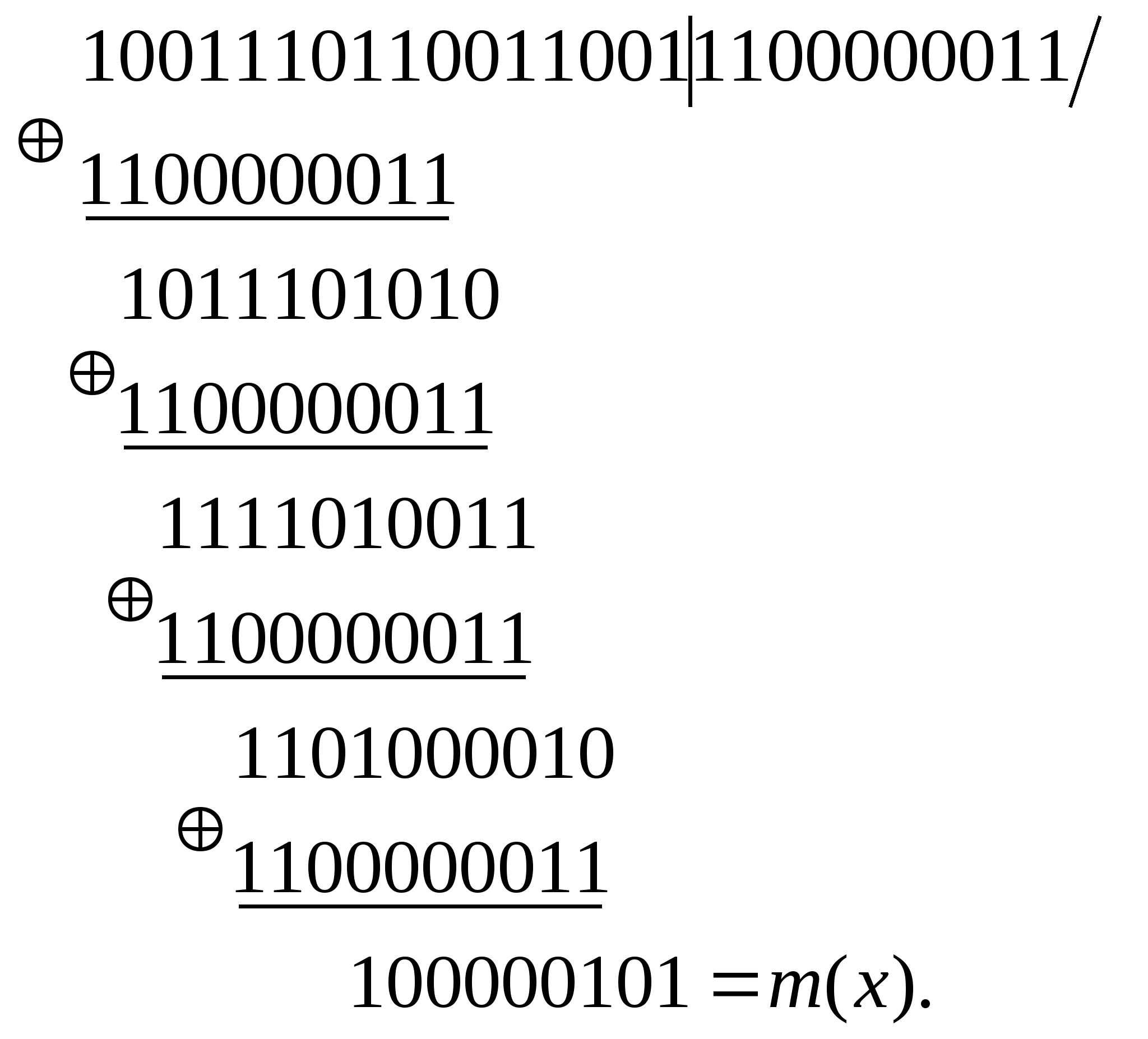
Мы получили обрамление в остатке => АО=П>6 >(единица внутри обрамления) и это ошибка в информационной части).

2. Ошибка в контрольной части

Передано: 1001100110011001 Принято: 1001100110010001

По форме остатка определяем, что ошибка в контрольной части КЦК. Единица указывает адрес ошибки АО= П>13>

Коррекция.

Для первого случая: инвертируем ошибочную позицию П>6 >: 1→0. Получаем 1001100110011001.

Для второго случая: инвертируем ошибочную позицию П>13 >0→1

Получаем 1001100110011001.

Декодирование.

Заключается в отбрасывании контрольных бит. Получаем 1001100.

Эффективность.

    Определяет и корректирует одну ошибку, широко применяется в станках с ЧПУ.

    Контрольные биты размещаются в конце информационной части кода. Значения контрольных бит вычисляются с помощью порождающего полинома.

    Диагностика наличия ошибки и вычисление ее адреса также выполняется с помощью порождающего полинома.

7.4 Корректирующий мажоритарный код: генерация, диагностика, коррекция, декодирование (другие названия – код по голосованию, К-удвоения)

Корректирующий мажоритарный код(КМК) иначе называют кодом по голосованию либо кодом удвоения.

Образуется КМК путём добавления к исходнику контрольной части, содержащей К удвоений, где К – нечетное число (К = 3, 5,7…).

Генерация КМК.

Пусть дано сообщение:

К = 1001101

n>и> = 7 бит

К исходнику добавляется контрольная часть, содержащая к

удвоений (к=3,5,7).

Запишем макет для 3-удвоения:

КМК(21;7)=

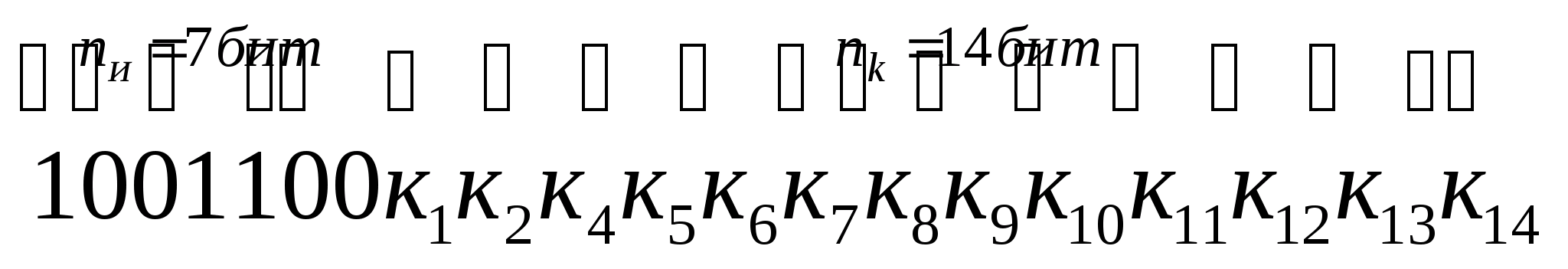
Значения контрольных бит равны соответствующим значениям информационных бит:

КМК(21;7)= 1001100 1001100 1001100.

Диагностика.

Для каждого инф. бита строится свой синдром. Если в синдроме биты одинаковые, то ошибки нет. Если разные, то ошибка в позиции с "наименьшим числом голосов".

Передано 1001100 1001100 1001100.

Принято 1101100 1001000 1001101.

Для П>1 >S>1>{П>1>,П>8>,П>15>}={1,1,1} => нет ошибки.

Для П>2> S>2>{П>2>,П>9>,П>16>}={1,0,0}=> есть ошибка, АО=П>2>

Для П>3> S>3>{П>3>,П>10>,П>17>}={0,0,0}=> нет ошибки

Для П>4> S>4>{П>4>,П>11>,П>18>}={1,1,1}=>нет ошибки

Для П>5> S>5>{П>5>,П>12>,П>19>}={1,0,1}=> есть ошибка, АО=П>12>

Для П>6> S>6>{П>6>,П>13>,П>20>}={0,0,0}=> нет ошибки

Для П>7> S>7>{П>7>,П>14>,П>21>}={0,0,1}=>есть ошибка, АО=П>21>

Для сильно зашумленных каналов применяют 7,9 удвоений.

Коррекция.

Инвертируем ошибочные позиции П>2> 1→0,

П>12> 0→1,

П>21> 1→0;

Получаем 1001100 1001100 1001100.

Декодирование.

Удаляем контрольные биты, получаем 1001100.

Эффективность.

    Обнаружение и коррекция кратных ошибок;

    Удобный, простой алгоритм генерации и диагностики;

    Большая избыточность: 200, 400, 500%.

7.5 Эффективность помехоустойчивых кодов

Помехоустойчивые коды предлагают простые и удобные алгоритмы генерации кода, диагностики, то есть обнаружения ошибок, а также их коррекции.

В состав помехоустойчивого кода входит определенное количество контрольных бит, из-за чего помехоустойчивые коды обладают большой избыточностью от 100 % до 600%.

8. Криптографическое кодирование (Создатель Клод Шеннон)

Крипта – латинское слово "тайна"

Криптография – тайная запись

Криптология – наука о тайнах состоит из двух частей:

Криптография – создание методов защиты информации от несанкционированного доступа (НСД);

Криптоанализ – разработка методов "взлома" систем защиты информации.

Принципы криптографии по Шеннону

    Перемешивание данных.

    Рассеивание данных. Изменение структуры данных

8.1 Требования к криптографическим алгоритмам

    Конфиденциальность – секретность;

    Целостность данных – нет замен, добавлений и удалений;

    Аутентичность – подлинность, истинность сообщения и абонента;

    Неотслеживаемость информации. Не устанавливается, кому и от

кого идет сообщение;

    Оперативность доступа для санкционированного пользователя и непреодолимая защита для остальных;

    Юридическая значимость электронного документа обеспечивается электронной цифровой подписью (ЭЦП);

    Криптостойкость алгоритма – способность алгоритма противостоять взлому. Обеспечивается ключом шифрования.

Криптографическое правило Кирхгофа

Криптоаналитику известно все (методы шифрования, программное обеспечение, фрагмент или весь шифротекст и т.д.), но не известен ключ шифрования.

Следствие.Ключ определяет криптостойкость алгоритма.

Абсолютно стойкий ключ по Шеннону

    Длина ключа равна длине сообщения ;

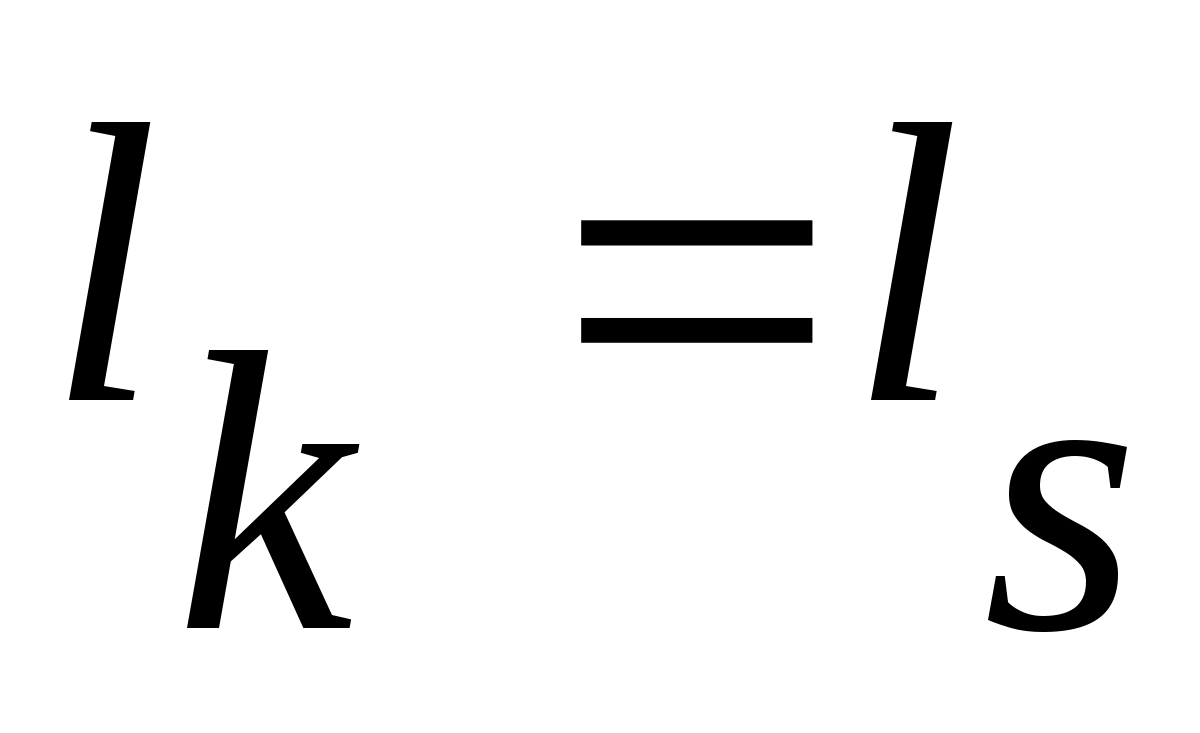    Ключ случайным образом выбирается из ключевого пространства;

    Ключ используется только один раз;

    Ключ создается на основе неразрешимой математической задачи, т.е. на основе этого принципа была создана открытая криптография (открытый ключ шифрования) и ЭЦП.

8.2 Жизненный цикл конфиденциальности данных

    Военная, тактическая информация ……….. минуты, часы

    Средства массовой информации (СМИ) …...……….... сутки

    Заявления о выпуске товара ……………….. неделя

    Бизнес проект ………………………........ месяцы, год

    Производственные секреты, технологии …………….. 10 лет

    Секрет создания водородной бомбы ………………. 40 лет

    Информация о разведчиках ………………...…… 50 лет

    Личная информация ………………… более 50 лет

    Дипломатическая тайна (государственная) …………. 65 лет

    Сведения о переписи населения ………………….… 100 лет

Критерии взлома ключа

    – критерий по времени;

– критерий по стоимости;

    Недостижимые ресурсы:

    вычислительные ресурсы (быстродействие, емкость памяти);

    объем перехвата сообщения, фрагмент шифротекста должен быть достаточно большим;

    неразрешимая математическая задача.

8.3 Классификация криптографических методов

Симметричные – шифрование происходит с помощью секретного ключа и дешифрование производится с помощью этого же ключа:

    Поточные методы, т.е. информация шифруется в потоке символ за символом. Шифрование ведется на основе простых и сложных замен. Существуют:

а) шифр Цезаря;

б) шифр Полибия;

в) шифр "Модульная арифметика";

г) шифр "Алфавитное сложение";

д) шифры на основе математических методов.

2. Блочные методы – методы перестановки:

а) шифр сцитала (с греческого – жезл);

б) стандартная перестановка;

в) вертикальная перестановка;

г) комбинированная перестановка;

д) магический квадрат;

е) квадратная и прямоугольная решетки Кордано.

    Многоалфавитные системы:

а) шифр квадрат Вижинера ();

    Шифр DES.

Несимметричные:

    Открытая криптография – работает два ключа: ключ секретный (личный), который никому не передается; ключ открытый (общедоступный):

а) RSA и др.;

    Электронная цифровая подпись (ЭЦП);

    Стеганография – скрывается факт передачи сообщения. Скрытие факта дешифрованного сообщения (решетки, микроточки и т.д.).

Физическая защита вычислительного центра и компьютера:

    Кодовые замки с антропологическим ключом (отпечаток пальца, сетчатка глаза и т.д.);

    Скремблеры (криптографический телефон);

    Генератор шума;

    Парольная система защиты компьютера, базы данных.

Применение в комплексе этих методов защиты обеспечивает выполнение требований криптографии.