Проектирование адаптивной сети нейро-нечеткого вывода для контроля критической зависимости параметров гемодинамики по модели измерений предрейсовых осмотров
Проектирование адаптивной сети нейро-нечеткого вывода для контроля критической зависимости параметров гемодинамики по модели измерений предрейсовых осмотров
COДЕРЖАНИЕ
СПИСОК СОКРАЩЕНИЙ
ВВЕДЕНИЕ
1. ПРОБЛЕМЫ ОПРЕДЕЛЕНИЯ НОРМЫ В МЕДИЦИНЕ. МЕТОДЫ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ НОРМЫ
1.1 АСПО как предметная область модели прогноза медицинской нормы в
системе безопасности на железнодорожном транспорте
1.2 Стандартные функции АСПО
1.3 Медицинские и психофизиологические аспекты выделения группы повышенного риска
1.3.1 Оценка параметров профессиональной пригодности
1.3.2 Критерии выделения «группы риска»
1.3.3 Расширенное психофизиологическое обследование по данным АСПО
1.3.3.1 Психологическая диагностика
1.3.3.2 Функциональная диагностика
1.4 Проблемы предоставления нормы в АСПО
2. АДАПТИВНАЯ НАСТРОЙКА СТАТИСТИЧЕСКОГО РАЗДЕЛЕНИЯ ПРИЗНАКОВ В СИСТЕМЕ НЕЙРО-НЕЧЕТКОГО ВЫВОДА
2.1 Основы принципа нечеткого вывода и идентификации
2.1.1 Нечеткая логика, лингвистическая оценка медицинских параметров
2.1.2 Направления исследований нечеткой логики по отношению к медицинским диагностическим заключениям
2.1.2.1 Символическая нечеткая логика и терминология предметной области.
2.1.2.2 Теория приближенных вычислений и стохастические измерения.
2.1.3 Идентификация с помощью иерархической системы нечеткого логического вывода
2.2 Задача разработки программных средств оценки критической зависимости гемодинамических показателей
2.2.1 Характеристики программной модели при обработке регрессионных измерений предрейсовых осмотров
2.2.2 Управление иерархией нечеткого вывода интерактивным пакетом ANFIS
2.2.3 Алгоритм диагностики
2.2.4 Усовершенствованный метод диагностики
2.2.5 Выводы и база знаний
2.2.6 Проектирование систем типа Сугено
2.2.7 Результаты проектирования нечеткого алгоритма предрейсовых медицинских осмотров на основе адаптивной сети нейро-нечеткого вывода
Заключение
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Список сокращений
медицинский осмотр нейро нечеткий сеть
ANFIS – Adaptive NeuroFuzzy Inference System (адаптивная нейро-нечеткая система вывода);
АСУ – автоматизированная система управления;
АСПО – автоматизированная система предрейсовых осмотров;
БД – база данных;
БП – база правил;
ИТ– информационные технологии;
МНК – метод наименьших квадратов;
ННС – нейро-нечеткие системы;
НС – нейронная сеть;
НЛ – нечеткая логика;
ОС – операционная система;
ПК – персональный компьютер;
ПО – программное обеспечение;
СУБД – система управления базами данных;
ЭВМ – электронная вычислительная машина;
Введение
Система предрейсовых осмотров актуальна в плане обеспечения безопасности транспортных перевозок, кроме того применяемый на данный момент принцип измерения и выбора медицинских наблюдаемых параметров позволяет усовершенствовать систему диагностики результата различными методами, начиная регрессионными и заканчивая современными интеллектуальными технологиями. Но в этом процессе должно совмещаться как экспертное знание так и числовая точность критериальной оценки состояния наблюдаемого субъекта. Соответственно здесь популярны гибридные схемы в подобных оценках. Экспертные базы требуют ввода лингвистической неопределенности в алгоритмы решения, а регрессионный характер измерений требует предварительной оценки их параметров и получение статистической модели с исключением аддитивных помех в наблюдаемом выходе.
Гибридные нейро-нечеткие системы (далее просто гибридные ANFIS системы) нашли самую большую область применения среди всех возможных методов синтеза нечетких множеств и нейронных сетей. Связано это с тем, что именно они позволяют наиболее полно использовать сильные стороны нечетких систем и НС. Характерной чертой гибридных систем является то, что они всегда могут быть рассмотрены как системы нечетких правил, при этом настройка функций принадлежностей в предпосылках и подзаключениях правил на основе обучающего множества производится с помощью НС. Существуют архитектуры гибридных систем, прогрессирующие от иерархической системы нечеткого выхода и от метода получения подзаключений по Сугено, учитывающие регрессионных характер исходных измерений. Эта схема вывода способна совместить предварительную настройку к стохастической среде получаемых данных методом регрессионного анализа и точную настройку к аппроксимируемому объекту по свойствам экспертного мнения. Кроме того, нужно учесть в пользу данного метода, что регрессионная часть выполняется матричным способом решения линейных уравнений и это составляет незначительную линейную трудность для алгоритма.
Проблема медицинской нормы, с точки зрения пространственного разделения признаков, состоит в том, что принимаемое во внимание среднеквадратичное отклонение нормального распределения по традиционной методике относится к одному медицинскому параметру, а центр распределения линейно связан с его средним значением. Если признаков несколько, то линейное геометрическое разделение по осям признаков составляет простейшую область для идеально нормального субъекта, что в реальности практически не достижимо и, кроме того, несовместимо с экспертным мнением, которое способно определять некоторые допуски к тем или иным параметрам. Та же проблема многоканального разделения признаков и в существующем АСПО, так как измерения многомерны – для оценки готовности к рейсу учитываются 7-14 параметров. В свою очередь возникает и экспертная сложность интеллектуального обобщения многомерных показателей в норму. Поэтому для решения этой актуальной проблемы принадлежности объекта к целевым классам нормы или ненормы самым оптимальным будет нелинейное разделение данных классов в пространстве признаков, которое идеально моделирует формула НС.
Нейро-нечеткие системы совмещают экспертные знания и оценки регрессионной среды как оптимальные аппроксиматоры целевых функций, но для разделения по признакам еще нужно обсудить некоторые особенности ННС. То есть, следует определить специфику ННС в решении проблем диагностики нормы исследуемых субъектов совместно с регрессионным анализом медицинских параметров. Итак, надо учесть, что ННС-аппроксиматоры образуют полносвязанную структуру без обратных связей. На выходе последнего слоя нет активационной функции, а формула квадратичной разности выхода и обучающего сигнала является функционалом, который зависит от параметров функций принадлежности экспертной базы и параметров выходного слоя вывода по Сугено. Величина изменения при настройке каждого параметра вычисляется как частная производная градиента функционала на выходе ННС, выполняя критерий его минимизации. Но исследуемая проблема требует ответа классификатора на пространстве признаков – принадлежит исследуемый субъект к целевой группе риска или нет. При этом подходе определяется пространство признаков размерности по числу параметров, предоставляемых с системе предрейсовых осмотров для диагностического заключения. Подобные измерения уже имеются в наличии у баз данных систем предрейсовых осмотров, в этом плане также отработана технология измерений. Но в этой системе экспертные представления фактически доминируют с существующими методами автоматизированной оценки норма/ненорма, так как исследуемые объекты в сущности являются сложными физиологическими системами с трудно формализуемыми математическими признаками целевого состояния в выполнении профессиональных действий. В этом случае ННС оптимально подходит для анализа признаков с учетом экспертных мнений, но традиционный выход системы требует соответствующей модификации, где необходимо обеспечить: аппроксимируемую непрерывную функцию выхода; активационную непрерывную функцию по формуле логистического распределения. Первая функция должна отображать стандартное нормальное распределение случайной величины, соответственно для нее будет подготовлены обучающие выборки гемодинамических показателей нормы. Аппроксимация центра распределения будет соответствовать активационному ответу «Нет» на принадлежность субъекта целевому классу риска. При смещении цента в случае выборки «ненорма» будет активирована функция выхода. С учетом того, что центр распределения может быть смещен выборкой «ненорма» в любую сторону оси, то выход аппроксимации несложно модифицируется инвертором уровня выхода и второй активационной функцией, а функции связаны с линией ответа посредством линейного сумматора. Таким образом, несложная адаптация к конкретной ситуации еще раз показывает универсализм иерархических ННС в управлении и настройке как регрессионных моделей, так и экспертных баз правил, где эти две структуры объединены нейросетевыми отношениями.
Актуальность работы: требования к качеству повышения обработки измерений с системах медицинского обеспечения безопасности на транспорте.
Целю работы является разработка системы на базе иерархии правил для нейросетевого принципа разделения признаков с использованием экспертных знаний достоверного анализа профессиональной пригодности работников транспорта.
Основные задачи, определенные в соответствии с поставленной целью квалификационной работы:
– анализ существующих методов, систем, типов и способов проводимых измерений в автоматизированных системах медицинского обеспечения безопасности на транспорте;
– ознакомление с типичными моделями ННС и выбор оптимальной с учетом особенностей организации АСПО;
– выбор способа определения медицинской нормы, который обладает свойством стохастичности с возможностью применения аппроксимирующей его ННС при ее обучении и использовании методов регрессионного анализа;
– выбор алгоритмов предварительного расчета регрессионных параметров вход-выход и градиентной весовой настройки правил;
– создание, на основе предложенных принципов и способов адаптации ННС к АСПО, алгоритмов ПО обучения и эксплуатации ННС в задачах АСПО;
– модернизация базовой технологии обеспечения безопасности грузопассажирских перевозок, учитывающей надежность «человеческого фактора», экспертной системой на базе ННС, способной к нелинейному разделению граничных условий норма/ненорма в пространстве признаков исходных измерений;
– составление ряда рекомендаций по использованию алгоритмов, свойств и параметров полученной программной модели иерархической системы нечеткого логического вывода контроля критической зависимости параметров гемодинамики.
1. ПРОБЛЕМЫ ОПРЕДЕЛЕНИЯ НОРМЫ В МЕДИЦИНЕ. МЕТОДЫ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ НОРМЫ
1.1 АСПО как предметная область моделирования прогноза медицинской нормы в системе безопасности на железнодорожном транспорте
Профессиональный отбор, предсменный и предрейсовый – все это является важнейшим направлением обеспечения безопасности движения на железнодорожном транспорте. В данной области медицинской практики можно рассмотреть аспекты адаптации к проблеме безопасности и внедрения вычислительных ресурсов компьютерных комплексов, функционирование которых базируется на различных по типу программных моделях медицинских исследований. Независимо от уровня чувствительности используемой аппаратуры получения исходных данных и средств визуализации результата, актуальным остается вопрос статистической обработки исходных измерений с целью выборки полезного сигнала с учетом знания определенной модели помехи наблюдения. Задачу подобной обработки данных в определенные моменты времени должны решать математические модели, используя классические методы идентификации. Но в плане моделирования динамики возникают проблемы с идентификацией параметров, т.к. стандартные методы дают несостоятельные оценки параметров при наличии ненаблюдаемых помех на входе и наблюдаемых на выходе. Это открывает направления научного исследования проблемы, одно из которых – модификация стандартных методов оценки параметров. Для возможности организации и внедрения программной обработки статистической выборки измерений, по математическим моделям моментного и динамического состояния медицинских показателей исследуемых работников, в качестве базовой разработки принимается действующая на Куйбышевской железной дороге АСПО на базе комплексов КАПД-01-СТ для медико-психологического обеспечения безопасности движения поездов (рисунок 1.1). Идеология АСПО заключается в следующем: интенсивность работы водителей транспорта имеет большое число факторов, влияющих на безопасность перевозок, требуются сведения о медицинских параметрах состояния здоровья участников перевозок и их обработка в едином информационном пространстве. В АСПО реализуется информационная технология (ИТ), позволяющая оптимизировать процессы управления за счет автоматизации рабочих мест, а также ИТ выполняет обеспечение процесса безопасности перевозок с учетом надежности «человеческого фактора».
Рисунок 1.1- Структурная ветвь базовой организации служб в АСПО на железной дороге
Необходимо помнить, что ИТ лишь автоматизируют существующий процесс, включая его недостатки. Например, полученный по датчикам поток измерений включает в себя аддитивные ошибки. Ошибка измерения (помеха) - объективный процесс, складывающийся с учетом: нелинейности физиологических процессов; поверхностного контакта датчиков; взаимной корреляции величин одной размерности, морфологии тканей, анизотропии биологических сред и т.п. В медицинской и биологической физике одним из основных направлений медицинских знаний является изучение физической сущности основных методов диагностики, их особенностей, приборной базы, а также оценка качества получаемой при этом информации. Следовательно, актуально разрабатывать численные методы идентификации полезного сигнала на базе математических моделей, адаптировать полученные программные продукты как расширение базовых ИТ, уже существующих в эксплуатации и не исключающих необходимости улучшения своего качества. По существу это задача реинжениринга - проектирования нового процесса, дающего основные результаты улучшения характеристик принимаемой к аналитической обработке информации. Это не только дополнительная автоматизация процессов управления, но и научно обоснованная возможность создать полностью новые, пересмотреть или оптимизировать уже существующие процессы и, следовательно, улучшить в несколько раз конечный продукт. В данном случае - повысить надежность «человеческого фактора» и, как следствие, увеличить безопасность грузопассажирских перевозок.
Новым процессом, реализованным в дипломном проекте для программных средств АСПО, является выявление «группы повышенного риска» и восстановление здоровья этой группы на основе математического моделирования статического и динамического распределения измерений медицинских параметров. «Процесс» - это ключевое слово в рассматриваемой концепции реинжениринга, означает не только использование специализированных технических средств и ИТ, но и постоянную работу всех участников, задействованных в обеспечении перевозок, направленную на выявление потенциальной опасности на ранней стадии и своевременного предупреждения. Все технические средства, начиная от средств измерений, сетевых решений, корпоративной базы данных до средств анализа подчинены этой цели. Фактически АСПО - это система управления, которая обеспечивает эффективное взаимодействие структурных подразделений транспортных предприятий и предприятий с высоким риском возникновения массовых катастроф в сочетании с автоматизацией предрабочего (предрейсового) медицинского осмотра. Структура АСПО четко определяет функциональные подразделения и их связи внутри нее. Это позволяет, на базе поставленных целей и решаемых задач, выявлять участки межструктурного взаимодействия, где можно применять методы идентификации полезной информации и расширять базу ИТ всей системы. В определении набора численных характеристик для клинического использования необходимо рассмотреть понятие медицинской нормы наблюдаемых параметров.
1.2 Стандартные функции АСПО
АСПО позволяет произвести выборки работников локомотивных бригад, относящихся к группе повышенного риска:
1. Выборки работников локомотивных бригад, относящихся к группе повышенно риска с помощью выбора математического ожидания и дисперсии. В заштрихованной зоне (АД свыше 140 мм.рт.ст. содержится группа работников, которая по показателям АДС может быть отнесена к группе повышенного риска).
2. Список этих работников локомотивных бригад, входящих в группу повышенного риска но показателю АДС > 140 мм.рт.ст. Задав минимальное количество осмотров, которое определяется в соответствии с выбранным промежутком времени (например, если запрос выполнен за 1 месяц, - от 5 до 15 осмотров) и процент попадания в выделенную зону (например 70 %), можно выделить значимую группу из всего состава.
3. Выделение фамилии работника для получения индивидуальных сведений. Предоставляется возможность выбора пороговых значений, анализ психофизиологических показателей и произвести запись в буфер для дальнейшего анализа.
4. Выполнение систематического обследования, входящих в группу работников с неадаптивной реакцией и срывом адаптации с помощью производственных врачей и психологов депо.
5. Применение такой методологии позволяет сделать существенно важные шаги для соединения медицинского, психологического и физиологического подходов к оценке здоровья работников локомотивных бригад. Например, начать определение взаимосвязи психологического фона возникающих заболеваний с конкретной диагностикой.
1.3 Медицинские и психофизиологические аспекты выделения группы повышенного риска
1.3.1 Оценка параметров профессиональной пригодности
Часто регистрируемые случаи профессиональных заболеваний – это болезни, связанные с воздействием на организм шума – нейросенсорная тугоухость – около 50%. Заболевания пылевой этиологии занимают второе место – 15–20% . На третьем месте стоят заболевания опорно-двигательного аппарата – 10–15%, далее вибрационная болезнь – около 10%.
По статистике, наибольшее число зарегистрированных случаев профессиональных заболеваний выявляются среди членов локомотивных бригад – около 30%.
По результатам предрейсовых медицинских осмотров с помощью автоматизированной системы предрейсового медицинского осмотра на базе аппаратно программного комплекса КАПД-01-СТ, выделяется группа риска по возможности развития патологических состояний и внезапного ухудшения самочувствия. За этот период времени стало ясно, что данная система может применяться для динамического контроля функционального состояния работников локомотивных бригад.
Группу риска по результатам медицинского и психологического обследований в основном составляют соматические заболевания около- 57%, психосоматические заболевания около 20% и около 23%- лица, у которых при медицинском обследовании признаков заболевания не обнаружено, т.е. с психологическими проблемами. Как видно из приведенных данных, около 43% работников локомотивных бригад, попадающих в группу риска, нуждаются в помощи психолога.
Такое положение и заставило объединить усилия медицинских работников и психологов локомотивных и мотор-вагонных депо в борьбе за здоровье и профессиональную работоспособность работников локомотивных бригад. Опыт работы психологов с группой риска дает право говорить о том, что комплекс КАПД-01-СТ и аналитические программы автоматизированной системы предрейсового медицинского осмотра позволяют выделять у работников локомотивных бригад такие состояния, как стрессовые, депрессивные, психоэмоциональную неустойчивость, накапливающееся утомление.
В исследовательском плане дальнейшая работа психофизиологических подразделений дорог направлена на уточнение корелляции между величинами индексов и психофизиологическим состоянием, состоянием здоровья работников локомотивных бригад.
Как показывает опыт работы, выделение группы риска по результатам предрейсового медицинского осмотра, на основе показателей индекса напряженности, SDR, Sit, показателям периферической гемодинамики, в основном происходит в период предболезни. По этой причине в инструкции психолога депо указано на необходимость консультации таких работников цеховым врачом с целью исключения соматического или психосоматического заболевания независимо от полученных им результатов обследования. Это делается с целью не просмотреть развитие болезни.
В зависимости от полученных результатов медицинского и психофизиологической» обследований, проводятся системные мероприятия: медицинские, восстановительные, реабилитационные.
В случае обнаружения соматического или психосоматического заболевания на первый план выступают медицинская и психотерапевтическая помощь. Если же признаков заболевания не удается обнаружить, на первый план выступает психологическая помощь.
Психофизиологическое обследование проводится параллельно с медицинским обследованием психологом локомотивного депо в первые 7 дней с момента отнесения работника локомотивной бригады к группе риска. Такое раннее обследование позволяет не только установить причину изменения функционального состояния, но и своевременно принять меры по проведению коррекционных мероприятий. Обследование проводится с использованием таких психологических методик, как СМИЛ, 16-факторный личностный опросник Р.Кеттела, шкала самооценки Ч.Спилбергера / Ю. Ханина, метод цветовых выборов, самооценки состояния (CAHL и психофизиологических методик таких как реакция на движущийся объект (РДО), простая двигательная реакция (ПДР), треморометрия.
Так например при психофизиологическом обследовании работника получены следующие результаты:
1) с низким показателем Sit: низкая тревожность, уравновешенность нервных процессов, эгоцентричен, обидчив, раним, проявляет неадекватные попытки упрямо отстаивать свои позиции, возможна ригидность характера, жесткость установок, стремится к поведению, ориентированному на одобрение окружающих, озабочен своим социальным статусом, склонен к отрицанию каких-либо затруднений, самооценка неадекватная;
- плохая бдительность, очень неустойчивое внимание, снижен контроль над эмоциональной сферой, проявляет себя осторожно, как будто бы чего-то опасается;
2) с высоким показателем Sit: преобладание процессов возбуждения, возбужден, тревожен, напряжен, насторожен, чувство неуверенности, тревога и опасение, восприимчив к внешним раздражителям;
- социально-психологическая дезадаптация, физическое и душевное перенапряжение, страх, чувство бесперспективности, утрата работоспособности;
3) с систолическим артериальным давлением более 140 мм рт. ст.: умеренная
реактивная тревожность, обидчив и раним, напряжен, характерна жесткость установок, ригидность характера.;
- высокая тревожность, физиологический дискомфорт, снижена работоспособность;
4) с высоким значением SDR и тахикардией: преобладание процессов возбуждения, отмечается затрудненность межличностных отношений и тенденция к усилению тяжести имеющихся затруднений и конфликтов, повышенная самооценка, самооценка не всегда адекватна, отмечаются черты аффективной ригидности, жесткость установок, агрессивность и эгоцентричность;
5) с неоднократным высоким значением SDR: неустойчивая работоспособность, раздражительная слабость, потребность в покое.
Таблица 1.1- Показатели для оценки психофизиологического состояния
|
Параметры |
Основной физиологический смысл |
|
ЧСС |
Артериальным пульсом называют ритмические колебания стенки артерии, обусловленные повышением давления в период систолы. Тахикардия (>90 уд/мин). Чаще всего является следствием физической нагрузки, сердечной недостаточности, нервно-эмоционального перенапряжения, утомления, переутомления, тиреотоксикоза (избыточно высокого давления гормонов щитовидной железы), физической нагрузки, повышения тонуса симпатического отдела автономной нервной системы. Брадикардия (<60 уд/мин) может быть физиологической как следствие тренированности занимающихся и занимавшихся ранее спортом обследуемых. Однако чаще снижение ЧСС происходит по причине гипертрофии сердца, повышения АД и нарушений проводимости. |
|
Систолическое давление |
Наибольшая величина давления в артериях (систолическое или максимальное) наблюдается во время прохождения вершины пульсовой волны. Заболевания: Артериальная гипертензия, гипертоническая болезнь, некоторые заболевания эндокринной системы. |
|
Диастолическое давление |
Наименьшая величина (диалистическое или минимальное давление) регистрируется во время прохождения основания пульсовой волны. Диалистическое АД определяют: а) преднагрузка сердца (количество притекаемой к сердцу крови); б) постнагрузка (тонус и состояние аорты); в) ритм сердца (отсутствие метаболических и других расстройств, нарушающих проводимость); г) сократимость сердца (способность создать достаточный конечнодиастолический объем после трех последовательных стадий систолы: пассивное заполнение левого желудочка, расслабление и фаза активного заполнения при систоле предсердий). |
|
Среднее гемодинамическое давление
|
Равнодействующая колебаний АД в разные фазы сердечного цикла. Характеризует эффективность работы системы кровообращения в обеспечении кровоснабжения отдельных органов и тканей. Особое значение показатель имеет при установлении диагноза гипотонической и гипертонической болезни при дифференциальной диагностике с нейроциркуляторной дистонией по гипертензивному типу. |
|
Пульсовое АД
|
Разница между систолическим и диастолическим АД. Зависит от количества крови, перекачиваемой сердцем с каждым ударом. Оценивать пульсовое давление необходимо, например, при патологии почек. Вторичный характер артериальной гипертензии определяет «обезглавленная гипертензия», т.е. пульсовое давление снижается до 20-10 мм.рт.ст. за счет замедленного повышения систоличесой компоненты. Снижение эластических свойств аорты и других крупных артериальных стволов (атеросклероз, эндартериит и т.п.) также определяет уменьшение значений показателя пульсового давления. Однако механизм этого понижения связан прежде всего с опережением роста показателей диастолического АД. |
|
Редуцированное давление
|
Отражает реакцию прекапиллярного русла, зависящую от объёма циркулирующей крови. |
|
SDR |
Отражает характер и механизмы системных расстройств при изменениях тонуса автономной (вегетативной) нервной системы, а также регуляции артериального давления и частоты сердечных сокращений. |
|
SIT |
Отражает состояние центральной нервной системы при различных типах реакции. В основном используется при определении состояний заторможенности или гиперактивности. |
|
Индекс напряжения регуляторных систем |
Отражает степень централизации управления сердечным ритмом и состояние баланса между центральной и периферической нервной системой. |
|
Мода (МО) |
Наиболее часто встречающееся значение интервала R-R, указывающее на доминирующий уровень функционирования синусового узла. |
|
Амплитуда моды (АМо) |
Количество кардиоциклов с наиболее часто встречающейся длительностью интервалов R-R, в %. |
|
Вариационный размах (^X) |
Разность между максимальным и минимальным значениями кардиоинтервалов. |
Продолжение таблицы 1.1
1.3.2 Критерии выделения «группы риска»
Критерием выделения в «группу риска» является:
• выход значений индексов регуляции (IN, SDR, SIT) или одного из них за пределы адаптивной реакции три и более раза в месяц;
• выход параметров частоты пульса и артериального давления за пределы установленных индивидуальных значений, приведший к отстранению от рейса два и более раза в месяц;
• признаки повышенной лабильности показателей гемодинамики три и более раза за 7 дней, в результате чего перед заступлением в рейс медицинским работником кабинета ПРМО проводились повторные измерения на автоматизированном комплексе;
• резкое снижение группы годности к поездной работе при периодическом психологическом обследовании;
• направление цехового терапевта;
• нарушение безопасности движения поездов, на основании Приказов по дисциплинарным нарушениям и направлению руководством локомотивного депо.
1.3.3 Расширенное психофизиологическое обследование по данным АСПО
1.3.3.1 Психологическая диагностика
Психологическая диагностика: исследование интеллекта (тест Амтхауэра), исследование личностных особенностей (MMPI), проверка операторской работоспособности (распределение внимания, скорость реакции, оперативность мыслительных процессов, скорость реакции выбора)
• Беседа (выясняются возможные причины отклонений по ПРМО, проговаривается график труда и отдыха, профилактические мероприятия по поддержанию требуемого уровня состояния здоровья и т.д.).
• Тест «САН» - методика оценки самочувствия, активности, настроения.
• Тест Спилбергера-Ханина — методика оценки личностной тревожности
и реактивной тревоги.
• ЧВ — методика оценки чувства времени.
• ПДР - методика оценки времени простой двигательной реакции.
• РДО - методика оценки реакции на движущийся объект.
• Метод цветовых выборов.
А также:
Определение нарушений функций мышления.
Определение нарушений функций внимания.
Определение нарушений функций памяти.
Диагностика мотивационной сферы:
Определение ценностных ориентаций
Мотивация избегания неуспеха – мотивация достижения
Диагностика направленности личности
Диагностика эмоционально-личностных качеств.
Диагностика коммуникативных навыков и особенностей межличностного взаимодействия:
Склонность к конфликтному и агрессивному поведению
Уровень субъективного контроля
Диагностика стиля взаимодействия
Диагностика профессиональной направленности и компетентности:
Профориентационные методики
Система «человек-человек»
Система «человек-техника»
Система «человек-знаковая система»
Система «человек-природа»
Творческий потенциал
1.3.3.2. Функциональная диагностика
Электроэнцефалография
Стабилография
Электрокардиография
Функциональные пробы
1.4 Проблемы предоставления нормы в АСПО
Основной целью автоматизированной системы предрейсовых осмотров является статистическое наблюдение распределение значений гемодинамики по частоте их измерения с предположением, что данное распределение, не зависимо от числа измерений, – нормально. Обсуждение проблемной части подобного подхода можно начинать, предварительно ознакомившись с целями и задачами АСПО.
АСПО на транспорте решает три задачи:
Первая - запретительная. По утвержденным критериям и их численным значениям осуществлять отстранение работников, не подготовленных к рейсу.
Вторая - предупредительная. С помощью мониторинга контроль этих же показателей и других критериев для осуществления активного вызова и выполнения лечебных и реабилитационных мероприятий.
Третья - исследовательская. Определение эффективно работающих критериев и их численных значений для решения задачи обеспечения безопасности движения поездов и других транспортных средств.
Также к основным задачам можно отнести:
- внедрение современных автоматизированных медицинских технологий для повышения качества и эффективности проведения предрейсовых медицинских осмотров локомотивных бригад;
- своевременное выявление лиц с нарушениями функционального состояния, явлениями острых и обострением хронических заболеваний;
- мониторинг состояния здоровья и функционального статуса работников локомотивных бригад на основе автоматизированной обработки и анализа результатов предрейсовых медицинских осмотров, в том числе с учетом данных углубленных осмотров;
- организационно-методическое обеспечение взаимодействия фельдшеров ПРМО, цеховых терапевтов, психологов (психофизиологов) локомотивных депо и других специалистов по вопросам медицинского и психофизиологического обеспечения локомотивных бригад;
- разработка индивидуальных критериев и пороговых значений физиологических показателей, оценка состояния здоровья различных возрастных групп работников локомотивных бригад, а также лиц, выполняющих иные виды движения;
- выделение групп повышенного риска по развитию психосоматических заболеваний, в том числе с симптомами недосыпания, переутомления, стрессовых, депрессивных и других нарушений функционального состояния:
- объективизация данных предрейсовых осмотров, автоматическая обработка и их систематизация, контроль качества и эффективности проводимых профилактических мероприятий;
- информационное сопряжение АСПО с ЛСУТ с разграничением прав доступа;
- интеграция результатов НИОКР: - «Автоматизированные методы оценки, в том числе дистантные и прогнозирование состояния здоровья и работоспособности работников локомотивных бригад на основе численных критериев функционального состояния в процессе предрейсового контроля» и «Обеспечение информационной безопасности в автоматизированных системах предрейсового осмотра и медико-психологического обеспечения работников локомотивных бригад» в программно-техническое обеспечение АСПО.
Не смотря на существенный перечень задач АСПО цеховыми терапевтами отмечается следующая закономерность: при малом числе измерений интервал нормы более объективен к рискованным отклонениям состояния здоровья членов исследуемой популяции. При большем числе измерений объективность скрывается интервалом нормы и отдельные краевые случаи состояния риска не каким образом не отражаются системой. Это сокрытие происходит за счет свойств нормального закона, который следуя закону больших чисел по вероятности с увеличением измерений будет приближать вычисляемую норму к «идеальной», скрывая факторы риска и прогрессирующие патологии. Для исправления подобных издержек информационной обработки сигналов АСПО поставлена цель и определены задачи настоящего проекта.
2. АДАПТИВНАЯ НАСТРОЙКА СТАТИСТИЧЕСКОГО РАЗДЕЛЕНИЯ ПРИЗНАКОВ В СИСТЕМЕ НЕЙРО-НЕЧЕТКОГО ВЫВОДА
2.1 Основы принципа нечеткого вывода и идентификации
2.1.1 Нечеткая логика, лингвистическая оценка медицинских параметров
Нечеткая логика это обобщение традиционной аристотелевой логики на случай, когда истинность рассматривается как лингвистическая переменная, принимающая значения типа: "очень истинно", "более-менее истинно", "не очень ложно" и т.п. Указанные лингвистические значения представляются нечеткими множествами. Лингвистической переменной называется переменная, принимающая значения из множества слов или словосочетаний некоторого естественного или искусственного языка.
2.1.2 Направления исследований нечеткой логики по отношению к медицинским диагностическим заключениям
В настоящее время существует по крайней мере два основных направления научных исследований в области нечеткой логики:
Нечеткая логика в широком смысле (Теория приближенных вычислений)
Нечеткая логика в узком смысле (Символическая нечеткая логика)
2.1.2.1 Символическая нечеткая логика и терминология предметной области
Символическая нечеткая логика основывается на понятии t-нормы. После выбора некоторой t-нормы (а её можно ввести несколькими разными способами) появляется возможность определить основные операции над пропозициональными переменными: конъюнкцию, дизъюнкцию, импликацию, отрицание и другие. Нетрудно доказать теорему о том, что дистрибутивность, присутствующая в классической логике, выполняется только в случае, когда в качестве t-нормы выбирается t-норма Гёделя. Кроме того, в силу определенных причин, в качестве импликации чаще всего выбирают операцию, называемую residium (она, вообще говоря, также зависит от выбора t-нормы). Определение основных операций, перечисленных выше, приводит к формальному определению базисной нечеткой логики, которая имеет много общего с классической булевозначной логикой (точнее, с исчислением высказываний). Существуют три основных базисных нечетких логики: логика Лукасевича, логика Гёделя и вероятностная логика (Product logic). Интересно, что объединение любых двух из трех перечисленных выше логик приводит к классической булевозначной логике.
2.1.2.2 Теория приближенных вычислений и стохастические измерения
Основное понятие нечеткой логики в широком смысле — нечеткое множество, определяемое при помощи обобщенного понятия характеристической функции. Затем вводятся понятия объединения, пересечения и дополнения множеств (через характеристическую функцию; задать можно различными способами), понятие нечеткого отношения, а также одно из важнейших понятий — понятие лингвистической переменной. Вообще говоря, даже такой минимальный набор определений позволяет использовать нечеткую логику в некоторых приложениях, для большинства же необходимо задать ещё и правило вывода (и оператор импликации).
2.1.3 Идентификация с помощью иерархической системы нечеткого логического вывода
Для моделирования многомерных
зависимостей "входы - выход"
целесообразно использовать иерархические
системы нечеткого логического вывода.
В этих системах выходная переменная
одной базы знаний является входной для
другой базы знаний. На рис. 2.1 приведен
пример иерархической нечеткой базы
знаний, моделирующей зависимостьвы
с
использованием трех баз знаний. Эти
базы знаний описывают такие зависимости:
,
и
.
Рисунок 2.1 - Пример иерархической нечеткой базы знаний
Применение иерархических нечетких баз знаний позволяет преодолеть "проклятие размерности". При большом количестве входов эксперту трудно описать причинно-следственные связи в виде нечетких правил. Это обусловлено тем, что в оперативной памяти человека может одновременно хранится не более 7±2 понятий-признаков. Следовательно, количество входных переменных в одной базе знаний не должно превышать это магическое число. Более поздние исследования показали, что хорошие базы знаний получаются, когда количество входов не превышает пяти шести. Поэтому, при большем количестве входных переменных необходимо их иерархически классифицировать с учетом приведенных выше рекомендаций. Обычно, выполнение такой классификации не составляет трудностей для эксперта, так как при принятии решений человек иерархически учитывает влияющие факторы.
Преимущество иерархических баз
знаний заключается еще и в том, что они
позволяют небольшим количество нечетких
правил адекватного описать многомерные
зависимости "входы - выход". Пусть,
для лингвистической оценки переменных
используется по пять термов. Тогда,
максимальное количество правил для
задания зависимости
с
помощью одной базы знаний будет равным
(конечно, для адекватного описания
зависимости "входы - выход" необходимо
значительно меньше нечетких правил).
Для иерархической базы знаний (рис.
2.1), описывающую ту же зависимость,
максимальное количество нечетких правил
будет равным
.
Причем, это "короие" правила с двумя
- тремя входными переменными.
Особенностью нечеткого логического вывода по иерархической базе знаний является отсутствие процедур дефаззификации и фаззификаци для промежуточных переменных (y>1> и y>2> на рис. 2.1). Результат логического вывода в виде нечеткого множества напрямую передается в машину нечеткого логического вывода следующего уровня иерархии. Поэтому, для описания промежуточных переменных в иерархических нечетких базах знаний достаточно задать только терм-множества, без определения функций принадлежностей.
2.2. Задача разработки программных средств оценки критической зависимости гемодинамических показателей
2.2.1 Характеристики программной модели при обработке регрессионных измерений предрейсовых осмотров
Назначение программы: инструментальный элемент анализа нормы гемодинамических показателей участников предрейсового осмотра: пульс, систолическое и диастолическое давление, психофизические показатели. Компоненты моделирования – текущее состояние и прогноз нормы как распределения при определенной частоте измерений, которые представляет динамическая модель с решением параметров модифицированным МНК в условиях ограниченной стохастичности входных сигналов. Выход программы – текущее и прогнозированное состояние нормы, в которой исключено влияние аддитивных помех типа белый шум, что позволяет представлять распределение значений по норме более объективными, учитывая тенденции риска по норме и возможности прогноза патологии по динамике нормы.
Программа моделирует совокупность компонентов исследования как некоторую часть объекта, который называется «Динамическая норма гемодинамики». Объект моделирования – есть программная модель как источник анализируемой информации.
Цель применения программы: анализ текущей и прогнозируемой нормы гемодинамики работников локомотивных бригад при медицинском обеспечении безопасности на железнодорожном транспорте.
Задачи: программа предназначена для интеграции в комплекс АСПО без привлечения дополнительных средств ее адаптации и обучения персонала. Программа выполняет задачу адаптации к системе данных АСПО и повышает качество измеряемого и анализируемого сигнала. Определяет текущее и прогнозируемое во времени состояние компонентов исследования для диагностического заключения о состоянии объекта с использованием графических вариантов выхода модели.
Функционирование программного обеспечения происходит на персональных компьютерах типа IBM PC не ниже класса Pentium при поддержке операционных систем (ОС) Windows 98, 2000, NT, XP, Vista. Учитывая целесообразность совмещения базы данных ведения картотеки пациентов и проводимых исследований на основе расчетов пространственно-временной модели, в программном обеспечении реализована концепция некоторой системы управления этими данными и численными методами расчетов. Проектирование системы начинается с обработки отношений в базе данных типа «Картотека медицинских исследований». Далее система адаптируется к СУБД, управления данными, использует определенную в АСПО технологию хранения и считывания данных приборов измерения параметров гемодинамики.
В качестве инструмента выполнения проекта управляющей системы выбраны: интерактивное ANFIS, объектно-ориентированный язык Object Pascal со стандартной библиотекой визуальных компонент проектирования. Концепция объектно-ориентированного программирования, реализованная в интерактивном ANFIS, позволяет рассмотреть средства статистической обработки данных параметров гемодинамики, как систему родословных отношений объектов, прогрессирующую по мере совершенствования существующих и новых перспективных моделей сбора, анализа исходной информации. Доступ к данным картотеки пациентов и измерениям происходит по типу «Клиент-сервер», осуществляется через компонентный интерфейс Delphi с системой доступа к базам данных (БД) фирмы Borland (Borland Database Engine, или BDE). Это первая функциональная часть управляющей системы. Вторая - реализация численных методов, описанных входными языками математических пакетов (Mathcad, Matlab и т.п.). Управление расчетами происходит на основе OLE (Object linking and embedding) технологии.
В качестве такого ресурса моделирования использовались входной язык, модули программирования и графической визуализации математической системы Mathcad версии 11.0а.
Результат: разработана программа управления системой ресурсов информационного обеспечения расчета параметров гемодинамики и имеющая расширение пространственно-временного анализа основных компонентов медицинской нормы, используются элементы графического вывода для целей интерпретации исходных данных и диагностического заключения.
Обмен административной оболочки пользователя с вычислительными ресурсами математических пакетов происходит по системной технологии OLE – вычислительные ресурсы методов идентификации и прогноза есть исходные данные COM сервера Mathcad для административной оболочки, выполненной по схеме многодокументного интерфейса.
2.2.2 Управление иерархией нечеткого вывода интерактивным пакетом ANFIS
ANFIS - это аббревиатура Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода. Она была предложена Янгом (Jang) в начале девяностых. ANFIS является одним из первых вариантов гибридных нейро-нечетких сетей - нейронной сети прямого распространения сигнала особого типа. Архитектура нейро-нечеткой сети изоморфна нечеткой базе знаний. В нейро-нечетких сетях используются дифференцируемые реализации треугольных норм (умножение и вероятностное ИЛИ), а также гладкие функции принадлежности. Это позволяет применять для настройки нейро-нечетких сетей быстрые алгоритмы обучения нейронных сетей, основанные на методе обратного распространения ошибки. Ниже описываются архитектура и правила функционирования каждого слоя ANFIS-сети.
ANFIS реализует систему нечеткого вывода Сугено в виде пятислойной нейронной сети прямого распространения сигнала. Назначение слоев следующее: первый слой - термы входных переменных; второй слой - антецеденты (посылки) нечетких правил; третий слой - нормализация степеней выполнения правил; четвертый слой - заключения правил; пятый слой - агрегирование результата, полученного по различным правилам.
Входы сети в отдельный слой не выделяются. На рис. 2.2. изображена ANFIS-сеть с двумя входными переменными (x>1> и x>2>) и четырьмя нечеткими правилами. Для лингвистической оценки входной переменной x>1> используется 3 терма, для переменной x>2> - 2 терма.
Рисунок 2.2 – Пример ANFIS-сети
Введем следующие обозначения, необходимые для дальнейшего изложения:
-
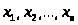входы сети;
-
выход сети;
-
нечеткое правило с порядковым номером
;
- количество
правил ,
;
-
нечеткий терм с функцией принадлежности
,
применяемый для лингвистической оценки
переменной
в r-ом правиле (,
);
-
действительные числа в заключении r-го
правила (,
).
ANFIS-сеть функционирует следующим образом.
Слой 1. Каждый
узел первого слоя представляет один
терм с колоколобразной функцией
принадлежности. Входы сети
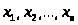соединены только со своими термами.
Количество узлов первого слоя равно
сумме мощностей терм-множеств входных
переменных. Выходом узла являются
степень принадлежности значения входной
переменной соответствующему нечеткому
терму:
,
(2.1)
где a, b и c - настраиваемые параметры функции принадлежности.
Слой 2. Количество
узлов второго слоя равно m. Каждый узел
этого слоя соответствует одному нечеткому
правилу. Узел второго слоя соединен с
теми узлами первого слоя, которые
формируют антецеденты соответствующего
правила. Следовательно, каждый узел
второго слоя может принимать от 1 до n
входных сигналов. Выходом узла является
степень выполнения правила, которая
рассчитывается как произведение входных
сигналов. Обозначим выходы узлов этого
слоя через
,.
Слой 3. Количество узлов третьего слоя также равно m. Каждый узел этого слоя рассчитывает относительную степень выполнения нечеткого правила:
.
(2.2)
Слой 4. Количество узлов четвертого слоя также равно m. Каждый узел соединен с одним узлом третьего слоя а также со всеми входами сети (на рис. 2.1. связи с входами не показаны). Узел четвертого слоя рассчитывает вклад одного нечеткого правила в выход сети:
.
(2.3)
Слой 5. Единственный узел этого слоя суммирует вклады всех правил:
.
(2.4)
Типовые процедуры обучения нейронных сетей могут быть применены для настройки ANFIS-сети так как, в ней использует только дифференцируемые функции. Обычно применяется комбинация градиентного спуска в виде алгоритма обратного распространения ошибки и метода наименьших квадратов. Алгоритм обратного распространения ошибки настраивает параметры антецедентов правил, т.е. функций принадлежности. Методом наименьших квадратов оцениваются коэффициенты заключений правил, так как они линейно связаны с выходом сети. Каждая итерация процедуры настройки выполняется в два этапа. На первом этапе на входы подается обучающая выборка, и по невязке между желаемым и действительным поведением сети итерационным методом наименьших квадратов находятся оптимальные параметры узлов четвертого слоя. На втором этапе остаточная невязка передается с выхода сети на входы, и методом обратного распространения ошибки модифицируются параметры узлов первого слоя. При этом найденные на первом этапе коэффициенты заключений правил не изменяются. Итерационная процедура настройки продолжается пока невязка превышает заранее установленное значение. Для настройки функций принадлежностей кроме метода обратного распространения ошибки могут использоваться и другие алгоритмы оптимизации, например, метод Левенберга-Марквардта.
2.2.3 Алгоритм диагностики
Информация,
полученная от врача и больного, включает
нечеткость, выраженную ЛЗИ. Для вычислений
необходимо преобразовать эти значения
в числовые значения истинности (ЧЗИ).
Для их количественной оценки использованы
функции принадлежности. В данной системе
такие понятия, как «немного», «очень»
для симптомов и «часто», «вероятно» и
др. для взаимосвязи между болезнями и
симптомами, представлены ЛЗИ (семь
уровней). При этом необходимо установить,
каким образом выбирать по функции
принадлежности каждого ЛЗИ значения
принадлежности. Такие значения назовем
а-сечением, а значение, выбранное для
,
обозначим
.
Обычно
имеет одно значение, но в целях сохранения
нечеткости в словах более естественно
использовать интервал значений, например
для ЛЗИ "UN" (неизвестное) введем
интервал [О, 1]. Таким образом будем
задавать интервал значений принадлежности
для всех ЛЗИ, т.е.
.
(2.5)
Связь между ЛЗИ, а-сечением и значениями принадлежности показана на рис. 2.3. В системе существует база данных, в которой все функции принадлежности и а-сечение являются координатами, константами и другими параметрами.
Алгоритм выводов следует из формул (2.6) и (2.7).
,
(2.6)
(2.7).
При этом
предполагается, что
-нечеткие
подмножества множества V ЛЗИ, т. е. очень
правдивые и выпуклые подмножества. Если
применить к формулам (2.6) и (2.7) нечеткие
правила «модус поненс» и «модус толлекс»,
то получатся следующие взаимосвязи
между болезнями и симптомами:
для
(2.8)
,
(2.9)
где
означает отрицание в нечеткой логике,
L
указывает нижнюю границу (см. дополнение
об операциях в нечеткой логике). Зададим
наблюдаемые симптомы
,-
и знания
,
Рисунок 2.3 Связь между ЛЗИ, а и значениями принадлежности
,
и обнаружим все болезни {
}.
можно получить, найдя общее решение
формул (2.8) и (2.9). При этом достоверности
знаний
,
,
можно определить через интервал их
значений ([нижнее значение, верхнее
значение]) следующим образом:
(2.10)
Кроме того, определим расстояние между симптомом и знаниями следующим образом:
,
(2.11)
.
(1.12)
Введем следующие множества интервалов значений для знаний и расстояний: для любых i, j
,
,
.
(2.13)
Записи
,
,
обозначают, что для любых i, j
,
,
.
(2.14)
Обратная задача для D.6) сводится к нахождению следующего вектора
,
(2.15)
где а-вектор, элементами которого являются множества интервалов значений. Используя алгоритм для обратной задачи, основанный на нечетких неравенствах, получаем решение
,
,
(2.16)
где
(2.17)
Где
,
(обозначения
,
объяснены в дополнении).
Кроме того, решение для выражения (2.9) можно получить, найдя вектор
,
(2.18)
Это решение имеет следующий вид:
,
.
(2.19)
Следовательно,
решение, удовлетворяющее формулам
(2.15), (2.19), для любых
имеет вид
,
,
(2.20)
где
определяется следующим образом:
. (2.21)
Если
,
решения не существует. В этом случае
можно рекомендовать следующие способы
решения:
1) уменьшить значение параметра а (а-сечение), отражающего точность выводов, и делать повторные выводы, приближая этот параметр к нулю;
2) повторно
расспросить больного о симптоме,
исправить данные на уточненные и вновь
сделать выводы.
Первый способ позволяет легко получить результаты с достаточно высокой степенью нечеткости в целом, но он не слишком эффективен. Поэтому целесообразно применить второй способ.
2.2.4 Усовершенствованный метод диагностики
Выше мы рассмотрели случай, когда существует решение обратной задачи при некотором заданном значении а. Однако, например, если а = 0,6, решение существует, но при а > 0,8 уже не существует, т. е. прийти к решению не всегда возможно. Обычно в подобных случаях недостаточно информации о симптомах, и лучше повторить диагностику после получения более полной информации. Следовательно, необходимо рассмотреть какие-либо методы выбора нужных симптомов. Например, в случае ошибочных исходных данных можно использовать усовершенствованную диагностику, которая позволяет прийти к правильному диагнозу. Такая диагностика состоит в следующем.
Прежде всего
рассмотрим следующий вектор
,
элементами которого являются ЛЗИ
элементов нечеткого множества болезней
по отношению к симптомам:
.
(2.22)
i-й базовый вектор А определим следующим образом:
,
,
(2.23)
где а. л. означает «абсолютная ложь».
-вектор,
в котором только i-й
элемент есть
,
а все остальные элементы - а.л. Другими
словами, учитывается только возможность
появления болезни i,
а уровень ЛЗИ для всех остальных болезней
есть а.л. Кроме того, предложим следующие
варианты ЛЗИ, относящиеся к
:
L = {ложь, неизвестно, истина, абсолютная истина}. Если применить к формулам (2.6), (2.7) правила нечеткий «модус поненс» и нечеткий «модус олленс» соответственно, то для i, j получим следующие формулы:
,
(2.24)
.
(2.25)
Приближение
(среднее арифметическое ожидаемое
значение)
полученное с помощью ЧЗИ для симптома,
предсказанного в случае
,
есть вектор, элементы которого имеют
следующий вид:
,
.
(2.26)
Аналогично
определим среднее арифметическое
значение b
для реально наблюдаемых симптомов.
Элементы
зададим следующим образом:
,
.
(2.27)
Направление
новых наблюдений можно определить с
учетом геометрической формы
и
,
т.е. чтобы определить группу симптомов,
которые следует проверить, вычислим
разность
и
.
Алгоритм вычислений заключается в
следующем. Сначала рассмотрим обычное
расстояние
:
.
(2.28)
есть разность
ожидаемых значений истинности симптомов
при
.
Это один из способов определения
расстояния, кроме него можно рассматривать
другие расстояния. Кратчайшее расстояние
определим следующим образом:
,
,
(2.29)
а именно
.
(2.30)
Запомним
,
удовлетворяющую следующему условию:
,
.
(2.31)
представляет
собой значение, при котором
является минимальным для
при любой болезни i.
При этом пусть
-это
,
задающее
.
Затем вычислим
такое,
что
.
(2.32)
определяет
для болезней, среди которых есть номер
болезни с самым маленьким
.
Учитывая значения истинности симптомов,
определим базовый вектор
для болезни, разность ожидаемых и
наблюдаемых значений для которой
наименьшая:
.
(2.33)
Этот вектор
позволяет создать относительный критерий
истинности значений для симптомов.
Кроме того, получим
,
т.е.
,
который можно сравнить с
для каждого элемента.
Итак, можно
указать группу симптомов, соответствующую
номеру с наибольшим значением
.
Если
прогнозируется появление одновременно
двух и более болезней, данный алгоритм
предполагается усовершенствовать,
например путем изучения комбинации
базовых векторов
.
2.2.5 Выводы и база знаний
В качестве методов нечетких выводов с использованием нечеткой информации известны продукционные правила, выводы с помощью нечетких отношений и другие методы. В данной системе из-за того, что знания имеют иерархическую структуру (что позволяет делать окончательную оценку с использованием промежуточных гипотез об оценке результатов обследования, рекомендаций по образу жизни и других гипотез) и есть необходимость запуска механизма выводов не в режиме диалога, а по факту ввода данных, использованы выводы с помощью продукционных правил с прямым построением цепочки рассуждений. По мере прослеживания правил метод построения цепочки увеличивает нечеткость, поэтому в системе результаты выдаются на втором или третьем уровне иерархии.
При вводе данных клинических анализов, информации, полученной при расспросе пациента, и при выводе тяжести болезни или других сведений используются непосредственные значения или лингвистические значения
ности. Механизм выводов является независимой подсистемой (рисунок 2.4). На входы поступают данные из базы фактов и базы знаний, а на выход передаются результаты выводов, их достоверность и объяснение процесса выводов.
Рисунок - 2.4 Схема механизма выводов.
Для выводов использован нечеткий «модус поненс», представляющий собой расширение правила «модус поненс» - дедуктивного вывода в классической логике. Это правило можно представить следующим образом:
Если
и
,
тогда
,
(2.34)
где
-нечеткие множества в полных пространствах
,
соответственно их элементы обозначим
через
.
Знак
обозначает импликацию.
Если можно
получить информацию
о пространстве U для нечеткого отношения
между некоторыми объектами
и
,
о которых имеется знание, то как результат
можно вывести информацию о V из
и
.
Нечетким
множествам в полном пространстве V можно
поставить в соответствие функции
принадлежности
,
где
обозначает меру принадлежности
элемента
.
Нечеткое множество а можно также
представить в виде
,
(2.35)
где
- объединение
на всем пространстве U, а знак «/» -
разделитель.
При нечетких
выводах необходимо задать метод
преобразования нечеткого условного
оператора
в нечеткое отношение
.
Кроме того, заключение можно получить
путем свертки фактических данных и
нечеткого отношения. Существует несколько
традиционных методов преобразования
и свертки. В данной системе выводы
делаются с помощью следующего метода,
обеспечивающего минимальный разброс
решений:
,
(2.36)
где
-заключение,
фактические данные.
Блок выводов работает следующим образом. Пусть в предпосылке правил записано несколько тезисов:
Если
,
тогда
.
(2.37)
Тогда, если
в базе фактических данных заданы
и
,
заключение
получается по следующей формуле:
,
(2.38)
где
-операция
максимум-минимум,
обозначает
.
Последовательность вывода показана на рис. 2.5.
База знаний для выводов составляется из функций принадлежности (в случае оценки входных и выходных значений), правил, диапазона входных и выходных значений и указаний к окончательным выходным данным. Функции принадлежности состоят из названия функции (уровня нечеткости) и значений принадлежности, в системе использованы следующие нечеткие уровни (ниже приведен процесс составления базы знаний):
1. Для каждого пункта клинических анализов, исключая качественные данные, в предпосылках используется пять уровней:
TRS (очень маленький) TPS (довольно малый)
ММ (обычный) ТРВ (довольно большой)
TRB (очень большой)
2. Для пунктов клинических анализов с качественными данными в предпосылках используются
ММ (-) TPS (+ - и ниже) РВ (+ -)
RB (+) ТРВ ( + и выше) ТРВ (+ + и выше)
VB ( + + +)
3. При расспросе о симптомах в предпосылках используются LT1 (не проявляется, проявляется временами, проявляется)
4. Для промежуточных гипотез и тяжести болезни в заключениях используются
CLA (классический) DEF (определенный)
PRO (вероятный) POS (возможный)
SUS (подозреваемый)
5. Для выбора диагноза на экране, выбора способа осмотра и промежуточных гипотез в предпосылках и заключениях используются
YES (да) NO (нет).
Пример функции принадлежности для уровней (1) приведен на рис. 2.6 а), для уровней (4)-на рис. 2.6 б). В правилах можно описать до десяти нечетких тезисов предпосылки и до двух нечетких тезисов заключения. Правила имеют следующую структуру:
Рисунок 2.5 Процесс выводов.
Если пункт введенных данных = уровень нечеткости,
тогда пункт выходных данных = уровень нечеткости.
а)
б)
Рисунок 2.6 функции принадлежности для уровней (1) на рис. а) и для уровней (4) на рис. б).
Кроме того, для уровней нечеткости, представленных функциями принадлежности, в тезисах можно использовать отрицание и логическую сумму.
Правила записаны в трех файлах: первичной оценки, вторичной оценки и указаний по охране здоровья. Файлы переключаются по соответствующей команде.
Приведем ниже примеры правил первичной оценки функционирования печени.
1. Если GOT = ТРВ, то функционирование печени = DEF.
2. Если GPT = ТРВ, то функционирование печени = DEF.
3. Если GGT = ТРВ, то функционирование печени = DEF.
4. Если (GOT = < GPT) = YES, то функционирование печени = DEF.
5. Если расспрос (легкая усталость) = LT1, то функционирование печени = PRO.
6. Если GOT = ММ & GPT = ММ & (GOT = < GPT) = NO & прошлый раз GOT = ТРВ, то функционирование печени = PRO.
2.2.6 Проектирование систем типа Сугено
Рассмотрим
основные этапы проектирования систем
типа Сугено
на примере создания системы нечеткого
логического вывода, моделирующей
зависимость
,
,
.
Моделирование
этой зависимости будем осуществлять с
помощью следующей базы знаний:
Если x1=Средний, то y=0;
Если x1=Высокий и x2=Высокий, то y=2x1+2x2+1;
Если x1=Высокий и x2=Низкий, то y=4x1-x2;
Если x1=Низкий и x2=Средний, то y=8x1+2x2+8;
Если x1=Низкий и x2=Низкий, то y=50;
Если x1=Низкий и x2=Высокий, то y=50.
Рисунок 2.7 Эталонная поверхность
Проектирование системы нечеткого логического вывода типа Сугэно состоит в выполнении следующей последовательности шагов.
Шаг 1. Для загрузки основного fis-редактора напечатаем слова fuzzy в командной строке. После этого откроется нового графическое окно, показанное на рис. 2.8.
Рисунок 2.8 Окно редактора FIS-Editor
Шаг 2. Выберем тип системы. Для этого в меню File выбираем в подменю New fis… команду Sugeno.
Шаг 3. Добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input.
Шаг 4. Переименуем первую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input1, введем новое обозначение x1 в поле редактирования имени текущей переменной и нажмем <Enter>.
Шаг 5. Переименуем вторую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input2, введем новое обозначение x2 в поле редактирования имени текущей переменной и нажмем <Enter>.
Шаг 6. Переименуем выходную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке output1, введем новое обозначение y в поле редактирования имени текущей переменной и нажмем <Enter>.
Шаг 7. Зададим имя системы. Для этого в меню File выбираем в подменю Export команду To disk и введем имя файла, например, FirstSugeno.
Шаг 8. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1.
Шаг 9. Зададим диапазон изменения переменной x1. Для этого напечатаем -7 3 в поле Range (см. рис. 2.9) и нажмем <Enter>.
Рисунок 2.9 Функции принадлежности переменной x1
Шаг 10. Зададим функции принадлежности переменной x1. Для лингвистической оценки этой переменной будем использовать, 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Зададим наименования термов переменной x1. Для этого делаем один щелчок левой кнопкой мыши по графику первой функции принадлежности (см. рис. 2.9). Затем напечатаем наименование терма Низкий в поле Name. Затем делаем один щелчок левой кнопкой мыши по графику второй функции принадлежности и вводим наименование терма Средний в поле Name. Еще раз делаем один щелчок левой кнопкой мыши по графику третьей функции принадлежности и вводим наименование терма Высокий в поле Name и нажмем <Enter>. В результате получим графическое окно, изображенное на рис. 2.9.
Шаг 11. Зададим функции принадлежности переменной x2. Для лингвистической оценки этой переменной будем использовать 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Для этого активизируем переменную x2 с помощью щелчка левой кнопки мыши на блоке x2. Зададим диапазон изменения переменной x2. Для этого напечатаем -4.4 1.7 в поле Range (см. рис. 2.10.) и нажмем <Enter>. По аналогии с предыдущим шагом зададим следующие наименования термов переменной x2: Низкий, Средний, Высокий. В результате получим графическое окно, изображенное на рис. 2.10.
Рисунок 2.10 Функции принадлежности переменной x2
Шаг 12. Зададим линейные зависимости между входами и выходом, приведенные в базе знаний. Для этого активизируем переменную y с помощью щелчка левой кнопки мыши на блоке y. В правом верхнем угле появилось обозначение трех функций принадлежности, каждая из которых соответствует одной линейной зависимости между входами и выходам. В базе знаний, приведенной в начале подраздела 2.2.6. указаны 5 различных зависимостей: y=50; y=4x1-x2; y=2x1+2x2+1; y=8x1+2x2+8; y=0. Поэтому добавим еще две зависимости путем выбора команды Add Mfs… меню Edit. В появившимся диалоговом окне в поле Number of MFs выбираем 2 и нажимаем кнопку OK.
Шаг 13. Зададим наименования и параметры линейных зависимостей. Для этого делаем один щелчок левой кнопкой мыши по наименованию первой зависимости mf1. Затем печатаем наименование зависимости, например 50, в поле Name, и устанавливаем тип зависимости – константа путем выбора опции Сonstant в меню Type. После этого вводим значение параметра – 50 в поле Params.
Аналогично для второй зависимости mf2 введем наименование зависимости, например 8+8x1+2x2. Затем укажем линейный тип зависимости путем выбора опции Linear в меню Type и введем параметры зависимости 8 2 8 в поле Params. Для линейной зависимости порядок параметров следующий: первый параметр – коэффициент при первой переменной, второй – при второй и т.д., и последний параметр – свободный член зависимости.
Аналогично для третьей зависимости mf3 введем наименование зависимости, например 1+2x1+2x2, укажем линейный тип зависимости и введем параметры зависимости 2 2 1.
Для четвертой зависимости mf4 введем наименование зависимости, например 4x1-x2, укажем линейный тип зависимости и введем параметры зависимости 4 -1 0.
Для пятой зависимости mf5 введем наименование зависимости, например 0, укажем тип зависимости - константа и введем параметр зависимости 0.
В результате получим графическое окно, изображенное на рис. 2.11.
Рисунок 2.11 Окно линейных зависимостей “входы-выход”
Шаг 14. Перейдем в редактор базы знаний RuleEditor. Для этого выберем в меню Edit команду Edit rules.... и введем правила базы знаний. Для ввода правила необходимо выбрать соответствующую комбинацию термов и зависимостей и нажать кнопку Add rule. На рис. 2.12. изображено окно редактора базы знаний после ввода всех шести правил.
На рис. 2.13. приведено окно визуализации нечеткого логического вывода. Это окно активизируется командой View rules... меню View. В поле Input указываются значения входных переменных, для которых выполняется логический вывод. Как видно из этого рисунка значение выходной переменной рассчитывается как среднее взвешенное значение результатов вывода по каждому правилу.
Рисунок 2.12 Нечеткая база знаний для системы типа Сугено
Рисунок 2.13 Визуализация нечеткого логического вывода для системы типа Сугено
На рис. 2.14. приведена поверхность “входы-выход”, соответствующая синтезированной нечеткой системе. Для вывода этого окна необходимо использовать команду View surface... меню View. Сравнивая поверхности на рис. 2.7. и на рис. 2.14. можно сделать вывод, что нечеткие правила достаточно хорошо описывают сложную нелинейную зависимость. При этом, модель типа Сугено более точная. Преимущество моделей типа Мамдани состоит в том, что правила базы знаний являются прозрачными и интуитивно понятными, тогда как для моделей типа Сугено не всегда ясно какие линейные зависимости “входы-выход” необходимо использовать.
Рисунок 2.14 Поверхность “входы-выход” для системы типа Сугено
2.2.7 Результаты проектирования нечеткого алгоритма предрейсовых медицинских осмотров на основе адаптивной сети нейро-нечеткого вывода
Для реализации в экспертной системе был выбран нечеткий логический вывод по Сугено: выходное нечеткое множество в этой схеме логического вывода является нечетким множеством первого порядка, то есть дискретным множеством, заданным на множестве четких чисел. Это позволяет избежать накопления нечеткости при его использовании в иерархических системах.
В
отличие от результата вывода Мамдани,
нечеткое множество является обычным
нечетким множеством первого порядка.
Оно задано на множестве четких чисел.
Результирующее значение выхода
определяется как суперпозиция линейных
зависимостей, выполняемых в данной
точке
n-мерного
факторного пространства. Для этого
дефаззифицируют нечеткое множество,
находя взвешенное среднее или взвешенную
сумму.
Рисунок 2.15 Функции слоев при аппроксимации нормы.
В гибридной схеме (рис. 2.15) иерархия нейронной сети адаптивно настраивает функции принадлежности в условиях и заключениях правил. Совмещение экспертных знаний и оценок регрессионной среды, как коэффициентов вывода по Сугено, позволяет получать оптимальные аппроксиматоры функций. Для целевого отделения признаков в работе был модифицирован выход сети. Добавление активационной логистической функции позволяет отследить изменение центра распределения в сторону риска.
Рисунок 2.16 Схема классификатора.
Отклонения от центра распределения – это есть значение минимизируемого функционала, обеспечивающего оптимальность решения относительно параметров правил. Регрессионный характер медицинских измерений учитывается при грубой настройке коэффициентов Сугено методом МНК. Точная подстройка функций правил осуществляется градиентным методом, где значением градиента является изменение функционала нормы, а аргументами частных производных – параметры гемодинамики (см. рис. 2.16).
Рисунок 2.17 - Схема статистического разделения нейротехнологии
Сигмоидальный выход характеризует с дробной вероятностью разделение входных признаков (рисунок 2.17). Грубая предварительная настройка по МНК приводит к общей области гистограмм разделения признаков. Точная настройка правил по обучающей выборке оптимально по вероятности обеспечивает минимальное пересечение классов.
Рисунок 2.18 Гистограммы указателя цели.
Алгоритм был применен к двум входным признакам гемодинамического артериального давления с одним выходом логического заключения, «есть риск, т.е. цель или нет». Грубой настройкой была получена вероятностная граница цели и не цели (рис. 2.18 (А, Б)). Точная настойка обучением обеспечила почти наверное разделение, смещая вероятностную границу вправо, в сторону риска(рис. 2.18 (В, Д)). Этим обеспечивается минимальная возможность ошибки.
Заключение
Произведенная теоретическая и практическая часть (в виде компьютерного программирования) работы достигает цели, поставленной при дипломном проектировании.
Разработанная система расспроса и предварительной диагностики позволяет получить достоверные результаты диагностирования и приемлемую скорость обработки при вводе симптомов, соответствующих базе знаний. Она дает превосходные методы обработки нечеткостей, которые свойственны всем медицинским данным, с помощью функций выводов. Наблюдения числовых характеристик полученной модели позволяют составить достоверный прогноз индивидуальных показателей нормы здоровья водителей транспортного средства. А это, в свою очередь, приводит к достижению цели обеспечения безаварийности перевозочного процесса и продления стажа опытных работников за счет планирования профилактических мероприятий по данным прогноза.
Все это подтверждает достижение цели, определенной поставленными перед выпускной работой актуальными проблемами современных систем управления в условиях лингвистической неопределенности.
ЛИТЕРАТУРА
1. Тэрано Т., Асаи К., Сугено М Прикладные нечеткие системы перевод с японского канд. техн. наук Ю. Н. Чернышова - Москва «Мир» 1993 – 363 с.
2. Норвиг А.М., Турсон И.Б. Построение функций принадлежности // Нечеткие множества и теория возможностей. Последние достижения: пер. с англ./ под ред. Р.Р. Ягера. – М.: Радио и связь, 1986. – 408 с.
3. Рыжов А.П. Элементы теории нечетких множеств и измерения нечеткости.– М.: Диалог –МГУ, 1998.
4. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику.-http://www.matlab.ru/fuzzylogic/book1/index.asp
5. Ярушкина Н.Г. Основы теории нечетких и гибридных систем. – М.: Финансы и статистика, 2004.
6. Круглов В. В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Радио и связь, 2000.
7. Катковник В. Я. Непараметрическая идентификация и сглаживание данных: метод локальной аппроксимации. - М.: Наука, 1985.
8. Заде Л. А., Понятие лингвистической переменной и его применение к принятию приближенных решений, Мир, М., 1976
9. Алексеев А.Н., Волков Н.И., Кочевский А.Н. Элементы нечёткой логики при программном контроле знаний // Открытое образование. 2004.Гроп Д. Методы идентификации. – М.: Наука, 1979.
10. Сейдж Э., Мелса Д. Индентификация систем управления. – М: Наука, 1974. – 247с.
11. Борисов В.В., Круглов В.В., Федулов А.С. Нечеткие модели и сети. – М.: Горячая линия – Телеком, 2007.