Программирование системы уравнений
Содержание
Введение
1 Постановка задачи
2 Решение системы уравнения методом Гаусса
3 Решение уравнения методами Ньютона, Хорд
4 Разработка блок схемы решения системы уравнения методом Гаусса
5 Разработка блок схемы решения уравнения методом Ньютона
6 Разработка блок схемы решения уравнения методом Хорд
7 Язык программирования Turbo Pascal
8 Разработка программы решения системы уравнения методом Гаусса при помощи Turbo Pascal
9 Разработка программы решения уравнения методом Ньютона при помощи Turbo Pascal
10 Разработка программы решения уравнения методом Хорд при помощи Turbo Pascal
Заключение
Список используемых источников
Введение
В основе того или иного языка программирования лежит некоторая руководящая идея, оказывающая существенное влияние на стиль соответствующих программ.
Исторически первой была идея структурирования программ, в соответствии с которой программист должен был решить, какие именно процедуры он будет использовать в своей программе, а затем выбрать наилучшие алгоритмы для реализации этих процедур. Появление этой идеи было следствием недостаточной изученности алгоритмической стороны вычислительных процессов, столь характерной для ранних программных разработок (сороковые — пятидесятые годы). Типичным примером процедурно-ориентированного языка является Фортран – первый и всё ещё один из наиболее популярных языков программирования. Последовательное использование идеи процедурного структурирования программ привело к созданию обширных библиотек программирования, содержащих множество сравнительно небольших процедур, из которых, как из кирпичиков, можно строить «здание» программы.
По мере прогресса в области вычислительной математики акцент в программировании стал смещаться с процедур в сторону организации данных. Оказалось, что эффективная разработка сложных программ нуждается в действенных способах контроля правильности использования данных. Контроль должен осуществляться как на стадии компиляции, так и при прогоне программ, в противном случае, как показала практика, резко возрастают трудности создания крупных программных проектов. Отчётливое осознание этой проблемы привело к созданию Ангола-60, а позже Паскаля, Модулы-2, Си и множества других языков программирования, имеющих более или менее развитые структуры типов данных. Логическим следствием развития этого направления стал модульный подход к разработке программ, характеризующийся стремлением «спрятать» данные и процедуры внутри модуля.
Начиная с языка Симула-67, в программировании наметился новый подход, который получил название объектно-ориентированного программирования (в дальнейшем ООП). Его руководящая идея заключается в стремлении связать данные с обрабатывающими эти данные процедурами в единое целое – объект. Характерной чертой объектов является инкапсуляция (объединение) данных и алгоритмов их обработки, в результате чего и данные, и процедуры во многом теряют самостоятельное значение.
1 Постановка задачи
Цель решения задачи курсовой работы – автоматизация решения системы уравнения методом Гаусса, а так же решения уравнения методами Хорд и Ньютона.
Выходная информация задачи выводиться на экран монитора.
Входная информация задачи поступает путем ввода пользователем данных для решения поставленной задачи
Прекращение решения задачи выполняется при выходе нового программного обеспечения, связанного с решением данной задачи или появление новой версии данного продукта.
2 Решение системы уравнения методом Гаусса
Метод Гаусса— классический метод решения системы линейных алгебраических уравнений (СЛАУ). Состоит в постепенном понижении порядка системы и исключении неизвестных.
Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах», составленном между I в. до н.э. и II в. н. э.
Описание метода
Пусть исходная система выглядит следующим образом
Тогда согласно свойству элементарных преобразований над строками эту систему можно привести к ступенчатому виду:
Переменные
называются
главными переменными.
Все остальные называются свободными.
Если
,
то рассматриваемая система несовместна.
Предположим,
что
.
Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом
(
,
где
—
номер строки):
,
где
Если свободным переменным системы (2) придавать все возможные значения и вычислить через них главные переменные, то мы получим все решения. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях полученное нами решение является решением системы (1).
Следствия:
1: Если в совместной системе все переменные главные, то такая система является определённой.
2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.
Условие совместности.
Упомянутое
выше условие
может
быть сформулировано в качестве
необходимого и достаточного условия
совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
1) На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получавшуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
2) На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
В простейшем случае алгоритм выглядит так:
Прямой ход:
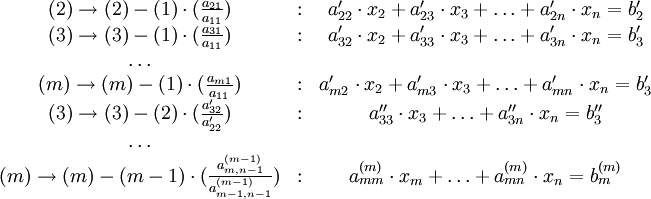
3) Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:
1) нахождения матрицы, обратной
к данной (к матрице справа приписывается
единичная такого же размера, что и
исходная:
,
после чего
приводится
к виду единичной матрицы методом
Гаусса—Жордана; в результате на месте
изначальной единичной матрицы справа
оказывается обратная к исходной матрица:
);
2) определения ранга матрицы (согласно следствию из теоремы Кронекера—Капелли ранг матрицы равен числу её главных переменных);
3) численного решения СЛАУ в вычислительной технике (ввиду погрешности вычислений используется Метод Гаусса с выделением главного элемента, суть которого заключена в том, чтобы на каждом шаге в качестве главной переменной выбирать ту, при которой среди оставшихся после вычёркивания очередных строк и столбцов стоит максимальный по модулю коэффициент).
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Система т линейных уравнений с п неизвестными имеет вид:
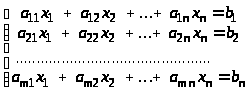
x>1> , x>2>, …, x>n> – неизвестные.
a>i>> >>j>> >- коэффициенты при неизвестных.
b>i> - свободные члены (или правые части)
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными, если они имеют одно и то же множество решений.
К элементарным преобразованиям системы отнесем следующее:
1) перемена местами двух любых уравнений;
2) умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
3) прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Элементарные преобразования переводят систему уравнений в равносильную ей.
Элементарные преобразования системы используются в методе Гаусса.
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
(
1 )
1-ый шаг метода Гаусса.
На первом шаге исключим неизвестное
х>1>
из всех уравнений системы (1), кроме
первого. Пусть коэффициент
.
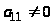Назовем его ведущим элементом. Разделим
первое уравнение системы (1) на а>11>.
Получим уравнение:
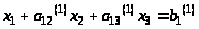( 2 )
где
Исключим х>1> из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х>1> (соответственно а>21> и а>31>).
Система примет вид:
( 3 )
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
2-ой шаг метода Гаусса.
На втором шаге исключим неизвестное
х>2>
из третьего уравнения
системы (3). Пусть коэффициент
.
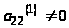Выберем его за ведущий элемент и разделим
на него второе уравнение системы (3),
получим уравнение:
(
4 )
где
Из третьего уравнения системы
(3) вычтем уравнение (4), умноженное на
Получим
уравнение:
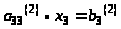
Предполагая, что
находим
В результате преобразований система приняла вид:
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х>3 >подставляют во второе уравнение системы (5) и находят х>2>. Затем х>2> и х>3 >подставляют в первое уравнение и находят х>1>.
В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.
Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными х>k>>+1>, … , x>k> переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х>1>, … , x>k>, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.
Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.
3 Решение уравнения методами Ньютона, Хорд
Метод хорд (способ пропорциональных частей) — численный метод уточнения корня трансцендентного уравнения.
Точный
корень
уравнения
находится
на отрезке
.
Производная
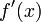на
этом промежутке непрерывна и сохраняет
постоянный знак. Приближенный корень
,
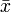при котором
,
можно найти используя метод хорд. Для
этого нужно взять начальное приближение
корня
и
применить к нему итерационную формулу:
линейный уравнение хорда гаусс ньютон
,
,
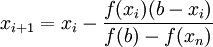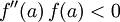
если
,
,
если
Погрешность вычислений:
,
,
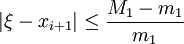В отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения, метод хорд использует пропорциональное деление интервала (рисунок 1).
|
Рис. 1. Метод хорд |
Рис.2. Метод касательных |
Здесь вычисляются значения функции на концах отрезка и строится “хорда”, соединяющая точки (a, f(a)) и (b, f(b)). Точка пересечения ее с осью абсцисс
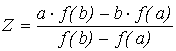
принимается за очередное
приближение к корню. Анализируя знак
f(z) в сопоставлении
со знаком f(x) на
концах отрезка, сужаем интервал до [a,z]
или [z,b] и продолжаем
процесс построения хорд до тех пор, пока
разница между очередными приближениями
не окажется достаточно малой (в пределах
допустимой погрешности) |Z>n>-Z>n-1>|<
.
Можно доказать, что истинная погрешность найденного приближения:
,
где X* - корень уравнения, Z>n> и Z>n+1> - очередные приближения, m и M – наименьшее.
Метод Ньютона
Пусть корень уравнения
отделен
на отрезке [a,
b],
причем
и
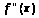непрерывны
и сохраняют определенные знаки при
.
Если на некотором произвольном шаге n
найдено приближенное значение корня
,
то можно уточнить это значение по методу
Ньютона. Положим
|
|
(1) |
где
считаем
малой величиной. Применяя формулу
Тейлора, получим:
Следовательно,
Внеся эту поправку в формулу (1), найдем следующее (по порядку) приближение корня
|
|
(2) |
Геометрически метод Ньютона
эквивалентен замене дуги кривой
касательной,
проведенной в некоторой точке кривой.
В самом деле, положим для определенности,
что
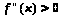при
и
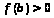(см.
рис.).
Выберем, например,
,
для которого
.
Проведем касательную к кривой
в
точке B>0>
с координатами
.
В качестве первого приближения
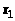корня
возьмем абсциссу точки пересечения
касательной с осью Ox.
Через точку
снова
проведем касательную, абсцисса точки
пересечения которой даст второе
приближение
корня
и т.д.
Формулу для уточнения корня
можно получить из прямоугольного
треугольника
,
образованного касательной, проведенной
в точке
,
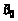осью абсцисс и перпендикуляром,
восстановленным из точки
.
Имеем
Так как угол образован касательной
и осью абсцисс, его тангенс численно
равен величине производной, вычисленной
в точке, соответствующей абсциссе точки
касания, т.е.
Тогда
или для любого шага n
.
В качестве начальной точки
можно
принять либо один из концов отрезка [a,
b],
либо точку внутри этого интервала. В
первом случае рекомендуется выбирать
ту границу, где выполняется условие
т.е. функция и ее вторая производная
в точке
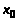должны
быть одного знака.
В качестве простейших условий окончания процедуры уточнения корня рекомендуется выполнение условия
Как следует из последнего
неравенства, требуется при расчете
запоминать три значения аргумента
.
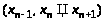В практических инженерных расчетах
часто применяют сравнение аргументов
на текущей и предыдущей итерациях:
При составлении программы решения
уравнения методом Ньютона следует
организовать многократный расчет
приближений
для
корня. Если удается получить аналитическое
выражение для производной, то ее
вычисление, а также вычисление
можно
оформить в виде функций.
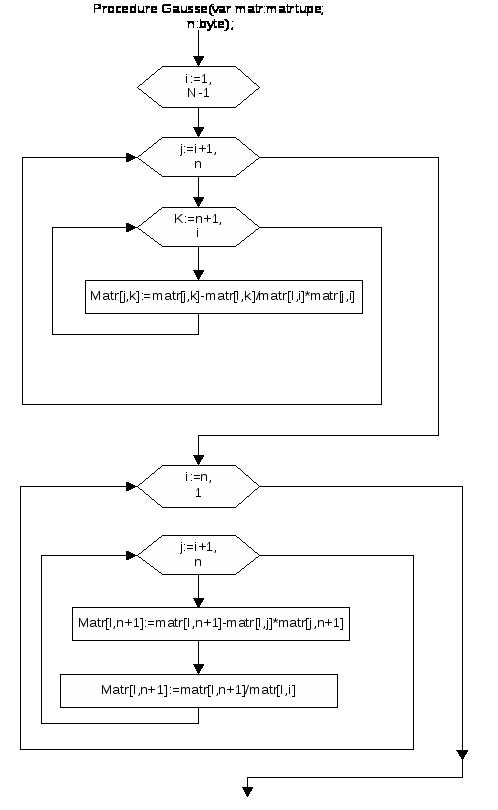
4 Разработка блок схемы решения системы уравнения методом Гаусса
5 Разработка блок схемы решения уравнения методом Ньютона
6 Разработка блок схемы решения уравнения методом Хорд
7 Язык программирования Turbo Pascal
Turbo Pascal является реализацией Pascal'я. Самая первая версия Pascal быля разработана на кафедре информатики Стэндфордского университета швейцарским ученым Николаусом Виртом в 1968 году.
С момента появления Pascal на рынке продуктов прошло много времени прежде чем он получил всеобщее признание. В середине 80-х годов американской фирмой Borland International, Inc была создана реализация языка Pascal, известная и по сей день под именем Turbo Pascal. Эта фирма объединила очень быстрый компилятор с редактором текста и добавила к стандартному Паскалю мощное расширение, что способствовало успеху первой версии этого языка.
В 1985 году на рынке ПЭВМ появился язык программирования Турбо Паскаль (версия 3.0) с компилятором стандартного Паскаля. С тех пор Паскаль стал применяться в общеобразовательных, профессионально-технических школах и в сфере высшего образования в качестве «первого» языка программирования. Благодаря простоте использования язык Турбо Паскаль получил широкое распространение и в любительских кругах. Повышению популярности Турбо Паскаля способствовал набор небольших сопутствующих программ (Toos), позволяющих получать чрезвычайно компактную, быструю и легко читаемую программу. Эти качества Турбо Паскаля были высоко оценены и в среде профессиональных программистов. Встроенный редактор текста использует достаточно широко распространенную систему команд, берущую начало от пакета WordStar и хорошо знакомую каждому, кто интенсивно использует ПЭВМ.
В появившемся со временем пакете Турбо Паскаль 4.0 было устранено большинство подвергавшихся критике ограничений компилятора и была повышена производительность системы. Кроме того, новый компилятор версии 4.0 имел существенные отличия от предыдущей версии. Наиболее важным нововведением была ИNIТ-концепция, заимствованная из языка Модула-2. Это дало возможность реализовать в рамках ТП разработку крупных программных продуктов.
С выходом в свет версии 5.0 ТП получил еще большие шансы на благосклонную реакцию со стороны профессиональных пользователей благодаря встроенному в среду программирования интегрированному отладчику, который позволил повысить производительность труда.
Существенно улучшила технические характеристики ТП реализация аппарата перекрытий (overlays), позволяющего строить мощные программные комплексы, рассчитанные на эксплуатацию в малых по объему областях памяти. Суть механизма перекрытий сводится к делению программы на части, поочередно загружаемые по мере необходимости с дискеты или жесткого диска в одну и ту же область памяти, заменяя при этом находившуюся там часть программы.
Кроме того, в ТП 5.0 были расширены возможности отладки программ и обеспечена возможность поддержки расширенной памяти в стандарте Lotus-Intel-Microsoft (SLIMS/EMS 4.0). Сокращение EMS обозначает Expanded Memory Specification (спецификация расширенной памяти). Нельзя путать этот вид дополнительной памяти с другим — Extended Memory. EMS имеется на обычных ПЭВМ класса XT, в то время как Extended Memory — только на машинах АТ-класса (с процессором 286, 386 и выше) при объеме памяти свыше 1 Мбайта.
В этой версии были также исправлены и улучшены библиотеки графических процедур, поставляемые вместе с пакетом ТП и обеспечивающие полную совместимость с графическими адаптерами класса VGA (Video Graphics Array).
В рамках версии ТП 5.5 были осуществлены дальнейшие преобразования в направлении улучшения технических характеристик пакета. Наряду с внутренними улучшениями и новыми возможностями встроенной справочной системы Help, а также большим набором учебных примеров, важным нововведением явилась реализация в языке концепции объектно-ориентированного программирования (ООП).
Через некоторое время на рынке появился ТП 6.0, в котором теоретическая концепция объектно-ориентированного программирования была реализована практически с полным набором объектов, которые могли использоваться для решения прикладных задач. Кроме того, реализация системы меню приведена в соответствие со стандартом SAA (Turbo Vision). В качестве практического примера использования новых возможностей был реализован текстовый редактор, встроенный в IDE ~ Integrated Development Environment — интегрированную инструментальную оболочку. При этом сторонники программирования на ТП 6.0 получили возможность не только работать со встроенным многооконным текстовым редактором, но и использовать мышь, которая значительно облегчает работу пользователя.
В 1992 году фирма Borland International представила пользователям очередную версию языка Паскаль — Турбо Паскаль 7.0. Наряду со всеми преимуществами, которые унаследованы от предыдущей версии (многооконный режим работы, возможность использования мыши, возможность использования языка программирования низкого уровня Ассемблер, возможность создавать объектно-ориентированные программы), в ТП 7.0 были произведены изменения и улучшения. Во-первых: появилась возможность выделять определенным цветом различные элементы исходного текста (зарезервированные слова, идентификаторы, числа и т. д.), позволяющая даже неопытным пользователям устранять ошибки на этапе ввода исходного текста. Во-вторых: язык программирования ТП 7.0 был расширен (появилась возможность использовать типизированный адресный оператор, открытые массивы и строки и т. д.), что предоставило пользователю дополнительные возможности при решении повседневных задач. В-третьих: был улучшен компилятор, вследствие чего «коды программ» стали более эффективными. В-четвертых: был улучшен интерфейс пользователя. Кроме того, в ТП 7.0 расширены возможности объектно-ориентированного программирования (в частности, расширены и улучшены возможности Turbo Vision).
8 Разработка программы решения системы уравнения методом Гаусса при помощи Turbo Pascal
program Gauss;
const
N=3;
A:array[1..N,1..N] of real = ((9.1, 5.6, 7.8),
(3.8, 5.1, 2.8),
(4.1, 5.7, 1.2));
B:array[1..N] of real = (9.8,
6.7,
5.8);
type
matrtype=array[1..N,1..N+1] of real;
var
i,j:byte;
matr:matrtype;
procedure Gausse(var matr:matrtype; N:byte);
var i,j,k:byte;
begin
for i:=1 to N-1 do
for j:=i+1 to N do
for k:=N+1 downto i do
matr[j,k]:=matr[j,k]-matr[i,k]/matr[i,i]*matr[j,i];
for i:=N downto 1 do
begin
for j:=i+1 to N do
Matr[i,N+1]:=Matr[i,N+1]-Matr[i,j]*Matr[j,N+1];
Matr[i,N+1]:=Matr[i,N+1]/Matr[i,i];
end;
end;
begin
clrscr;
writeln('reshenie sistemi iz ',N,' linear yravnenii');
for i:=1 to N do
begin
writeln('vvodim yravnenie',i,':');
for j:=1 to N do
begin
write('A[',i
,',',j,']=');
read(A[i,j]);
end;
write('B[',i,']=');
readln(B[i]);
end;
writeln('Sistema linear yravnenii');
for i:=1 to N do
begin
for j:=1 to N do
write(A[i,j]:5:2);
writeln(B[i]:5:2);
end;
for i:=1 to N do
begin
for j:=1 to N do
matr[i,j]:=A[i,j];
matr[i,N+1]:=B[i];
end;
Gausse(matr,N);
writeln('reshenie sistemi yravnenii:');
for i:=1 to N do
writeln('X',i,'=',matr[i,N+1]:5:2);
readkey;
end.
9 Разработка программы решения уравнения методом Ньютона при помощи Turbo Pascal
uses crt;
var
a,b,Exp,s : real;
i : integer;
function Func(x : real) : real;
begin
Func:=2*x*x*x-3*x*x-12*x+10;
end;
function PFunc(x : real) : real;
begin
PFunc:=6*x*x-6*x-12;
end;
Begin
clrscr;
Writeln('Vvedite verhnij predel:');
readln(b);
Writeln('Vvedite to4nost'':');
readln(Exp);
i:=0;
repeat
a:=b-Func(b)/PFunc(b);
s:=b;
b:=a;
i:=i+1;
Writeln('Shag ',s:5:2,' X-',a:5:2,' f(x)=',Func(b));
until(abs(a-s)>Exp);
Writeln('Otvet: ',b:5:2);
readln;
end.
10 Разработка программы решения уравнения методом Хорд при помощи Turbo Pascal
program hord;
var x,a,b,eps,s:real;
function f(x:real):real;
begin
f:=2*x*x*x-3*x*x-12*x+10;
end;
begin
write('vvedite levuiu granicu');
readln(a);
write('vvedite pravuiu granicu');
readln(b);
write('vvedite epsilon');
readln(eps);
while f(b)-f(a)>=eps do
begin
s:=b-f(b)/(f(b)-f(a))/(b-a);
a:=b; b:=s;
end;
writeln(s:5:2);
readln;
end.
Заключение
В соответствии с заданием курсовой работы была осуществлена программная реализация задачи. В ходе выполнения работы были получены навыки программирования системы уравнений.
Список используемых источников
1) Блашкин И.И., Буров А.А. Новые возможности Turbo-Pascal 7.1. — Спб.: Изд-во “Макет”, 2005.
2) Бородич Ю.С. и др. Паскаль для персональных компьютеров: Справ. Пособие/ Ю.С. Бородич, А.Н. Вальвачев, А.И.Кузьмич. — Мн.: Выш. Шк.: БФ ГИТМП “НИКА”, 2001.
3)Васильев П.П. Турбо Паскаль — мой друг: М.: Компьютер, ЮНИТИ, 2006.
4) Джордейн Р. Справочник программиста персональных компьютеров типа IBM PC, XT, AT: Пер. с англ./ Предисл. Н.В. Гайского. — М.: Финансы и статистика, 2001.
5) Зуев Е.А. Язык программирования Turbo Pascal 7.1. — М.: Унитех, 2005.
2