Чисельне розв’язання задач оптимального керування
ЧИСЕЛЬНЕ РОЗВ’ЯЗАННЯ ЗАДАЧ оптимального керування
1 Дискретизація задачі із закріпленим лівим і вільним правим кінцем. Необхідні умови оптимальності
Розглянемо неперервну задачу оптимального керування
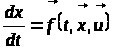 ,(1)
,(1)
 ,(2)
,(2)
 ,
,
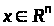 ,
,
 . (3)
. (3)
Виконаємо
дискретну апроксимацію даної задачі.
Для цього розіб’ємо відрізок
 точками
точками
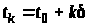 ,
,
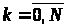 і будемо обчислювати значення цільового
функціонала і закону руху тільки в
точках розбиття:
і будемо обчислювати значення цільового
функціонала і закону руху тільки в
точках розбиття:
 ,
,
 ,
,
 .
Закон руху в цьому випадку можна записати
у вигляді:
.
Закон руху в цьому випадку можна записати
у вигляді:
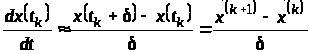 .
.
Тепер дискретна задача оптимального керування, що апроксимує неперервну задачу (1) – (3), матиме вигляд:
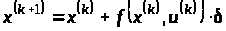 ,
,
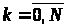 , (4)
, (4)
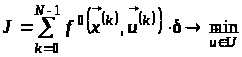 , (5)
, (5)
 (6)
(6)
 ,
,
 . (7)
. (7)
Для пошуку оптимального розв’язку отриманої дискретної задачі може бути застосований метод множників Лагранжа. Функція Лагранжа має вигляд:
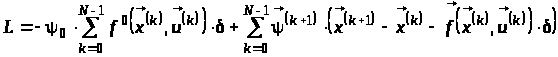 ,
,
 ,(8)
,(8)
де
 .
.
Обмеження
на керування введемо далі, під час
реалізації чисельного методу. Відзначимо,
що перед першим доданком стоїть знак
«–», оскільки
 і якщо не додавати «–», то характер
екстремуму початкової функції зміниться.
і якщо не додавати «–», то характер
екстремуму початкової функції зміниться.
Якщо
 – локально-оптимальний процес для
задачі (4) – (7), то існують такі нерівні
одночасно нулю множники Лагранжа
– локально-оптимальний процес для
задачі (4) – (7), то існують такі нерівні
одночасно нулю множники Лагранжа
 ,
,
 ,
,
 ,
,
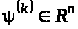 ,
що матимуть місце наступні умови:
,
що матимуть місце наступні умови:
1.
 або
або
 ,
,
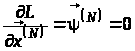 ,
,
 . (10)
. (10)
2.
 або
або
 ,
,
 .
(11)
.
(11)
Із
(9) одержимо ітераційні співвідношення
для спряжених змінних
 ,
а з (10) – співвідношення для
,
а з (10) – співвідношення для
 :
:

 ,
(12)
,
(12)
 . (13)
. (13)
Перепишемо співвідношення (12) у вигляді:
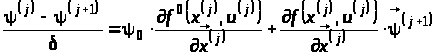 .
.
Очевидно, що останнє співвідношення є аналогом спряженої системи для неперервних задач керування. Дійсно,
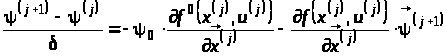 .
.
Якщо
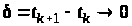 ,
то з останнього співвідношення одержимо
,
то з останнього співвідношення одержимо
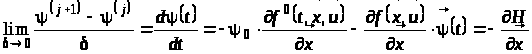 .
.
Зі
співвідношення (13) випливає, що
 .
.
Сформулюємо
критерій оптимальності для задачі (4) –
(7). Вважатимемо, що функції
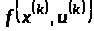 ,
,
 неперервно-диференційовані за змінними
неперервно-диференційовані за змінними
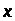 і опуклі за
і опуклі за
 .
Тоді для локально-оптимального процесу
.
Тоді для локально-оптимального процесу
 існують такі множники Лагранжа
існують такі множники Лагранжа
 ,
,
 ,
,
 ,
,
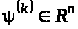 ,
не всі рівні нулю одночасно, що матимуть
місце необхідні умови екстремуму:
,
не всі рівні нулю одночасно, що матимуть
місце необхідні умови екстремуму:
1)
умови стаціонарності в точці
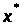 :
:
 ;
;
2)
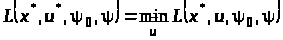 .
(14)
.
(14)
Розпишемо (14), використовуючи вираз для функції Лагранжа:

Перетворимо
вираз під знаком мінімуму, переходячи
до довільного
 :
:

Або

Якщо
 ,
то з останнього співвідношення одержимо
,
то з останнього співвідношення одержимо
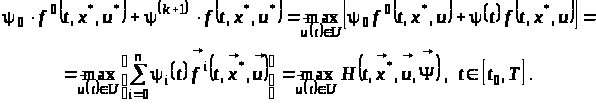
2 Ітераційний метод розв’язання дискретної задачі оптимального керування з двійним перерахуванням
Розглянемо
ітераційний метод пошуку оптимального
керування задачі (4) – (7). Суть методу
полягає в тому, що на кожній ітерації
обчислюються два вектори:
 і
і
 .
Перший із них містить
.
Перший із них містить
 -е
наближення для керувань у моменти часу
-е
наближення для керувань у моменти часу
 для системи (14), при
для системи (14), при
 ,
а другий –
,
а другий –
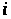 -е
наближення для фазових станів системи
в ці ж моменти часу. Отже, на кожній
ітерації ми одержуємо процес
-е
наближення для фазових станів системи
в ці ж моменти часу. Отже, на кожній
ітерації ми одержуємо процес
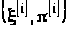 ,
що є
,
що є
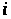 -м
наближенням до шуканого оптимального
процесу.
-м
наближенням до шуканого оптимального
процесу.
Контроль у методі подвійного перерахування полягає в повторному перерахуванні результатів задачі і порівнянні отриманих даних для різних значень кроку розбиття. У випадку розбіжності виконується корекція і обчислення повторюються.
Розглянемо алгоритм методу.
1.
Задаємо крок розбиття
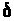 та точність обчислень
та точність обчислень
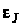 .
.
2. Задаємо початкове наближення – припустимий набір керувань на кожному кроці – початкову стратегію керування:
 ,
,
 ,
,
 ,
,
де
 – наближення керування в момент
– наближення керування в момент
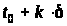 на ітерації
на ітерації
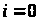 .
.
3.
За визначеною в п. 2 стратегією керування
 будуємо фазову траєкторію процесу
будуємо фазову траєкторію процесу
 ,
,
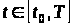 ,
,
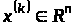
на
початкової ітерації
 ,
використовуючи початкові умови і
різницеві співвідношення, що апроксимують
рівняння руху:
,
використовуючи початкові умови і
різницеві співвідношення, що апроксимують
рівняння руху:

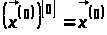 ,
,
 .
.
4.
Визначаємо початкове наближення
 відповідно до (5).
відповідно до (5).
5. Знаходимо спряжені змінні за формулами (12) – (13).
Визначаємо
наступні наближення до оптимального
керування
 ,
,

в
момент
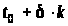 як розв’язки задачі (15) або (16):
як розв’язки задачі (15) або (16):
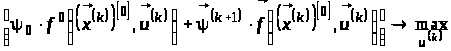 ,
,
 .
.
7.
Обчислюємо відповідну стратегії
 траєкторію
траєкторію

за формулами (4), (6):
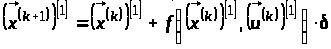 ,
,
 ,
,
 .
.
8. Знаходимо наступне наближення цільового функціонала
 за формулою (5).
за формулою (5).
9.
Якщо
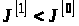 ,
то переходимо до п. 10, інакше вважаємо,
що
,
то переходимо до п. 10, інакше вважаємо,
що
 ,
,
 ,
,
 і переходимо до п. 13.
і переходимо до п. 13.
10. Перевіряємо, чи виконується задана точність обчислень. Якщо
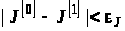 і
і
 ,
,
то переходимо до п. 13, інакше – до п. 11.
11. Позначаємо
 ,
,
 ,
,
 .
.
12. Виконуємо наступний крок ітераційного методу – п. 5.
13. Позначаємо
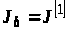 ,
,
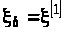 ,
,
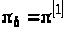 – розв’язок, отриманий із кроком
розбиття
– розв’язок, отриманий із кроком
розбиття
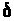 .
.
1
Якщо крок
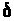 не ділився, то переходимо до п. 15, інакше
– до п. 1
не ділився, то переходимо до п. 15, інакше
– до п. 1
15. Ділимо крок
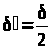 .
Тоді
.
Тоді
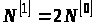 і переходимо до п. 2 при
і переходимо до п. 2 при
 .
.
1 Перевіряємо задану точність. Якщо
 і
і
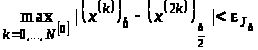 ,
,
то переходимо до п. 18, інакше переходимо до п. 17.
17. Позначаємо
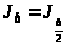 ,
,
 ,
,
 ,
,
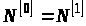 ,
і переходимо до п. 15 – наступного кроку
подвійного перерахування.
,
і переходимо до п. 15 – наступного кроку
подвійного перерахування.
18.
 ,
,
 ,
,
 – розв’язок задачі.
– розв’язок задачі.
Кінець алгоритму.
3. Оптимальне стохастичне керування: формулювання із зовнішнім інтегралом
Розглянемо
відображення
 ,
що задане формулою
,
що задане формулою
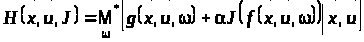 , (17)
, (17)
за таких припущень:
параметр
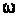 приймає значення з вимірного простору
приймає значення з вимірного простору
 .
Для будь-якої фіксованої пари
.
Для будь-якої фіксованої пари
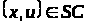 задана ймовірнісна міра
задана ймовірнісна міра
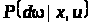 на просторі
на просторі
 ,
а символ
,
а символ
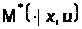 у формулі (12) означає зовнішній інтеграл
відносно цієї міри. Отже,
у формулі (12) означає зовнішній інтеграл
відносно цієї міри. Отже,
 ;
;
функції
 і
і
 відображують множину
відображують множину
 відповідно в множини
відповідно в множини
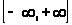 і
і
 ,
тобто
,
тобто
 ,
,
 ;
;
скаляр
 додатний.
додатний.
Формули
(1), (6) є окремими випадками відображення
 з (12). Очевидно, що відображення (1) для
детермінованої задачі випливає з (12),
якщо множина
з (12). Очевидно, що відображення (1) для
детермінованої задачі випливає з (12),
якщо множина
 складається з єдиного елемента, а
відображення (6) (для стохастичної задачі
зі зліченним простором збурень) відповідає
випадку, коли множина
складається з єдиного елемента, а
відображення (6) (для стохастичної задачі
зі зліченним простором збурень) відповідає
випадку, коли множина
 зліченна, а
зліченна, а
 є
є
 -алгеброю,
складеною із всіх підмножин
-алгеброю,
складеною із всіх підмножин
 .
.
Очевидно,
що відображення
 з (12) задовольняє припущенню монотонності.
Якщо на множини
з (12) задовольняє припущенню монотонності.
Якщо на множини
 ,
,
 і функції
і функції
 ,
,
 і
і
 накласти вимоги вимірності, то витрати
за
накласти вимоги вимірності, то витрати
за
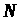 кроків
кроків
 можна визначити в термінах звичайного
інтегрування для будь-якої стратегії
можна визначити в термінах звичайного
інтегрування для будь-якої стратегії
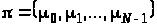 ,
для якої функції
,
для якої функції
 ,
,
 вимірні.
вимірні.
Для
початкового стану
 і стратегії
і стратегії
 ймовірнісні міри
ймовірнісні міри
 ,
...,
,
...,

у сукупності із системою рівнянь
 ,
,
 (18)
(18)
визначають
єдину міру
 на
на
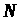 -кратному
прямому добутку
-кратному
прямому добутку
 копій простору
копій простору
 .
У випадку, якщо
.
У випадку, якщо
 ,
,
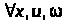 ,
і виконується одна з умов
,
і виконується одна з умов
 або
або
 ,
,
то
функція витрат за
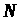 кроків, що відповідає вимірній стратегії
кроків, що відповідає вимірній стратегії
 ,
приводиться до звичайного вигляду
,
приводиться до звичайного вигляду
 ,
,
де
стани
 ,
,
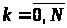 виражено як функції змінних
виражено як функції змінних
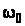 ,
...,
,
...,
 за допомогою рівнянь (13) та початкового
стану
за допомогою рівнянь (13) та початкового
стану
 .
.
Рекурентне співвідношення методу динамічного програмування для розв’язання багатоетапних задач оптимального стохастичного керування зі скінченним горизонтом можна записати так:
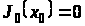 ,
,
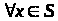 ,
,

де
 – щільність розподілу величини
– щільність розподілу величини
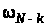 .
.
4 Оптимальне стохастичне керування: мультиплікативний функціонал витрат
Розглянемо відображення
 ,
що задане формулою
,
що задане формулою
 , (19)
, (19)
за
припущення, що параметр
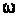 приймає значення зі зліченної множини
приймає значення зі зліченної множини
 відповідно до заданого розподілу
ймовірностей, що залежать від стану
відповідно до заданого розподілу
ймовірностей, що залежать від стану
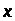 і керування
і керування
 .
Вважатимемо також, що
.
Вважатимемо також, що
 ,
,
 ,
,
 ,
,
 .
Тоді відображення
.
Тоді відображення
 з формули (14) задовольняє припущенню
монотонності.
з формули (14) задовольняє припущенню
монотонності.
Якщо
 ,
,
 ,
то задача оптимального керування з
мультиплікативним функціоналом витрат
і скінченним горизонтом
,
то задача оптимального керування з
мультиплікативним функціоналом витрат
і скінченним горизонтом
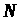 матиме такий вигляд:
матиме такий вигляд:
 , (20)
, (20)
 . (21)
. (21)
а відповідна задача з нескінченним горизонтом:
 , (22)
, (22)
 . (23)
. (23)
Границя
в (23) існує, якщо
 :
:
 або
або
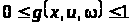 .
.
Самостійний інтерес становить задача з експоненціальною функцією витрат
 ,
,
 ,
,
де
 .
.
Для розв’язання багатоетапних задач оптимального стохастичного керування з мультиплікативним функціоналом витрат використовується таке рекурентне співвідношення алгоритму динамічного програмування:
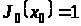 ,
,
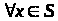 ,
,

де
 – щільність розподілу величини
– щільність розподілу величини
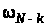 .
.
5. Мінімаксне керування
Розглянемо
задачу керування системою, у якій
некерованими впливами є стратегії
супротивника (або явища природи)
 ,
,
 ,
що обираються залежно від поточного
стану
,
що обираються залежно від поточного
стану
 і керування
і керування
 .
Вважатимемо, що припустимі стратегії
супротивника приймають значення із
множини
.
Вважатимемо, що припустимі стратегії
супротивника приймають значення із
множини
 ,
,
 .
Будемо обчислювати стратегію керування
.
Будемо обчислювати стратегію керування
 ,
орієнтуючись на найгіршу поведінку
супротивника. Розглянемо відображення
,
орієнтуючись на найгіршу поведінку
супротивника. Розглянемо відображення
 ,
задане формулою
,
задане формулою
 ,
,
за таких припущень:
параметр
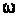 приймає значення з деякої множини
приймає значення з деякої множини
 ,
а
,
а
 – непуста підмножина
– непуста підмножина
 при будь-яких
при будь-яких
 ,
,
 ;
;
функції
 і
і
 відображують множину
відображують множину
 в множини
в множини
 та
та
 відповідно, тобто
відповідно, тобто
 ,
,
 ;
;
скаляр
 додатний.
додатний.
За
таких умов припущення про монотонність
для відображення
 має місце. Якщо при цьому
має місце. Якщо при цьому
 ,
,
 і
і
 для всіх
для всіх
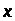 ,
,
 ,
,
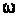 ,
то відповідну
,
то відповідну
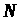 -крокову
задачу мінімаксного керування можна
сформулювати так:
-крокову
задачу мінімаксного керування можна
сформулювати так:
 , (17)
, (17)
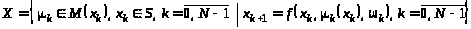 .
(18)
.
(18)
Задача з нескінченним горизонтом формулюється аналогічно:
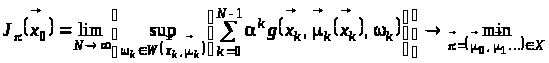 ,
(24)
,
(24)
 . (25)
. (25)
Границя у співвідношенні (25) існує при виконанні будь-якої з умов:
 ,
,
 ,
,
 ,
,
 ;
;
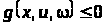 ,
,
 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ,
,
 ,
,
 і деякого
і деякого
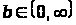 .
.
Для розв’язання багатокрокових мінімаксних задач оптимального стохастичного керування рекурентне співвідношення алгоритму динамічного програмування використовується у такому вигляді:
 ,
,
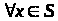 ,
,
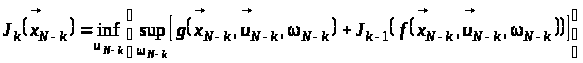 ,
,
 .
.