Задачи синтеза оптимальных систем управления
Предмет: Теория Автоматического Управления
Тема:
ЗАДАЧИ СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
Задачи синтеза оптимальных систем управления
Статистический синтез заключается в отыскании и реализации оптимальных в определенном смысле свойств (структуры и параметров) системы по заданным статистическим характеристикам входных воздействий.
Существуют различные методы статистической оптимизации. Рассмотрим задачу, сформулированную Винером-Колмогоровым.
Постановка задачи Винера–Колмогорова.
Д
ано:
x (t) - полезный
сигнал; z (t) - помеха;
K>и> (p) - оператор
преобразования.
Рис. 1
Определить: оптимальную передаточную функцию - K>0> (p).
Передаточная функция K>0> (p) должна быть устойчивой и физически реализуемой. Если полезный сигнал - x (t) и помеха - z (t) представляют собой Гауссовские случайные процессы, то решение может быть найдено в классе линейных стационарных систем, в противном случае решение находится в классе нелинейных систем.
В зависимости от оператора К>и> (р) рассматриваются следующие задачи:
К>и> (р) = 1 - воспроизведения;
К>и> (р) = 1/р - статистического интегрирования;
К>и> (р) = р - статистического дифференцирования;
К>и>
(р) =
 -
статистического упреждения, экстраполяции,
прогнозирования.
-
статистического упреждения, экстраполяции,
прогнозирования.
Таким образом, задача Винера-Колмогорова решается при следующих предположениях:
Сигнал и помеха представляют собой Гауссовские процессы.
Искомая система должна принадлежать к классу линейных систем.
Критерий оптимальности - минимум средней квадратичной ошибки.
Решение: Определим выражение для средней квадратичной ошибки

Средняя квадратичная ошибка равна

Мы получили некоторый функционал, в котором неизвестно к (). Необходимо найти такое к (), при котором ошибка будет минимальной.
Это задача минимизации функционала: она решается с использованием вариационного анализа.
Пусть
 ;
;
где:
 - оптимальная функция веса;
- оптимальная функция веса;
 - приращение.
- приращение.
Подставим это в исходное уравнение для ошибки и получим:
 ;
;
где А - функция, которая не зависит от а; В - функция, которая зависит от а; С - функция, которая зависит от а2.
Найдем экстремум по параметру а

к () -оптимально если а = 0 т.е. В = 0.

Откуда можно получить следующее выражение
 (1)
(1)
Это интегральное уравнение Винера-Хопфа, оптимальная передаточная функция должна удовлетворять этому уравнению.
Решение уравнение Винера-Хопфа.
Строгое решение этого уравнения сложно, решим это уравнение простым путем предложенным Шенноном. Уравнению Винера-Хопфа в частотной области соответствует следующее выражение:
 (2)
(2)
Откуда
 (3)
(3)
Но это уравнение физически нереализуемо так как к>0> () = 0 при < 0 т.е. K>0> (j) содержит физически реализуемую и нереализуемую часть.
Для выделения физически реализуемой части воспользуемся свойством формирующего фильтра.
Используя операцию факторизации суммарную спектральную плотность сигнала и помехи можно представить в виде:
 (4)
(4)
Используя операцию расщепления, представим выражение для частотной характеристики оптимальной системы в виде реализуемой и нереализуемой части
 (5)
(5)
где [] >+> - реализуемая часть; [] - нереализуемая часть.
Определим

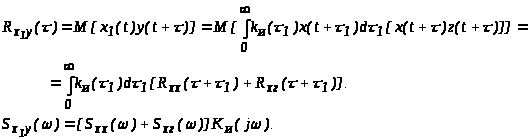
Отбросив нереализуемую часть, можно записать следующее выражение для частотной характеристики оптимальной системы с учетом физической реализуемости:
 (6)
(6)
Это формула Винера-Колмогорова.
Примеры решений задач
Пример 1. Рассмотрим задачу фильтрации с воспроизведением. Определить оптимальную передаточную функцию - K>0> (p) устойчивой и физически реализуемой системы рис.2).
Дано: Полезный сигнал - X (t) и помеха - Z (t), представляющие собой Гауссовские случайные процессы.
K>и>
(p) = 1;

Р
ис. 2Решение: Так как полезный сигнал - X (t) и помеха - Z (t) представляют собой Гауссовские случайные процессы, то решение может быть найдено в классе линейных стационарных систем.
Выражение для частотной характеристики оптимальной системы с учетом физической реализуемости имеет вид:

Так как сигнал и помеха некоррелированы и K>и> (p) = 1, то выражение имеет вид:

Определим К>ф> (j)

Используя операцию расщепления, представим выражение для частотной характеристики оптимальной системы в виде реализуемой и нереализуемой части

При этом

Значения А и В найдем методом неопределенных коэффициентов

С учетом полученных выражений

При этом передаточная функция представляет аппериодическое звено

Где

Пример 2. Рассмотрим задачу фильтрации с дифференцированием. Определить оптимальную передаточную функцию - K>0> (p) устойчивой и физически реализуемой системы рис.3.
Дано: Полезный сигнал - X (t) и помеха - Z (t), представляющие собой Гауссовские случайные процессы.
K>и> (p) = р;
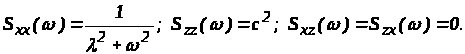

Р
ис. 3Решение: Так как полезный сигнал - X (t) и помеха - Z (t) представляют собой Гауссовские случайные процессы, то решение может быть найдено в классе линейных стационарных систем.
Выражение для частотной характеристики оптимальной системы с учетом физической реализуемости имеет вид:

Так как сигнал и помеха некоррелированны то выражение имеет вид:

Определим К>ф> (j)

где
Используя операцию расщепления, представим выражение для частотной характеристики оптимальной системы в виде реализуемой и нереализуемой части
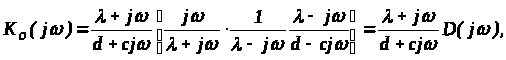
Где

Значения А и В найдем методом неопределенных коэффициентов

С учетом полученных выражений

При этом передаточная функция представляет апериодическое звено

где

Литература
Гуляев В.И., Баженов В.А., Попов С.Л. Прикладные задачи теории нелинейных колебаний механических систем, 1989.
Меркин Д.Р. Введение в теорию устойчивости движения, 1985.
Светлицкий В.А., Стасенко И.В. Сборник задач по теории колебаний, 1973.