Дослідження перехідних характеристик цифрових САК
Лабораторна робота №1
ДОСЛІДЖЕННЯ ПЕКРЕХІДНИХ ХАРАКТЕРИСТИК ЦИФРОВИХ САК
Мета робота: Дослідити перехідні характеристики цифрових систем автоматичного керування для типових вхідних сигналів.
Порядок виконання роботи
1. Згідно з заданим варіантом (№51)випишемо вихідні параметри досліджуваної цифрової (Ц) САК, наведеної на рис. 1.1.
Рис. 1.1. Структурна схема досліджуваної цифрової САК
w0(s) =
- неперервна дискретна САК.
2. Визначимо передатні функції розімкненої
та замкненої САК відносно вхідного
сигналу в загальному випадку. Для цього
виконаємо z-перетворення
Лапласа Z
за допомогою таблиць перетворень
Лапласа, виконавши наступні дії:
1)
.
2) Для зручності перетворення розкладемо
функцію
на прості дроби
.
Маємо (4A+C)s2 + (A+4B)s + B = 4, тоді s0| B = 4;
s1| A+4B = 0, A = -16;
s2| 4A+C = 0, C = -64.
Тобто
.
3) Виконаємо z-перетворення
Z
4) Отримаємо передаточну функцію розімкненої САК в z-формі:
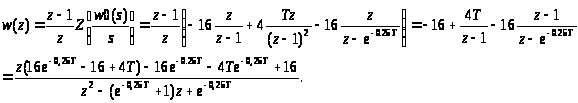
5) Передаточна функція замкнено САК:
Ф(z) =
.
3. Визначимо передатні функції розімкненої та замкненої САК відносно вхідного сигналу для двох значень періоду квантування Т>к >= 0,2, Т>к >= 0,8:
а) при Т>к >= 0,2:
1) передаточна функція розімкненої САК:
2) передаточна функція замкненої САК:
Ф(z)
=
б) при Т>к >= 0,8:
1) передаточна функція розімкненої САК:
2) передаточна функція замкненої САК:
Ф(z)
=
.
4. Визначимо аналітично перехідні
характеристики ЦСАК Y(z)
= Ф(z)*G(z),
де G(z)
=
- зображення вхідного одиничного сигналу.
Тобто
а) при Т>к >= 0,2 Y(z)
=
.
б) при Т>к >= 0,8 Y(z)
=
.
5. Побудуємо графіки перехідних процесів, попередньо розклавши перехідні характеристики в ряд Лорана:
а) при Т>к >= 0,2
_
_
_
_
Тобто C>1> = 0,01967, C>2> = 0,077, C>3> = 0,1686, C>4> = 0,2839, C>5> = 0,4176. За цими даними побудуємо графік-гістограму перехідного процесу (рис. 1.2).
Рис. 1.2. Перехідна характеристика досліджуваної ЦСАК з періодом квантування Т>к> = 0,2
б) при Т>к >= 0,8
_
_
_
_
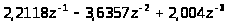
Таким чином, C>1> = 0,2997, C>2> = 1,0353, C>3> = 1,8233, C>4> = 2,2118, C>5> = 1,9358.
Побудуємо графік ЦСАК, враховуючи, що період квантування Т>к> = 0,8 (рис. 1.3).
Рис. 1.3. Перехідна характеристика досліджуваної ЦСАК з періодом квантування Т>к> = 0,8
6. Проведемо моделювання цифрової та неперервної САК із використання MatLab:
» k=4
k = 4
» T=4
T = 4
» w0=tf([k],[T 1 0])
Transfer function:
4
---------
4 s^2 + s
» wz1=c2d(w0,0.2)
Transfer function:
0.01967 z + 0.01935
----------------------
z^2 - 1.951 z + 0.9512
Sampling time: 0.2
» wz2=c2d(w0,0.8)
Transfer function:
0.2997 z + 0.2804
----------------------
z^2 - 1.819 z + 0.8187
Sampling time: 0.8
» Fz1=wz1/(wz1+1)
Transfer function:
0.01967 z^3 - 0.01904 z^2 - 0.01904 z + 0.0184
----------------------------------------------
z^4 - 3.883 z^3 + 5.691 z^2 - 3.731 z + 0.9232
Sampling time: 0.2
» Fz2=wz2/(wz2+1)
Transfer function:
0.2997 z^3 - 0.2647 z^2 - 0.2645 z + 0.2295
----------------------------------------------
z^4 - 3.338 z^3 + 4.681 z^2 - 3.243 z + 0.8999
Sampling time: 0.8
» Step(Fz1,60)
» Step(Fz2,60)
» F0=w0/(w0+1)
Transfer function:
16 s^2 + 4 s
-----------------------------
16 s^4 + 8 s^3 + 17 s^2 + 4 s
» Step(F0,20)
Приведемо графіки перехідних процесів, отримані за допомогою програмного пакету MatLab.
Рис. 1.4. Перехідна характеристика досліджуваної ЦСАК отримана за допомогою MatLab, період квантування Т>к> = 0,2
Рис. 1.5. Перехідна характеристика досліджуваної ЦСАК отримана за допомогою MatLab, період квантування Т>к> = 0,8
Рис. 1.6. Перехідна характеристика неперервної САК
Висновок
Виконуючи дану роботу, ми провели дослідження цифрових систем автоматичного керування. Я переконалася в правильності власних теоретичних розрахунків, порівнюючи отримані результати з результатами обчислень в програмі MatLab. Виявилося, що зі збільшенням періоду дискретизації цифрової САК правильність роботи системи страждає, тобто якість системи погіршується. Виконуючи лабораторну роботу, я також закріпила навички z-перетворення Лапласа функцій.