Дискретное преобразование Фурье (работа 1)

Министерство образования Республики Беларусь

Белорусский государственный университет информатики и радиоэлектроники

Кафедра Электронных вычислительных средств

Отчет по лабораторной работе

"Дискретное преобразование Фурье"

Выполнила:

Студентка гр. 610701

Лыпка Ю.А.

Проверил: Родионов М. М.

Минск 2009

1. Цель работы

Программирование дискретного преобразования Фурье в пакете Matlab. Изучение свойств ДПФ.

2 Выполнение заданий.

Задание 1-2

Разработайте функцию DFT, вычисляющую ДПФ от входного вектора, не используя функцию Matlab FFT, и рисующую графики действительной и мнимой частей входного вектора и результата преобразования, а также амплитудный спектр.

clear all;

close all;

clc;

n = 0:99;

k=(2*pi/length(n)).*n

s = (n >= 0) & (n <= 9);

figure(1);

sub>plot(221);

stem(n, real(s),'x');

title('Re(s(n))');

sub>plot(222);

stem(n, imag((s)),'x');

title('Im(s(n))');

sub>plot(223);

stem(k, abs(dft(s)),'x');

xlabel('\omega');

title('|S(k)|');

sub>plot(224);

stem(k, abs(dft(s)),'x');

title('|S(k)| cherez fft');

xlabel('\omega');

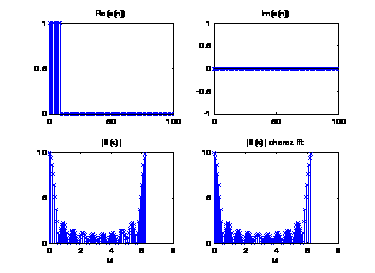
Рисунок 1 – Реальная и мнимая часть входного вектора, амплитудный спектр.

Задание 3

Исследуйте свойства симметрии ДПФ при следующих входных сигналах: действительном; мнимом; действительном четном; мнимом четном; действительном нечетном; действительном симметричном четном. Длину входного вектора выберите в соответствии с вариантом 2: N=35.

clear all;

%% 3 zadanie

N = 35;

n = 0:2*pi/N:2*pi;

figure;

sub>plot(311);

x = sin(n) + cos(n); % действительный входной сигнал

plot(n,x,'x');

title('real signal');

xlabel('n');

ylabel('Re(x)');

sub>plot(312);

plot(n, real(fft(x)));

title('real part of real signal');

xlabel('n');

ylabel('Re(x)');

sub>plot(313);

plot(n, imag(fft(x)));

title('image part of real signal')

xlabel('n');

ylabel('Im(x)');

Рисунок 2 – Real, image часть действительного входного сигнала

figure;

sub>plot(311);

x = j*(sin(n) + cos(n)); % мнимый входной сигнал

plot(n,imag(x),'x');

title('image signal')

xlabel('n');

ylabel('Im(x)');

sub>plot(312);

plot(n, real(fft(x)));

title('real part of image signal');

xlabel('n');

ylabel('re of Im(x)');

sub>plot(313);

plot(n, imag(fft(x)));

title('image part of image signal');

xlabel('n');

ylabel('Im of Im(x)');

Рисунок 3 – Real, image часть мнимого входного сигнала

figure;

sub>plot(311);

x = cos(n); % действительный чётный сигнал

plot(n,x,'x');

title('real even signal');

xlabel('n');

ylabel('Re(s)');

sub>plot(312);

plot(n, real(fft(x)));

title('real part of real even signal');

xlabel('n');

ylabel('Re of Re(x)');

sub>plot(313);

plot(n, imag(fft(x)));

title('Image part of real even signal');

xlabel('n');

ylabel('Im of Re(s)');

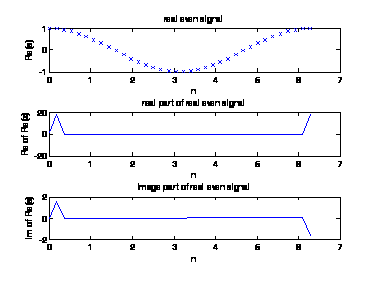
Рисунок 4 – Real, image часть действительного четного входного сигнала

figure;

sub>plot(311);

x = j*cos(n); % мнимый чётный сигнал

plot(n,imag(x),'x')

title('image even signal');

xlabel('n');

ylabel(' Even Im(x)');

sub>plot(312);

plot(n, real(fft(x)));

title('real part of image even signal');

xlabel('n');

ylabel('Re of Even Im(x)');

sub>plot(313);

plot(n, imag(fft(x)));

title('Image part of image even signal');

xlabel('n');

ylabel(' Im of Even Im(x)');

Рисунок 5 – Real, image часть мнимого четного входного сигнала

figure;

sub>plot(311);

x = sin(n); % действительный нечётный сигнал

plot(n,x,'x');

title('real odd signal')

xlabel('n');

ylabel('Re odd(x)');

sub>plot(312);

plot(n, real(fft(x)));

title('real part of real odd signal');

xlabel('n');

ylabel('Re of Re(x)');

sub>plot(313);

plot(n, imag(fft(x)));

title('image part of real odd signal')

xlabel('n');

ylabel('Im of Re(s)');

Рисунок 6 – Real, image часть мнимого нечетного входного сигнала

figure;

sub>plot(311);

n = -N/2:N/2;

x = n.^2; % действительный симметричный сигнал

plot(n,x,'x');

title('real symmetrical signal');

xlabel('n');

ylabel('Re(x)');

sub>plot(312);

plot(n, real(fft(x)));

title('real part of real symmetrical signal');

xlabel('n');

ylabel('Re of Re(x)');

sub>plot(313);

plot(n, imag(fft(x)));

title('Image part of real symmetrical signal');

xlabel('n');

ylabel('Im Of Re(x)');

Рисунок 7 – Real, image часть действительного симметричного входного сигнала

Задание 4

Разработайте функцию, позволяющую с помощью ДПФ формировать вектор, содержащий целое число периодов заданной функции. Длину выходного вектора, число периодов и функцию выберите в соответствии с вариантом 2: функция = – cos(x), длинна 90, число периодов 4.

function [x] = cosinus(leng, period);

%генерация функции -cos(x) длиной leng и числом периодов period

X = zeros(1,leng);%инициализируем нулями наш Фурье образ

X(period+1) = (leng-1)/2;%

X(leng-period + 1)= (leng-1)/2;

x = ifft(X);

figure;

Period = 4;

LengV = 90;

stem(cosinus(LengV,Period));

title('Function -cos(x)');

Рисунок 8 – Преобразование Фурье функции –cos(x)

Задание 5

Разработайте функцию, вычисляющую ДПФ для двух действительных векторов одной длины с помощью однократного вызова функции Matlab FFT. Продемонстрируйте ее работу.

%% 5 zadanie

N = 40;

n = 0:N-1;

k=(2*pi/length(n)).*n

x1 = cos(k);

x2 = sin(k);

x = real(x1) + j*real(x2);

y = fft(x);

y(N + 1) = y(1);

for k = 1:N+1

re1(k) = 0.5*(real(y(k)) + real(y(N - k + 2)));

im1(k) = 0.5*(imag(y(k)) - imag(y(N - k + 2)));

re2(k) = 0.5*(imag(y(k)) + imag(y(N - k + 2)));

im2(k) = 0.5*(real(y(N - k + 2)) - real(y(k)));

end;

y1 = re1 + j*im1;

y2 = re2 + j*im2;

sub>plot(221);

stem(0:N, real(y1));

title('real y1');

sub>plot(222);

stem(0:N, imag(y1));

title('imag y1');

sub>plot(223);

stem(0:N, real(y2));

title('real y2');

sub>plot(224);

stem(0:N, imag(y2));

title('imag y2');

Рисунок 9 – ДПФ для двух действительных векторов х1 и х2

Вывод по работе

При выполнении лабораторной работы мы ознакомились с дискретным преобразованием Фурье, его свойствами и реализацией. В ходе работы были исследованы свойства ДПФ при различных входных сигналах, применено обратное преобразование Фурье при генерации периодической функции косинуса, а также показана возможность вычисления ДПФ двух действительных векторов одинаковой длинны , с помощью однократного вызова функции ДПФ.