ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения системы алгебраических уравнений

Министерство Топлива и Энергетики Украины

СЕВАСТОПОЛЬСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

ЯДЕРНОЙ ЭНЕРГИИ И ПРОМЫШЛЕННОСТИ

Тема:

Севастополь 2008

План

1. Данные варианта задания

Операции численного решения системы линейных алгебраических уравнений

2.1 Решение системы линейных алгебраических уравнений методом последовательного исключения неизвестных (метод Гаусса)

2.2 Решение системы линейных алгебраических уравнений методом последовательного исключения неизвестных (метод Холесского)

2.3 Решение системы линейных алгебраических уравнений методом определителей

2.4 Решение системы линейных алгебраических уравнений методом обратной матрицы

2.5 Решение однородной системы линейных алгебраических уравнений

Выводы по работе №2

1. Данные варианта задания

Коэффициенты квадратной матрицы А и вектора b

Таблица1. Коэффициенты квадратной матрицы А и вектора b.

№

вар

Коэффициенты квадратной матрицы А и вектора b системы линейных алгебраических уравнений

а_>11>

а_>12>

а_>13>

а_>14>

а_>21>

а_>22>

а_>23>

а_>24>

а_>31>

а_>32>

а_>33>

а_>34>

а_>41>

а_>42>

а_>43>

а_>44>

b_>1>

b_>2>

b_>3>

b_>4>

2,4

1,4

1,6

1,8

2,6

0,6

4,0

-0,8

0,85

0,1

0,2

0,4

1,2

1,0

1,5

0,1

0,2

-0,4

0,6

2. Операции численного решения системы линейных алгебраических уравнений

a11·x1+ a12·x2+ a13·x3+ a14·x4=b1

a21·x1+ a22·x2+ a23·x3+ a24·x4=b2 (1)

a31·x1+ a32·x2+ a33·x3+ a34·x4=b3

a41·x1+ a42·x2+ a43·x3+ a44·x4=b4

Составим расширенную матрицу системы (1):

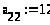
Преобразуем матрицу А, для чего умножим первую строку расширенной матрицы на а_>21>/а_>11> и вычтем из второй строки расширенной матрицы, затем первую строку умножим на а_>31>/а_>11> и вычтем из третьей строки расширенной матрицы, далее первую строку на а41/а11 и вычтем из четвёртой строки, что с помощью Mathcad будет выглядеть так:

Получили новые коэффициенты матрицы А:

Далее аналогично умножаем и вычитаем из второй строки:

Получили новые коэффициенты матрицы А, где число нулевых членов увеличилось.

Далее аналогично умножаем и вычитаем из третьей строки.

Проверим правильность нахождения корней:

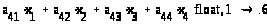
Ответ: х1≈0,1 х2≈-0,67 х3≈-2,1 х4≈2,31

Метод Холесского заключается в представлении матрицы в виде произведения двух треугольных матриц L и U , имеющих следующий вид: диагональные элементы L матрицы равны единице, а элементы выше главной диагонали равны нулю; у матрицы U равны нулю элементы, лежащие ниже главной диагонали. Тогда можно записать:

что эквивалентно двум треугольным системам,

которые можно решить способом изложенным выше. Элементы l_>ij>, и u_>ij> матриц L и U можно найти, образуя произведение матриц LU и приравнивая его элементы последовательно элементам а_>11>, а_>11>……. а_>nn> матрицы А.

Последовательно приравниваем элементы полученной матрицы к элементам а_>11>, а_>11>……. а_>nn> матрицы А и находим элементы l_>ij>, и u_>ij> .

По первой строке:

По второй строке:

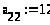
По третьей строке:

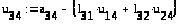
По четвёртой строке:

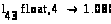
Далее вычисляем значения ξ:

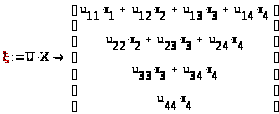
2.3 Решение системы линейных алгебраических уравнений методом определителей

Система уравнений с неизвестными, определитель которой не равен нулю, всегда имеет единственное решение. Это решение определяется так: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном столбцом свободных членов.

Ответ: х1≈0,1 х2≈-0,67 х3≈-2,1 х4≈2,31

2.4 Решение системы линейных алгебраических уравнений методом обратной матрицы

Если требуется решить систему для фиксированных значений a_>ij>, но для различных значений вектора В, то выгодно построить обратную матрицу А^-1 и затем воспользоваться соотношением

Ответ: х1≈0,1 х2≈-0,67 х3≈-2,1 х4≈2,31

2.5 Решение однородной системы линейных алгебраических уравнений

Однородной системой линейных алгебраических уравнений называют такую систему, свободные члены которой равны нулю, т.е.:

a11·x1+ a12·x2+ a13·x3+ a14·x4=0

a21·x1+ a22·x2+ a23·x3+ a24·x4=0

a31·x1+ a32·x2+ a33·x3+ a34·x4=0

a41·x1+ a42·x2+ a43·x3+ a44·x4=0

Однородная линейная система допускает нулевое решение х1=0, х2=0, х3=0, х4=0 и, следовательно, всегда совместна. Интересно выяснить случаи, когда однородная система имеет ненулевые решения. Это будет, если определитель равен нулю.

Найдем значение коэффициента а, при котором определитель равен нулю:

Решение системы будем искать, исключив из нее первое уравнение. Убедимся, что для новой системы уравнений определитель матрицы А не равен нулю:

a21·x1+ a22·x2+ a23·x3 =- a24·x4

a31·x1+ a32·x2+ a33·x3=- a34·x4

a41·x1+ a42·x2+ a43·x3=-a44·x4

Решение системы линейных алгебраических уравнений выполним методом последовательного исключения неизвестных (метод Гаусса). Увеличим для более точных расчётов число знаков после запятой:

В результате будем иметь систему, решение которой определит неизвестные для произвольного значения х_>4> :

Выводы по работе №2

В результате выполнения практического занятия №2 были изучены некоторые возможности математического пакета MathCad в среде Windows 98 для использования матричной алгебры и решения системы линейных алгебраических уравнений, а также изучены методы решения систем линейных алгебраических уравнений. В процессе работы я научился:

Задавать шаблоны матриц и векторов.

Работать с массивами, векторами и матрицами.

Решать системы линейных алгебраических уравнений различными методами.

Интересно признать, что решение систем уравнений в курсе высшей математики занимало большое количество времени. Например, решение системы методом последовательного исключения неизвестных (метод Гаусса) довольно громоздкий для ручного расчёта и намного быстрее производится с помощью MathCad , причём с точностью до 18 знаков после запятой. Наиболее наглядным является метод определителей, а самым простым и быстрым - метод обратной матрицы. Результаты расчётов, полученные разными методами, совпадают.