ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения дифференциального уравнения n-го порядка
Министерство Топлива и Энергетики Украины
СЕВАСТОПОЛЬСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ЯДЕРНОЙ ЭНЕРГИИ И ПРОМЫШЛЕННОСТИ
Практическое занятие №3
по дисциплине
«Использование ЭВМ в инженерных расчетах электротехнических систем»
Тема : ЭВМ С ИСПОЛЬЗОВАНИЕМ МАТЕМАТИЧЕСКОГО ПАКЕТА MathCad В СРЕДЕ WINDOWS ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ N-го ПОРЯДКА.
Вариант №8
Выполнил: студент группы ЭСЭ 22-В
Левицкий П.В.
Проверил:_______________________
Севастополь 2008
ПЛАН
1. Данные варианта задания.
2. Решение дифференциального уравнения N-го порядка
2.1. Решение дифференциальных уравнений N-го порядка методом интегрирования при помощи характеристического уравнения:
при y(t) = 0 и заданных начальных условиях ;
при y(t) = 1(t) и нулевых начальных условиях;
при y(t) = 1(t) и заданных начальных условиях;
при y(t) = cos(aּπּt) и нулевых начальных условиях;
2.2. Решение дифференциальных уравнений N-го порядка операторным методом:
при y(t) = 0 и заданных начальных условиях;
при y(t) = 1(t) и нулевых начальных условиях;
при y(t) = 1(t) и заданных начальных условиях;
при y(t) = cos(aּπּt) и нулевых начальных условиях;
1. Данные варианта задания
ПРИЛОЖЕНИЕ №1
( к практическому занятию №3)
Дифференциальное уравнения 4-го порядка


Т а б л и ц а № 1
|
№ вар |
Коэффициенты дифференциальногоуравнения 4–го порядка |
Правая часть уравнения и начальные условия |
||||||
|
а>0> |
а>1> |
а>2> |
а>3> |
а>4> |
b>0> |
y(t) = 1(t) x0(0) = 1 x1(0) = x2(0)= x3(0) = 0 |
y(t) = cos(aּπּt) x0(0) = -1 x1(0) = x2(0)= x3(0) = 0 |
|
|
8 |
10 |
20 |
1.7 |
0.16 |
0.08 |
10 |
a = 0.35 |
2. Решение дифференциального уравнения N-го порядка
2.1 Решение дифференциальных уравнений N-го порядка методом интегрирования при помощи характеристического уравнения
2.1.1 При y(t) = 0 и заданных начальных условиях
Дифференциальное уравнение 4-го порядка, описывающее динамические процессы электротехнической системы имеет вид:
Водим уравнение, пользуясь панелью «Исчисления» в Mathcad.

При заданных по условию значениях коэффициентов, уравнение примет вид:







Данное линейное дифференциальное уравнения 4-го порядка преобразуем
в систему дифференциальных уравнений первого порядка (в нормальную форму Коши). Обозначим:






Зададим вектор начальных значений:

СПРАВКА: В Mathcad 11 имеются три встроенные функции, которые позволяют решать поставленную в форме (2—3) задачу Коши различными численными методами.
rkfixed(y0, t0, t1, M, D) — метод Рунге-Кутты с фиксированным шагом,
Rkadapt(y0, t0, t1, M, D) — метод Рунге-Кутты с переменным шагом;
Buistoer(y0, t0, t1, M, D) — метод Булирша-Штера;
у0 — вектор начальных значений в точке to размера NXI;
t0 — начальная точка расчета,
t1 — конечная точка расчета,
M — число шагов, на которых численный метод находит решение;
D — векторная функция размера NXI двух аргументов — скалярного t и векторного у При этом у — искомая векторная функция аргумента t того же размера NXI.
Таким образом, воспользуемся функцией rkfixed(y0, t0, t1, M, D) -получим матрицу решения системы обыкновенных дифференциальных уравнений численным методом Рунге-Кута на интервале от t0 до t1 при M фиксированных шагах решения и правыми частями уравнений, записанными в D. Тогда решение уравнения динамики электротехнической системы с помощью встроенной функции rkfixed выглядит так:
Зададим интервал интегрирования t0 - t1, количество шагов интегрирования М, вектор заданных начальных условий ic и правую часть дифференциального уравнения y(t):





Сформируем матрицу системы дифференциальных уравнений, соответствующую заданному дифференциальному уравнению 4-го порядка.

Применим функцию:


-Интервал времени.

-Значение искомой координаты.

Рисунок1. Матрица решений системы уравнений.
По этой таблице можно определять расчётные значения исходного вектора на заданном шаге.
Результаты численного решения дифференциального уравнения можно вывести в виде таблицы с прокруткой времени и искомой неизвестной (см файл в Mathcad). Согласно выбранному М получили 1500 строк.




Рисунок2. Результаты пошагового решения дифференциального уравнения, представленные в виде таблицы.
Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат представлено на рисунке 3. График изображён так, что можно проверить значения строки 1500. При Т=150, Х=4,563*10^130


Рисунок 3. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = 0 и заданных начальных условиях.
2.1.2 При y(t) = 1(t) и нулевых начальных условиях
В этом случае необходимо изменить начальные условия и задать правую часть дифференциального уравнения.









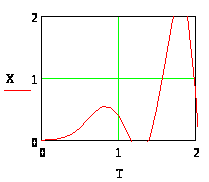
Рисунок 4. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = 1(t) и нулевых начальных условиях.
2.1.3 При y(t) = 1(t) и заданных начальных условиях
Изменим условия решения дифференциального уравнения. Зададим начальные условия для искомой переменной х>0>(0) = 1, начальные условия для других переменных равны нулю.( x1(0) = x2(0)= x3(0) = 0).См.таблицу1.

Рисунок 5. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = 1(t) и ненулевых начальных условиях. х>0>(0) = 1
Зададим начальные условия для искомой переменной х>0>(0) =- 1, начальные условия для других переменных равны нулю.( x1(0) = x2(0)= x3(0) = 0).




Рисунок 6. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = 1(t) и ненулевых начальных условиях х>0>(0) =- 1.
2.1.4 При y(t) = cos(aּπּt) и нулевых начальных условиях.
a = 0.35








Рисунок 7. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат.
При y(t) = cos(aּπּt) и нулевых начальных условиях(a = 0.35)._
При y(t) = cos(aּπּt) и ненулевых начальных условиях.
a = 0.35
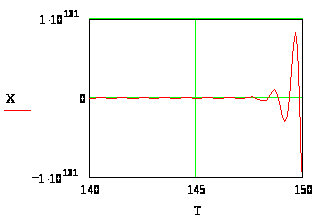

Рисунок 8. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = cos(aּπּt) и нулевых начальных условиях(a = 0.35; x0(0) = -1).
2.2. Решение дифференциальных уравнений N-го порядка операторным методом.
2.2.1 При y(t) = 0 и заданных начальных условиях (см. Табл.№1 )
К дифференциальному уравнению 4-го порядка применим преобразование Лапласа при заданных начальных условиях и у(t) = 0 и запишем его относительно изображения искомой переменной:
К линейные дифференциальным уравнениям с постоянными коэффициентами применим преобразование Лапласа, чтобы переменные вещественного аргумента t заменить на переменные комплексного аргумента S, дифференцирование заменим умножением на S, повторное дифференцирование- умножением на S^2 и т.д.



Используя обратное преобразование Лапласа, найдем оригинал искомой переменной:


На рис. 9. показаны графики изменения переменной, полученных в результате решения заданного дифференциального уравнения путем интегрирования (кривая Х) и операторным методом (Н(t)).

Рисунок 9. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = 0 и заданных начальных условиях.
2.2.2 При y(t) = 1(t) и нулевых начальных условиях
 -Изображение
по Лапласу y(t)
= 1(t)
-Изображение
по Лапласу y(t)
= 1(t)





Рисунок10. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = 1(t) и нулевых начальных условиях.
2.2.3 При y(t) = 1(t) и заданных начальных условиях





Рисунок11. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = 1(t) и заданных начальных условиях.
2.2.4 При y(t) = cos(aּπּt) и нулевых начальных условиях




Рисунок11. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = cos(aּπּt) и нулевых начальных условиях;
3. Выводы по работе №3
В процессе данной практической работы я изучил возможности математического пакета MathCad в среде Windows для решения дифференциальных уравнений N-го порядка, используемых в инженерных расчетах электротехнических систем. Были выполнены численные методы решения дифференциальных уравнений N-го порядка. Заданное уравнение 4-го порядка описывает динамические процессы электротехнической системы. Оно было преобразовано в систему дифференциальных уравнений первого порядка (в нормальную форму Коши). Мы воспользовались функцией rkfixed(y0, t0, t1, M, D) -получили матрицу решения системы обыкновенных дифференциальных уравнений численным методом Рунге-Кута на интервале от t0 до t1 при M фиксированных шагах решения и правыми частями уравнений, записанными в D. Получено численное и графическое представление результатов.
Решение уравнения операторным методом предполагает применение преобразования Лапласа. В данной работе мы использовали преобразование Лапласа к искомой переменной системы, в частности, теорему о дифференцировании оригинала и свойство линейности преобразования Лапласа. Мы применили преобразование Лапласа (функция laplace), чтобы переменные вещественного аргумента t заменить на переменные комплексного аргумента s, дифференцирование заменить умножением на s, повторное на s в квадрате и т.д. Из полученных в комплексной области алгебраических уравнений нашли отношение выходной характеристики к входной. Это изображение обычно представляет собой передаточную функцию системы автоматического управления. Используя обратное преобразование Лапласа( функция invlaplace), найден оригинал искомой переменной.
Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами совпадают.