Числові методи
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ
ЧЕРНІВЕЦЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
ІМ. Ю. ФЕДЬКОВИЧА
КОНТРОЛЬНА РОБОТА
з дисципліни " Числові методи "
Варіант 16.
Виконав
студент 2-го курсу
кафедри ЕОМ
Перевірив
м. Чернівці
Завдання 1
Задана СЛАР

а) розв’язати цю систему методом Гауса за схемою з частковим вибором головного елементу;
б)розв’язати цю систему за формулою
 .
.
 –
вектор невідомих,
–
вектор невідомих,
 –
вектор вільних членів,
–
вектор вільних членів,
 –
обернена матриця до матриці
–
обернена матриця до матриці
 з коєфіцієнтів при невідомих.
з коєфіцієнтів при невідомих.
Обернену матрицю знай ти методом Гауса - Жордана за схемою з частковим вибором головного елемента.
Рішення.
а) Прямий хід методу Гауса.
( )
)
Запишемо матрицю
 .
.

1-й крок.
Серед елементів першого стовпчика шукаємо максимальний:
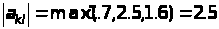


Перше і друге рівняння міняємо місцями.

Розділимо рівняння (1) на 2.5
 (1)
(1)
Від рівняння (2) віднімемо 1.7Р1 .


 (2)
(2)


 (3)
(3)
Таким чином в кінці першого кроку отримуємо систему

2-й крок.
Порядок рівнянь зберігається.

 (2)
(2)


 (3)
(3)
Після другого кроку система рівнянь стала такою:

Зворотній хід.
З рівняння (3)
 ;
;
з рівняння (2)
 ;
;
з рівняння (1)
 ;
;
Для рішення системи лінійних рівнянь методом Гауса призначена програма Work1_1.
//------------------------------------------------------------
// Work1_1.cpp
//------------------------------------------------------------
// "Числові методи"
// Завдання 1
// Рішення системи лінійних рівнянь методом Гауса
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
const int nMax=5; // максимальна кількість рівнянь
const float ZERO=.0000001;
int fGaus(float A[nMax][nMax],float B[nMax],int n,float X[nMax])
/* Функція розв'язує систему лінійних рівнянь методом Гауса за схемою з
частковим вибором головного елементу.
Вхідні дані:
A- масив з коефіцієнтами при невідомих;
В- масив з вільними членами СЛАР;
n- порядок матриці А(кількість рівнянь системи);
Вихідні дані:
Х- масив з коренями системи;
функція повертає код помилки:
0- сисетма успішно розв’язана;
1- матриця А вироджена. */
{float aMax,t; // максимальний елемент , тимчасова змінна
int i,j,k,l;
for(k=0; k<n; k++) // шукаємо головний елемент, мах за модулем
{aMax=A[k][k]; l=k;
for (i=k+1; i<n; i++)
if (fabs(A[i][k])>fabs(aMax))
{aMax=A[i][k];
l=i;}
// якщо модуль головного елементу aMax менший за програмний 0 (ZERO)
if ( fabs(aMax)<ZERO ) return 1;
// якщо потрібно, міняємо місцями рівняння Pk i Pl
if ( l!=k)
{for( j=0; j<n; j++)
{ t=A[l][j]; A[l][j]=A[k][j]; A[k][j]=t; }
t=B[l]; B[l]=B[k]; B[k]=t;}
// ділимо k-те рівняння на головний елемент
for (j=0; j<n; j++) A[k][j]/=aMax;
B[k]/=aMax;
// обчислюємо коефіцієнти A[i][j] та вільні члени решти рівнянь
for (i=k+1; i<n; i++)
{t=A[i][k]; B[i]-=t*B[k];
for (j=0; j<n; j++) A[i][j]-=t*A[k][j];}
} // for (k)
// Зворотній хід
for ( k=n-1; k>=0; k--)
{X[k]=0;
for (l=k+1; l<n; l++) X[k]+=A[k][l]*X[l];
X[k]=B[k]-X[k];}
return 0;
} // fGaus()
void main()
{float A[nMax][nMax];
float B[nMax];
float X[nMax];
int n,i,j;
char *strError="\n Error of file !";
FILE *FileIn,*FileOut;
FileIn=fopen("data_in.txt","r"); // відкриваємо файл для читання
if (FileIn==NULL)
{cout << " \"Data_in.txt\": Error open file or file not found !!!\n";
goto exit;}
FileOut=fopen("data_out.txt","w"); // відкриваємо файл для запису
if (FileOut==NULL)
{cout << " \"Data_out.txt\": Error open file !!!\n";
goto exit;}
if(fscanf(FileIn,"%d",&n)==NULL)
{ cout << strError; goto exit;};
for (i=0; i<n; i++)
for(j=0; j<n; j++)
fscanf(FileIn,"%f",&(A[i][j]));
for (i=0; i<n;i++)
if(fscanf(FileIn,"%f",&(B[i]))==NULL)
{ cout << strError; goto exit;}
if(fGaus(A,B,n,X)!=0)
{ cout << "\n det|A|=0 !"; goto exit;}
// Вивід результатів
for (i=0; i<n; i++)
{printf(" x[%d]= %f ",i+1,X[i]);
fprintf(FileOut," x[%d]= %f ",i+1,X[i]);}
fclose(FileIn);
fclose(FileOut);
exit: cout << "\n Press any key ...";
getch();}
Результат роботи програми:
x[1]= 3.017808 x[2]= 0.356946 x[3]= -0.302131
б) Знайдемо обернену
матрицю
 .
.
0-й крок.
А
 Е
Е

1-й крок.






 ;
;



2-й крок.



 ;
;



3-й крок.
 ;
;
 ;
;






 .
.
Даний алгоритм рішення системи лінійних рівнянь реалізований в програмі Work1_2.
//------------------------------------------------------------
// Work1_2.cpp
//------------------------------------------------------------
// "Числові методи"
// Завдання 1
// Рішення системи лінійних рівнянь методом Гауса-Жордана
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
const int nMax=5; // максимальна кількість рівнянь
const float ZERO=.0000001;
int fGausJordan(int n,float A[nMax][nMax],float Ainv[nMax][nMax])
/* Функція знаходить обернену матрицю
Вхідні дані:
A- масив з коефіцієнтами при невідомих;
n- порядок матриці А(кількість рівнянь системи);
Вихідні дані:
Ainv- матриця обернена до матриці А;
функція повертає код помилки:
0- помилки немає;
1- матриця А вироджена. */
{float aMax,t; // максимальний елемент , тимчасова змінна
int i,j,k,l;
// формуємо одиничну матрицю
for(i=0; i<n; i++)
for (j=0; j<n; j++)
Ainv[i][j] = (i==j)? 1. : 0.;
for (k=0; k<n; k++)
{// знаходимо мах по модулю елемент
aMax=A[k][k]; l=k;
for (i=k+1; i<n; i++)
if (fabs(A[i][k])>fabs(aMax))
{ aMax=A[i][k]; l=i; }
// якщо модуль головного елементу aMax менший за програмний 0 (ZERO)
if ( fabs(aMax)<ZERO ) return 1;
// якщо потрібно, міняємо місцями рівняння Pk i Pl
if ( l!=k)
for( j=0; j<n; j++)
{t=A[l][j]; A[l][j]=A[k][j]; A[k][j]=t;
t=Ainv[l][j]; Ainv[l][j]=Ainv[k][j]; Ainv[k][j]=t;}
// ділимо k-й рядок на головний елемент
for (j=0; j<n; j++) { A[k][j]/=aMax; Ainv[k][j]/=aMax; }
// обчислюємо елементи решти рядків
for (i=0; i<n; i++)
if( i!=k )
{t=A[i][k];
for (j=0; j<n; j++)
{A[i][j]-=t*A[k][j];
Ainv[i][j]-=t*Ainv[k][j];}}}
return 0;
} // fGausJordana()
void fDobMatr(int n, float A[nMax][nMax], float B[nMax],float X[nMax])
// функція знаходить добуток матриці А на вектор В і результат повертає в
// векторі Х
{int i,j;
float summa;
for (i=0; i<n; i++)
{summa=0;
for (j=0; j<n; j++)
{summa+=A[i][j]*B[j];
X[i]=summa;}}
} // fDobMatr
void main()
{float A[nMax][nMax],Ainv[nMax][nMax];
float B[nMax];
float X[nMax];
int n,i,j;
char *strError="\n Error of file !";
FILE *FileIn,*FileOut;
FileIn=fopen("data_in.txt","r"); // відкриваємо файл для читання
if (FileIn==NULL)
{cout << " \"Data_in.txt\": Error open file or file not found !!!\n";
goto exit;}
FileOut=fopen("data_out.txt","w"); // відкриваємо файл для запису
if (FileOut==NULL)
{cout << " \"Data_out.txt\": Error open file !!!\n";
goto exit;}
if(fscanf(FileIn,"%d",&n)==NULL)
{ cout << strError; goto exit;};
for (i=0; i<n; i++)
for(j=0; j<n; j++)
fscanf(FileIn,"%f",&(A[i][j]));
for (i=0; i<n;i++)
if(fscanf(FileIn,"%f",&(B[i]))==NULL)
{ cout << strError; goto exit;}
if(fGausJordan(n,A,Ainv)!=0)
{ cout << "\n det|A|=0 !"; goto exit;}
fDobMatr(n,Ainv,B,X);
// Вивід результатів
for (i=0; i<n; i++)
{printf(" x[%d]= %f ",i+1,X[i]);
fprintf(FileOut," x[%d]= %f ",i+1,X[i]);}
fclose(FileIn);
fclose(FileOut);
exit: cout << "\n Press any key ...";
getch();}
Результат роботи програми:
x[1]= 3.017808 x[2]= 0.356946 x[3]= -0.302131
Завдання 2
Задана задача Коші
 ,
,

а) Знайти розв’язок
 в табличній формі методом Рунге-Кутта:
в табличній формі методом Рунге-Кутта:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 ,
,
 ,
,

 .
.
б) Інтерполювати цю функцію кубічним сплайном. Систему рівнянь для моментів кубічного сплайну розв’язати методом прогонки. Вибрати крайові умови для кубічного сплайну у вигляді
 .
.
в) Використовуючи
кубічний сплайн з пункту б) обчислити
 методом Сімпсона .
методом Сімпсона .
Взяти
 (
( –
кількість відрізків розбиття).
–
кількість відрізків розбиття).
Рішення.
а) Метод Рунге-Кутта
Розрахунок будемо проводити за наступними формулами :
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Цей алгоритм реалізовується в програмі Work2_1.
//------------------------------------------------------------
// Work2_1.cpp
//------------------------------------------------------------
// "Числові методи"
// Завдання 2
// Рішення задачі Коші методом Рунге-Кутта
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
typedef float (*pfunc)(float,float); // pfunc - вказівник на функцію
const int nMax=5; // максимальна кількість відрізків розбиття
void fRunge_Kutta(pfunc f, float x0, float y0,float h, int n, float Y[nMax])
/* Функція знаходить табличне значення функції методом Рунге-Кутта
Вхідні дані:
f - функція f(x,y)
x0,y0 - початкова точка;
h - крок;
n- кількість точок розбиття;
Вихідні дані:
Y- вектор значень функції*/
{float k1,k2,k3,k4,x; // максимальний елемент , тимчасова змінна
int i;
x=x0; Y[0]=y0;
for (i=0; i<n-1; i++)
{k1=f(x,Y[i]);
k2=f(x+h/2, Y[i]+k1*h/2);
k3=f(x+h/2, Y[i]+k2*h/2);
k4=f(x+h, Y[i]+h*k3);
Y[i+1]=Y[i]+(h/6)*(k1+2*k2+2*k3+k4);
x+=h;}}
float Myfunc(float x,float y)
{return log10(cos(x+y)*cos(x+y)+2)/log10(5);}
void main()
{float Y[nMax],h,x0,y0;
int n,i;
char *strError="\n Error of file !";
FILE *FileIn,*FileOut, *FileOut2;
FileIn=fopen("data2_in.txt","r"); // відкриваємо файл для читання
if (FileIn==NULL)
{cout << " \"Data2_in.txt\": Error open file or file not found !!!\n";
goto exit;}
FileOut=fopen("data2_out.txt","w"); // відкриваємо файл для запису
if (FileOut==NULL)
{cout << " \"Data2_out.txt\": Error open file !!!\n";
goto exit;}
FileOut2=fopen("data2_2in.txt","w"); // відкриваємо файл для запису
if (FileOut==NULL)
{cout << " \"Data2_2in.txt\": Error open file !!!\n";
goto exit;}
if(fscanf(FileIn,"%d%f%f%f,",&n,&h,&x0,&y0)==NULL)
{ cout << strError; goto exit;};
fRunge_Kutta(Myfunc,x0,y0,h,n,Y);
// Вивід результатів
for (i=0; i<n; i++)
{printf(" x[%d]= %4.2f ",i,Y[i]);
fprintf(FileOut," x[%d]= %4.2f ",i,Y[i]);
fprintf(FileOut2,"%4.2f ",Y[i]);}
fclose(FileIn);
fclose(FileOut);
exit: cout << "\n Press any key ...";
getch();}
Результат роботи програми (файл "data2_out.txt"):
x[0]= 1.00 x[1]= 1.05 x[2]= 1.10 x[3]= 1.14 x[4]= 1.18
б) В загальному вигляді кубічний сплайн виглядає наступним чином:
 ,
,

Параметри кубічного сплайну будемо обчислювати , використовуючи формули:
 ;
;
 ;
;
 ;
;
 ,
де
,
де
 –
моменти кубічного
сплайну.
–
моменти кубічного
сплайну.
Моменти мають задовольняти такій системі рівнянь:

 .
.
Для

 ;
;
 ;
;
 .
.
Якщо прийняти до уваги
граничні умови
 ,
то систему можна записати так
,
то систему можна записати так


 .
.
В даному випадку матриця з коефіцієнтів при невідомих є тридіагональною
 ,
,
тому для знаходження моментів кубічних сплайнів застосуємо метод прогонки.
На прямому ході обчислюємо такі коефіцієнти.
 ;
;
 ;
;
На зворотньому ході обчислюємо значення моментів кубічного сплайну.
 ;
;
 .
.
Для знаходження коефіцієнті вкубічного сплайну призначена програма Work2_2.
//------------------------------------------------------------
// Work2_2.cpp
//------------------------------------------------------------
// "Числові методи"
// Завдання 2
// Інтерполювання функції кубічним сплайном
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
const int nMax=4; // максимальна кількість відрізків розбиття
const float x0=0.;// початкова точка сітки
const float h=0.1;// крок розбиття
// вектори матриці А
float a[]={0., 0.5, 0.5};
float b[]={2., 2., 2.};
float c[]={0.5, 0.5, 0.};
//void fMetodProgonku( int n,float a[nMax],float b[nMax],float c[nMax],float d[nMax], float M[nMax+1])
/* Функція знаходить моменти кубічного сплайну методом прогонки
Вхідні дані:
a,b,c -вектори матриці А ;
d - вектор вільних членів;
n- степінь матриці А;
Вихідні дані:
М- вектор моментів кубічного сплайну.*/
{float k[nMax],fi[nMax];
int i;
// прямий хід
for (i=0; i<n; i++)
{k[i] = (i==0)? -c[i]/b[i] : -c[i]/(b[i]+a[i]*k[i-1]);
fi[i] = (i==0)? d[i]/b[i] : (-a[i]*fi[i-1]+d[i])/(b[i]+a[i]*k[i-1]);}
//зворотній хід
for (i=n; i>0; i--)
M[i] = (i==n)? fi[i-1] : k[i-1]*M[i+1]+fi[i-1];}
void fSplain( int n,float h,float Y[nMax+1],float M[nMax+1],float Ak[nMax][4])
/* Функція обчислює коефіцієнти кубічного сплайну
Вхідні дані:
n- кількість відрізків розбиття;
H - крок розбиття відрізку [X0; Xn]]
М- вектор моментів кубічного сплайну.
Y- вектор значень функції f(x,y) в точках x[0],x[1],...x[n].
Вихідні дані:
Ak- матриця коефіцієнтів кубічного сплайну.*/
{int i;
for (i=0; i<n; i++)
{Ak[i][0] = Y[i];
Ak[i][1] = (Y[i+1]-Y[i])/h-h/6*(2.*M[i]+M[i+1]);
Ak[i][2] = M[i]/2;
Ak[i][3] = (M[i+1]-M[i])/6*h;}}
void main()
{float Y[nMax+1],d[nMax],M[nMax+1],Ak[nMax][4];
int n,i,j;
n=nMax;
M[0]=0; M[n]=0; //крайові умови
char *strError="\n Error of file !";
FILE *FileIn,*FileOut,*FileOut2;
FileIn=fopen("data2_2in.txt","r"); // відкриваємо файл для читання
if (FileIn==NULL)
{ cout << " \"Data2_2in.txt\": Error open file or file not found !!!\n";
goto exit; }
FileOut=fopen("data2_2ou.txt","w"); // відкриваємо файл для запису
if (FileOut==NULL)
{ cout << " \"Data2_2ou.txt\": Error open file !!!\n";
goto exit; }
FileOut2=fopen("data2_3in.txt","w"); // відкриваємо файл для запису
if (FileOut2==NULL)
{ cout << " \"Data2_3in.txt\": Error open file !!!\n";
goto exit; }
// читаємо вектор Y
for (i=0; i<=n; i++)
if(fscanf(FileIn,"%f,",&(Y[i]))==NULL)
{ cout << strError; goto exit;};
// обчислюємо вектор d
for (i=1; i<n; i++) d[i-1]=3/(h*h)*(Y[i+1]-2*Y[i]+Y[i-1]);
//fMetodProgonku(n-1,a,b,c,d,M);
fSplain( n,h,Y,M,Ak);
// Вивід результатів в тому числі і для наступного завдання
fprintf(FileOut2,"%d\n",n); // n - кількість відрізків
// координати точок сітки по Х
for(float xi=x0,i=0; i<n; i++) fprintf(FileOut2,"%2.2f ",xi+h*i);
fprintf(FileOut2,"\n");
for (i=0; i<n; i++)
{for (j=0; j<4; j++)
{printf("a[%d,%d]= %4.4f ",i,j,Ak[i][j]);
fprintf(FileOut,"a[%d,%d]= %4.4f ",i,j,Ak[i][j]);
fprintf(FileOut2,"%4.4f ",Ak[i][j]);}
cout << endl;
fprintf(FileOut,"\n");
fprintf(FileOut2,"\n");}
fclose(FileIn);
fclose(FileOut);
exit: cout << "\n Press any key ...";
getch();}
Результат роботи програми (" data2_2uo.txt"):
a[0,0]= 1.0000 a[0,1]= 0.5104 a[0,2]= 0.0000 a[0,3]= -0.0104
a[1,0]= 1.0500 a[1,1]= 0.4793 a[1,2]= -0.3107 a[1,3]= 0.0118
a[2,0]= 1.0960 a[2,1]= 0.4525 a[2,2]= 0.0429 a[2,3]= -0.0068
a[3,0]= 1.1410 a[3,1]= 0.4407 a[3,2]= -0.1607 a[3,3]= 0.0054
в) Розіб’ємо відрізок
 на
на
 частин.
частин.
Складова формула Сімпсона буде мати вигляд:
 ;
;
де
 -
крок розбиття,
-
крок розбиття,
 –
значення функції
–
значення функції
 в точках сітки.
в точках сітки.
Замінимо
 значеннями кубічних сплайнів із пункту
б) цього завдання.
значеннями кубічних сплайнів із пункту
б) цього завдання.

Для оцінки похибки
використаємо правило Рунге. Для цього
обчислимо наближені значення інтегралу
з кроком
 (
( ),
а потім з кроком
),
а потім з кроком
 (
( ).
).
За наближене значення
інтегралу, обчисленого за формулою
Сімпсона з поправкою по Рунге приймемо:
 .
.
//------------------------------------------------------------
// Work2_3.cpp
//------------------------------------------------------------
// "Числові методи"
// Завдання 2
// Обчислення інтегралу методом Сімпсона з використанням кубічного сплайну
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
#include <math.h>
// визначення сплайнового класу
class Tsplain
{public:
int kol; // кількість рівнянь (відрізків розбиття)
float ** Ak; // масив коефіцієнтів
float * Xi; // вектор початків відрізків
float vol(float x); // функція повертає значення сплайну в точці х
Tsplain(int k); // constructor};
Tsplain::Tsplain(int k)
{kol=k;
Xi=new float[kol];
Ak=new float*[kol];
for(int i=0; i<kol; i++) Ak[i]=new float[kol];}
float Tsplain::vol(float x)
{float s=0.;
int i,t;
// шукаємо відрізок t де знаходиться точка х
for (i=0; i<kol; i++) if (x>=Xi[i]) { t=i; break; }
s=Ak[t][0];
for (i=1; i<kol; i++)
s+=Ak[t][i]*pow((x-Xi[t]),i);
return s;}
float fSimps(float down,float up, int n, Tsplain *spl)
/* Функція обчислює інтеграл методом Сімпсона з використанням кубічного сплайну
Вхідні дані:
down,up -границі інтегрування ;
n- число відрізків , на яке розбиваєтьться відрізок інтегрування ;
spl - вказівник на об’єкт класу Tsplain ( кубічний сплайн );
Вихідні дані:
функція повертає знайдене значення інтегралу.*/
{float s=0;
float h=(up-down)/(float)n;
int i;
s=spl->vol(down)+spl->vol(up-h);
for (i=2; i<n; i+=2)
s+=2*(spl->vol(down+i*h));
for (i=1; i<n; i+=2)
s+=4*(spl->vol(down+i*h));
return s*h;}
void main()
{int kol; // кількість рівняннь кубічного сплайну
float down,up;
float I1,I2,I,eps;
int n,i,j;
char *strError="\n Error of file !";
FILE *FileIn,*FileOut;
FileIn=fopen("data2_3in.txt","r"); // відкриваємо файл для читання
if (FileIn==NULL)
{ cout << " \"Data2_3in.txt\": Error open file or file not found !!!\n";
goto exit; }
FileOut=fopen("data2_3ou.txt","w"); // відкриваємо файл для запису
if (FileOut==NULL)
{ cout << " \"Data2_3ou.txt\": Error open file !!!\n";
goto exit; }
// читаємо kol
if(fscanf(FileIn,"%d,",&kol)==NULL)
{ cout << strError; goto exit;};
Tsplain *sp;
sp=new Tsplain(kol);
// читаємо вектор Xi
for(i=0; i<kol; i++) fscanf(FileIn,"%f,",&(sp->Xi[i]));
// читаємо масив Ak
for (i=0; i<kol; i++)
for (j=0; j<kol; j++) fscanf(FileIn,"%f,",&(sp->Ak[i][j]));
// читаємо n - кількість відрізків розбиття відрізку інтегрування
if(fscanf(FileIn,"%d,",&n)==NULL)
{ cout << strError; goto exit;};
down=sp->Xi[0];
up=sp->Xi[sp->kol-1]+(sp->Xi[sp->kol-1]-sp->Xi[sp->kol-2]);
I1=fSimps(down,up, n, sp);
I2=fSimps(down,up, 2*n, sp);
eps=(I2-I1)/15;
I=I2+eps;
// Вивід результатів
printf("I= %5.5f\n",I);
printf("EPS= %5.5f\n",eps);
fprintf(FileOut,"I= %5.5f\n",I);
fprintf(FileOut,"EPS= %5.5f\n",eps);
fclose(FileIn);
fclose(FileOut);
exit: cout << "\n Press any key ...";
getch();}
Результат роботи програми ("data2_3ou.txt")
I= 1.32213
EPS= 0.00004
Завдання 3
Знайти розв’язок системи нелінійних рівнянь
 ,
,

Рішення.
Умову завдання перепишемо наступним чином
 .
.
Приймаючи що
 і
і
 то коротко систему рівнянь можна записати
так
то коротко систему рівнянь можна записати
так
 .
.
Якщо відомо деяке
наближення
 кореня
кореня
 системи рівнянь, то поправку
системи рівнянь, то поправку
 можна знайти рішаючи систему
можна знайти рішаючи систему
 .
.
Розкладемо ліву частину
рівняння по степеням малого вектору
 ,
обмежуючись лінійними членами
,
обмежуючись лінійними членами


 .
.
 =
= =
= – матриця похідних (матриця Якобі) (
– матриця похідних (матриця Якобі) ( ).
).
Складемо матрицю похідних (матрицю Якобі):

Якщо
 , то
, то
 ,
,
де
 – матриця обернена до матриці Якобі.
– матриця обернена до матриці Якобі.
Таким чином послідовне наближення кореня можна обчислити за формулою
 або
або
 .
.
Умовою закінчення ітераційного процесу наближення корення вибираємо умову
 ,
,
 –
евклідова відстань
між двома послідовними наближеннями
;
–
евклідова відстань
між двома послідовними наближеннями
; –
число, що задає мінімальне наближення.
–
число, що задає мінімальне наближення.
Для рішення систем нелінійних рівнянь за даним алгоритмом призначена програма
Work3.cpp
//------------------------------------------------------------
// Work3.cpp
//------------------------------------------------------------
// "Числові методи"
// Завдання 3
// Розв’язування системи нелінійних рівнянь методом Ньютона
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
#include <math.h>
#include "matrix.h"
const int N=2; // степінь матриці Якобі (кількість рівнянь)
typedef void (*funcJ) (float[N], float[N][N]);
void fJakobi(float X[N],float J[N][N])
// функції , які складають матрицю Гессе
{J[0][0]=cos(X[0]); J[0][1]=cos(X[1]);
J[1][0]=2*X[0]; J[1][1]=-2*X[1]+1;}
typedef void (*funcF) (float[N], float[N]);
void fSist(float X[N],float Y[N])
{Y[0]=sin(X[0])+sin(X[1])-1;
Y[1]=X[0]*X[0]-X[1]*X[1]+X[1];}
//int NelinSist(float X[N], funcJ pJakobi, funcF pSist,float eps)
/* Функція знаходить кореня системи нелінійних рівнянь методом Ньютона.
Вхідні дані:
X[N] - вектор значень початкового наближення
pSist - вказівник на функцію, яка обчислює по
заданим значенням X[] значення функції f(X) ;
pJakobi - вказівник на функцію, яка обчислює по
заданим значенням X[] елементи матриці W ;
Вихідні дані:
X[N] - вектор наближеного значення мінімуму.
Функція повертає код помилки
0 - система рівнянь успішно розв’язана
1 - det W=0 */
{int n=N;
float len;
float W[N][N],Winv[N][N],Y[N],deltaX[N];
do
{pJakobi(X,W);
if(invMatr(n,W,Winv)) return 1;
pSist(X,Y);
DobMatr(n,Winv,Y,deltaX);
X[0]-=deltaX[0];
X[1]-=deltaX[1];
len=sqrt(deltaX[0]*deltaX[0]+deltaX[1]*deltaX[1]);}
while (len>eps);
return 0;}
//int main()
{float X[N],eps;
// початкові умови
eps=.0001;
X[0]=0.0; X[1]=1.0;
if (NelinSist(X,fJakobi,fSist,eps))
{ cout << "Error of matrix: detW=0"; return 1;}
printf("X= %5.4f Y= %5.4f\n",X[0],X[1]);
cout << "\n Press any key ...";
getch();}
Результат роботи програми:
X= 0.1477 Y= 1.0214
Завдання 4
Знайти точку мінімуму та мінімальне значення функції
 ,
,

методом Ньютона.
Рішення.
 ;
;
Матриця Гессе
 .
.
Ітераційний процес послідовного наближення мінімуму функції буде таким:
 ,
,
де
 –
матриця обернена до матриці Гессе.
–
матриця обернена до матриці Гессе.
Для закінчення ітераційного процесу використаємо умову
 або
або
 .
.
Для пошуку мінімуму функції за методом Ньютона призначена програма Work4.cpp
//------------------------------------------------------------
// matrix.h
//-----------------------------------------------------------
const int nMax=2; // кількість рівнянь
const float ZERO=.00000001;
int invMatr(int n,float A[nMax][nMax],float Ainv[nMax][nMax])
/* Функція знаходить обернену матрицю
Вхідні дані:
A- масив з коефіцієнтами при невідомих;
n- порядок матриці А(кількість рівнянь системи);
Вихідні дані:
Ainv- матриця обернена до матриці А;
функція повертає код помилки:
0- помилки немає;
1- матриця А вироджена. */
{float aMax,t; // максимальний елемент , тимчасова змінна
int i,j,k,l;
// формуємо одиничну матрицю
for(i=0; i<n; i++)
for (j=0; j<n; j++)
Ainv[i][j] = (i==j)? 1. : 0.;
for (k=0; k<n; k++)
{// знаходимо мах по модулю елемент
aMax=A[k][k]; l=k;
for (i=k+1; i<n; i++)
if (fabs(A[i][k])>fabs(aMax))
{ aMax=A[i][k]; l=i; }
// якщо модуль головного елементу aMax менший за програмний 0 (ZERO)
if ( fabs(aMax)<ZERO ) return 1;
// якщо потрібно, міняємо місцями рівняння Pk i Pl
if ( l!=k)
for( j=0; j<n; j++)
{t=A[l][j]; A[l][j]=A[k][j]; A[k][j]=t;
t=Ainv[l][j]; Ainv[l][j]=Ainv[k][j]; Ainv[k][j]=t;}
// ділимо k-й рядок на головний елемент
for (j=0; j<n; j++) { A[k][j]/=aMax; Ainv[k][j]/=aMax; }
// обчислюємо елементи решти рядків
for (i=0; i<n; i++)
if( i!=k )
{t=A[i][k];
for (j=0; j<n; j++)
{A[i][j]-=t*A[k][j];
Ainv[i][j]-=t*Ainv[k][j];}}}
return 0;}
void DobMatr(int n, float A[nMax][nMax], float B[nMax],float X[nMax])
// функція знаходить добуток матриці А на вектор В і результат повертає в
// векторі Х
{int i,j;
float summa;
for (i=0; i<n; i++)
{summa=0;
for (j=0; j<n; j++)
{summa+=A[i][j]*B[j];
X[i]=summa;}}
} // DobMatr
//------------------------------------------------------------
// Work4.cpp
//------------------------------------------------------------
// "Числові методи"
// Завдання 4
// Пошук мінімуму функції методом Ньютона
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
#include <math.h>
#include "matrix.h"
const int N=2; // степінь матриці Гессе
float myFunc(float x[N])
{ return exp(-x[1])-pow(x[1]+x[0]*x[0],2); }
typedef void (*funcH) (float[N], float[N][N]);
void fHesse(float X[N],float H[N][N])
// функції , які складають матрицю Гессе
{H[0][0]=-4.*X[1]-6.*X[0]*X[0]; H[0][1]=-4.*X[0];
H[1][0]=-4; H[1][1]=exp(-X[1])-21;}
typedef void (*funcG) (float[N], float[N]);
void fGrad(float X[N],float Y[N])
{Y[0]=-4*X[1]*X[0]-3*X[0]*X[0]*X[0];
Y[1]=exp(-X[1])-2.*X[1]-2*X[0]*X[0];}
//int fMin(float X[N], funcG pGrad, funcH pHesse,float eps)
/* Функція знаходить точку мінімуму рівняння методом Ньютона.
Вхідні дані:
X[N] - вектор значень початкового наближення
pGrad - вказівник на функцію, яка обчислює по
заданим значенням X[] значення grad f(X) ;
pHesse - вказівник на функцію, яка обчислює по
заданим значенням X[] елементи матриці H ;
Вихідні дані:
X[N] - вектор наближеного значення мінімуму.
Функція повертає код помилки
0 - система рівнянь успішно розв’язана
1 - det H=0 */
{int n=N;
float modGrad;
float Hesse[N][N],HesseInv[N][N],Grad[N],deltaX[N];
do
{pHesse(X,Hesse);
if(invMatr(n,Hesse,HesseInv)) return 1;
pGrad(X,Grad);
DobMatr(n,HesseInv,Grad,deltaX);
X[0]-=deltaX[0];
X[1]-=deltaX[1];
modGrad=sqrt(deltaX[0]*deltaX[0]+deltaX[1]*deltaX[1]);}
while (modGrad>eps);
return 0;}
//int main()
{float X[N],eps;
// початкові умови
eps=.0001;
X[0]=0.5; X[1]=0.5;
if (fMin(X,fGrad,fHesse,eps))
{ cout << "Error of matrix: detH=0"; return 1;}
printf("X= %5.5f Y= %5.4f\n f(x,y)= %4.3f\n ",X[0],X[1],myFunc(X));
cout << "\n Press any key ...";
getch();}
Результат роботи програми:
x= -0.0000 y= 0.3523
f(x,y)= 0.579
Завдання 5
Розкласти в ряд Фурьє
функцію
 на відрізку [-1; 1].
на відрізку [-1; 1].
Рішення.
В загальному вигляді
ряд Фурьє функції
 виглядає так:
виглядає так:


 , де
, де
 =0,
1, 2, …
=0,
1, 2, …
В нашому випадку
відрізок розкладення функції – [-1; 1],
тому проводимо лінійну заміну змінної
 :
:
 .
Тоді умова завдання стане такою:
.
Тоді умова завдання стане такою:


Для наближеного обчислення коефіцієнтів ряду Фурьє використаємо квадратурні формули, які утворюються при інтерполяції алгебраїчним многочленом підінтегральних функцій
 і
і
 :
:
 (1)
(1)
 (2)
(2)
 (3)
(3)
де
 –
число вузлів квадратурної формули;
–
число вузлів квадратурної формули;
 –
вузли квадратурної
формули ,
–
вузли квадратурної
формули ,
 =0,
1, 2, …, 2
=0,
1, 2, …, 2
Для обчислення наближених значень коефіцієнтів ряду Фурьє по формулам (1), (2), (3) призначена процедура (функція) Fourier.
//---------------------------------------------------------
// Work5.h
//---------------------------------------------------------
#include <math.h>
const double Pi=3.141592653;
// функція повертає і-й вузол квадратурної формули, 2N+1-кілікість вузлів
inline double FuncXi(int N, int i) {return -Pi+(2*Pi*i)/(2*N+1);}
typedef double (*Func)(double); // опис типу вказівника на функцію
char Fourier(Func F_name, int CountN, int CountK,double **Arr)
/* функція обчислює коефіцієнти ряду Фурьє
Вхідні дані:
F_mame - вказівник на функцію(функтор), яка обчислює значення функції
f(x) на відрізку [-п; п];
CountN - число, яке задає розбиття відрізка [-п; п] на рівні частини
довжиною 2п/(2*CountN+1);
CountK - кількість обчислюваних пар коефіцієнтів;
Вихідні дані:
Arr - двомірний масив розміру [CountK+1][2], в якому
знаходяться обчислені коефіцієнти ряду Фурьє.
Функція повертає значення коду помилки:
Fourier=0 - помилки немає;
Fourier=1 - якщо CountN<CountK;
Fourier=2 - якщо CountK<0;*/
{double a,b,sumA,sumB;
int i,k;
if (CountN < CountK) return 1;
if (CountK < 0) return 2;
// обчислення а0
sumA=0;
for (i=0; i< 2*CountN+1; i++) sumA+=F_name(FuncXi(CountN,i));
a=1./(2*CountN+1)*sumA;
Arr[0][0]=a;
// обчислення коефіцієнтів аk,bk
for (k=1; k<=CountK; k++)
{sumA=sumB=0;
for (i=0; i<2*CountN+1; i++)
{sumA+=F_name(FuncXi(CountN,i))*cos(2*Pi*k*i/(2*CountN+1));
sumB+=F_name(FuncXi(CountN,i))*sin(2*Pi*k*i/(2*CountN+1));}
a=(2./(2*CountN+1))*sumA;
b=(2./(2*CountN+1))*sumB;
Arr[k][0]=a;
Arr[k][1]=b;}
return 0;}
//------------------------------------------------------------
// Work5.cpp
//------------------------------------------------------------
// "Числовы методи"
// Завдання 5
// Розрахунок коэфіцієнтів ряду Фурьє
#include "Work5.h"
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
double f(double x)
// функція повертає значення функції f(x)
{return sqrt(Pi*Pi*x*x+1);}
const int N=20; // константа, яка визначає розбиття відрізка [-п; п]
// на рівні частини
const int CountF=15; // кількість пар коефіцієнтів ряду
void main()
{double **data;
data = new double *[CountF+1];
for ( int i=0; i<=CountF; i++) data[i] = new double [2];
if (Fourier(f,N,CountF,data) != 0)
{cout << "\n Помилка !!!";
return;}
// Вивід результатів
printf("a0= %lf\n",data[0][0]);
for (int i=1;i<=CountF;i++)
printf("a%d = %lf , b%d = %lf\n",i,data[i][0],i,data[i][1]);
cout << " Press any key ...";
getch();}
Результат роботи програми Work5.cpp












