Розробка програми Sierpins, яка реалізує побудову рекурсивних кривих Серпінського
3
ЗМІСТ
Вступ
Розділ 1. Криві Серпінського.
Розділ 2. Методи та засоби розв'язку задачі
Розділ 3. Практична реалізація розв'язку задачі
Висновки
Список використаної літератури.
Додаток а. Блок-схема алгоритму.
Додаток б. Текст програми
Додаток в. Тест програми
Вступ
Мови програмування - це формальні мови зв'язку людини з машиною‚ призначені для опису даних та алгоритмів(програм) їх обробки на ЕОМ. Алгоритмічні мови‚ існують в наш час‚ поділяються на три великих класи: машинно-орієнтовані‚ процедурно-орієнтовані та проблемно-орієнтовані. До машинно-орієнтованих відносяться мови‚ в яких з однієї сторони явно виражений зв'язок з конкретною ЕОМ (структура команд‚ пам'яті‚ зовнішніх пристроїв)‚ а з другої - в мову введено елементи‚ які спрощують і автоматизують процес програмування (символьне позначення команд і комірок пам'яті‚ широке застосування звичних для людини позначень і т.д.). Процедурно-орієнтовані мови є вищим рівнем мов програмування, призначені для різних сфер застосування ЕОМ і враховують специфіку їх застосування.
Особливий клас утворюють мови‚ призначені для опису спеціальних проблем і які носять назву проблемно-орієнтованих мов. Програма, реалізована на такій мові програмування містять крім опису умови задачі вказівку розв'язати задачу даного класу. Прикладом такої мови є, наприклад, мова Stress‚ яка призначається для опису задач конструювання. Програма на цій мові містить ряд загальних характеристик системи (розмірності‚ число вершин та ін.) і дані‚ а також вказівку - розв'язати задачу і представити певні дані у вигляді деякої таблиці.
Програмна реалізація курсового проекту здійснювалась на алгоритмічній мові Lisp. Мова Lisp є процедурно-орієнтованою мовою і відноситься до групи мов програмування‚ призначених для обробки списків (сюди ж відносяться мови. IL-V, КОМИТ). Мова IPL-V використовується для досліджень в області штучного інтелекту.
Особливістю мови Lisp є використання ланцюжкової адресації - кожен член списку містить інформацію про себе у вигляді безпосереднього значення чи адреси та адресу наступного елемента списку. Мова є зручним засобом при створенні програм обробки інформації‚ зміст та об'єм якої наперед невідомі.
Розділ 1. Криві Серпінського
Оригінальний візерунок на малюнку 1 складається із суперпозиції чотирьох кривих. Ці криві відповідають деякому регулярному образу. Алгоритм для побудови цих кривих на екрані монітора чи на графобудівнику під керуванням обчислювальної машини описаний у [1].
Задача проекту – реалізувати цей алгоритм у виді програми функціональною мовою програмування Lisp.
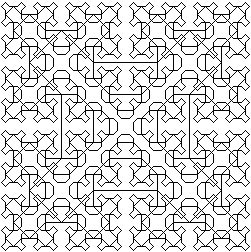
Малюнок 1
Аналізуючи малюнок 1, можна переконатись, що він отриманий шляхом накладення один на одного декількох кривих. Перші дві з них показані на малюнку 2. Крива S>i> називається кривою Серпінського І-го порядку. Необхідно з'ясувати, яка рекурсивна схема цих кривих.

Малюнок 2
Головна особливість кривої Серпінського полягає в тому, що вона замкнута й у ній немає перетинань. Це означає, що основна рекурсивна схема повинна давати розімкнуту криву лінію, чотири частини якої з'єднуються лініями, що не належать самому рекурсивному образу. І дійсно, ці замикаючі лінії являють собою відрізки прямих у чотирьох зовнішніх кутах, на малюнку 2 вони виділені жирними лініями. Можна вважати, що вони належать до не порожньої початкової кривої S – квадрату, який «стоїть» на одному куті. Тепер досить легко скласти рекурсивну схему.
Чотири складових образи, для наочності, позначимо через A, B, C, D, а процедури, що малюють сполучні прямі, будемо позначати стрільцями, що указують відповідному напрямку. Треба відзначити, що чотири рекурсивних образи власне кажучи ідентичні, але лише повертаються на 90°.
Розділ 2. Методи та засоби розв'язку задачі
Основний образ кривих Серпінського задається схемою:
S: A B C D
а рекурсивні складові (горизонтальні і вертикальні відрізки – подвійної довжини):
A: A B D A
B: B C A B
C: C D B C
D: D A C D
Припустимо,
що для побудови частини прямої в нашому
розпорядженні є процедура Line,
що пересуває перо в заданому напрямку
на задану відстань, причому напрямок
задається цілочисленим параметром i,
як
 градусів. Якщо одиничну пряму позначити
через h,
то за допомогою рекурсивних звертань
до аналогічно складених процедур для
B
і D
і до самої процедури A
досить просто написати процедуру, що
відповідає схемі А.
градусів. Якщо одиничну пряму позначити
через h,
то за допомогою рекурсивних звертань
до аналогічно складених процедур для
B
і D
і до самої процедури A
досить просто написати процедуру, що
відповідає схемі А.
( defun A ( k )
( cond ( ( > k 0 )
( A ( - k 1 ) ) ( Line 1 h )
( B ( - k 1 ) ) ( Line 0 ( * 2 h ) )
( D ( - k 1 ) ) ( Line 7 h )
( A ( - k 1 ) ))))
Ця процедура ініціюється головною програмою по одному разу для кожної кривої Серпінського, що утворять зображений вище малюнок. Уживання фактичного параметра для рівня гарантує закінчення роботи, тому що глибина рекурсії не може бути більше k. Головна програма будується за зразком S. Її задача - установити початкову точку (центр) кривої, тобто вихідні координати пера (P>x> і P>y>) і одиничну довжину збільшення h. Квадрат, де малюється крива, міститься в середині екрана заданої ширини і висоти.
Графічне зображення отриманого алгоритму представлено в додатку А.
В порівнянні з такою рекурсивною побудовою еквівалентні програми, де уникали вживання рекурсії, виглядають украй складними й заплутаними.
Розділ 3. Практична реалізація розв'язку задачі
Програма рисування кривих Серпінського реалізована мовою Lisp. Текст програми наведено в додатку Б.
Програма на мові Lisp прдставляє собою рекурсивну функцію символьних виразів‚ яка будується аналогічно до арифметичних функцій з допомогою умовного оператора та оператора суперпозиції. Умовний оператор має вигляд
(p>1> → l>1>;→ ... ;p>n> →l>n> )
Результатом його виконання буде p>і>‚ якщо l>і >прийме істине значення. В мові є п'ять елементарних функцій:
atom - логична функция‚ яка визначає чи є досліджуваний вираз атомом - неподільною частиною інформації;
eq - логична функцияё яка встановлює рівність двох атомів;
car, cdr -функції, які виділяють зі списку перший елемент‚ та елементи‚ що залишились;
cons - об'єднання двох списків у один.
Крім елементарних‚ в мові Lisp є ряд більш складних функцій‚ які будуються з них‚ наприклад‚ підстановка в у вираз z замість всіх входжень символу y виразу x запишеться у вигляді наступної функції
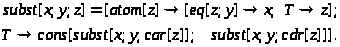
цей запис представляє собою приклад програми на мові Lisp.
В даному курсовому проекті на мови Lisp розроблено програму Sierpins, яка реалізує побудову рекурсивних кривих Серінського.
На початку програми встановлюється значення змінної *VMode*‚ яка керує установкою відео режиму, і за замовчуванням встановлена в значення 18. Ця установка відповідає режиму 640x480 Color, і працює на більшості систем. У випадку проблеми з установкою цього режиму необхідно вибрати значення цієї змінної відповідно до документації на устаткування. Розмір області для побудови кривих встановлюється константою *SquareZize*, значення якої в даному випадку становить 256.
Далі з допомогою операцій
h = SquareSize/4
x>0> = MaxX/2
y>0> = MaxY/2
обчислюється довжина лінії h та координати початкової точки (x>0>,y>0>) для малювання кривої .
Рисування кривої здійснюється в циклі по змінній і‚ котра визначає порядок кривої Серпінського (при тестовому запуску програми пропонувалось 4). В циклі виконуються такі операції:
1. обчислення координат початкової точки для малювання та визначення довжини одиничної лінії за формулами

2. установка пера в точку з координатами P>x> P>y>
3. визначення і установка кольору для малювання
4. малювання рекурсивної частини кривої з допомогою процедур A(i), B(i), C(i) D(i).
Потім виконується збільшення лічильника циклу на 1 і перевірка умови закінчення циклу. При досягненні лічильником циклу значення змінної Count здійснюється вихід з циклу й побудова кривої Серпінського і-го порядку завершується. На цьому програма завершує свою роботу.
При роботі з програмою встановлюються такі вимоги до системи:
x86 персональний комп'ютер (386 мінімум; 486, Pentium, чи Pentium Pro рекомендується)
Microsoft DOS 3.30 чи вище
Microsoft Windows 3.1, Microsoft Windows for Workgroups, Microsoft Windows 95, Microsoft Windows NT 3.51 чи 4.0
512 Kb RAM
5 Kb вільного простору на жорсткому диску
Встановлений інтерпретатор XLisp версії 2.1 чи вище
Для запуску програми необхідно:
Увімкнути комп'ютер
Завантажити інтерпретатор XLisp c параметром «Sierpins.lsp»: C:\XLISP\XLISP.EXE SIERPINS.LSP1
У відповідь на запрошення XLisp увести: (SierpinskiCurve 4)
Висновки
Завершивши роботу над курсовим проектом можна зробити висновок про те, що мені вдалося досягти своєї мети і розробити програму побудови кривих Серпінського. За допомогою засобів алгоритмічної мови Lisp було створено програму Serp‚ яка дозволяє будувати криві Серпінського за допомогою рекурсивних процедур. Використання чотирьох рекурсивних процедур дало змогу досить просто справитись з поставленою задачею..
Розробка даної програми дала мені змогу оволодіти основними засобами програмування на алгоритмічній мові Lisp та здобути практичні навички розробки програм з використанням інтерпретатора PC-Lisp версії 3.0.
Завдяки використанню мови програмування Lisp розроблена програма вийшла лаконічною і водночас легкою для читання й розуміння, а розроблені рекурсивні графічні процедури можуть бути використані при розв'язуванні інших, можливо набагато складніших програм.
Список використаної літератури
“Алгоритм + структура даних = програма”, H.Вірт.
“XLisp-Plus 2.1 Programmers Manual”, David Michael Betz
Додаток А. Блок-схема алгоритму

Схема алгоритму процедури A
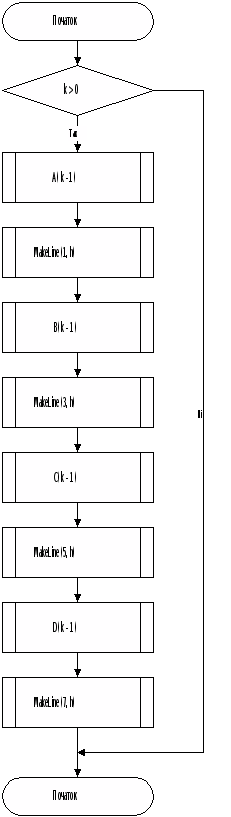
Додаток Б. Текст програми
;; SIERPINS.LSP для XLISP версії 2.1
;; ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
;; Програма побудови кривих Серпінського i-го порядку.
;;
;; ЗАПУСК: > (SierpinskiCurve 4)
;;
;;
( defvar *VMode* 18 ) ;Відео режим за замовчуванням
( defvar *Max* 640 ) ;Максимальна ширина екрана за замовчуванням
( defvar *Max* 480 ) ;Максимальна висота екрана за замовчуванням
( defvar *SquareSize* 256 ) ;Розмір області для побудови
;;
;; Функція ініціалізує графічний режим, установлює перемінні
;; *Max* *Max* *SquareSize* відповідно до обраного режиму
;;
(
defun InitGraph()
(
case *VMode*
( 4 ;320x200 Color
( mode 4 )
( setq *MaxX* 320 *MaxY* 200 *SquareSize* 128 ) )
( 16 ;640x350 Color
( mode 16 )
( setq *MaxX* 640 *MaxY* 350 *SquareSize* 128 ) )
( 18 ;640x480 Color
( mode 18 ) )
( 106 ;800x600 Color
( mode 106 106 800 600 )
( setq *MaxX* 800 *MaxY* 600 *SquareSize* 512 ) )
( t ( error Unsupported graphics mode: *VMode* ) )
)
)
;;
;; Функція реалізує затримку на заданий час
;;
(
defun pause ( time )
( let ( ( fintime ( + ( * time internal-time-units-per-second )
( get-internal-run-time ) ) ) )
( loop ( when ( > ( get-internal-run-time) fintime )
( return-from pause ) ) ) )
)
;;
;; Функція цілочисленого розподілу
;;
(
defun div ( a b ) ( round ( / a b ) )
)
;;
;; Функція малювання прямої:
;; Параметри: <Direction> - напрямок малювання (0-7)
;; <Size> - довжина прямої
;;
(
defun Line( Direction Size )
( setq x Px y Py )
(
case Direction
( 0 ( setq x ( + x Size) ) )
( 1 ( setq x ( + x Size ) y ( - y Size ) ) )
( 2 ( setq y ( - y Size) ) )
( 3 ( setq x ( - x Size ) y ( - y Size ) ) )
( 4 ( setq x ( - x Size) ) )
( 5 ( setq x ( - x Size ) y ( + y Size ) ) )
( 6 ( setq y ( + y Size) ) )
( 7 ( setq x ( + x Size ) y ( + y Size ) ) )
)
( move Px Py x y )
( setq Px x Py y )
)
;;
;; Функції A, B, C, D - рекурсивні функції малювання
;;
(
defun A ( k )
( cond ( ( > k 0 )
( A ( - k 1 ) ) ( Line 1 h )
( B ( - k 1 ) ) ( Line 0 ( * 2 h ) )
( D ( - k 1 ) ) ( Line 7 h )
( A ( - k 1 ) )
) )
)
(
defun B ( k )
( cond ( ( > k 0 )
( B ( - k 1 ) ) ( Line 3 h )
( C ( - k 1 ) ) ( Line 2 ( * 2 h ) )
( A ( - k 1 ) ) ( Line 1 h )
( B ( - k 1 ) )
) )
)
(
defun C ( k )
( cond ( ( > k 0 )
( C ( - k 1 ) ) ( Line 5 h )
( D ( - k 1 ) ) ( Line 4 ( * 2 h ) )
( B ( - k 1 ) ) ( Line 3 h )
( C ( - k 1 ) )
) )
)
(
defun D ( k )
( cond ( ( > k 0 )
( D ( - k 1 ) ) ( Line 7 h )
( A ( - k 1 ) ) ( Line 6 ( * 2 h ) )
( C ( - k 1 ) ) ( Line 5 h )
( D ( - k 1 ) )
) )
)
;;
;; Головна процедура
;; Параметри: <Count> - кількість ітерацій
;;
(
defun SierpinskiCurve ( Count )
( InitGraph ) ;Установка графічного режиму
( setq h ( div *SquareSize* 4 ) ) ;Обчислення довжини лінії
( setq x0 ( div *Max* 2 ) ) ;Обчислення початкової точки
( setq y0 ( + ( div *Max* 2 ) h ) ) ;для малювання
( ;Основний цикл
do (( i 1 )) ;Ініціалізація лічильника
(( eql i ( + Count 1 ) ) 'Done ) ;Умова завершення
( setq x0 ( - x0 h ) ) ;Обчислення координат початкової
( setq h ( div h 2 ) ) ;крапки для малювання і
( setq y0 ( + y0 h ) ) ;одиничної довжини лінії
( setq Px x0 Py y0 ) ;Установка пера
( color i ) ;Установка кольору для малювання
( A i ) ( Line 1 h ) ;Малювання
( B i ) ( Line 3 h )
( C i ) ( Line 5 h )
( D i ) ( Line 7 h )
( pause 1.0 ) ;Затримка
( setq i ( + i 1 )) ;Інкремент лічильника
) ;Кінець основного циклу
)
( print Try (SierpinskiCurve 4) ) ;Підказка
Додаток В. Тест програми
Тест проводився на робочій станції з наступною конфігурацією:
Pentium 166
32 Mb RAM
SyncMaster 17Glsi
S3 Trio64V+
Windows 95
Інтерпретатор XLisp був запущений у вікні MS-DOS.
Програма тестувалась при значеннях параметра Count від 1 до 4. У результаті тестів були отримані наступні зображення на екрані монітора :
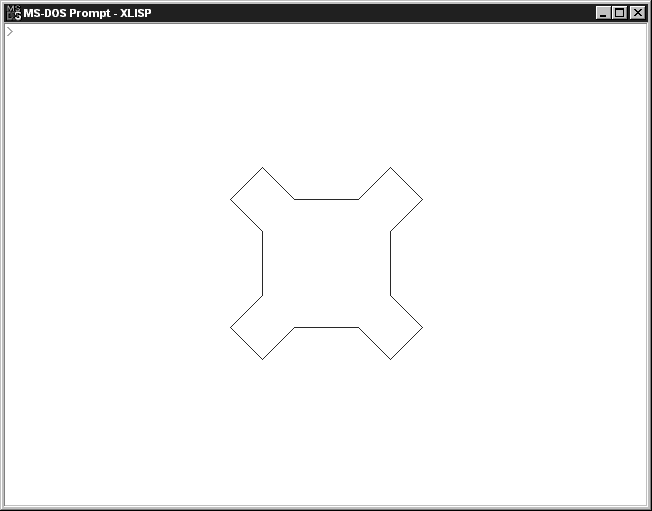
Малюнок 3

Малюнок 4

Малюнок 5

Малюнок 6
1 Даний приклад передбачає, що XLisp встановлено в каталозі C:\XLISP и його запуск проводиться в режимі MS-DOS.