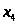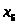Розв’язання задач лінійного програмування

Міністерство освіти та науки України

Вінницький національний технічний університет

Інститут автоматики та комп’ютерних систем управління

Факультет автоматики та комп’ютерних систем управління

Розв’язання задач лінійного програмування(А)

Пояснювальна записка

з дисципліни «Математичне програмування та дослідження операцій»

до курсової роботи за спеціальністю

«Системи управління та автоматики»

08-01.МПДО.342.00.000-ПЗ

Вінниця, ВНТУ 2007

Анотація

В даній курсові роботі розглянуто методи розв’язку задач лінійного програмування. Такі задачі досить поширені у повсякденному житті. Тому в даній роботі розглянуто рішення на окремій задачі, а також розглянуто як їх можна розв’язувати вручну і за допомогою спеціального програмного продукту.

Було розроблено математичну модель і програмне забезпечення. Дана задача вирішується симплекс методом, тому досліджується основний принцип метода, особливості і переваги в порівнянні з іншими методами.

Зміст

Вступ

1 Опис існуючих методів розв’язку задач лінійного програмування

1.1 Постановка задачі

1.2 Графічний метод

1.3 Симплекс-метод

1.4 Двоїстий симплекс метод

1.5 Транспортна задача

1.6 Вибір методу розв’язку задачі

2 Опис метода розв’язку задачі

3 Розробка моделі розв’язку задачі

4 Розробка програмного забезпечення

4.1 Призначення програми

4.2 Вибір середовища програмування

4.3 Опис вхідних та вихідних даних

4.4 Розробка структури програми

4.5 Розробка схеми алгоритму

4.6 Розробка тестів

4.7 Аналіз результатів тестування

4.8 Інструкція користувачеві

Висновки

Література

Додаток А.

Технічне завдання

Вступ

В даний час лінійне програмування є одним з найбільш популярних апаратів математичної теорії оптимального управління рішень, у тому числі і у фінансовій математиці. Для вирішення завдань лінійного програмування розроблено складне програмне забезпечення, що дає можливість ефективно і надійно вирішувати практичні завдання великих об'ємів. Ці програми і системи забезпечені розвиненими системами підготовки початкових даних, засобами їх аналізу і представленням отриманих результатів. У розвиток і вдосконалення цих систем вкладена праця і талант багатьох математиків, досвід вирішення тисяч завдань. Знання системи лінійного програмування необхідні кожному спеціалісту в області прикладної математики.

У класичній математиці методи пошуку оптимальних рішень розглядають у розділах класичної математики, зв'язаних з вивченням екстремумів функцій, у математичному програмуванні.

Існує багато розділів в математичному програмуванні, серед них лінійне і нелінійне програмування, опукле і квадратичне, і багато інших. Але всі вони зводяться до отримання оптимального рішення у великій кількості задач різних промислових і виробничих гілках суспільства. Розглянемо лінійне програмування та визначимо основні принципи і алгоритми даного розділу математичного програмування.

Лінійне програмування є найбільш часто використовуваним методом оптимізації. До завдань лінійного програмування можна віднести:

    раціональне використання сировини і матеріалів;

    завдання оптимального розкрою;

-оптимізації виробничої програми підприємств;

-оптимального розміщення і концентрації виробництва;

-складання оптимального плану перевезень, роботи транспорту;

-управління виробничими запасами і ін.

Для великої кількості практично цікавих завдань цільова функція виражається лінійно – через характеристики плану, причому допустимі значення параметрів підпорядковані лінійній рівності або нерівностям. Знаходження за даних умов абсолютного екстремуму цільової функції носить назву лінійного програмування.

Першим дослідженням по лінійному програмуванню є робота Л. В. Кантфовіча “Математичні методи організації і планування виробництва”, яке було опубліковане в 1939 р. У ньому розміщена постановка завдань лінійного програмування, розроблений метод результуючих множників вирішення завдань лінійного програмування і дано його теоретичне обґрунтування.

Головна мета лінійного програмування є математичне формулювання проблеми складання такого плану використання різних способів виробництва, який дозволяє отримати максимальну кількість однорідного продукту при ресурсах, що є в наявності.

1 Опис існуючих методів розв’язку задач лінійного програмування

Лінійне програмування розв’язує велику кількість задач з різними типами обмежень. Тому їх можна розв’язати різними методами. Розглянемо їх принцип.

      Постановка задачі

Методи лінійного програмування - чисельні методи вирішення оптимізаційних задач, що зводяться до формальних моделей лінійного програмування[1].

Як відомо, будь-яке завдання лінійного програмування може бути приведене до канонічної моделі мінімізації лінійної цільової функції з лінійними обмеженнями типу рівності. Оскільки число змінних в завданні лінійного програмування більше числа обмежень (), то можна отримати рішення, прирівнявши нулю () змінних, які називаються вільними. Решта m змінних, які називаються базисними, можна легко визначити з системи обмежень звичайними методами лінійної алгебри. Якщо рішення існує, то воно називається базисним. Якщо задача лінійного програмування має оптимальні рішення, то хоча б один із них є базисним.

Приведені міркування означають, що при пошуку оптимального рішення задачі лінійного програмування досить обмежитися перебором базисних допустимих рішень. Те, що не всі базисні рішення є допустимими, істотно проблеми не міняє, оскільки щоб оцінити допустимість базисного рішення, його необхідно отримати.

В загальному постановка задачі має вигляд:

Нехай маємо деякі змінні і функцію цих змінних, яка називається цільовою функцією. Потрібно найти екстремум (максимум чи мінімум) цільової функціїпри умові,що змінні належать деякій області :

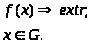(1.1.1)

В залежності від виду функції і області G розрізняють розділи математичного програмування: квадратичне програмування, випукле і ін.

Лінійне програмування характеризується тим, що функція і лінійною функцією змінних і область G визначається системою лінійних рівнянь чи нерівностей.

      Графічний метод

Якщо модель містить тільки дві змінні, задачу можна розв’язати графічно. У випадку трьох змінних графічний розв’язок стає менш наочним, а при більшому числі змінних - взагалі неможливим. Незважаючи на це, розгляд графічного методу дасть змогу зробити висновки, що послужать основою для розробки загального методу розв’язання задач лінійного програмування[2].

Перший крок при використанні графічного методу полягає в поданні області допустимих розв’язків, у якій водночас задовольняються всі обмеження моделі. Нехай шукана область (простір) розв’язків задачі показана. Умови невід’ємності змінних обмежують область їх допустимих значень.> >Інші межі простору розв’язків потрібно зобразити прямими лініями, побудованими по рівняннях, що отримані заміною знака «≤» чи «≥» знаком “=" в обмеженнях. Області, в яких відповідні обмеження виконуються як нерівності, указуються стрілками, спрямованими вбік допустимих значень змінних. Отримуємо простір розв’язків задачі. У кожній точці, що належить внутрішній області або межам, всі обмеження виконуються, тому розв’язки, що відповідають цим точкам, є допустимими. Серед безкінечного числа таких точок можна знайти точку оптимального розв’язку, якщо з'ясувати, в якому напрямку зростає цільова функція. На графік наносять лінію рівня цільової функції 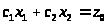, де > >- довільне значення . Будують вектор , що є нормаллю до ліній рівня цільової функції й визначає напрямок оптимізації . Лінію рівня зрушують паралельно самій собі вздовж вектора доти, поки вона не вийде за межі області допустимих розв’язків. Остання точка цієї області й буде точкою оптимуму.

Значення > >та 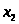в розв’язуючій точці визначаються шляхом розв’язання системи рівнянь.

Зазначимо, що у випадку, коли лінії рівня мають такий самий нахил, як пряма зв’язуючого обмеження (тобто такого, що проходить через оптимальну точку), матимемо безліч оптимумів на відрізку.

Графічний спосіб розв'язування ґрунтується на геометричній інтерпретації задачі лінійного програмування, тому він досить простий для розуміння. Недоліком є те, що графічним способом можна розв’язати задачу, в якій в обмеженнях є лише дві змінні, потрібно намагатися малювати лінії з найбільшою точністю, в протилежному випадку можна отримати велику похибку, а в результаті неправильне рішення.

1.3 Симплекс-метод

Симплекс-метод застосовується до рішення будь-якої задачі лінійного програмування[3].

Симплекс метод в порівнянні з графічним методом забезпечує більш раціональне рішення задачі. Розпочинаючи з будь-якої вершини багатокутника, твореного обмеженнями, переходять до розрахунку тільки тієї вершини, в якій значення лінійної форми буде більшим, чим в попередніх. Решту варіантів не обчислюють. Тоді при кінцевому числі кроків може бути найдений оптимальний план. Таким чином, виконується впорядкований перебір вершин, при яких відбувається постійне збільшення лінійної форми. Тому симплекс-метод також називають методом послідовного покращення оптимального плану. Рішення задачі симплекс-методом включає в себе два етапи. Спочатку потрібно найти вершину багатокутника обмежень, координати якої визначають початковий опорний план. Потім послідовно переходимо від однієї вершини багатокутника до іншої, яка сусідня попередній. Так як прилеглих вершин багато, то кожний раз вибирається така вершина, при переході до якої забезпечується найбільший приріст лінійної форми. На кожному кроці процесу покращення плану виконується перевірка на оптимальність. Очевидно, що план буде оптимальний, якщо серед вершин, які прилягають до даної, немає такої, при переході до якої відбувається ріст лінійної функції.

За звичай, симплекс-метод реалізується у вигляді симплекс-таблиць. У першому стовпчику цієї таблиці зазначають вектори, які входять в базис. У другому – коефіцієнти цільової функції, які відповідають векторам, що входять в базис. Третій стовпчик – компоненти опорного плану.

Головною перевагою симплекс-методу є його універсальність, будь-яку задачу лінійного програмування можна з легкістю вирішити як за допомогою програмного забезпечення так і вручну. Якщо обчислення і створення симплекс-таблиць пишеться вручну, то єдиною трудністю може стати обчислення: якщо велика кількість обмежень через неуважність можна отримати хибне рішення.

1.4 Двоїстий симплекс-метод

Двоїстий симплекс-метод і симплекс-метод за алгоритмом досить схожі. Однак двоїстий симплекс-метод можна застосовувати при рішенні задач лінійного програмування, вільні члени системи рівнянь якої можуть бути будь-якими числами (при рішенні задачі симплексним методом ці числа передбачалися ненегативними).

Нехай за умовою задачі потрібно визначити максимальне значення функції:

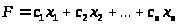.(1.4.1)

Нехай

(1.4.2)

де 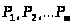- одиничні вектори.

Для того, щоб вирішити задачу двоїстим симплекс-методом потрібно виконати дві умови. Спочатку необхідно знайти так званий псевдо план задачі. Рішення системи лінійних рівнянь(1.4.2), приймаючи до уваги базис(одиничні вектори), називається псевдопланом задачі, якщо всі умови даної системи задоволені. Потім рішення зводиться до перевірки отриманого псевдоплану. Якщо він оптимальний, то отримане значення і є розв’язком задачі. Якщо ж ні, то потрібно знову встановлювати псевдоплан. Після цього, вибирають рядок, що дозволяє, за допомогою визначення найбільшого по абсолютній величині негативного числа стовпця вектора 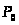і результуючого стовпчика, знаходження найменшого по абсолютній величині відношення елементів () і рядка до відповідного негативним елементам результуючого рядка. Знаходять новий псевдоплан і цикл розв’язку задачі повторюється.

В порівнянні з методами, описаними раніше, двоїстий симплекс-метод дає змогу вирішувати задачі лінійного програмування, системи обмежень яких при позитивному базисі містять вільні члени будь-якого знаку. Цей метод дозволяє зменшити кількість перетворень системи обмежень, а також розміри симплексної таблиці.

1.5 Транспортна задача

В найпростішому варіанті транспортна задача формулюється наступним чином: є n постачальників із запасами однорідного штучного товару 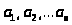та m споживачів із потребами цього товару . Не порушуючи загальності, можна вважати транспортну задачу закритою, тобто, що сума всіх запасів дорівнює сумі всіх потреб, в противному разі задача є відкритою і простими відомими методами (введенням фіктивного постачальника чи фіктивного споживача) зводиться до закритої. Нехай матриця 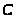є матрицею цін перевезень, тобто кожен її елемент 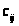є ціною за перевезення одиниці продукції від i–го постачальника j–му споживачу, а матриця такої ж розмірності є планом перевезень, тобто кожне є цілим невід’ємним числом, що дорівнює кількості товару, що перевозиться від i–го постачальника j–му споживачу. Метою розв’язку транспортної задачі є пошук такого плану перевезень Х, при якому загальна вартість перевезень була б найменшою з можливих за умови, що весь товар від постачальників перевозиться до споживачів. Транспортна задача є задачею цілочислового лінійного програмування. З основами лінійного програмування можна ознайомитись, з науковим обґрунтуванням алгоритмів розв’язку задач лінійного програмування, зокрема транспортної задачі. Відзначимо лише, що по-перше, жоден з відомих алгоритмів не є досконалим, а по-друге, зажди пропонується шукати один оптимальний план перевезень, а решта оптимальних планів залишається або без уваги, або в кращому випадку залишається на розгляд методами після оптимізаційного аналізу. Досі було важко запропонувати достойну альтернативу цим методам через відсутність потужної обчислювальної техніки, але тепер це можливо[4].

Для сучасної ЕОМ не представляє ніяких складностей вирішення задач за допомогою даного методу, що можна сміливо віднести до першої переваги методу розв’язку транспортної задачі. Навіть враховуючи те, що кількість варіантів дуже швидко ростиме зі збільшенням кількостей постачальників, споживачів, запасів та потреб, в багатьох випадках ЕОМ розв’яже задачу цим методом швидше, ніж людина – іншим методом. Зазначимо, що описаний алгоритм підрахунку кількості можливих варіантів є водночас і алгоритмом власне перебору цих варіантів.

Другою перевагою цього методу є те, що в ході перебору легко отримати не один, а всі оптимальні плани перевезень , для яких досягається спільне мінімальне значення вартості перевезень, які в свою чергу, для зручності аналізу можна згрупувати по кількості відмінних елементів.

Третьою суттєвою перевагою цього методу є його прозорість (порівняно з іншими методами) та можливість легкого програмування. Єдиним недоліком цього методу є те, що при великих розмірах матриці та великих значеннях обсягів потреб та запасів час роботи програми може складати кілька годин, хоча і такий час може бути виправданий, коли мова йде про конкретну практичну задачу.

1.6 Вибір методу розв’язку задачі

Так як симплекс-метод є універсальним, будь-яку задачу лінійного програмування можна з легкістю вирішити як за допомогою програмного забезпечення так і вручну, то для вирішення заданої задачі він підійде найкраще. За допомогою програми можна буде вирішувати велику кількість схожих задач.

    Опис метода розв’язку задачі

Нехай у задачі представлено n видів виробничої діяльності, інтенсивності використання котрих (шукані величини) складають 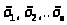. Для здійснення усіх видів виробничої діяльності є в наявності видів ресурсів, можливі обсяги споживання яких обмежені значеннями 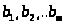. Витрати і-го ресурсу на одиницю продукції j-го виду виробництва дорівнюють 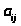. Тому сума, яка являє собою загальний обсяг і-го ресурсу, що використовується n видами виробництва, не може перевищувати величини .

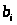Структура цільової функції відбиває внесок кожного виду виробничої діяльності в загальний результат. У випадку максимізації величина 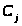являє собою прибуток від j-го виду виробничої діяльності на одиницю відповідної продукції, а у випадку мінімізації 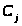характеризує питомі витрати. Зауважимо, що «корисність» деякого виду виробничої діяльності не можна встановити тільки за значенням відповідного коефіцієнта цільової функції, оскільки обсяг споживання обмежених ресурсів також є важливим чинником. Оскільки усі види виробничої діяльності, подані в моделі, претендують на використання обмежених ресурсів, відносна корисність деякого виду виробництва (у порівнянні з іншими видами виробничої діяльності) залежить як від величини коефіцієнта цільової функції , так і від інтенсивності споживання ресурсів 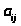. Тому можлива ситуація, коли через занадто великі витрати обмежених ресурсів деякий j-й вид виробничої діяльності, що характеризується високим прибутком, використовувати недоцільно (тобто в оптимальному розв’язку відповідна змінна виявиться небазисною).

В основі симплекс-методу є процес побудови початкової симплекс-таблиці, та перехід від однієї симплекс-таблиці до наступної згідно певних правил. Такі переходи виконуються доти, доки не буде виконано критерій оптимальності або не стане зрозумілим, що розв’язку не існує. Перехід від однієї симплекс-таблиці до наступної здійснюється наступним чином. Згідно певних критеріїв вибирається провідний елемент таблиці (b>k,l>), який стоїть на перетині рядка, який виводиться з базису, та стовпчика, який буде введено до базису. Елементи таблиці перераховуються так:

. (2.

)> >

Очевидним чином дану формулу можна спростити до наступної:

. (2.2)

тобто всі елементи нової таблиці матимуть вигляд a>i,j >/ x, де х – провідний елемент попередньої таблиці (зауваження: якщо дроби можна скоротити, то цього НЕ слід робити для правильності подальших міркувань).

Нехай тепер маємо симплекс-таблицю, що складається з цілих чисел (тобто коефіцієнти рівнянь цілі чи раціональні, що зводяться до цілих). Після першого кроку перетворень отримується така таблиця (провідний елемент дорівнює х):

Таблиця 2.1 – Симплекс-таблиця

¼

¼

¼

a/x

b/x

¼

¼

c/x

d/x

¼

¼

¼

Нехай на другому кроці провідним буде елемент d/x. Тоді елемент a/x перераховується за загальним правилом:

(2.3)

причому легко переконатися, що чисельник (ad-bc)/x буде цілим числом.

Отже, після другого кроку всі елементи знову мають загальний вигляд зі спільним знаменником, що дорівнює чисельнику провідного елемента попередньої таблиці. А в наступній таблиці чисельники будуть знову скорочуватись на цей знаменник і будуть цілими.

Якщо більш розгорнуто записати декілька переходів від однієї таблиці до іншої, то можна помітити, що числа у чисельниках та знаменниках є мінорами різних порядків, які складені з елементів початкової таблиці. Позначимо через > 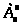> мінор, що складений з елементів перетину рядків зі стовпцями початкової таблиці. Сама таблиця матиме вигляд:

Таблиця 2.2 – Симплекс-таблиця

A>1>1

A>2>1

...

A>n>1

A>1>2

A>2>2

...

A>n>2

...

...

...

...

A>1>m

A>2>m

...

A>n>m

Процес переходу від попередньої таблиці до наступної взагалі спрощується: достатньо дописати номер рядка та стовпчика провідного елемента до всіх мінорів таблиці, що стоять у чисельниках, крім елементів того ж рядка, та до всіх мінорів знаменників (в початковій таблиці знаменник рівний одиниці).

Але слід звернути увагу на такий випадок: якщо провідний елемент опинився у тому ж рядку, що і раніше введений елемент, то “більш застарілий” слід викинути з мінору, а новий загальним чином дописати в кінець списку рядків та стовпчиків мінору відповідно. Звідси випливає, що рядки в мінорі не можуть повторюватись, тобто їх не може бути більше, ніж рівнянь обмежень, і мінори не будуть нескінченно розростатись. Але може зустрітися випадок, коли в списку стовпців, з яких складається мінор, зустрінуться однакові стовпці, тобто мінор рівний нулю. Це якраз відповідає нульовим елементам таблиці на відповідному кроці і вписується в загальне правило.

За допомогою даного методу можна набагато точніше обчислювати розв’язки задач лінійного програмування без накопичування похибки (при використанні комп’ютера), яка виникає при діленні. Цього можна досягти, якщо зберігати чисельники окремо, а знаменники взагалі завжди однакові.

    Розробка моделі розв’язку задачі

За умовою задачі необхідно знайти оптимальний варіант розподілу бюджету на різний вид реклами, завдяки якому він в результаті дав би найбільшій прибуток фірмі.

Для розрахунку здачі введемо деякі позначення:

- витрати бюджету фірми на телерекламу;

- витрати на рекламу по радіо;

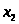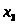- витрати на рекламу у газетах.

В результаті потрібно отримати прибуток, тому цільова функція буде максимізуватися. Завдяки досвіду минулих років, відомо, який прибуток буде отриманий фірмою, при витраті одного долара на різні види реклами, тому можна записати цільову функцію, вона матиме наступний вигляд:

(3.1)

За умовою задачі витрати не повинні перевищувати 10000, тому можемо записати перше обмеження:

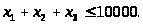(3.2)

Витрати на теле- та радіорекламу не повинна перевищувати шістдесят відсотків бюджетних коштів, тому можна записати друге обмеження:

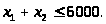(3.3)

За умовою витрати на газетну рекламу не повинні перевищувати більш як удвічі витрати на радіо рекламу:

(3.4)

Обов’язково потрібно врахувати наступні нерівності, адже вони суттєво вплинуть на розв’язок задачі:

(3.5)

Оскільки дана задача буде розв'язуватись симплекс методом, приведемо модель до вигляду, який буде зручним для використання симплекс методу. Всі вище записані обмеження об’єднаємо до системи і отримаємо:

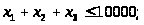
(3.6)

Для того, щоб розв’язати задачу симплекс-методом необхідно систему обмежень, яка містить нерівності, перетворити до системи рівнянь. Для цього введемо додаткові змінні . При використанні симплекс методу, цільова функція повинна мінімізуватися, для цього помножимо її на -1 та додамо додаткові змінні з відповідними коефіцієнтами. Тоді функція мети перетвориться до наступного вигляду:

(3.7)

Розв'язок цієї моделі наведений у розділі тестування даної курсової роботи.

    Розробка програмного забезпечення

В даному розділі розглянемо логічний опис та структуру програми, вхідні та вихідні дані, зробимо аналіз отриманих результатів.

      Призначення програми

Дана програма призначена для розв’язку задач лінійного програмування за допомогою симплекс методу. Вона дозволяє отримати швидкий розв’язок задачі за умови введення коректних даних та виконання умов використання програми. Програма виконує розв’язок задачі, обмеження якої задаються системою рівнянь. Можна розв’язувати задачі з різною кількістю змінних і знаходити як мінімум так і максимум функції мети.

4.2 Вибір середовища програмування

Microsoft Office є єдиним пакетом, встановленим на більшості комп'ютерів. Excel — це організатор будь-якого типа даних, будь вони числовими, текстовими або якими-небудь ще. Оскільки в цій програмі є багато вбудованих обчислювальних можливостей, більшість людей звертаються до Excel, коли потрібно створити таблиці для фінансових розрахунків, працювати із статистичними даними. За допомогою даної програми можна зробити свої звіти професіональнішими і виконати додаткове фінансування за допомогою красивих ділових презентацій. За допомогою даного пакету можна створювати різноманітні графіки і діаграми для більш наочного представлення результатів.

Excel — це великий охоронець списків (хоча їх прийнято називати в Excel базами даних) і творець таблиць. Тому Excel як не можна краще підходить для відстежування інформації про товари, що продаються, про обслуговуваних клієнтів, про службовців, яких контролює будь-яка організація і т.д.

Кожна одиниця інформації (ім'я, адреса, число продажів в місяць і ін.) займає свою власну клітинку в створюваній робочій таблиці. У кожній робочій таблиці 256 стовпців (з яких в новій робочій таблиці на екрані видно, як правило, тільки перші 10 або 11 (від А до J) і 65 536 рядків (з яких зазвичай видні тільки перші 15-20). Кожна нова робоча книга містить три чистих листа робочої таблиці.

Вся інформація, що поміщається в електронну таблицю, зберігається в окремих клітинках робочої таблиці. Але ввести інформацію можна тільки в поточну клітинку. За допомогою адреси в рядку формул і табличний курсор Excel вказує, який з 16 мільйонів клітинок робочої таблиці є поточним.

Excel є чудовим інструментом для виконання розрахунків по формулах, а також для зберігання інформації у вигляді списків і таблиць. Це дає можливість набагато спростити роботу із статистичними даними, які розраховуються по складних формулах. В програмі закладені багато груп формул, в тому числі і статистичні, або користувач сам може записати формулу.

Тому можна зробити висновок, що даний програмний пакет найкраще підходить для розв’язку задач лінійного програмування.

      Опис вхідних та вихідних даних

Дана програма написана в Excel. В ній задаються обмеження і значення цільової функції, які можна змінювати. Потім програма проводить розрахунки і в клітинках, яким попередньо були присвоєнні спеціальні імена, записує розв’язок функції мети і значення змінних, при яких цей оптимальний розв’язок був отриманий. Розглянемо всі введення даних детальніше.

Вхідними даними для даної задачі є виражені з обмежень значення кожної змінної та вираз для обчислення цільової функції. Значення змінних вводяться в поле «Ограничения» в меню інструменту Пошук розв'язку. Вираз значення цільової функції вводиться в комірку робочого аркуша.

Вихідними даними є значення кожної змінної та максимальне значення цільової функції, які будуть записані у визначених клітинках робочої таблиці.

      Розробка структури програми

Щоб отримати розв'язок задачі лінійного програмування за допомогою Excel потрібно виконати наступні дії:

1. В заданій задачі три змінних, тому клітинкам потрібно присвоїти імена відповідно - витрати на рекламу по телебаченню; - витрати на радіорекламу; - витрати на рекламу у газетах. Для цього викликаємо команду Вставка → Имя → Присвоить. У вікні, що появилося записуємо ім’я, яке хочемо присвоїти клітинці, для першої клітинки це буде , і натиснути Enter. Для двох решти клітинок, що залишилися виконуємо аналогічні дії у присвоєнні імені. Після цього у клітинці аналогічно, як і для змінних, присвоюємо ім’я 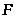, в ній програма запише розв’язок даної задачі (рисунок 4.4.1):

Рисунок 4.4.1 – Вікно для присвоєння імені для комірки цільової функції

    Після цього у цій же комірці записуємо формулу для обчислення значення цільової функції у наступному вигляді:

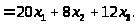
    Запускаємо програму. Спочатку натискаємо на вкладку Сервис, що знаходиться на панелі інструментів, і в меню, що появилося, вибираємо Поиск решения (рисунок 4.4.2):

Рисунок 4.4.2 – Заповнення вікна Поиск решения

В даному діалоговому вікні встановлюємо значення цільової клітинки 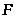та зазначаємо пошук максимуму цільової функції. Задаємо клітинки, в яких буде розв'язок даної задачі — діапазон клітинок від 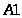до 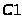. За допомогою кнопки Добавить додаємо обмеження у вигляді восьми обмежень (рисунок 4.4.3):

Рисунок 4.4.3 – Вікно для додавання обмежень

В меню Параметры відмічаємо, що модель лінійна (рисунок 4.4.4):

Рисунок 4.4.4 – Вікно для визначення параметрів

Натиснувши на кнопку Вьполнить отримуємо розв'язок задачі (рисунок 4.4.5):

Рисунок 4.4.5 – Розв’язок даної задачі

В комірках отримали відповідні значення , а в комірці максимальне значення цільової функції.

4.5 Розробка схеми алгоритму

На рисунку 4.5.1 приведена схема алгоритму програми:


Рисунок 4.5.1 – Схема алгоритму програми

4.6 Розробка тестів

У якості тесту будемо використовувати розв'язок задачі, отриманий вручну. Для цього отриману у третьому розділі даної роботи модель заносимо до симплекс таблиці (таблиця 4.6.1):

Таблиця 4.6.1 – Ітерація 1

1

1

1

1

0

0

10000

1

1

0

0

1

0

6000

0

2

-1

0

0

1

0

20

8

12

0

0

0

0

Знаходимо базисний елемент: шукаємо стовпчик з максимальним коефіцієнтом 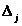і рядок з мінімальним відношенням /.

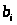Отриманий елемент є базисним елементом. Тепер змінну 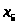виводимо з базису, а 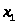вводимо в базис. Кожний елемент вибраного рядка ділимо на базисний елемент і перераховуємо таблицю за правилом прямокутника.

Елементи 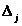перераховуємо за коефіцієнтами. Отримуємо симплекс-таблицю 4.6.2.

Таблиця 4.6.2 – Ітерація 2

0

0

1

1

-1

0

4000

1

1

0

0

1

0

6000

0

2

-1

0

0

1

0

0

-12

12

0

-20

0

-120000

Перевіряємо елементи рядка 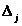. Оскільки вони всі не від’ємні і не нульові, продовжуємо розрахунок далі. Отримуємо базисний елемент. Перераховуємо таблицю, як було показано раніше. Отримуємо симплекс-таблицю 4.6.3.

Таблиця 4.6.3 – Ітерація 3

0

0

1

1

-1

0

4000

1

1

0

0

1

0

6000

0

2

0

1

-1

1

4000

0

-12

0

-12

-8

0

-168000

Як бачимо, всі елементи 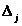від’ємні або дорівнюють нулю. Отже, знайдений розв’язок. Запишемо його у вигляді:

Значення змінних: .

Так як за умовою задачі необхідно було знайти максимум функції, але симплекс-метод дозволяє знайти лише мінімум і тому було попередньо змінено знак цільової функції, то отриманий розв’язок задачі знову потрібно помножити на -1, тому ми отримаємо наступне значення:

Цільова функція: .

4.7 Аналіз результатів тестування

Проаналізувавши отримані результати бачимо, що значення цільової функції однакове як при вирішені задачі вручну так i при обрахунку програми.

За звичай, при обрахунку вручну появляється деяка похибка, але в даній задачі цього не відбувається, так як числа за умовою досить прості і при обрахунку ніяких заокруглень не робимо, тому отримаємо точно такі самі значення, що і при розрахунку з використання програми.

4.8 Інструкція користувачеві

Для вирішення заданої задачі відкриваємо файл «Kursach.xls». Перед користувачем відкриється на перший погляд майже чистий лист робочої таблиці Excel, лише в комірці буде записаний нуль, але це не так. Потрібно натиснути на вкладку Сервис, що знаходиться на панелі інструментів, і в меню, що появилося, вибрати Поиск решения (див. рисунок 4.4.2). Потім у вікні, що появилося натиснути на кнопку Выполнить(див. рисунок 4.4.4) і програма все зробить сама.

Перед користувачем з’явиться розв’язок даної задачі у вигляді як це показано на рисунку 4.4.5.

При необхідності можна змінити цільову функцію і значення параметрів. Для того, щоб змінити цільову функцію необхідно в комірці ввести ту формулу, яку необхідно. А якщо необхідно змінити обмеження, то це можна зробити у вікні Поиск решения так, як це було описано у пункті 4.4.

Висновки

В процесі написання даної роботи я усвідомила різницю в трактуванні понять “модель” і “метод”, необхідність поглибленого оволодіння математичними та статистичними знаннями. Приведені в роботі приклади з застосуванням математичних моделей, на мою думку, досить добре проілюстрували весь процес прийняття рішення з боку даної методології.

Незалежно від обраної професії, незалежно від життєвої ситуації людина повинна приймати раціональне рішення. Для того щоб запобігти помилок і отримати необхідну користь, потрібно розуміти весь процес прийняття рішення. Отже стає зрозуміло, що методи науки управління підвищують якість рішень, що приймаються за рахунок використання наукового підходу, системної орієнтації та моделей.

Дана курсова робота складається з багатьох розділів, що дозволяють повність зрозуміти суть проблеми, зв’язаної з оптимізацією, а також розібратися з програмним забезпеченням, що вирішує задану задачу.

Метою виконаної курсової роботи є вирішення конкретної задачі та створення програми для обчислення даних. Робота виконана з детальним описом кожного з розділів. Також приведений опис аналітичного розв'язку задачі, та порівняння результатів з розрахунком вручну.

При розв’язку задачі як в ручну так і за допомогою програми було отримано значення цільової функції та значення шуканих змінних. Тобто визначивши всі витрати на рекламу, можна отримати максимальний прибуток фірмі.

Результатом виконання даної курсової роботи є розроблена програма у найпоширенішому програмного пакеті Excel, що вирішує задачу симплекс-методом та виводить результат.

Програму можна використовувати для розрахунку різних видів оптимізації і не тільки витрат, а інших коштів, що проходять через будь-яку організацію.

Література

    http://www.kgtu.runnet.ru/WD/TUTOR/lp/lp01.html#$lp01.1;

    http://semenets.by.ru/public/graphic.html;

    http://dl.sumdu.edu.ua/e-pub/mo/rus/m_simpl.html;

    http://www.kgtu.runnet.ru/WD/TUTOR/lp/lp05.html;

    http://dl.sumdu.edu.ua/e-pub/mo/rus/m_excel.html - Приклад розв’язку задач лінійного програмування в Excel;

    Гавриленко В., Пархоменко Л., "Решение задач аппроксимации средствами MS EXCEL", "Компьютеры+программы", №12/2002р., с.42.http://imcs.dvgu.ru/lib/nurmi/finmath/node42.html.

Додаток А

Міністерство освіти і науки України

Вінницький національний технічний університет

Інститут автоматики, електроніки і комп’ютерних систем управління

Факультет управління та комп’ютерних систем управління

Кафедра комп’ютерних систем управління

ТЕХНІЧНЕ ЗАВДАННЯ

на виконання курсової роботи на тему:

“ Розв’язок задач лінійного програмування ”

з дисципліни

“Математичне програмування та дослідження операцій”

Мета: Метою курсової роботи є розробка програмного забезпечення для розв’язку симплекс задачі

Для цього необхідно виконати наступні етапи:

1.1 Найменування та галузь застосування об’єкта розробки: Дана робота присвячена розробці програмного забезпечення для розв’язку симплекс задачі .

1.2 Підстава для проведення робіт: Підставою для розробки програмного забезпечення є навчальний план спеціальності 7.091401, робоча програма для

33

дисципліни “Математичне програмування та дослідження операцій”, індивідуальне завдання.

1.3 Дата початку роботи: “__” “______”2007р.

1.4 Дата закінчення роботи: “__” “_______”2007р.

1.5 Мета призначення розробки: Метою даної роботи є розробка програмного забезпечення для автоматизації роботи симплекс задачі.

1.6 Вимоги до надійності: Надійність даного проекту забезпечується використанням структурного програмування; а також тим, що програма працює під керівництвом єдиного меню; в ній передбачені переривання, тобто програма реагує на невірні дії користувача, вказуючи на дії, які необхідно виконати.

Все програмне забезпечення та супроводжуюча техніка документація повинні задовольняти наступним ГОСТам:

ГОСТ 19.701-90

ІСО 5807 – 85 ГОСТ на розробку програмних документів, схем, алгоритмів програм, даних та систем.

ГОСТ 19.781 – 74 – Вимоги до розробки програмного забезпечення

ГОСТ 19.101-77(СТ СЭВ 1626 - 79) – Держстандарт на розробку програмної документації, видів програм та програмних документів.

ГОСТ 29.401-78- Текст програми. Вимоги до змісту та оформлення.

ГОСТ 19.106-78- Вимоги до програмної документації.

ГОСТ 7.1- 84 та ДСТУ 3008- 95- Розробка технічної документації.

1.7 Стадії та етапи розробки:

1. Уточнення постановки задачі та розробка технічного завдання на виконання курсової роботи “Розв’язок симплекс задачі” (до 14.09.07).

2. Варіантний аналіз існуючих методів розв’язання поставленої задачі та вибір програмного середовища для вирішення задачі курсової роботи “Розв’язок симплекс задачі” (до28.09.07).

3. Розробка структури програми та наповнення файлів бази даних для розв’язку симплекс задачі (до 12.10.07).

34

4. Розробка програмного забезпечення для розв’язку симплекс задачі (до 2.11.07).

5. Розробка інтерфейсу , планування, тестування розробленої програми та створення бази даних для розв’язку симплекс задачі (до 20.11.07).

6. Демонстрація програмного забезпечення для розв’язку симплекс (до 30.11.07).

7. Розробка пояснювальної записки (до 7.12.07).

8. Захист курсової роботи (до 21.12.07).

1.8 Вимоги до безпеки: Розроблене програмне забезпечення повинно відповідати сучасним вимогам СНІП та ДЕСТів до робочого місця операторів ЕОМ.