Решение финансовых задач при помощи Microsoft Excel
Лабораторная работа № 1 Вариант № 6
Задание:
Управляющему банком были представлены 4 проекта, претендующие на получение кредита в банке. Ресурс банка в каждый период, потребности проектов и прибыль по ним приведены в таблице (тыс. долл.).
|
Проект |
Потребность проекта в объемах кредитов |
Прибыль |
|||
|
Период 1 |
Период 2 |
Период 3 |
Период 4 |
||
|
А |
8 |
8 |
10 |
10 |
21 |
|
Б |
7 |
9 |
9 |
11 |
18 |
|
В |
5 |
7 |
9 |
11 |
16 |
|
Г |
9 |
8 |
7 |
6 |
17,5 |
|
Ресурс банка |
22 |
25 |
38 |
30 |
При выборе проектов следует принять во внимание потребность проектов в объемах кредитов и ресурс банка для соответствующих периодов.
Какие проекты следует финансировать, если цель состоит в том, чтобы максимизировать прибыль?
Математическая модель:
Введем по числу проектов переменную X>i>, где i= А, Б, В, Г. переменная X>i>=1, ели проект с номером i будет финансироваться и X>i>=0- не будет финансироваться.
Целевая функция:
max (21x>1>+18 x>2>+16 x>3>+17,5 x>4>)
Ограничения:
Период 1
8 x>1>+7 x>2>+5 x>3>+9 x>4 >≤22
Период 2
8 x>1>+9 x>2>+7 x>3>+8 x>4 >≤25
Период 3
10 x>1>+9 x>2>+9 x>3>+7 x>4 >≤38
Период 4
10 x>1>+11 x>2>+11 x>3>+6 x>4 >≤30
Условие отрицательности:
x>1,2,3,4 >≥ 0
Найти max (21x>1>+18 x>2>+16 x>3>+17,5 x>4>)
 Создаем
форму для ввода условий задачи в Microsoft
Excel:
Создаем
форму для ввода условий задачи в Microsoft
Excel:
Введем исходные данные:

Введем зависимость для целевой функции:
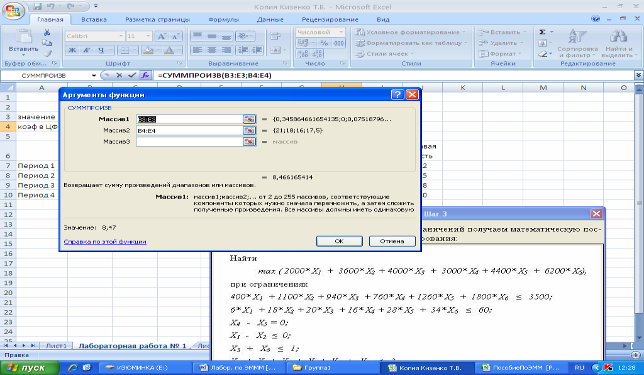
Введем зависимость для ограничений:

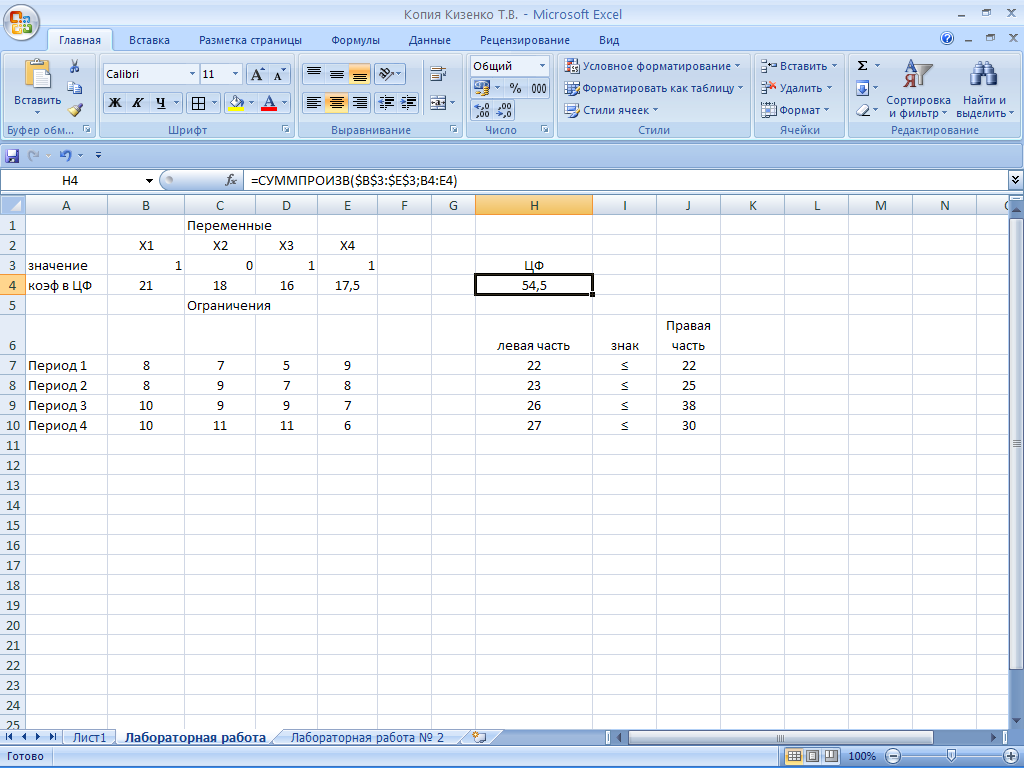
Вывод: В результате решение рассматриваемой задачи получено оптимальное решение, указывающее, что целесообразно финансировать проекты А и В.
Целевая функция (ожидаемая прибыль) = 54,5 тыс.долл
Лабораторная работа № 2 Вариант № 6
Задание: В распоряжении некоторой компании имеется 6 торговых точек и 6 продавцов. Из прошлого опыта известно, что эффективность работы продавцов в различных торговых точках неодинакова. Коммерческий директор компании произвел оценку деятельности каждого продавца в каждой торговой точке. Результаты этой оценки представлены в таблице.
|
Продавец |
Объемы продаж по торговым точкам, USD/тыс.шт. |
|||||
|
I |
II |
III |
IV |
V |
VI |
|
|
A |
66 |
72 |
75 |
- |
75 |
69 |
|
B |
56 |
60 |
58 |
63 |
61 |
59 |
|
C |
35 |
38 |
40 |
45 |
25 |
27 |
|
D |
40 |
42 |
47 |
45 |
53 |
36 |
|
E |
62 |
70 |
68 |
67 |
69 |
70 |
|
F |
65 |
63 |
69 |
70 |
72 |
68 |
(Назначение первого продавца на четвертую торговую точку недопустимо по медицинским показателям, т.е. в матрице объемов продаж проставлен запрет – «-».)
Как коммерческий директор должен осуществить назначение продавцов по торговым точкам, чтобы достичь максимального объема продаж?
Математическая модель:
X>ij> – факт назначения или не назначения i-го продавца на j-ый объем продаж по торговой точке
I= 1, 2, 3, 4, 5, 6
J= 1, 2, 3, 4, 5, 6
X>ij >=1, если i-ый продавец назначен на j-ый объем продаж по торговой точке, и равен 0, если i-ый продавец не назначен на j-ый объем продаж по торговой точке
Найти
max(68x>11>+72 x>12>+75 x>13>+0 x>14>+75 x>15>+69 x>16>+56 x>21>+60 x>22>+58 x>23>+63 x>24>+61 x>25>+59 x>26>+35 x>31>+38 x>32>+40 x>33>+45 x>34>+25 x>35>+27 x>36>+40 x>41>+42 x>42>+47 x>43>+45 x>44>+53 x>45>+36 x>46>+62 x>51>+70 x>52>+68 x>53>+67 x>54>+69 x>55>+70 x>56>+65 x>61>+63 x>62>+69 x>63>+70 x>64>+72 x>65>+68 x>66>)
При ограничениях
x>11> +x>12>+ x>13>+ x>14>+ x>15>+ x>16>≤1
x>21> +x>22>+ x>23>+ x>24>+ x>25>+ x>26>≤1
x>31> +x>32>+ x>33>+ x>34>+ x>35>+ x>36>≤1
x>41> +x>42>+ x>43>+ x>44>+ x>45>+ x>46>≤1
x>51> +x>52>+ x>53>+ x>54>+ x>55>+ x>56>≤1
x>61> +x>62>+ x>63>+ x>64>+ x>65>+ x>66>≤1
x>11> + x>21>+ x>31>+ x>41> + x>51>+ x>61>=1
x>12>+x>22>+ x>32>+ x>42>+ x>52>+ x>62>=1
x>13> +x>23>+ x>33>+ x>43>+ x>53>+ x>63>=1
x>14> +x>24>+ x>34>+ x>44>+ x>54>+ x>64>=1
x>15> +x>25>+ x>35>+ x>45>+ x>55>+ x>65>=1
x>16> +x>26>+ x>36>+ x>46>+ x>56>+ x>66>=1
Введем исходные данные:

Введем зависимость для ограничений:
