Расчет структурной надежности системы (работа 1)
Федеральное агентство по образованию РФ
ГОУ ВПО "Российский химико-технологический университет
им. Д.И. Менделеева"
Новомосковский институт (филиал)
Кафедра "ВТИТ"
Предмет "Надежность, эргономика, качество"
Расчетное задание
"РАСЧЕТ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМЫ"
Вариант № 39
Студент: Голубков Д.С.
Группа: АС-05-2
Преподаватель: Прохоров В.С.
Новомосковск, 2009 год
Исходные данные
По структурной схеме надежности
технической системы в соответствии с
вариантом задания, требуемому значению
вероятности безотказной работы системы
и значениям интенсивностей отказов ее
элементов
(табл.6.1) требуется:
1. Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 - 0.2.
2. Определить
- процентную наработку технической
системы.
3. Обеспечить увеличение
- процентной наработки не менее, чем в
1.5 раза за счет:
а) повышения надежности элементов;
б) структурного резервирования элементов системы.
Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.
На схемах обведенные пунктиром m элементов являются функционально необходимыми из n параллельных ветвей.
Вариант 39
|
№ |
, |
Интенсивности отказов элементов, , x10-6 1/ч |
||||||||||||||
|
вар. |
% |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
39 |
90 |
8.0 |
3.0 |
5.0 |
2.0 |
Выполнение
1. В исходной схеме элементы 2 и 3 образуют
параллельное соединение. Заменяем их
квазиэлементом А. Учитывая, что
,
получим
.
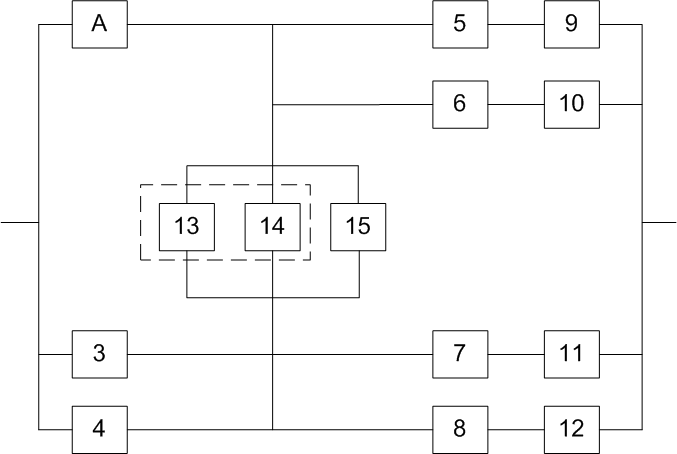
2. Элементы 3 и 4 также образуют параллельное
соединение, заменив которое элементом
В и учитывая, что
,
получим
3. Элементы 5 и 9 исходной схеме соединены
последовательно. Заменяем их элементом
С1
.
4. Элементы 6 и 10 исходной схеме соединены
последовательно. Заменяем их элементом
С2
.
5. Элементы С1 и С2 с параллельным
соединением заменяем элементом С,
причем, так как
,
то
6. Так как
,
то заменяем элементы 7, 8, 11, 12 элементом
D, равным элементу С.
7. Элементы 13, 14 и 15 образуют соединение
“2 из 3”, которое заменяем элементом E.
Так как
,
то для определения вероятности безотказной
работы элемента E можно
воспользоваться методом прямого
перебора:
|
№ состояния |
Состояние элемента |
Состояние системы |
Вероят. состояния системы |
||
|
1 |
2 |
3 |
|||
|
1 |
+ |
+ |
+ |
+ |
|
|
2 |
+ |
+ |
- |
+ |
|
|
3 |
+ |
- |
+ |
||
|
4 |
- |
+ |
+ |
||
|
5 |
+ |
- |
- |
|
|
|
6 |
- |
+ |
- |
||
|
7 |
- |
- |
+ |
||
|
8 |
- |
- |
- |
- |
|
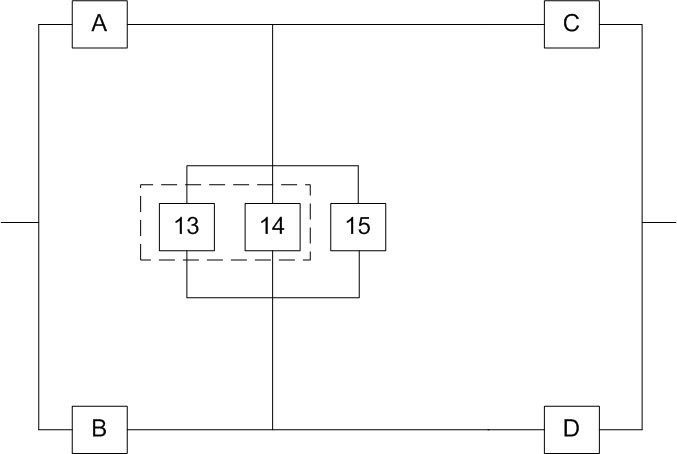
8. Элементы A, B, C, D и Е образуют мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента, в качестве которого выберем элемент E. Тогда
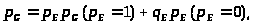(7.7)
где
- вероятность безотказной работы
мостиковой схемы при абсолютно надежном
элементе E:
- вероятность безотказной работы
мостиковой схемы при отказавшем элементе
E:.
9. Таблица 1.
|
Элемент |
i, |
Наработка t, x 106 ч |
|
|
|
|
|
|
|
|
x10-6 ч-1 |
0,01 |
0,03 |
0,05 |
0,07 |
0,09 |
0,11 |
0,13 |
|
1,2,3,4 |
8 |
0,923116347 |
0,78662786 |
0,67032 |
0,57121 |
0,48675 |
0,41478 |
0,35345 |
|
5,6,7,8 |
3 |
0,970445534 |
0,91393119 |
0,86071 |
0,81058 |
0,76338 |
0,71892 |
0,67706 |
|
9,10,11,12 |
5 |
0,951229425 |
0,86070798 |
0,7788 |
0,70469 |
0,63763 |
0,57695 |
0,52205 |
|
13,14,15 |
2 |
0,980198674 |
0,94176453 |
0,90484 |
0,86936 |
0,83527 |
0,80252 |
0,77105 |
|
A, B |
- |
0,994088904 |
0,95447233 |
0,89131 |
0,81614 |
0,73658 |
0,65752 |
0,58198 |
|
C1, С2 |
- |
0,923116347 |
0,78662786 |
0,67032 |
0,57121 |
0,48675 |
0,41478 |
0,35345 |
|
C,D |
- |
0,994088904 |
0,95447233 |
0,89131 |
0,81614 |
0,73658 |
0,65752 |
0,58198 |
|
E |
- |
0,99883925 |
0,99022089 |
0,97456 |
0,95326 |
0,92753 |
0,89841 |
0,86675 |
|
P |
- |
0,999930039 |
0,99582183 |
0,97604 |
0,93143 |
0,86058 |
0,76887 |
0,66528 |
|
1-4` |
5,267 |
0,94869303 |
0,85384124 |
0,76847 |
0,69164 |
0,62249 |
0,56025 |
0,50424 |
|
5-12` |
2,634 |
0,974003872 |
0,92402144 |
0,8766 |
0,83162 |
0,78894 |
0,74846 |
0,71005 |
|
P` |
- |
0,999986125 |
0,99907896 |
0,99413 |
0,98131 |
0,95763 |
0,92166 |
0,87367 |
|
A``,B``,C``,D`` |
|
0,999965059 |
0,99792723 |
0,98819 |
0,96619 |
0,93061 |
0,88271 |
0,82526 |
|
P`` |
|
0,999999792 |
0,99990038 |
0,99854 |
0,99234 |
0,97561 |
0,94263 |
0,89007 |
|
Элемент |
|
|
|
|
|
|
|
T и P |
T, P`, P`` |
|
|
0,15 |
0,17 |
0, 19 |
0,21 |
0,23 |
0,25 |
0,27 |
0,07973804 |
0,11960706 |
|
1,2,3,4 |
0,30119 |
0,25666 |
0,21871189 |
0,18637 |
0,15881743 |
0,135335286 |
0,115325124 |
0,528398622 |
0,384098415 |
|
5,6,7,8 |
0,63763 |
0,6005 |
0,565525442 |
0,53259 |
0,50157607 |
0,472366556 |
0,44485807 |
0,787246301 |
0,698499248 |
|
9,10,11,12 |
0,47237 |
0,42741 |
0,386741027 |
0,34994 |
0,31663677 |
0,286504801 |
0,259240264 |
0,671198609 |
0,54989095 |
|
13,14,15 |
0,74082 |
0,71177 |
0,683861412 |
0,65705 |
0,63128365 |
0,606530663 |
0,582748256 |
0,852590363 |
0,787246301 |
|
A, B |
0,51167 |
0,44745 |
0,38958889 |
0,33801 |
0,29241188 |
0,252354932 |
0,217350363 |
0,777592141 |
0,620665238 |
|
C1, С2 |
0,30119 |
0,25666 |
0,21871189 |
0,18637 |
0,15881743 |
0,135335286 |
0,115325124 |
0,528398622 |
0,384098415 |
|
C,D |
0,51167 |
0,44745 |
0,38958889 |
0,33801 |
0,29241188 |
0,252354932 |
0,217350363 |
0,777592141 |
0,620665238 |
|
E |
0,8333 |
0,79866 |
0,763361241 |
0,72782 |
0,69240002 |
0,657378008 |
0,622989184 |
0,941217502 |
0,883467816 |
|
P |
0,55912 |
0,45797 |
0,36686319 |
0,28833 |
0,22298245 |
0,170111991 |
0,128305675 |
0,900000031 |
0,719996796 |
|
1-4` |
0,45382 |
0,40845 |
0,367610991 |
0,33086 |
0,29777712 |
0,268004908 |
0,241209366 |
0,657059795 |
0,532607577 |
|
5-12` |
0,67361 |
0,63905 |
0,606251723 |
0,57514 |
0,54562683 |
0,517627197 |
0,491064403 |
0,810559933 |
0,72975604 |
|
P` |
0,81533 |
0,74925 |
0,678456118 |
0,60595 |
0,53436478 |
0,46583755 |
0,401900718 |
0,971261919 |
0,900037955 |
|
A``,B``,C``,D`` |
0,76153 |
0,69468 |
0,627398277 |
0,56177 |
0,49931906 |
0,441026853 |
0,387459546 |
0,950534744 |
0,856105138 |
|
P`` |
0,81835 |
0,73158 |
0,636087979 |
0,53872 |
0,4454249 |
0,360448125 |
0,286218627 |
0,985888039 |
0,919896102 |
10. График 1
P-вероятность безотказной работы исходной системы
P` - вероятность безотказной работы системы с повышенной надежностью
P`` - вероятность безотказной работы системы со структурным резервированием
По графику находим время, где вероятность безотказной работы исходной системы равна 90%, это 79738,04 ч.
11. Расчет показывает (таблица 1), что наименьшее значение вероятности безотказной работы имеют элементы A,B,C,D. Поэтому увеличение надежности работы этих элементов даст наибольшие увеличение надежности всей системы в целом.
Для того чтобы система при
ч система в целом имела вероятность
безотказной работы
,
необходимо, чтобы элементы A,B,C,D
имели вероятность безотказной работы
найденную из формулы.
Т. к.
,
то
,
решив данное уравнение в Excel
получим.
=
0,781502
A,B,C,D являются квазиэлементами, найдем вероятности элементов:
Т. к. в уравнении появились 2 неизвестные,
и
будем считать равными.
Т. к. по условию все элементы работают в периоде нормальной эксплуатации и подчиняются экспотенциальному закону, то
λ1-4=5,267
λ5-12=2,634
Для увеличения γ-% наработки, необходимо снизить интенсивность отказов элементов 1, 2, 3, 4 в 1,519 раза, элементов 5,6,7,8 в 1,139 раза, элементов 9, 10, 11, 12 в 1,898 раза.
12. Увелим вероятность безотказа исходной системы методом структурного резервирования, выбирая те же элементы, что и в предыдущем случае. Для повышения надежности, добавляем следующие элементы:
Где элементы A,B,C,D,F,G,H равны.
Вновь упростив схему до мостиковой, и
подставив в формулу
новые значения, посчитаем с помощью Excel γ-% наработку, при заданном времени.
Из Таблицы 1 видно, что при 119607,06 часах работы, вероятость безотказной работы будет равна ≈ 92%, что нас устраивает.
Таким образом образом для увеличения надежности системы, нужно ввести следующие элементы:
1=2=3=4=20=21
5=6=16=18=7=8=22=24
9=10=17=19=11=12=23=25
13=14=15
Анализ зависимостей вероятностей безотказной работы показал, что способ структурного резервирования предпочтительнее, т.к в период наработки до 119607,06 часов вероятность безотказной работы системы при структурном резервировании выше, чем при увеличении надежности элементов. С точки зрения технической реализации системы, метод структурного резервирования также предпочтительнее, т.к не всегда технически возможно увеличить надежность элемента.