Разработка программы поиска решения системы дифференциальных уравнений двумя методами: Рунге-Кутта и Рунге-Кутта-Мерсона
Введение
В курсовой работе в соответствии с заданием на проектирование решается задача разработки программы поиска решения системы дифференциальных уравнений двумя методами: Рунге-Кутта и Рунге-Кутта-Мерсона.
В данной пояснительной записке проводится описание последовательности шагов по составлению программы на алгоритмическом языке Turbo Pascal. Рассматриваются вопросы математической формулировки и алгоритмизации задачи, разработки блок-схемы алгоритма её решения, составления исходной Pascal-программы и реализации вычислений по составленной программе.
Выбор метода вычисления, обращение к справке по программе и выход из программы обеспечивается с помощью специального меню. Ввод исходных данных и вывод результатов вычисления выполняется в отдельном для каждого метода вычислений окне.
В пояснительной записке приводится также сравнения точности вычислений корней системы уравнений использованными методами.
1. Постановка задачи
Ставится задача составить программу решения системы дифференциальных уравнений:
 (1)
(1)
Требуется найти решение системы дифференциальных уравнений (1) методом Рунге-Кутта и методом Рунге-Кутта-Мерсона. Выбор метода решения посредствам меню, при помощи клавиш управления курсором.
Таким образом, программа должна обеспечивать возможность:
выбора пользователем численного метода поиска решения системы дифференциальных уравнений;
предоставить пользователю возможность получить краткую справку о программе;
вывода результатов вычисления на дисплей в удобном для восприятия виде.
В результате сформулируем следующую задачу по созданию программы:
вид системы дифференциальных уравнений должен задаваться в подпрограмме – процедуре;
вид правой части уравнений должен задаваться в подпрограмме – функции;
программа после загрузки должна выводить на дисплей исходное окно-заставку, в которой отображаются общие сведения о статусе программы и её авторе;
после выполнения указанной в строке подсказки процедуры перехода должно выводиться вертикальное меню с пунктами: «Справка», «Метод Рунге-Кутта», «Метод Рунге-Кутта-Мерсона» и «Выход»
при выборе в меню пункта «Справка» должна выводиться краткая справка о назначении программы;
после выбора в меню варианта численного метода должно открываться отдельное окно, в котором будут вводиться начальные условия и выводиться результат поиска выбранным методом;
при выборе пункта меню «Выход» программы должна завершать работу.
2. Математическая формулировка задачи
Задача Коши заключается в решении систем обыкновенных дифференциальных уравнений (1) первого порядка, представляемых в виде:
 (1.1)
(1.1)
Где j=1 N-номер
каждой зависимой переменной y>j>,
x-независимая
переменная .
N-номер
каждой зависимой переменной y>j>,
x-независимая
переменная .
Решение системы (1.1) при заданных начальных условиях x=x>0>, y>1>(x>0>)=y>10>,…,y>2>(x>0>)=y>20>, y>N>(x>0>)=y>N>>0> сводиться к нахождению зависимостей (интегральных кривых) y>1>(x),…,y>2>(x), y>N>(x), проходящих через точки (x>0>,y>10>), (x>0>,y>20>),…, (x>0>,y>N>>0>). Задача Коши сводиться к интегрированию дифференциальных уравнений. Порядок метода численного интегрирования при этом определяется и порядок метода решения (1).
2.1 Метод Рунге-Кутта
Этот метод является наиболее
распространенным методом решения систем
(1.1) при шаге h=const.
Его достоинством является высокая
точность-погрешность
 - и меньшая склонность к возникновению
неустойчивости решения. Алгоритм
реализации метода заключается в
циклических вычислениях Y>j>>(>>i>>+1)>
на каждом i+1
шаге по следующим формулам:
- и меньшая склонность к возникновению
неустойчивости решения. Алгоритм
реализации метода заключается в
циклических вычислениях Y>j>>(>>i>>+1)>
на каждом i+1
шаге по следующим формулам:
 (2)
(2)

 (3)
(3)
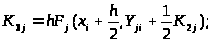 (4)
(4)
 (5)
(5)
 (6)
(6)
При переходе от одной формулы к другой задаются или вычисляются соответствующие значения x и Y>j>> >и находятся по подпрограмме значения функции F>j>(x,Y>j>).
2.2 Метод Рунге-Кутта-Мерсона
Автоматическое изменение шага
в ходе решения систем дифференциальных
уравнений необходимо, если решение
требуется получить с заданной точностью.
При высокой точности (погрешность
 )
и решении в виде кривых с сильно
различающейся крутизной автоматическое
изменение шага обеспечивает уменьшение
общего числа шагов в несколько раз,
резко уменьшается вероятность числовой
неустойчивости, даёт более равномерное
расположение точек графика кривых
(решений) при их выводе на печать. Данный
метод обеспечивает приближённую оценку
погрешностей на каждом шаге интегрирования.
Погрешность интегрирования имеет
порядок h5.
Этот метод реализуется
следующим алгоритмом: Задаём число
уравнений N,
погрешность ε=E,
начальный шаг интегрирования h=H
и начальное значение
y>10>,…,y>N>>0>.
С помощью пяти циклов с управляющей
переменной J=1,2,..,N
вычисляем коэффициенты:
)
и решении в виде кривых с сильно
различающейся крутизной автоматическое
изменение шага обеспечивает уменьшение
общего числа шагов в несколько раз,
резко уменьшается вероятность числовой
неустойчивости, даёт более равномерное
расположение точек графика кривых
(решений) при их выводе на печать. Данный
метод обеспечивает приближённую оценку
погрешностей на каждом шаге интегрирования.
Погрешность интегрирования имеет
порядок h5.
Этот метод реализуется
следующим алгоритмом: Задаём число
уравнений N,
погрешность ε=E,
начальный шаг интегрирования h=H
и начальное значение
y>10>,…,y>N>>0>.
С помощью пяти циклов с управляющей
переменной J=1,2,..,N
вычисляем коэффициенты:
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
Находим (в последнем цикле) значение (12)
 (12)
(12)
И погрешность
 (13)
(13)
Проверяем выполнения условий
 (14)
(14)
 (15)
(15)
Если условие (14) не выполняется, то делим шаг h на 2 и повторяем вычисления. Если это условие выполняется и выполняется условие (15), значение x>i>>+1>=x>i>+h и Y>j>>(>>i>>+1)>, то считаем, что решение системы дифференциальных уравнений найдено с заданной точностью. Если условие (15) не выполняется , шаг h увеличивается вдвое и вычисления повторяются.
3. Алгоритмизация задачи
В соответствии с постановленной в разделе 2 задачей целесообразно реализовать алгоритм, использующий обращение к соответствующим подпрограммам из головной программы.
Алгоритм работы головной программы следующий:
Скрыть курсор с использованием подпрограммы - процедуры скрытия курсора и вывести в специальном окне заставку программы, содержащую сведения о назначении программы, исполнителе и руководителе курсовой работы, а также подсказку для пользователя о последующих действиях, с использованием подпрограммы - процедуры заставки.
Запустить подпрограмму-процедуру вертикального меню при нажатии любой клавиши с использованием подпрограмм-процедур построения окна, вывода рамки окна и скрытия курсора.
Запустить подпрограмму-процедуру справки и вывести в специальном окне справочные сведения о работе с программой при выборе пункта меню «Справка» с использованием строки-подсказки о возврате в меню.
Запустить подпрограмму-процедуру поиска решения системы дифференциальных уравнений методом Рунге-Кутта при выборе пункта меню «Метод Рунге-Кутта» с использованием включения курсора, а также строки-подсказки о возврате в меню.
Запустить подпрограмму-процедуру поиска решения системы дифференциальных уравнений методом Рунге-Кутта-Мерсона при выборе пункта меню «Метод Рунге-Кутта-Мерсона» с использованием включения курсора, а также строки-подсказки о возврате в меню.
Завершить работу программы при выборе пункта меню «Выход».
Алгоритм поиска решения системы уравнения методом Рунге-Кутта в подпрограмме-процедуре runkut включает следующие шаги:
Создать окно для ввода исходных данных и вывода результатов вычисления.
Восстановить отображение курсора нормального размера соответствующей подпрограммой - процедурой.
Задать начальный шаг-h и начальные значение x>о>,y>10>,…,y>N>>0> .
В подпрограмме-функции задаём вид правой части уравнений.
В подпрограмме-процедуре задаём вид системы дифференциальных уравнений.
Организовать цикл для поиска коэффициентов погрешности по формулам (2-5)
По формуле (6) найти решение системы дифференциальных уравнений.
Вывести результаты вычислений в том же окне.
Вывести в окне запрос о продолжении вычислений с новыми исходными данными.
Выполнить анализ кода нажатой в ответ на запрос клавиши: при нажатии “Y” повторить ввод снова, при нажатии “N” перейти в окно с меню.
Алгоритм поиска решения системы уравнений методом Рунге-Кутта-Мерсона в подпрограмме процедуре rukutm включает:
Создание окно для ввода исходных данных и вывода результатов вычисления.
Восстановления отображение курсора нормального размера соответствующей подпрограммой - процедурой.
Задание начального шаг-h, начальных значений x>о>,y>10>,…,y>N>>0> и точности вычисления- ε.
Подпрограмме-процедуре задаём вид системы дифференциальных уравнений
В подпрограмме-функции задаём вид правой части уравнений
С помощью пяти циклов с управляющей переменной J=1,N вычисляем коэффициенты по формулам (7)-(11).
В последнем цикле находим решение системы дифференциальных уравнений по формуле (12) и погрешность по формуле (13).
Проверка выполнение условий (14) и (15). Если первое условие не выполняется то h:=h/2 и переходим к п.5.
Если выполняются оба условия, то значение x>i>>+1>=x>i>+h и Y>j>>(>>i>>+1)> выводим на экран.
Если второе условие не выполняется, то h:=h+h и переходим к п.5.
Вывести результаты вычислений в том же окне.
Вывести в окне запрос о продолжении вычислений с новыми исходными данными.
Выполнить анализ кода нажатой в ответ на запрос клавиши: при нажатии “Y” пoвторить ввод снова , при нажатии “N” перейти в окно с меню.
4. Идентификаторы программы
Для указания соответствия обозначений переменных в формулах математической формулировки и их идентификаторов в программе сведем их в таблицу 1:
Таблица 1
|
Обозначение параметров |
Смысл параметра |
|
|
В формулах |
В программе |
|
|
Y>1…>Y>n> |
Y[1]…Y[n] |
Начальные приближения |
|
ε |
E |
Точность результата |
|
h |
H |
Шаг интегрирования |
|
К>ij> |
K[j] |
Коэффициенты погрешности |
|
N |
n |
Количество уравнений |
|
|
F[1] |
Первое уравнение системы |
|
|
F[2] |
Второе уравнение системы |
Остальные идентификаторы являются промежуточными или служебными.
5. Блок-схема алгоритма
5.1 Блок-схема алгоритма головной программы

Нет Да
# 72 #80
72 #80
Да Нет Да Нет
5.2 Блок-схема алгоритма подпрограммы–процедуры runkut

























 j
j








Д
 а Нет
а Нет


Д
 а
а




j:=1,2



 Нет
Нет




j







j:=1,2
5.3 Блок-схема алгоритма подпрограммы–процедуры rukutm





e[j]:=f[j]*H; y[j]:=W[j]+(a[j]+4*d[j]+e[j])/6; e2:= abs(-2*a[j]+9*c[j]-8*d[j]+e[j])/30;








Н















 ет Да
ет Да

Н


 ет Да
ет Да
e3:=0;
d2:=d2+1
Д
 а
Нет
а
Нет














j:=1,2





 j
j





j

j:=1,2

















 j
j

J:=1,2
Д а
а


Нет
5.4 Блок-схема подпрограммы–процедуры moymenu

5.5 Блок-схема подпрограммы–процедуры ur

5.6 Блок-схема подпрограммы–функции f1

5.7 Блок-схема подпрограммы– функции f2

5.8 Блок-схема подпрограммы–процедуры CursorSize

5.9 Блок-схема подпрограммы–процедуры HiddeCursor

5.10 Блок-схема подпрограммы–процедуры NormCursor

5.9 Блок-схема подпрограммы–процедуры Spravka

5.10 Блок-схема подпрограммы–процедуры Zastavka

6. Текст исходной программы
program Kursovoy;
Uses CRT, DOS;
Const N=2;
Label 11;
Type
mas=Array[1..4] of String[60];
Const
menu:mas= ('Справка ',
'Метод Рунге-Кутта ',
'Метод Рунге-Кутта-Мерсона',
'Выход ' );
var
i,s,p:integer;
h,v,x,e1,e2,e3 : real;
y,w,k,f,e,a,c,d:array[1..10] of real;
j,d2:integer;
k2:byte;
stop:boolean;
eps,dx,dy,x0,y0:real;
f11,f22:real;
c1,kod,k10:Char;
pass:string;
ch:char;
function f1 (x1,y1,y2:real):real;
begin
f1:=y1+y2-x1*x1+x1-2;
end;
function f2(x1,y1,y2:real):real;
begin
f2:=-2*y1+4*y2+2*x1*x1-4*x1-7;
end;
procedure ur;
begin
f[1]:=f1(x,y[1],y[2]);
f[2]:=f2(x,y[1],y[2]);
end;
Procedure CursorSize(Size:word);
var
Regs: Registers;
begin
With Regs do
begin
AH:=$01;
CH:=Hi(size);
Cl:=Lo(Size);
intr($10,Regs);
end;
end;
procedure HiddeCursor;
begin
CursorSize($2000);
end;
Procedure NormCursor;
begin
CursorSize($0607);
end;
Procedure ramka (x1,y1,x2,y2:byte);
const
a=#201;
b=#205;
c=#187;
d=#186;
e=#188;
f=#200;
begin
TextColor(15);
TextBackground(4);
Clrscr;
GoToxy(x1,y1);
write(a);
for i:=x1+1 to x2-1 do write(b);
write(c);
for i:=y1+1 to y2-1 do
begin
gotoxy(x1,i);
write(d);
Gotoxy(x2,i);
write(d);
End;
GoToxy(x1,y2);
write(f);
for i:=x1+1 to x2-1 do write(b);
write(e);
End;
Procedure Okno(x1,y1,x2,y2,Fcolor,Tcolor:byte);
Begin
Clrscr;
TextMode(3);
HiddeCursor;
Ramka(x1,y1,x2,y2);
Window(x1+1,y1+1,x2-1,y2-1);
TextBackground(Fcolor);
TextColor(Tcolor);
Clrscr;
Gotoxy(1,1);
End;
Procedure Zastavka;
begin
Okno(1,1,79,23,3,15);
GoToXY(3,1);
writeln(' ');
Writeln(' Министерство образования Республики Беларусь');
Writeln(' Белорусский национальный технический университет');
GoToXY (1,6);
writeln(' Программа решения системы дифференциальных уравнений ');
writeln;
writeln;
writeln;
writeln;
writeln(' Курсовая работа ');
writeln(' по дисциплине "Информатика" ');
GoToXY(1,15);
Writeln(' Исполнитель: Неверовская Я.Б') ;
writeln(' гр.102826 ');
writeln(' Руководитель: Петренко С.М.');
writeln;
writeln;
writeln(' Минск 2008');
Window(0,0,80,25);
gotoxy(40,23);
TextColor(15);
gotoxy(1,79);
writeln(' Для продолжения нажмите любую клавишу... ');
repeat until keypressed;
while keypressed do c1:=readkey;
clrscr;
End;
Procedure Spravka;
var
ch:char;
Begin
Okno(1,1,79,23,3,15);
Writeln(' СПРАВКА ' );
Writeln;
Writeln(' Данная программа позволяет найти решения системы дифференциальных уравнений. ') ;
Writeln(' В частности системы уравнений:');
Writeln(' y`1=y1+y2-x1*x1+x1-2 ');
Writeln(' y`2=-2*y1+4*y2+2*x1*x1-4*x1-7 ');
Writeln;
Writeln(' методом Рунге-Кутта или методом Рунге-Кутта-Мерсона. ') ;
Writeln(' Правые части системы дифференциальных уравнений заданы в подпрограммах ');
Writeln(' функциях f1 и f2 соответственно. В данных подпрограммах можно задать');
Writeln(' свои функции вместо исходных.');
Writeln(' После перехода в меню выберите клавишами управления курсора');
Writeln(' необходимый пункт.');
Writeln('При выборе пунктов меню "Метод Рунге-Кутта " или "Метод');
Writeln('Рунге-Кутта-Мерсона " введите исходные данные , программа выведет’);
writeln(' полученные результаты.');
Window(2,2,79,24);
Textcolor(15);
gotoxy(5,20);
write( ' Для возврата в меню нажмите любую клавишу... ' ) ;
ch:=readkey;
End;
Procedure moymenu;
begin
clrscr;
Okno(10,5,60,20,3,15);
For i:=1 to 4 do
begin
Gotoxy(15,i+5);
if i=p then Textbackground(4) else
Textbackground(3);
write(Menu[i]);
end;
End;
procedure Exitfrom;
begin
writeln;
gotoxy(50,26);
Writeln(' Для прдолжения вычисления нажмите Y, для выхода -N');
ch:=readkey;
if ch=#121 then moymenu else Zastavka;
end;
Procedure runkut ;
label 2;
begin
clrscr;
textcolor(15);
NormCursor;
Writeln('Метод Рунге-Кутта ');
2: Write('Задайте положительный начальный h=');
read(h);
if h<=0 then
goto 2
else begin
write ('Задайте начальное Xo=');
read (x);
for j:=1 to n do
begin
Write('Задайте начальные y0[',j,']=');
readln(W[j]);
y[j]:=W[j];
end;
ur;
for j:=1 to n do
begin
v:=H*f[j];
k[j]:=v;
y[j]:=W[j]+v/2;
end;
ur;
for j:=1 to n do
begin
v:=H*f[j];
k[j]:=k[j]+2*v;
y[j]:=W[j]+v/2;
end;
ur;
for j:=1 to n do
begin
v:=H*f[j];
k[j]:=k[j]+2*v;
y[j]:=W[j]+v;
end;
ur;
Textcolor(5);
Writeln('решение системы дифференциальных уравнений:');
for j:=1 to n do
begin
y[j]:=W[j]+(k[j]+h*f[j])/6;
writeln('y[',j,']=',y[j]:12:9);
W[j]:=y[j];
end;
HiddeCursor;
textcolor(14);
gotoxy(1,24);
writeln('Для продолжения вычисления нажмите <Y>,');
writeln('для выхода <N>');
ch:=readkey;
if ch=#121 then runkut else moymenu;
end;end;
Procedure rukutm;
label 3;
begin
clrscr;
textcolor(15);
NormCursor;
Writeln('Метод Рунге-Кутта-Мерсона ');
3: Write('задайте положительный начальный шаг h=');
read(h);
if h<=0 then
goto 3
else begin
Write('Задайте погрешность вычислений e=');
read(e1);
write ('Задайте начальное Xo=');
read (x);
for j:=1 to n do
begin
write('Введите начальное Y0[',j,']=');
readln(w[j]);
y[j]:=W[j];
end;
k2:=0;
e3:=0;
ur;
d2:=0;
for j:=1 to n do
begin
a[j]:=f[j]*H;
y[j]:=W[j]+a[j]/3;
end;
x:=x+h/3;
ur;
for j:=1 to n do
begin
y[j]:=W[j]+(a[j]+f[j]*H)/6;
end;
ur;
for j:=1 to n do
begin
c[j]:=f[j]*H;
y[j]:=W[j]+a[j]/8+0.375*c[j];
end;
x:=x+h/6;
ur;
for j:=1 to n do
begin
d[j]:=f[j]*H;
y[j]:=W[j]+a[j]/2-1.5*c[j]+2*d[j];
end;
x:=x+h/2;
ur;
for j:=1 to n do
begin
e[j]:=f[j]*H;
y[j]:=W[j]+(a[j]+4*d[j]+e[j])/6;
e2:=abs(-2*a[j]+9*c[j]-8*d[j]+e[j])/30;
if e2<=e1 then
if e2<e1/20 then d2:=d2+1 else
e3:=0;
end;
if e3<>0 then begin
x:=x-h;
for j:=1 to n do begin
y[j]:=W[j];
end;
H:=H/2;
end
else k2:=1;
if d2=n then H:=H+H;
Textcolor(5);
Writeln('решение системы дифференциальных уравнений:');
for i:=1 to n do begin
writeln('y[',i,']=',y[i]:12:9);
W[i]:=y[i];
end;
HiddeCursor;
textcolor(14);
gotoxy(1,24);
writeln('Для продолжения вычисления нажмите <Y>,');
writeln('для выхода <N>');
ch:=readkey;
if ch=#121 then rukutm else moymenu;
end; end;
BEGIN
Clrscr;
Zastavka;
11: hiddecursor;
p:=1;
moymenu;
k10:=readkey;
while k10<>#13 do
begin
Case k10 of
#72: if p=1 then p:=4 else p:=P-1;
#80: if p=4 then p:=1 else p:=p+1;
end;
moymenu;
k10:=readkey;
end;
Case p of
1: Spravka;
2: runkut;
3: rukutm;
4: exit;
end;
goto 11;
END.
7. Результаты работы программы
После запуска программы в соответствии с поставленной задачей на проектирование выводится окно заставки программы, приведенное на рисунке 1.

Рисунок 1. Окно заставки.
После нажатия любой клавиши выводится окно с меню, представленное на рисунке 2.

Рисунок 2. Окно с меню.
При выборе пункта меню «Справка» открывается соответствующие окно в котором находится справочная информация о программе. Пример такого окна представлен на рисунке 3.

Рисунок 3. Окно справки.
При выборе пункта меню « Метод Рунге-Кутта » или «Метод Рунге-Кутта-Мерсона» открывается соответствующие окна, в которых вводятся исходные данные и выводятся результаты вычисления. Примеры таких окон представлены на рисунках 4 ( Метод Рунге-Кутта ) и 5 (Метод Рунге-Кутта-Мерсона).

Рисунок 4. Вычисление методом Рунге-Кутта.

Рисунок 5. Вычисление методом Рунге-Кутта-Мерсона.
8. Анализ результатов
Для анализа результатов сведем данные нескольких расчетов в таблицу.
Таблица 2 – Результаты расчетов
|
№ |
Метод Рунге-Кутта-Мерсона |
Метод Рунге-Кутта |
|||||||
|
Y>01> |
Y>02> |
Х>о> |
h |
E |
Y>01> |
Y>02> |
Х>о> |
h |
|
|
1 |
2 |
1 |
1 |
0.02 |
0,001 |
2 |
1 |
1 |
0.02 |
|
Y>1> |
2.018133460 |
2,018237453 |
|||||||
|
Y>2> |
0,812223824 |
0,0812215653 |
Сравнение методов показывает, что они обеспечивают примерно одинаковое решение.
В большинстве случаев метод
Рунге-Кутта-Мерсона даёт более точный
результат (погрешность
 ).
Кроме того, хотя он громоздок в реализации,
но быстрая сходимость метода компенсирует
увеличение числа вспомогательных
операций и, резко уменьшает вероятность
числовой неустойчивости.
).
Кроме того, хотя он громоздок в реализации,
но быстрая сходимость метода компенсирует
увеличение числа вспомогательных
операций и, резко уменьшает вероятность
числовой неустойчивости.
9. Инструкция по работе с программой
Файл NYBKURSO.pas с исходным текстом Паскаль-программы находится по адресу E:\2 kurs\Неверовская. Результат компиляции исходной программы NYBKURSO.exe находится в той же папке.
Необходимо запустить на выполнение NYBKURSO.exe либо загрузить Turbo Pascal, сделать текущим каталог Неверовская, открыть файл с исходной Паскаль-программой NYBKURSO.pas и запустить ее на выполнение командой Run\ Run.
После вывода заставки программы нажать любую клавишу для перехода в меню и открыть окно справки. После ознакомления со справкой нажатием любой клавиши возвратится в окно меню, с помощью клавиш управления курсором выбрать метод вычисления и ввести по запросу программы значения, а также погрешность.
Результаты вычисления выводятся в том же окне, где вводились исходные данные.
Для продолжения вычислений следует ответить на запрос программы нажатием клавиши ‘Y’, что обеспечит переход к повторному вводу данных. Нажатие клавиши ‘N’ приводит к переходу в меню программы.
Завершение работы с программой реализуется выбором пункта меню “Выход”.
Заключение
В данной курсовой работе разработана блок-схема и реализована средствами языка программирования Турбо-Паскаль программа, позволяющая решить систему дифференциальных уравнений :

методом Рунге-Кутта-Мерсона и методом Рунге-Кутта.
Программа по запросу пользователя сообщает общие сведения по работе с программой и производит вычисления, выбор метода вычисления производится посредством меню, ввод данных осуществляется с клавиатуры по запросу программы.
Из анализа результатов вычисления можно сделать вывод о большей точности вычисления по методу Рунге-Кутта-Мерсона.

