Представление сигналов в базисе несинусоидальных ортогональных функций
НАЦИОНАЛЬНИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ УКРАИНЫ
“КИЕВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ”
ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ
Кафедра физико–технических средств защиты информации
Лабораторная работа
по предмету Обработка широкополосных сигналов
Представление сигналов в базисе несинусоидальных ортогональных функций
Выполнил студент гр. ФЕ-21
Коваленко А.С.
Киев 2008
Введение
Представление сигналов в базисе несинусоидальных ортогональных функций. Обобщенный ряд Фурье. Функции Радемахера. Представление сигнала с конечной энергией в базисе функций Хаара.
Цель работы: Изучение особенностей кусочно-постоянных ортогональных функций Радемахера и Хаара. Получение практических навыков расчета спектров сложных сигналов, используя преобразование Хаара.
Теоретические сведения
Обобщенный ряд Фурье
Обобщенный ряд
Фурье сигнала
 в выбранном базисе
в выбранном базисе
 для сигнала с конечной энергией
для сигнала с конечной энергией

может быть представлен в виде ряда
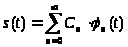 ,
,
где
 – коэффициент разложения, определяющий
спектр сигнала;
– коэффициент разложения, определяющий
спектр сигнала;
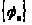 – система ортонормированных вещественных
функций (базис), причем для произвольных
функций, ортонормированных на интервале
– система ортонормированных вещественных
функций (базис), причем для произвольных
функций, ортонормированных на интервале
 ,
можно записать
,
можно записать

Коэффициенты
разложения
 определяются следующим образом
определяются следующим образом
 .
.
Для минимизации
времени вычислений необходимо выбирать
систему базисных функций по возможности
более согласованную по форме с исследуемым
сигналом. Причем необходимо также
учитывать возможность более простой
аппаратной или программной реализации
базиса. Для импульсных сигналов
представляет интерес разложение
 в базисах функций Хаара, Уолша и др.
в базисах функций Хаара, Уолша и др.
Дискретное преобразование Фурье (ДПФ)
Спектральная
плотность
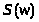 дискретного сигнала
дискретного сигнала
 определяется выражением
определяется выражением
 ,
(1.1)
,
(1.1)
где n – номер
дискретного отсчета непрерывной функции;
 -
период дискретизации непрерывной
функции x(t).
-
период дискретизации непрерывной
функции x(t).
Согласно выражению (1.1) спектр дискретного сигнала сплошной. Но таковым он бывает только лишь при условии, что объем выборки дискретного сигнала бесконечен. В приложениях выборка отсчетов сигнала всегда конечномерна. Кроме того, по многим причинам желательно вычислять преобразование Фурье на ЭВМ. Это означает, что конечномерной является не только выборка дискретных отсчетов сигнала, но и соответствующее этой выборке число гармоник спектра дискретного сигнала.
Каждая
спектральная линия состоит из амплитудной
и фазовой составляющих. Следовательно,
из N данных отсчетов можно получить
амплитуды и фазы для N/2 дискретных
частот, которые находятся в интервале
от
 до
до
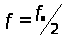 ,
где
,
где
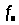 -
частота дискретизации равная
-
частота дискретизации равная
 .
.
Соответствующие
спектральные линии повторяются в
интервале от
 до
до
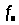 .
В области от
.
В области от
 до
до
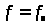 можно построить N линий для частот
можно построить N линий для частот
 ,
,
где k = 0, 1, …, N
–1. Если в уравнении (1.1) заменить
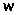 на
на ,
то получим уравнение полностью дискретное
как по времени, так и по частоте и поэтому
удобное для вычислений на ЭВМ.
,
то получим уравнение полностью дискретное
как по времени, так и по частоте и поэтому
удобное для вычислений на ЭВМ.
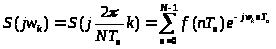 ;
;
 ,
,
где k = 0, 1, …, N –1.
Выражение для обратного ДПФ следующее:
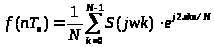 ,
,
где n = 0, 1, …, N –1.
Быстрое преобразование Фурье (БПФ)
Классические
формы прямого и обратного ДПФ просты и
легко реализуемы на ЭВМ. Однако их
практическое применение ограничивается
большими объемами вычислений, которые
растут в квадратичной зависимости от
объема выборки
 .
Так, если число отсчетов временной
функции
.
Так, если число отсчетов временной
функции
 составляет N, то полный спектр
составляет N, то полный спектр -мерной
последовательности дискретных сигналов
определяется посредством приблизительно
-мерной
последовательности дискретных сигналов
определяется посредством приблизительно
 комплексных операций умножения и
сложения. При достаточно больших
комплексных операций умножения и
сложения. При достаточно больших
 может оказаться, что ресурса даже
высокопроизводительных ЭВМ недостаточно
для вычисления спектра в реальном
времени (т.е. в темпе поступления входных
данных). Существуют различные способы
сокращения объема вычисления при
определении дискретно спектра, которые
приводят к алгоритмам быстрого
преобразования Фурье. Алгоритмы БПФ
основаны на устранении избыточности
вычислений. Покажем на примере.
может оказаться, что ресурса даже
высокопроизводительных ЭВМ недостаточно
для вычисления спектра в реальном
времени (т.е. в темпе поступления входных
данных). Существуют различные способы
сокращения объема вычисления при
определении дискретно спектра, которые
приводят к алгоритмам быстрого
преобразования Фурье. Алгоритмы БПФ
основаны на устранении избыточности
вычислений. Покажем на примере.
Допустим, что нужно рассчитать число А
А = ac + ad + bc + bd
В записанном виде расчет содержит четыре операции умножения и три сложения. Если число А нужно считать много раз для разных множеств данных, то его представляют в эквивалентной форме:
А = (a+b) (c+d)
которая требует выполнения лишь одной операции умножения и двух операций сложения.
Основная идея
БПФ заключается в разделении исходной
 -
точечной последовательности входных
сигналов на две более короткие
последовательности, ДПФ которых можно
скомбинировать таким образом, чтобы
получилось ДПФ исходной
-
точечной последовательности входных
сигналов на две более короткие
последовательности, ДПФ которых можно
скомбинировать таким образом, чтобы
получилось ДПФ исходной
 -
точечной последовательности. Так,
например, если
-
точечной последовательности. Так,
например, если
 – четное, а исходная
– четное, а исходная
 -
точечная последовательность разбита
на две
-
точечная последовательность разбита
на две
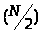 -
точечные последовательности, то для
вычисления искомого
-
точечные последовательности, то для
вычисления искомого
 -
точечного ДПФ потребуется
-
точечного ДПФ потребуется
 комплексных
операций умножения, т.е. вдвое меньше
по сравнению с прямым вычислением ДПФ.
Здесь множитель
комплексных
операций умножения, т.е. вдвое меньше
по сравнению с прямым вычислением ДПФ.
Здесь множитель
 равен числу умножений, необходимых для
определения
равен числу умножений, необходимых для
определения
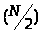 -
точечного ДПФ, а множитель 2 соответствует
двум ДПФ, которые должны быть вычислены.
Эту операцию можно повторить, вычисляя
вместо
-
точечного ДПФ, а множитель 2 соответствует
двум ДПФ, которые должны быть вычислены.
Эту операцию можно повторить, вычисляя
вместо
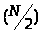 -
точечного ДПФ две
-
точечного ДПФ две
 точечные ДПФ (предполагая, что
точечные ДПФ (предполагая, что
 – четное) и сокращая тем самым объем
вычислений еще в два раза. Выигрыш в два
раза является приблизительным, поскольку
не учитывается, каким образом из ДПФ
меньшего размера образуется искомое
– четное) и сокращая тем самым объем
вычислений еще в два раза. Выигрыш в два
раза является приблизительным, поскольку
не учитывается, каким образом из ДПФ
меньшего размера образуется искомое
 -
точечное ДПФ.
-
точечное ДПФ.
Функции Радемахера и их представление
Функции
Радемахера составляют неполную систему
ортонормированных функций, что
ограничивает их применение. Но их широкое
использование обусловлено тем, что на
их основе можно получить полные функций,
например, Хаара и Уолша. Непрерывная
Функция Радемахера с индексом m, которая
обозначается как rad(m,x), имеет вид
последовательности прямоугольных
импульсов, содержит
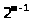 периодов на полуоткрытом интервале
[0;1) и принимает значения +1 или –1.
Исключением является rad (0,x), которая
имеет вид единичного импульса. Функции
Радемахера периодические с периодом
1, т.е. rad(m,x) = rad(m,x+1). Кроме того, они
периодические и на более коротких
интервалах:
периодов на полуоткрытом интервале
[0;1) и принимает значения +1 или –1.
Исключением является rad (0,x), которая
имеет вид единичного импульса. Функции
Радемахера периодические с периодом
1, т.е. rad(m,x) = rad(m,x+1). Кроме того, они
периодические и на более коротких
интервалах:
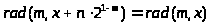 ,
,
 ,
,
 Их можно получить с помощью рекуррентного
соотношения:
Их можно получить с помощью рекуррентного
соотношения:
 ,
,

Получить функции Радемахера можно также с помощью следующего соотношения:
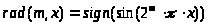
Первые четыре функции Радемахера представлены на рис.1.1 а, б


а) б)
Рис. 1.1. Первые четыре непрерывные функции Радемахера:
a) на интервале [0; 1); б) на интервале [-0.5; 0.5);
Пример разложения функции f(x) в базисе функций Радемахера, используя общую формулу (1.2) представлен на рис 1.2.
 ,
(1.2)
,
(1.2)
где

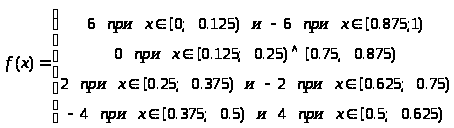

Рис.1.2. Пример разложения в базисе функций Радемахера.
Дискретные функции Радемахера
Дискретные функции Радемахера являются отсчетами непрерывных функций Радемахера. Каждый отсчет расположен в середине связанного с ним элемента непрерывной функции. Обозначаются дискретные функции Радемахера как Rad(m,x). Для дискретных функций Радемахера удобно использовать матрицу, каждая строка которой является дискретной функцией Радемахера. Например, для третьей диады (m=3) имеем: (для удобства обозначим “+1” как “+”, а “–1” как “–” )

Rad(0,x)
Rad(1,x)
Rad(2,x)
Rad(3,x)

Функции Хаара и их представление
Множество
непрерывных функций Хаара
 составляет периодическую, ортонормированную
и полную систему функций. Широкое
распространение функции Хаара получили
в вэйвлет-анализа и сжатии изображений.
Рекуррентное соотношение, которое дает
возможность сформировать непрерывную
функцию
составляет периодическую, ортонормированную
и полную систему функций. Широкое
распространение функции Хаара получили
в вэйвлет-анализа и сжатии изображений.
Рекуррентное соотношение, которое дает
возможность сформировать непрерывную
функцию
 ,
имеет вид:
,
имеет вид:


где
 и
и
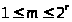 ,
N – общее количество функций.
,
N – общее количество функций.
Первые восемь функций Хаара представлены на рис. 1.3.

Рис.1.3. Первые восемь непрерывных функции Хаара.
Дискретные функции Хаара
По аналогии с
дискретными функциями Радемахера
дискретные функции Хаара являются
отсчетами непрерывных функций Хаара.
Каждый отсчет расположен в середине
связанного с ним элемента непрерывной
функции. Обозначаются дискретные функции
Хаара как
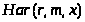 .
.
Построим матрицу дискретных значений
функций Хаара для
 ,
в которой каждая строка отвечает
соответствующей функции.
,
в которой каждая строка отвечает
соответствующей функции.
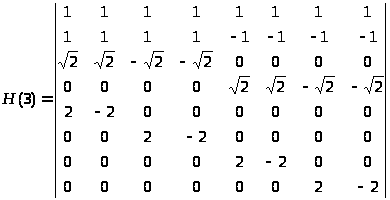
Нar(0,0,x)
Har(0,1,x)
Har(1,1,x)
Har(1,2,x)
Har(2,1,x)
Har(2,2,x)
Har(2,3,x)
Har(2,4,x)
При цифровой обработке сигналов, вэйвлет-анализе, сжатии изображений, анализе и синтезе логических функций, часто применяются ненормированные функции Хаара, которые на отдельных участках принимают одно из трех значений +1; 0; –1.
Преобразование Хаара
Любую интегрируемую
на интервале
 функцию
функцию
 можно представить рядом Фурье по системе
функций Хаара:
можно представить рядом Фурье по системе
функций Хаара:
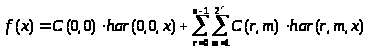 ,
где
,
где
 (1.3)
(1.3)
с коэффициентами
 .
(1.4)
.
(1.4)
Домашнее задание
Выражения для непрерывных функций Радемахера


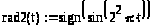



Матрица для системы дискретных функций Радемахера при N = 5.
|
Rad(0,t) |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Rad(1,t) |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|
Rad(2,t) |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|
Rad(3,t) |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
|
Rad(4,t) |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
|
Rad(5,t) |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
Графики функций от
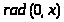 до
до
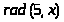 .
.

Выражение для нормированных функций Хаара.



Графики нормированных функций от
 до
до
 .
.Графики ненормированных функций от
 до
до
 .
.
Выполнение работы
Используя преобразование Хаара рассчитаем амплитудный и фазовый спектр заданного сигнала
А. Используем нормированные функции Хаара.

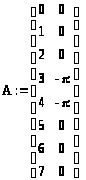

Б. Используем ненормированные функции Хаара

Синтезируем заданный сигнал и построим графики для обоих случаев
А. Используем нормированные функции Хаара

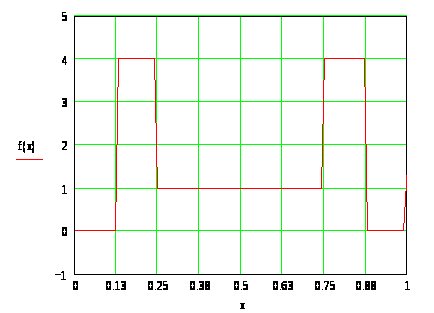
Б. Используем ненормированные функции Хаара


Выводы по работе
