Построение и использование имитационных моделей
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
Кафедра компьютерных образовательных технологий
КУРСОВАЯ РАБОТА
Тема: Построение и использование имитационных моделей
Работу выполнил студент
Машков Андрей Сергеевич
Техническое задание
1. Наименование темы: Построение и исследование имитационных моделей
2. Срок сдачи студентом законченной работы 05.06.07
3. Техническое задание и исходные
данные к работе Разработать программу
для имитационного моделирования системы
массового обслуживания с 2 устройствами.
В системе интервалы времени между
поступлением требований являются
независимыми случайными величинами со
средним временем поступления требований
 =10
(с). Когда требование поступает, а
устройство свободно, обслуживание
начинается немедленно. Время обслуживания
является случайной величиной
некоррелированной с интервалами
поступления требований. Среднее значение
времени обслуживания требований
=10
(с). Когда требование поступает, а
устройство свободно, обслуживание
начинается немедленно. Время обслуживания
является случайной величиной
некоррелированной с интервалами
поступления требований. Среднее значение
времени обслуживания требований
 =10
(c).
Если при поступлении требования
устройства заняты, требование становится
в очередь.
=10
(c).
Если при поступлении требования
устройства заняты, требование становится
в очередь.
Дисциплина обслуживания: циклическая с квантом q=1c.
Оценке подлежат следующие параметры:
коэффициент использования
системы
 ;
;
средняя задержка в очереди
 ;
;
среднее время ожидания
 ;
;
среднее по времени число
требований в очереди
 ;
;
среднее по времени число
требований в системе
 .
.
4. Содержание курсовой работы (перечень подлежащих разработке вопросов):
Анализ задачи и обзор аналогов;
Выбор входных распределений;
Логика работы программы;
Построение генераторов случайных чисел;
Статистический анализ выходных данных моделирования;
Рекомендации по использованию результатов моделирования.
5. Перечень графического материала (с указанием обязательного материала):
Графики функций распределения вероятностей;
Графики функций плотности распределения вероятностей;
График по времени числа требований в очереди;
График по времени числа требований в системе;
График по времени коэффициента использования системы;
Блок-схемы алгоритмов.
6. Исходные материалы и пособия
1. Кельтон В., Лоу А. Имитационное моделирование. Классика CS. 3-ие изд. – СПб.:Питер; Киев: Издательская группа BHV, 2004. – 847 c.
Содержание
Введение
1. Анализ задачи и обзор аналогов
2. Выбор входных распределений. Построение генераторов случайных чисел
3. Оценка входных параметров
3.1 Оценки средних значений
3.2 Интервальные оценки
3.3 Проверка статистических гипотез
3.4 Метод гистограмм
4. Логика работы программы
4.1 Блок-схема алгоритма программы
4.2 Интерфейс
5. Планирование эксперимента
5.1 Статический анализ выходных данных моделирования
5.2 Построение факторного плана
5.3 Эффекты взаимодействия и уравнения регрессии
6. Рекомендации по использованию результатов моделирования
Заключение
Приложение А
Приложение Б
Список литературы
Введение
На производстве, в быту, военном деле, науке и т. д. часто встречаются процессы, которые, не вдаваясь в детали, можно описать следующим образом: с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой — происходит постоянное удовлетворение этих запросов. Та часть процесса, в которой возникают запросы, называется обслуживаемой системой, а та, которая принимает запросы и удовлетворяет их,— обслуживающей. Совокупность обслуживающей и обслуживаемой систем составляет систему массового обслуживания. Под системой массового обслуживания (СМО) понимают динамическую систему, предназначенную для эффективного облуживания случайного потока требований при ограниченных ресурсах системы.
Модели системы массового обслуживания являются наиболее часто используемым классом моделей со случайными факторами, что определяется повсеместным распространением систем такого типа.
К настоящему времени разработано много моделей систем массового обслуживания, имеющих аналитическое решение. Но они далеко не исчерпывают все способы функционирования реальных обслуживающих систем. Кроме того, на практике не всегда выполняются предпосылки, лежащие в основе имеющихся аналитических моделей.
Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания.
Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и простоев каналов обслуживания.
Эффективным методом решения задач теории массового обслуживания, как и многих других, не имеющих аналитического решения, является метод статистического моделирования, предусматривающий, имитацию на ЭВМ процессов, протекающих в исследуемой системе. Математическое описание процесса в этом случае задается алгоритмически. Моделирующий алгоритм многократно воспроизводит изучаемый случайный процесс, накапливает сведения о его протекании, и после обработки выдает оценки показателей работы системы. Целью любого компьютерного эксперимента является сбор информации о значениях переменных модели, наблюдаемых в процессе проведения эксперимента, и состояниях очередей, возникающих в процессе моделирования.
Построение программы имитации поведения СМО основано на программировании цепочки событий, начиная от входных требований, поступающих в случайные моменты времени, занятия и освобождения серверов в соответствии со случайным характером длительности обработки каждого требования. Итогом работы программы является получение статистических отчетов о процессах в системе.
В данной курсовой работе требуется разработать программу для имитационного моделирования системы массового обслуживания с двумя устройствами. В системе интервалы времени между поступлениями требований являются независимыми случайными величинами со средним временем Ā = 10 секунд. Когда требование поступает, а устройство свободно, обслуживание начинается немедленно. Время обслуживания является случайной величиной, некоррелированной с интервалами поступления требований. Среднее значение обслуживания требований – Ŝ = 10 секунд. Если при поступлении требования устройства заняты, то требование становится в очередь. Дисциплина обслуживания циклическая с квантом q=1c.
Оценке подлежат следующие параметры:
коэффициент использования системы;
средняя задержка в очереди;
среднее время ожидания;
среднее по времени число требований в очереди;
среднее по времени число требований в системе.
1. Анализ задачи и обзор аналогов
Основными элементами СМО являются: входящий поток требований, очередь требований, обслуживающие устройства, (каналы) и выходящий поток требований. Изучение СМО начинается с анализа входящего потока требований. Входящий поток требований представляет собой совокупность требований, которые поступают в систему и нуждаются в обслуживании. Входящий поток требований изучается с целью установления закономерностей этого потока и дальнейшего улучшения качества обслуживания.
В данной работе СМО предназначена для обслуживания какого-то потока требований, поступающих в какие-то случайные моменты времени. Так как система циклично содержит квант q, то по истечению этого цикла если требование успело обслужиться, то оно покидает систему, в противном случае требование поступает в конец очереди. Далее время обработки этого требования уменьшается на квант q.
Задача данной СМО – установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что требование будет обслужена; математического ожидания числа обслуженных требований и т.д.) от входных показателей (количества каналов в системе, параметров входящего потока требований и т.д.). Результирующими показателями или интересующими нас характеристиками СМО являются – показатели эффективности СМО, которые описывают, способна ли данная система справляться с потоком требований.
Модель такой системы представлена на рисунке 1.1.

Рисунок 1.1 – Модель циклическая с квантом q
В действительности, многие системы работают по такому принципу:
Задача продавца газет. Партии товара Q поступают регулярно через Т, через этот промежуток продается случайное количество товара R, к моменту поставки новой партии старый товар теряет свои потребительские свойства.
2. Выбор входных распределений. Построение генераторов случайных чисел
Для многих реальных процессов поток требований достаточно хорошо описывается законом распределения Пуассона. Такой поток называется простейшим.
Простейший поток обладает такими важными свойствами:
Свойством стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку в среднем в сутки должно быть одинаковым для различных периодов времени, к примеру, в начале и в конце декады.
Отсутствия последействия, которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени. Например, число автомобилей, прибывших за материалами в десятый день месяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца.
Свойством ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).
Таким образом, при моделировании
мы генерируем две экспоненциально
распределенные псевдослучайные
последовательности с заданными средними
значениями
 ,
,
 .
.
Чтобы смоделировать экспоненциально распределенную случайную величину сначала генерируется стандартно равномерно распределенная случайная величина U, которая затем преобразуется в величину с экспоненциальным законом распределения согласно формуле:
X = – ln(U),(2.1)
где - математическое ожидание.
Для генерации стандартно равномерно распределенной случайной величины U используется мультипликативный генератор:
 ,
(2.2)
,
(2.2)
где: a = 630360016, m = 2147483647.
Рассмотрим вид входных распределений
на основе последовательностей из 1000
элементов с входными параметрами
генераторов ( –
случайная величина поступления требований
(среднее значение 10),
–
случайная величина поступления требований
(среднее значение 10),
 –
случайная величина обработки требований
(среднее значение 10)):
–
случайная величина обработки требований
(среднее значение 10)):
 (
( )
=46382 ,
)
=46382 ,
 (
( )
= 94215.
)
= 94215.
3. Оценка входных параметров
3.1 Оценки средних значений
Оценка математического ожидания случайных величин X вычисляется по формуле:

(3.1)
где n – количество элементов.
Для случайных величин
 и
и
 она равна:
она равна:


Оценка дисперсии случайных величин вычисляется по формуле:
 . (3.2)
. (3.2)
Для случайных величин
 и
и
 она
равна:
она
равна:


Оценка корреляции случайных величин вычисляется по формулам:
 , (3.3)
, (3.3)
где j = 1,…,n.
Графики корреляции показаны на рисунках 3.1. и 3.2.

Рисунок 3.1 – Корреляция величины

Рисунок 3.2 – Корреляция величины S
Графики зависимости последующего значения от предыдущего представлены на рисунках 3.3 и 3.4.

Рисунок 3.3
– Зависимость
 от
от


Рисунок 3.4 – Зависимость
 от
от

3.2 Интервальные оценки
Доверительный интервал для оценки математического ожидания случайной величины определяется формулой:
 , (3.4)
, (3.4)
где
= 0.95 – доверительная вероятность,
 - квантиль порядка
- квантиль порядка
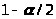 ,
,
 =
=
 - оценка дисперсии.
- оценка дисперсии.
 = 1.96 для доверительной вероятности 0.95.
= 1.96 для доверительной вероятности 0.95.
Доверительные интервалы для
оценки математического ожидания
случайных величин
 и
и
 равны:
равны:
(9.5886; 10.8315),
 –
попадает в полученный доверительный
интервал;
–
попадает в полученный доверительный
интервал;
(9.5627; 10.7928),
 –
попадает в полученный доверительный
интервал.
–
попадает в полученный доверительный
интервал.
3.3 Проверка статистических гипотез
Проверка гипотез об экспоненциальном распределении величин A и S осуществляется с помощью метода 2.
Выдвигаем гипотезу о том, что случайные величины A и S распределены экспоненциально.
Статистическая функция вычисляется по формуле:
 , (3.5)
, (3.5)
где
 -
это частота попадания в k
–й интервал, p>i>
- вероятность попадания, которая
вычисляется следующим образом
-
это частота попадания в k
–й интервал, p>i>
- вероятность попадания, которая
вычисляется следующим образом
 ,
(3.6)
,
(3.6)
Расчет проводился на k
= 20. Если
 ,
то гипотеза принимается, если
,
то гипотеза принимается, если
 ,
гипотеза отвергается. По данным таблицы
для k=20
и
,
гипотеза отвергается. По данным таблицы
для k=20
и
 =0.05,
критерий 2
= 31.4.
=0.05,
критерий 2
= 31.4.
В результате были получены
следующие значения
 и
и

Таким образом, обе гипотезы принимаются.
Интервалы: [0 0,4879), [0.4879 1.0008), [1.0008 1.5415), [1.5415 2.1131), [2.1131 2.7193), [2.7193 3.3647), [3.3647 4.0547), [4.0547 4.7957), [4.7957 5.5962), [5.5962 6.4663), [6.4663 7.4194), [7.4194 8.4730), [8.4730 9.6508), [9.6508 10.9861), [10.9861 12.5276), [12.5276 14.3508), [14.3508 16.5823), [16.5823 19.4591), [19.4591 23.5138) .
3.4 Метод гистограмм
На рисунках 3.5 и 3.6 изображены гистограммы с функциями плотностей распределения вероятностей для A и S.

Рисунок 3.5 –Гистограмма величины A
Эта гистограмма показывает, что смоделированная случайная величина A распределена по экспоненциальному закону. Математическое ожидание случайной величины А равно 10.

Рисунок 3.6 –Гистограмма величины S
На гистограмме видно, что смоделированная случайная величина S распределена по экспоненциальному закону. Математическое ожидание случайной величины S равно 10.
На рисунках 3.7 и 3.8 изображены графики функций распределения вероятностей для A и S.

Рисунок 3.7 – Функция распределения величины A

Рисунок 3.8 – Функция распределения величины S
4 Логика работы программы
4.1 Блок-схема алгоритма программы
На рисунке 4.1 представлена логика работы системы массового обслуживания с дисциплиной – циклическая с квантом q.


Генерация входных параметров

Инициализация


Нет





Поступление требования в очередь
 Да
Да
Блок поступления требования в устройство

Блок ухода требования и дополнительной обработки


Рисунок 4.1- Блок-схема алгоритма программы
На рисунке 4.2 представлена блок-схема блока поступления требования в устройство.


Планирование времени поступления требования


Нет
Да



Функция, обеспечивающая обработку требования
Увеличиваем число требований в очереди на единицу





Рисунок 4.2 – Блок-схема поступления требования
На рисунке 4.3 представлена блок-схема функции, обеспечивающей обработку требования, где q - максимальное время обслуживание требования.
На рисунке 4.4 представлена блок-схема блока ухода требования и дополнительной обработки.


Уменьшение числа требований в очереди на единицу
и вычисление времени обслуживания этого требования

Уменьшение на q оставшегося времени обслуживание для этого требования

Занесение требования в устройство

Планирование события завершения обслуживания для прохождения этого требования


Рисунок 4.3 – Блок-схема функции обработки требования


Удаление требование с обслуживания






Да Нет
Увеличение числа требований на единицу
Прибавляем единицы к числу обработанных требования





Рисунок 4.4- Блок-схема дополнительной обработки или ухода требования
4.2 Интерфейс
К графическому интерфейсу относится управление параметрами системы, такими как изменение входных параметров.
На рисунке 4.5 представлено основное диалоговое окно графического интерфейса.

Рисунок 4.5 - Основное диалоговое окно графического интерфейса
Здесь имеются поля для ввода входных параметров, кнопки управления происходящим процессом.
При нажатии на клавишу «Запуск» мы видим диалоговое окно, представленное на рисунке 4.6. Здесь можно заметить, что поля ввода входных параметров неактивны для изменения. Так же в графе «Выходные параметры системы» результаты показываются только по двум пунктам: системное время и время поступления следующей заявки. Кнопка «Графики» неактивна. Соответственно происходит выполнение работы программы.

Рисунок 4.5 – Диалоговое окно при нажатии на кнопку «Запуск»
При нажатии на кнопку «Стоп» происходит активация полей ввода «Параметры моделируемой системы». Так же выводится информация о промежуточных подсчётах. Можно посмотреть полученные графики. Это можно посмотреть на рисунке 4.6.

Рисунок 4.6 - Диалоговое окно при нажатии на кнопку «Стоп»
После окончательного прогона моделирования системы массового обслуживания и нажатия на кнопку «Графики» мы увидим:
график изменения коэффициента использования системы во времени на рисунке 4.7;
график текущего по времени числа заявок в очереди на рисунке 4.8;
график текущего по времени числа заявок в системе на рисунке 4.9;
график среднего по времени числа заявок в очереди и системе на рисунке 4.10.

Рисунок 4.7 - Изменения коэффициента использования системы во времени

Рисунок 4.8 - Текущее по времени число заявок в очереди

Рисунок 4.9 - Текущее по времени число заявок в системе

Рисунок 4.10 - Среднего по времени числа заявок в очереди и системе
5 Планирование эксперимента
5.1 Статический анализ выходных данных моделирования
Для анализа выходных параметров моделирования необходимо рассчитать количество экспериментов для построения факторного плана. Расчет количества экспериментов производится по формуле:
 , (5.1)
, (5.1)
где
 -
дисперсия,
-
дисперсия,
 -
5% от математического ожидания на 10
значениях каждого выходного параметра,
-
5% от математического ожидания на 10
значениях каждого выходного параметра,
 =1.96
– квантиль порядка
=1.96
– квантиль порядка
 .
.
Результаты расчетов необходимого количества экспериментов приведены в таблице 5.1.
Таблица 5.1 – Количество экспериментов
|
A1 |
S1 |
p |
d |
w |
Q |
L |
|
|
1 |
254789 |
251463 |
0,425622 |
9,23302 |
19,0935 |
0,564 |
2,2317 |
|
2 |
62315 |
56514 |
0,42811 |
10,1712 |
20,7671 |
0,609816 |
2,24761 |
|
3 |
54789623 |
1263532 |
0,500968 |
10,0617 |
20,1693 |
0,757584 |
2,54167 |
|
4 |
658765 |
459877 |
0,480135 |
8,99325 |
18,8155 |
0,549471 |
2,24218 |
|
5 |
678678 |
967567 |
0,421836 |
8,863665 |
18,111 |
0,477824 |
2,04563 |
|
6 |
872343 |
976723 |
0,490978 |
8,75354 |
18,384 |
0,53815 |
2,24663 |
|
7 |
98745 |
874509 |
0,476293 |
9,028 |
18,873 |
0,552332 |
2,27674 |
|
8 |
2148963 |
1247896 |
0,482266 |
9,24245 |
19,2856 |
0,534981 |
2,21667 |
|
9 |
2652567 |
4589642 |
0,411253 |
8,32548 |
17,9225 |
0,432992 |
2,0688 |
|
10 |
829192 |
873292 |
0,472514 |
9,23085 |
19,0708 |
0,622302 |
2,36714 |
|
n |
8,090238 |
5,737406 |
3,266298 |
37,26833 |
5,93063 |
В таблице 5.1 приняты следующие обозначения: A1 – начальное значение величины A (поступления требования); S1 - начальное значение величины S (обработки требования); p, d, w, Q, L – выходные параметры, соответственно коэффициент использования, системы, средняя задержка в очереди, среднее время ожидания, среднее по времени число требований в очереди, среднее по времени число требований в системе; n – необходимое количество экспериментов вычисленное по формуле 5.1.
Было определено максимальное значение n равное 37.
5.2 Построение факторного плана
В данной СМО входными переменными модели, т.е. факторами являются:
количество устройств;
среднее время поступления требований;
среднее время обработки требований.
Выходными показателями работы СМО, т.е. откликами являются:
коэффициент использования системы;
средняя задержка в очереди;
среднее время ожидания;
среднее по времени число требований в очереди;
среднее по времени число требований в системе.
В таблице 5.2 приведены уровни факторов и их значения.
Таблица 5.2 – Значения уровней и факторов
|
Фактор |
- |
+ |
|
Количество устройств (m) |
1 |
2 |
|
Среднее значение
|
11 |
12 |
|
Среднее значение
|
8 |
9 |
Значения факторов были подобраны эмпирически, основываясь на том, что нужно увеличить загруженность системы (повысить коэффициент использования системы), но при этом не должно создаваться ситуации, когда очередь постоянно возрастает. Т.е. значения двух факторов должны быть ограничены.
Для планирования экспериментов
был построен факторный план
 значения которого приведены в таблице
5.3 .В Приложении
А приведены графики контрольных прогонов
для каждого эксперимента факторного
плана.
значения которого приведены в таблице
5.3 .В Приложении
А приведены графики контрольных прогонов
для каждого эксперимента факторного
плана.
Таблица 5.3 – Факторный план
|
N |
M |
|
|
ρ |
d |
W |
Q |
L |
|
1 |
- |
- |
- |
0,615924 |
24,9953 |
32,8826 |
1,74527 |
2,52777 |
|
2 |
+ |
- |
- |
0,364636 |
7,10077 |
15,1911 |
0,271809 |
1,48011 |
|
3 |
- |
+ |
- |
0,641983 |
19,9019 |
27,7597 |
1,13215 |
1,84383 |
|
4 |
+ |
+ |
- |
0,282609 |
6,37251 |
13,9526 |
0,1287 |
1,08477 |
|
5 |
- |
- |
+ |
0,799233 |
31,835 |
40,4347 |
2,48326 |
3,37997 |
|
6 |
+ |
- |
+ |
0,395812 |
7,81768 |
16,8574 |
0,265331 |
1,56789 |
|
7 |
- |
+ |
+ |
0,619495 |
25,401 |
33,9974 |
1,56838 |
2,34359 |
|
8 |
+ |
+ |
+ |
0,356732 |
7,57915 |
16,4351 |
0,237693 |
1,45666 |
Полный факторный план
Таблица А.1 - Результаты работы системы 1/11/8
|
№ |
A |
S |
ρ |
d |
w |
Q |
L |
|
1 |
25698 |
25745 |
0,6755528 |
20,4441 |
28,3593 |
1,27841 |
2,05395 |
|
2 |
35861 |
91752 |
0,680536 |
21,3554 |
29,1991 |
1,37816 |
2,14923 |
|
3 |
11867 |
378922 |
0,639325 |
19,8888 |
27,7547 |
1,21289 |
1,97175 |
|
4 |
26598 |
524568 |
0,657458 |
22,4653 |
30,3462 |
1,51871 |
2,31604 |
|
5 |
258569 |
256985 |
0,667673 |
20,8268 |
28,4641 |
1,35581 |
2,11021 |
|
6 |
585458 |
112362 |
0,596395 |
17,0318 |
24,4552 |
0,975926 |
1,69182 |
|
7 |
554265 |
556963 |
0,692 |
20,7156 |
28,8005 |
1,29098 |
2,08363 |
|
8 |
659123 |
456321 |
0,640571 |
22,6587 |
30,8684 |
1,38142 |
2,13753 |
|
9 |
542369 |
758963 |
0,713228 |
24,5171 |
32,0071 |
1,82475 |
2,60021 |
|
10 |
369258 |
741258 |
0,753513 |
30,4055 |
38,7389 |
2,30473 |
3,15114 |
|
11 |
456321 |
321456 |
0,639594 |
17,5491 |
25,3863 |
0,973815 |
1,71901 |
|
12 |
258321 |
123698 |
0,72446 |
29,3316 |
37,4017 |
2,24594 |
3,07944 |
|
13 |
546132 |
963659 |
0,734653 |
27,3305 |
35,6129 |
1,91317 |
2,72048 |
|
14 |
658741 |
336559 |
0,695646 |
23,1381 |
31,4143 |
1,4804 |
2,27275 |
|
15 |
439157 |
496326 |
0,711085 |
22,194 |
30,3506 |
1,39806 |
2,1861 |
|
16 |
486248 |
684268 |
0,694425 |
26,9778 |
35,1111 |
1,89538 |
2,68753 |
|
17 |
139852 |
369562 |
0,633895 |
20,6619 |
28,2276 |
1,33358 |
2,07694 |
|
18 |
341254 |
851147 |
0,705575 |
29,6748 |
37,9012 |
2,14604 |
2,94536 |
|
19 |
112354 |
774584 |
0,644321 |
17,6122 |
25,5628 |
0,961498 |
1,70932 |
|
20 |
546378 |
796541 |
0,761192 |
28,0322 |
36,2059 |
2,11432 |
2,95728 |
|
21 |
595985 |
747856 |
0,695619 |
23,7853 |
32,0953 |
1,52594 |
2,31901 |
|
22 |
446623 |
332256 |
0,781548 |
25,304 |
33,4814 |
1,77277 |
2,58992 |
|
23 |
882654 |
996548 |
0,743595 |
26,5645 |
34,6843 |
1,92301 |
2,74851 |
|
24 |
654845 |
695658 |
0,574422 |
17,751 |
25,1839 |
1,03218 |
1,74265 |
|
25 |
502508 |
360268 |
0,645467 |
23,8161 |
31,7211 |
1,65099 |
2,44626 |
|
26 |
459543 |
302369 |
0,591592 |
22,7245 |
30,5422 |
1,4158 |
2,13354 |
|
27 |
201301 |
800961 |
0,629991 |
27,2424 |
35,1988 |
1,92285 |
2,69709 |
|
28 |
548545 |
965236 |
0,727015 |
25,9111 |
33,9255 |
1,91621 |
2,74568 |
|
29 |
502401 |
658025 |
0,68132 |
23,6408 |
31,7551 |
1,57362 |
2,36523 |
|
30 |
990065 |
365852 |
0,673105 |
21,8759 |
29,6414 |
1,51489 |
2,31478 |
|
31 |
326587 |
562389 |
0,662329 |
21,9148 |
29,5617 |
1,47498 |
2,23395 |
|
32 |
743652 |
780954 |
0,723818 |
28,8251 |
36,8655 |
2,1632 |
2,98105 |
|
33 |
559658 |
412365 |
0,634386 |
31,1898 |
39,2282 |
2,42949 |
3,2553 |
|
34 |
678151 |
511247 |
0,666739 |
25,5455 |
33,4027 |
1,78458 |
2,5574 |
|
35 |
548545 |
965236 |
0,727015 |
25,9111 |
33,9255 |
1,91621 |
2,74568 |
|
36 |
502401 |
658025 |
0,68132 |
23,6408 |
31,7551 |
1,57362 |
2,36523 |
|
37 |
654845 |
695658 |
0,574422 |
17,751 |
25,1839 |
1,03218 |
1,74265 |
|
38 |
585458 |
112362 |
0,596395 |
17,0318 |
24,4552 |
0,975926 |
1,69182 |
Таблица А.2 - Результаты работы системы 2/11/8
|
№ |
A |
S |
ρ |
d |
w |
Q |
L |
|
1 |
543550 |
543550 |
0,338698 |
6,63765 |
14,8306 |
0,0359895 |
1,07935 |
|
2 |
546328 |
925328 |
0,325319 |
6,78376 |
14,7786 |
0,182953 |
1,322 |
|
3 |
512657 |
14751 |
0,314471 |
6,63436 |
14,1134 |
0,218668 |
1,28283 |
|
4 |
65412 |
365984 |
0,32293 |
6,79088 |
14,8843 |
0,155927 |
1,24995 |
|
5 |
541025 |
850257 |
0,312803 |
6,04349 |
13,5354 |
0,100849 |
1,11726 |
|
6 |
132052 |
956201 |
0.362961 |
6.90582 |
14.8984 |
0.227443 |
1.41849 |
|
7 |
548561 |
523659 |
0.319346 |
6.95141 |
14.6858 |
0.238178 |
1.32071 |
|
8 |
745695 |
652354 |
0.325195 |
6.68655 |
14.9192 |
0.147331 |
1.3253 |
|
9 |
569852 |
258741 |
0.357333 |
7.1276 |
15.5344 |
0.205545 |
1.43516 |
|
10 |
789632 |
123698 |
0.342605 |
6.81135 |
14.9676 |
0.192304 |
1.39074 |
|
11 |
120325 |
669520 |
0.316259 |
6.58486 |
14.6634 |
0.125711 |
1.21964 |
|
12 |
885695 |
336511 |
0.329522 |
6.72872 |
14.6084 |
0.167234 |
1.24897 |
|
13 |
125496 |
695124 |
0.308968 |
6.95665 |
14.969 |
0.175414 |
1.23178 |
|
14 |
23584 |
255963 |
0.316783 |
6.70453 |
14.7566 |
0.148303 |
1.22348 |
|
15 |
352147 |
357159 |
0.336722 |
7.22136 |
15.7185 |
0.193198 |
1.37311 |
|
16 |
645123 |
973451 |
0.338016 |
6.27922 |
13.9954 |
0.105584 |
1.19676 |
|
17 |
645121 |
782223 |
0.326981 |
6.54399 |
14.4811 |
0.106791 |
1.17305 |
|
18 |
203265 |
213025 |
0.372122 |
6.76579 |
14.807 |
0.192739 |
1.38204 |
|
19 |
112354 |
565239 |
0.319334 |
6.73003 |
14.6728 |
0.162247 |
1.23175 |
|
20 |
459548 |
365824 |
0.361309 |
6.80957 |
14.9258 |
0.15476 |
1.28074 |
|
21 |
659369 |
147524 |
0.318654 |
6.87234 |
15.0754 |
0.140456 |
1.2272 |
|
22 |
584215 |
753268 |
0.365926 |
6.56857 |
14.3551 |
0.163679 |
1.25831 |
|
23 |
787789 |
989989 |
0.366771 |
6.52882 |
14.4654 |
0.187632 |
1.4107 |
|
24 |
123235 |
654546 |
0.384813 |
7.60551 |
16.1285 |
0.2599 |
1.42453 |
|
25 |
636963 |
147414 |
0.344725 |
6.57443 |
14.6367 |
0.135911 |
1.2607 |
|
26 |
459543 |
302369 |
0.295819 |
6.812 |
14.6297 |
0.17923 |
1.2025 |
|
27 |
645123 |
973451 |
0.338016 |
6.27922 |
13.9954 |
0.105584 |
1.19676 |
|
28 |
645121 |
782223 |
0.326981 |
6.54399 |
14.4811 |
0.106791 |
1.17305 |
|
29 |
915475 |
984123 |
0.358508 |
6.68446 |
14.6201 |
0.188477 |
1.37552 |
|
30 |
990065 |
365852 |
0.336152 |
6.43067 |
14.1962 |
0.149999 |
1.29115 |
|
31 |
745695 |
652354 |
0.325195 |
6.68655 |
14.9192 |
0.147331 |
1.3253 |
|
32 |
569852 |
258741 |
0.357333 |
7.1276 |
15.5344 |
0.205545 |
1.43516 |
|
33 |
659369 |
147524 |
0.318654 |
6.87234 |
15.0754 |
0.140456 |
1.2272 |
|
34 |
65412 |
365984 |
0,32293 |
6,79088 |
14,8843 |
0,155927 |
1,24995 |
|
35 |
541025 |
850257 |
0,312803 |
6,04349 |
13,5354 |
0,100849 |
1,11726 |
|
36 |
512657 |
14751 |
0,314471 |
6,63436 |
14,1134 |
0,218668 |
1,28283 |
|
37 |
546328 |
925328 |
0,325319 |
6,78376 |
14,7786 |
0,182953 |
1,322 |
|
38 |
512657 |
14751 |
0,314471 |
6,63436 |
14,1134 |
0,218668 |
1,28283 |
Таблица А.3 - Результаты работы системы 1/12/8
|
№ |
A |
S |
ρ |
d |
w |
Q |
L |
|
1 |
990065 |
365852 |
0,61843 |
18,8208 |
26,5865 |
1,09074 |
1,82072 |
|
2 |
256585 |
6523 |
0,638141 |
20,3544 |
28,4439 |
1,14575 |
1,87597 |
|
3 |
555368 |
333652 |
0,603842 |
24,9082 |
33,3464 |
1,52609 |
2,28326 |
|
4 |
352648 |
333652 |
0,558157 |
21,6328 |
30,0966 |
1,17218 |
1,89695 |
|
5 |
666666 |
335225 |
0,54776 |
18,0408 |
25,6844 |
0,975644 |
1,66246 |
|
6 |
132052 |
568112 |
0,727417 |
24,3047 |
32,7124 |
1,53687 |
2,32258 |
|
7 |
223311 |
996633 |
0,603162 |
23,24 |
31,0355 |
1,43715 |
2,14018 |
|
8 |
562551 |
336221 |
0,57625 |
16,0752 |
23,782 |
0,781477 |
1,46213 |
|
9 |
448444 |
112110 |
0,629062 |
19,5658 |
27,5804 |
1,10843 |
1,84356 |
|
10 |
541523 |
236523 |
0,652206 |
24,5259 |
32,6706 |
1,54672 |
2,2922 |
|
11 |
120325 |
339911 |
0,584455 |
19,407 |
27,2744 |
1,04603 |
1,72192 |
|
12 |
885225 |
335221 |
0,571277 |
18,5817 |
26,3752 |
1,05846 |
1,7859 |
|
13 |
654485 |
225650 |
0,577097 |
18,1954 |
26,37 |
0,883966 |
1,57177 |
|
14 |
541263 |
325852 |
0,564309 |
16,6183 |
24,3225 |
0,807201 |
1,47055 |
|
15 |
116633 |
111856 |
0,599607 |
22,5597 |
30,7084 |
1,29238 |
2,00157 |
|
16 |
774123 |
336214 |
0,629704 |
20,499 |
28,2943 |
1,21975 |
1,9422 |
|
17 |
555236 |
502899 |
0,584854 |
20,4274 |
28,3354 |
1,12509 |
1,8123 |
|
18 |
203265 |
213025 |
0.372122 |
6.76579 |
14.807 |
0.192739 |
1.38204 |
|
19 |
112354 |
565239 |
0.319334 |
6.73003 |
14.6728 |
0.162247 |
1.23175 |
|
20 |
459548 |
365824 |
0.361309 |
6.80957 |
14.9258 |
0.15476 |
1.28074 |
|
21 |
659369 |
147524 |
0.318654 |
6.87234 |
15.0754 |
0.140456 |
1.2272 |
|
22 |
584215 |
753268 |
0.365926 |
6.56857 |
14.3551 |
0.163679 |
1.25831 |
|
23 |
787789 |
989989 |
0.366771 |
6.52882 |
14.4654 |
0.187632 |
1.4107 |
|
24 |
123235 |
654546 |
0.384813 |
7.60551 |
16.1285 |
0.2599 |
1.42453 |
|
25 |
636963 |
147414 |
0.344725 |
6.57443 |
14.6367 |
0.135911 |
1.2607 |
|
26 |
459543 |
302369 |
0.295819 |
6.812 |
14.6297 |
0.17923 |
1.2025 |
|
27 |
645123 |
973451 |
0.338016 |
6.27922 |
13.9954 |
0.105584 |
1.19676 |
|
28 |
645121 |
782223 |
0.326981 |
6.54399 |
14.4811 |
0.106791 |
1.17305 |
|
29 |
915475 |
984123 |
0.358508 |
6.68446 |
14.6201 |
0.188477 |
1.37552 |
|
30 |
990065 |
365852 |
0.336152 |
6.43067 |
14.1962 |
0.149999 |
1.29115 |
|
31 |
745695 |
652354 |
0.325195 |
6.68655 |
14.9192 |
0.147331 |
1.3253 |
|
32 |
569852 |
258741 |
0.357333 |
7.1276 |
15.5344 |
0.205545 |
1.43516 |
|
33 |
659369 |
147524 |
0.318654 |
6.87234 |
15.0754 |
0.140456 |
1.2272 |
|
34 |
65412 |
365984 |
0,32293 |
6,79088 |
14,8843 |
0,155927 |
1,24995 |
|
35 |
990065 |
365852 |
0,61843 |
18,8208 |
26,5865 |
1,09074 |
1,82072 |
|
36 |
256585 |
6523 |
0,638141 |
20,3544 |
28,4439 |
1,14575 |
1,87597 |
|
37 |
555368 |
333652 |
0,603842 |
24,9082 |
33,3464 |
1,52609 |
2,28326 |
|
38 |
352648 |
333652 |
0,558157 |
21,6328 |
30,0966 |
1,17218 |
1,89695 |
5.3 Эффекты взаимодействия и уравнения регрессии
Главные эффекты первого, второго и третьего факторов вычисляются по следующим формулам:
 ,
,
 ,
(5.2)
,
(5.2)
 ,
,
где
 >
>– отклики системы.
>
>– отклики системы.
Эффекты взаимодействия первого и второго, первого и третьего, второго и третьего, первого и второго и третьего факторов вычисляются по следующим формулам:
 ,
,
 ,
(5.3)
,
(5.3)
 ,
,
 ,
,
где
 >
>– отклики системы.
>
>– отклики системы.
Значения эффектов для каждого выходного параметра представлены в таблице 5.4.
Таблица 5.4 – Значения эффектов
|
Параметр |
e>1> |
e>2> |
e>3> |
e>12> |
e>13> |
e>23> |
e>123> |
|
p |
-0,3192115 |
-0,0686965 |
0,06653 |
-0,6994355 |
-0,642834 |
-0,0686965 |
0,062186 |
|
d |
-18,315773 |
-3,1235475 |
3,5655875 |
-25,774998 |
-25,052413 |
-3,1235475 |
0,4575825 |
|
w |
-18,15955 |
-3,30525 |
4,48465 |
-34,1838 |
-32,7314 |
-3,30525 |
0,5327 |
|
Q |
-1,5063818 |
-0,424687 |
0,3191838 |
-1,7749518 |
-1,7066363 |
-0,4246868 |
0,10430775 |
|
L |
-1,1264325 |
-0,556723 |
0,4529075 |
-2,6504325 |
-2,4088725 |
-0,5567225 |
0,1591375 |
Общий вид уравнения регрессии представлен ниже:
 ,
(5.4)
,
(5.4)
где
 - коэффициенты уравнения регрессии.
- коэффициенты уравнения регрессии.
Значения коэффициентов уравнения регрессии представлены в таблице 5.5. Пример вычисления коэффициентов представлен в приложении Б.
Значения коэффициентов уравнения регрессии представлены в таблице 5.5.
Таблица 5.5 – Значения коэффициентов уравнения регрессии
|
Ρ |
d |
W |
Q |
L |
|
-43,2915 |
-235,808 |
-45,0088 |
-59,9977 |
-85,6907 |
|
24,04419 |
144,1403 |
66,1593 |
36,02849 |
57,9095 |
|
3,770473 |
15,9089 |
0,5527 |
4,668797 |
6,93938 |
|
5,335393 |
47,84272 |
27,3329 |
9,391359 |
12,49551 |
|
-2,09804 |
-10,2775 |
-4,1604 |
-2,86784 |
-4,8038 |
|
-0,45454 |
-3,17093 |
-1,445 |
-0,71899 |
-0,98899 |
|
-2,88832 |
-26,2564 |
-17,3224 |
-5,33401 |
-7,76647 |
|
0,248744 |
1,83033 |
1,1306 |
0,417231 |
0,63655 |
Уравнения регрессии для каждого из откликов:
ρ = - 43.2915 +
24.04419m + 3.770473 + 5.335393
+ 5.335393 - 2.09804
- 2.09804 - 0.45454
- 0.45454
 - 2.88832m
- 2.88832m + 0.248744m
+ 0.248744m
 ;
;
d = - 235.808 + 144.1403m + 15.9089 + 47.84272
+ 47.84272 - 10,2775m
- 10,2775m - 3.17093
- 3.17093
 - 26.2564m
- 26.2564m + 1.83033m
+ 1.83033m
 ;
;
w = - 45.0088+ 66.1593m + 0.5527 + 273329
+ 273329 -
4.1604m
-
4.1604m - 1.445
- 1.445
 - 17.3224m
- 17.3224m + 1.1306m
+ 1.1306m
 ;
;
Q= - 59.9977 + 36.02849m + 4.668797 + 9.391359
+ 9.391359 - 2.86784m
- 2.86784m - 0.71899
- 0.71899
 - 5.33401m
- 5.33401m + 0.417231m
+ 0.417231m
 ;
;
l
= -85.6907 + 57.9095m
+ 6.93938 + 12.49551
+ 12.49551 - 4.8038m
- 4.8038m - 0.98889
- 0.98889
 - 7.76647m
- 7.76647m + 0.63655m
+ 0.63655m
 .
.
По уравнениям регрессии для
значения для входных параметров m=2,
 =10,
=10,
 =10
получаем:
=10
получаем:
ρ = 0.4231; d =8.2874; w = 18.1298; Q = 0.1710; l =1.4828.
Для проверки адекватности
уравнений регрессии используем метод
малых приращений. Так, для значений m,
 ,
,
 значения были получены выше. В таблице
5.6 представлены результаты при малом
приращении с (dm
= 0,04),
значения были получены выше. В таблице
5.6 представлены результаты при малом
приращении с (dm
= 0,04),
 (d
(d = 0,2),
= 0,2), (d
(d =0,2):
=0,2):
Таблица 5.6 – Метод малых приращений
|
N |
Dm |
d |
d |
Ρ |
d |
w |
Q |
L |
|
1 |
0 |
0 |
0 |
0.4231 |
8.2874 |
18.1298 |
0.1710 |
1.4828 |
|
2 |
-0,04 |
0 |
0 |
0.4609 |
9.8100 |
19.5541 |
0.3417 |
1.6483 |
|
3 |
0,04 |
0 |
0 |
0.3853 |
6.7568 |
16.7055 |
0.0003 |
1.3173 |
|
4 |
0 |
-0,2 |
0 |
0.4223 |
8.2331 |
18.0510 |
0.1535 |
1.4482 |
|
5 |
0 |
0,2 |
0 |
0.4239 |
8.3336 |
18.2086 |
0.1886 |
1.5174 |
|
6 |
0 |
0 |
-0,2 |
0.4255 |
8.2380 |
17.9598 |
0.1954 |
1.5221 |
|
7 |
0 |
0 |
0,2 |
0.4208 |
8.3288 |
18.2998 |
0.1466 |
1.4435 |
6. Рекомендации по использованию результатов моделирования
После исследования данной имитационной модели массового обслуживания и ее анализа, были получены следующие данные, о том что коэффициент использования системы с тремя заданными параметрами равен 46%, среднее время ожидания 19 секунды, средняя задержка в очереди 9,2 секунды, среднее по времени количество требований в очереди 0,56, среднее по времени количество требований в системе 2,24.
Полученные выходные параметры, свидетельствует о том, что смоделированная нами система массового обслуживания является недогруженной и не достаточно эффективной.
Опираясь на анализ выходных данных моделирования можно сделать следующий вывод: система массового обслуживания будет достаточно эффективной при коэффициенте использования системы 79,9%, который достигается при минимальном количестве устройств равном 1, минимальном времени поступления требования равным 11 секунд и максимальном времени обработки требования равным 9 секунд. При таких входных параметрах системы мы получим среднее время ожидания равное 40 секундам, среднюю задержку в очереди 31,8, среднее по времени количество требований в очереди 2,5, среднее по времени количество требований в системе 3,4.
Следует отметить, что увеличение показателей среднего времени ожидания, средней задержки в очереди, среднего по времени количества требований в очереди и среднего по времени количества требований в системе являются допустимыми для достижения оптимального коэффициента использования системы.
Графики рекомендуемых параметров (коэффициент использования системы, по времени числа требований в очереди и системе) представлены в приложении A на рисунках А.9 и А.10.
Заключение
В процессе роботы над курсовым проектом «Построение и использование имитационных моделей» была разработана и создана программа имитационной модели системы массового обслуживания с циклической дисциплиной с квантом q, тремя входными факторами и пятью выходными параметрами. Задачи, поставленные в ходе курсового проекта, считаются выполненными. На основе статистического анализа выходных данных были даны рекомендации по выбору оптимальных параметров системы.
Список литературы
Кельтон В., Лоу А. Имитационное моделирование. Классика CS. 3-ие изд. – СПб.: Питер; Киев: Издательская группа BHV, 2008.
Советов Б.Я.Моделирование систем: Учебник для вузов 3-е изд., стер. - М.: Высшая школа.,2009.-295с.
Крылов Н.П., Самосвалов И.Т. Учебник по имитационному моделированию экономических процессов. 3-е изд, - Москва 2009- 458с.
Труб И.И. Объектно-ориентированное моделирование на C++, издательство СПб.: Питер; 2008- 346с.
Приложение А
На рисунках А.1, А.2, А.3, А.4, А.5, А.6, А.7, А.8 приведены графики контрольных прогонов для каждого эксперимента факторного плана представлены

Рисунок А.1 – Среднее число
требований в очереди и системе для
факторов m=1,
 =11,
=11,
 =8
=8

Рисунок А.2 – Среднее число
требований в очереди и системе для
факторов m=2,
 =11,
=11,
 =8
=8

Рисунок А.3 – Среднее число
требований в очереди и системе для
факторов m=1,
 =12,
=12,
 =8
=8

Рисунок А.4 – Среднее число
требований в очереди и системе для
факторов m=2,
 =12,
=12,
 =8
=8

Рисунок А.5 – Среднее число
требований в очереди и системе для
факторов m=21,
 =11,
=11,
 =9
=9

Рисунок А.6 – Среднее число
требований в очереди и системе для
факторов m=1,
 =12,
=12,
 =9
=9

Рисунок А.7 – Среднее число
требований в очереди и системе для
факторов m=2,
 =12,
=12,
 =9
=9
Так же рекомендуемыми параметрами использования системы являются параметры, указанные на графике А.9

Рисунок А.9 – Рекомендуемые
параметры использования системы m=1,
 =11,
=11,
 =9
=9

Рисунок А.9 – Рекомендуемый параметр коэффициента использования системы
Приложение Б
Расчет коэффициентов уравнения регрессии для коэффициента использования системы представлены ниже.

где

Для всех остальных выходных параметров коэффициенты уравнения регрессии рассчитываются аналогично.