МПС цифрового оброблення сигналів

Полтавський Військовий Інститут Зв’язку

Кафедра схемотехніки радіоелектронних систем

ОБЧИСЛЮВАЛЬНА ТЕХНІКА ТА МІКРОПРОЦЕСОРИ

напрям підготовки 0924 «Телекомунікації»

МПС цифрового оброблення сигналів.

Полтава – 2006

Навчальна література.

Мюллер, Скотт. Модернізація і ремонт ПК, 16-е изд.: – М.: Издательский дом «Вильямс», 2006. с. 677 – 723.

ЗМІСТ ЛЕКЦІЇ ТА МЕТОДИКА ЇЇ ВИКЛАДЕННЯ

Загальні поняття про МПС ЦОС

Алгоритми ЦОС використовуються для виконання таких операцій, як фільтрація, формування сигналів, виділення сигналів на фоні перешкод, розпізнавання образів і багатьох інших. Раніше ці задачі вирішувалися традиційними методами аналогового оброблення сигналів, але дані методи мають багато недоліків, а саме: невисоку точність перетворень, нестабільність характеристик, низьку надійність, і інші. Використання методів ЦОС дозволяє досягнути якісного поліпшення характеристик реалізованої апаратури.

Сучасні системи ЦОС будуються на основі процесорів цифрових сигналів (ПЦС).

Сигнальними мікропроцесорами (СМП) або процесорами цифрових сигналів називають спеціалізовані процесори, призначені для виконання алгоритмів цифрової обробки сигналів (ЦОС) у реальному масштабі часу.

Стандартна схема МПС ЦОС зображена на рис.1.

Рис. 1. Схема МПС ЦОС

Аналоговий сигнал X(t) перетворюється в цифрову форму в аналого-цифровому перетворювачі (АЦП) і, у вигляді послідовності багаторозрядних двійкових слів X(kt), надходить у СМП. СМП виконує перетворення вхідної послідовності у вихідну Y(kt) відповідно до визначеного алгоритму ЦОС.

Вихідна послідовність двійкових слів Y(k) надходить на вхід цифроаналогового перетворювача (ЦАП), де формується вихідний аналоговий сигнал Y(t). Fg тут – сигнал опорної частоти, яка є частотою дискретизації АЦП та тактовою частотою СМП одночасно.

У процесі аналого-цифрового перетворення можна виділити три етапи: дискретизацію за часом, квантування за рівнем і кодування. Розглянемо сутність цих процесів. При цьому будемо вважати, що в цифрову форму перетвориться сигнал, поданий у формі змінної напруги (див. рис.2).

101

011

010

011

100

101

д)

Рис. 2. Перетворення аналогового сигналу у цифровий

Хай сигнал Uc, що підлягає перетворенню має вигляд, показаний на рис.2а.

Дискретизація за часом полягає в тому, що перетворений сигнал Uc подається не безперервної послідовністю своїх значень, а лише окремими вибірками, відліками Uд, узятими через однакові проміжки часу Тд, називані інтервалами часової дискретизації (див. рис.2в).

Очевидно, що чим менше інтервал дискретизації Тд (чим вище частота дискретизації Fд, тим більше відліків буде узято за одиницю часу), тим точніше дискретний сигнал буде відтворювати вхідний аналоговий. Зі збільшенням же Тд ступінь спотворень перетвореного сигналу зростає.

Для точного відтворення характеру зміни безперервного сигналу його дискретними вибірками необхідно виконати умова теореми дискретизації (теореми Котельникова):

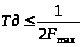або ,

де F_>max> –складова у спектрі безперервного сигналу, що має найбільшу частоту.

Тобто, частота дискретизації (проходження вибірок сигналу) повинна перевищувати (чи, як мінімум, дорівнювати) подвоєну максимальну частоту спектра сигналу, що перетворюється в цифровий вигляд.

Квантування за рівнем полягає в наступному. Створюється (наприклад, за допомогою набору компараторів) сітка так званих рівнів квантування (див. рис.2с), строго фіксованих і зсунутих відносно один одного на величину , що назівають кроком квантування. Далі отримані в результаті дискретизації значення відліків вхідної напруги Uд замінюються найближчими до них рівнями із сітки, що, зрозуміло, породжує помилки квантування сигналу. Помилка квантування значень сигналу (шум квантування) виявляється в межах:

Отже, зі збільшенням числа рівнів квантування в заданому діапазоні значень напруги, тобто зі зменшенням кроку квантування , шум квантування зменшується.

Кодування полягає у заміні рівнів квантування, що є вибірками перетвореного сигналу на їхні порядкові номери (див. рис.2с), подані у двійковому коді. Отримана послідовність двійкових чисел (див. рис.2д), є результатом перетворення аналогового сигналу на цифровий. Зрозуміло, що збільшення числа рівнів квантування з метою зменшення шумів квантування приводить до необхідності збільшення розрядності двійкового коду, який відображує відліки цифрового сигналу.

Аналого-цифрові перетворювачі.

Основними характеристиками АЦП є:

точність;

роздільна здатність, що визначається розрядністю АЦП і максимальним діапазоном вхідної аналогової напруги;

швидкодія, що характеризується часом перетворення, тобто інтервалом часу від моменту зміни сигналу на вході до появи на виході сталого коду.

По своїй структурі (способу побудови) АЦП поділяються на два типи: із застосуванням ЦАП і без них.

2.1. АЦП із проміжним перетворенням напруги в часовий інтервал.

Схема АЦП із проміжним перетворенням вхідної напруги в часовий інтервал подана на рис.3, а тимчасові діаграми, що пояснюють його роботу – на рис.4. Відповідні один одному діаграми на рис.4 і точки схеми на рис.3 позначені однаковими цифрами.

До складу перетворювача входять: ГЛЗН – генератор напруги, що лінійно змінюється ; ГІП – генератор імпульсної послідовності; К1 і К2 – компаратори, лічильник, JK-тригер, кон’юнктор.

Компаратор є, по суті, диференціальним підсилювачем, але з обмеженою вихідною напругою. Він порівнює наявні на двох його входах напруги. У залежності від того, яка з них більша, на виході компаратора одержуємо чи позитивну, чи негативну напругу Us. Слід зазначити, що Us лише по своєму знаку, але не за абсолютним значенням залежить від різниці напруг на входах. Це абсолютне значення залишається постійним незалежно від того, яку різницю напруг – позитивну чи негативну маємо на входах компаратора. Тому +Us може бути використане в якості логічної 1, а Us – у якості логічного 0.

Робочий цикл перетворювача може бути описаний у такий спосіб. Черговий тактовий імпульс, що надходить на вхід ТИ (діаграма 1), встановлює в нульовий стан лічильник і одночасно запускає ГЛЗН (діаграма 2).

Рис. 3. АЦП з перетворенням напруги на часовий інтервал.

Рис. 4. Часові діаграми, що пояснюють роботу АЦП.

Вихідна напруга ГЛЗН надходить на входи компараторів К1 і К2, на інші входи яких подаються відповідно вхідна та нульова напруги. У момент часу, що коли напруга, що лінійно змінюється, зростаючи, проходить нульове значення, компаратор К2 видає імпульс (діаграма 3). JK-тригер переднім фронтом цього імпульсу встановлюється в одиничний стан. При досягненні напругою ГЛІН значення, рівного величині вхідної напруги, імпульс видає компаратор К1 (діаграма 4), повертаючи тригер у нульовий стан.

Очевидно, що час Т, протягом якого тригер знаходиться в одиничному стані (діаграма 5) прямо пропорційний величині вхідної напруги. Протягом цього інтервалу імпульси з ГІП (діаграма 6) через кон’юнктор надходять на вхід лічильника (діаграма 7). Таким чином, число що встановлюється протягом робочого циклу у лічильнику пропорційне значенню вхідної напруги.

З надходженням чергового тактового імпульсу робочий цикл повторюється.

2.2 Схеми АЦП з застосуванням ЦАП

Наявність у схемі АЦП ГЛЗН може бути джерелом значної амплітудної похибки перетворення через нелінійність характеристики генератора. Цей недолік усувається в схемах АЦП, що не містять у своєму складі ГЛЗН. Широко поширені, наприклад, перетворювачі, побудовані за схемою зі зворотним зв'язком, що включає в себе ЦАП.

АЦП зі зворотним зв'язком

Рис. 5. Схема АЦП зі зворотним зв'язком.

Як і в попередній схемі, на початку робочого циклу перетворювача черговий тактовий імпульс, що надходить на вхід ТИ, встановлює в нульовий стан лічильник. На виході ЦАП, код, записаний у лічильнику, перетворюється у нульову напругу Uзс=0. При наявності на вході схеми Uвх>Uзс компаратор К подає на вхід елемента ТА рівень логічної одиниці. При цьому імпульси ГІП проходять на вхід лічильника. Кожен імпульс, що надійшов на вхід лічильника, збільшує на одиницю записане до нього число і збільшує напругу на виході ЦАП на одну «елементарну сходинку». Таким чином, Uзс росте по східчастому законі.

У момент часу, коли Uзс досягає рівня, що перевищує Uвх, компаратор видає на виході рівень логічного 0, імпульси ГІП перестають потрапляти на вхід лічильника. Записане на цей моменту часу у лічильнику число буде пропорційним напрузі Uвх.

АЦП стежачого типу

Обидві розглянуті схеми АЦП працюють у циклічному режимі. У них кожен черговий тактовий імпульс установлює перетворювач у вихідний стан, після чого починається процес перетворення. Очевидно, що швидкодія таких перетворювачів обмежена, головним чином, швидкодією лічильника, що у кожнім циклі починає свою роботу з нульового стану.

На практиці часто використовується нециклічний перетворювач, структурна схема якого показана на рис.6.

Рис. 6. Схема АЦП стежачого типу

Ця схема відрізняється від попередньої тем, що в ній використовується реверсивний лічильник, керований сигналами з виходу компаратора. При Uвх>Uзс лічильник встановлюється в режим прямого рахування, імпульси що надходять на його вхід з ГІП послідовно збільшують записане у ньому число. Напруга Uзс зростає доти, доки не досягне рівня напруги Uвх. При Uвх<Uзс лічильник переходить до режиму зворотного рахування, при якому число, записане в лічильнику, зменшується і, отже, зменшується Uзс, поки не дорівнюватиме Uвх.

Таким чином, усі зміни вхідної напруги Uвх у часі відслідковуються напругою Uзс на виході ЦАП.

Числа, пропорційні значенням Uвх, як і в попередньо розглянутих схемах, знімаються з виходу лічильника.

3. Цифро-аналогові перетворювачі.

Цифро-аналогові перетворювачі (ЦАП) – це пристрої, що перетворюють цифровий код у миттєве значення аналогового сигналу. ЦАП будуються за принципом додавання напруг чи струмів, пропорційних ваговим коефіцієнтам двійкового коду.

Розглянемо принцип побудови ЦАП з додаванням напруг.

Найбільш проста схема ЦАП являє собою вагову резистивну матрицю (Рис.7), на входи якої надходять розряди двійкового кодового слова, наприклад, з виходів паралельного регістра. У такому перетворювачі сума струмів ∑In, що протікають через загальний резистор R_>0>, пропорційна ваговим коефіцієнтам двійкових розрядів, а вихідна напруга (при R_>0><<R)

Uвых = ∑In_>0>

пропорційна двійковому числу.

Рис.7. Найпростішій ЦАП.

об збільшити розрядність перетворюваного двійкового числа, варто підключити резистори 16R_>0>, 32R_>0> і т.д. Найбільші вимоги пред'являються до точності резисторів старших розрядів, оскільки розкид струмів у них не повинний перевищувати струму молодшого розряду.

Головним недоліком ЦАП із ваговими резистивними матрицями є саме те, що в матриці потрібно використовувати велика кількість високоточних резисторів різних номіналів. Виготовлення таких матриць в інтегральному виконанні з необхідною точністю параметрів викликає певні труднощі.

Для подолання цього недоліку використовують окремі вагові матриці для молодших, середніх і старших розрядів двійкового коду з додатковим (пропорційним) розподілом вихідних напруг матриць не старших розрядів - так називані резистивні матриці типу R-2R. У них використовуються резистори усього лише двох номіналів, такі матриці набагато простіше у виготовленні.

Схеми ЦАП з підсумовуванням струмів на резистивних матрицях відрізняються від розглянутих схем тим, що замість джерел стабільних напруг у них використовуються джерела стабільних струмів.

Замість регістра в схемах ЦАП може бути використаний двійковий лічильник прямого рахування. Якщо подати на вхід цього лічильника послідовність імпульсів, то з приходом кожного чергового імпульсу число в лічильнику буде збільшуватися на одиницю і напруга на виході ЦАП буде зростати на квант, що відповідає одиниці молодшого розряду лічильника. Таким чином, напруга на виході ЦАП буде мати східчасту форму, як показано на рис.8.

Після надходження 2ⁿ-1 імпульсів, де n – число станів лічильника, усі розряди лічильника будуть містити 1, на виході ЦАП утвориться максимальна вихідна напруга U_>выхmax>, далі черговим імпульсом лічильник буде скинутий у нульовий стан, нульовим стане і вихідна напруга на виході ЦАП. Після цього лічильник починає знов рахувати імпульси і на виході ЦАП знову формується напруга східчастої форми. Очевидно, що робота такої схеми ЦАП носить циклічний характер. Така схема ЦАП може бути використана, наприклад, у зворотному зв'язку АЦП зі зворотним зв'язком.

Рис.8. До пояснення принципу роботи ЦАП.

кщо в схемі ЦАП використовувати реверсивний лічильник, то він стане нециклічним перетворювачем. Така схема ЦАП може бути використана в схемі АЦП

стежачого типу.

Загальне графічне позначення ЦАП (варіанти показані на рис.9) указує характер перетворення: В чи # –двійковий код, А чи ^ – аналогова інформація.

По такому ж принципі формуються й умовні графічні позначення АЦП.

Рис.9. Умовне графічні позначення ЦАП (варіанти).

В И С Н О В О К

Сучасні системи ЦОС будуються на основі процесорів цифрових сигналів (ПЦС). Сигнальними мікропроцесорами (СМП) або процесорами цифрових сигналів називають спеціалізовані процесори, призначені для виконання алгоритмів цифрової обробки сигналів (ЦОС) у реальному масштабі часу.

У процесі аналого-цифрового перетворення можна виділити три етапи: дискретизацію за часом, квантування за рівнем і кодування. При виконанні дискретизації необхідно забезпечити виконання теореми дискретизації.

Робота великої частини розповсюджених схем АЦП заснована на принципі перетворення рівня вхідної напруги в пропорційне йому кількість імпульсів що надходять до лічильника.

Найпростіші ЦАП будуються за принципом додавання напруг чи струмів, пропорційних ваговим коефіцієнтам двійкового коду на основі резистивних матриц. Для збільшення вихідного сигналу в схемах ЦАП використовують операційні підсилювачі з негативним зворотним зв'язком.