Моделювання процесу обробки сигналів датчика у вихровому потоковимірювачі

Міністерство освіти і науки України

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

Моделювання процесу обробки сигналів датчика

у вихровому потоковимірювачі

Харків 2009р.

Зміст

Вступ

1.Підстава для НДР

2. Мета і призначення НДР

3. Вимоги до виконання НДР

4. Матеріали, що подаються по закінченні НДР

5. Техніко-економічні показники НДР

6. Стадії та етапи виконання НДР

7. Порядок контролю та приймання НДР

Вступ

Серед засобів вимірювання потоку рідини або газу найпростіші за конструкцією та здатністю працювати із засміченими потоками є вихрові потоковимірювачі.

В процесі вимірювання параметрів потоків рідини та газів, що рухаються, з використанням тіла обтікання постає проблема при використанні п’єзоелектричних та тензодатчиків. Вона виникає при вимірюваннях на нижніх частотах, коли амплітуда корисного сигналу, що надходить від датчика, зменшується пропорційно зменшенню інтенсивності потоку газу чи рідини. При зменшенні швидкості потоку в сигналі від датчика буде зменшуватися кількість імпульсів але тільки до критичної межі, а потім, при зменшенні інтенсивності потоку газу чи рідини, різко почне підвищуватися частота імпульсів і лічильник швидкості потоку буде показувати неіснуюче підвищення швидкості потоку. Це обумовлено тим, що амплітуда корисного сигналу зменшується нижче рівня шумів і після формування імпульсів лічильник починає рахувати сигнали від різних перешкод, пов’язаних з роботою насосів та вентиляторів, процесів вихороутворення в місцях опору (вентилі, клапани, коліна, звуження та ін.), вібраційними та акустичними коливаннями, що розходяться по трубопроводу та корпусу пристрою.

Приводом для цієї науково-дослідної роботи (НДР) стала проблема, описана вище, що постала при проведенні експериментів на кафедрі турбінобудування НТУ “ХПІ”. На цій кафедрі зібрали установку для підрахунку швидкості потоку за допомогою вихрового потоковимірювача.

1 Підстава для НДР

Підставою для розробки є тема дипломної роботи:

“Моделювання процесу обробки сигналів датчика у вихровому потоковимірювачі”, видана на кафедрі ОТП НТУ ”ХПI” відповідно до наказу від “08” 11 2004 р. № 2310 – ІІІ.

2 Мета і призначення НДР

В процесі виконання дипломної роботи потрібно розглянути можливі способи обробки сигналів від датчика вихрового потоковимірювача та можливості їх поліпшення.

В даній роботі потрібно проведені числові експерименти з метою з’ясування критичної межі, коли потрібно буде зупинити підрахунок потоку.

Для проведення експериментів потрібно вибрати модель завади та дослідити її характеристики. В процесі проведення числових експериментів потрібно промоделювати та зробити оцінки стосовно можливого використання деяких моделей шумів та фільтрів для них. Також потрібно розглянуті можливі методи для розширення діапазону вимірювань та обрані оптимальні для конкретного випадку.

Призначення НДР полягає у тому, щоб розробити оптимальний метод, алгоритм для обробки даних від датчика вихрового потоковимірювача.

3 Вимоги до виконання НДР

В процесі виконання НДР потрібно:

повинні бути розглянути описану проблему та вже відомі методи вирішення схожих задач;

на базі результатів проведеного аналізу потрібно визначити подальший напрямок роботи;

потрібно розглянути різні можливості отримання псевдовипадкового сигналу для моделювання шуму та визначити параметри отриманих послідовностей;

треба промоделювати декілька можливих варіантів фільтрації вхідної послідовності;

потрібно розглянути та запропонувати інші варіанти по обробці вхідної послідовності викривленого сигналу;

повинні бути запропоновані, на базі результатів проведених експериментів, оптимальні методи обробки послідовностей від датчика вихрового потоковимірювача з оптимальними параметрами.

4 Матеріали, що подаються по закінченні НДР

До складу програмної документації входять:

відомість проекту;

технічне завдання;

пояснювальна записка.

5 Техніко-економічні показники

При розробці програмного забезпечення необхідно виконати техніко-економічне обґрунтування науково-дослідної роботи.

6 Стадії й етапи виконання НДР

Отримання завдання;

збір початкових матеріалів;

огляд літератури й обґрунтування необхідності розробки;

розробка технічного завдання.

техніко-економічне обґрунтування розробки;

розробка та реалізація допоміжних алгоритмів для проведення

експериментів;

оцінка розробки по охороні праці і навколишнього середовища;

оформлення звіту з НДР.

7 Порядок контролю і приймання

При прийманні перевіряється:

комплексність, зміст і оформлення документації НДР;

відповідальність програмного продукту згідно вимогам, висунутим в п. 3 цього документу.

Приймання здійснюється державною екзаменаційною комісією.

ВСТУП

В процесі вимірювання швидкості проходження потоку рідини або газу з використанням вихрового потоковимірювача з тілом обтікання виникає проблема. Вона пов’язана з неможливістю вимірювання з достатньою точністю параметрів потоку за малих інтенсивностей потоку. При зменшенні потоку після деякого критичного значення у сигналі від датчика починається дуже різко підвішується кількість імпульсів. Це пояснюється зменшенням амплітуди корисного сигналу до рівня перешкод. Для точного вимірювання потоку на малих інтенсивностях потрібно додатково обробляти вхідні данні. Це необхідно для діставання з них інформації про корисний сигнал.

В даній роботі були проведені числові експерименти з метою з’ясування критичної межі, коли потрібно буде зупинити підрахунок потоку. В процесі проведення числових експериментів були промодельовані та зроблені оцінки стосовно можливого використання деяких моделей шумів та фільтрів для них. Також були розглянуті можливі методи для розширення діапазону вимірювань та обрані оптимальні для конкретного випадку.

Робота проводилася на підставі технічного завдання на дипломну роботу, виданого на кафедрі «Обчислювальна техніка і програмування» Національного технічного університету «Харківський політехнічний інститут» і затвердженого _________ ______________ 2005 р.

1 Постановка проблеми

Приводом для цієї розробки стала проблема, описана вище, що постала при проведенні експериментів на кафедрі турбінобудування НТУ “ХПІ”. На цій кафедрі зібрали установку для підрахунку швидкості потоку за допомогою вихрового потоковимірювача. Дані отримані при проведені експериментів наведені на рисунку 1.1.

Для визначення частоти синусоїдального сигналу можна скористатися способом наведеним нижче. Частота синусоїдального сигнал викривленого перешкодою буде невизначеною через статичні флуктуації випадкової перешкоди (рисунок 1.2).

Рисунок 1.1 – Залежність частоти імпульсів від швидкості потоку

Особлива легко можна визначити частоту суміші шляхом обчислення статистичного математичного очікування кількості нулів за одиницю часу. Для чистої синусоїди частота гц кількість нулів за секунду дорівнює (рисунок 1.3). Перешкода викликає відхилення математичного відхилення цієї кількості.

Рисунок 1.2 – Суміш синусоїдального сигналу та перешкоди.

Рисунок 1.3 – Синусоїда з частотою = 9 гц і = 18 нулями за секунду.

Цей метод може бути прийнятний для визначення частоти синусоїди, яка має набагато більше амплітуду ніж перешкода.

Коли амплітуда перешкоди сумірна або більше амплітуди корисного сигналу, тоді потрібно приймати заходи для захисту від вібраційних та акустичних перешкод чутливих елементів або використовувати додаткову обробку вхідних даних. Перший метод потребує додаткових складних доробок що можуть бути неприйнятними у багатьох конкретних випадках. Другий метод потребує лише додати між датчиком, що відображає або реєструє пристроєм додатковий елемент, де основним елементом буде мікроконролеру, що буде обробляти вхідні дані та з невеликою затримкою видавати більш чистий, позбавлений, значно, від перешкоди далі для подальшої обробки (рисунок 1.4).

Рисунок 1.4 – Відфільтрований та оброблений сигнал.

Безпосередньо завданням для даної роботі було проведення моделювання процесу обробки сигналу від датчику для з’ясування наскільки покращується сигнал після різних типів обробки та визначити найкращій алгоритм обробки або комбінацію алгоритмів.

2 Опис принципів вихрового обліку потоку рідини або газу

2.1 Турбулентні течії

Течії рідких і газоподібних середовищ бувають двох типів: 1) спокійні, плавні і 2) нерегулярні, зі значним перемішуванням об’ємів середовища і хаотичною зміною швидкостей і інших параметрів. Перші називають ламінарними, а для других англійський фізик У. Томсон запропонував термін "турбулентні" (від англ. turbulent - бурхливий, безладний). Більшість течій у природі й техніку ставляться саме до другого, найменш вивченій групі. У цьому випадку застосовують статистичні (пов'язані з усередненням за часом і простором) способи опису. По-перше, тому, що практично неможливо встежити за пульсаціями в кожній точці течії, а по-друге, ці дані марні: їх не можна використати в конкретних прикладних програмах [2].

Оскільки турбулентність - одне з найглибших явищ природи, при самому загальному підході до його вивчення воно змикається з філософським проникненням у суть речей. Знаменитий учений Т. Кишеня дуже образно це охарактеризував, сказавши, що, коли стане перед Творцем, перше одкровення, про яке буде просити, - розкрити таємниці турбулентності.

Найбільший практичний інтерес представляють такі плини, які відповідають досить більшим числам Рейнольдса.

Число Рейнольдса визначає співвідношення інерційних сил і сил тертя (в'язкості).

Re = v_>0>R/, (2.1)

де Re – число Рейнольдса;

v_>
0> – середня швидкість;

R – поперечний розмір каналу;

- коефіцієнт в’язкості.

З ім’ям англійського фізика і інженера О. Рейнольдса нерозривно пов’язана наука о турбулентних течіях. Йому належить основні початкові результати в даній області, з його робіт почався важливий етап дослідження турбулентності.

Інженерні задачі гідродинаміки потребували систематизації відомостей про важливі макроскопічні властивості турбулентних течій. Така систематизація проводилася. Встановлювалися емпіричні закономірності (для середньої швидкості і розподілення середніх швидкостей по перерізу труби для ефективної в’язкості та ін.), добре узгоджуваний в той чи іншій області вимірювання параметрів з експериментальними даними. Встановлення та використання емпіричних законів – необхідний етап в вивченні та освоєнні будь-якого явища, однак на цьому етапі багато численних “як?” і “чому?” не тільки не знаходять відповіді, але, як правило, не дуже часто і виходять на перший план. Саме працям, які в 1876 р. почав Рейнольдс, було призначено з часом покласти край емпіричній течії у вивченні турбулентності. Систематизуючи та аналізуючи дані про течію рідини по трубах, він основну увагу приділяв переходу ламінарної течії води у турбулентне. Рейнольдс виявив, що перетворення “прямого” руху рідини у “звивистий” відбувається за де якої критичної швидкості , яка зменшується зі збільшення радіусу труби і зі зменшенням в’язкості. Але Головним було те, що йому вдалося встановити закон: безрозмірне відношення.

, (2.2)

де R – радіус труби;

- швидкість течії;

- коефіцієнт в’язкості.

Число Рейнольдса повинно досягти приблизно 2000, щоб ламінарний потік став турбулентним. Наведене відношення – назване на честь Рейнольдса його ім’ям, - дозволяє записати встановлений критерій у вигляді:

, (2.3)

де Re – число Рейнольдса;

- критичне значення числа Рейнольдса, що розділяє ламінарні та турбулентні потоки.

Рейнольдс робив спроби теоретично оцінити і навіть отримав правдоподібні оцінки, але йому не вдалося зробити цього строго.

2.2 Вихороутворення при обтіканні нерухомих тіл

Вихрові об’ємні витратоміри з об’єктом обтікання застосовуються для вимірювання витрат рідини та газів широкому динамічному діапазоні. За основу перетворювачів для вимірювань взяли ефект вихороутворювання у досліджувальному потоці. Згаданий ефект вигідно відрізняється від відомих методів відсутністю рухливих елементів у вимірювальному середовищі, природним частотним виходом сигналу, який легко, без додаткової похибки погоджується з інформаційною системою та обчислювальною технікою, результатами, що добре відтворюється.

Звичайна в’язкість – це макроскопічне проявлення молекулярного руху та перемішування.

Тіло з дуже сильно вираженими розмірами за умов, коли його обтікає речовина, слугує джерелом вихрових коливань.

В’язкість середовища, що обтікає нерухоме тіло, призводить до утворення вихорів у початковому потенціальному потоку. Швидкість потоку на поверхні тіла через приставання рідини дорівнює нулю. Подалі від поверхні вона набуває значення близьке до швидкості набігаючого потоку. Ця зміна швидкості відбувається у межуючому шарі, у якому дія в’язких напруг можливо порівняти зі значенням ефекту, який викликається інерцією.

Товщина межуєчого шару залежить від числа Рейнольдса та довжини шару .

, (2.4)

де - товщина межуєчого шару;

- довжина межуєчого шару;

Re - числа Рейнольда.

Існування прикордонного шару призводить до помітних змін течії позаду тіла. Там з’являється зворотна течія, що має назву точка відриву прикордонного шару. Зворотна течія утворює вихор, що поступово збільшується приблизно до розмірів тіла, який в решті решт відривається від тіла. Те саме має місце і у нижній точці відриву. Але розвиток вихору з одного боку заважає його утворенню з іншого. Тому розвиток вихорів та їх відрив відбувається по черзі то з одного боку то з іншого. Вихорі, що відриваються, утворюють позаду тіла подвійний ланцюжок Кармана. Позаду тіла обтікання потік набуває хвилеподібного характеру течії через періодичні утворення по черзі з протилежних боків. Регулярні вихрові доріжки утворюються, коли число Рейнольда приблизно знаходиться в інтервалі віл 60 до 50000. Для обтікання циліндру і для тіл з гострими гранями до 10000. Для чисел Рейнольдсаа нижче 60 течія позаду циліндру ламінарна, а понад 5000-10000 відбувається повне турбулентне перемішування.

При скінченній довжині тіла, що обтикається, з урахуванням характеру обтікання у місцях закладання порушується когерентність частоти вихороутворення на окремих ділянках тіла. З іншого боку, процес вихороутворення залежить від стану потоку перед тілом обтікання, тому що характер попередніх збурень потоку впливає на місце та час відриву прикордонного слою. Для підвищення стабільності процесів вихороутворення, зменшення лобового спротиву та збільшення інтервалу чисел Рейнольдса, при яких відбувається регулярне вихороутворення, в тілі обтікання передбачають пристрій для підсосу пограничного слою. З цією метою у стінці тіла, що обтикається, паралельно утворюючій циліндра прорізають вузьку щілину, через яку призупинена рідина, що тече у прикордонному шарі, відсмоктується усередину тіла.

Цей спосіб суттєво стабілізує формування завихрень та робить їх незалежними від зовнішніх збурень, зменшує лобовий спротив тіла, що обтикається, тому повне згорнення та відрив вихрової формації не відбувається.

У загальному вигляді частоту перетоків у каналі можна визначити відношенням (2.5) по методу розмірностей з величин, що характеризують потік, який обтікає тіло.

, (2.5)

де - частота вихороутворення;

- безрозмірний критерій, що характеризує потік, який обтікає тіло (число Струхаля);

- швидкість потоку;

- характерній розмір.

Для шару та циліндру під мають на увазі їх діаметри. Для пластинки, що має ширину та товщину , яка стоїть під кутом атаки до потоку,

, (2.6)

де - характерній розмір пластинки;

- ширина пластинки;

- кутом атаки пластинки до потоку;

- товщина пластинки.

При такому визначенні отримаємо з опитних даних, що для циліндру S = 0.2 - 0.21 у зоні ; для пластинки S = 0,165 – 0,18 у зоні при куті атаки від 20 до 90^о. Шахове розташування вихорів на доріжці стале для широкого класу збурень при умові , де - відстань між вихорами по ширині; - відстань між вихорами по довжині.

Вихороутворення у потоці характеризується декількома параметрами, які відрізняють їх від іншої однорідної частини потоку.

Ядро вихору відрізняється зниженим тиском відносно до тиску у потоці, підвищеним значенням швидкості, зниженою густиною у газовому потоці, підвищеною тепловіддачею; ядро вихору прецесує у зоні розширення формуючого патрубку, поступово-обертаючий потік має знижений коефіцієнт витрат у порівнянні з поступовим потоком. Лобовий опір у течії з вихороутворенням швидко збільшується. Вихрові коливання можуть збуджувати резонансну порожнину.

Для виявлення вихрових формацій у потоці за ознакою зниженого тиску у ядрі вихору застосовуються датчики тиску, які розташовують у зоні розширення формуючого патрубку або за тілом обтікання.

Датчик тиску, який розміщують за тілом у регулярну вихрову доріжку, реагує на проходження кожної вихрової формації.

Кожний вихор може бути виділений у потоці по дуже вираженому переважанню тангенціальній складовій швидкості. Датчик у цьому випадку роблять у вигляді нагрітого термоанемометра. Він змінює свій опір пропорційно зміні швидкості ц вихровій формації.

У якості датчика, який реагує на появу вихрового утворення, у потоці може бути використаний малоінерційний термометр, що розміщується у зазначеному місті. При цьому нагрівачем здійснюються нагрів ядра вихору або прикордонного шару на тілі обтікання.

Збільшення необоротних втрат напору, який створюються обертаючої струї збільшенням лобового опору тіла при обтіканні його потоку з вихороутворенням, може бути змінено дифманометром, який визначає різницю тиску у ядрі обертаючої струї та на ЇЇ периферії. Для тіла, яке обтикається, різниця тиску до та після тіла.

У газових потоках процесах вихороутворення пов’язані зі змінами локальної густини. Зменшення тиску у ядрі вихора викликає зменшення густини. Зміну густини у потоці фіксується спрямованим ультразвуковими коливаннями.

Індикація вихрових формацій у пороці може бути здійснена по відбиттю ультразвукової хвилі або по розсіюванню прямої хвилі.

Аналогічна задача може бути розв’язана методами оптичного фіксування. Можна скористатися фотоелектричним способом реєстрації показників тіньового пристрою.

Індикація вихрових коливань може здійснюватися спрощеним методом, якщо у зоні прецесії обертаючого потоку або у зоні вихороутворення за тілом обтікання помістити феромагнітне тіло, яке робить коливання під дією вихорових коливань. Форма феромагнітного тіла може бути обрана найрізноманітнішою: куля, циліндр, крило, лопата.

Під дією знакозмінної реактивної сили, яка викликається порушенням симетрії потоку, що обтікає вихороутворювач, у процесі вихороутворення, тіло обтікання, закріпленого на гнучкій опорі, відбуваються періодичні коливання, частота, яких пропорційна частоті вихороутворенням.

2.3 Приймачі-перетворювачі вихрових коливань

Вихрові коливання, які утворюються тілами обтікання у досліджувальному потоці, сприймаються й перетворюються у електричну форму приймачами-перетворювачами. Приймачі (датчики) розташовують у регулярній вихровій стежці зі тілом або безпосередньо у тілі, використовуючи знакозмінний перетік середовища, який був викликаний процесами вихороутворення.

Приймачі-перетворювачі поділяються на дві основні групи: нерухомі та здійснюючі коливання з частотою вихороутворення. До першої групи відносяться термоанемометри та термістори, мембрана з тензометром, ультразвукові коливання. До другої групи можна віднести коливання, що існують у вихровій доріжці: куля, прапорець, сам вихороутворювач, закріплений на гнучкій основі.

В залежності від типу вимірюваних коливань приймачі-перетворювачі можуть реагувати на коливання тиску, швидкості, температури.

У якості приймачів-перетворювачів тиску частіше використовуються п’єзоелектричні перетворювачі.

У якості перетворювача для датчика з термістором використовується RC-генератор, де термістор є R - елемент генератора.

Датчики тиску та швидкості окремо мають ряд переваг та недоліків. Нагріті термоанемометри не реагують на шумові завади та пульсації тиску, що поширюються у потоці, але верхня межа частотного діапазону їх роботи обмежена тепловою інерційністю термістору, а їх чутливість зменшується зі збільшенням витратами потоку, через те що збільшується інтенсивність охолодження. Датчик тиску п’єзоелектричного типу практично не мають обмежень за частотою перетворюваного сигналу, але потребують вжиття спеціальних засобів для захисту від сторонніх шумів та пульсацій потоку, який вимірюється. Крім цього, при малих витратах різниця тисків між периферією вихору та його центральною зоною невелика, тому виокремити корисний сигнал з малою інтенсивністю фоні шуму дуже важко (рисунок 2.1).

Рисунок 2.1 – корисний сигнал на фоні завади

Для збільшення діапазону вимірюваних витрат можна використовувати комбінацію п’єзоелектричного датчику тиску та нагрітого мікроанемометру.

2.4 Аналіз вихідних сигналів вихрових датчиків

Вихідні сигнали вихрових датчиків в загальному вигляді можна визначити як періодичні полігармонічні процеси. Для тіла обтікання з формою трикутної призми максимум амплітуди сигналу складає третя або п’ята гармоніка. У енергетичному розподілі третя гармоніка досягає 50% , тоді як перша усього лише 18-20% [1]. Для тіла обтікання у формі циліндру також домінує третя гармоніка, але значення першої гармоніки більше. Наскрізні отворі та протоки, перпендикулярні до осі тіла та ті, що мають виходи у зоні вихороутворення, дуже сильно змінюють картину спектрального розподілу. Перша гармоніка стає 80%, третя та п’ята гармоніка дуже зменшуються, у деяких випадках не перевищує 5-6%. Для тіл обтікання у формі трикутної призми, яку повернули вістря до потоку, з паралельною пластиною у основі спектр стає приблизно однорідний без дуже сильно виражених окремих гармонік до третьої.

Енергія більш високих гармонік різко зменшується.

Вихрові генератори (датчик з вихороутворювачем) утворюють перекручування вихідного сигналу через:

накладання на основний сигнал пульсуючих коливань швидкості та тиску. Такі пульсації обумовленні роботою насосів та вентиляторів, процесів вихороутворення в місцях опору (вентилі, клапани, коліна, звуження та ін.);

вібраційні та акустичні коливання, що розходяться по трубопроводу та корпусу пристрою;

фазові викривлення, які виникають в сигналі через зсув розташування точок збору сигналу.

Викривлення по першому пункту значні у генераторах, де знімання сигналу здійснюються одним швидкісним перетворювачем (анемометром, терморезистором та ін.). Використання в якості приймача перетворювача тиску, який з парафазним виходом підключають по диференціальній схемі, значно зменшує рівень завад по першому пункту. Швидкісні приймачі не чутливі до викривлень, що утворюються за першим пунктом. У перетворювачів тиску, що використовують п’єзоелектричні чутливі елементи, вживають заходи для захисту від вібраційних та акустичних завад.

Розглянемо деякі кількісні характеристики.

Можна очікувати лінійну залежність між швидкістю та частотою вихідного сигналу. Цю залежність можна описати лінійним рівнянням регресії:

, (2.7)

де - швидкість вихідного сигналу;

- частота вихідного сигналу;

- нульовий коефіцієнт лінійної регресії;

- перший коефіцієнт лінійної регресії.

Коефіцієнти цього лінійного рівняння регресії обчислюються по відношенням:

, (2.8)

. (2.9)

Коефіцієнт кореляції між об’ємними витратами і частотою основної гармоніки:

, (2.10)

де R - коефіцієнт кореляції;

, - відповідні значення дисперсій [1].

Коефіцієнт кореляції між об’ємними витратами і частотою основною гармоніки дорівнює 0.999. Коефіцієнт кореляції для інших гармонік дорівнює майже нулю. Звідсіля можна зробити висновок, що інформація про змінний параметр має тільки основна гармоніка. Зв’язок між кінетичної енергією потоку, що обертається, та амплітудою першої гармонікою описується нелінійним рівнянням регресії типу

(2.11)

При цьому коефіцієнт кореляції між вказаним значенням наближається до 0,995. Зв’язком інших гармонік зі значенням енергії обертаючого потоку у точці вимірювань можна знехтувати з достатньою точністю. Для вихрових генераторів з тілами обтікання також характерний лінійний зв’язок між частотою вихороутворення і швидкістю потоку у точці обтікання.

Коефіцієнт кореляції для третьої гармоніки наближається до 0,99. У випадку використання тіл обтікання з перпендикулярними отворами коефіцієнт кореляції для першої гармоніки складає 0,98 – 0,99 [1].

Можна зробити деякі висновки про інформаційних характеристиках вихрових генераторів.

Вихрові генератори з тілом обтікання у широкому діапазоні густин окремо для газів та рідини забезпечують лінійну функціональну залежність між частотою однієї з гармонік та значенням витрат в точці обтікання. Зміна в’язкості середовища, яке вимірюють, робить відчутній вплив на значення коефіцієнта кореляції, тому цей тип вихрового генератору знайде, переважно, застосування для вимірювань у газових середовищах.

Амплітуда гармоніки вихідного сигналу, по якій відбувається вимірювання, залежить від енергії вихрової формації. В процесі вимірювання у діапазоні змін швидкості потоку амплітуда змінюється не дуже сильно.

Характерна особливість, яка властива п’єзоелектричним перетворювачам. В момент відкриття та закриття клапану відбувається зміна тиску в системі, що призводить до появи на обкладинках п’єзоелементу статичного заряду. Перезаряд вхідного конденсатору створює на виході підсилювача декілька імпульсів завади, від яких можна позбавитися за допомогою більш ретельного налагодження приймачів перетворювачів тиску.

3 Обчислювальні експерименти з різними моделями завад та фільтрів

Межі вимірювань при використанні вихрових потоковимірювачів кінцеві. Тому що у них частота вихорів при зниженні швидкості зменшується разом з суттєвим зменшенням амплітуди сигналу датчика [3]. Так, експериментально отримана залежність між швидкістю потоку й частотою сформованих імпульсів виглядала як на рисунку 3.1:

Рисунок 3.1 - Залежність частоти імпульсів від швидкості потоку.

Підставою для припинення вимірів є досягнення допустимого рівня похибки, що у свою чергу можна здійснити, оцінюючи кількість “зайвих” сформованих імпульсів при вимірюванні частот сигналу низького рівня.

З наведеного вище рисунка видно, що існує певний рівень, при досягненні якого відбувається нарощування зайвих імпульсів. При низьких частотах і малих рівнях сигналу шуми перебувають в області верхніх вимірюваних частот і фільтрація шумів може шкодити корисним сигналам в області верхніх частот діапазону вимірів, таким чином, коли потік стає ламінарним, спостерігається нагромадження зайвих імпульсів (помилки внаслідок відносного збільшення рівня шуму над корисним сигналом).

При високих частотах, коли частота сигналу більше частоти шуму, може виникнути ситуація, коли амплітуда шуму буде більше амплітуди сигналу. У цьому випадку також будуть помилки.

Вважаємо за можливе при відповідному ускладненні приладу визначати ситуацію, коли варто припинити рахувати імпульси і сповістити користувача або супутні системи про це.

Вираз для обчислення математичного очікуванної кількості нулів для суми фіксованого синусоїдального сигналу й нормального випадкового шуму, запропонований Райсом [4] і отриманий пізніше Бендатом іншим шляхом, за свідченням Бендата «занадто складний для практичних цілей і не узгодиться з результатами крім як у нецікавому випадку, коли синусоїдальна складова відсутня».

У вираз входить інтеграл, що може бути обчислений лише чисельними методами. Для окремих випадків, наприклад, для білого шуму з обмеженою смугою частот, Бендат [5] пропонує вираз:

, (3.1)

де - кругова частота;

p – відношення сигналу до шуму;

a 1 і b 1 константи такі що , де - частота синусоїдального сигналу, - смуга частот, які пропускаються фільтром.

У даній формулі частота синусоїди вважається постійною.

Трохи іншим аспектам присвячена робота [6]. Кедем у своїй роботі [7] застосовує до рішення цього питання спектральний аналіз, а в роботі [8] робить аналіз кількості перетинань методом вищих порядків (Higher Order Crossings). Ідея методу полягає в тому, щоб поєднувати підрахунок кількості переходів через нуль із фільтрами. Пізніше Кедем разом з Барнеттом визначали число переходів через нуль у добутках гаусових процесів [9].

В поданому розділі була проведена робота по визначенню і порівнянню оцінок кількості переходів через нуль, отриманих аналітичним шляхом і шляхом обчислювального експерименту.

Для перевірки виконання на практиці формули (3.1) був проведений експеримент на ПК. Для того, щоб надалі використати отриману модель генератора для розробки алгоритму обробки сигналу.

Проведені розрахунки більш наближені до реальних датчиків.

Параметри, які є незмінними у всіх експериментах наведені нижче:

- мінімальна кількість точок дискретизації на період синусоїди 10;

- мінімальна частота корисного сигналу 20 Гц;

- максимальна частота корисного сигналу 500 Гц;

- довжина випадкової реалізації 4096;

3.1 Обчислювальні експерименти без урахування квадратичної залежності амплітуди від частоти

3.1.1 Фільтрація ковзкого згладжування

Генератором випадкового шуму був обраний стандартний генератор псевдовипадкових чисел c нормальним розподілом у MathCad2001 і генератор псевдовипадкових чисел на зсувних регістрах c зворотним зв'язком, що використовує поліном [10]:

, (3.1)

де - значення самого поліному;

ⁿ – значення відповідних розрядів, де n – номер розряду у вхідному числі.

Були визначені характеристики отриманих псевдовипадкових послідовностей.

До цього шуму був доданий корисний сигнал, що являє собою синусоїду. Формула (1) призначена для обмеженої смуги частот, тому отриману нами суміш шуму й корисного сигналу потрібно пропустити через фільтр.

Для фільтрації обраний метод ковзного згладжування з двома проходами. У першому проході вибірку здійснювали по n=8 елементи, а в другому по n =6.

Потім для отриманої суміші шуму й корисного сигналу в процесі експерименту був проведений підрахунок кількості переходів через нульовий рівень (зі співвідношенням сигнал/шум, що дорівнює: 0.1, 0.5, 1, 5).

На рисунку 3.1 показані залежності, отримані з використанням стандартного генератора псевдовипадкових чисел і на рисунку 3.2 - з використанням генератора псевдовипадкових чисел на ЗРЗЗ.

З використанням формули 3.1 були отримані залежності кількості переходів через нульовий рівень від частоти (при таких же співвідношеннях сигнал/шум). Цей графік подано на рисунку 3.3.

Експеримент з використанням стандартного генератору псевдовипадкових чисел c нормальним розподілом у MathCad2001 був проведений з наступними параметрами:

максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда шуму (середньоквадратичне відхилення) обиралася в залежності від відношення сигнал-шум та діючого значення амплітуди шуму;

Експеримент з використанням генератора псевдовипадкових чисел на ЗРЗЗ був проведений з наступними параметрами:

- максимальна амплітуда шуму 2048

- амплітуда синусоїди 1.5 В (ефективне значення);

- амплітуда синусоїди (ефективне значення) обиралася в залежності від відношення сигнал-шум та середньоквадратичного відхилення шуму.

Рисунок 3.1 - Залежність кількості перетинань нульового рівня від частоти отримані з використанням стандартного генератора псевдовипадкових чисел.

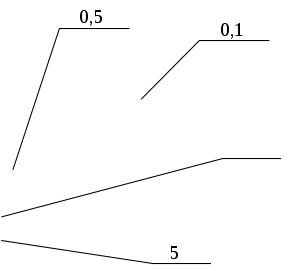
Рисунок 3.2 - Залежність кількості перетинань нульового рівня від частоти отримані з використанням генератора псевдовипадкових чисел на ЗРЗЗ.

Рис. 3.3 - Залежність кількості перетинань нульового рівня від частоти, отримана з використанням формули 3.1.

Як видно з отриманих результатів, характеристики, отримані аналітично й експериментально, мають спільні риси. Причому, є точка перетинання всіх кривих. Однак, у формулі 3.1 не враховується квадратична залежність амплітуди сигналу від частоти. Обчислюється математичне очікування кількості нулів не за певну кількість періодів, а за одиницю часу для суми синусоїдального сигналу й білого шуму з обмеженою смугою частот.

3.1.2 Аперіодичний фільтр

На практиці складно реалізувати фільтр ковзного згладжування, а RC-фільтр набагато простіше. Тому проводимо ще один експеримент де фільтрацію зробимо за допомогою RC-фільтра. Гранична частота при фільтрації 500 Гц.

- максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- фільтра для частоти 500 Гц дорівнює 3,183 *10^-4;

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

Експеримент з використанням генератора псевдовипадкових чисел на СРОС був проведений з наступними параметрами:

- максимальна амплітуда шуму 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда синусоїди (ефективне значення) обиралася в залежності від відношення сигнал-шум та середньоквадратичного відхилення шуму;

- фільтра для частоти 500 Гц дорівнює 3,183 *10^-4;

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

Результати експерименту з використанням генератора псевдовипадкових чисел на СРОС можна побачити на рисунку 3.4.

Результати експерименту з використанням стандартного генератору псевдовипадкових чисел у MathCad2001 можна побачити на рисунку 3.5. Помітні розбіжності спостерігаються при співвідношенні 0,1.

3.2 Обчислювальні експерименти з урахування квадратичної залежності амплітуди від частоти

3.2.1 Фільтрація ковзкого згладжування

Як було вище сказано, у сигналі від реального датчика присутній квадратична залежність амплітуди сигналу від частоти. Обчислюється математичне очікування кількості нулів не за визначену кількість періодів, а за одиницю часу для суми синусоїдального сигналу й білого шуму з обмеженою смугою частот. У подальших експериментах використовується квадратична залежність і підрахунок перетинань на однаковій кількості перетинань.

максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда шуму (середньоквадратичне відхилення) обиралася в залежності від відношення сигнал-шум (відношення сигнал-шум дорівнює 1, коли 1В синусоїди на 500 Гц відповідає шум з амплітудою 1мВ) та діючого значення амплітуди шуму;

- фільтр ковзного згладжування з двома проходами, у першому проході вибірку здійснювали по n=8 елементи, а в другому по n =6.

Результати експерименту з використанням генератора псевдовипадкових чисел на СРОС можна побачити на рисунку 3.6.

- максимальна амплітуда шуму 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда синусоїди (ефективне значення) обиралася в залежності від відношення сигнал-шум (відношення сигнал-шум дорівнює 1, коли 1В синусоїди на 500 Гц відповідає шум з амплітудою 1мВ); та середньоквадратичного відхилення шуму;

Результати експерименту з використанням стандартного генератору псевдовипадкових чисел c нормальним розподілом у MathCad2001 можна побачити на рисунку 3.7. Границя достовірних вимірів за умов використання генератору MathCad2001 у два рази зсунулася у бік високих частот до частоти 130 Гц.

3.2.2 Аперіодичний фільтр

- максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- фільтра для частоти 500 Гц дорівнює 3,183 *10^-4;

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

Результати експерименту з використанням генератора псевдовипадкових чисел на СРОС можна побачити на рисунку 3.8.

- максимальна амплітуда шуму 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- фільтра для частоти 500 Гц дорівнює 3,183 *10^-4;

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

Результати експерименту з використанням стандартного генератору псевдовипадкових чисел у MathCad2001 можна побачити на рисунку 3.7.

3.3 Результати експериментів

Характеристики, отримані аналітично й експериментально без врахування квадратичної залежності між частотою та амплітудою, мають спільні риси. Причому, є точка перетинання всіх кривих. Також були проведені розрахунки більш наближені до реальних датчиків з врахуванням квадратичної залежності амплітуди сигналу від частоти. Обчислювання математичного очікування кількості нулів відбувалося на певному часовому інтервалі так і за певну кількість періодів.

За умов використання фільтрації ковзного згладжування з параметрами, коли при фільтрації залишалися частоти до 600 – 700 Гц, тоді отримані графіки нагадували рис. 4 та рис. 5. При цьому на частоті 500 Гц коефіцієнт передачі падав до 0,2-0,3. Коли фільтрацію зробили після 1000 Гц, на 500 Гц коефіцієнт піднявся до 0,8 – 0,9, тоді отримані графіки стали відповідати отриманим аналітичним шляхом.

При використанні RC-фільтрації з параметром 500 Гц були отримані ті самі рисунок 3.4 та рисунок 3.5.

Такі результати експериментів пояснюються тим, що в теоретичних розрахунках Бендат [5] використовував ідеальний фільтр який має коефіцієнт передачі 1 на частотах, що проходять крізь фільтр і 0 – на тих що фільтруються. Звичайно таку фільтрацію за реальних умов забезпечити неможливо, тому можна спостерігати розбіжності з отриманими результатами експериментальним шляхом.

Експеримент з урахування квадратичної залежності амплітуди від частоти нічого несподіваного не показав. Було підтверджено що за умови збільшення процентної присутності шуму у сигналі межа зменшується з боку низьких частот. Визначили числові значення цих частот за різних співвідношень сигнал/шум.

За умов використання фільтрів, як і очікувалося відбувається збільшення області достовірних вимірів в залежності від співвідношення сигнал/шум.

Результати отримані за умов використання двох різних фільтрів загалом однакові, але з практичної точки зору RC-фільтр набагато простіше зробити. Тому рекомендується використовувати цей фільтр у практичних експериментах.

4 Визначення кількості перетинів корисного сигналу з нульовим рівнем за допомогою методики для квантованого у часі сигналУ

4.1 Визначення дискретної частоти за допомогою перетинів нульового значення

В даному розділі будуть наведені методи ті, що використовують ітеративні фільтраційні процедури для визначення частот сигналів, схованих у шумі компонент. Подана методика використовує параметричну фільтрацію для рекурсивного визначення частот дискретних спектральних компонент.

Визначення частоти – класична задача аналізу часових рядів. Майже сотні років періодограми широко застосовувалися для аналізу та визначення спектрів. Швидке перетворення Фур’є (FFT), що являє собою ефективний алгоритм для оцінки періодограм у частотах Фур’є, підтримує популярність цього важливого інструмента. Але на протязі більш ніж десяти останніх років багато авторів пропонували методи ітеративної фільтрації для визначення частот дискретних гармонік [8, 11-14].

Корисна математична модель, так саме, як і та, що ми використовуємо у цьому прикладі, це наступна суміш сигналів стаціонарного процесу,

, (4.1)

де, - дискретні значення часу;

А та В всі не корельовано, - математичне відхилення, та - дисперсія.

Взагалі, приймаємо - підкрашений стаціонарний шум з нульовим середнім значенням і дисперсією , незалежною від А та В. Шум, приймаємо, має абсолютно неперервну спектральну функцію зі спектральною щільністю , . Для нашої мети ми приймаємо, що {Z_>t>} – Гаусів процес. Але Гаусовість не є необхідною для параметричної фільтрації за методом Яковітца [16]. Також покажемо, що частота для нас є низка упорядкованих констант в межах (0,) [15],

, (4.2)

Загальна задача це визначити частоти , використовуючи кінцеву довжину реалізації (спостереження) з часового ряду Z_>1>, Z_>2>, ...,Z_>N>.

Іншими словами, наша основна стратегія це фільтрувати спостереження Z_>1>, Z_>2>, ...,Z_>N> за допомогою фільтру з параметричного сімейства лінійних фільтрів, спостерігати статистику перетинів нуля виходу фільтру, а потім обирати інший фільтр (зміною параметра) з сімейства на базі статистики, що спостерігається. При деяких умовах ця ітеративна процедура сходиться і точне значення частоти може бути отримане.

4.2 Очікуване число перетинів нуля Гаусова процесу

Нижче подано формули для визначення очікуваної кількості перетинів нуля Гаусова процесу. Наведемо обидва випадки: безперервного та дискретного часу.

Якщо стаціонарний Гаусів процес {Z_>t>}, для , з нормалізованою автокореляційною функцією має дуже гладку форму, що середнє число перетинів нуля за одиницю часу, дорівнює за формолою Райса [4].

, (4.3)

де D – число перетинів нуля у реалізації {Z_>t>} для t у одиничному інтервалі [0, 1];

є друга похідна нормалізованої автокореляційної функції від {Z_>t>} у нулі.

Ялвісакер в 1965 довів формулу Райса строго при пом’якшуючих умовах і показав, що очікувана кількість перетинів нулів скінченна якщо, і тільки якщо, автокореляційна функція двічі може бути диференційована в точці .

Аналогічна формула для дискретного часу, для процесу з нульовим середнім, для стаціонарної Гаусової послідовності {Z_>к>}, була отримана багатьма авторами [7] і виглядає як:

, (4.4)

або, еквівалентно, в інверсній формі:

, (4.5)

де D_>1> – число змін знаків або перетинів нуля у реалізаціях Z_>1>, ...,Z_>N>;

- кореляція послідовності {Z_>к>};

- очікувана число перетинів нуля при дискретному часі.

Ця формула (4.5) має назву – косинусна формула. Спостерігаємо, що через стаціонарність очікуване число перетинів нуля - не залежить від N. Взагалі повинен бути кореляцією, див. Кедем (1991). Оскільки лінійна фільтрація Гаусова процесу дає результат Гаусів процес, косинусна формула придатна для фільтрованого процесу, де кореляційний коефіцієнт і число перетинів нуля фільтрованого процесу використано у косинус ній формулі (4.5). Для точності, нехай буде вихід у момент t з лінійного з незмінними у часі параметрами фільтру L_>a>, що був застосований до процесу {Z_>t>}. Використовуючи косинусну формулу (4.5) і спектральне подання для стаціонарних процесів, коефіцієнти кореляції першого порядку фільтрованого процесу отримаємо вираз [15]:

, (4.6)

де D_>a> – число перетинів нуля в {L_>a>(Z)_>1>, ...,L_>a>(Z)_>N>,};

- функція спектрального розподілу процесу {Z_>t>};

- квадрат коефіцієнту передачі фільтру L_>a>.

Перетини нуля D_>a>фільтрованого часового ряду називаємо “Перетини вищого порядку” або НОС [7].

Для даного з нульовим середнім часового ряду {Z_>к>} і сімейства параметричних фільтрів з пространством параметрів , , відповідає НОС сімейство помічено як .

4.3 НК – алгоритм. Параметричний фільтр АR(1)

Ітеративна схема, наведена нижче, ілюструє метод для виявлення однієї частоти у Гаусовому шумі. Наша модель це (4.1) з р = 1 та білим Гаусовим шумом. Алгоритм має собою наступні гарантії збіжності НОС послідовності до частоти у нашій моделі. Сімейство фільтрів це експоненціальний фільтр, що згладжує, або авторегрсійний порядку 1, АR(1)-фільтр.

Фільтр АR(1), відомий як ( - фільтр) визначається операцією:

, (4.7)

або еквівалентно в його рекурсивній формі:

, (4.8)

де квадрат коефіцієнта передачі фільтру заданий виразом:

(4.9)

де

Параметричний фільтр АR(1) має фундаментальні властивості відносно білого шуму [15].

(4.10)

Тому НОС послідовність та на практиці емпіричні числа або ті, що спостерігаються, перетинів нуля обчислюються по формулі Е[D_>ak>] на кожній стадії в ітерації і шумовий процес не обов’язково повинен бути білим – він повинен бути з неперервним спектром. На рисунку 4.1 можна побачити як підстроюється параметр в залежності від вхідного сигналу у конкретному випадку при використанні даного алгоритму на практиці.

Рисунок 4.1 - Зміна параметра на протязі двадцяти ітерацій.

На рисунку 4.2 показано, як в процесі двадцяти ітерацій змінюється спектр сигналу. Можна побачити, як коефіцієнт передачі, рівномірний по всіх частотах, поступово переходить у бік низьких частот, тим самим виділяючи потрібну частоту корисного сигналу.

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 N

Рисунок 4.2 – Зміна спектру сигналу під час обробки алгоритмом НК.

К – енергетична складова гармонік, N – кількість перетинів нульового рівня

Далі буде показана реалізація алгоритму HK з використанням фільтру AR(1). Реалізація цього алгоритми була виконана з наступними параметрами:

- параметр , де k = 20 – кількість проходів по вхідної послідовності, N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність , D – число перетинів нуля на попередніх інтервалах;

- кількість точок на одному інтервалі N_>i> дорівнює 512;

- кількість періодів синусоїди в одному інтервалі дорівнює 10 і відповідно

кількість перетинів нульового рівня – 20;

- загальна довжина вхідної послідовності дорівнює 16384 точок;

- точок відліку на один період припадає 51;

- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;

- частота синусоїди дорівнює 20.0784 Гц;

- загальна довжина вхідної послідовності 16 секунд;

- кількість перетинів нуля вхідної послідовності 639.

Для проведення експерименту по виявленню корисного сигналу на фоні завади, була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Перед використанням алгоритму HK з фільтру AR(1) попередньо синусоїду з відомими параметрами змішуємо з отриманим шумом. Далі, під час проведення експерименту, можна простежити, як цей алгоритм знаходить у зашумованому сигналі потрібну частоту. Цей процес на протязі двадцяти ітерацій, з новим обчисленням параметру після проходження усієї вхідної послідовності, можна спостерігати на рисунку 4.3.

Рисунок 4.3 - Пошук потрібної кількості перетинів нульового рівня вхідним сигналом. N_>і> - номер ітерації алгоритму, N – кількість перетинів нульового рівня.

Зміну поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру після кожного інтервалу вхідної послідовності, можна спостерігати на рисунку 4.4.

Рисунок 4.4 - Пошук потрібної кількості перетинів нульового рівня вхідним сигналом.

На рисунку 4.4 спостерігаються підвищення поточної кількості перетинів нульового рівня вхідним сигналом рівномірно через однакові проміжки часу. Це пов’язано з тим, що алгоритм починає проходження вхідної послідовності з початку, а історія обчислень була накопичена на інтервалах в кінці послідовності і послідовність була змінена. Тому відбувається швидке підстроювання параметрів під нові інтервали.

З метою визначення ефективності даного алгоритму при обробці сигналу, в якому ефективно значення шуму відносно сигналу дорівнює, більше та менше. Для зручності співвідношення сигнал/завада обираємо наступними: 2, 1, 0,5. Також паралельно провадилися експерименти з ініціалізацією початкового значення параметру наступними значеннями 0,1, 0,5, 0,9, -0,1, -0,5, -0,9.

За для зручності аналізу отриманих результатів було прийнято рішення подавати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожен графік буде подавати інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

Описані експерименти проводилися для двох різновидів алгоритмів HK з використанням фільтру сімейства AR(1).

У першому варіанті алгоритму проводилася зміна поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру після кожного інтервалу вхідної послідовності.

У другому варіанті алгоритму проводилася зміна поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру після проходження усієї вхідної послідовності.

Для отримання моделі завади була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Її амплітуда при генерації задавалася за допомогою стандартного математичного відхилення. Для порівняння амплітуди синусоїди з завадою використовувалося діюче значення амплітуди сигналу синусоїди.

На рисунку 4.5 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5.

Рисунок 4.5 - Залежність кількості перетинів нульового рівня від частоти. Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.1 та А.2.

На рисунку 4.6 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0.5.

Рисунок 4.6 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку 4.7 наведене у збільшеному масштабі результати попереднього експерименту. Це було зроблено для того, щоб більш детально розглянути момент в роботі алгоритму HK з використанням фільтру сімейства AR(1), коли проводиться зміна поточного кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру після кожного інтервалу вхідної послідовності. Це потрібно для щоб детально показати які стрибки відбуваються під час переходу обробки вхідного сигналу з кінця на початок і як їх амплітуда залежить від обирання початкового значення параметру .

Рисунок 4.7 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.3 та А.4.

З проведених експериментів можна зробити висновки стосовно обирання початкового значення параметру для отримання потрібної частоти за найменшу кількість ітерацій, ефективності двох типів алгоритмів HK з використанням фільтру сімейства AR(1), швидкості знаходження потрібної частоти в залежності від співвідношення сигнал/шум.

Висновки такі:

- як і очікувалося, при збільшенні співвідношення сигнал/шум швидкість сходження алгоритму до конкретного значення збільшується;

- найкращі результати були отримані при використанні початкового значення = 0.9;

- результати використання обох алгоритмів НК приблизно однакові.

4.4 Параметричний фільтр МА(1)

Фільтр МА(1) задовольняє фундаментальній властивості відносно білого шуму (4.10). МА(1) – сімейство подібно до - фільтру.

Нехай наша модель буде (4.1) з {Z_>t>}, стаціонарною з нульовим середнім Гаусовими часовими рядами, визначеними як:

, (4.11)

де , ми обмежуємо для зручності.

Вважаємо сімейство {L_>r>} ковзного згладжування першого порядку МА(1), фільтрів , що індексується параметром r, і визначається як:

, (4.12)

і піднесений до квадрату коефіцієнт передачі є

, (4.13)

де ,

Це сімейство складається з простого з імпульсним відкликом фільтром, який демонструє характеристики фільтру нижніх частот для відповідних значень параметра r, який позитивний і демонструє характеристики фільтру високих частот для негативних значень параметру.

Фундаментальна властивість вимагає щоб [15]:

, (4.14)

оскільки нам потрібно щоб шум був білий. Але обчислення невласного інтегралу дає [15]:

, (4.15)

Таким чином нам потрібна репараметризація. Для отримання ре параметризації, яка задовольняє фундаментальній властивості, водимо параметр:

(4.16)

та роз’язуємо відносно r:

(4.17)

Таким чином, вимога фундаментальної властивості задовольняється сімейством, що було репараметризовано за допомогою . Зазначимо, що , тому є привід обмежити .

Наступні експерименти були проведені з метою з’ясування можливостей алгоритму НК з використанням сімейств фільтрів МA(1), визначення кількості перетинів нульового рівня корисним сигналом, що складається з однієї гармоніки постійної за параметрами на всій довжині вхідної послідовності.

Далі буде показана реалізація алгоритму HK з використанням фільтру МA(1). Реалізація цього алгоритми була виконана з наступними параметрами:

- N = 20 – кількість проходів по вхідної послідовності;

- N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність;

- D – число перетинів нуля на попередніх інтервалах;

- кількість точок на одному інтервалі N_>i> дорівнює 512;

- кількість періодів синусоїди в одному інтервалі дорівнює 10 і відповідно кількість перетинів нульового рівня – 20;

- загальна довжина вхідної послідовності дорівнює 16384 точок;

- точок відліку на один період припадає 51;

- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;

- частота синусоїди дорівнює 20.0784 Гц;

- загальна довжина вхідної послідовності 16 секунд;

- кількість перетинів нуля вхідної послідовності 639.

На одному графіку будуть показані результати експериментів з ініціалізацією початкового значення параметру наступними значеннями 0,1, 0,5, 0,9.

Описані експерименти проводилися для двох різновидів алгоритмів HK з використанням фільтру сімейства AR(1).

З метою отримання моделі завади була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Її амплітуда при генерації задавалася за допомогою стандартного математичного відхилення. Для порівняння амплітуди синусоїди з завадою використовувалося діюче значення амплітуди сигналу синусоїди.

На рисунку 4.8 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1.

Рисунок 4.8 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Алгоритм НК з використанням сімейства фільтрів МА(1).

Експерименти з іншими параметрами наведені в додатку А на рисунках А.5.

З наведених результатів експериментів можна зробити висновки стосовно того, що використання сімейства фільтрів МА(1) дає трохи гірші результати.

4.5 Корисний сигнал з двома і більше гармоніками

Наступні експерименти були проведені з метою з’ясування можливостей алгоритму НК з використанням сімейств фільтрів AR(1) визначати кількість перетинів нульового рівня корисним сигналом, що складається з двох гармонік.

Для проведення цього експерименту було зроблено генерування корисного сигналу, що складається з двох гармонік. Для першого випадку з першої та другої гармоніки (рисунок 4.9) і для другого - з першої та третьої (рисунок 4.10).

Рисунок 4.9 - Сигнал з двох гармонік для першого випадку.

Рисунок 4.10 - Сигнал з двох гармонік для другого випадку.

При проведенні експериментів був використаний алгоритм HK з фільтру AR(1). Реалізація цього алгоритми була виконана з наступними параметрами:

- загальна довжина вхідної послідовності дорівнює 16384 точок;

- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;

- загальна довжина вхідної послідовності 16 секунд;

Експерименти були проведені, по схемі вже описаній у підрозділі 4.3.

Отримані результати було прийнято рішення подати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожний графік подає інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

На рисунку 4.11 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5.

Рисунок 4.11 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.6 та А.7.

На рисунку 4.12 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5

Рисунок 4.12 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.8 та А.9.

З наведених результатів експериментів можна зробити висновки стосовно того, що алгоритму НК з використанням сімейств фільтрів AR(1) можна використовувати для визначення кількості перетинів корисного сигналу, після його перекручування завадою.

Висновки:

- результати при використанні двох підтипів алгоритмів сходяться до різних значень через різні гармонічні складові вхідного корисного сигналу;

- завдяки де яким технічним доробкам, що були наведені у другому розділі, основна енергія корисного сигналу концентрується в першій гармоніці. Це дозволяє використовувати описаний алгоритм при обробці даних, що будуть надходити від вихрового потоковимірювача з дослідженими варіантами вхідного сигналу.

4.6 Корисний сигнал, що змінює частоту у часі

Наступні експерименти були проведені з метою з’ясування можливостей алгоритму НК з використанням сімейств фільтрів AR(1) визначати кількість перетинів нульового рівня корисним сигналом, який динамічно змінює власну частоту випадковим чином.

Для проведення цього експерименту було зроблено генерування синусоїди з випадковою зміною частоти. Після розбивання отриманого сигналу на тридцять два інтервали було з’ясовано, що на кожний інтервал у середньому припало приблизно 19.8 перетинів нульового рівня.

- загальна довжина вхідної послідовності дорівнює 16384 точок;

- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;

- загальна довжина вхідної послідовності 16 секунд;

Експерименти були проведені по схемі вже описаній у підрозділі 4.3.

Після отримання результатів для їх відображення було прийнято рішення подати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожний графік подає інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

На рисунку 4.13 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5

Рисунок 4.13 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.10 та А.11.

На рисунку 4.14 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5

Рисунок 4.14 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.12 та А.13.

З наведених результатів експериментів можна зробити висновки стосовно того, що, при використанні алгоритму НК з сімейств фільтрів AR(1), для виявлення кількості перетинів нульового рівня корисним сигналом, який динамічно змінює власну частоту випадковим чином.

Висновки такі:

- вихідні результати мають досить велику похибку.

- для того щоб обійти цю заваду потрібно буде розбивати вхідну послідовність на невеликі частини, щоб зміна частоти у ній була не дуже значною. За таких умов описаний алгоритм можна буде використовувати для обробки даних від вихрового потоковимірювача;

- також потрібно дослідити (попередньо реальні умови яких будуть проходити вимірювання швидкості потоків) на наявність швидких, різких та частих змін параметрів потоку. У реальних потоків дуже швидко параметри не змінюються, зазвичай, через згладжування різких коливань.

5 Комбінування алгоритму НК з попередньою фільтрацією фільтром низьких частот

У подальших дослідженнях було прийнято рішення поєднати два методи для отримання кращих результатів. Спочатку проводиться фільтрація вхідної послідовності за допомогою фільтра нижніх частот, а потім проводиться обробка отриманої послідовності за допомогою алгоритму AR(1) для виявлення частоти корисного сигналу більш точним методом, ніж простим підрахунком перетинів корисного сигналу з нульовим рівнем.

Довжина вхідної послідовності зменшувалася пропорцій зменшенню частоти сигналу для того, щоб кількість перетинів нульового рівня залишалася постійною і дорівнювала 32 перетинам.

У сигналі від реального датчика присутній квадратична залежність амплітуди сигналу від частоти. Обчислюється математичне очікування кількості нулів за одиницю часу для суми синусоїдального сигналу й білого шуму з обмеженою смугою частот. У подальших експериментах використовується квадратична залежність між частотою та ефективним значенням амплітуди корисного сигналу

В процесі проведення цього експерименту синусоїда генерувалася кожного разу заново для нової частоти на всьому діапазоні частот, що досліджуються. Для отримання моделі перешкоди була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Її амплітуда при генерації задавалася за допомогою математичного відхилення. Для порівняння амплітуди синусоїди з перешкодою використовувалося діюче значення амплітуди сигналу синусоїди. Амплітуда синусоїди обиралася в залежності співвідношення сигнал/шум на початку експерименту.

- , де k = 20 – кількість проходів по вхідної послідовності, N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність, D – число перетинів нуля на попередніх інтервалах;

- мінімальна кількість точок дискретизації на період синусоїди 10;

- мінімальна частота корисного сигналу 20 Гц;

- максимальна частота корисного сигналу 500 Гц;

- довжина випадкової реалізації 4096;

- максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

За для зручності аналізу отриманих результатів було прийнято рішення подавати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожний графік подає інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

З метою визначення ефективності даного алгоритму при обробці сигналу, в якому перешкода відносно сигналу дорівнює, більше та менше. Для зручності співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

Початкове значення коефіцієнту ініціалізується значеннями: 0,5;

Обробка еквівалентна проходженню через інтегруючий RC-фільтр.

На рисунку 5.1 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму на ЗРЗЗ;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

Рисунок 5.1 - Залежність числа перетинів нульового рівня від частоти. Використаний генератор псевдовипадкових чисел на ЗРЗЗ.

Обробка еквівалентна проходженню через інтегруючий RC-фільтр.

На рисунку 5.2 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму стандартний з середовища Mathcad;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

Рисунок 5.2 - Залежність числа перетинів нульового рівня від частоти. Використаний генератор псевдовипадкових чисел стандартний з середовища Mathcad.

Обробка еквівалентна проходженню через інтегруючий RC-фільтр та подальшій обробці за допомогою AR(1) алгоритму.

На рисунку 5.3 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму на ЗРЗЗ;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

Рисунок 5.3 - Залежність числа перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел на ЗРЗЗ.

Додаткова обробка за допомогою НК алгоритму.

На рисунку 5.4 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму стандартний з середовища Mathcad;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

Рисунок 5.4 - Залежність числа перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел стандартний з середовища Mathcad.

Додаткова обробка за допомогою НК алгоритму.

Висновки такі:

- на високих частотах на корисний сигнал від датчика завада майже не впливає, але на низьких, коли амплітуда корисного сигналу значно зменшується, через заваду дуже стрімко починаються з’являтися зайві перетини нульового рівня;

- після поєднання двох методів, які окремо покращували результати обробки, результати експериментів покращились;

- отримані результати суттєво розширили у бік низьких частот можливий діапазон вимірювань потоків при вимірювані за допомогою вихрового потоковимірювача.

6 ОХОРОНА ПРАЦІ І НАВКОЛИШНЬОГО СЕРЕДОВИЩА

6.1 Загальні питання охорони праці

Охорона праці — це система законодавчих актів, соціально-економічних, технічних, гігієнічних, лікувально-профілактичних заходів і засобів, що забезпечують безпеку, збереження здоров’я і працездатності людини в процесі труда.

Максимальне зменшення числа шкідливих впливів, створення комфорту — от головні задачі охорони праці.

Тема дипломної роботи — “Моделювання процесу обробки сигналів датчика у вихровому потоковимірювачі”.

Машинний зал ПЕОМ є помешканням з підвищеною небезпекою поразки людини електричним струмом, тому що в даному помешканні присутня можливість одночасного доторку людини до металоконструкцій будинків і т.п., які мають сполучення з землею, з одного боку, і до металевих корпусів електроустаткування - з іншого.

По характеру навколишнього середовища, машинний зал ПЕОМ відноситься до класу нормальних, тому що в ньому відсутні ознаки властиві помешканням жарким, курним і з хімічно активним середовищем. По характеру зорової роботи, робота відноситься до середньої точності, розряд зорової роботи IV, підрозряд зорової роботи В, найменший розмір об'єкта розрізнення 0,5-1,0 мм, контраст великий, фон темний.

При виконанні науково-дослідницької роботи зростає нервово-емоційна напруга. Причиною її виникнення може бути відхилення реального результату від запланованого, невідповідність інтенсивності інформаційних потоків індивідуальним можливостям людини, несприятливий вплив виробничого середовища й інших факторів, що викликають негативні емоції.

Тому для науково обгрунтованого підходу до оптимізації розумової праці, одержання необхідних даних оптимальних умов праці повинно здійснюватися комплексно з застосуванням знань по промисловій санітарії й ергономіці.

Розроблення програмних продуктів відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи оператора і науковця при проектуванні або дослідженні об'єкта.

6.2 Характеристика помешкання для роботи на ЕОМ

У цьому пункті розглядається характеристика помешкання по небезпеці поразки електричним струмом та характеристика помешкання по пожежній небезпеці.

Помешкання повинно бути світлим, сухим і теплим. Підлоги робляться рівними, без вибоїв, щільними, мають не слизьку і зручну для чищення поверхню, і утримуються в чистоті.

Радіатори і трубопроводи опалювальної і водопровідної систем обладнюються діелектриками. Закриваються огородженнями. Не можна застосовувати огородження з ДСП, шаруватого паперового пластика і т.п.

Категорія помешкання по пожежній небезпеці — В, тому що присутні тверді спалимі речовини і матеріали.

Клас помешкання по пожежній небезпеці — П-IIа, відповідно до ПУЭ-87 «Правила устройства электроустановок» [21], ступінь вогнестійкості будинку – II, тому що максимальна кількість поверхів у будинку – 3.

6.3 Виробнича санітарія

Продуктивність праці багато в чому залежить від умов на виробництві, таких як: освітлення, склад повітря, шуми, шкідливі випромінювання. Ці параметри по окремості й у комплексі впливають на організм людини, визначаючи його самопочуття.

Категорію роботи враховуємо по фізичному навантаженню.

По енерговитратах організму науково-дослідна робота відноситься до категорії 1а (легкої), тому що робота відбувається сидячи, не потребує систематичної фізичної напруги або підняття і перенесення тяжкостей (витрата енергії при виконанні роботи до 150 ккал/година).

6.4 Метеорологічні умови при роботі

Метеорологічні умови на виробництві або мікроклімат визначають наступні параметри: температура (C), рухливість (м/с), відносна вологість повітря (%) і теплове випромінювання.

Оскільки науково-дослідна робота відноситься до легкої фізичної роботи, але характеризується напруженою розумовою працею, то керуючись ГОСТ 12.1.005-88 «Общие санитарно-гигиенические требования к воздуху рабочей зоны» [22], оптимальні параметри мікроклімату для виконання роботи повинні знаходитися в межах, зазначених у таблиці 6.1. Параметри є оптимальними, тому що категорія розумової роботи напружена.

Категорію роботи враховуємо по фізичному навантаженню. Наша робота відноситься до категорії Iа, тобто витрата енергії при виконанні роботи до 120 ккал/година і не потребує фізичної напруги.

Таблиця 6.1 — Оптимальні параметри мікроклімату

Категорія роботи

(фізична)

Період року

Температура

t, С

Відносна вологість,

Швидкість руху повітря

V, м/с

Легка робота Iа

Холодний

22...24

40...60

0,1

Легка робота Iа

Теплий

23...25

40...60

0,1

Для забезпечення вищевказаних оптимальних метеорологічних умов у помешканні передбачена система опалення (загальне парове), вентиляції (загальна приточно-витяжна штучна) і кондицюювання відповідно до СНиП 2.04.05-86 «Строительные нормы и правила. Отопление. Вентиляция и кондиционирование воздуха» [23].

Розрахунок необхідної кількості кондиціонерів, повинен здійснюватися по теплонадлишкам від машин, людей, сонячної радіації.

Режим роботи кондиціонера повинен забезпечити максимально можливе надходження зовнішнього повітря, але не менше 50% від продуктивності кондиціонера.

При проектуванні дисплейних класів ВУЗів необхідно передбачати приточно-витяжну вентиляцію. Подача повітря повинна відбуватися у верхню зону малими швидкостями з розрахунку створення рухливості повітря на робочому місці студента менше 0,1 м/с, краще через підшивну гофровану стелю. Витяжка — природна з верхньої зони стіни, протилежної віконним прорізам.

Якісний состав повітря: утримання кисню в дисплейному класі повинно бути в межах 21-22 об.%. Двоокис вуглецю не повинна перевищувати 0,1 об.% , озон — 0,1 мг/м³, аміак — 0,2 мг/м³, фенол — 0,01 мг/м³, хлористий звинувачував — 0,005 мг/м³, формальдегід — 0,003 мг/м³.

Значення надлишку явного тепла не перевищує 23 Дж/м³. Для підтримування в помешканні даного температурного режима відповідно до вимоги СНиП 2.04.05-86 «Строительные нормы и правила. Отопление. Вентиляция и кондиционирование воздуха» [23] є централізоване опалення (загальне парове), штучна вентиляція (загальна приточно-витяжна штучна).

6.5 Освітлення

В даний час багато видів науково-дослідницьких робіт виконуються на ЕОМ. Особливістю роботи за дисплеєм ЕОМ є постійна і значна напруга функцій зорового аналізатора, обумовленого необхідністю розходження об'єктів, що самосвітяться, (символів, знаків і т.п.), при наявності відблисків на екрані, рядковій структурі екрана, мерехтінням зображення, недостатньою чіткістю об'єктів розходження.

Працездатність оператора багато в чому залежить від освітлення. Незадовільне освітлення кількісно або якісно стомлює не тільки зір, але і викликає стомлення організму в цілому, впливає на продуктивність праці оператора.

Для забезпечення нормального освітлення застосовуються природне і штучне освітлення, а також змішане, що нормуються будівельними нормами і правилами СНиП II-4-79 «Строительные нормы и правила. Естественное и искусственное освещение» [24].

6.5.1 Природне освітлення

Всі виробничі помешкання, із постійним перебуванням у них людей, відповідно до санітарних норм і правил, мають природне освітлення.

У нашому випадку використовується бічне двостороннє природне освітлення. Природне освітлення нормується коефіцієнтом природного освітлення (КПО) по СНиП II-4-79 «Строительные нормы и правила. Естественное и искусственное освещение» [24].

Нормовані значення КПО для будинків, розташованих у IV поясі світлового клімату визначаються по такій формулі:

(6.1)

де — значення КПО для III пояса світлового клімату СНД, складає 1,5;

m — коефіцієнт світлового клімату (для м.Харкова m=0,9%);

c — коефіцієнт сонячності клімату, дорівнюється 0,8.

6.5.2 Штучне освітлення

У лабораторії застосовується загальне штучне освітлення, у холодні періоди року — сполучене.

Результати розрахунку параметрів освітлення приведені в таблиці 6.2.

Таблиця 6.2 - Параметри освітлення

Мінімальний розмір об'єкта розрізнення, Мм	Фон	Контраст	Розряд, подрозряд зорової роботи	Нормоване значення
Природне освітлення	Штучне освітлення
,%	,%	Е, лк	Тип ламп
Від 0,5 до 1,0	темний	середній	IV, б	1,5	1,08	500	газоразрядні

Дослідження параметрів освітлення показали, що характеристика зорової роботи є середньої точності.

У якості джерела світла рекомендується використовувати люмінісцентні лампи потужністю 40 Вт або енергоекономні потужністю 36 Вт типу ЛБ, ЛХБ, або ЛДЦ як найбільше ефективні і прийнятні з погляду спектрального складу, колірна температура (Т_>ца>) випромінювання яких знаходиться в діапазоні 3500-4200 К.

При проектуванні ОП з люмінісцентними світильниками в дисплейному класі доцільно вибирати коефіцієнт запасу, рівний 1,4. Відповідно до СниП II-4-79 «Строительные нормы и правила. Естественное и искусственное освещение» — «Природное и искусственное освещение. Нормы проектирования» [24].

Допустима величина дискомфорту, одного з якісних параметрів ОП що регламентується для обмеження прямої блескості, не повинна перевищувати 15. При проектуванні ОП варто користуватися інженерним методом оцінки сліпучої дії ОП по дискомфорті.

Розмір коефіцієнта пульсації не повинен перевищувати 10%, для чого варто застосовувати багатолампові світильники з компенсуючими ПРА, здійснювати розфазування світильників при електромонтажі ОП.

Для освітлення дисплейного класу рекомендується застосовувати світильники серії ЛП013, ЛП031, ЛП033 виконання 001 і 006, ЛС002, ЛС004. З металевою решіткою, що екранує, і непрозорими боковинами.

6.5.3 Розрахунок освітлення робочого місця

Виконаємо розрахунок коефіцієнта освітлення робочого міста. Коефіцієнт природного освітлення приблизно розраховується за наступною формулою:

, (6.2)

де _>ок> — світлова характеристика вікна;

К_>з> —коефіцієнт запаса, який враховує зниження освітленості в процесі експлуатації осклення;

S_>n>=A∙B площина підлоги приміщення;

К_>зд> — коефіцієнт, який враховує затемнення вікон будівлями, які розташовані напроти;

_>ок> — загальний коефіцієнт світлопропускання:

_>ок>= _>1>+ _>2>+ _>3>+ _>4>, (6.3)

де _>1> — коефіцієнт, який враховує вид світлопропускаючого матеріала;

_>2> — коефіцієнт, який враховує вид переплетення;

_>3> — коефіцієнт, який враховує вид несущих конструкцій покрівель;

_>4> — коефіцієнт, який враховує загублення світла в сонцезахисних пристроях;

r_>1> — коефіцієнт, який враховує вплив відображеного світла при боковому освітленні;

е_>н> — нормоване значення КПО в відсотках з урахуванням характера зорової роботи, вида освітлення та світлового клімата в районі розташування будівлі.

(6.4)

де е^ІІІ — значення КПО з урахуванням характера зорової роботи та вида освітлення;

m — коефіцієнт світлового клімата (m=0,9);

с — коефіцієнт сонячності клімата (с=1).

Отримуємо норомоване значення КПО: е_>н>=1,35%.

Площина приміщення дорівнює S_>n>=А∙В=6∙5=30м². Висота приміщення h=3,5м.

Знаходимо значення світлової характеристики _>ок> при відношенні глибини приміщення В до його висоти від рівня умовної робочої поверхні до верха вікна h_>1>.

h_>1>= h-0,4-0,7=2,4м.

В/ h_>1>=5/2,4=2,08, А/В=6/5=1,2.

При даних параметрах значення характеристики _>ок>=15.

Коефіцієнт запаса К_>з>=1,2.

Знайдемо _>ок>. Вид світлопропускаючого матеріала _>1>=0,8 (скло віконне листове подвійне), вид перетину _>2>=0,65 (перетин для вікон житлових будівель деревяниі подвійні розділені), несучі поверхні _>3>=0,8 (балки та рамі суцільні при висоті січення 50см та більше), сонцезахисні пристрої, вироби та матеріали _>4>=0,75 (стаціонарні жалюзі вертикальні). Виходячи з цих даних, _>ок>=0,312.

Для розрахунку r_>1> необхідно знайти відношення відстані l розрахункової точки від наружної стіни до глибини приміщення В та коефіцієнт віддзеркалення стелі, стін та підлоги. В нашому випадку l=4 (точка, яка розташована в одному метрі від стіни напроти віконних отворів). Таким чином відношення l/B=4/5=0,8. Коефіцієнт віддзеркалення 0,5. Маємо r_>1>=3,1.

Коефіцієнт К_>зд> враховує затемнення вікон будівлями, які розташовано напроти, в залежності від відстані між будівлями. В нашому випадку коефіцієнт дорівнює 1, тому що не маємо будівель, які розташовано напроти.

Тепер перейдемо до розрахунку коефіцієнта освітлення робочого місця.

(6.5)

Таким чином отримали коефіцієнт, який являє собою сумарну площину віконних отворів.

6.6 Шум

У помешканні лабораторії причиною шуму є апарати, прилади й устаткування (друкувальні пристрої, комп’ютери і т.д.). Відповідно до вимог ГОСТ 12.1.003-83 «Шум. Общие требования безопасности» [25], рівні звука в помешканні лабораторії, де працює обслуговуючий персонал, не перевищують 50 дБА.

Крім чуйного діапазону частот у дисплейному класі можуть бути присутнім і шуми що не відчуваються слуховим апаратом людини: інфразвук (<20 Гц) і ультразвук (>20000 Гц), що надають шкідливий вплив на організм і психіку людини.

Для зниження рівня шуму відповідно до ГОСТ 12.1.003-83 «Вибрация. Общие требования безопасности» [26], стеля або стіни вище панелей (1,5 -1,7 м. від підлоги), а іноді і стіни і стеля повинні обиватися звуковбирним матеріалом із максимальним коефіцієнтом звукопоглинання в області частот 63-8000 Гц.

Додатковим звукопоглинанням у дисплейному класі можуть бути занавеси, підвішені в складку на відстані 15-20 см. від огородження, виконаного з щільної важкої тканини. Ширина занавеси повинна бути в два рази більше ширини віконного прорізу.

Вібрація буває загальною (транспортна, транспортно-технологічна, технологічна) і локальна. У нашому випадку присутня загальна вібрація, джерелом якої є кондиціонери, копіювальна техніка (зокрема принтери) і системні блоки ЕОМ. Критерій впливу вібрації «комфорт».

Вібрація, як і шум, робить шкідливий вплив на організм і психіку людини (особливо низькочастотна вібрація). Вібрація з частотою до 10 Гц є найбільше небезпечною, тому що збігається з частотою коливання внутрішніх органів.

Основними методами захисту від шуму і вібрації є:

- зниження шуму і вібрації в джерелі (підставки, шумопоглинаючі корпуса);

- зниження шуму і вібрації на шляху поширення (ширми, шумопоглинаючі стійки);

- застосування індивідуальних засобів захисту;

- організаційно-профілактичні методи захисту.

6.7 Випромінювання від екрана

ЕЛТ генерує декілька типів випромінювання, у тому числі: гама тормозне, рентгенівське, радіочастотне, мікроволнове, видиме, ультрафіолетове й інфрачервоне випромінювання. Рівні цих випромінювань не перевищують діючих норм.

Конструктивне рішення екрана дисплея таке, що рентгенівське випромінювання від екрана на відстані 10 см не перевищує 100 мкР/г.

У помешканнях із дисплеями необхідно контролювати аероіонізацію. У таблиці 6.3 наведені рівні іонізації повітря робочої зони ОЦ.

Таблиця 6.3 – Рівні іонізації повітря робочої зони ОЦ

Значення рівнів	Кількість іонів на см3 повітря
П+	П-
1) Мінімально необхідна кількість іонів	400	600
2) Оптимальна кількість іонів	1500-3000	3000-5000
3) Максимально допустима кількість іонів	50000	50000

Варто враховувати, що м'яке рентгенівське випромінювання, що виникає при напрузі на аноді 20-22 кВ, а також напруга на струмоведучих ділянках схеми викликає іонізацію повітря з утворенням позитивних іонів, що вважаються несприятливими для людини.

6.8 Техніка безпеки

Через те, що лабораторія, де знаходяться ЕОМ, не є помешканням із підвищеним утриманням механічних, теплових або радіаційних небезпек, але є споживачем електричної енергії (трифазна мережа перемінного струму напругою 220 В та частотою 50 Гц), в даному помешканні є небезпека поразки людини електричним струмом. Тому при розгляді питань техніки безпеки обмежимося розглядом електробезпеки.

Передбачено такі міри електробезпеки:

- конструктивні заходи електробезпеки;

- схемно-конструктивні заходи електробезпеки;

- експлуатаційні заходи електробезпеки.

6.8.1 Конструктивні заходи електробезпеки

Конструктивні заходи безпеки спрямовані на запобігання можливості дотику людини до струмоведучих частин.

Для усунення можливості дотику оператора до струмоведучих частин, усі рубильники встановлені в закритих корпусах, усі струмоведучі частини розміщені в захисному корпусі або мають захисний прошарок ізоляції, що виключає можливість дотику до них, застосовується блоковий монтаж. Живлячий електричний ланцюг має ізоляцію, виконану відповідно до ГОСТ_14254-80 «Электрооборудование напряжением до 1000 В. Оболочки. Степени защиты» [27]. Ступінь захисту устаткування відповідає IР44 (де 4 захист від твердих тіл розміром більш 1 мм; 4 — захист від бризг) відповідно до ПУЭ-87 «Правила устройства электроустановок».

Відповідно до ГОСТ 12.2.007.0-75* «Изделия электротехнические. Общие требования безопасности» [28] приймаємо I клас захисту від поразки електричним струмом обслуговуючого персоналу тому, що комп'ютер має робочу ізоляцію й елементи занулення.

6.8.2 Схемно-конструктивні заходи електробезпеки

Забезпечують безпеку дотику людини до металевих не струмоведучих частин електричних апаратів при випадковому пробої їхньої ізоляції і виникнення електричного потенціалу на них.

Живлення здійснюється від трьохпровідної мережі: фазовий дріт, нульовий робочий дріт, нульовий захисний дріт.

Тому що напруга менше 1000 В, але більше 42 В, то відповідно до ГОСТ 12.1.030-81 «Электробезопасность. Защитное заземление. Зануление» [29] із метою захисту від ураження електричним струмом застосовуємо занулення, тому що лабораторія є помешканням із підвищеною небезпекою поразки людини електричним струмом, так як можливий одночасний дотик людини до металоконструкціями будинків, маючим з’єднання з землею, і т.п. з одного боку, і до металевих корпусів електронного устаткування — з іншого боку.

Занулення — навмисне електричне з’єднання з нульовим захисним провідником металевих не струмоведучих частин, що можуть виявитися під напругою.

Принцип діяї занулення — перетворення пробою на корпус в однофазне коротке замикання з метою викликати великий струм, здатний забезпечити спрацьовування захисту і тим самим автоматично відключити ушкоджену установку від живлячої мережі.

Занулення потребує наявності в мережі нульового дроту, глухого заземлення нейтралі джерела струму і повторного заземлення нульового дроту (Рис. 6.8.1).

По засобу захисту від поразки електричним струмом проектована система відноситься до I класу відповідно до ГОСТ 12.2.007.0-75* «Изделия электротехнические. Общие требования безопасности» [28].

U_>Ф> I_>КЗ> I_>КЗ>

I_>н> I_>ПЗ> I_>ПЗ> NP I_{>З NЗ}>

I_>З> 2

R_>0> R_>п>

I_>З> 1 I_>З>

I_>З>

Рис. 6.1 — Принципова схема занулення

Умовні позначення:

1 – корпус електроустановки;

2 – апарати захисту від струмів КЗ (запобіжники);

R_>o> – опір заземлення середньої точки обмотки джерела струму;

R_>п> – опір повторного заземлювача нульового захисного провідника;

I_>КЗ>– струм короткого замикання;

I_>н>– частина струму короткого замикання, що протікає через нульовий захисний провідник;

I_>з>– частина струму короткого замикання, що протікає через землю.

Призначення елементів занулення:

- призначення нульового захисного провідника — забезпечити необхідне для відключення установки значення струму однофазного короткого замикання шляхом створення для цього струму ланцюга з малим опором;

- призначення заземлення середньої точки - зниження напруги занулених корпусів (а отже, нульового захисного провідника) щодо землі до безпечного значення при замиканні фази на землю;

- призначення повторного заземлення захисного провідника - зниження напруги щодо землі занулених конструкцій у період замикання фази на корпус як при справній схемі занулення, так і у випадку обриву нульового захисного дроту.

Таким чином, занулення здійснює дві захисних дії - швидке автоматичне відключення ушкодженої установки від живлячої мережі і зниження напруги занулених металевих не струмоведучих частин, що виявилися під напругою, щодо землі.

6.8.3 Експлуатаційні заходи електробезпеки

Первинним джерелом живлення ПЕВМ є трьохпровідна мережа: фазовий дріт, нульовий робочий дріт, нульовий захисний дріт. Електроживлення здійснюється від електроустановки (трансформатора) із регульованою напругою під навантаженням. Напруга мережі подається в розподільну шафу.

У помешканні лабораторії прокладена шина повторного захисного заземлення (заземлюєчий провідник) виконана відповідно до ГОСТ 12.1.030-81 «Электробезопасность. Защитное заземление. Зануление» [23], що металево з'єднується з заземленою нейтраллю електроустановки.

Опір заземлюючого пристрою, до якого приєднана нейтраль, не більш 0,6 Ом. Шина повторного захисного заземлювача доступна для огляду.

Для роботи з пристроями під високою напругою необхідні наступні запобіжні заходи:

- не підключати і не відключати рознімання кабелів при напрузі мережі;

- технічне обслуговування і ремонтні роботи допускається виробляти тільки при виключеному живленні мережі;

- до роботи допускаються особи, які навчені і які мають групи допуску до роботи на машинах відповідно до ПУЭ-87 «Правила устройства

электроустановок» [21].

6.9 Пожежна безпека

Пожежна безпека — стан об’єкта при якому із установленою ймовірністю виключається можливість виникнення і розвитку пожежі, а також забезпечується захист матеріальних цінностей.

Причини, що можуть викликати пожежу в розглянутому помешканні:

- несправність електропроводки і приладів;

- коротке замикання електричних ланцюгів;

- перегрів апаратури;

- блискавка.

Помешкання обчислювального центру по пожежній безпеці відноситься до категорії В відповідно до ОНТП-24-86 «Строительные нормы и правила. Противопожарные нормы проектирования зданий и сооружений», тому що в обігу знаходяться тверді спалимі речовини і матеріали. Ступінь вогнестійкості будинку — II відповідно до СНиП 2.01.02-85 «Пожарная безопасность. Общие требования», клас помешкання по пожежній небезпеці П-IIа, відповідно до ПУЭ-87 «Правила устройства электроустановок».

Пожежна безпека відповідно до ГОСТ 12.1.004-91 «Пожарная безопасность. Общие требования» забезпечується системами запобігання пожежі, пожежного захисту, організаційно-технічними заходами.

Система запобігання пожежі:

- контроль і профілактика ізоляції;

- наявність плавких вставок і запобіжників в електронному устаткуванні;

- для захисту від статичної напруги використовується заземлення;

- захист від блискавок будівель і устаткування.

Для даного класу будівель і місцевості із середньою грозовою діяльністю 10 і більш грозових годин у рік, тобто для умов м. Харкова встановлена III категорія захисту від блискавок.

Ступінь захисту відповідному класу помешкання П II-а IР44 для устаткування і IР2Х для світильників.

Система пожежного захисту:

- аварійне відключення і переключення апаратури;

- наявність первинних засобів пожежегасіння, вогнегасників ОУ-5, тому що вуглекислота має погану електропровідність, або порошкових вогнегасників;

- система оповіщення, світлова і звукова сигналізація;

- захист легкозаймистих частин устаткування, конструкцій захисними матеріалами;

- використання негорючих матеріалів для акустичної обробки стін і стель;

- у помешканнях, де немає робочого персоналу встановлена автоматична система пожежного захисту.

Для успішної евакуації персоналу при пожежі розміри дверей робочого помешкання повинні бути наступними: ширина дверей не менше 1,5 м., висота дверей не менше 2,0 м., ширина коридора 1,8 м.; робоче помешкання повинно мати два виходи; відстань від найбільше віддаленого робочого місця не повинне перевищувати 100 м.

Організаційні заходи пожежної профілактики:

- навчання персоналу правилам пожежної безпеки;

- видання необхідних інструкцій і плакатів, плану евакуації персоналу у випадку пожежі.

Будівля обчислювального центру відповідає вимогам пожежної безпеки.

6.10 Рекомендації до добору колірної гами обробки помешкання

Для забезпечення оптимальних умов зорової роботи операторів ОЦ є рекомендації по колірній обробці помешкань із телеекранами в залежності від яскравості, кольоровості інформації і кольоровості захисного світофільтра. Так, при використанні екранів із яскравістю інформації 100-150 кд/м² зеленого кольору і при наявності зеленого світофільтра рекомендується офарблювати стіну помешкання, протилежну екранам, у зелений колір із коефіцієнтом відбитка =40%, а інші стіни - у жовтий колір із =62%. Для екранів із максимальною яскравістю зображення 15 кд/м² червонясто-жовтогарячого кольору стіна, протилежна екранам, офарблюється в темно-коричневий колір із =17%, інші стіни - у червоно-коричневий колір із  = 35%.

При сприйнятті інформації на екрані зеленого кольору для підвищення чутливості очей доцільно офарблювати стіну, на якій спрямований погляд оператора, у маслиново-зелений колір із =40% (припустимою є фарбування в червоно-сірий колір). У забарвленні навколишніх поверхонь, що випадково можуть потрапити в поле зору оператора (стіни, устаткування, меблі), також повинні бути присутнім червонуваті відтінки. Фарбуванню внутрішніх поверхонь варто надавати матову фактуру, тому що в поле зору оператора не повинні потрапляти блискучі поверхні, здатні створити відблиски відбитка на екрані.

7 ТЕХНІКО-ЕКОНОМІЧНЕ ОБГРУНТУВАННЯ НАУКОВО-ДОСЛІДНОЇ РОБОТИ

7.1 Мета та призначення

У якості нового інтелектуального продукту пропонується науково-дослідна розробка з питання виміру швидкостей потоків газів та рідини за допомогою вихрового потоковимірювача та обробки даних, що надходять від нього.

Вимірювальна система, побудована на базі вищевказаної розробки, дозволяє проводити облік проходження по трубах різних речовин. Дана розробка дозволяє проводити вимірювання у агресивних середовищах з домішками твердих тіл.

Основними потенційними покупцями пропонованої вимірювальної системи можуть бути підприємства, робота яких пов’язана з переміщенням по трубах різноманітні гази або рідини. Це можуть бути електростанції, підприємства по очищенню води та ін., хімічні підприємства та ін.

Перевагою розробки є її істотна простота й дешевина в порівнянні із закордонними аналогами, а також відсутність аналогічних систем українського виробництва для роботи в агресивних середовищах.

7.2 Дослідження й аналіз ринку збуту

При аналізі ринку збуту перед нами ставиться завдання відповісти на наступні питання: хто, чому, у якому обсязі, коли й за якою ціною купить пропонований до розробки продукт [11].

Мета цього дослідження - сегментація ринку й визначення ємності сегмента.

Ємність товарного ринку - це показник, що характеризує принципово можливий обсяг збуту товару. Місткість ринку визначається обсягом (у фізичних одиницях або вартісному вираженні) реалізованих на ньому товарів протягом року й складається з ємності його сегментів. Джерела відомостей про місткості ринку статистичні, галузеві й фірмові довідники, бюлетені іноземної комерційної інформації. Знаючи місткість ринку й тенденції її зміни, можна оцінити перспективність ринків збуту.

Сегмент ринку - це особливим образом виділена частина ринку, група споживачів, продуктів або підприємств, що володіють певними загальними ознаками. Продукти можуть групуватися по характері використання або області застосування.

Сегментація ринку - один з найважливіших інструментів маркетингу. Від правильності вибору сегмента ринку багато в чому залежить успіх підприємства в конкурентній боротьбі.

У таблиці 7.1 представлена сегментація ринку по основних споживачах даної наукової розробки.

Таблиця 7.1 - Сегменти ринку по основних споживачах

Галузь використання	Код споживача	Споживач
1	2	3	4
1 Хімічні підприємства	А	+		+
2 Очисні підприємства	Б	+		+
3 Електростанції	В	+		+
4 Інші промислові підприємства	Г	+	+	+
5 Галузеві НДІ	Д				+

1 - інженери по обслуговуванню;

2 - інженери-конструктори;

3 - механіки-ремонтники;

4 - наукові співробітники.

Дані про аналіз ємності сегментів ринку наведені в таблиці 6.2

Таблиця 7.2 - Аналіз ємності сегментів

Код сегмента	Кількість збутів	Передбачуване число продажів одиниць об'єкта	Передбачувана ємність
А	7	2	14
Б	5	1	5
В	8	2	16
Г	15	2	30
Д	2	1	3
Разом місткість ринку:	68

Висновок: таким чином, місткість ринку дорівнює 68.

Параметрична сегментація ринку виробляється шляхом виділення параметрів продукту й оцінки ступеня важливості кожного параметрів продукту й оцінки ступеня важливості кожного параметра для кожного споживчого сегмента по п'ятибальній шкалі [11].

Параметрична сегментація ринку наведена в таблиці 6.3

Таблиця 7.3 - Параметрична сегментація ринку

Параметри продукту	Оцінка споживачів	Ітогова оцінка	Питома вага, %
А	Б	В	Г	Д
1 Ціна	4	4	5	5	5	23	15,71
2 Надійність	5	5	5	5	5	25	17,14
3 Точність	5	5	5	5	5	25	17,14
4 Простота використання	5	4	5	5	4	23	15,71
5 Рівень сервісу	5	5	5	5	5	25	17,14
6 Швидкість роботи	5	5	5	5	5	25	17,14
Разом:	146

Як видно з таблиці, найбільш важливими параметрами на споживчому ринку є швидкість роботи й рівень сервісу.

7.3 Технічна підготовка НДР

Сітковий графік складається на обсяг робіт, виконуваний для розробки комплексу досліджень і документації, пов'язаної із цими дослідженнями. Для скорочення строку розробки й з метою ведення робіт паралельним методом можуть залучатися додаткові виконавці, крім посадового состава виконавців, передбаченого типовими нормами [11].

З метою визначення тривалості виконуваних робіт варто використати типові нормативи, питомі співвідношення окремих етапів і розділів робіт у загальній трудомісткості певної стадії розробки.

Визначимо тривалість розробки в нормо-годинах:

, (7.1)

де - кількість місяців, потрібна для розробки НДР, (=5 міс.);

- кількість робочих днів у місяці, (=22 дня);

- кількість робочих годин за день, (=8 год.);

н-г.

Розрахуємо трудомісткість і тривалість кожного з етапів розробки й дані занесемо в таблицю 7.4

Таблиця 7.4 - Перелік робіт сіткового графіка НДР

Номер роботи	Найменування роботи	Питома вага, %	Трудоміст-кість, н-г.	Кількість виконавців	Трива-лість, дн.
1	2	3	4	5	6
1	Постановка завдань досліджень	1	8,8	1	1
2	Аналіз методів обліку швидкості потоків рідини та газів	6	53	1	9
3	Аналіз апаратних засобів обліку швидкості потоку	7	62	2	6
4	Аналіз та вивчення методів роботи з турбулентними течіями	7	62	1	11
5	Обирання приймача перетворювача вихрових коливань	8	70	1	12
6	Аналіз вихідних сигналів вихрових генераторів	6	53	2	5
7	Обчислювальні експерименти без урахування квадратичної залежності амплітуди від частоти	8	70	2	6
8	Обчислювальні експерименти з урахування квадратичної залежності амплітуди від частоти	3	26	2	2
9	Визначення кількості перетинів корисного сигналу з нульовим рівнем з допомогою методики для квантованого у часі сигналом	5	44	1	8
10	Очікуване число перетинів нуля для Гаусова процесу	5	44	1	8
1	2	3	4	5	6
11	Параметричний фільтр МА(1)	5	44	2	4
12	Експериментування з корисним сигналом з двома і більше гармоніками	3	26	1	5
13	Експериментування з корисним сигналом, що змінює частоту у часі	3	26	1	5
14	Комбінування алгоритму AR(1) з попередньою фільтрацією фільтром низьких частот	5	44	2	4
15	Перспективи подальших досліджень в області обробки даних від вихрових потоковимірювачів	5	44	2	4
16	Розгляд питань, пов'язаних з техніко-економічним обґрунтуванням НДР	5	44	1	8
17	Розгляд питань, пов'язаних з охороною праці й навколишнього середовища	5	44	1	8
18	Підготовка НДРС	5	44	1	8
19	Оформлення графічного матеріалу	7	62	2	6
20	Написання доповіді	2	18	1	3
		100	880

Тривалість і-того етапу розробки знайдемо по формулі:

, (7.2)

де - трудомісткість і-того етапу дослідницької розробки;

- коефіцієнт узгодження, що враховує можливість збільшення трудомісткості етапу (=1,2);

z - кількість виконавців;

q - тривалість робочого дня (q =8 год.);

- коефіцієнт виконання норм часу ();

- коефіцієнт перекладу робочих днів у календарні дні (=0,72).

За даними таблиці 7.4 складемо сітковий графік НДР (рисунок 7.1)

Рисунок 7.1 - Сітковий графік НДР

Для розрахунку вихідних характеристик сіткового графіка може бути використана мова подій і мова робіт. Допускається також застосування спрощених методів розрахунку, розрахунок параметрів безпосередньо на сітковому графіку, за допомогою матриці ручного світла, алгоритму Форда й ін.

У випадку застосування мови робіт, розрахунок характеристик мережі здійснюється по наступних формулах [11]:

- ранній початок роботи:

, (7.3)

- раннє закінчення роботи:

, (7.4)

де – тривалість останньої роботи;

пізніший початок роботи:

, (7.5)

де – самий довгий шлях від першої роботи до останнього;

– раннє закінчення роботи у зворотному зв'язку;

- пізніше закінчення роботи:

, (7.6)

- повний резерв часу:

, (7.7)

- вільний резерв часу:

, (7.8)

де j - наступна робота;

i - дана робота.

Розрахункові дані, згідно з вищевказаними формулами, приведені в таблиці 7.5

Таблиця 7.5 - Розрахунок параметрів сіткового графіка НДР

Номер роботи	Тривалість, дн.	Ранні строки	Пізні строки	Резерви часу

1	2	3	4	5	6	7	8
1	1	0	1	0	1	0	0
2	9	1	10	1	10	0	0
3	6	10	16	10	16	0	0
4	11	16	27	23	34	6	6
5	12	16	28	16	28	0	0
6	5	28	33	29	34	0	0
7	6	28	34	28	34	1	1
8	2	28	30	32	34	3	3
9	8	34	42	34	42	0	0
10	8	42	50	49	57	0	0
11	4	50	54	57	61	0	0
12	5	54	59	61	66	0	0
13	5	54	59	61	66	0	0
14	4	42	46	42	46	7	7
15	4	46	50	46	50	3	3
16	8	50	58	50	58	1	1
17	8	58	66	58	66	9	9
18	8	66	74	66	74	0	0
19	6	74	80	74	80	0	0
20	3	80	83	80	83	0	0

7.4 Розрахунок собівартості

Собівартість являє собою виражені в грошовій формі поточні витрати підприємства, науково-технічних інститутів на виробництво й реалізацію продукції. У ході виробничо-господарської діяльності ці витрати повинні відшкодовуватися за рахунок виторгу від продажу [12].

Використання показників собівартості в практиці у всіх випадках вимагає забезпечення однаковості витрат, що враховують у її составі. Для забезпечення такої однаковості конкретний состав витрат, які відносять на собівартість, регламентується Типовим положенням по плануванню, обліку й калькулюванню собівартості продукції (робіт, послуг) у промисловості (постанова КМ 19.08.2002 р. N 27/4248).

Метою планування собівартості є економічно обґрунтоване визначення величини витрат, необхідних у планованому періоді для виробництва кожного виду й всієї промислової продукції підприємства, що відповідає вимогам по її якості.

Метою обліку собівартості продукції є повне й достовірне визначення фактичних витрат, пов'язаних з розробкою, виробництвом і збутом продукції.

Витрати, що включаються у собівартість продукції (робіт, послуг), групуються по наступних елементах:

а) матеріальні витрати;

б) витрати на оплату праці;

в) відрахування на соціальні заходи;

г) інші витрати.

7.4.1 Матеріальні витрати

До складу елемента «Матеріальні витрати» включаються витрати на сировину й матеріали [12].

Розрахунок ведеться по формулі:

(7.9)

де Нр_>i>_>>- норма витрати i-го матеріалу на одиницю продукції;

Ц_>i> - ціна одиниці i-го виду матеріалу;

m - кількість видів матеріалу;

С_>0> - вартість відходів. Приймаємо С_>0>= 0 % від вартості матеріалів.

У таблиці 6.6 наведені витрати на матеріали й покупні вироби при розробці даної науково-дослідної роботи.

Таблиця 7.6 - Витрати на матеріали й покупні вироби

Перелік матеріалів і покупних виробів	Кількість	Ціна одиниці, грн.	Вартість, грн
1 Дискети	1	2,40	2,40
2 Картридж для принтера	1	150,60	150,60
3 Папір формату А4	250		9,80
Разом:	162,80

7.4.2 Витрати на оплату праці

До елемента «Витрати на оплату праці» ставляться основна й додаткова заробітна плата персоналу, зайнятого безпосередньо на виконанні даної теми: науковці, науково-технічний, науково-допоміжний персонал і виробничі робітники [12]. Розрахунок витрат на основну заробітну плату по темі представлений у таблиці 7.7

Таблиця 6.7 - Розрахунок витрат на основну заробітну плату

Посада	Оклад, грн.	Кількість місяців	Участі на паях, %	Сума, грн.
Керівник теми	500,00	5	20	500,00
Інженер	293,00	5	80	1172,00
Разом:	1672,00

7.4.3 Додаткова заробітна плата

Вона включає доплати й надбавки до тарифних ставок і посадових окладів у розмірах, передбачених чинним законодавством, премії й заохочення робітником, керівникам, фахівцям і іншому службовцям за виробничі результати; гарантійні й компенсаційні виплати; оплата іншого невідпрацьованого часу й інші витрати на оплату праці [12].

Додаткову заробітну плату приймаємо 10 % від основної З_>ОСН>:

З_>ДОД>=0,1·З_>ОСН,>(7.10)

З_>ДОД> =1672,00 · 0,1=167,20 грн.

7.4.4 Відрахування на соціальні заходи

До елемента "Відрахування на соціальні заходи" ставляться:

а) відрахування на державне (обов'язкове) пенсійне страхування (у Пенсійний фонд) – 32 % від ():

= 0,32·(), (7.11)

=0,32·(1672,00+167,20) =588,54 грн.;

б) відрахування на державне (обов'язкове) соціальне страхування, включаючи відрахування на обов'язкове медичне страхування – 2,5 % від ():

= 0,025·(), (7.12)

=0,025·(1672,00+167,20) =45,98 грн.;

в) відрахування у Фонд сприяння зайнятості населення 2,5 % від ():

=0,025·(), (7.13)

=0,025·(1672,00+167,20) =45,98 грн.;

г) страхування по травматизму 0,85% від ():

=0,0085·(), (7.14)

=0,0085·(1672,00+167,20) =15,63 грн.

7.4.5 Експлуатаційні витрати

При розробці даної науково-дослідної роботи для обробки результатів виміру й оформлення пояснювальної записки використався персональний комп'ютер. Розрахуємо витрати на машинний час:

З_>екс>=·n_>дн>··T, (7.15)

де - кількість місяців, потрібна для розробки НДР (=5 міс.);

- кількість робочих днів у місяці (=22 дня);

- кількість робочих годин за день на ЕОМ (=2 год.);

Т – тариф за використання ЕОМ, за годину (Т=2 грн.).

З_>екс>=5.·22·2.·2=440,00 грн.

7.4.6 Накладні витрати

Накладні витрати у відмінності від прямих витрат пов'язані із забезпеченням загальних умов при розробці науково-дослідної роботи з урахуванням амортизаційних відрахувань. При складанні кошторисів накладні витрати визначаються непрямим шляхом - установленою нормою стосовно витрат або стосовно основної заробітної плати. Накладні витрати становлять 30 % від З_>ОСН>:

З_>НВ>=0,3·З_>ОСН>; (7.16)

З_>НВ>=0,3·1672,00=501,60 грн.

7.4.7 Калькуляція собівартості

За результатами проведених розрахунків становимо калькуляцію собівартості, що представлена в таблиці 7.8.

Проведені розрахунки показують, що ціна продажу, рівна 4913,64 грн., прийнятна для представників малого й середнього бізнесу, а також і для державних підприємств, а вартість розробки склала 3639,73 грн., що говорить про те, що проведену роботу можна вважати економічно ефективної, що має високий науковий і економічний рівень.

Таблиця 7.8 - Калькуляція собівартості науково-дослідної роботи

Найменування статей калькуляції	Сума, грн
1 Матеріали	162,80
2 Основна заробітна плата	1672,00
3 Додаткова заробітна плата	167,20
4 Відрахування на соціальні заходи А) пенсійне страхування Б) соціальне страхування В) зайнятість населення Г) травматизм	588,54 45,98 45,98 15,63
5 Експлуатаційні витрати	440,00
6 Накладні витрати	501,60
7 Собівартість	3639,73
8 Прибуток 35 %	1273,91
9 Ціна продажу	4913,64

7.5 Економічна ефективність НДР

Специфічною особливістю проведення ефективності НДР є їхній прогнозний характер, а також наявність невизначеності в області застосування й обсягах використання результатів НДР, у рівні витрат на виробництво, в оцінці впливу характеристик приладів на характеристики більше складних систем.

Визначення економічної ефективності НДР базується на загальних методах розрахунку порівняльної економічної ефективності нової техніки.

Кількісне визначення економічної ефективності НДР можливо, якщо є база для порівняння, відомі область і обсяг промислового використання результатів НДР. Однак, специфіка розрахунку економічної ефективності НДР полягає в тім, що результати НДР самостійного значення не мають, а дають економічний ефект у народному господарстві тільки будучи опосередкованими через довгий ланцюжок стадій технічного прогресу. Тому економічна ефективність НДР оцінюється по участі у відсотках від економічної ефективності нової техніки в цілому відповідно до ГОСТ 20779-81 [12] по формулі:

, (7.17)

де - частина річного ефекту, що доводиться на і-ту організацію або етап;

Э - загальний річний економічний ефект від створення й впровадження нової техніки або нового методу робіт;

- коефіцієнт участі у відсотках і-ої організації або і-го етапу робіт:

(7.18)

де - витрати на заробітну плату і-ої організації або і-го етапу робіт;

- коефіцієнт значимості і-го етапу;

m - число організацій або етапів.

Економічну ефективність деяких пошукових і прикладних НДР розрахувати не вдається. У такому випадку приводять якісний опис соціально-економічної ефективності НДР за методикою, сутність якої полягає в тому, що на основі оцінок роботи визначається коефіцієнт науково-дослідного ефекту НДВКР [12]:

, (7.19)

де - ваговий коефіцієнт і-ої ознаки науково-технічного ефекту (таблиця 7.9);

- кількісна оцінка і-ої ознаки науково-технічного ефекту НДР.

Кількісна оцінка рівня новизни визначається по таблиці 7.10; теоретичний рівень отриманих результатів - на основі експертних оцінок з обліком даних таблиці 7.11; можливість реалізації наукових результатів - на основі суми значень балів таблиці 7.12 і таблиці 7.13

Таблиця 7.9 - Коефіцієнт вагомості ознак

Ознака науково-технічного ефекту НДОКР	Значення вагового коефіцієнта
1 Рівень новизни	0,6
2 Теоретичний рівень	0,4
3 Можливість реалізації	0,2

Таблиця 7.10 - Ознака наукової новизни

Рівень новизни розробки	Характеристика новизни	Бали
Абсолютно нова	Робота носить інноваційний характер в Україні. Вимірювання швидкості потоків в агресивних.	8-10

Таблиця 7.11 - Ознака теоретичного рівня

Теоретичний рівень отриманих результатів	Бали
Розробка способу (алгоритм, програма заходів, пристрій і т.д.)	7-9

Таблиця 7.12 - Ознака часу реалізації

Час реалізації	Бали
Перші чотири роки	10

Таблиця 7.13 - Масштаби реалізації

Масштаби реалізації	Бали
Народне господарство	10

балів,

де 0,6 - рівень новизни нашого виробу;

8 - нова розробка;

0,4 - теоретичний рівень;

7 - розробка способу;

0,2 - можливість реалізації;

20 = 10+2,

де 10 - можливість реалізації протягом перших чотирьох років;

2 - народним господарством.

На кожній розробці встановлюється ступінь наближення у відсотках отриманих значень науково-технічного ефекту до максимально можливого:

, (6.20)

де балів – максимальне значення узагальнюючого показника науково-технічного ефекту.

З наведеного вище розрахунку економічної ефективності видно, що новий виріб доцільно розробляти.

Основні техніко-економічні показники наведені в таблиці 7.14

Таблиця 7.14 - Техніко-економічні показники

Найменування показника	Одиниці виміру	Значення
2 Кошторисна вартість	грн.	4913,64
3 Прибуток	грн.	1273,91
4 Строк розробки	дн.	83
5 Економічний ефект	%	96,6

Результат розрахунку коефіцієнта науково-технічного ефекту (Н_>Т>=96,6 %) показує доцільність проведення даної роботи, а також подальших досліджень у цій області.

Висновки

В дипломній роботі було розглянуто декілька моделей фільтрів та зроблена їх оцінка стосовно їх можливого використання у розробці вихрового потоковимірювача. Розглянуті результати фільтрації непогано узгоджуються з аналітичними розрахунками Бендат Дж. [5]. Використання фільтрів розширює діапазон вимірювання за допомогою вихрового потоковимірювача. В процесі моделювання були використані два різних генератора псевдовипадкових чисел та була зроблена оцінка параметрів отриманих псевдовипадкових послідовностей. Були реалізований алгоритм НК з використанням сімейств фільтрів AR(1) та MА(1) що використовує параметричну фільтрацію для рекурсивного визначення частот дискретних спектральних компонент. Ці алгоритми мають покращити характеристики вихрового потоковимірювача. Для покрашення результатів обробки було досліджено вплив проведеної попередньо фільтрації з пригніченням високочастотних завад використанням алгоритму НК з використанням фільтру сімейства AR(1). Отримані результати дають змогу суттєво розширити у бік низьких частот можливий діапазон вимірювань потоків при вимірювані за допомогою вихрового потоковимірювача.

Список джерел інформації

1. Киясбейли А.Ш., Перельштейн М. Е. Вихревые измерительные приборы. Б-ка приборостроителя. М., «Машиностроение», 1978, 152 с.

2. Белоцерковский С. М. Турбулентность и вихревая аэродинамика.

3. Бакай А.С., Сигов Ю.С. Многоликая турбулентность,М.: Знание,1989. С.3-12

4. Rice S. Mathematical analysis of random noise // Bell Syst. Tech. J., Vol.24, 1945.P.46-156.

5. Бендат Дж. Основы теории случайных шумов и ее применения,М.: Наука, 1965. С.429-431

6. Gajic B., Paliwal K. Robust speech recognition using features based on zero crossings with peak amplitudes // IEEE Intern. Conf. on Acoustics, Speech and Signal Processing, Vol.1, 2003.P. 64-67.

7. Kedem B. Spectral Analysis and Discrimination by Zero-Crossings // IEEE, Vol. 74, 1986.P.1475-1493.

8. He S., Kedem B. Higher Order crossings Spectral Analysis of an Almost Periodic Random Sequence in Noise // IEEE, Vol.35, 1989.P.360-370.

9. Barnett, J., Kedem B. Zero-crossing rates of mixtures and products of Gaussian processes // IEEE, Vol.44, 1998.P.1672-1677.

10. Питерсон У. Коды, исправляющие ошибки.М.: МИР,1964.С.288-307.

11. Troendle, J.F., An Iterative Filtering Method of Frequency Detection in a Mixed Spectrum Model. Doctoral Dissertation, Department of Mathematics, University of Maryland, College Park, 1991.

12. Matausek, M.R., S.S. Stankovic, and D.V. Radovic, "Iterative inverse filtering approach to the estimation of frequencies of noisy sinusoids," IEEE Tr. on Acoust. Speech Sig. Proc., ASSP-31, No. 6, pp. 1456-1463, 1983.

13. Li, T. and B. Kedem, "Improving Prony's estimator for multiple frequency estimation by a general method of parametric filtering," ICASSP-93, vol. IV, pp. 256-259, April 1993.

14. Dragosevic, M.V. and S.S. Stankovic, "A generalized least squares method for frequency estimation," IEEE Trans. Acoust., Speech, Signal Process., 37, No. 6, pp. 805-819, 1989.

15. J.T.Barnett., Zero-Crossing Rates of Some Non-Gaussian Processes with Application to Detection and Estimation, 1996.

16. Yakowitz, S., "Some contributions to a frequency location method due to He and Kedem," IEEE Trans. Infor. Theory, 37, No. 4, pp. 1177-1182, 1991.

17. Федоров А.А. Курс лекций по дисциплине: “Экономика и организация производства”.

18. Федоров А.А., Ланько А.В., Статейко Т.Г. Методические указания по технико-экономическому обоснованию дипломных работ (конструкторская часть)

АП-факультет.

19. Котлер Д.Н. Маркетинг, 2000г.

20. Омаров К.С. Организация производства.

21. ПУЭ-87. Правила устройства электроустановок.

- М.:Энергоатомиздат, 1987. - 648 с.

22. ГОСТ 12.1.005-88.ССБТ. Общие санитарно-гигиенические требования к воздуху рабочей зоны. - Введ. 01.01.89.

23. СНиП 2.04.05-86.Строительные нормы и правила. Отопление. Вентиляция и кондиционирование воздуха.-М.:Стройиздат, 1987-110с.

24. СНиП II-4-79. Строительные нормы и правила. Естественное и искусственное освещение. - М.: Стройиздат, 1980. - 48с.

25. ГОСТ 12.1.003-83.ССБТ. Шум. Общие требования безопасности.

-Введ. 01.07.84.

26. ГОСТ 12.1.012-90.ССБТ. Вибрация. Общие требования безопасности.

-Введ. 01.07.87.

27. ГОСТ 14254-80. Электрооборудование напряжением до 1000 В. Оболочки. Степени защиты. -Введ. 01.01.81.

28. ГОСТ 12.2.007.0-75 .ССБТ. Изделия электротехнические. Общие требования безопасности. -Введ. 01.01.78.

29. ГОСТ 12.1.030-81 .ССБТ. Электробезопасность. Защитное заземление. Зануление. -Введ. 01.07.82.

30. ДБН. В.1.1.-7-2002.

31. ГОСТ 12.1.004-91.ССБТ. Пожарная безопасность. Общие требования.

-Введ. 01.07.92.

32. ДСТУ 3008-95. Державний стандарт України. Документація. Звіти у сфері науки і техніки. Структура і правила оформлення.

33. СТВУЗ-ХПІ-2.01-2003. Система стандартів з організації навчального процесу. Дипломні роботи. Загальні вимоги. -Введ. 19.02.03.

34. СТВУЗ-ХПІ-2.03-2003. Система стандартів з організації навчального процесу. Дипломні науково-дослідні роботи. Порядок виконання. –Введ. 19.02.03.

Додаток А

На рисунку А.1 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1.

Рисунок А.1 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.2 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 2.

Рисунок А.2 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.3 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1.

Рисунок А.3 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.4 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 2.

Рисунок А.4 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.5 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1.

Рисунок А.5 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Алгоритм НК з використанням сімейства фільтрів МА(1).

На рисунку А.6 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1

Рисунок А.6 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.7 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 2

Рисунок А.7 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.8 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1

Рисунок А.8 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.9 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 2

Рисунок А.9 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.10 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1

Рисунок А.10 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.11 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 2

Рисунок А.11 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.12 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1

Рисунок А.12 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

На рисунку А.13 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 2

Рисунок А.13 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Моделювання процесу обробки сигналів датчика у вихровому потоковимірювачі

Міністерство освіти і науки України

Моделювання процесу обробки сигналів датчика

“Моделювання процесу обробки сигналів датчика у вихровому потоковимірювачі”, видана на кафедрі ОТП НТУ ”ХПI” відповідно до наказу від “08” 11 2004 р. № 2310 – ІІІ.

Споживач

А

Б

Код сегмента

Постановка завдань досліджень

Значення вагового коефіцієнта

Рівень новизни розробки

Характеристика новизни

Бали

Абсолютно нова

Бали

Час реалізації

Бали

Масштаби реалізації

Бали

Найменування показника

Одиниці виміру

Значення