Моделі і методи прийняття рішень
1
Моделі і методи прийняття рішень
(реферат)
1. Планування цілеспрямованих дій і прийняття рішень
1.1 Оптимізаційні задачі
Інтелектуальна система спочатку аналізує зовнішню ситуацію, потім планує цілеспрямовані дії і приймає рішення про вибір певної дії.
Широкий клас завдань у рамках прийняття рішення можна сформулювати у вигляді класичної оптимізаційної задачі: знайти рішення, за яким цільова функція досягає максимуму при заданих обмеження. Оптимізацій ні задачі є предметом науки „дослідження операцій”.
Формально оптимізацій на задача описується у вигляді:
знайти рішення х=(х>1>, ...х>n>), для якого цільова функція f(x) досягає максимуму (або мінімуму) і задовольняються обмеження g>i>(x)>=0.
Приклад. Мандрівник збирається у дорогу. Він може взяти в рюкзак певну кількість x>i> предметів різних типів. Нехай є n типів предметів, наявна кількість і-го предмета становить r>і>. Кожний предмет має власну цінність c>i> та вагу q>i>. Потрібно зібрати рюкзак таким чином, щоб сумарна цінність узятих предметів була максимальною, але щоб сумарна вага не перевищувала межі u.
Математично задача
про рюкзак формулюється так:
знайти х=(х>1>,
...х>n>),
для якого
 та задовольняються
обмеження
та задовольняються
обмеження
 ,
де x>i>
- цілі числа, x>i>>=0;
x>i><=r>i>.
,
де x>i>
- цілі числа, x>i>>=0;
x>i><=r>i>.
Будь-який елемент х, що задовольняє обмеженням g>i>(x)>=0, називається допустимим рішенням задачі. Якщо умова максимізації не висувається, то йдеться про задачу пошуку допустимих рішень. Якщо обмежень немає, то йдеться про безумовну оптимізацію.
Якщо потрібно вирішити задачу мінімізації, то вона переводиться до задачі максимізації зміною знаку в цільовій функції.
Залежно від вигляду цільової функції та обмежень розрізняють:
лінійне програмування – цільова функція і обмеження лінійні;
нелінійне програмування - цільова функція і обмеження нелінійні;
дискретне програмування – всі х>і> є цілими числами (як у задачі про рюкзак).
Розглянемо основні методи вирішення оптимізацій них задач
1.2 Метод перебору
Метод повного перебору – це очевидний і універсальний метод вирішення оптимізаційних задач, якщо множина допустимих рішень М обмежена. Метод є точним, тобто гарантує оптимальний розв’язок.
Недолік перебору – для практичних задач кількість варіантів надто велика.
Іноді можна пожертвувати точністю розв’язку і знайти субоптимальне рішення за рахунок значного зменшення часу розрахунку. В цьому полягає суть евристичних алгоритмів.
2. Евристичний пошук
Евристичний пошук – процедура систематизованого перебору варіантів. Загальна схема методу така:
Вибрати певну дію з області можливих дій
Здійснити дію, що приведе до зміни ситуації.
Оцінити нову ситуацію.
Якщо досягнуто успіху – кінець, інакше повернутися на крок 1.
Здійснити дію можна реально (стратегія спроб і помилок) або уявно (планування).
Одним з важливих варіантів евристичного пошуку є метод послідовних поліпшень.
2.1 Експоненційна складність евристичного пошуку
Розглянемо складність рішення оптимізацій них задач на прикладі задачі про виконуваність булевого виразу, яка формулюється так: для будь-якого виразу від n змінних знайти хоча б один набір значень (x>1>, … x>n>), для якого вираз приймає значення 1.
Найпростіша схема евристичного пошуку така: надаємо одне з можливих значень (0/1) першій, другій і т.д. змінним. Після встановлення значень всіх змінних перевіряється значення виразу: 1 – задача вирішена, не 1 – повернутися на початок.
Таку задачу можна розглядати як задачу пошуку на певному дереві перебору. Кожна вершина цього дерева відповідає певному набору встановлених значень x>1>, …x>k>. Ми можемо встановити змінну x>k>>+1> в 0 або в 1, тобто маємо вибір з двох дій. Тоді кожній з цих дій відповідає одна з двох дуг, які йдуть від цієї вершини. Тобто вершина (x>1>, …x>k>) має двох нащадків (x>1>, …x>k>, 0) і (x>1>, …x>k>, 1).
При n=3 дерево перебору /можливостей/ матиме вигляд (рис.1).

Рис.1. Дерево перебору (вершини – значення змінних, дуги – рішення), зафарбовані вершини відповідають виразу (х>1>х>2>) = х>3>
З рис.1 видно, що вирішення задачі зводиться до перебору листів (гілок) дерева з пошуком набору, що відповідає умові задачі. Для виразу (х>1>х>2>) = х>3> такими наборами будуть 000, 010, 100, 111.
Якщо n=3, дерево має 23=8 листів. Тобто число варіантів експоненційно залежить від n (2n=exp(n ln2).
Не кожний перебірний алгоритм є експоненційним (алгоритм пошуку максимального елемента в масиві – лінійний).
Із збільшенням розмірності задачі будь-який поліноміальний алгоритм стає ефективнішим за експоненційний.
2.2 Пошук у глибину і у ширину
Є дві основні стратегії пошуку потрібної вершини на дереві:
1) пошук у ширину;
2) пошук у глибину (перебір з поверненнями, бектрекінг).
Процедура пошуку у ширину передбачає аналіз на кожному кроці нащадків усіх вершин (паралельна перевірка всіх можливих альтернатив).
Процедура пошуку в глибину передбачає першочерговий аналіз нащадків тих вершин, що були проаналізовані останніми. Всі альтернативи аналізуються послідовно; аналіз деякої альтернативи завершується лише тоді, коли встановлюється, приводить вона до успіху чи ні. Якщо ж альтернатива зумовлює невдачу, відбувається повернення і розгляд інших альтернатив.
На рис.2 показана послідовність перегляду вершин при пошуку в ширину, на рис.3 – пошуку в глибину.

Рис.2. Процедура пошуку в ширину
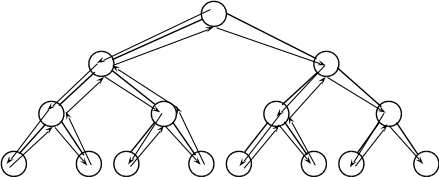
Рис.3. Процедура пошуку в глибину
Пошук в глибину (більш поширений) дозволяє зекономити пам’ять, оскільки при його реалізації не потрібно запам’ятовувати все дерево, а лише вершини, що мають відношення до поточної альтернативи.
2.3. Простір задач і простір станів
При плануванні в просторі станів заданим вважається деякий набір станів (ситуацій). Відомі дії, які може здійснювати система та які визначають перехід з одного стану в інший.
Графом станів задачі називається орієнтований граф, вершини якого відповідають можливим станам предметної області, а дуги – методам переходу від стану до стану.
Дуги можуть мати мітки, які інтерпретуються як вартість або довжина відповідного переходу. Тоді вирішення задачі являє собою пошук шляху від початкового стану до цільового; при цьому типовою вимогою є оптимізація даного рішення (пошуку найкоротшого шляху).
Класичний приклад планування в просторі станів – задача комівояжера.
Планування в просторі задач передбачає декомпозицію початкової задачі на підзадачі, поки не буде досягнути зведення до задач, для яких вже готові алгоритми рішення. Таку декомпозицію можна уявити у вигляді І/АБО графа.
Існують також комбінації планування у просторі задач істанів.
2.4 Автоматний спосіб задання алгоритму
В комп’ютері вхідна послідовність бітів перетворюється у вихідну за допомогою логічних схем. Логічні схеми поділяються на комбінаційні схеми і схеми з пам’яттю (скінченні автомати).
У комбінаційних схемах значення вихідних змінних залежать лише від стану вхідних і не залежать від поточного стану схеми. Будь-яка комбінаційна схема реалізує булеву (0/1) функцію від своїх вхідних змінних.
Скінчений автомат є перетворювачем, вихід якого залежить від входу, але й від поточного стану автомата. При цьому кількість вхідних і вихідних змінних, їх значень є скінченою. Поточний стан автомата – в пам’яті.
Найуніверсальнішою моделлю комп’ютерних обчислень є машина Тьюринга.
Автомати мають пам’ять у вигляді стрічки і пристрій для читання з неї. Стрічка розбита на квадрати з символами. Автомат розглядає символи по черзі, виконує обчислення і розв’язує задачі.
Формально скінчений автомат описується так:
FA=<Q, A, b, q>0>, F>
де Q=(q>1>,
q>2>,
…, q>n>)
- скінченна множина станів керування;
A=(a>1>,
a>2>,
.., a>m>)
- вхідний алфавіт;
b:
Q*A→Q
- функція переходів;
q>0>
- початковий стан;
 - множина заключних
станів керування.
- множина заключних
станів керування.
Приклад. Потрібно побудувати скінчений автомат який допускає тільки послідовності 0/1, при цьому в послідовності розпізнавання кількість одиниць повинна бути парною, а нулів – непарною.
Згідно з умовою задачі А складатиметься з символів 0, 1, #, де # позначатиме довільний символ, відмінний від 0 і 1. Тобто, А=<0, 1, #>.
Множину станів виберемо так:
Q=(q>1>, q>2>, …, q>5>),
де q>0> - початковий стан;
q>1 - >стан помилки;
q>2> - кількість нулів непарна, а одиниць – парна;
q>3> – кількість нулів і одиниць непарна;
q>4> – кількість нулів і одиниць парна;
q>5> – кількість нулів парна, а одиниць – непарна;
Згідно з умовою задачі F=<q>2>>
Функції переходів визначаються так:
|
q>0>#→q>1> |
q>0>0→q>2> |
q>3>0→q>5> |
|
q>1>→q>1> |
q>0>1→q>5> |
q>3>1→q>2> |
|
q>2>→q>1> |
q>1>0→q>1> |
q>4>0→q>2> |
|
q>3>→q>1> |
q>1>1→q>1> |
q>4>1→q>5> |
|
q>4>→q>1> |
q>2>0→q>4> |
q>5>0→q>3> |
|
q>5>→q>1> |
q>2>1→q>3> |
q>5>1→q>4> |
Автомати зручно задавати таблично:
|
# |
0 |
1 |
← |
|
|
q>0> |
q>1> |
q>2> |
q>5> |
|
|
q>1> |
q>1> |
q>1> |
q>1> |
|
|
q>2> |
q>1> |
q>4> |
q>3> |
|
|
q>3> |
q>1> |
q>5> |
q>2> |
|
|
q>4> |
q>1> |
q>2> |
q>5> |
|
|
q>5> |
q>1> |
q>3> |
q>4> |
Рис.1. Табличне задання автомата
Рядки таблиці позначаються станами множини Q, а стовпці – символами вхідного алфавіту. Символ ← позначає заключні допустимі стани.
Графічний опис автомата полягає у побудові графа, де вершини q>i> і q>j> з’єднуються дугою a якщо виконується команда q>i>a→q>j>. Заключні допустимі вершини позначаються подвійним колом.

Рис.2. Графічне задання автомата
Спеціальним типом автомата є машина Тьюринга. Універсальна машина Тьюринга може обчислити будь-який інтуїтивний алгоритм.
3. Складність алгоритмів
Універсальним обчислювальним пристроєм називатимемо пристрій, на якому можна промоделювати роботу машини Тьюринга.
Машини Тьюринга дозволяють обчислювати тільки рекурсивні функції.
Частково рекурсивні функції – визначена не при всіх значеннях аргумента.
Теза Тьюринга: Клас функцій, частково обчислюваних за Тьюрингом, збігається з класом частково рекурсивних функцій.
Теза Чорча: клас частково рекурсивних функцій збігається з класом частково обчислюваних функцій.
Теза Чорча еквівалентна тезі Тьюринга.
Моделі РАМ і РАСП
Машина Тьюринга дуже незручна для програмування через послідовний доступ до комірок пам’яті (стрічка), неструктурованість записів на стрічці (потрібно використовувати розподільники), відсутні основні арифметичні операції та ін.
Модель РАМ – довільний доступ до пам’яті, одна стрічка – для читання, друга – для запису.
РАСП – програма перебуває в регістрах і може сама себе змінювати.
Під складністю алгоритму розуміється часова оцінка його роботи або ємність необхідної пам’яті.
Апріорний аналіз алгоритму – теоретично, тестування – практична перевірка.
Розмірність задачі (вхідних даних) – це число (ціле), яке характеризує розмір вхідних даних задачі (розмірність одномірних, двомірних масивів, ...).
Часова складність алгоритму – час вирішення проблеми у залежності від розмірності задачі.
Асимптотична часова складність – поведінка часової складності при збільшенні розмірності задачі.
Задачі з великої часової складністю неможливі для реальних комп’ютерів (млрд. років).
При аналізі алгоритмів використовують такі позначення.
Запис f(n)=O(g(n)) означає: функція має порядок g(n) тоді, існують дві додатні константи с i n>0>, що f(n)<=c[g(n)] для всіх n>n>0>.
Звичайно f(n)=O(g(n)) визначає час обчислень;
 .
.
Теорема. Якщо
A(n)=a>m>nm + … a>1>n + a>0>
є поліномом ступеня m, тоді
A(n)=O(nm).
Нехай є два алгоритми з часовою оцінкою обчислень O(n) і O(n2). Час виконання першого алгоритму - c>1>n, а другого - c>2>n2 (с - константи). Тоді при n<c>1>/c>2> перевагу має перший алгоритм, а при n>c>1>/c>2> – другий.
При великих n значення констант несуттєві.
Найбільш типові часові оцінки алгоритмів: O(1) - константна, O(log n) - логарифмічна, O(n) - лінійна, O(nm) - поліноміальна, O(2n) - експоненційна. Для досить великих n:
O(1) < O(log n) < O(n) < O(n log n) < O(n2) < O(n3) < O(2n)
Ω(g(n)) - мінінімальна часова оцінка.
Задачі класу P I NP
Якщо розмірність задачі n, то P задача може бути розв’язана за поліноміальний час O(nm).
Задача NP може бути вирішена за поліноміальний час для недетермінованої машини Тьюринга (така машина породжує на кожному кроці певну кількість нових машин).
Більшість дискретних і комбінаторних задач можна вирішити шляхом перебору. Проте перебірні методи мають експоненційну складність.
Проблема: знайти метод вирішення експоненційних задач за поліноміальний час.
3.1 Планування в просторі станів. Основні поняття теорії графів
Граф – сукупність вершин і дуг. Для комп’ютерного опису графу використовуються: матриця інцидентності, матриця суміжності та списки суміжності.
Поширена структура даних в програмуванні – лінійні списки.
Лінійний список – скінченна послідовність однотипних елементів (певної довжини). Списки бувають однозв’язні (лінійні), двозв’язні (циклічні) і т.п. Лінійний список L, що складається з l>1>, l>2>,.. l>n> елементів , записується у вигляді L=< l>1>, l>2>,.. l>n> >

Рис..1. Графічне зображення списку
Існує два основних методи задання списків: послідовний (масиви) і зв’язний (динамічні змінні).
Стек – список, в якому занесення і видалення елементів можна проводити тільки через один початковий елемент (вершину стеку). Стек працює за принципом: останній зайшов – перший вийшов (Last In First Out - LIFO)
Чергою називають список, в якому всі вставки здійснюються в кінець списку (змінна rear), а всі видалення відбуваються з голови (початку) списку (змінна front).
Черга працює за принципом : перший зайшов – перший вийшов (First In First Out - FIFO).
Поняття граф ввів у 1736 році Ейлер. Граф G містить дві множини G=(V,E), де V - множина вершин (вузлів 1...n), E - множина ребер. Коли пари вершин впорядковані - то граф орієнтований, інакше - неорієнтований. Впорядкована пара позначається <i,j>, невпорядкована – (i,j). У зважених графах кожне ребро має вагу.
Ступенем вершини називається число суміжних вершин. В орієнтованому графі виділяють півстепінь входу (число вхідних ребер) та півстепінь виходу (число вихідних ребер).
Шляхом називається послідовність вершин між двома вершинами p і q.
Циклом називається шлях, у якого початкова і кінцева вершини збігаються. Граф називається зв’язним, якщо для довільної пари вершин існує між ними шлях.

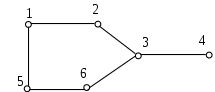
а) б)
Рис.2. Зображення орієнтованого (а) і неорієнтованого (б) графів.
3.2 Способи задання графів
Існує послідовний і зв’язний спосіб задання графів.
Послідовна форма використовує квадратну таблицю (Graf(n,n), n - вершин), яку називають матрицею суміжності. Якщо є зв’язок між вершинами, то Graf(I,j)=1, інакше Graf(I,j)=0.
а) б)
б)

Рис.3. Матриці суміжності графів з рис.2.: а – неорієнтованого, б – орієнтованого
Матриця інцидентності відображає зв’язок n вершин за допомогою m дуг, розмір матриці інцидентності (n*m), але вона менш зручна, ніж матриця суміжності.
Інша форма задання графу – список зв’язності. Граф з n вершинами буде задаватися списками – по одному для кожної вершини. Список для вершини і містить вершини, суміжні з і.
3.3 Дерева
Дерево – це орієнтований ациклічний граф, для якого виконуються такі умови:
1) існує одна вершина, в яка не входить жодне ребро (корінь);
2) у будь-яку вершину, крім кореня, входить лише одне ребро;
3) з кореня можна знайти унікальний шлях до кожної вершини дерева.
Орієнтований граф з кількох вершин – ліс. Бінарне дерево – кожна вершина має два нащадки. При пошуку певного вузла у дереві використовують пряме і зворотне проходження вузлів.
Способи зберігання дерев
Послідовне зберігання ділиться на рівневі і діжкове.
Рівневе: для кожного рівня дерева послідовно вказаються його вузли.
Дужкове: дужками вказуються нащадки даного вузла.
Зв’язне зберігання – списки, кожен список містить вказівними на нащадків.
Пошук у глибину і ширину
Пошук в глибину – послідовно відвідуються всі нові вершини –нащадки (якщо вершина була відвідана, то вона перестає бути новою).
Пошук у ширину – перевіряються суміжні вершини одного рівня, потім – перехід на нижчий рівень.
Остові дерева
Довільне дерево <V, T> неорієнтованого графу G=<V, E> називається остовим.
Ейлерові шляхи
Для вирішення багатьох прикладних проблем використовуються ейлерові шляхи. Ейлеревими називають шляхи, які проходять через кожне ребро графу один раз. Якщо початковий вузол є кінцевим, то такий граф називається ейлеревим циклом.
Задача про Кенігсбергські мости.
Теорема. У графі існує ейлерів шлях тільки тоді, коли граф зв’язний і містить не більше двох вершин непарного ступеня.
Знаходження найкоротших шляхів у графі
Потрібно знайти
мінімальний шлях (контур) у навантаженому
графі, де d(u,v)
- відстань між вершинами u
і v,
якщо не існує шляху, то d(u,v)=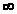 .
.
4. Загальна схема алгоритму Харта, Нельсона і Рафаеля
Узагальненням алгоритмів пошуку найкоротшого шляху на графах є алгоритм Харта, Нельсона і Рафаеля.
Введемо такі позначення:
s - початкова вершина;
q - цільова вершина;
c(i,j) - довжина ребра між вершинами і та j;
d(i, j) - довжина найкоротшого шляху між і-ю та j-ю вершинами;
g(n) - довжина найкоротшого шляху між від початкової вершини до n-ї;
h(n) - довжина найкоротшого шляху між від n-ї вершини до цільової;
f(n) - довжина найкоротшого шляху між від початкової вершини до цільової, які проходять через вершину n, при цьому f(n)=g(n)+h(n);
g*(n) – оцінка довжини найкоротшого шляху між від початкової вершини до n-ї;
h*(n) – евристична функція, яка задає оцінку довжини найкоротшого шляху між від n-ї вершини до цільової;
f*(n)=g*(n)+h*(n) - оцінка f(n);
L(n) - множина всіх наступників вершини n.
Введемо робочі множини: OPEN I CLOSE.
Загальна схема пошуку найкоротшого шляху:
Сформувати шраф пошуку G, який спочатку складається з початкової вершини s. Занести s до OPEN. Прокласти g*(s)=g(s)=0.
Сформувати множину CLOSE, яка спочатку буде порожня.
Якщо множина OPEN порожня, то вихід – потрібного шляху не існує;
Взяти з множини OPEN перший елемент m (відповідно до порядку, встановленого кроком 9), вилучити m з OPEN та занести її до CLOSE.
Якщо m - цільова вершина, то успіх. Відновити шлях від s до m на основі відновлюючи вказівників, що встановлені на кроках 6-8 і завершити алгоритм.
Розкрити вершину m,
отримати множину наступників L(m).
Додати до графу G
всі вершини, які належать L(m),
але не належать G,
разом з відповідними дугами. Додати ці
вершини до OPEN.
Для кожної вершини
 обчислити оцінки f*(k)=g*(k)+h*(k),
поклавши g*(k)=g*(m)+c(m,k),
встановити з k
до m
відновлюючий вказівник;
обчислити оцінки f*(k)=g*(k)+h*(k),
поклавши g*(k)=g*(m)+c(m,k),
встановити з k
до m
відновлюючий вказівник;
Для кожної вершини n з тих, які потрапили до L(m), але вже належали OPEN або CLOSE, переобчислити оцінки g*(n)=min((g*(m)+c(m,n), g*(n)). Якщо оцінка зменшилася, то перевстановити з неї відновлюючий вказівник до m.
Для всіх вершин з L(m), які до цього знаходилися в CLOSE, перевстановити відновлюючи вказівними для кожного з наступників цих вершин у напрямі найкоротшого шляху.
Перевпорядкувати множину OPEN за зростанням значень f*.
Повернутися на крок 3.
Якщо евристична функція не використовується, тобто h*(n)=0 і f*(n)=g*(n), то отримується алгоритм Дейкстри.
Якщо взяти g*(n)=0, утворюється алгоритм Дорана і Мічі.
4.1 Планування в просторі задач. І-АБО граф
Планування в просторі задач полягає в розбитті задачі на підзадачі, поки під задача не зведеться до елементарної (для якої існує готовий алгоритм розв’язку).
Для планування в просторі задач втрадиційно використовують І-АБО графи.
І-АБО графом називають орієнтований граф, вершини якого відповідають задачам, а дуги – відношенням між задачами (І - АБО).
І-АБО графи фактично є фрагментами мереж виведення продукційних систем. Розглянемо продукцій ну систему
A → C
B → C
D, C → G
Для такої системи існує І-АБО граф
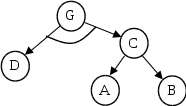
Рис.15.1. І-АБО граф
Вершина C пов’язана з вершинами A i B відношенням АБО (достатньо виконання однієї підзадачі), а вершина G пов’язана з вершинами D i C відношенням І (необхідне виконання всіх підзадач).
4.2 Метод „Поділяй і пануй”
Нехай потрібно вирішити задачу для елементів масиву початкових даних від p до q.
Метод „поділяй і пануй”, або поділ на підзадачі, можна записати у вигляді рекурсивної процедури sub>Task.
Булeва функція Small(p, q) визначає, чи не зведена під задача до елементарної. Якщо задача елементарна, то знаходиться її розв’язок за допомогою функції G(p,q).
Якщо задача не елементарна, то вона ділиться на дві частини функцією Divide(p,q). Процедура Combine рекурсивно викликає на виконання процедуру sub>Task, але для меншої розмірності вхідних даних. Процес рекурсивно продовжується до тих пір, поки всі задачі не будуть зведені до елементарних.
procedure sub>Task(p, q:integer);
Var m:integer;
Begin
if Small(p, q) then G(p,q);
else
begin
m:=Divide(p,q); { p <= m < q }
Combine (sub>Task(p,m), sub>Task(m+1,q));
end;
End;