ЛИСП-реализация основных операций над нечеткими множествами
СОДЕРЖАНИЕ
Введение
1. Постановка задачи
2. Математические и алгоритмические основы решения задачи
2.1 Понятие нечеткого множества
2.2 Операции над нечеткими множествами
2.2.1 Содержание
2.2.2 Равенство
2.2.3 Пересечение
2.2.4 Объединение
2.2.5 Разность
2.2.6 Произведение
2.2.7 Отрицание
2.2.8 Дизъюнктивная сумма
2.2.3 Наглядное представление операций над нечеткими множествами
3. Функциональные модели и блок-схемы решения задачи
4. Программная реализация решения задачи
5. Пример выполнения программы
Заключение
Список использованных источников и литературы
ВВЕДЕНИЕ
Наверное, самым впечатляющим у человеческого интеллекта является способность принимать правильные решения в условиях неполной и нечеткой информации. Построение моделей приближенных размышлений человека и использование их в компьютерных системах представляет сегодня одну из важнейших проблем науки.
Основы нечеткой логики были заложены в конце 60-х лет в работах известного американского математика Латфи Заде. Исследования такого рода было вызвано возрастающим неудовольствием экспертными системами. Хваленый "искусственный интеллект", который легко справлялся с задачами управления сложными техническими комплексами, был беспомощным при простейших высказываниях повседневной жизни, типа "Если в машине перед тобой сидит неопытный водитель - держись от нее подальше". Для создания действительно интеллектуальных систем, способных адекватно взаимодействовать с человеком, был необходим новый математический аппарат, который переводит неоднозначные жизненные утверждения в язык четких и формальных математических формул. Первым серьезным шагом в этом направлении стала теория нечетких множеств, разработанная Заде. Его работа "Fuzzy Sets", опубликованная в 1965 году в журнале "Information and Control", заложила основы моделирования интеллектуальной деятельности человека и стала начальным толчком к развитию новой математической теории. Он же дал и название для новой области науки - "fuzzy logic" (fuzzy - нечеткий, размытый, мягкий).
Чтобы стать классиком, надо немного опередить свое время. Существует легенда о том, каким образом была создана теория "нечетких множеств". Один раз Заде имел длинную дискуссию со своим другом относительно того, чья из жен более привлекательна. Термин "привлекательная" является неопределенным и в результате дискуссии они не смогли прийти к удовлетворительному итогу. Это заставило Заде сформулировать концепцию, которая выражает нечеткие понятия типа "привлекательная" в числовой форме.
Дальнейшие работы профессора Латфи Заде и его последователей заложили фундамент новой теории и создали предпосылки для внедрения методов нечеткого управления в инженерную практику.
Аппарат теории нечетких множеств, продемонстрировав ряд многообещающих возможностей применения - от систем управления летательными аппаратами до прогнозирования итогов выборов, оказался вместе с тем сложным для воплощения. Учитывая имеющийся уровень технологии, нечеткая логика заняла свое место среди других специальных научных дисциплин - где-то посредине между экспертными системами и нейронными сетями.
Свое второе рождение теория нечеткой логики пережила в начале восьмидесятых годов, когда несколько групп исследователей (в основном в США и Японии) всерьез занялись созданием электронных систем различного применения, использующих нечеткие управляющие алгоритмы. Теоретические основы для этого были заложены в ранних работах Коско и других ученых.
Третий период начался с конца 80-х годов и до сих пор. Этот период характеризуется бумом практического применения теории нечеткой логики в разных сферах науки и техники. До 90-ого года появилось около 40 патентов, относящихся к нечеткой логике (30 - японских). Сорок восемь японских компаний создают лабораторию LIFE (Laboratory for International Fuzzy Engineering), японское правительство финансирует 5-летнюю программу по нечеткой логике, которая включает 19 разных проектов - от систем оценки глобального загрязнения атмосферы и предвидения землетрясений до АСУ заводских цехов. Результатом выполнения этой программы было появление целого ряда новых массовых микрочипов, базирующихся на нечеткой логике. Сегодня их можно найти в стиральных машинах и видеокамерах, цехах заводов и моторных отсеках автомобилей, в системах управления складскими роботами и боевыми вертолетами.
В США развитие нечеткой логики идет по пути создания систем для большого бизнеса и военных. Нечеткая логика применяется при анализе новых рынков, биржевой игре, оценки политических рейтингов, выборе оптимальной ценовой стратегии и т.п. Появились и коммерческие системы массового применения.
Целью данной курсовой работы является ЛИСП – реализация основных операций над нечеткими множествами.
1.Постановка задачи
Требуется реализовать основные операции над нечеткими множествами:
содержание;
равенство;
пересечение;
объединение;
разность;
произведение;
отрицание;
дизъюнктивная сумма.
Пример 1.
Пусть:
 ;
;
 .
.
Решение:
Содержание: так как
 ,
B
доминирует A.
,
B
доминирует A.
Равенство: так как
 ,
следовательно A не равно
B.
,
следовательно A не равно
B.
Пересечение:
 .
.
Объединение:
 .
.
Разность:
 .
.
Произведение:

Отрицание:
 ,
,
 .
.
Дизъюнктивная сумма:
 .
.
Пример 2.
Пусть:
 ;
;
 .
.
Решение:
Содержание: так как
 ,
B доминирует A.
,
B доминирует A.Равенство: так как
 ,
следовательно A равно B.
,
следовательно A равно B.Пересечение:
 .
.
Объединение:
 .
.
Разность:
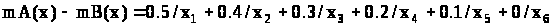 .
.
Произведение

7. Отрицание:
 ,
,
 .
.
Дизъюнктивная сумма:
 .
.
2. Математические и алгоритмические основы решения задачи
2.1 Понятие нечеткого множества
Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. в статье "Fuzzy Sets" (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1.
Под нечётким множеством A понимается совокупность
 ,
,
где— X
универсальное множество, а
 — функция принадлежности (характеристическая
функция), характеризующая степень
принадлежности элемента нечёткому
множеству A.
— функция принадлежности (характеристическая
функция), характеризующая степень
принадлежности элемента нечёткому
множеству A.
Функция
 принимает значения в некотором вполне
упорядоченном множестве M.
Множество M
называют множеством принадлежностей,
часто в качестве M
выбирается отрезок
принимает значения в некотором вполне
упорядоченном множестве M.
Множество M
называют множеством принадлежностей,
часто в качестве M
выбирается отрезок
 .
Если
.
Если
 ,
то нечёткое множество может рассматриваться
как обычное, чёткое множество.
,
то нечёткое множество может рассматриваться
как обычное, чёткое множество.
2.2 Операции над нечеткими множествами
Пусть A и B - нечеткие множества на универсальном множестве E.
2.2.1 Содержание
Говорят, что A содержится в B, если
 .
.
Обозначение: A М B.
Иногда используют термин "доминирование", то есть в случае если A М B, говорят, что B доминирует A.
2.2.2 Равенство
A и B равны, если
 .
.
Обозначение: A = B.
2.2.3 Пересечение
Пересечением нечётких множеств A и B называется наибольшее нечёткое подмножество, содержащееся одновременно в A и B:
 .
.
2.2.4 Объединение

- наименьшее нечеткое подмножество, которое включает как А, так и В, с функцией принадлежности:

2.2.5 Разность
 с функцией принадлежности:
с функцией принадлежности:
 .
.
2.2.6 Произведение
Произведением нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности:
 .
.
2.2.7 Отрицание
Отрицанием множества A
при
 называется множество
называется множество
 с функцией принадлежности:
с функцией принадлежности:
 .
.
2.2.8 Дизъюнктивная сумма
Дизъюнктивной суммой нечетких множеств A и B называется множество с функцией принадлежности:
 .
.
2.3 Наглядное представление операций над нечеткими множествами
Для нечетких множеств можно применить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значение mA(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами.
Пусть A нечеткий интервал между 5 до 8 и B нечеткое число около 4, как показано на рисунке 1 и 2.


Рисунок 1. Множество A Рисунок 2. Множество B
Проиллюстрируем нечеткое множество между 5 AND 8 около 4 (синяя линия).

Рисунок 3. Пересечение множеств А и В
Нечеткое множество между 5 OR 8 около 4 показано на следующем рисунке (синяя линия).

Рисунок 4. Объединение множеств А и В
Следующий рисунок иллюстрирует операцию отрицания. Синяя линия - это отрицание нечеткого множества A.

Рисунок 5. Отрицание множества А
На следующем рисунке заштрихованная
часть соответствует нечеткому множеству
A и изображает область значений А и всех
нечетких множеств, содержащихся в A.
Остальные рисунки изображают соответственно
 .
.




Рисунок 6. Множества

3. Функциональные модели и блок-схемы решения задачи
Функциональные модели и блок-схемы решения задачи представлены на рисунке 7 – 14.
Условные обозначения:
X1 – первое множество;
X2 – второе множество;
X – множество.

Рисунок 7 – Функциональная модель решения задачи для функции CONTENT (содержание)

Рисунок 8 – Функциональная модель решения задачи для функции EQUAL_ (равенство)

Рисунок 9 – Функциональная модель решения задачи для функции CROSSING (пересечение)

Рисунок 10 – Функциональная модель решения задачи для функции UNION (объединение)

Рисунок 11 – Функциональная модель решения задачи для функции sub>TR (разность)

Рисунок 12 – Функциональная модель решения задачи для функции MULT (произведение)

Рисунок 13 – Функциональная модель решения задачи для функции ADDITION (отрицание)

Рисунок 14 – Функциональная модель решения задачи для функции DIZ_SUMM (дизъюнктивная сумма)
4. Программная реализация решения задачи
;СОДЕРЖАНИЕ mA(x) < mB(x)
;РАВЕНСТВО mA(X) = mB(X)
;ПЕРЕСЕЧЕНИЕ min( mA(x), mB(x))
;ОБЪЕДИНЕНИЕ max(mA(x), m B(x))
;РАЗНОСТЬ А - B = АЗ с функцией принадлежности: mA-B(x) = mA З (x) = min( mA(x), 1 - m B(x))
;ПРОИЗВЕДЕНИЕ mA(x)* m B(x)
;ОТРИЦАНИЕ A^ = 1-mA(X)
;ДИЗЪЮНКТИВНАЯ СУММА АЕB = (А - B)И(B - А) = (А З ) И( З B) с функцией принадлежности:
;mA-B(x) = max{[min{m A(x), 1 - mB(x)}];[min{1 - mA(x), mB(x)}] }
;СОДЕРЖАНИЕ
;ЕСЛИ МНОЖЕСТВО A СОДЕРЖИТСЯ В МНОЖЕСТВЕ B - РЕЗУЛЬТАТОМ ФУНКЦИИ БУДЕТ 0
(DEFUN CONTENT (X1 X2)
(COND
((NULL X1) 0)
((ATOM X1) (IF (> X1 X2) 1 0))
(T (+ (CONTENT (CAR X1) (CAR X2)) (CONTENT (CDR X1) (CDR X2))))
)
)
;РАВЕНСТВО
;ЕСЛИ МНОЖЕСТВО A РАВНО МНОЖЕСТВУ B - РЕЗУЛЬТАТОМ ФУНКЦИИ БУДЕТ 0
(DEFUN EQUAL_ (X1 X2)
(COND
((NULL X1) 0)
((ATOM X1) (IF (EQUAL X1 X2) 0 1))
(T (+ (EQUAL_ (CAR X1) (CAR X2)) (EQUAL_ (CDR X1) (CDR X2))))
)
)
;ПЕРЕСЕЧЕНИЕ
(DEFUN CROSSING (X1 X2)
(MIN X1 X2)
)
;ОБЪЕДИНЕНИЕ
(DEFUN UNION (X1 X2)
(MAX X1 X2)
)
;РАЗНОСТЬ
(DEFUN sub>TR (X1 X2)
(MIN X1 (- 1 X2))
)
;ПРОИЗВЕДЕНИЕ
(DEFUN MULT (X1 X2)
(* X1 X2)
)
;ОТРИЦАНИЕ
(DEFUN ADDITION (X)
(- 1 X)
)
;ДИЗЪЮНКТИВНАЯ СУММА
(DEFUN DIZ_SUMM (X1 X2)
(MAX (MIN X1 (- 1 X2)) (MIN (- 1 X1) X2))
)
;РЕАЛИЗАЦИЯ ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ
;С ПОМОЩЬЮ ОПИСАННЫХ РАННЕЕ ФУНКЦИЙ
;----------------------------------------------
;ПОЛУЧАЕМ МНОЖЕСТВА
(SETQ INPUT (OPEN " D:\MULTITUDE.TXT" :DIRECTION :INPUT))
(SETQ A (READ INPUT))
(SETQ B (READ INPUT))
(CLOSE INPUT)
;СОДЕРЖАНИЕ
(SETQ CONTENT_AB (IF (= (CONTENT A B)) "Mnowestvo A soderzitsya v mnowestve B" "Mnowestvo A NE soderzitsya v mnowestve B"))
;РАВЕНСТВО
(SETQ EQUAL_AB (IF (= (EQUAL_ A B) 0) "Mnowestvo A ravno B" "Mnowestvo A NE ravno B"))
;ПЕРЕСЕЧЕНИЕ
(SETQ CROSS_AB (MAPCAR 'CROSSING A B))
;ОБЪЕДИНЕНИЕ
(SETQ UNION_AB (MAPCAR 'UNION A B))
;ПРОИЗВЕДЕНИЕ
(SETQ MULT_AB (MAPCAR 'MULT A B))
;РАЗНОСТЬ
(SETQ sub>TR_AB (MAPCAR 'sub>TR A B))
;ОТРИЦАНИЕ
(SETQ A_ (MAPCAR 'ADDITION A))
(SETQ B_ (MAPCAR 'ADDITION B))
;ДИЗЪЮКТИВНАЯ СУММА
(SETQ DIZ_SUMM_AB (MAPCAR 'DIZ_SUMM A B))
;ЗАПИСЫВАЕМ РЕЗУЛЬТАТ ОПЕРАЦИЙ В ФАЙЛ
(SETQ OUTPUT (OPEN "D:\RESULT_OPERATIONS.TXT" :DIRECTION :OUTPUT))
(PRINT (LIST 'A A) OUTPUT)
(PRINT (LIST 'B B) OUTPUT)
(PRINT 'OPERATIONS OUTPUT)
(PRINT '------------------------- OUTPUT)
(PRINT (LIST 'CONTENT_AB CONTENT_AB) OUTPUT)
(PRINT (LIST 'EQUAL_AB EQUAL_AB) OUTPUT)
(PRINT (LIST 'CROSS_AB CROSS_AB) OUTPUT)
(PRINT (LIST 'UNION_AB UNION_AB) OUTPUT)
(PRINT (LIST 'MULT_AB MULT_AB) OUTPUT)
(PRINT (LIST 'sub>TR_AB sub>TR_AB) OUTPUT)
(PRINT (LIST 'A_ A_) OUTPUT)
(PRINT (LIST 'B_ B_) OUTPUT)
(PRINT (LIST 'DIZ_SUMM_AB DIZ_SUMM_AB) OUTPUT)
(TERPRI OUTPUT)
(CLOSE OUTPUT)
;КОНЕЦ
5. Пример выполнения программы
Пример 1.

Рисунок 15 – Входные данные

Рисунок 16 – Выходные данные
Пример 2.

Рисунок 17 – Входные данные

Рисунок 18 – Выходные данные
Пример 3.

Рисунок 19 – Входные данные

Рисунок 20 – Выходные данные
ЗАКЛЮЧЕНИЕ
Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда нечеткое множество является четким (обычным), эти операции переходили в обычные операции теории множеств, то есть операции над нечеткими множествами должны обобщать соответствующие операции над обычными множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств.
Итогом работы можно считать созданную функциональную модель реализации основных операций над нечеткими множествами. Созданная функциональная модель и ее программная реализация могут служить органической частью решения более сложных задач.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы
Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н.Бронштейн, К.А.Семендяев. – М.: Наука, 2007. – 708 с.
Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений [Электронный ресурс] / Заде Л. – М.: Мир, 1976. С. 166.
Кофман А. Введение в теорию нечетких множеств [Текст] / А.Кофман. – М.: Радио и связь, 1982. С. 432.
Круглов, В.В. Нечёткая логика и искусственные нейронные сети. [Текст] / В.В. Круглов, М.И. Дли, Р.Ю. Голунов. – М.: Питер, 2001. C. 224.
Нечеткое множество [Электронный ресурс] – Режим доступа: http://ru.wikipedia.org/wiki/Нечеткое_множество
Симанков, В.С. Основы функционального программирования [Текст] / В.С.Симанков, Т.Т.Зангиев, И.В.Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
Хювенен Э. Мир Лиспа [Текст] / Э.Хювенен, Й.Сеппянен. – М.: Мир, 1990. – 460 с.