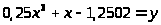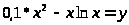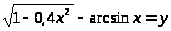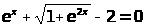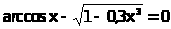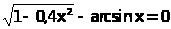Компьютерные технологии MS EXEL
КОНТРОЛЬНАЯ РАБОТА ПО ИНФОРМАТИКЕ
ЦЕЛЬ РАБОТЫ
Закрепление знаний и практических навыков работы на персональном компьютере с использованием современных компьютерных технологий MS EXEL.
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
Контрольная работа состоит из 5 заданий, решение которых должно быть представлено в виде электронного варианта книги MS Excel и пояснительной записки, составленной в MS Word.
Задание 1. Табулировние и построение графиков функций.
Задание 2. Вычисление суммы функционального ряда.
Задание 3 Вычисление корней нелинейного (трансцендентного) уравнения, используя инструмент Подбор параметра.
Задание 4. Финансовый анализ в Excel на примерах использования: Подбор параметра и Диспетчера сценариев.
Задание 5. Применение возможностей Excel на примерах решения практических задач.
Задание 1
Тема: Табулирование и построение графиков функций
Постановка задачи.
Построить графики двух функций Y=cos2x
и Z=sin2x
“по точкам” на отрезке -2π≤X≤2π
c
шагом
 ,
где n-число
разбиения отрезка.
,
где n-число
разбиения отрезка.
Решение
Строим математическую модель и определяем исходные и результирующие данные.
Исходные данные: начало и конец отрезка, число разбиений отрезка.
Результаты: столбец - аргумента X и два столбца функцийY и Z, которые вычисляются в каждой точке отрезка с шагом H. В нашем случае шаг вычисляется по формулеH=4π/n, где n=20.
Технология создания рабочего листа.
Переименуем рабочий лист в “Табулирование”. Для этого дважды щелкнем мышкой по вкладке текущего рабочего листа и на вкладке листа введем имя “Табулирование”.
Введем исходные данные с пояснениями и расчетные формулы для вычисления X,Y,Z,H в следующей последовательности:
Ввод в ячейку F2 числа разбиений=20;
Вычисление шага H: E2=4*ПИ()/$F$2;
Формула вычисления начального значения X: B2=-2*ПИ();
Удобно задавать описание X как функцию, в которой последующее значение X определяется через предыдущее,X=X+H.Тогда, сменив число разбиения n, автоматически произойдет пересчет по всем формулам на рабочем листе;
Вычисление последующего значения X определяется по формуле B3=B2+$E$2;
Формулы для вычисления начальных значений функций Y и Z определяются по формулам: C2=(cos(B2))^2; D2=sin(2*B2).
Далее формулы X ,Y, Z копируем вниз до последнего значения X.
Полученные результаты приведены на рабочем листе ”Табулирование” (рис.1), который представлен в режиме отображения значений. Внимательно посмотрите, правильно ли набраны формулы. Для этого представим рабочий лист в режиме отображения формул, который устанавливается нажатием клавиш Ctrl+ `(` этот значок на клавише, расположенной в левом верхнем углу клавиатуры, где ~ (тильда)), или командой Сервис/Параметры/Вкладка Вид/Параметры окна-Формула. Проанализировав формулы, выполнив ту же последовательность команд, вернемся в режим отображений значений.
Построение графиков по точкам.
Графики (диаграммы) можно создать с помощью команды Вставка/ Диаграмма или нажатием кнопки Мастер диаграмм на стандартной панели инструментов. Последовательность действий создания диаграммы:
Выделите на рабочем листе данные, которые нужно отобразить- диапазон B1:D22;
Нажмите на кнопку Мастер диаграмм;
Выберите тип диаграммы – Точечный и нажмите на кнопку Далее;
Выберите расположение данных-По строкам или По столбцам. Выберите По столбцам и нажмите на кнопку Далее;
На соответствующих вкладках задайте параметры: заголовки и надписи данных и нажмите на кнопку Далее;
Укажите, где должна находиться новая диаграмма, - На отдельном листе или уже Существующем. Выберите – На существующем листе и нажмите кнопку Готово.
На текущем рабочем листе появится Диаграмма-график. Как и любой объект, его можно выделить и перетащить с помощью мыши на новое место листа (рис.3).
Замечание.
Для построения одного графика Z=F(X) нужно Мастеру диаграмм задать несмежные области листа B2:B22 и D2:D22 , которые можно выделить при нажатой клавише Ctrl.
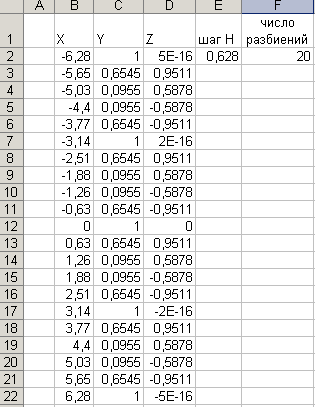
Рис 1.
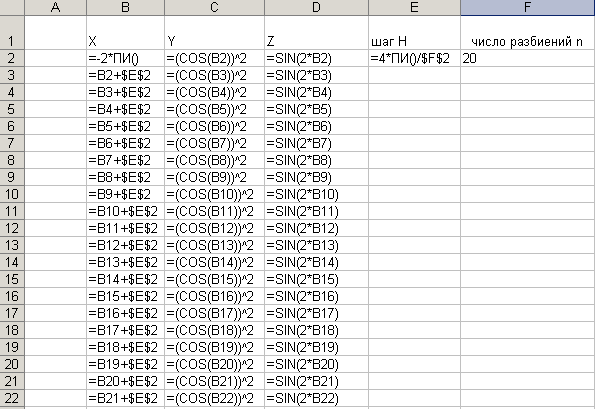
Рис.2
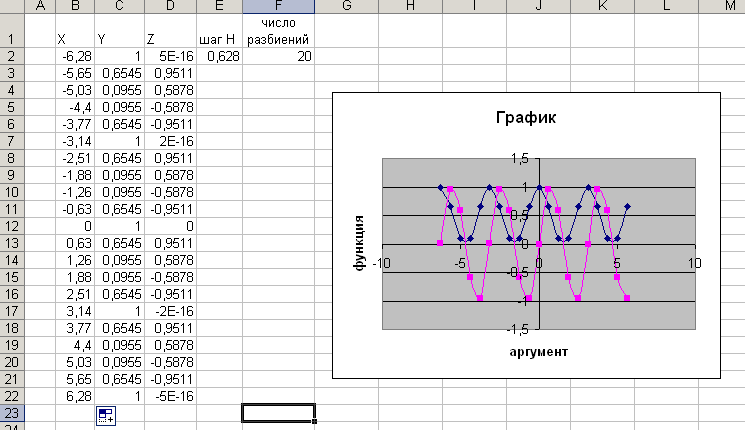
Рис. 3
Варианты заданий
|
№ |
Уравнение y=f(x) |
Уравнение z=f(x) |
Отрезок, содержащий корень |
Шаг |
|
1 |
|
|
[2; 3] |
0,1 |
|
2 |
|
|
[0; 2] |
0,2 |
|
3 |
|
|
[0,4; 1] |
0,05 |
|
4 |
|
|
[0, 0,85] |
0,05 |
|
5 |
|
|
[1; 2] |
0,1 |
|
6 |
|
|
[0; 0,8] |
0,05 |
|
7 |
|
|
[0; 1] |
0,1 |
|
8 |
|
|
[2; 4] |
0,2 |
|
9 |
|
|
[1; 2] |
0,1 |
|
10 |
|
|
[0; 2] |
0,1 |
|
11 |
|
|
[0.1; 1] |
0,1 |
|
12 |
|
|
[1; 3] |
0,2 |
|
13 |
|
|
[1,2; 2] |
0,08 |
|
14 |
ex+lnx-10x=н |
|
[3; 4] |
0,1 |
|
15 |
|
|
[1; 2] |
0,1 |
|
16 |
1-x+sinx-ln(1+x)=y |
|
[0; 1,5] |
0,15 |
|
17 |
3x-14+ex-e-x=y |
|
[1; 3] |
0,2 |
|
18 |
|
|
[0; 1] |
0,1 |
|
19 |
x+cos(x0,52+2)=y |
|
[0,5; 1] |
0,05 |
|
20 |
3ln2x+6lnx-5=y |
|
[1; 3] |
0,2 |
|
21 |
sinx2+cosx2-10x=y |
|
[0; 1] |
0,1 |
|
22 |
x2 – ln(1+x) – 3=y |
|
[2; 3] |
0,1 |
|
23 |
2x*sinx – cosx=y |
|
[0,4; 1] |
0,05 |
|
24 |
|
|
[-1; 0] |
0,1 |
|
25 |
lnx – x + 1,8=y |
|
[2; 3] |
0,1 |
|
26 |
|
|
[0,2; 1] |
0,05 |
|
27 |
|
|
[1; 2] |
0,1 |
|
28 |
|
|
[1; 2] |
0,1 |
|
29 |
|
|
[0; 1] |
0,1 |
|
30 |
0,6*3x-2,3*x – 3=y |
|
[2; 3] |
0,1 |
Задание 3
Нахождение корней нелинейных (трансцендентных) уравнений, используя инструмент «Подбор параметра»
Пример. Найти
корни уравнения

Из рис.1 видно, что функция меняет знак между значениями X диапазона [3,2;3,3]. Значит, в этом диапазоне существует корень. В качестве начального приближения Xкорень берем ячейку F3=3, значение функции Y задаем в ячейке F4=3*F3-4*ln(F3)-5.
Теперь выберем команду Сервис, Подбор параметра и заполним диалоговое окно Подбор параметра. Заполнение окна смотрите на рис.1.
После нажатия кнопки OK средство Подбора параметров находит приближенное значение корня, которое помещает в ячейку F3, а корень-результат в ячейку F4(смотрите рис.2).

Рис.1

Рис.2
Варианты к заданию 3
|
№ |
Уравнения |
Отрезок, содержащий корень |
Приближенное значение |
|
1 |
1-x+sinx-ln(1+x)=0 |
[0; 1,5] |
1,1474 |
|
2 |
3x-14+ex-e-x=0 |
[1; 3] |
2,0692 |
|
3 |
|
[0; 1] |
0,5768 |
|
4 |
x+cos(x0,52+2)=0 |
[0,5; 1] |
0,9892 |
|
5 |
3ln2x+6lnx-5=0 |
[1; 3] |
1,8832 |
|
6 |
sinx2+cosx2-10x=0 |
[0; 1] |
0,1010 |
|
7 |
x2 - ln(1+x) - 3=0 |
[2; 3] |
2,0267 |
|
8 |
2x*sinx - cosx=0 |
[0,4; 1] |
0,6533 |
|
9 |
|
[-1; 0] |
- 0,2877 |
|
10 |
lnx - x + 1,8=0 |
[2; 3] |
2,8459 |
|
11 |
|
[0,2; 1] |
0,5472 |
|
12 |
|
[1; 2] |
1,0769 |
|
13 |
|
[1; 2] |
1,2388 |
|
14 |
|
[0; 1] |
0,4538 |
|
15 |
0,6*3x-2,3*x - 3=0 |
[2; 3] |
2,4200 |
|
16 |
|
[2; 3] |
2,2985 |
|
17 |
|
[0; 2] |
1,0001 |
|
18 |
|
[0,4; 1] |
0,7376 |
|
19 |
|
[0; 0,85] |
0,2624 |
|
20 |
|
[1; 2] |
1,1183 |
|
21 |
|
[0; 0,8] |
0,3333 |
|
22 |
|
[0; 1] |
0,5629 |
|
23 |
|
[2; 4] |
3,2300 |
|
24 |
|
[1; 2] |
1,8756 |
|
25 |
|
[0; 1] |
0,7672 |
|
26 |
|
[0; 1] |
0,8814 |
|
27 |
|
[1; 3] |
1,3749 |
|
28 |
|
[1,2; 2] |
1,3077 |
|
29 |
ex+lnx-10x=0 |
[3; 4] |
3,5265 |
|
30 |
|
[1; 2] |
1,0804 |
Задание 4. Финансовый анализ в Excel
Excel предоставляет большой спектр функций финансового анализа: от нахождения платы по процентам, амортизации оборудования, регулярных выплат по займу до оценки эффективности капиталовложений. Рассмотрим функции финансового анализа Excel на большом количестве конкретных примеров.
Пример 1
Постановка задачи. Вычислить финансовую функцию ППЛАТ(ПЛТ) расчета 30-летней ипотечной ссуды со ставкой 8% годовых при начальном взносе 20% от цены покупки и ежемесячной (ежегодной) выплате.
Функция ППЛАТ(ПЛТ) вычисляет величину постоянной периодической выплаты ренты (кредита) при постоянной процентной ставке.
Синтаксис:
=ППЛАТ (ПЛТ) (ставка; кпер; ос; остаток; тип)
Аргументы:
ставка Процентная ставка за период;
кпер количество периодов выплат;
ос Общая сумма кредита, которую составят будущие платежи;
остаток Остаток или баланс наличности, который нужно достичь после последней выплаты. Если остаток опущен, то он полагается равным 0;
тип Число 0 или 1, обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 — то в начале периода.
Очень важно быть последовательным в выборе единиц измерения для задания аргументов ставка и кпер. Например, если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12% годовых, то для задания аргумента ставка используйте 12%/12, а для задания аргумента кпер — 4*12. Если вы делаете ежегодные платежи по тому же займу, то для задания аргумента ставка используйте 12%, а для задания аргумента кпер — 4.
Замечание. Обратите внимание, что в функциях, связанных с интервалами выплат, выплачиваемые вами деньги, такие как депозит на накопление, представляются отрицательным числом, а деньги, которые вы получаете, такие как чеки на дивиденды, представляются положительным числом. Например, депозит в банк на сумму 1000 руб. представляется аргументом -1000, если вы вкладчик, и аргументом 1000, если вы — представитель банка, т.е. что отдается банку-аргумент с минусом, при получении от банка-аргумент с плюсом.
Рабочий лист (рис.1) приведен в режиме отображения значений, а на рис.2-в режиме формул.

Рис.1.Расчет ипотечной ссуды

Рис. 2. Формулы для расчета ипотечной ссуды
Пример 2 расчета эффективности неравномерных капиталовложений с помощью функций НПЗ и инструмента Подбор параметра
Постановка задачи. Вас просят дать в долг 10000 руб. и обещают вернуть через год 2000руб., через два года— 4000руб., через три года— 7000 руб. Определить при какой годовой процентной ставке эта сделка выгодна? Для решения задачи будем использовать финансовую функцию НПЗ(ЧПС).
Функция НПЗ(ЧПС) возвращает чистый текущий объем вклада, вычисляемый на основе ряда последовательных поступлений наличных.
Синтаксис: НПЗ(ЧПС) (ставка; 1-е значение; 2-е значение; ...)
Аргументы: ставка Процентная ставка за период;
1-е значение, От 1 до 29 аргументов, представляющих расходы и доходы;
2-е значение 1-е значение, 2-е значение,. . . должны быть равномерно распределены по времени и осуществляться в конце каждого периода. НПЗ использует порядок аргументов 1-е значение, 2-е значение,.. для определения порядка поступлений и платежей.
На рабочем листе (рис.3) введем исходные данные с пояснениями и расчетные формулы в следующей последовательности:
Ввод текста и значений в диапазон A2:B6;
В ячейку C6 введем формулу
C6==ЕСЛИ(Вб=1;"год";ЕСЛИ(И(В6>=2;Вб<=4);"года";"лет"))
Первоначально в ячейку В7 введем произвольный процент, например 3%.
В ячейку B8 введем формулу вычисления текущего вклада B8=НПЗ(ЧПС)(B7;B3;B5).
Ввод исходных данных завершен.

Рис.3.Расчет годовой процентной ставки
Далее выполняем команду Сервис, Подбор параметра и заполняем открывшееся диалоговое окно Подбор параметра, как показано на рис.4

Рис. 4. Диалоговое окно Подбор параметра при расчете годовой процентной ставки
В поле Значение указываем 10000 — размер ссуды. В поле Изменяя значение ячейки даем ссылку на ячейку В7, в которой вычисляется годовая процентная ставка. После нажатия кнопки ОК средство подбора параметров определит, при какой годовой процентной ставке чистый текущий объем вклада равен 10000 руб. Результат вычисления выводится в ячейку В7. В нашем случае годовая учетная ставка равна 11,79%. Вывод: если банки предлагают большую годовую процентную ставку, то предлагаемая сделка не выгодна.
Пример 3 расчета эффективности капиталовложений с помощью функции ПЗ(ПС)
Постановка задачи. Допустим, что у вас просят в долг 10000 руб. и обещают возвращать по 2000 руб. в течение 6 лет. Будет ли выгодна эта сделка при годовой ставке 7%?
На рабочем листе ( рис.5) в ячейку В5 введена формула
=ПЗ(ПС)(В4;В2;-В3)
На рабочем листе введем исходные данные в диапазон A1:B4.
В ячейки введем следующие формулы:
[B5]=ПЗ(B4;В2;-В3);
=ЕСЛИ(В2=1;"год";ЕСЛИ(И(В2>=2;В2<=4);"года";"лет"));
=ЕСЛИ (В1<В5; "Выгодно дать деньги в долг"; ЕСЛИ (В5=В1; "Варианты равносильны"; "Выгоднее деньги положить под проценты")).

Рис. 5. Расчет эффективности капиталовложений
Функция ПЗ(ПС)возвращает текущий объем вклада на основе постоянных периодических платежей. Функция ПЗ(ПС) аналогична функции ПЗ(ПС). Основное различие между ними заключается в том, что функция ПЗ(ПС) допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. Кроме того, в отличие от функции ПЗ(ПС), денежные взносы в функции ПЗ(ПС) должны быть постоянными на весь период инвестиции.
Синтаксис:
ПЗ(ПС) (ставка; кпер; выплата; остаток; тип)
Аргументы:
ставка Процентная ставка за период
кпер Общее число периодов выплат
выплата Величина постоянных периодических платежей
остаток Будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если аргумент бз опущен, он полагается равным 0 (например, будущая стоимость займа равна 0)
тип Число 0 или 1, обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 — то в начале периода
В данном разделе была рассмотрена задача с двумя результирующими функциями: числовой — чистым текущим объемом вклада и качественной, оценивающей, выгодна ли сделка. Эти функции зависят от нескольких параметров. Некоторыми из них вы можете управлять, например, сроком и суммой ежегодно возвращаемых денег. Часто бывает удобно проанализировать ситуацию для нескольких возможных вариантов параметров. Команда Сервис, Сценарии предоставляет такую возможность с одновременным автоматизированным составлением отчета. Рассмотрим способ применения этой команды для следующих трех комбинаций срока и суммы ежегодно возвращаемых денег: 6, 2000; 12, 1500 и 7, 1500.
Выберем команду Сервис, Сценарии. В открывшемся диалоговом окне Диспетчер сценариев для создания первого сценария нажмите кнопку Добавить (рис.6).

Рис.6.Диалоговое окно Диспетчер сценариев
В диалоговом окне Добавление сценария в поле Название сценария введите, например ПЗ1, а в поле Изменяемые ячейки — ссылку на ячейки В2 и ВЗ, в которые вводятся значения параметров задачи (срок и сумма ежегодно возвращаемых денег) (рис. 7).
После нажатия кнопки ОК появится диалоговое окно Значения ячеек сценария, в поля которого введите значения параметров для первого сценария (рис.8).
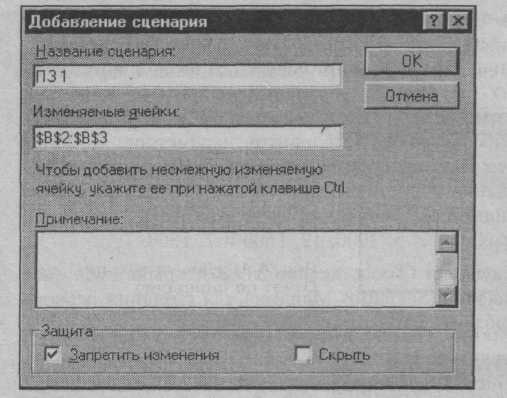
Рис.7.Диалоговое окно Добавление сценария
С помощью кнопки Добавить последовательно создайте нужное число сценариев. После этого диалоговое окно Диспетчер сценариев будет иметь вид, показанный на рис. 9.
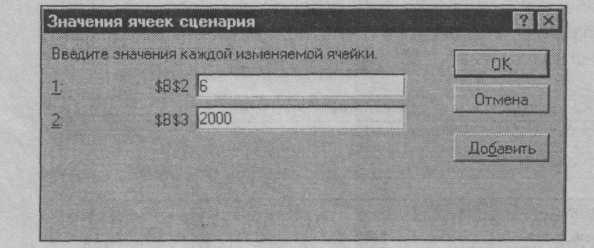
Рис.8.Диалоговое окно Значения ячеек сценария

Рис.9.Вывод сценариев на рабочий лист с помощью диалогового окна Диспетчер сценариев
С помощью кнопки Вывести можно вывести результаты, соответствующие выбранному сценарию. Нажатие кнопки Отчет открывает диалоговое окно Отчет по сценарию (рис. 10).

Рис.10.Диалоговое окно Отчет по сценарию
В этом окне в группе Тип отчета необходимо установить переключатель в положение Структура или Сводная таблица , а в поле Ячейки результата дать ссылку на ячейки, где вычисляются значения результирующих функций. После нажатия кнопки ОК создается отчет. На рис. 11 показан отчет по сценариям типа Структура.

Рис.11.Отчет по сценарию типа Структура
Пример 4 Финансовые функции ПЛПРОЦ и СНПЛАТ
Постановка задачи. Вычислить основные платежи, платы по процентам, общей ежегодной платы и остатка долга на примере ссуды 100000 руб. на срок 5 лет при годовой ставке 2% (рис. 12).
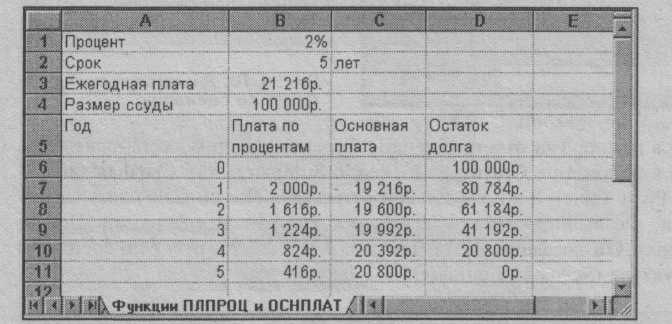
Рис. 12. Вычисление основных платежей и платы по процентам
Ежегодная плата вычисляется в ячейке ВЗ по формуле:
В3=ППЛАТ(В1;В2;-В4).
За первый год плата по процентам в ячейке В7 вычисляется по формуле:
В7=D6*0,02.
Основная плата в ячейке С7 вычисляется по формуле:
С7=$B$3-B7.
Остаток долга в ячейке D7 вычисляется по формуле:
=D6-C7
В оставшиеся годы эти платы определяются с помощью протаскивания маркера заполнения выделенного диапазона B7:D7 вниз по столбцам. Отметим, что основную плату и плату по процентам можно было непосредственно найти с помощью функций оснплат (ррмт) и плпроц (ipmt), соответственно.
Функция плпроц возвращает платежи по процентам за данный период на основе периодических постоянных выплат и постоянной процентной ставки.
Синтаксис:
ПЛПРОЦ(ставка; период; клер; нз; бз; тип)
Функция оснплат возвращает величину выплаты за данный период на основе периодических постоянных платежей и постоянной процентной ставки.
Синтаксис:
ОСНПЛАТ(ставка; период; кпер; нз; бз; тип)
Аргументы функций плпроц: и оснплат:
Период Период, за который требуется найти прибыль (должен находиться в интервале от 1 до кпер)
Ставка Процентная ставка за период
кпер Общее число периодов выплат
нз Текущее значение, т. е. общая сумма, которую составят будущие платежи
бз Будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если аргумент бз опущен, он полагается равным 0 (например, будущая стоимость займа равна 0)
тип Число 0 или 1, обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 — то в начале периода
Пример 5. Финансовая функция БЗ
Функция БЗ(БС) вычисляет будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки. Функция БЗ(БС) подходит для расчета итогов накоплений при ежемесячных банковских взносах.
Синтаксис:
БЗ(БС) (ставка; кпер; выплата; нз; тип)
Аргументы:
ставка Процентная ставка за период
кпер Общее число периодов выплат
выплата Величина постоянных периодических платежей
нз Текущее значение, т. е. общая сумма, которую составят будущие платежи
тип Число 0 или 1, обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 — в начале периода
Пример использования функции БЗ(БС) . Предположим, вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, вы собираетесь вложить 1000 руб. при годовой ставке 6%. Вы собираетесь вкладывать по 100 руб. в начале каждого месяца в течение года. Сколько денег будет на счете в конце 12 месяцев?
С помощью формулы
=БЗ(б%/12; 12; -100; -1000; 1)
получаем ответ: 2 301.40р.
Провести расчет, когда общее число периодов выплат –годовое.
Варианты заданий упражнения 4
Пример 1. Вычислить n-годичную ипотечную ссуду покупки квартиры за P руб. с годовой ставкой i%и начальным взносом А%. Сделать расчет для ежемесячных и ежегодных выплат.
 Варианты
n
Р i
A
Варианты
n
Р i
A
7 70000 5 100
70000 5 100
8 200000 6 100
9 220000 7 200
10 300000 8 200
11 350000 9 150
7 210000 10 150
8 250000 11 300
9 310000 12 300
9 10 320000 13 250
10 11 360000 14 250
11 7 300000 8 100
12 8 200000 6 100
13 9 220000 7 200
14 11 300000 8 200
15 10 350000 9 150
16 12 210000 10 150
17 8 250000 11 300
18 7 310000 12 300
19 10 320000 13 250
20 11 360000 14
250
Пример 2. Вас просят дать в долг Р руб. и обещают вернуть Р>1> руб. через год, P>2> руб. — через два года и т. д., наконец, Р>п> руб. — через п лет. При какой годовой процентной ставке эта сделка имеет смысл?
Варианты п Р Р>1 >Р>2> Р>3> Р>4> Р>5>
3 17000 5000 7000 8000
4 20000 6000 6000 9000 7000
5 22000 5000 8000 8000 7000 5000
3 30000 5000 10000 18000
4 35000 5000 9000 10000 18000
5 21000 4000 5000 8000 10000 11000
3 25000 8000 9000 10000
4 31000 9000 10000 10000 15000
5 32000 8000 10000 10000 10000 11000
3 36000 10000 15000 21000
4 20000 6000 6000 9000 7000
5 22000 5000 8000 8000 7000 5000
3 30000 5000 10000 18000
4 35000 5000 9000 10000 18000
5 21000 4000 5000 8000 10000 11000
3 25000 8000 9000 10000
4 31000 9000 10000 10000 15000
5 32000 8000 10000 10000 10000 11000
3 36000 10000 15000 21000
20 3 36000 10000 15000 21000

Пример 3. Вас просят дать в долг Р руб. и обещают возвращать по А руб. в течение п лет. При какой годовой процентной ставке эта сделка имеет смысл?
Вариант п Р А
7 170000 30000
8 200000 31000
9 220000 33000
10 300000 34000
11 350000 41000
7 210000 32000
8 250000 37000
9 310000 40000
9 10 320000 35000
10 11 360000 41000
11 7 170000 30000
12 8 200000 31000
13 9 220000 33000
14 10 300000 34000
15 11 350000 41000
16 7 210000 32000
17 8 250000 37000
18 9 310000 40000
19 10 320000 35000
20 11 360000 41000
Пример 4. Вычислить основные платежи, плату по процентам, общую ежегодную выплату и остаток долга на примере ссуды Р руб. под годовую ставку i'% на срок п лет.
Вариант п Р i
8 200000 6
9 220000 7
10 300000 8
11 350000 9
7 210000 10
8 250000 11
9 310000 12
9 10 320000 13
10 11 360000 14
11 8 200000 6
12 9 220000 7
13 10 300000 8
14 11 350000 9
15 7 210000 10
16 8 250000 11
17 9 310000 12
18 10 320000 13
19 11 360000 14
20 8 250000 11
Задание 5
Создание таблиц заданной структуры на примерах решений практических задач
Пример 1. Конвертирование валюты.
Создать таблицу конвертирования цены товара. При внешнеторговых операциях расчет с поставщиками выполняется в долларах, а расчет с внутренними покупателями - в рублях. Ввиду этого нужно иметь возможность конвертирования в рубли исходной (в момент поступления) и текущей ("на сегодня") цены товара. Вся необходимая информация хранится в двух таблицах: таблице курса доллара и таблице расчета рублевого эквивалента товара.
 Рис.
Лист Курс
Рис.
Лист Курс
Для удобства пользователя этот материал мы разнесем на два листа рабочей книги – лист Курс и лист Товар
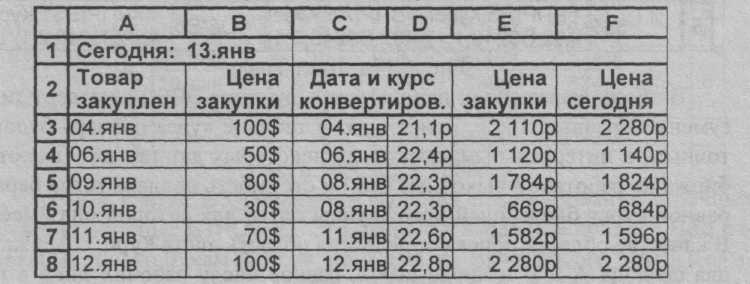
Рис.1 Лист Товар
Содержимое первого (на рисунке изображен только фрагмент листа) очевидно, - это последовательные значения дат и стоимости доллара. На листе Товар в клетке В1 предъявляется текущая дата (функция СЕГОДНЯ()), а также содержатся сведения о дате закупки товара и о закупочной цене (столбцы А и В). В столбце Е вычисляется рублевый эквивалент этой цены, но прежде формируются два столбца, нужные только для сведения оператора. В столбце С предъявляется ближайшая, найденная в листе Курс, дата (СЗ=ВПР (АЗ;Курс!А$2:В$240;1;1)), по курсу которой (столбец D) и производится конвертирование доллара в рубли. Делается это ради того, чтобы пользователь мог контролировать правильность конвертирования. Так, например, если обнаруживается, что дата конвертирования сильно отстает от даты закупки, можно предположить, что курсовая таблица содержит не все данные и ее следует просмотреть и, возможно, дополнить.
В столбце D показывается найденный курс доллара, по которому будет осуществляться конвертирование цены товара DЗ=ВПР(А3; Курс!А$2:В$240;2;1). На основании его и находится закупочная цена товара в рублях E3=D3*B3.
В столбце F определяется рублевый эквивалент цены “товара на сегодня” F3=ВПР(B$1;Курс!A$2:B$240;2;1)).
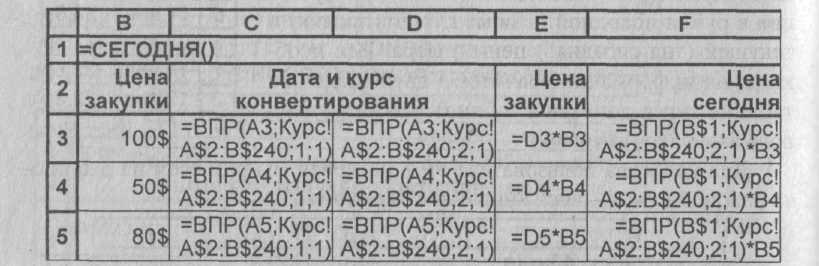
Рис.2 Лист Товар
В обоих выражениях используется функция ВПР() с четвертым аргументом равным 1, т.е. поиск даты в таблице курса доллара будет не точным, а интервальным, поскольку некоторых дат там нет (валютная биржа не работает в выходные дни) и стоимость доллара тогда берется равной курсу ближайшей предыдущей даты, для которой она имеется. В качестве области поиска определена область листа Курс, содержащая два столбца А и В и число строк, равное числу рабочих дней в году (около 240).
1