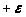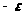Исследование операций (работа 1)
Министерство образования и науки Российской Федерации
Южно-Уральский государственный университет
Кафедра системы управления
Курсовая работа
по дисциплине: исследование операций
Вариант 9
_
Челябинск
2004 г.
Содержание
Задание 1 3
Задание 2 6
Задание 3 9
Задание 4 11
Литература 17
Задание 1
Задача 9
Условие:
Из трех видов сырья необходимо составить смесь, в состав которой должно входить не менее a ед. химического вещества А, b ед. – вещества В и c ед. – вещества С. Количество единиц химического вещества, содержащегося в 1 кг. сырья каждого вида, указано в таблице. Там же приведена цена 1 кг. сырья каждого вида. Составить смесь, содержащую не менее нужного количества веществ данного вида и имеющую минимальную стоимость.
|
Вещество |
Количество единиц вещества, содержащегося в 1 кг сырья |
||
|
1 |
2 |
3 |
|
|
А |
d>11> |
d>12> |
d>13> |
|
В |
d>21> |
d>22> |
d>23> |
|
С |
d>31> |
d>32> |
d>33> |
|
Цена 1 кг сырья |
D>1> |
D>2> |
D>3> |
|
№ вар. |
d>11> |
d>12> |
d>13> |
d>21> |
d>22> |
d>23> |
d>31> |
d>32> |
d>33> |
|
9 |
1 |
1 |
0 |
2 |
0 |
3 |
1 |
2 |
4 |
|
D>1> |
D>2> |
D>3> |
а |
b |
c |
|
5 |
6 |
7 |
26 |
30 |
24 |
Решение:
Составим математическую модель задачи.
Обозначим через n1, n2, n3 количество кг сырья 1, 2, 3 соответственно.
Тогда, целевая функция будет
L=D1n1+ D2n2+D3n3 = 5n1+ 6n2+7n3 →min
Система ограничений:
_ EMBED Equation.3 ___
Приведем систему ограничений к виду основной задачи линейного программирования. Введем целевую функцию с противоположным знаком L', и новые переменные n4, n5, n6, которые входят в целевую функцию с нулевыми коэффициентами.
L’=0-(5n1+ 6n2+7n3) →max
_ EMBED Equation.3 ___
Выберем n1, n2, n3 свободными переменными, а n4, n5, n6 – базисными и приведем к стандартному виду для решения с помощью симплекс-таблицы:
L’=0-(5n1+ 6n2+7n3)
_ EMBED Equation.3 ___
Составим симплекс-таблицу.
Это решение не опорное, т.к. свободные члены не положительны.
Выберем в первой строке отрицательный элемент, например на пересечении n1 и n4, тогда разрешающий столбец n1, а разрешающий элемент – n5 (минимальный по отношению свободного члена к элементам разрешающего столбца).
Таблица 1.1
|
|
b |
n>1> |
n>2> |
n>3> |
|||||
|
L’ |
0 |
|
5 |
|
6 |
|
7 |
|
|
|
|
-75 |
|
2,5 |
|
0 |
|
-8 |
||
|
n>4> |
-26 |
|
-1 |
|
-1 |
|
0 |
|
26/1=26 |
|
|
15 |
-1 |
|
0 |
|
1,5 |
|||
|
n>5> |
-30 |
-2 |
|
0 |
|
-3 |
|
30/2=15min |
|
|
|
15 |
|
-1 |
|
0 |
|
1,5 |
||
|
n>6> |
-24 |
|
-1 |
|
-2 |
|
-4 |
|
24/1=24 |
|
|
15 |
|
-1 |
|
0 |
|
1,5 |
Меняем n>1 >и n>5.>
Таблица 1.2
|
|
b |
n>5> |
n>2> |
n>3> |
|||||
|
L’ |
-75 |
|
2,5 |
|
6 |
|
-0,5 |
|
|
|
|
-45 |
|
5 |
|
-10 |
|
25 |
||
|
n>4> |
-11 |
-0,5 |
|
-1 |
1,5 |
|
11/0,5=22 |
||
|
|
9 |
|
-1 |
2 |
|
-5 |
|||
|
n>1> |
15 |
|
-0,5 |
|
0 |
|
1,5 |
|
|
|
|
9 |
|
-1 |
|
2 |
|
-5 |
||
|
n>6> |
-9 |
-0,5 |
|
-2 |
-2,5 |
|
9/0,5=18min |
||
|
|
18 |
|
-2 |
|
4 |
|
5 |
Меняем n>5 >и n>6.>
Таблица 1.3
|
|
b |
n>6> |
n>2> |
n>3> |
||||
|
L’ |
-120 |
|
5 |
-4 |
|
25 |
|
|
|
|
-10 |
5 |
|
5 |
|
-18 |
||
|
n>4> |
-2 |
-1 |
1 |
|
-4 |
|
||
|
|
2 |
-1 |
|
-1 |
2,5 |
|||
|
n>1> |
24 |
|
-1 |
|
2 |
|
-3 |
|
|
|
2 |
|
-1 |
|
-1 |
|
3,5 |
|
|
n>5> |
18 |
|
-2 |
4 |
|
5 |
|
|
|
|
4 |
|
-2 |
|
-2 |
|
7 |
Меняем n>4 >и n>6>.
Таблица 1.4
|
|
b |
n>4> |
n>2> |
n>3> |
||||
|
L’ |
-130 |
|
5 |
|
1 |
|
7 |
|
|
|
|
|
|
|
|
|
||
|
n>6> |
2 |
|
-1 |
|
-1 |
|
3,5 |
|
|
|
|
|
|
|
|
|
|
|
|
n>1> |
26 |
|
-1 |
|
-1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
n>5> |
22 |
|
-2 |
|
2 |
|
12 |
|
|
|
|
|
|
|
|
|
|
Т.к. коэффициенты при всех ni положительны, то это и есть оптимальное решение.
Тогда n4 = n2 = n3 =0, n6 =2, n1 =26, n5 =22, L’= -130, следовательно, L=130.
Необходимо взять 26 кг первого сырья, и тогда получим смесь, содержащую не менее нужного количества веществ данного вида и имеющую минимальную стоимость 130.
Ответ: для получения смеси с минимальными затратами необходимо взять 26 кг только первого сырья.
Задание 2
Задача 29
Условие:
Решение задачи линейного программирования.
С помощью симплекс–таблиц найти решение задачи линейного программирования: определить экстремальное значение целевой функции Q=CTx при условии Ax ( (B,
где (( = ( (1 (2 . . . (6 (( , В( = ( b1 b2 . . . b6 (( ,
(( = ( (1 (2 . . . (6(( , А= ((((( ((=1,6; (=1,3).
|
№ вар. |
С>1> |
с>2> |
с>3> |
с>4> |
с>5> |
с>6> |
b>1> |
b>2> |
b>3> |
|
29 |
0 |
5 |
1 |
–1 |
1 |
0 |
2 |
2 |
10 |
|
Знаки ограничений |
a>11> |
a>12> |
a>13> |
a>14> |
||
|
1 |
2 |
3 |
||||
|
|
|
|
–1 |
1 |
1 |
0 |
|
a>15> |
a>16> |
a>21> |
a>22> |
a>23> |
a>24> |
a>25> |
a>26> |
|
0 |
0 |
1 |
–2 |
0 |
1 |
0 |
0 |
|
a>31> |
a>32> |
a>33> |
a>34> |
a>35> |
a>36> |
Тип экстрем. |
|
2 |
1 |
1 |
1 |
2 |
0 |
max |
Решение:
Составим систему:
_ EMBED Equation.3 ___
Целевая функция Q= 0x1+5x2+x3 –x4+x5 →max
Приведем систему ограничений к виду основной задачи линейного программирования.
_ EMBED Equation.3 ___
Пусть х1, х2 , х3, х4, х5 – свободные переменные, х6, х7, х8 – базисные.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
Q= 0-(-5x2-x3 +x4- x5)
_ EMBED Equation.3 ___
Составим симплекс-таблицу:
Это опорное решение т.к. коэффициенты bj>0. Будем искать оптимальное решение. Т.к. коэффициенты при свободных членах <0 (кроме при x1), то разрешающим может быть любой столбец. Пусть x2, тогда на пересечении x2 и x6 получим разрешающий элемент.
Таблица 2.1
|
|
b |
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
|||||||
|
Q |
0 |
|
0 |
|
-5 |
|
-1 |
|
1 |
|
-1 |
|
|
|
|
10 |
|
-5 |
|
5 |
|
5 |
|
0 |
|
0 |
||
|
x>6> |
2 |
|
-1 |
|
1 |
|
1 |
0 |
|
0 |
|
2/1=2min |
|
|
|
2 |
|
-1 |
|
1 |
1 |
|
0 |
|
0 |
|||
|
x>7> |
2 |
|
1 |
|
-2 |
|
0 |
|
1 |
|
0 |
|
|
|
|
4 |
|
-2 |
|
2 |
|
2 |
|
0 |
|
0 |
||
|
x>8> |
10 |
|
2 |
|
1 |
|
1 |
1 |
|
2 |
|
10/2=5 |
|
|
|
-2 |
|
1 |
|
-1 |
|
-2 |
|
0 |
|
0 |
Меняем x>2 >и x>6.>
Таблица 2.2
|
|
b |
x>1> |
x>6> |
x>3> |
x>4> |
x>5> |
||||||
|
Q |
10 |
|
-5 |
|
5 |
|
4 |
|
1 |
|
-1 |
|
|
|
4 |
1,5 |
|
-1 |
-1 |
|
0,5 |
0,5 |
||||
|
x>2> |
2 |
|
-1 |
|
1 |
|
1 |
|
0 |
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
x>7> |
6 |
|
-1 |
2 |
|
2 |
1 |
|
0 |
|
||
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
0 |
||
|
x>8> |
8 |
|
3 |
-1 |
|
-1 |
1 |
2 |
|
|||
|
|
4 |
|
6 |
|
-2 |
|
-2 |
|
2 |
|
0,5 |
Меняем x>5 >и x>8.>
Таблица 2.3
|
|
b |
x>1> |
x>6> |
x>3> |
x>4> |
x>8> |
||||||
|
Q |
14 |
|
-3.5 |
|
4,5 |
|
3,5 |
|
1,5 |
|
0,5 |
|
|
|
21 |
5,25 |
|
-2,625 |
-2,625 |
|
2,625 |
|
2,625 |
|||
|
x>2> |
2 |
|
-1 |
|
1 |
|
1 |
|
0 |
|
0 |
|
|
|
8/3 |
|
2/3 |
|
-1/3 |
|
-1/3 |
|
1/3 |
|
1/3 |
|
|
x>7> |
6 |
|
-1 |
2 |
|
2 |
1 |
0 |
|
|||
|
|
8/3 |
2/3 |
|
-1/3 |
|
-1/3 |
|
1/3 |
|
1/3 |
||
|
x>5> |
4 |
1,5 |
-0,5 |
|
-1 |
0,5 |
0,5 |
|
||||
|
|
8/3 |
|
2/3 |
|
-1/3 |
|
-1/3 |
|
1/3 |
|
1/3 |
Меняем x>5 >и x>1.>
Таблица 2.4
|
b |
x>5> |
x>6> |
x>3> |
x>4> |
x>8> |
|
|
Q |
35 |
5,25 |
1,875 |
0,875 |
4,125 |
3,125 |
|
x>2> |
14/3 |
2/3 |
2/3 |
2/3 |
1/3 |
1/3 |
|
x>7> |
26/3 |
2/3 |
5/3 |
5/3 |
4/3 |
1/3 |
|
x>1> |
8/3 |
2/3 |
-1/3 |
-1/3 |
1/3 |
1/3 |
Получили оптимальное решение, т.к. все коэффициенты положительны.
Следовательно Q=35; x5=x6= x3=x4=x8=0; x1=8/3; x2=14/3; x7=26/3.
Ответ: Q=35; x5=x6= x3=x4=x8=0; x1=8/3; x2=14/3; x7=26/3.
Задание 3
Задача 9
Условие:
Решение транспортной задачи:
1. Записать условия задачи в матричной форме.
2. Определить опорный план задачи.
3. Определить оптимальный план задачи.
4. Проверить решение задачи методом потенциалов.
Таблица 1
|
№вар. |
а>1> |
а>2> |
а>3> |
b>1> |
b>2> |
b>3> |
b>4> |
b>5> |
с>11> |
с>12> |
с>13> |
|
9 |
300 |
700 |
1000 |
200 |
100 |
400 |
600 |
200 |
23 |
40 |
10 |
|
с>14> |
с>15> |
с>21> |
с>22> |
с>23> |
с>24> |
с>25> |
с>31> |
с>32> |
с>33> |
с>34> |
с>35> |
|
12 |
21 |
25 |
21 |
20 |
50 |
18 |
15 |
30 |
32 |
25 |
50 |
Решение:
Составим таблицу транспортной задачи.
Таблица 2
|
|
B1 |
B2 |
B3 |
B4 |
B5 |
a |
|
A1 |
|
|
|
|
|
|
|
23 |
40 |
10 |
12 |
21 |
300 |
|
|
A2 |
|
|
|
|||
|
25 |
21 |
20 |
50 |
18 |
700 |
|
|
A3 |
|
|
|
|
|
|
|
15 |
30 |
32 |
25 |
50 |
1000 |
|
|
b |
200 |
100 |
200 |
600 |
200 |
|
Заметим, что сумма запасов превышает заявки. Это транспортная задача с избытком запасов. Для того чтобы привести к транспортной задаче с правильным балансом, введем фиктивный пункт назначения В5 с нулевыми перевозками. Добавим недостающее число заявок b5=700. Теперь количество заявок равно количеству запасов и равно 2000.
Заполним таблицу. Для этого не будем использовать метод северо-западного угла, т.к. он принесет много хлопот, будем заполнять клетки слева направо от заявок к запасам, исходя из наименьшей цены.
Таблица 3
|
|
B1 |
B2 |
B3 |
B4 |
B5 |
В6 |
a |
|
A1 |
|
|
|
300 |
|
|
|
|
23 |
40 |
10 |
12 |
21 |
0 |
300 |
|
|
A2 |
100 |
200 |
|
200 |
200 |
|
|
|
25 |
21 |
20 |
50 |
18 |
0 |
700 |
|
|
A3 |
200 |
|
|
300 |
|
500 |
|
|
15 |
30 |
32 |
25 |
50 |
0 |
1000 |
|
|
b |
200 |
100 |
200 |
600 |
200 |
700 |
2000 |
Это будет опорный план.
Количество заполненных ячеек – 6. r=m+n-1=3+6-1=8>6, значит, план является вырожденным, т.к. не хватает 2 базисных клеток. Добавим их, и сделаем план невырожденным. Для этого изменим в некоторых клетках количество запасов и заявок на малую величину _ EMBED Equation.3 ___
Таблица 4
|
|
B1 |
B2 |
B3 |
B4 |
B5 |
В6 |
a |
|
A1 |
|
|
|
300 |
|
|
300 |
|
23 |
40 |
10 |
12 |
21 |
0 |
||
|
A2 |
|
100 |
200 |
|
200 |
200 |
700 |
|
25 |
21 |
20 |
50 |
18 |
0 |
||
|
A3 |
200 |
|
|
300 |
|
500 |
1000 |
|
15 |
30 |
32 |
25 |
50 |
0 |
||
|
b |
200 |
100 |
200 |
600 |
200 |
700 |
2000 |
Проверим методом потенциалов:
Примем α1=0, тогда βj = cij – αi (для заполненных клеток).
Если решение верное, то во всех пустых клетках таблицы Δij = cij – (αi+ βj) ≥ 0
Очевидно, что Δij =0 для заполненных клеток.
В результате получим следующую таблицу:
Таблица 5
|
|
β1=2 |
β2=8 |
β3=7 |
β4=12 |
β5=6 |
β6=-13 |
a |
|
α1=0 |
|
|
|
300 |
|
|
300 |
|
23-2>0 |
40-8>0 |
10-7>0 |
12-12=0 |
21-6>0 |
0-(-13)>0 |
||
|
α2=13 |
100 |
200 |
|
200 |
200 |
700 |
|
|
25-13-2>0 |
21-8-13=0 |
20-7-13=0 |
50-12-13>0 |
18-6-13=0 |
0-13+13=0 |
||
|
α2=13 |
200 |
|
|
300 |
|
500 |
1000 |
|
15-13-2=0 |
30-13-8>0 |
32-13-7>0 |
25-13-2=0 |
50-13-6>0 |
0-13+13=0 |
||
|
b |
200 |
100 |
200 |
600 |
200 |
700 |
2000 |
Таким образом, решение верное, т.к. Δij > 0 для всех пустых клеток и Δij =0 для всех заполненных.
Тогда сумма всех перевозок:
L=200*15+10*21+200*20+300*12+300*25+200*18+200*0+500*0=23800
Ответ:
|
|
B1 |
B2 |
B3 |
B4 |
B5 |
В6 |
a |
|
A1 |
|
|
|
300 |
|
|
|
|
23 |
40 |
10 |
12 |
21 |
0 |
300 |
|
|
A2 |
100 |
200 |
|
200 |
200 |
|
|
|
25 |
21 |
20 |
50 |
18 |
0 |
700 |
|
|
A3 |
200 |
|
|
300 |
|
500 |
|
|
15 |
30 |
32 |
25 |
50 |
0 |
1000 |
|
|
b |
200 |
100 |
200 |
600 |
200 |
700 |
2000 |
Задание 4
Задача 54
Условие:
Определить экстремум целевой функции вида
( = (11(12+(22(22+(12(1(2+(1(1+(2(2
при условиях:
(11(1+(12(2<=>(1
(21(1+(22(2<=>(2 .
Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
Составить функцию Лагранжа.
Получить систему неравенств в соответствии с теоремой Куна-Таккера.
Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
Дать ответ с учетом условий дополняющей нежесткости.
|
№ |
b>1> |
b>2> |
c>11> |
c>12> |
c>22> |
extr |
a>11> |
a>12> |
a>21> |
a>22> |
p>1> |
p>2> |
Знаки огр. 1 2 |
|
|
|
–7 |
–2 |
4 |
1.5 |
–2 |
min |
–2 |
1.5 |
4 |
–3 |
18 |
9 |
|
|
Решение:
1) Целевая функция: F=4x12-2x22 +1,5x1x2-7x1-2x2→min
Рассмотрим F’=-4x12+2x22 -1,5x1x2+7x1+2x2→max
Ограничения g1(x) и g2(x): _ EMBED Equation.3 ___ →_ EMBED Equation.3 ___
Определим относительный максимум функции F’, для этого определим стационарную точку (х10, х20):
_ EMBED Equation.3 ___→ _ EMBED Equation.3 ___→ _ EMBED Equation.3 ___
2) Исследуем стационарную точку на максимум, для чего определяем выпуклость или вогнутость функции:
F’11 (х10, х20) = -8 < 0
F’12 (х10, х20) = -1,5
F’21 (х10, х20) = -1,5
F’22 (х10, х20) = 4
_ EMBED Equation.3 ___
Т.к. условие выполняется, то целевая функция является строго выпуклой в окрестности стационарной точки
3) Составляем функцию Лагранжа:
L(x,u)=F’(x)+u1g1(x)+u2g2(x)=
=-4x12+2x22 -1,5x1x2+7x1+2x2+u1(_ EMBED Equation.3 ___)+u2(_ EMBED Equation.3 ___)
Получим уравнения седловой точки, применяя теорему Куна-Таккера:
_ EMBED Equation.3 ___ i=1;2
Объединим неравенства в систему А, а равенства в систему В:
Система А:
_ EMBED Equation.3 ___
Система В:
_ EMBED Equation.3 ___
Перепишем систему А:
_ EMBED Equation.3 ___
4)Введем новые переменные
V={v1,v2}≥0; W={w1,w2}≥0
в систему А для того, чтобы неравенства превратить в равенства:
_ EMBED Equation.3 ___
Тогда
_ EMBED Equation.3 ___.
Значит , система В примет вид:
_ EMBED Equation.3 ___ - это условия дополняющей нежесткости.
5) Решим систему А с помощью метода искусственных переменных.
Введем переменные Y={y1; y2} в 1 и 2 уравнения системы
_ EMBED Equation.3 ___
Затем создадим псевдоцелевую функцию Y=My1+My2→min
Y’=-Y= -My1-My2→max.
Пусть свободные переменные: х1, х2, v1, v2, u1, u2;
а базисные y1, y2, w1, w2.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
_ EMBED Equation.3 ___
_ EMBED Equation.3 ___
Решим с помощью симплекс-таблицы. Найдем опорное решение:
|
|
b |
x1 |
x2 |
u1 |
u2 |
v1 |
v2 |
||||||||
|
Y'/M |
-9 |
|
-9,5 |
|
2,5 |
|
0,5 |
|
1 |
|
1 |
|
1 |
|
|
|
|
8,3125 |
1,1875 |
|
1,7813 |
-2,375 |
|
-4,75 |
-1,188 |
|
0 |
|||||
|
y1 |
7 |
|
8 |
|
1,5 |
|
-2 |
|
-4 |
|
-1 |
|
0 |
|
|
|
|
0,875 |
0,125 |
|
0,1875 |
-0,25 |
|
-0,5 |
-0,125 |
|
0 |
|||||
|
y2 |
2 |
|
1,5 |
|
-4 |
|
1,5 |
|
3 |
|
0 |
|
-1 |
|
|
|
|
-1,313 |
-0,188 |
|
-0,281 |
0,375 |
|
0,75 |
0,1875 |
|
0 |
|||||
|
w1 |
18 |
|
-2 |
|
1,5 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
1,75 |
|
0,25 |
|
0,375 |
|
-0,5 |
|
-1 |
|
-0,25 |
|
0 |
||
|
w2 |
9 |
|
-4 |
3 |
|
0 |
0 |
|
0 |
0 |
|
||||
|
|
3,5 |
|
0,5 |
|
0,75 |
|
-1 |
|
-2 |
|
-0,5 |
|
0 |
||
|
|
b |
y1 |
x2 |
u1 |
u2 |
v1 |
v2 |
||||||||
|
Y'/M |
-0,69 |
|
1,1875 |
|
4,2813 |
|
-1,875 |
|
-3,75 |
|
-0,188 |
|
1 |
|
|
|
|
0,6875 |
-0,188 |
|
-4,281 |
1 |
|
3,75 |
0,1875 |
|
-1 |
|||||
|
x1 |
0,875 |
|
0,125 |
|
0,1875 |
|
-0,25 |
|
-0,5 |
|
-0,125 |
|
0 |
|
|
|
|
0,0917 |
|
-0,025 |
|
-0,571 |
0,1333 |
|
|
0,025 |
|
-0,133 |
||||
|
y2 |
0,688 |
|
-0,188 |
|
-4,281 |
|
1,875 |
|
3,75 |
|
0,1875 |
|
-1 |
|
|
|
|
0,3667 |
|
-0,1 |
|
-2,283 |
|
0,5333 |
|
2 |
|
0,1 |
|
-0,533 |
||
|
w1 |
19,75 |
0,25 |
1,875 |
|
-0,5 |
-1 |
|
-0,25 |
|
0 |
|
||||
|
|
0,1833 |
|
-0,05 |
|
-1,142 |
|
0,2667 |
|
1 |
|
0,05 |
|
-0,267 |
||
|
w2 |
12,5 |
|
0,5 |
|
3,75 |
|
-1 |
-2 |
|
-0,5 |
0 |
|
|||
|
|
0,3667 |
|
-0,1 |
|
-2,283 |
|
0,5333 |
|
2 |
|
0,1 |
|
-0,533 |
||
|
|
b |
y1 |
x2 |
y2 |
u2 |
v1 |
v2 |
||||||||
|
Y'/M |
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x1 |
0,967 |
|
|
|
|
|
0,1333 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
u1 |
0,367 |
|
-0,1 |
|
-2,283 |
|
0,5333 |
|
2 |
|
0,1 |
|
-0,533 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
w1 |
19,93 |
|
|
0,2667 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
w2 |
12,87 |
|
|
|
0,5333 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т. о, u2=x2=y1=y2=v1=v2=0; x1=0,967; u1=0,367; w1=19,93; w2=12,87;
б) Условия дополняющей нежесткости выполняются (u2w2=0), значит решения исходной задачи квадратичного программирования существует.
ОТВЕТ: существует.
Литература
Курс лекций Плотникова Н. В.