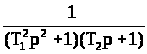Исследование нелинейных систем

Кафедра: Автоматика и информационные технологии

ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ И ИМПУЛЬСНЫХ СИСТЕМ

Екатеринбург 2005

Оглавление

Введение 3

1. Изучение типичных нелинейностей 4

2. Исследование нелинейных систем методом фазовой плоскости 19

3. Исследование нелинейных систем методом гармонического баланса 32

4. Синтез дискретной системы с максимальным быстродействием 53

Список литературы 66

Введение

Изучение раздела «Нелинейные системы» предусматривает выполнение трех лабораторных работ. Последняя, четвертая работа посвящена разделу «Импульсные системы автоматического управления». Работы выполняются с использованием пакета Matlab. Предполагается, что студенты получили опыт использования данного пакета в процессе выполнения лабораторных работ по курсу «Линейные системы» и в ходе самостоятельного изучения.

Для сохранения результатов работы каждой бригаде необходимо создать на компьютере в папке, предназначенной для работы пользователей, папку группы, внутри нее папку бригады, где и следует размещать поддиректории с результатами лабораторных работ. После окончания лабораторной работы все результаты необходимо сохранить на дискете.

1.Изучение типичных нелинейностей

В работе рассматриваются типичные нелинейности с симметричными характеристиками, представленными на рис. 1.1.

Рис. 1.1. Характеристики нелинейных элементов: а – идеальное двухпозиционное реле; б – усилитель с ограничением и зоной нечувствительности; в-трехпозиционное реле; г – двухпозиционное реле с гистерезисом; д – люфт

Цель работы  моделирование указанных нелинейностей и фиксация процессов на входе и выходе каждого нелинейного звена средствами пакета Matlab (c использованием его расширения – пакета моделирования динамических систем Simulink). В качестве источника (генератора) входного воздействия следует использовать свободные колебания на выходе колебательного звена, описываемого передаточной функцией при ненулевых начальных условиях. Варьируя декремент затухания (коэффициент демпфирования) и постоянную времени Т или другие связанные с ними параметры колебательного звена, можно добиться как гармонических, так и затухающих колебательных процессов. Гармонический сигнал различной амплитуды позволяет протестировать работу нелинейности «по частям», т.е. наблюдать влияние отдельных участков характеристики нелинейности на преобразование входного сигнала. При помощи затухающего тестового сигнала можно проверить работу нелинейности в целом, наблюдая за время затухания процесса все возможные эволюции сигнала на выходе нелинейного элемента (НЭ), связанные с его воздействием, а также построить характеристику НЭ (при этом максимальное значение амплитуды тестового сигнала, естественно, должно быть задано бóльшим, чем значение параметров b или b>2>, в зависимости от типа нелинейности).

Выбор значений параметров нелинейных элементов и генератора

Параметры НЭ и время затухания колебательного процесса на выходе генератора следует задавать в соответствии с вариантом, приведённым в табл. 1.1. Номер варианта соответствует номеру бригады.

Таблица 1.1 Значения параметров нелинейных элементов и генератора

Параметры

Номер варианта

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

c

1

1.5

2

2.5

3

3.5

4

4.5

5

5.5

6

6.5

7

7.5

8

b

0.1

0.2

0.25

0.25

0.3

0.35

0.4

0.5

0.5

0.6

0.8

1

1.2

1.3

1.5

b>2>

1.1

1.7

2.25

2.75

3.3

3.85

4.4

5

5.5

6.1

6.8

7.5

8.2

8.8

9.5

t>з>

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

        Найти угловую частоту затухающих колебаний и коэффициент затухания колебательного звена в соответствии с заданным в табл. 1.1 временем затухания колебательного процесса и числом периодов, равным 10  20 на интервале .

Уравнение, описывающее свободные колебания на выходе колебательного звена, имеет следующий вид:

, (1.1)

,

где t – время; А – амплитуда гармонических колебаний (при ) или амплитуда затухающих колебаний в начальный момент времени (при ); – угловая частота гармонических колебаний.

Амплитуда А задается произвольно, а параметры и необходимо увязать с исходными данными о требуемом времени затухания колебательного процесса и заданным количеством периодов колебаний за это время.

Затухание процесса можно считать окончившимся в момент времени, приблизительно равный трем постоянным времени экспоненты, т.е.

,

а угловую частоту следует вычислять по уравнению

,

где N – задаваемое количество колебаний (периодов) за время затухания процесса.

Решая систему уравнений

получим выражение для :

, (1.2)

после чего можно вычислить .

В итоге рассчитываются коэффициент затухания по формуле и угловая частота по формуле или .

        Для проведения моделирования создать 2 файла: файл-сценарий TN_prog.m и файл модели TN_mod.mdl. Они взаимосвязаны: переменные, определенные в m файле, используются при задании параметров блоков модели, модель запускается на выполнение также командой из m файла, а при проведении моделирования в Simulink результаты записываются в рабочую область памяти (Workspace), откуда считываются при построении итоговых графиков командами из m файла. Пример файла TN_prog.m приводится ниже.

Изучение типичных нелинейностей

Используемые обозначениЯ:

НЭ – нелинейный элемент.

clear all % очистка памЯти

close all % закрытие всех предыдущих рисунков

Задание значениЯ переменной, определЯющей положение переключателЯ

%конфигурации в файле TN_mod.mdl

%1 – НЭ-идеальное двухпозиционное реле

%2 – НЭ-усилитель с ограничением и зоной нечувствительности

%3 – НЭ-трехпозиционное реле без гистерезиса

%4 – НЭ-двухпозиционное реле с гистерезисом

%5 – НЭ-люфт

config = 5;

%Определение значениЯ строковой переменной nlin

switch config

case 1,

nlin = 'ид. 2 х поз. реле';

case 2,

nlin = 'ус-ль с огр. и зоной нечувст.';

case 3,

nlin = '3 х поз. реле без гист.';

case 4,

nlin = '2 х поз. реле с гист.';

case 5,

nlin = 'люфт';

end

%Константы, описывающие нелинейные элементы

c = 6;

b = 1;

b2 = 7;

%Параметры моделированиЯ

t_end = 10; %времЯ моделированиЯ, с

step = 1e 3;%шаг моделированиЯ, с

%Описание генератора затухающих колебаний

N = 15; %количество колебаний за времЯ моделированиЯ

A = 10; %амплитуда в начальный момент времени

lambda = 2*pi*N/t_end; %угловаЯ частота затухающих колебаний

ksi = 1.5/sqrt((pi*N)^2+2.25); %декремент затуханиЯ

%ksi = 0;

omega = (2*pi*N)/(t_end*sqrt (1 ksi^2));%угловаЯ чатота гармонических колебаний

gamma = ksi*omega; %коэффициент затуханиЯ

%вызов модели

open_system ('TN_mod.mdl');

%запуск моделированиЯ

sim ('TN_mod');

%Построение процессов во времени (рис. 1)

figure(1) %открытие окна рисунка

title(['Процессы e(t) и y(t). НЭ – ', nlin, ', b=', num2str(b), ', b2=', num2str(b2),…

', c=', num2str(c)]) %заголовок рисунка

xlabel ('t – времЯ, c') %название оси Х

ylabel ('e – вход НЭ, g – выход НЭ') %название оси Y

grid on %включение сетки

hold on

plot (t, e, '-r') %построение первого графика рисунка с указанием

%имен массивов точек, выводимых по осЯм X и Y, и

%установкой цвета и типа линии графика

plot (t, g, '-b') %второй график – аналогично

legend ('вход НЭ', 'выход НЭ', 4)%вывод на рисунок поЯснЯющей надписи, показывающей

%соответствие между цветом графика и его названием

%Построение характеристики нелинейности (рис. 2)

figure(2)

title(['Хар-ка нелин-ти g(e). НЭ – ', nlin, ', b=', num2str(b), ', b2=', num2str(b2),…

', c=', num2str(c)])

xlabel ('e – вход НЭ')

ylabel ('g – выход НЭ')

%ручнаЯ установка пределов по осЯм X и Y: [Xmin, Xmax, Ymin, Ymax]

if config == 5

axis ([-A*1.1 A*1.1 – (A-b)*1.1 (A-b)*1.1])

else

axis ([-A*1.1 A*1.1 – c*1.1 c*1.1])

end

grid on

hold on

plot (e, g, '-r')

Все команды Matlab, использованные при создании данной программы, описаны в приложении.

В файле-сценарии необходимо задать значения констант, описывающих нелинейности, задать шаг и время моделирования, равное времени затухания колебаний на выходе генератора, а также значение переменной config, управляющей конфигурацией нелинейной части модели. В процессе выполнения m файла рассчитываются параметры генератора, вызывается и запускается модель, результаты в виде временных процессов на входе и выходе НЭ, а также зависимость выходного сигнала от значений входного при помощи команд построения двумерных графиков выводятся в отдельные графические окна.

Файл модели должен содержать генератор и соединенный с ним нелинейный элемент. Можно предусмотреть одновременное наличие в схеме всех пяти рассматриваемых НЭ, а их выбор производить при помощи селектора (рис. 1.2). Учитывая возможность переименования функциональных блоков в Matlab, рекомендуется давать им содержательные названия.

В настройках параметров моделирования следует указывать специально предназначенные для этой цели переменные, значения которых заданы в файле-сценарии. Параметры моделирования должны быть указаны в окне «Simulation parameters», доступном через меню Simulation\Simulation parameters окна, в котором открыт mdl файл (рис. 1.3).

В дальнейшем в настройках блоков используются переменные, заданные в m файле. Такой подход помогает экономить время при настройке и перенастройке модели.

Рис. 1.2. Структурная схема модели

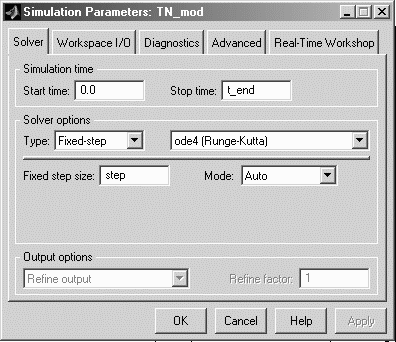
Рис. 1.3. Настройка параметров моделирования

При помощи блоков Constant (константа) из библиотеки Sources, Gain (коэффициент усиления) из библиотеки Math и переменной config можно задавать различное значение управляющего входа переключателя конфигурации нелинейной части (блока Multiport Switch из библиотеки Nonlinear).

В качестве генератора свободных колебаний можно использовать блок Fcn из библиотеки Functions & Tables с записанным в него выражением для свободных колебаний по формуле (1.1). Настройки блока Fcn показаны на рис. 1.4.

Рис. 1.4. Настройки блока Fcn

На вход блока Fcn следует подключить источник модельного времени – блок Clock из библиотеки Sources (рис. 1.5).

Рис. 1.5. Настройки блока Clock

Для создания пяти изучаемых НЭ следует воспользоваться четырьмя блоками библиотеки Nonlinear: Backlash (люфт), Dead Zone (усилитель с единичным коэффициентом усиления и зоной нечувствительности), Saturation (усилитель с единичным коэффициентом усиления и ограничением), Relay (двухпозиционное реле с гистерезисом).

В качестве двухпозиционного реле с гистерезисом следует использовать блок Relay (рис. 1.6).

Рис. 1.6. Настройки двухпозиционного реле с гистерезисом

Идеальное двухпозиционное реле – это блок Relay с нулевой шириной зоны гистерезиса (рис. 1.7).

Рис. 1.7. Настройки блока Relay при моделировании идеального
двухпозиционного реле

Усилитель с ограничением и зоной нечувствительности – это последовательное соединение трех звеньев: Dead Zone, Gain и Saturation (рис. 1.8, 1.9).

Рис. 1.8. Схема моделирования усилителя с ограничением
и зоной нечувствительности

а б

в

Рис. 1.9. Настройки блоков, входящих в состав усилителя с ограничением и зоной нечувствительности: а – блока Dead Zone; б – блока Saturation; в-блока Gain

Трехпозиционное реле без гистерезиса можно организовать при помощи параллельного соединения двух идеальных двухпозиционных реле (рис. 1.10, 1.11).

Рис. 1.10. Схема моделирования трехпозиционного реле

а б

Рис. 1.11. Настройки блоков, входящих в состав трехпозиционного реле: а – блока Relay1; б – блока Relay2

Для организации НЭ «Люфт» необходим блок Backlash (рис. 1.12).

Рис. 1.12. Настройки блока Backlash

Значения текущего модельного времени, а также сигналов на входе и выходе нелинейности следует выводить в рабочую область памяти при помощи блоков To Workspace (из библиотеки Sinks), указав в каждом блоке имя переменной, предназначенной для хранения данных в выбранном формате. По завершении моделирования в Simulink сохраненная информация будет использована при построении графиков в процессе дальнейшего выполнения файла-сценария.

При использовании блока To Workspace для вывода в рабочую область памяти текущего модельного времени для этого блока необходимо сделать следующие настройки:

    формат записи (Save format)  Array (массив);

    имя массива (Variable name)  t;

    количество точек в массиве (Limit data points to last) не ограничивается  inf;

    такт работы блока (Simple time) наследуется от предыдущего  (-1);

    прореживание массива (Decimation) не осуществляется  1 (в память записывается значение времени на каждом такте работы блока).

Окно настроек блока показано на рис. 1.13.

Рис. 1.13. Настройки блока To Workspace, отвечающего за вывод в рабочую область памяти текущего модельного времени

Программа работы

        Разместить созданные при подготовке файл-сценарий и файл модели в рабочей директории. Открыть TN_prog.m, проверить соответствие записанных в него исходных данных номеру варианта и при помощи переменной config выбрать для моделирования один из нелинейных элементов. Для обеспечения работы генератора в режиме с затуханием выходного сигнала рассчитывать значение коэффициента демпфирования в соответствии с формулой (1.2). Значение начальной амплитуды сигнала должно превышать значение параметра b>2> нелинейности в случае усилителя с ограничением и зоной нечувствительности, 0 – в случае идеального двухпозиционного реле и b – во всех остальных случаях.

        Запустить m файл на выполнение. В случае безошибочной организации файла-сценария и файла модели будет запущено моделирование в Simulink, а по его завершении построены три результирующих графика (совмещенные зависимости входного и выходного сигналов НЭ от времени и характеристика нелинейности, т.е. зависимость выходного сигнала от значений входного). Наличие на графиках изломов является признаком выбора слишком крупного шага моделирования; в этом случае следует провести повторный эксперимент, уменьшив шаг моделирования.

        Скопировать информацию, выведенную в графические окна путем выполнения команды меню «Edit\Copy Figure», после чего сохранить ее при помощи какого-либо приложения, например текстового редактора MS Word.

        Установить нулевое значение коэффициента демпфирования и провести 2–3 эксперимента при разной амплитуде гармонического сигнала на выходе генератора (0<A<b, b<A<b2, A>b2 – для усилителя с ограничением и зоной нечувствительности; 0<A<b, A>b – во всех остальных случаях, кроме идеального двухпозиционного реле, для которого подобный эксперимент не требуется). При этом значение времени моделирования должно быть выбрано таким, чтобы на интервале моделирования «укладывалось» 2–3 периода гармонического сигнала. Амплитуда тестового сигнала также не должна быть выбрана чрезмерно большой, чтобы при совмещении графиков временных зависимостей выходной сигнал НЭ не «потерялся» на фоне входного. При выполнении этого пункта следует сохранять только графики временных зависимостей входного и выходного сигналов НЭ.

        Повторить пп. 1.4.1 – 1.4.4 для других изучаемых в данной лабораторной работе нелинейностей.

Содержание отчета

        Исходные данные лабораторной работы: название работы, цель работы, характеристики исследуемых НЭ, номер варианта и соответствующие ему значения параметров НЭ и генератора.

        Текст файла лабораторной работы и схема моделирования.

        Результаты моделирования каждой нелинейности:

    график с характеристикой нелинейности (зависимость «выход-вход» НЭ);

    совмещенные графики зависимостей входного и выходного сигналов НЭ от времени при затухающем тестовом сигнале и гармоническом тестовом сигнале различной амплитуды.

При оформлении результатов моделирования необходимо обратить внимание на информационное сопровождение рисунков: оси должны быть снабжены обозначениями, рисунки иметь подрисуночные надписи. Кроме того, на всех графиках должны быть отмечены характерные точки с указанием числовых значений по осям, т.е. точки, которые связаны с параметрами НЭ (b, b>2>, c) и амплитудой А тестового сигнала. Также по графикам следует рассчитать величину фазового сдвига между входным и выходным сигналами НЭ.

Объяснение полученных результатов по каждому НЭ. Объяснения требуют такие события, как наличие или отсутствие сигнала на выходе НЭ, ограничение сигнала, различие в амплитудах входного и выходного сигналов НЭ, фазовый сдвиг выходного сигнала НЭ относительно входного. Описывающие эти события числовые данные графиков должны быть подтверждены аналитическим расчетом.

Выводы.

Отчет оформляется на листах формата А4, допускается рукописное, печатное или комбинированное оформление.

Контрольные вопросы

Колебательное звено: передаточная функция, характеристическое уравнение, полюсы, названия и взаимосвязь параметров.

Текст программы: назначение переменной config.

Текст программы: из каких соображений выбирается шаг моделирования и время моделирования?

Модель в Simulink: возможные способы организации генератора.

Модель в Simulink: создание усилителя с ограничением и зоной нечувствительности из стандартных блоков библиотеки Nonlinear.

Модель в Simulink: создание трехпозиционного реле без гистерезиса из стандартных блоков библиотеки Nonlinear. Как организовать трехпозиционное реле с гистерезисом?

2.Исследование нелинейных систем методом фазовой плоскости

В работе исследуется нелинейная система с нелинейным элементом (идеальным двухпозиционным реле или реле с гистерезисом) и линейной частью второго порядка (двумя интеграторами с коэффициентом усиления или инерционным звеном и интегратором).

На рис. 2.1 представлена структурная схема системы со следующими обозначениями: u – входной сигнал системы; e – сигнал на входе нелинейного элемента (НЭ); g – сигнал на выходе НЭ; x – выходной сигнал системы; y – его производная (скорость изменения); – коэффициент обратной связи по скорости (); k – статический передаточный коэффициент; c, b – параметры НЭ; – передаточная функция линейной части.

Рис. 2.1. Структурная схема системы

Целью работы является изучение процессов в данной системе на фазовой плоскости и во временной области при помощи пакета математического моделирования Matlab и его расширения – пакета моделирования динамических систем Simulink.

Выбор значений параметров нелинейных элементов
и линейной части

Параметры НЭ и линейной части (ЛЧ) следует задавать в соответствии с вариантом, приведённым в табл. 2.1. Номер варианта соответствует номеру бригады.

Таблица 2.1 Значения параметров нелинейного элемента и линейной части

Параметры

Номер варианта

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

c

1

1.5

2

2.5

3

3.5

4

4.5

5

5.5

6

6.5

7

7.5

8

b

0.1

0.2

0.25

0.25

0.3

0.35

0.4

0.5

0.5

0.6

0.8

1

1.2

1.3

1.5

k

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

T

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

1.1

1.2

1.3

1.4

1.5

Подготовительная часть работы

        В процессе подготовки к данной лабораторной работе необходимо эскизно с построением линий переключения изобразить фазовые портреты для четырех вариантов конфигурации системы, изображенной на рис. 2.1:

    идеальное двухпозиционное реле + линейная часть ;

    идеальное двухпозиционное реле + линейная часть ;

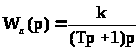    двухпозиционное реле с гистерезисом + линейная часть ;

    двухпозиционное реле с гистерезисом + линейная часть ;

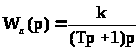        Для каждой конфигурации проанализировать, при каких возникает скользящий режим.

        Подготовить текст программы (m файл) и модель в Simulink (mdl файл). Как и в предыдущей работе, удобно связать их друг с другом: переменные, определенные в m файле, используются при задании параметров блоков модели, модель запускается на выполнение также командой из m файла, а при проведении моделирования в Simulink результаты записываются в рабочую область памяти (Workspace), откуда считываются при построении итоговых графиков командами из m файла. Пример m файла (FP_prog.m) приведен ниже.

%Исследование нелинейной системы методом фазовой плоскости (файл FP_prog.m)

%Подключаемый файл: FP_mod.mdl.

%Используемые обозначениЯ: НЭ – нелинейный элемент, ЛЧ – линейнаЯ часть.

%Очистка всех переменных в памЯти и закрытие всех предыдущих рисунков

clear all

close all

%Задание значениЯ переменной, определЯющей положение переключателЯ

%конфигурации нелинейной системы в файле FP_mod.mdl

%1 – НЭ-идеальное двухпозиционное реле, ЛЧ – k/p^2

%2 – НЭ-идеальное двухпозиционное реле, ЛЧ – k/[(Tp+1) p]

%3 – НЭ-двухпозиционное реле с гистерезисом, ЛЧ – k/p^2

%4 – НЭ – двухпозиционное реле с гистерезисом, ЛЧ – k/[(Tp+1) p]

config = 1;

%Определение значений строковых переменных nlin и lin

switch config

case 1,

nlin = 'ид. 2 х поз. реле'; lin = 'k/p^2';

case 2,

nlin = 'ид. 2 х поз. реле'; lin = 'k/[(Tp+1) p]';

case 3,

nlin = '2 х поз. реле с гист.'; lin = 'k/p^2';

case 4,

nlin = '2 х поз. реле с гист.'; lin = 'k/[(Tp+1) p]';

end

%времЯ моделированиЯ, c

t_end = 20;

%ограничение шага моделированиЯ

step_max = 0.005;

%параметры нелинейного элемента

b = 0.1;

c = 1;

%параметры линейной части

k = 1;

T = 0.4;

%коэффициент обратной свЯзи по скорости

alfa = 0.0;

%Начальные условиЯ:

%задаваЯ различные начальные условиЯ длЯ системы, получаем набор

%фазовых траекторий, т.е. фазовый портрет в системе координат Oxy;

%множество начальных условий по х: [x0_min, x0_max];

%множество начальных условий по y: [y0_min, y0_max];

%при переборе начальных условий движемсЯ снизу вверх с шагом dy

%и слева направо с шагом dx

%Назначение диапазонов изменениЯ начальных условий

x0_min = -1.5;

y0_min = -1.5;

x0_max = 1.5;

y0_max = 1.5;

%Шаг при переборе начальных условий

dx = 0.8;

dy = 0.9;

%Исходные значениЯ начальных условий

x0 = x0_min;

y0 = y0_min;

%Задание цветовой гаммы длЯ рисованиЯ фазовых траекторий

%'r' – red, красный;

%'g' – green, зеленый;

%'c' – cyan, голубой;

%'m' – magenta, пурпурный;

%'k' – black, черный;

%'y' – yellow, желтый;

%'b' – blue, синий

color = ['r';'g';'c';'m';'k'];%многоцветнаЯ картинка

%color = 'r'; %одноцветнаЯ картинка

%Подготовка рисунка с фазовым портретом

figure(1)

xlabel('x')

ylabel('y')

title(['Фазовый портрет. НЭ – ', nlin, ', b=', num2str(b), ', c=', num2str(c), '; ЛЧ – ',…

lin, ', k=', num2str(k), ', T=', num2str(T), '; alfa=', num2str(alfa)])

hold on

grid on

%вызов модели

open_system ('FP_mod.mdl');

%начальнаЯ установка номера цвета

i=0;

%перебор начальных условий; при каждом варианте начальных условий запускаетсЯ

%моделирование, а после его окончаниЯ строитсЯ фазоваЯ траекториЯ

while x0 <= x0_max

i = i+1; %номер текущего цвета

if i == length(color)+1

i=1;

end

x0_ = x0; %запоминание значений НУ

y0_ = y0; %длЯ текущей фазовой траектории

sim ('FP_mod'); %запуск моделированиЯ

gr1 = plot (x, y); %x и y – массивы из workspace

set (gr1, {'Color'}, {color(i)});

y0 = y0 + dy;

if y0 > y0_max

y0 = y0_min;

x0 = x0 + dx;

end

end

%рисование линии / линий переключениЯ

y1 = [-2.5; 2.5];

if (config == 1) | (config == 2)

x1 = – alfa.*y1; %уравнение линии переключениЯ, НЭ – ид. 2 х поз. реле

gr2 = plot (x1, y1);

set (gr2, {'Color'}, {'b'});

else

x11 = – alfa.* y1 + b; %уравнениЯ линий

x12 = – alfa.* y1 – b; %переключениЯ, НЭ – 2 х поз. реле с гист.

gr2 = plot (x11, y1);

set (gr2, {'Color'}, {'b'});

gr2 = plot (x12, y1);

set (gr2, {'Color'}, {'b'});

end

%построение процессов во времени, соответствующих

%последней фазовой траектории

figure(2)

xlabel ('t, cек')

ylabel ('x, y')

title(['x(t) и y(t). НЭ – ', nlin, ', b=', num2str(b), ', c=', num2str(c), '; ЛЧ – ',…

lin, ', k=', num2str(k), ', T=', num2str(T), '; alfa=', num2str(alfa),…

'; x0=', num2str (x0_), '; y0=', num2str (y0_)])

hold on

grid on

gr3 = plot (time, x);

set (gr3, {'Color'}, {'r'});

gr4 = plot (time, y);

set (gr4, {'Color'}, {'b'});

legend ('x(t)', 'y(t)', 4);

Все команды Matlab, использованные при составлении данной программы, описаны в приложении.

В m файле необходимо задать значения констант – параметров нелинейностей и линейной части, значение коэффициента обратной связи по скорости, задать шаг и время моделирования, диапазоны изменения начальных условий для сигналов х и у, шаг при их переборе и их исходные значения, а также значение переменной config, управляющей конфигурацией модели.

В процессе выполнения m файла происходит подготовка графического окна для вывода фазового портрета, вызов и циклический запуск модели нелинейной системы при различных начальных условиях по x и y. По результатам моделирования строятся фазовый портрет системы и временные процессы х(t) и y(t), соответствующие последней из воспроизведенных на фазовом портрете фазовых траекторий. Для получения рисунка с изображением только одной фазовой траектории необходимо задать одинаковые значения для границ изменения начальных условий по х и у.

При составлении модели в Simulink используются элементы библиотек Simulink (Math, Nonlinear, Sinks и Sources) и Simulink Extras (Additional Linear), доступные через Simulink Library Browser. Схема моделирования из файла-примера FP_mod.mdl представлена на рис. 2.2.

Интегрирующие и инерционные звенья с возможностью установки начальных условий по выходу находятся в дополнительной библиотеке Simulink  Simulink Extras\Additional Linear.

Управление переключателем конфигурации системы осуществляется через переменную config, значение которой задается в m файле.

Как и в предыдущей работе, в настройках параметров моделирования следует указывать специально предназначенные для этой цели переменные, значения которых заданы в файле-сценарии. Параметры моделирования должны быть указаны в окне «Simulation parameters», доступном через меню Simulation\Simulation parameters окна, в котором открыт mdl файл (рис. 2.3).

Рис. 2.2. Схема моделирования

Рис. 2.3. Параметры моделирования

Установку параметров различных функциональных блоков модели поясняют рис. 2.4 – 2.6. В настройках блоков используются переменные, заданные в m файле. Такой подход помогает экономить время при настройке и перенастройке модели.

Рис. 2.4. Параметры блока To Workspace

а б

Рис. 2.5. Параметры нелинейных элементов модели:
а – идеального двухпозиционного реле; б – двухпозиционного реле с гистерезисом

а б

в

Рис. 2.6. Параметры блоков линейной части системы: а – интегрирующего звена; б – инерционного звена; в-интегратора

Выполнение работы

        Получите и зафиксируйте фазовый портрет системы с идеальным двухпозиционным реле и линейной частью без обратной связи по скорости. Для одного варианта начальных условий получите изображения фазовой траектории и процессов во времени x(t) и y(t).

        Введите отрицательную обратную связь по скорости (0.1 – 0.5) так, чтобы при этом не происходило возникновение скользящего режима. Зафиксируйте фазовый портрет, фазовую траекторию и временные процессы.

        Увеличьте значение  до величины, при которой в системе возникает скользящий режим и изображающая точка перемещается по линии переключения. Зафиксируйте фазовый портрет, фазовую траекторию и временные процессы.

        Измените конфигурацию модели системы, активировав комбинацию блоков «идеальное двухпозиционное реле + линейная часть «, после чего повторите действия пп. 2.4.1 – 2.4.3.

        Измените конфигурацию модели системы, активировав комбинацию блоков «двухпозиционное реле с гистерезисом + линейная часть « и отключив обратную связь по скорости. Зафиксируйте фазовый портрет системы, при этом диапазон изменения и шаг изменения начальных условий следует задать таким образом, чтобы получить фазовые траектории, берущие начало как в области между линиями переключения (), так и вне ее (). Для одного варианта начальных условий получите изображения фазовой траектории и процессов во времени x(t) и y(t).

        Введите в модель обратную связь по скорости (0.1 – 0.5) так, чтобы при этом не происходило возникновение скользящего режима. Зафиксируйте фазовый портрет системы, обеспечив такие варианты начальных условий, при которых фазовые траектории начинаются как в области между линиями переключения, так и вне ее: а) ; б) . Постройте две фазовые траектории и соответствующие им процессы во времени для таких вариантов начальных условий.

        Увеличьте  до величины, при которой в системе возникает скользящий режим и изображающая точка перемещается в данном случае между двумя линиями переключения. Зафиксируйте фазовый портрет, две фазовых траектории и соответствующие им временные процессы аналогично п. 2.4.6.

        Измените конфигурацию модели системы, активировав комбинацию блоков «двухпозиционное реле с гистерезисом + линейная часть «. Зафиксируйте фазовый портрет, фазовую траекторию и временные процессы при отсутствии обратной связи по скорости.

        Введите обратную связь по скорости и зафиксируйте фазовый портрет, фазовую траекторию и временные процессы как при отсутствии, так и при наличии скользящего режима.

        Содержание отчёта

        Вариант задания, схемы моделирования, цель работы.

        Подготовительная часть: эскизы фазовых портретов и сопровождающие расчеты (дифференциальные уравнения, описывающие линейную часть; уравнения, описывающие нелинейные элементы; уравнения фазовых траекторий и линий переключения).

        Результаты моделирования (фазовые портреты, фазовые траектории, временные процессы x(t) и y(t)).

        Анализ результатов (нахождение соответствия между видами фазовых траекторий и процессов во времени, анализ влияния коэффициента обратной связи на вид фазового портрета, на возникновение скользящего режима в системе и др.). Выводы (аргументированное подтверждение соответствия предварительных расчетов и результатов эксперимента).

Отчет оформляется на листах формата А4, допускается рукописное, печатное или комбинированное оформление.

        Контрольные вопросы

        Определение фазовой траектории и фазового портрета.

        Определение линии переключения. От чего зависит наклон линии (линий) переключения?

        Определение скользящего режима. Условия его появления.

        Предельный цикл: определение, условия возникновения и графическое изображение на фазовой плоскости.

        Определение системы, устойчивой / неустойчивой в малом / большом.

        Приведите пример фазовой траектории и найдите соответствующий ему процесс во времени.

        В чем схожесть фазовых портретов устойчивых (неустойчивых, на границе устойчивости) систем?

3.Исследование нелинейных систем методом гармонического баланса

В работе необходимо провести исследование нелинейной системы, приведенной на рис. 3.1, средствами пакета Matlab и его расширения – пакета Simulink. Используются следующие обозначения:

НЭ – нелинейный элемент: двухпозиционное реле с гистерезисом (рис. 3.2, а), трехпозиционное реле без гистерезиса (рис. 3.2, б) или люфт (рис. 3.2, в);

W>л >(р) – передаточная функция линейной части (ЛЧ); в табл. 3.1 приведены возможные варианты передаточной функции.

Рис. 3.1. Структурная схема системы

а б в

Рис. 3.2. Характеристики нелинейных элементов: а – двухпозиционное реле с гистерезисом, б – трехпозиционное реле без гистерезиса, в-люфт

Таблица 3.1 Варианты линейной части

Номер ЛЧ

Передаточная функция ЛЧ

1

2

3

4

Метод гармонического баланса позволяет определить, могут ли в нелинейной системе возникнуть периодические колебания, и если да, то оценить их амплитуду А>п> и частоту >п,> а также оценить устойчивость этих периодических режимов. Метод применяется, если выполняется гипотеза фильтра, т.е. линейная часть обеспечивает подавление высокочастотных составляющих входного негармонического сигнала, который поступает с выхода нелинейного элемента. Условием возникновения периодического режима является прохождение эквивалентной частотной передаточной функции через критическую точку (-1, j0), т.е. выполнение равенства

,

которое для решения представляется в более удобном виде:

.

Целями работы являются: графическое решение данного уравнения; определение, если возможно, А>п> и >п,> оценка устойчивости периодических режимов; моделирование нелинейной системы и определение параметров колебаний по полученному процессу; проверка выполнения гипотезы фильтра.

Подготовительная часть работы

По данным рис. 3.2 и табл. 3.1 и 3.2 в соответствии со своим вариантом выбрать:

    передаточную функцию линейной части и значения ее параметров;

    типы нелинейных элементов и значения их параметров.

Эксперименты будут проводиться для выбранного варианта линейной части и нелинейности сначала первого типа, а затем второго.

Для каждого типа нелинейности своего варианта подготовьте на основании справочных данных выражения для коэффициентов гармонической линеаризации q(A) и q1(A) и запишите эквивалентный комплексный передаточный коэффициент .

Запишите комплексный передаточный коэффициент линейной части своего варианта W>л>(j), постройте (эскизно) ее ЛАЧХ и ФЧХ, после чего для каждого типа нелинейности приведите совместные характеристики линейной части (АФХ линейной части W>л>(j)) и нелинейности .

Таблица 3.2 Значения параметров линейной части и нелинейных элементов

        Номер

        варианта

        1

        2

        3

        4

        5

        6

        7

        8

        W>л>(р)

        W>л1>

        W>л2>

        W>л3>

        W>л4>

        W>л1>

        W>л2>

        W>л3>

        W>л4>

        Типы НЭ

        НЭ>1,>

        НЭ>2>

        НЭ>2,>

        НЭ>3>

        НЭ>1,>

        НЭ>3>

        НЭ>1,>

        НЭ>3>

        НЭ>2,>

        НЭ>3>

        НЭ>1,>

        НЭ>3>

        НЭ>1,>

        НЭ>2>

        НЭ>1,>

        НЭ>3>

        Параметры

        k

        6

        5

        3

        4

        15

        2

        10

        8

        T>1>

        0.1

        0.2

        10

        0.4

        0.5

        0.6

        9

        0.8

        T>2>

        0.2

        0.4

        5

        0.8

        1.0

        1.2

        6

        1.6

        T>3>

        1

        -

        0.1

        -

        5

        -

        0.2

        -

        b

        0.1

        0.2

        0.25

        0.25

        0.3

        0.35

        0.4

        0.5

        c

        1

        1.5

        2

        2.5

        3

        3.5

        4

        4.5

        Номер варианта

        9

        10

        11

        12

        13

        14

        15

        16

        W>л>(р)

        W>л1>

        W>л2>

        W>л3>

        W>л4>

        W>л1>

        W>л2>

        W>л3>

        W>л4>

        Типы НЭ

        НЭ>1,>

        НЭ>3>

        НЭ>1,>

        НЭ>2>

        НЭ>1,>

        НЭ>2>

        НЭ>1,>

        НЭ>3>

        НЭ>1,>

        НЭ>2>

        НЭ>2,>

        НЭ>3>

        НЭ>1,>

        НЭ>3>

        НЭ>1,>

        НЭ>3>

        Параметры

        k

        15

        10

        9

        6

        7

        8

        5

        7

        T>1>

        0.9

        1.0

        7

        0.6

        0.2

        0.3

        9

        0.7

        T>2>

        1.8

        2.0

        5

        1.2

        0.3

        0.5

        4

        1.5

        T>3>

        9

        -

        0.3

        -

        1.5

        -

        0.2

        -

        b

        0.5

        1.0

        0.5

        0.35

        0.3

        0.35

        0.35

        0.45

        c

        5

        6

        5.5

        3

        2

        2.5

        3

        4

        Проведите качественное исследование системы: оцените возможность возникновения периодических режимов и их устойчивость. Там, где это возможно, запишите выражения для критического коэффициента усиления ЛЧ, при котором в нелинейной системе возникают автоколебания.

        Изучите текст программы (файл GB_prog.m) и структуру моделей (файлы GB_mod.mdl и R_Fourie.mdl).

Графический расчет параметров периодических режимов c использованием метода гармонического баланса производится по сценарию, записанному в файле GB_prog.m. Моделирование нелинейной системы осуществляется при помощи файлов GB_prog.m и GB_mod.mdl, а анализ спектрального состава периодического режима на выходе линейной части – при помощи файлов GB_prog.m и R_Fourie.mdl.

Cодержание файла GB_prog.m:

%Исследование нелинейных систем методом гармонического баланса

%Используемые файлы: GB_prog.m, GB_mod.mdl и R_Fourie.mdl.

%Используемые обозначениЯ: НЭ – нелинейный элемент, ЛЧ – линейнаЯ часть.

%Очистка всех переменных в памЯти

clear all

%закрытие всех предыдущих рисунков

set (0,'ShowHiddenHandles', 'on')

delete (get(0,'Children'))

%Задание значениЯ переменной, определЯющей положение переключателЯ

%конфигурации нелинейной части в файле GB_mod.mdl

%1 – НЭ-двухпозиционное реле с гистерезисом

%2 – НЭ-трехпозиционное реле без гистерезиса

%3 – НЭ-люфт

config_nlin = 2;

%Задание значениЯ переменной, определЯющей положение переключателЯ

%конфигурации линейной части в файле GB_mod.mdl

%1 – ЛЧ – Wл1 (p)=k/[(T1*p+1) (T2*p+1) (T3p+1)]

%2 – ЛЧ – Wл2 (p)=k/[(T1*p+1) (T2*p+1) p]

%3 – ЛЧ – Wл3 (p)=[k (T1*p+1)]/[(T2*p 1)^2 (T3*p+1)^2]

%4 – ЛЧ – Wл4 (p)=[k (T1*p+1)]/[(T2*p 1) p]

config_lin = 2;

k = 5;

T1 = 0.1;

T2 = 0.2;

T3 = 1;

b = 0.1;

c = 1;

%Графический расчет параметров периодических режимов c использованием

%метода гармонического баланса

%описание линейной части

switch config_lin

case 1,

%начальное значение, шаг и конечное значение частоты (в рад)

w = [0.02:0.01:100];

%комплексный передаточный коэффициент ЛЧ

W_lin = k./ ((T1*j*w+1).* (T2*j*w+1).*(T3*j*w+1));

%определение значениЯ строковой переменной lin

lin = 'Wл1 (p)';

case 2,

%начальное значение, шаг и конечное значение частоты (в рад)

w = [2:0.01:100];

%комплексный передаточный коэффициент ЛЧ

W_lin = k./ ((T1*j*w+1).* (T2*j*w+1).*(j*w));

%определение значениЯ строковой переменной lin

lin = 'Wл2 (p)';

case 3,

%начальное значение, шаг и конечное значение частоты (в рад)

w = [0.01:0.01:300];

%комплексный передаточный коэффициент ЛЧ

W_lin = (k*(T1*j*w+1))./ ((T2*j*w 1).^2.*(T3*j*w+1).^2);

%определение значениЯ строковой переменной lin

lin = 'Wл3 (p)';

case 4,

%начальное значение, шаг и конечное значение частоты (в рад)

w = [1:0.01:100];

%комплексный передаточный коэффициент ЛЧ

W_lin = (k*(T1*j*w+1))./ ((T2*j*w 1).*(j*w));

%определение значениЯ строковой переменной lin

lin = 'Wл4 (p)';

end

%описание ЛЧ как частотной характеристики через W_lin(jw)

SYSL = frd (W_lin, w);

%–

%Описание нелинейной части

switch config_nlin

case 1,

%начальное значение, шаг и конечное значение амплитуды на входе НЭ

A = [b:0.01:3.0];

%коэффициенты гармонической линеаризации

q = 2*c/(pi*b).* ((2*b./A).* sqrt (1 – (b./A).^2));

q1 = -2*c/(pi*b).* 2*(b./A).^2;

%определение значениЯ строковой переменной nlin

nlin = '2 х поз. реле с гист.';

case 2,

%начальное значение, шаг и конечное значение амплитуды на входе НЭ

A = [b+0.0001:0.005:b*sqrt(2)];

A_ = [b*sqrt(2):0.005:3.0];

%коэффициенты гармонической линеаризации

q = (4*c./ (pi*A)).* sqrt (1 – (b./A).^2);

q1 = 0;

q_ = (4*c./ (pi*A_)).* sqrt (1 – (b./A_).^2);

q1_ = 0;

%эквивалентный комплексный передаточный коэффициент W_nlin(jA) НЭ

W_nlin_ = q_ + j*q1_;

%характеристика -1/W_nlin(jA)

S_ = -1./W_nlin_;

%описание НЭ как амплитудной характеристики через -1/W_nlin(jA)

SYSN_ = frd (S_, A_);

%определение значениЯ строковой переменной nlin

nlin = '3 х поз. реле без гист.';

case 3,

%начальное значение, шаг и конечное значение амплитуды на входе НЭ

A = [b+0.001:0.01:100];

%коэффициенты гармонической линеаризации

alfa = asin (1–2*b./A);

q = (1/pi)*(pi/2+alfa+0.5*sin (2*alfa));

q1 = – (4*b).* (1 b./A)./ (pi*A);

%определение значениЯ строковой переменной nlin

nlin = 'люфт';

end

%эквивалентный комплексный передаточный коэффициент W_nlin(jA) НЭ

W_nlin = q + j*q1;

%характеристика -1/W_nlin(jA)

S = -1./W_nlin;

%описание НЭ как амплитудной характеристики через -1/W_nlin(jA)

SYSN = frd (S, A);

%–

%ВизуализациЯ

%Построение W_lin(jw) и -1/W_nlin(jA) при помощи plot (общий вид)

figure(1)

gr_W_lin = plot (real(W_lin), imag (W_lin));

set (gr_W_lin, {'Color'}, {'r'});

hold on

gr_S = plot (real(S), imag(S));

set (gr_S, {'Color'}, {'b'});

title(['Расчет гарм. баланса. НЭ – ', nlin, ', b=', num2str(b), ', c=', num2str(c), '; ЛЧ – ',…

lin, ', k=', num2str(k), ', T1=', num2str(T1), ', T2=', num2str(T2),…

', T3=', num2str(T3)])

xlabel ('re(W lin), re(S)');

ylabel ('im(W lin), im(S)');

legend ('W lin(jw)', 'S(jA)', 0);

grid on

%–

%построение W_lin(jw) и -1/W_nlin(jA) при помощи LTI Viewer

if config_nlin == 2

ltiview({'nyquist'}, SYSL, '-b', SYSN, '-r')

ltiview({'nyquist'}, SYSL, '-b', SYSN_, '-r')

else

ltiview({'nyquist'}, SYSL, '-b', SYSN, '-r')

end

%–

%Завершение графического расчета параметров периодических режимов

%c использованием метода гармонического баланса

%====================================================

%^^^^^^^^^^^^^^Моделирование нелинейной системы (НС)^^^^^^^^^^^^^^^^^^^^^

% с определением параметров автоколебаний

%задание времени моделированиЯ

t_end = 15;

%ограничение шага моделированиЯ сверху

step_max = 0.005;

%задание амплитуды сигнала на выходе ЛЧ в начальный момент времени

y0 = 0.5;

%вызов модели

open_system ('GB_mod.mdl');

%запуск модели

sim ('GB_mod');

%считывание фактических параметров моделированиЯ

Max_Step_Size = get_param ('GB_mod', 'MaxStep');

Stop_Time = get_param ('GB_mod', 'StopTime');

%извлечение последнего элемента из векторов vec_period и vec_amp

%(определение установившихсЯ значений периода и амплитуды автоколебаний

%с использованием данных, записанных в рабочую область памЯти)

clc % очистка командного окна

period = vec_period (length(vec_period));

clear vec_period;

amp_kol = vec_amp (length(vec_amp))%вывод в командное окно

clear vec_amp;

%расчет частоты сигнала на выходе ЛЧ (используетсЯ длЯ последующего

%расчета амплитуды гармоник)

frequency = 1/period;

w_kol = 2*pi*frequency %вывод в командное окно

%Построение процесса во времени на выходе ЛЧ

figure(2)

gr = plot (t_and_y(:, 1), t_and_y(:, 2));

set (gr, {'Color'}, {'r'});

title(['Процесс y(t). НЭ – ', nlin, ', b=', num2str(b), ', c=', num2str(c), '; ЛЧ – ',…

lin, ', k=', num2str(k), ', T1=', num2str(T1), ', T2=', num2str(T2),…

', T3=', num2str(T3), ', y0=', num2str(y0)])

xlabel(['t, cек Амп.кол.=', num2str (amp_kol), ', Wкол=', num2str (w_kol), 'c^-1']);

ylabel('y');

grid on

%–

%закрытие модели

%close_system ('GB_mod', 1)

%=====================================================

%^^^^^^^^^^^^^^^^Анализ спектра автоколебательного процесса^^^^^^^^^^^^^^

%вызов программы, определЯющей амплитуды гармоник сигнала на выходе ЛЧ

open_system ('R_Fourie.mdl');

%транслЯциЯ параметров моделированиЯ НС 'GB_mod.mdl' в файл R_Fourie.mdl

set_param ('R_Fourie', 'MaxStep', Max_Step_Size);

set_param ('R_Fourie', 'StopTime', Stop_Time);

%запуск программы, вычислЯющей амплитуды гармоник

sim ('R_Fourie');

%закрытие программы

%close_system ('R_Fourie', 1)

%извлечение последнего элемента из каждого вектора, содержащего амплитуды

%гармоник (определение установившихсЯ значений амплитуд гармоник с

%использованием данных, записанных в рабочую область памЯти)

magn_0=vec_magn_0 (length(vec_magn_0));

clear vec_magn_0;

magn_1=vec_magn_1 (length(vec_magn_1));

clear vec_magn_1;

magn_2=vec_magn_2 (length(vec_magn_2));

clear vec_magn_2;

magn_3=vec_magn_3 (length(vec_magn_3));

clear vec_magn_3;

magn_4=vec_magn_4 (length(vec_magn_4));

clear vec_magn_4;

magn_5=vec_magn_5 (length(vec_magn_5));

clear vec_magn_5;

%Проверка гипотезы фильтра

filtration = magn_1/magn_3

%построение гистограммы

figure(3);

bar([0 1 2 3 4 5], [magn_0 magn_1 magn_2 magn_3 magn_4 magn_5]);

grid on

title(['Гарм. состав y(t). НЭ – ', nlin, ', b=', num2str(b),…

', c=', num2str(c), '; ЛЧ – ', lin, ', k=', num2str(k), ', T1=', num2str(T1),…

', T2=', num2str(T2), ', T3=', num2str(T3)])

xlabel(['Номер гармоники ГФ: A1/A3=', num2str(filtration)]);

ylabel ('Амплитуда гармоники');

Все команды Matlab, использованные при составлении данной программы, описаны в приложении.

В m файле задаются значения параметров линейной части и нелинейного элемента, а также начальные условия по выходу линейной части, указывается время моделирования и шаг моделирования.

Для проведения графического расчета параметров периодических режимов m файл содержит описания ЛЧ (через комплексный передаточный коэффициент) и нелинейности (через коэффициенты гармонической линеаризации и эквивалентный комплексный передаточный коэффициент). Совместное воспроизведение характеристик W>л>(j) и осуществляется двумя способами: при помощи команды plot и команды ltiview. Первая позволяет совместно вывести на рисунок указанные характеристики без вывода комплексно-сопряженных характеристик W>л>(-j) и , но не позволяет по точке их пересечения определить частоту и амплитуду периодических режимов. При помощи второй одновременно выводятся все четыре характеристики, но имеется возможность определения частоты и амплитуды по точке пересечения: команда zoom контекстного меню, вызываемого правой клавишей мыши, позволяет увеличить нужную область рисунка, после чего нужно поместить указатель мыши на требуемую характеристику и нажать на ее левую клавишу – на графике появятся отметка и информационное окно, которые можно переместить мышью в точку пересечения. Для случая системы с идеальным трехпозиционным реле предусмотрено раздельное построение характеристики до и после точки экстремума при помощи двух команд ltiview.

После завершения графического расчета производится вызов и запуск модели нелинейной системы (GB_mod.mdl). По окончании моделирования строится временной процесс y(t) на выходе линейной части, определяются частота и амплитуда автоколебаний (их значения можно увидеть в командном окне и на созданном рисунке).

На этапе анализа спектрального состава периодического режима на выходе линейной части производится вызов и запуск модели (R_Fourie.mdl), определяющей амплитуды гармоник сигнала y(t), записанного в рабочую область памяти, и строится результирующая гистограмма «Номер гармоники – амплитуда гармоники». В командное окно и окно с гистограммой выводится отношение амплитуд первой и третьей гармоник, что позволяет сделать заключение о выполнении / невыполнении гипотезы фильтра.

При составлении моделей в Simulink (GB_mod.mdl и R_Fourie.mdl) используются элементы библиотек Simulink (Math, Linear, Nonlinear, Signals & Systems, Sinks и Sources), Simulink Extras (Additional Linear) и Power System Blockset (Extra Library\Measurements), доступные через Simulink Library Browser (рис. 3.3 – 3.6). В модели нелинейной системы GB_mod.mdl, показанной на рис. 3.3, предусмотрены переключатели конфигурации линейной и нелинейной частей, управление ими осуществляется соответственно через переменные config_lin и config_nlin, значения которых задаются в m файле GB_prog.m.

Параметры моделирования должны быть указаны в окне Simulation parameters, доступном через меню Simulation\Simulation parameters окна, в котором открыт mdl файл (рис. 3.7, 3.8).

Установку параметров различных функциональных блоков моделей GB_mod.mdl и R_Fourie.mdl поясняют рис. 3.9 – 3.15.

Рис. 3.4. Организация трехпозиционного реле без гистерезиса
(файл GB_mod.mdl)

Рис. 3.5. Подсистема определения периода и амплитуды автоколебаний (файл GB_mod.mdl)

Рис. 3.6. Модель в Simulink, вычисляющая амплитуду гармоник в составе периодического процесса на выходе линейной части (файл R_Fourie.mdl)

Рис. 3.7. Параметры моделирования для файла GB_mod.mdl

Рис. 3.8. Параметры моделирования для файла R_Fourie.mdl

а б

Рис. 3.9. Параметры блоков в составе трехпозиционного реле без гистерезиса (файл GB_mod.mdl): а – блока Relay1; б – блока Relay2

а б

Рис. 3.10. Параметры нелинейностей (файл GB_mod.mdl): а – люфта; б – двухпозиционного реле с гистерезисом

а б

Рис. 3.11. Параметры блоков линейной части (файл GB_mod.mdl): а – инерционного звена; б – интегрирующего звена

Рис. 3.12. Параметры блока To Workspace (файл GB_mod.mdl)

а б

Рис. 3.13. Параметры блоков подсистемы определения периода и амплитуды автоколебаний (файл GB_mod.mdl): а – блока ограничения сигнала Saturation2; б – блока памяти Memory1

Рис. 3.14. Параметры блока Fourier (файл R_Fourie.mdl)

Рис. 3.15. Параметры блока From Workspace (файл R_Fourie.mdl)

        Выполнение работы

        Модернизируйте файл сценария (m файл) в соответствии со своим вариантом: установите значения переменных конфигурации, т.е. выберите передаточную функцию линейной части и первую из двух нелинейностей вашего варианта; установите заданные значения параметров ЛЧ и нелинейности.

        Запустите m файл на исполнение. Зафиксируйте совместно воспроизведенные командой plot частотную характеристику линейной части W>л>(-j) и характеристику нелинейности –1/W>н>(jA). По точкам их пересечения определите А>п> и >п>, используя LTI Viewer.

        Оцените устойчивость найденных периодических режимов, задавая различные начальные условия (н.у.) по выходу ЛЧ (для каждого периодического режима достаточно двух значений из окрестности значения А>п> – y(0)<А>п> и y(0)>А>п>). Следует провести несколько экспериментов, запуская m файл с разными значениями н.у. и фиксируя процессы во времени y(t).

        Для устойчивого периодического режима зафиксируйте значения амплитуды и частоты автоколебаний, гистограмму с их гармоническим составом и соотношение амплитуд первой и третьей гармоник, при этом с помощью осциллографа «Гармоники», находящегося в модели R_Fourie.mdl, проконтролируйте достижение амплитудами гармоник своих установившихся значений, т.е. убедитесь в том, что выбранное время моделирования является достаточным для завершения переходных процессов в системе; в противном случае увеличьте его и повторите эксперимент.

        Найдите критический коэффициент усиления ЛЧ: подберите такое значение параметра k, при котором точка пересечения характеристик нелинейности и ЛЧ начинает исчезать. Сравните с теоретически рассчитанным значением.

        Выберите вторую из двух нелинейностей вашего варианта, установив соответствующее значение конфигурационной переменной config_nlin в m файле, и повторите действия из пп. 3.3.2  3.3.5.

Содержание отчёта

        Вариант задания, схемы моделирования, цель работы.

        Материалы, подготовленные по пп. 3.2.2  3.2.4.

        Результаты моделирования (совмещенные характеристики нелинейности и линейной части, построенные на комплексной плоскости, с указанием значений параметров периодических режимов, найденных по точкам пересечения; процессы во времени y(t) при различных вариантах начальных условий с указанием значений параметров установившихся периодических режимов; гистограммы гармонического состава установившихся периодических режимов).

        Анализ результатов (нахождение соответствия между результатами предварительной подготовки, графического расчета по методу гармонического баланса и моделирования нелинейной системы в отношении устойчивости / неустойчивости периодических режимов, в отношении значения амплитуды и частоты автоколебаний, значения критического коэффициента).

        Выводы (сделать заключение о выполнении / невыполнении гипотезы фильтра, о погрешностях определения значений параметров периодических режимов по методу гармонического баланса).

Отчет оформляется на листах формата А4, допускается рукописное, печатное или комбинированное оформление.

Контрольные вопросы

        Метод гармонического баланса: назначение, условия применения, основное уравнение. Суть метода гармонической линеаризации и гипотезы фильтра. Метод Д-разбиений: основные положения. Определение комплексного передаточного коэффициента нелинейного звена.

4.Синтез дискретной системы с максимальным быстродействием

В работе необходимо с использованием методов модального синтеза провести проектирование цифрового алгоритма управления непрерывным объектом из условий обеспечения максимального быстродействия и единичной статики по командному сигналу.

Методы модального синтеза основаны на обеспечении желаемого расположения собственных чисел матрицы динамики системы. Из теории известно, что в линейных импульсных системах можно обеспечить окончание переходных процессов за минимальное время, равное произведению порядка дифференциальных уравнений объекта на период квантования по времени. Для этого все собственные числа матрицы динамики системы должны быть нулевыми. Если не все координаты вектора состояния объекта являются измеримыми, то в алгоритм управления необходимо ввести наблюдатель с целью получить оценки неизмеримых координат вектора состояния. Собственные числа наблюдателя в рассматриваемой задаче также целесообразно задать равными нулю. Управляющий сигнал, который будет подан на вход объекта управления, вычисляется как произведение оценки вектора состояния объекта на матрицу обратной связи, полученную в результате модального синтеза.

Целями работы являются:

      закрепление знаний по теории модального синтеза;

      ознакомление с возможностями пакета MATLAB в части модального синтеза;

      анализ процессов при наличии и при отсутствии наблюдателя;

      анализ грубости (чувствительности) системы по отношению к параметрам линейной модели объекта;

      анализ быстродействия при наличии ограничений сигнала управления.

        Подготовительная часть работы

        По данным табл. 4.1 и в соответствии с предложенным преподавателем вариантом и значениями параметров проанализировать свойства объекта.

        Таблица 4.1 Варианты передаточной функции объекта

        Номер варианта

        W>ob>(p)

        Параметры

        Номер варианта

        W>ob>(p)

        Параметры

        1

        6

        T>1>=0.2;

        T>2>=0.1;

        ξ = 0.1

        2

        T>1>=0.1

        7

        Т>1>=2;

        T>2>=1;

        T>3>=1

        3

        T>1>=2; ξ=0.1

        8

        T>1>=0.2;

        ξ=0.1

        4

        T>1>=2;

        T>2>=1

        9

        T>1>=2;

        T>2>=1

        5

        T>1>=5

        10

        T>1>=2;

        ξ=0.1

        Изучите текст программы (файл SSOpt_d.m) и структуру моделей SSLOpt_dSim.mdl (система с обратной связью по вектору состояния) и SSLKOpt_dSim.mdl (система с наблюдателем).

        Содержание файла SSOpt_d.m:

%Синтез дискретной системы с максимальным быстродействием

%–

clc

close_system ('SSLOpt_dSim', 1); %Закрытие mdl файла

close_system ('SSLKOpt_dSim', 1); %Закрытие mdl файла

clear all

close all

set (0, 'ShowHiddenHandles', 'on')

delete (get(0,'Children'))

%Параметры моделированиЯ

hMO = 0.01; %Шаг моделированиЯ объекта, с

T0 = 0.35; %Шаг работы цифровой части, с

T_end = 8% 2.5; %ВремЯ окончаниЯ моделированиЯ, с

top_lim_u = 5000; %заданное ограничение управлениЯ сверху

low_lim_u = -5000; %заданное ограничение управлениЯ снизу

%ОбъЯвление комплексной переменной p

p = zpk('p');

%Передаточная функция объекта

% (непрерывной части системы)

%Параметры передаточной функции непрерывной части

T1 = 0.2; T2 = 0.1; T3 = 1; ksi = 0.1;

%Варианты передаточной функции непрерывной части

disp ('ПередаточнаЯ функциЯ непрерывной части')

Wn_1 = 1/p^2;

Wn_2 = 1/((T1*p+1)^2);

Wn_3 = 1/(T1^2*p^2+2*ksi*T1*p+1);

Wn_4 = (T1*p+1)/(p*(T2*p+1));

Wn_5 = 1/(p*(T1*p 1));

Wn_6 = 1/(p*(T1*p+1)^3*(T2^2*p^2+2*ksi*T2*p+1));

Wn_7 = (T1*p+1)/(p*(T2*p 1)*(T3*p+1));

Wn_8 = 1/(p*(T1^2*p^2+2*ksi*T1*p+1));

Wn_9 = 1/((T1^2*p^2+1)*(T2*p+1));

Wn_10 = 1/(p*(T1^2*p^2–2*ksi*T1*p+1));

%Выбор варианта передаточной функции

Wn = Wn_10

%:

%Как получить различную информацию об объекте

%(напоминание о видах операторов, используемых для этого)

disp ('Нули, полюсы и К передаточной функции непрерывного объекта')

[zn_ob, pn_ob, kn_ob] = zpkdata (Wn, 'v')

disp ('Коэффициенты полиномов числителЯ R и знаменателЯ Q передаточной функции')

[num_n_ob, den_n_ob] = tfdata (Wn, 'v')

disp ('Матрицы непрерывного объекта')

[An_ob, Bn_ob, Cn_ob, Dn_ob] = ssdata(Wn)

n_ob = size (An_ob);%n_ob(1) – порЯдок непрер. объекта

%:

%Переход к дискретному объекту

sys_n_ob = ss(Wn); %Переход к вект.-матр. описанию объекта

sys_d_ob = c2d (sys_n_ob, T0); %Переход к дискр. объекту в вект.-матр. форме

[Ad_ob, Bd_ob, Cd_ob, Dd_ob] = ssdata (sys_d_ob) %Матрицы дискретного объекта

%Переходные функции непрерывного и дискретизированного объекта

ltiview ('step', sys_n_ob, 'r-', sys_d_ob, 'b-');

grid on

%:

%Синтез управлениЯ длЯ дискретной системы

disp ('Желаемые полюсы замкнутой дискретной системы')

Pd = zeros (1, n_ob(1))%Нулевой вектор-строка

disp ('Матрица оптимальной обратной свЯзи дискретной системы')

Ld = acker (Ad_ob, Bd_ob, Pd)

%Ld = place (Ad_ob, Bd_ob, Pd) – не работает при кратных полюсах замкнутой системы

%:

%Матрицы замкнутой дискретной системы

%Матрица динамики

Ad_z = Ad_ob-Bd_ob*Ld;

%Матрицы B, C, D

Bd_z = Bd_ob;

Cd_z = Cd_ob;

Dd_z = Dd_ob;

%:

%Проверка полюсов замкнутой системы

sys_d_z = ss (Ad_z, Bd_z, Cd_z, Dd_z);%Описание замкн. дискр. сист-мы в вект.-матр. форме

disp ('Фактические полюсы замкнутой дискретной системы (сравнить с желаемыми)')

poles_sys_d_z = eig (sys_d_z)

%:

%^Вычисление коэфф-та при командном сигнале, обеспечивающего единичную статику

%Векторы коэффициентов полиномов числителЯ и знаменателЯ дискретной передаточной

%функции замкнутой системы

[num_d_z, den_d_z] = tfdata (sys_d_z, 'v');

disp ('Коэффициент при командном сигнале, обеспечивающий единичную статику')

%Величина, обратнаЯ сумме коэффициентов числителЯ дискретной ПФ замкнутой системы

Kv = 1/sum (num_d_z)

%:

%Моделирование в Simulink системы с обратной свЯзью

%по вектору состоЯниЯ

%Для того, чтобы провести моделирование, необходимо иметь доступ к вектору состояния объекта. Поэтому в файле SSLOpt_dSim.mdl при задании объекта в векторноматричной форме (блок State-Space) нужно вместо матрицы Cn_ob указать единичную

%матрицу Сх, а в качестве матрицы Dn_ob – нулевой вектор-столбец Dx соответств-щих

%размерностей

Cx = eye (n_ob(1)); %ЕдиничнаЯ матрица

Dx = zeros (n_ob(1), 1); %Нулевой вектор-столбец

open_system ('SSLOpt_dSim.mdl'); %Вызов mdl файла

sim ('SSLOpt_dSim'); %Запуск моделированиЯ

%:

disp ('Желаемые собственные числа дискретного наблюдателЯ')

P_obs_d = zeros (1, n_ob(1))

%Матрица невЯзки дискретного наблюдателЯ

Все команды Matlab, использованные при составлении данной программы, описаны в приложении.

При составлении моделей в Simulink (SSLOpt_dSim.mdl и SSLKOpt_dSim.mdl) используются элементы из таких разделов библиотеки Simulink, как Math, Linear, Discrete, Nonlinear, Function & Tables, Signals & Systems, Sinks и Sources. Схемы моделирования и настройки элементов моделей представлены на рис. 4.1 – 4.8. Параметры моделирования нужно указать в окне «Simulation parameters», доступном через меню Simulation\Simulation parameters окна, в котором открыт mdl файл (рис. 4.9).

Рис. 4.3. Настройки блока «Фиксатор нулевого порядка»

Рис. 4.4. Настройки блока «Ограничитель входного сигнала»

Рис. 4.5. Настройки блока «Коэффициент усиления командного сигнала»

Рис. 4.6. Настройки блока «Матрица коэффициентов обратной связи»

Рис. 4.7. Настройки блока «Объект»

Рис. 4.8. Настройки блока «Наблюдатель»

Рис. 4.9. Параметры моделирования

        Составьте план экспериментов в соответствии с целями лабораторной работы (см. п. 4.1).

Выполнение работы

        Выберите передаточную функцию объекта и значения её параметров в соответствии с вашим вариантом.

        Установите необходимые параметры моделирования: шаг моделирования объекта, такт работы системы управления (первоначально около 0.4 c), время моделирования; снимите ограничения на уровень управляющего сигнала.

        Ознакомьтесь с работой программного комплекса. Обратите внимание на данные, появляющиеся в командном окне во время решения.

        Проанализируйте влияние наблюдателя на процессы, происходящие в системе, выясните роль начальных условий по вектору состояния наблюдателя. Зафиксируйте переходные процессы в системе без наблюдателя и с наблюдателем.

        Исследуйте влияние периода квантования T0 на требуемый диапазон изменения управляющего сигнала в системе с наблюдателем. Результаты фиксируйте в таблице.

        Введите ограничение на величину управляющего сигнала и выберите оптимальный период квантования Т0. Зафиксируйте переходные функции системы с наблюдателем при оптимальном и неоптимальном значениях Т0.

        Вследствие того, что параметры реального объекта могут изменяться с течением времени, важно знать, как это сказывается на основных показателях качества процессов управления (времени регулирования, перерегулировании). На примере системы с наблюдателем проведите анализ «грубости» (чувствительности) синтезированного алгоритма управления по отношению к параметрам объекта. Для этого необходимо в m файле после осуществления синтеза системы управления непосредственно перед запуском моделирования в Simulink пересчитать матрицы объекта в соответствии с изменившимся значением какого-либо параметра и зафиксировать поведение системы в таких условиях. Количество значений для каждого параметра должно быть не менее пяти. Результаты эксперимента следует оформить в виде таблиц и построить соответствующие графики.

Во время лабораторной работы необходимо вести протокол, в котором следует фиксировать все промежуточные и конечные результаты. Основные результаты согласовывать с преподавателем по мере их получения, соответствующие комментарии отражать в протоколе.

Содержание отчёта

        Цель работы, вариант задания, структура программы, схемы моделирования.

        План проведения лабораторной работы.

        Значения матрицы обратной связи и матриц наблюдателя, полученные при выполнении п. 4.3.3.

        Графические зависимости, характеризующие систему с наблюдателем и без наблюдателя, полученные при выполнении п. 4.3.4.

        Результаты выполнения п. 4.3.5 в виде таблицы и соответствующая графическая зависимость.

        Результаты выполнения п. 4.3.6 – графики переходных функций системы при введении ограничений на величину управляющего сигнала. Обоснование выбора периода квантования по времени T>0>.

        Результаты выполнения п. 4.3.7 – таблицы и графические зависимости, характеризующие «грубость» синтезированных алгоритмов.

Контрольные вопросы

        Перечислить операторы пакета Matlab, необходимые для модального синтеза и синтеза наблюдателя.

        Сформулировать основные отличия и общие черты синтеза непрерывных и дискретных систем управления.

        Из каких соображений выбирается период квантования по времени в дискретной системе?

        Структура наблюдателя Люенбергера.

        Что такое матрица невязки наблюдателя?

        Как вычисляется коэффициент усиления по командному сигналу, обеспечивающий единичную статику в дискретной системе?

        Как вычислить размерности матриц A, B, C, D объекта и наблюдателя?

        Как обеспечить максимальное быстродействие при синтезе дискретной системы управления и чему оно будет равно?

Список литературы

    Бесекерский В.А. Теория систем автоматического регулирования / В.А. Бесекерский, Е.П. Попов. М.: Наука, 1975. 768 с.

    Теория автоматического управления / под ред. А.А. Воронова. М.: Высшая школа, 1986. Ч. 2. 504 с.

    Теория автоматического управления / под ред. А.В. Нетушила. М.: Высшая школа, 1972. Ч. 2. 430 с.

    Попов Е.П. Теория нелинейных систем автоматического регулирования и управления / Е.П. Попов. М.: Наука, 1988. 256 с.

    Цыпкин Я.З. Основы теории автоматических систем / Я.З. Цыпкин. М.: Наука, 1977. 560 с.

    Сборник задач по теории автоматического регулирования и управления. 5 е изд., перераб. и доп. / под ред. В.А. Бесекерского. М.: Наука, 1978. 512 с.

    Задачник по теории автоматического управления. 2 е изд., перераб. и доп. / под ред. А.С. Шаталова. М.: Энергия, 1979. 545 с.

    Ануфриев И.Е. Самоучитель Matlab 5.3/6.x / И.Е. Ануфриев. СПб.: БХВ-Петербург, 2002. 736 с.

    Дьяконов В. Matlab: учебный курс / В. Дьяконов. СПб.: Питер, 2001. 560 с.

    Дьяконов В. Simulink 4. Специальный справочник / В. Дьяконов. СПб.: Питер, 2002. 528 с.