Исследование линейных систем (работа 1)

Кафедра: ИТ

Лабораторная работа

"ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ СИСТЕМ"

Цель работы

В данной лабораторной работе средствами пакета Matlab (c использованием его расширения – пакета моделирования динамических систем Simulink) должно быть выполнено моделирование линейной системы, зафиксированы процессы, соответствующие элементам матричной весовой и переходной функций и проведено их сравнение с аналитически полученными зависимостями. Структурная схема системы представлена на рис. 1.1, коэффициенты структурной схемы  в табл. 1.1. Номер варианта для бригады указывается преподавателем.

1. Расчет матричных весовых и переходных функций

Рис. 1.1. Структурная схема системы

Таблица 1.1 Значения параметров структурной схемы

Номер

варианта

1

2

3

4

5

6

7

8

9

10

a>1>

0,1

0,1

3

0,3

0,4

0,8

1

2

2

2

a>2>

0.1

0,3

0,2

0,5

0,6

1,2

3

3

4

6

k>1>

0,1

0,015

0,4

5

3

0,48

1,5

1

4

24

k>2>

0,1

2

1

0,03

0,08

2

2

6

2

0,5

Номер

варианта

11

12

13

14

15

16

17

18

19

20

a>1>

3

0,8

0,9

0,9

0,9

1,2

3

4

4

5

a>2>

7

0,4

0,5

0,7

0,9

1,8

2

3

5

6

k>1>

0,5

0,5

2

0,12

0,5

0,1

4

2

6

4

k>2>

42

0,24

0,025

0,25

0,02

1,6

0,5

3

2

5

Подготовительная часть работы

        Составить векторно-матричное описание системы.

        Вычислить передаточную функцию (матрицу ) с использованием резольвенты матрицы динамики А:

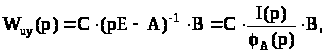
где В-матрица входов; С – матрица выходов; I(p) – присоединенная матрица для матрицы А; 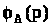– характеристический полином матрицы А (I(p) и 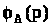могут быть определены по методу Фаддеева-Леверье).

Найти элементы матричной весовой функции по формуле

,

где – элемент i й строки и j го столбца матричной весовой функции, интерпретируемый как реакция i й координаты вектора выхода на дельта-функцию в j й координате вектора входа .

        Вычислить матричную весовую функцию по формуле

,

где 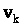и – соответственно k й правый и k й левый собственные векторы матрицы А. Убедиться в идентичности результатов, полученных в пп. 1.2.2 – 1.2.3.

        Вычислить элементы матричной переходной функции по формуле

,

где – элемент i й строки и j го столбца матричной переходной функции, интерпретируемый как реакция i й координаты вектора выхода на единичную функцию в j й координате вектора входа .

Программа работы

В ходе проведения лабораторной работы требуется в среде Matlab подготовить схему моделирования исследуемой системы, провести модельный эксперимент и зафиксировать его результаты.

Изучаемая в данной работе система описана двумя способами: при помощи структурной схемы (см. рис. 1.1) и в виде векторно-матричных уравнений, полученных в ходе подготовки к работе. Поэтому предлагается провести моделирование для двух вариантов описания системы и сравнить его результаты (процессы, соответствующие элементам матричной весовой и переходной функций) с аналитически полученными зависимостями.

Рекомендуется создать две отдельных модели: одну – для получения и фиксации 4 процессов, соответствующих элементам матричной весовой функции, вторую – для 4 процессов, соответствующих элементам матричной переходной функции.

Таким образом, должно быть зафиксировано 8 процессов, причем каждый из них будет представлен в трех вариантах, совмещенных на одном графике (т. к. моделируется система, описанная, во-первых, в виде структурной схемы и, во-вторых, – в векторно-матричной форме, а также, в-третьих, получены аналитические зависимости для и ).

        Для проведения моделирования должны быть созданы 5 файлов.

1) Файл-сценарий w_h_init.m, содержащий определения всех необходимых переменных в моделях:

%Файл определениЯ переменных

%

%Параметры моделированиЯ длЯ mdl файла

t_end = 1; %максимальный шаг моделированиЯ

h_max = 0.01; %времЯ завершениЯ моделированиЯ

%Параметры исследуемой системы

a1 = 2;

a2 = 3;

k1 = 1;

k2 = 6;

Время моделирования t_end и максимальный шаг моделирования h_max должны быть выбраны такими, чтобы все процессы смогли достигнуть своих установившихся значений, а графики не имели изломов и искажений.

2), 3) Файлы с моделями Simulink w.mdl и h.mdl, предназначенные для расчета и визуализации элементов соответственно весовой и переходной функций (рис. 1.2 и 1.3).

Параметры моделирования следует задать в окне Simulation Parameters, доступном через меню Simulation\Simulation parameters окна, в котором открыт mdl файл (рис. 1.4).

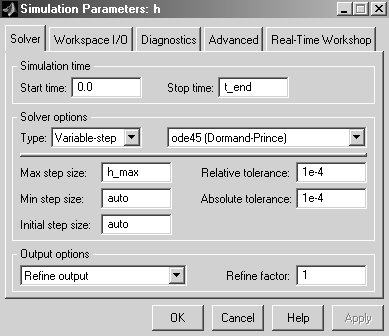
Рис. 1.4. Настройка параметров моделирования

Промоделировать систему, описанную в векторно-матричной форме, позволяет блок State-Space раздела Continuous основной библиотеки блоков Simulink. Структурная схема системы также может быть создана на основе блоков этой же библиотеки. Начальные условия следует принять нулевыми. Полученные структуры рекомендуется объединить в подсистемы, выделив все их элементы и выполнив команду Create sub>system меню Edit или нажав на сочетание клавиш Ctrl+G.

Рис. 1.5. Подсистема «Система в виде структурной схемы»

Рис. 1.6. Подсистема «Система с описанием
в векторно-матричной форме»

При организации источника входного воздействия (единичной или дельта-функции) следует использовать блоки Step и Pulse Generator раздела Sources. Обратите внимание на то, что необходимо подобрать длительность входного импульса, который бы воспринимался системой как дельта-функция (площадь импульса должна быть равна 1), т.е. значение длительности должно быть таким, чтобы его уменьшение уже не приводило к изменению отклика системы.

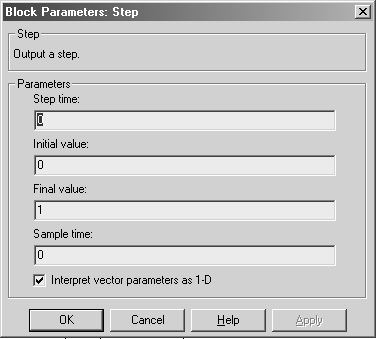
а б

Рис. 1.7. Настройки блоков:
а – Pulse Generator; б – Step

Графики найденных аналитически временных зависимостей можно получить при помощи блока MATLAB Fcn раздела Function&Tables и источника времени моделирования Clock.

Рис. 1.8. Настройки блока Matlab Fcn, содержащего аналитическое описание элементов матричной весовой функции

Для визуализации процессов, соответствующих элементам матричной весовой и переходной функций, рекомендуется выводить их, а также текущее время моделирования в рабочую область памяти Mаtlab при помощи блоков To Workspace раздела Sinks, а затем строить их графики, используя команды построения графиков функций одной переменной. В этом случае не возникает проблем с переносом полученных результатов в электронную версию отчета по лабораторной работе и имеется возможность соблюсти все необходимые правила оформления графиков.

Рис. 1.9. Настройки блока To Workspace

Вывод графиков может быть продублирован с использованием осциллографов (блоков Scope раздела Sinks).

4), 5) Файлы-сценарии w_stop.m и h_stop.m, предназначенные для построения графиков процессов, соответствующих элементам матричной весовой и переходной функций, в стандартных графических окнах Figure.

%Построение графиков элементов матричной весовой функции (файл w_stop.m)

%

close all

figure

plot (t_, w11_s, 'r-', t_, w11_vm, 'b–', t_, w11_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('w11')

title ('Графики элемента w11 матричной весовой функции')

legend ('w11 struct', 'w11 VM', 'w11 analit', 0)

figure

plot (t_, w21_s, 'r-', t_, w21_vm, 'b–', t_, w21_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('w21')

title ('Графики элемента w21 матричной весовой функции')

legend ('w21 struct', 'w21 VM', 'w21 analit', 0)

figure

plot (t_, w12_s, 'r-', t_, w12_vm, 'b–', t_, w12_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('w12')

title ('Графики элемента w12 матричной весовой функции')

legend ('w12 struct', 'w12 VM', 'w12 analit', 0)

figure

plot (t_, w22_s, 'r-', t_, w22_vm, 'b–', t_, w22_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('w22')

title ('Графики элемента w22 матричной весовой функции')

legend ('w22 struct', 'w22 VM', 'w22 analit', 0)

%Построение графиков элементов матричной переходной функции (файл h_stop.m)

%

close all

figure

plot (t_, H21_s, 'r-', t_, H21_vm, 'b–', t_, H21_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('H21')

title ('Графики элемента H21 матричной переходной функции')

legend ('H21 struct', 'H21 VM', 'H21 analit', 0)

figure

plot (t_, H31_s, 'r-', t_, H31_vm, 'b–', t_, H31_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('H31')

title ('Графики элемента H31 матричной переходной функции')

legend ('H31 struct', 'H31 VM', 'H31 analit', 0)

figure

plot (t_, H22_s, 'r-', t_, H22_vm, 'b–', t_, H22_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('H22')

title ('Графики элемента H22 матричной переходной функции')

legend ('H22 struct', 'H22 VM', 'H22 analit', 0)

figure

plot (t_, H32_s, 'r-', t_, H32_vm, 'b–', t_, H32_a, 'm – .')

grid on

xlabel ('t, c')

ylabel('H32')

title ('Графики элемента H32 матричной переходной функции')

legend ('H32 struct', 'H32 VM', 'H32 analit', 0)

Назначение всех функций пакета Matlab, использованных при создании программ (m файлов), приводится в приложении.

Организовать все указанные файлы следует самостоятельно (файлы-примеры выдаваться не будут) с целью получения навыков работы с редактором-отладчиком m файлов и редактором схем Simulink.

Открыть и запустить файл w_h_init.m для задания значений всем необходимым переменным в рабочей области памяти Matlab (Workspace).

Открыть и запустить модель из файла w.mdl и проверить соответствие результатов домашнего расчета элементов матричной весовой функции результатам компьютерного моделирования. В случае несоответствия найти и устранить ошибки.

По завершении моделирования в Simulink открыть и запустить файл w_stop.m. Скопировать информацию, выведенную в графические окно путем выполнения команды меню «Edit\Copy Figure», после чего сохранить ее при помощи какого-либо приложения, например текстового редактора MS Word.

Выполнить пп. 1.3.3 и 1.3.4, используя файлы h.mdl и h_stop.m.

Замечание. Запуск файлов w_h_init.m и w_stop.m (h_stop.m) до и после проведения моделирования можно автоматизировать, связав mdl файл с соответствующими m файлами. Для этого необходимо:

    убедиться в том, что mdl- и m – файлы находятся в одной директории и она является текущей;

    открыть mdl файлы;

    в командном окне выполнить следующие команды:

set_param ('w', 'InitFcn', 'w_h_init')

set_param ('w', 'StopFcn', 'w_stop')

set_param ('h', 'InitFcn', 'w_h_init')

set_param ('h', 'StopFcn', 'h_stop')

    в Simulink для каждого mdl файла выполнить команду меню Edit\Update Diagram и сохранить файлы.

Содержание отчёта

        Исходные данные лабораторной работы: название работы, цель работы, структурная схема исследуемой системы, номер варианта и соответствующие ему значения параметров схемы.

        Результаты предварительной подготовки.

        Использованные схемы моделирования с необходимыми пояснениями (например, по выбору параметров того или иного блока).

        Графики элементов w(t) и h(t), количество – 8 графиков.

        Выводы о взаимном соответствии результатов предварительной подготовки и компьютерного моделирования.

Отчет оформляется на листах формата А4, допускается рукописное, печатное или комбинированное оформление.

1.Изучение типовых звеньев

Цель работы

Целью работы является расчет весовых и переходных функций, логарифмических амплитудно-частотных и фазочастотных характеристик (ЛАЧХ и ЛФЧХ), амплитудно-фазовых характеристик (АФХ) типовых динамических звеньев систем автоматического управления, а также анализ влияния их параметров на перечисленные выше характеристики. В работе предусматривается исследование звеньев, перечень которых приведен в табл. 2.1.

Таблица 2.1 Перечень типовых звеньев

Номер

звена

Звено

Передаточная функция

1

Интегрирующее

2

Инерционное

3

Реальное

дифференцирующее

4

Интегро-дифференцирующее

5

Колебательное

6

Номинально-фазовое первого порядка

7

Неустойчивое первого порядка

8

Неустойчивое второго порядка

9

Режекторный фильтр

Обязательными для изучения являются первые пять звеньев, указанные в табл. 2.1, а также любые два звена из звеньев №6–9.

Подготовительная часть работы

Для каждого типового звена необходимо выполнить следующее.

        Вывести и записать дифференциальные уравнения.

        Вывести и записать выражения для модуля и фазы комплексных передаточных коэффициентов.

        Вывести и записать выражения для весовых и переходных функций и привести их примерное графическое изображение.

        Построить (эскизно) логарифмические асимптотические амплитудно-частотные характеристики и фазовые частотные характеристики. Обратить внимание на масштабирование по оси абсцисс.

        Привести примерное изображение амплитудно-фазовых характеристик.

        Спланировать проведение экспериментов.

Все рассматриваемые звенья, за исключением интегратора, имеют 2 или 3 настраиваемых параметра. В отдельных случаях при изучении влияния параметра на характеристики звена достаточно варьировать его независимо от остальных, а в других ситуациях имеет смысл учитывать соотношения нескольких параметров и варьировать их совместно. Поэтому для каждого исследуемого звена следует провести предварительный анализ необходимого количества и содержания экспериментов.

При проведении подготовки рекомендуется использовать учебную и справочную литературу по курсу «Линейные непрерывные системы регулирования» (ТАУ).

Особое внимание следует уделить информационному сопровождению приводимых в подготовительной части работы эскизных рисунков: для каждого процесса необходимо отметить его характерные особенности, которые зависят от каких-либо параметров исследуемого звена. Так, для временных процессов  это начальное и установившееся значения, постоянная времени, период колебаний, перерегулирование; для ЛАЧХ – сопрягающие частоты, наклон в децибелах на декаду (дб/дек) для наклонных участков и значения модуля комплексного передаточного коэффициента для горизонтальных участков; для ЛЧХ – сопрягающие частоты, асимптоты, точки экстремума (если есть); для АФХ – точки на комплексной плоскости (, соответствующие , , пересечению с мнимой или действительной осями, точка максимального значения модуля комплексного передаточного коэффициента.

Выполнение работы

        Описать передаточные функции изучаемых звеньев в файле-функции Matlab. Например, создать файл TF_zv.m следующего содержания:

%ФункциЯ описаниЯ звена в виде передаточной функции

%

function W = TF_zv (N_zv, inp_param)

p = tf('p');

switch N_zv

case 1, %интегрирующее звено, N_zv = 1, inp_param = [k]

k = inp_param(1);

W = k/p;

case 2, %инерционное звено, N_zv = 2, inp_param = [k, T]

k = inp_param(1);

T = inp_param(2);

W = k/(T*p+1);

case 3, %реальное дифференцирующее звено, N_zv = 3, inp_param = [k, T]

k = inp_param(1);

T = inp_param(2);

W = (k*p)/(T*p+1);

case 4, %интегро-дифференцирующее звено, N_zv = 4, inp_param = [T1, T2]

T1 = inp_param(1);

T2 = inp_param(2);

W = (T1*p+1)/(T2*p+1);

case 5, %колебательное звено, N_zv = 5, inp_param = [k, T, ksi]

k = inp_param(1);

T = inp_param(2);

ksi = inp_param(3);

W = k/(T^2*p^2+2*ksi*T*p+1);

case 6, %неминимально-фазовое звено 1 го пор., N_zv = 6, inp_param = [T1, T2]

T1 = inp_param(1);

T2 = inp_param(2);

W = (1 T1*p)/(1+T2*p);

case 7, %неустойчивое звено 1 го пор., N_zv = 7, inp_param = [k, T]

k = inp_param(1);

T = inp_param(2);

W = k/(T*p 1);

case 8, %неустойчивое звено 2 го пор., N_zv = 8, inp_param = [k, T, ksi]

k = inp_param(1);

T = inp_param(2);

ksi = inp_param(3);

W = k/(T^2*p^2–2*ksi*T*p+1);

case 9, %режекторный фильтр, N_zv = 9, inp_param = [T, ksi1, ksi2]

T = inp_param(1);

ksi1 = inp_param(2);

ksi2 = inp_param(3);

W = (T^2*p^2+2*ksi1*T*p+1)/(T^2*p^2+2*ksi2*T*p+1);

end

%end of function TF_zv

Назначение всех использованных при создании этого файла функций Matlab приводится в приложении.

В программе звенья пронумерованы в соответствии с табл. 2.1, указание на номер моделируемого звена выполняется с помощью параметра N_zv рассматриваемой функции TF_zv. Второй параметр inp_param является векторным и предназначен для передачи значений параметров звена; в зависимости от вида звена он может содержать от одного до трех элементов. Для организации выбора описания звена служит оператор switch…case, при помощи которого производится анализ значения переменной N_zv и переход на вычисление соответствующей передаточной функции.

        Для каждого звена написать файл-сценарий с целью получения графиков требуемых временных и частотных характеристик. Например, для изучения колебательного звена следует создать файл kol_zv.m следующего содержания:

%Изучение типовых динамических звеньев: колебательное звено

%Очистка всех переменных в памЯти

clear all

%Очистка командного окна

clc

%Закрытие всех предыдущих рисунков

set (0,'ShowHiddenHandles', 'on')

delete (get(0,'Children'))

%Описание колебательного звена (N_zv = 5) через его передаточную функцию

%при различных значениЯх параметров. Параметры колебательного звена

%задаютсЯ вектором inp_param = [k, T, ksi] (см. текст файла TF_zv.m)

%изменЯем k

W_11 = TF_zv (5, [1,1,0.707]);

W_12 = TF_zv (5, [2,1,0.707]);

W_13 = TF_zv (5, [3,1,0.707]);

%изменЯем Т

W_21 = TF_zv (5, [1,0. 354,0.707]);

W_22 = TF_zv (5, [1,0. 707,0.707]);

W_23 = TF_zv (5, [1,1. 414,0.707]);

%изменЯем ksi

W_31 = TF_zv (5, [1,0. 5,0.3]);

W_32 = TF_zv (5, [1,0. 5,0.5]);

W_33 = TF_zv (5, [1,0. 5,0.7]);

%изменЯем T и ksi

W_41 = TF_zv (5, [1,0. 3,0.3]);

W_42 = TF_zv (5, [1,0. 5,0.5]);

W_43 = TF_zv (5, [1,0. 7,0.7]);

%Построение требуемых характеристик при различных k

%ЛАЧХ и ЛФЧХ

ltiview({'bode'}, W_11,'b-', W_12,'r-', W_13,'k-')

%АФХ

ltiview({'nyquist'}, W_11,'b-', W_12,'r-', W_13,'k-')

%весоваЯ функциЯ w(t)

ltiview({'impulse'}, W_11,'b-', W_12,'r-', W_13,'k-')

%переходнаЯ функциЯ h(t)

ltiview({'step'}, W_11,'b-', W_12,'r-', W_13,'k-')

%Построение требуемых характеристик при различных T

%ЛАЧХ и ЛФЧХ

ltiview({'bode'}, W_21,'b-', W_22,'r-', W_23,'k-')

%АФХ

ltiview({'nyquist'}, W_21,'b-', W_22,'r-', W_23,'k-')

%весоваЯ функциЯ w(t)

ltiview({'impulse'}, W_21,'b-', W_22,'r-', W_23,'k-')

%переходнаЯ функциЯ h(t)

ltiview({'step'}, W_21,'b-', W_22,'r-', W_23,'k-')

%Построение требуемых характеристик при различных ksi

%ЛАЧХ и ЛФЧХ

ltiview({'bode'}, W_31,'b-', W_32,'r-', W_33,'k-')

%АФХ

ltiview({'nyquist'}, W_31,'b-', W_32,'r-', W_33,'k-')

%весоваЯ функциЯ w(t)

ltiview({'impulse'}, W_31,'b-', W_32,'r-', W_33,'k-')

%переходнаЯ функциЯ h(t)

ltiview({'step'}, W_31,'b-', W_32,'r-', W_33,'k-')

%Построение требуемых характеристик при различных T и ksi

%ЛАЧХ и ЛФЧХ

ltiview({'bode'}, W_41,'b-', W_42,'r-', W_43,'k-')

%АФХ

ltiview({'nyquist'}, W_41,'b-', W_42,'r-', W_43,'k-')

%весоваЯ функциЯ w(t)

ltiview({'impulse'}, W_41,'b-', W_42,'r-', W_43,'k-')

%переходнаЯ функциЯ h(t)

ltiview({'step'}, W_41,'b-', W_42,'r-', W_43,'k-')

Назначение всех использованных при создании этой программы функций Matlab приводится в приложении.

Обратите внимание: в данном m файле используется внешняя функция TF_zv, описанная в п. 2.3.1, в связи с этим файлы kol_zv.m и TF_zv.m должны находиться в одной директории.

Для построения временных и частотных характеристик динамического звена используется команда ltiview, первый параметр которой – строковая переменная, заключенная в фигурные скобки, – служит для указания типа отображаемой характеристики, а следующие за ним пары параметров – для указания имени системы и свойств выводимой линии (цвета, типа линии и т.д. аналогично оформлению двумерных графиков при использовании команды plot).

Для каждого изучаемого звена произвести запуск программы и зафиксировать результаты моделирования.

При выполнении команды ltiview появляется графическое окно, в котором отображается график указанной характеристики. Дополнительные настройки доступны при нажатии правой клавиши мыши и через команды меню. Необходимой настройкой является включение сетки grid.

Для сохранения содержимого графического окна LTI Viewer необходимо воспользоваться командой меню File\Print to Figure, после чего открывается новое окно Figure, содержащее тот же самый рисунок, скопировать который можно путем выполнения команды меню Edit\Copy Figure.

При изучении влияния какого-либо параметра на характеристики рассматриваемого звена он (отдельно или в сочетании с другими параметрами) должен варьироваться не менее трех раз. Это позволяет впоследствии достаточно легко выявить основную тенденцию в изменении вида характеристик. Таким образом, результатом эксперимента с варьированием какого-либо параметра звена является четыре рисунка (ЛАЧХ и ЛФЧХ, АФХ, весовые функции, переходные функции), содержащие не менее трех графиков.

Замечания

1. При оформлении результатов компьютерного моделирования необходимо, как и в подготовительной части, обратить внимание на информационное сопровождение рисунков: оси должны быть снабжены обозначениями, рисунки иметь подрисуночные надписи, каждому графику должен быть поставлен в соответствие тот набор параметров, при котором проводилось моделирование звена. Кроме того, на графиках должны быть отмечены характерные точки (с указанием числовых значений по осям) и показано их соответствие теоретически рассчитанным характерным точкам.

2. На АФХ проставить оцифровку (не менее 8 значений ).

Содержание отчета

Исходные данные лабораторной работы: название работы, цель работы, список выбранных для изучения звеньев с их передаточными функциями.

Подготовительная часть, оформленная в соответствии с требованиями п. 2.2.

Результаты компьютерного моделирования, оформленные в соответствии с требованиями п. 2.3.3.

Качественный анализ влияния параметров каждого из рассмотренных звеньев на вид частотных и временных характеристик.

Выводы.

Приложение: текст файла-функции и одного из файлов-сценариев с указанием в комментариях номера группы, состава бригады и даты проведения работы.

Отчет оформляется на листах формата А4, допускается рукописное, печатное или комбинированное оформление.

2.Частотные характеристики систем и критерий устойчивости Найквиста

Цель работы

Целью работы является анализ частотных характеристик разомкнутых и замкнутых систем, получение навыков по использованию критерия устойчивости Найквиста.

В работе предусматривается исследование трех систем, различающихся видом передаточной функции (ПФ) разомкнутого контура. Варианты значений параметров ПФ приведены в табл. 3.1. Замкнутая система построена по типу классической следящей системы, ее структурная схема представлена на рис. 3.1.

Таблица 3.1 Значения параметров передаточной функции

Номер варианта

1

2

3

4

5

6

7

8

9

10

Система

1

T>1>

0,5

0,5

1,0

1,0

2,0

2,0

3,0

3,0

5,0

5,0

T>2>

0,1

0,1

0,2

0,2

0,4

0,4

0,6

0,6

1,0

1,0

T>3>

0,5

1,0

1,0

2,0

2,0

4,0

3,0

6,0

5,0

10,0

Система

2

T>1>

1

1

2

2

4

4

6

6

8

8

T>2>

0,02

0,1

0,04

0,2

0,08

0,4

0,12

0,6

0,16

0,8

Система

3

T>1>

1

2

3

4

5

6

7

8

9

10

T>2>

4,705

9,41

14,15

18,82

23,53

28,23

32,94

37,64

42,35

47,05

Номер варианта

11

12

13

14

15

16

17

18

19

20

Система

1

T>1>

0,25

0,25

0,5

0,5

1,0

1,0

2,0

2,0

4,0

4,0

T>2>

0,1

0,1

0,2

0,2

0,4

0,4

0,8

0,8

1,6

1,0

T>3>

2,0

3,0

4,0

6,0

8,0

120

16

24

32

48

Система

2

T>1>

10

10

20

20

40

40

60

60

80

80

T>2>

0,2

1

0,4

2

0,8

4

1,2

6

1,6

8

Система

3

T>1>

1

2

3

4

5

6

7

8

9

10

T>2>

5,671

11,34

17,01

22,68

28,36

34,03

38,70

45,37

51,04

56,71

Подготовительная часть

Для каждой из трех систем в соответствии с заданным вариантом произвести следующее:

Записать уравнения для модуля и фазы комплексного передаточного коэффициента.

Построить (эскизно) логарифмическую асимптотическую амплитудную и фазовую частотные характеристики разомкнутой системы.

Построить (эскизно) амплитудно-фазовую характеристику разомкнутой системы, провести ее расширение, если это необходимо.

Проанализировать устойчивость замкнутой системы, применяя критерий устойчивости Найквиста или его формулировку с использованием понятия переходов. По критерию Гурвица найти критическое значение передаточного коэффициента k разомкнутого контура системы, а также его значения (в виде неравенств), приводящие замкнутую систему в устойчивое или неустойчивое состояние.

Выполнение работы

Создать файл-сценарий, содержащий описание исследуемых систем и обеспечивающий построение частотных характеристик и переходных процессов. Также необходимо предусмотреть расчет значений полюсов для каждой из систем в замкнутом состоянии. Рекомендуется организовать файл следующим образом:

%Исследование устойчивости систем (частотные характеристики систем

%и критерий устойчивости Найквиста), файл prog.m

%Очистка всех переменных в памЯти

clear all

%Очистка командного окна

clc

%Закрытие всех предыдущих рисунков

set (0,'ShowHiddenHandles', 'on')

delete (get(0,'Children'))

%Параметры систем длЯ варианта #20

T1_s1 = 4;

T2_s1 = 1;

T3_s1 = 48;

K_s1 = 1;

T1_s2 = 80;

T2_s2 = 8;

K_s2 = 1;

T1_s3 = 10;

T2_s3 = 56.71;

K_s3 = 1;

%Описание разомкнутой и замкнутой систем через передаточные функции

p = tf('p');

R_s1 = K_s1*(T1_s1*p+1);

Q_s1 = (T2_s1*p+1)*(T3_s1*p 1)*p;

W_s1_r = R_s1/Q_s1;

W_s1_z = R_s1/(Q_s1+R_s1);

R_s2 = K_s2*(T1_s2*p+1)^2;

Q_s2 = (T2_s2*p+1)^2*p^3;

W_s2_r = R_s2/Q_s2;

W_s2_z = R_s2/(Q_s2+R_s2);

R_s3 = K_s3;

Q_s3 = (T1_s3^2*p^2+1)*(T2_s3*p+1)^3;

W_s3_r = R_s3/Q_s3;

W_s3_z = R_s3/(Q_s3+R_s3);

%Выбор номера исследуемой системы

sys_num = 1;

%Построение требуемых характеристик

switch sys_num

case 1,

%ЛАЧХ и ЛФЧХ разомкнутой системы

ltiview({'bode'}, W_s1_r);

%АФХ разомкнутой системы

ltiview({'nyquist'}, W_s1_r);

%переходный процесс в замкнутой системе

ltiview({'step'}, W_s1_z);

%собственные числа замкнутой системы – полюсы ее ПФ

[zeros_s1_z, poles_s1_z, koef_s1_z] = zpkdata (zpk(W_s1_z), 'v');

poles_s1_z

case 2,

%ЛАЧХ и ЛФЧХ разомкнутой системы

ltiview({'bode'}, W_s2_r);

%АФХ разомкнутой системы

ltiview({'nyquist'}, W_s2_r);

%переходный процесс в замкнутой системе

ltiview({'step'}, W_s2_z);

%собственные числа замкнутой системы – полюсы ее ПФ

[zeros_s2_z, poles_s2_z, koef_s2_z] = zpkdata (zpk(W_s2_z), 'v');

poles_s2_z

case 3,

%ЛАЧХ и ЛФЧХ разомкнутой системы

ltiview({'bode'}, W_s3_r);

%АФХ разомкнутой системы

ltiview({'nyquist'}, W_s3_r);

%переходный процесс в замкнутой системе

ltiview({'step'}, W_s3_z);

%собственные числа замкнутой системы – полюсы ее ПФ

[zeros_s3_z, poles_s3_z, koef_s3_z] = zpkdata (zpk(W_s3_z), 'v');

poles_s3_z

end

Назначение всех использованных функций Matlab приводится в приложении.

Переменной sys_num необходимо присвоить значение номера той системы, изучение которой производится в данный момент. В результате для этой системы при выбранных значениях ее параметров будут построены все требуемые характеристики с использованием LTI Viewer, а в командное окно будут выведены значения полюсов ПФ замкнутой системы.

Запустить созданный файл-сценарий, предварительно выбрав систему №1 и задав значения ее параметров в соответствии со своим вариантом (значение коэффициента усиления k разомкнутой системы принять равным 1). Сравнить полученные ЛАЧХ, ЛФЧХ и АФХ разомкнутой системы с результатами домашней подготовки. По совмещенным ЛАЧХ и ЛФЧХ разомкнутой системы вычислить значение k, при котором

– замкнутая система будет находиться на границе устойчивости (k=k>кр>);

– замкнутая система будет неустойчива (k=k>ну>);

– замкнутая система будет устойчива (k=k>у>) с запасом по модулю не менее 10 дБ.

Проверить соответствие значений коэффициента, рассчитанных при подготовке и по результатам компьютерного моделирования.

        Для каждого из трех найденных значений k провести повторный запуск программы и убедиться в том, что замкнутая система находится в соответствующем значению k состоянии. Для этого:

– проверить значения запасов устойчивости по модулю, используя ЛЧХ разомкнутой системы, оценить состояние замкнутой системы;

– проанализировать взаимное расположение АФХ разомкнутой системы и точки (-1, j0) на комплексной плоскости, определить количество переходов расширенной АФХ разомкнутой системы, сделать вывод об устойчивости системы в замкнутом состоянии;

– проанализировать расположение полюсов замкнутой системы на комплексной плоскости, сделать вывод о ее устойчивости;

– проверить состояние замкнутой системы по ее переходной характеристике.

Эксперимент по изучению устойчивости рассматриваемой системы считается завершенным только в случае непротиворечивости всех полученных результатов.

Сохранить в файл совмещенные ЛАЧХ и ЛФЧХ разомкнутой системы при k=1, также сохранить все частотные характеристики разомкнутой системы, переходный процесс в замкнутой системе и ее собственные значения при k= k>кр>, k>ну>, k>у> (т.е. всего 1+ рисунка + 3 текстовых блока для рассматриваемой системы). Наличие сетки на графиках обязательно. На ЛАЧХ должны быть отмечены сопрягающие частоты и ее наклон на каждом из участков. На АФХ должна присутствовать оцифровка.

Повторить пп. 3.3.2 – 3.3.4 для систем №2 и 3.

Содержание отчета

Исходные данные лабораторной работы: название работы, цель работы, перечень ПФ исследуемых систем с указанием значений параметров, соответствующих номеру варианта.

Подготовительная часть, оформленная в соответствии с требованиями п. 3.2.

Результаты компьютерного моделирования, оформленные в соответствии с требованиями п. 3.3.4.

Анализ полученных результатов – на основании выводов, сделанных в пп. 3.3.2 и 3.3.3.

Текст файла-сценария с указанием в комментариях номера группы, состава бригады и даты проведения работы.

Отчет оформляется на листах формата А4, допускается рукописное, печатное или комбинированное оформление.

3.Модальный синтез управления в линейных непрерывных системах

Цель работы

Данная лабораторная работа предназначена для первого практического ознакомления с применением модального метода для синтеза управления. Ее целью является исследование взаимосвязи между расположением собственных чисел и качеством процессов и выработка обоснованного подхода к выбору желаемых полюсов системы при осуществлении модального синтеза.

В качестве неизменяемой части системы следует принять одну из систем, заданную передаточной функцией в работе №3, с теми же значениями параметров (номер системы выбирается из табл. 4.1 согласно варианту).

Таблица 4.1 Выбор исследуемой системы (см. также табл. 3.1)

Номер варианта

1

2

3

4

5

6

7

8

9

10

Номер системы

1

2

3

1

2

3

1

2

3

1

Номер варианта

11

12

13

14

15

16

17

18

19

20

Номер системы

2

3

1

2

3

1

2

3

1

2

Подготовительная часть

        По передаточной функции разомкнутой системы (объекта) записать соответствующие векторно-матричные уравнения.

        Записать в общем виде уравнение обратной связи, т.е. выражение для синтезируемого управляющего сигнала (входного сигнала объекта) в векторно-матричной форме. Дать определение и вычислить размерности всех входящих в уравнение переменных.

        Записать векторно-матричные уравнения замкнутой системы.

        По результатам выполнения пп. 4.2.1 и 4.2.2 составить подробную структурную схему замкнутой системы (т.е. системы «регулятор + объект управления») с показом структуры объекта и обратных связей по каждому элементу вектора состояния.

        Дать описание алгоритма вычисления матрицы обратной связи.

        Привести описание алгоритма вычисления коэффициента усиления по командному сигналу.

        Изучить материалы лекций по темам «Основные показатели качества», «Обратная связь по состоянию, обеспечивающая заданное (желаемое) расположение собственных чисел в замкнутой системе с одним (скалярным) входом», а также проанализировать данные, полученные в процессе выполнения лабораторных работ №2 и 3, где требовалось проводить анализ влияния собственных чисел систем на их динамические свойства.

Выполнение работы

        Подготовить файл-сценарий, реализующий процедуру модального синтеза управления для изучаемой системы. Реализовать в Simulink структурную схему замкнутой системы, предусмотрев возможность наблюдения сигнала на входе и выходе объекта. Пример модели для системы №1 (sys1_mod.mdl) представлен на рис. 4.1 и 4.2, а содержание
        m файла (sys1.m) будет следующим:

%Модальный синтез управлениЯ в линейных непрерывных системах

%Система #1

%Вывод информации – в командное и графические окна

%Очистка всех переменных в памЯти

clear all

%Очистка командного окна

clc

%Закрытие всех предыдущих рисунков

set (0,'ShowHiddenHandles', 'on')

delete (get(0,'Children'))

%Установка параметров моделированиЯ для mdl файла

h_max = 0.01;%максимальный шаг моделированиЯ

t_end = 20; %времЯ завершениЯ моделированиЯ

%задание переменной преобразованиЯ Лапласа длЯ последующего описаниЯ

%системы в виде передаточной функции

p = tf('p');

%Параметры системы #1 длЯ варианта #20

T1_s1 = 4;

T2_s1 = 1;

T3_s1 = 48;

%Описание разомкнутой системы через передаточную функцию

disp ('ПередаточнаЯ функциЯ системы #1 в разомкнутом состоЯнии');

disp([' ' num2str (T1_s1) '*p+1'])

disp ('–');

disp([' (' num2str (T2_s1) '*p+1)*(' num2str (T3_s1) '*p 1)*p']);

R_s1 = T1_s1*p+1;

Q_s1 = (T2_s1*p+1)*(T3_s1*p 1)*p;

W_s1_r = R_s1/Q_s1

%Преобразование описаниЯ в ss форму (получение описаниЯ через матрицы % A, B, C, D)

sys1_r = ss (W_s1_r);

[A_s1_r, B_s1_r, C_s1_r, D_s1_r] = ssdata (sys1_r);

disp ('Матрицы A, B, C, D разомкнутой системы');

A_s1_r

B_s1_r

C_s1_r

D_s1_r

%Вычисление нулей и полюсов ПФ разомкнутой системы

[zeros_s1_r, poles_s1_r, koef_s1_r] = zpkdata (zpk(W_s1_r), 'v');

disp ('Нули и полюсы ПФ разомкнутой системы');

zeros_s1_r

poles_s1_r

%Проверка правильности вычислениЯ матрицы динамики при домашней подготовке

%путем вычислениЯ ее собственных чисел и сравнениЯ их c poles_s1_r

disp ('Cобств. числа матрицы динамики разомк. сис-мы (из домашней подготовки)');

poles_s1_r_dp = eig([-47/48 1/48 0; 1 0 0; 0 1 0])

%Желаемые полюсы замкнутой системы (задаютсЯ после анализа расположениЯ

%полюсов разомкнутой системы)

disp ('Желаемые полюсы замкнутой системы');

poles_s1_z_g = [-2+2*j; -2–2*j; -0.25]

%Расчет матрицы обратных свЯзей L, реализующей желаемое расположение

%полюсов замк. сис.

[L_s1, PREC_s1, MESSAGE_s1] = PLACE (A_s1_r, B_s1_r, poles_s1_z_g);

disp ('Матрица обратных свЯзей');

L_s1

%Матрица динамики замкнутой системы

A_s1_z = A_s1_r-B_s1_r*L_s1;

%Матрицы B, C, D замкнутой системы

B_s1_z = B_s1_r;

C_s1_z = C_s1_r;

D_s1_z = D_s1_r;

%Описание замкнутой системы в ss форме

sys1_z = ss (A_s1_z, B_s1_z, C_s1_z, D_s1_z);

%Расчет коэффициента усилениЯ по командному сигналу (должен обеспечивать

%единичную статику)

W_s1_z = tf (sys1_z);

[num_s1, den_s1] = tfdata (W_s1_z, 'v');

disp ('Коэффициент усилениЯ по командному сигналу');

%Вычисление коэффициента усилениЯ по командному сигналу

%как отношениЯ свободных членов полиномов знаменателЯ и числителЯ,

%передаточной функции замкнутой системы, т.е. последних элементов

%в векторах коэффициентов знаменателЯ и числителЯ

Kv_s1 = den_s1 (length(den_s1))/num_s1 (length(num_s1))

%Описание итоговой замкнутой системы в ss форме

B_s1_z = Kv_s1*B_s1_r;

sys1_z = ss (A_s1_z, B_s1_z, C_s1_z, D_s1_z);

%Фактические собственные числа итоговой замкнутой системы

%(сравнить с заказанными)

[zeros_s1_z_f, poles_s1_z_f, koef_s1_z_f] = zpkdata (zpk(sys1_z), 'v');

disp ('Нули и полюсы замкнутой системы с синтезированным управлением');

zeros_s1_z_f

poles_s1_z_f

%Рисунок, отображающий расположение нулей и полюсов до и после

%замыканиЯ обратных свЯзей

figure

plot (real(poles_s1_r), imag (poles_s1_r), 'rs', real (zeros_s1_r), imag (zeros_s1_r), 'ro')

hold on

plot (real(poles_s1_z_f), imag (poles_s1_z_f), 'bs', real (zeros_s1_z_f),…

imag (zeros_s1_z_f), 'bo', 'MarkerSize', 14)

grid on

title ('Расположение нулей и полюсов до и после замыканиЯ обратных свЯзей')

xlabel ('real(z)');

ylabel ('imag(z)');

legend ('poles of sys1 (razomk)', 'zeros of sys1 (razomk)',…

'poles of sys1 (zamkn)', 'zeros of sys1 (zamkn)', 0);

%переходный процесс в замкнутой системе c синтезированным управлением

ltiview({'step'}, sys1_z, t_end);

grid on

%вызов модели

open_system ('sys1_mod.mdl');

%запуск моделированиЯ

sim ('sys1_mod');

Назначение всех использованных при создании данной программы функций Matlab приводится в приложении.

Как следует из текста вышеприведенного файла, процедура модального синтеза управления предполагает выполнение следующих шагов:

    описание объекта (ввод исходных данных);

    преобразование описания объекта к ss форме и нахождение матриц A, B, C, D;

    вычисление нулей и полюсов ПФ разомкнутой системы;

    анализ расположения нулей и полюсов разомкнутой системы и назначение желаемых полюсов замкнутой системы;

    расчет матрицы обратных связей, реализующей желаемое расположение полюсов замкнутой системы;

    вычисление передаточной функции полученной замкнутой системы и коэффициента усиления по командному сигналу (т.е. как отношения свободных членов полиномов знаменателя и числителя передаточной функции замкнутой системы).

Результаты вычислений на каждом из этапов выводятся в командное окно.

Также в программе предусмотрено проведение ряда проверок (с использованием данных из командного окна): сравнение собственных чисел матрицы динамики разомкнутой системы, полученной в ходе предварительной подготовки, с собственными числами разомкнутой системы, рассчитанными в Matlab; проверка правильности работы процедуры расчета матрицы обратных связей – вычисление фактических значений полюсов полученной замкнутой системы и сравнение их со значениями желаемых полюсов.

Кроме того, по завершении процедуры модального синтеза будет выведено графическое окно с расположением нулей и полюсов системы на комплексной плоскости до и после замыкания обратных связей, построен график переходного процесса для замкнутой системы и запущена модель Simulink, содержащая структурную схему замкнутой системы.

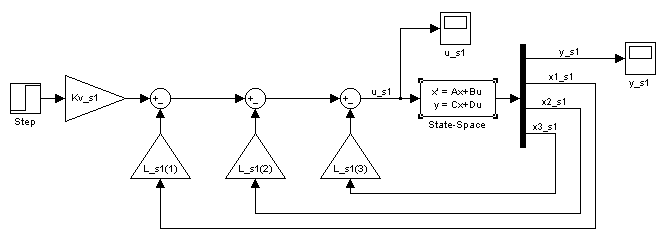
Рис. 4.1. Структурная схема замкнутой системы в Simulink

а б

Рис. 4.2. Настройка параметров: а – моделирования; б – в блоке State-Space

В тексте описанного выше файла-сценария скорректировать исходные данные в соответствии с номером варианта, задать матрицу динамики, рассчитанную при домашней подготовке, и задать некоторое желаемое расположение полюсов замкнутой системы. Скорректировать описание объекта в блоке State-Space модели, если это необходимо. Запустить программу на выполнение, после чего проверить правильность предварительных расчетов и корректность работы встроенной в Matlab процедуры расчета матрицы обратных связей place. Убедиться в правильности описания замкнутой системы при помощи структурной схемы в Simulink, сравнив переходный процесс в графическом окне и на экране осциллографа. В случае отсутствия ошибок сохранить полученные файл-сценарий и структурную схему в файл.

Выявить взаимосвязь между расположением нулей и полюсов замкнутой системы на комплексной плоскости и качеством процессов управления, варьируя желаемые собственные значения и фиксируя при помощи встроенных средств LTI Viewer (описание LTI Viewer см. в приложении) значения времени регулирования tp и перерегулирования  (основных показателей качества переходного процесса). Величину допуска («трубки») принять равной 5%. Также необходимо фиксировать максимальные значения управляющего воздействия umax по осциллографу в модели замкнутой системы в Simulink. Результаты необходимо оформить, заполнив табл. 4.2, 4.3 и 4.4.

Выполнение этого пункта лабораторной работы может существенно облегчить следующий подход: стремиться располагать полюсы замкнутой системы таким образом, чтобы приблизить ее к системе 2 го порядка, так как обеспечить требуемое качество управления в такой системе значительно проще; принимать во внимание тот факт, что значения показателей качества зависят от расположения на комплексной плоскости полюсов, ближайших к мнимой оси.

Тогда, во-первых, необходимо обеспечить расположение всех полюсов слева от мнимой оси (система должна быть устойчива в замкнутом состоянии); во-вторых, ближайшей к мнимой оси должна быть пара комплексно сопряженных полюсов, не считая полюсов, компенсирующих нули системы; в-третьих, все остальные полюсы должны находиться значительно левее, чтобы не оказывать влияния на характер переходной функции (соответствующие им моды будут обладать меньшим временем переходного процесса и вносить меньший вклад в выходной сигнал). Однако следует помнить, что чрезмерный сдвиг полюсов влево может привести к значительному увеличению коэффициентов обратных связей, росту пиковых значений управляющего воздействия и появлению нелинейных эффектов в реальных системах, поскольку для них всегда производится ограничение управляющего сигнала.

Изучение поведения систем второго порядка на примере колебательного звена показывает, что время переходного процесса определяется расстоянием пары комплексно сопряженных полюсов p>1,2 >= j до мнимой оси (это время равно приблизительно утроенной обратной величине их действительной части, t>p>3/||), а от соотношения ||/|| мнимой и действительной частей зависит колебательность процесса.

Таблица 4.2. Зависимость максимального значения управляющего воздействия от расстояния до мнимой оси наиболее удаленного от нее полюса замкнутой системы

Таблица 4.3. Зависимость времени регулирования от расстояния до мнимой оси ближайших к ней собственных значений замкнутой системы

0.05

0.075

0.15

0.5

1.5

0.1

0.15

0.3

1.0

3.0

, с

0.1

0.15

0.3

1.0

3.0

0.1

0.15

0.3

1.0

3.0

, с

0.5

0.75

1.5

5

15

0.1

0.15

0.3

1.0

3.0

, с

Таблица 4.4 Зависимость перерегулирования от соотношения мнимой и действительной частей ближайших к мнимой оси собственных значений замкнутой системы

0.07

0.1

0.15

0.3

0.8

0.7

1

1.5

3

8

, %

0.35

0.5

0.75

1.5

4

0.7

1

1.5

3

8

, %

Данные таблиц представить в виде соответствующих графиков, используя средства Matlab. Сохранить графики в файл.

Обеспечить требуемое качество процессов управления в замкнутой системе: время регулирования t>р >= 6 с, перерегулирование 15–20%. Сохранить протокол работы, выводимый в командное окно, расположение нулей и полюсов на комплексной плоскости, переходный процесс и управляющий сигнал в замкнутой системе.

Критерием успешного завершения лабораторной работы считается существенное сокращение времени на выбор расположения полюсов, обеспечивающих требуемое качество управления в замкнутой системе. В конце занятия преподаватель проводит проверку и просит обеспечить произвольное значение времени регулирования и перерегулирования переходного процесса в замкнутой системе.

Содержание отчета

Исходные данные лабораторной работы: название работы, цель работы, ПФ исследуемой системы с указанием значений параметров, соответствующих номеру варианта.

Подготовительная часть, оформленная в соответствии с требованиями п. 4.2.

Текст файла-сценария и структурная схема модели в Simulink.

Результаты компьютерного моделирования, оформленные в соответствии с требованиями пп. 4.3.3 и 4.3.4.

Аргументированные выводы о влиянии собственных значений на характер переходных процессов.

Отчет оформляется на листах формата А4, допускается рукописное, печатное или комбинированное оформление.

Список литературы

    Бесекерский В.А. Теория систем автоматического регулирования / В.А. Бесекерский, Е.П. Попов. М.: Наука, 1975. 768 с.

    Теория автоматического управления / под ред. А.А. Воронова. М.: Высшая школа, 1986. Ч. 1. 367 с.

    Теория автоматического управления / под ред. А.В. Нетушила. М.: Высшая школа, 1968. Ч. 1. 424 с.

    Попов Е.П. Теория линейных систем автоматического регулирования и управления / Е.П. Попов. М.: Наука, 1989. 304 с.

    Цыпкин Я.З. Основы теории автоматических систем / Я.З. Цыпкин. М.: Наука, 1977. 560 с.

    Ту Ю.Т. Современная теория управления / Ю.Т. Ту. М.: Машиностроение, 1971. 472 с.

    Деруссо П. Пространство состояний в теории управления / П. Деруссо, Р. Рой, С. Клоуз. М.: Наука, 1970. 620 с.

    Сборник задач по теории автоматического регулирования и управления. 5-е изд., перераб. и доп. / под ред. В.А. Бесекерского. М.: Наука, 1978. 512 с.

    Задачник по теории автоматического управления. 2-е изд., перераб. и доп. / под ред. А.С. Шаталова. М.: Энергия, 1979. 545 с.

    Дьяконов В. Simulink 4. Специальный справочник / В. Дьяконов. СПб.: Питер, 2002. 528 с.

    Дьяконов В. Matlab: учебный курс / В. Дьяконов. СПб.: Питер, 2001. 560 с.

    Ануфриев И.Е. Самоучитель Matlab 5.3/6.x / И.Е. Ануфриев. СПб.: БХВ-Петербург, 2002. 736 с.

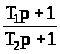
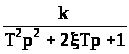
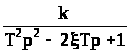
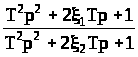
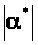
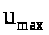
    Медведев В.С. Control System Toolbox. MATLAB 5 для студентов / В.С. Медведев, В.Г. Потемкин; под общ. ред. В.Г. Потемкина. М.: ДИАЛОГ-МИФИ, 1999. 287 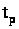с.