Использование команд преобразования выражений Maple для математических вычислений

Кафедра: Информационные Технологии

Лабораторная работа

На тему:

"Использование команд преобразования выражений Maple для математических вычислений"

Москва, 2008 г

Цели работы:

 знать команды, наиболее часто используемые при выполнении аналитических вычислений;

 уметь применять указанные команды для решения математических задач.

1. Команды преобразования выражений

Процесс работы в Maple состоит в том, что пользователь создает переменные, присваивает им символьные выражения и производит над ними некоторые действия в соответствии с алгоритмом решения поставленной задачи, использую стандартные функции или написанные собственные процедуры.

Синтаксис вызова стандартной команды следующий:

команда (пар_1, пар_2,…, пар_n);

Здесь команда – это имя вызываемой функции, а пар_1, пар_2,… означают необходимые для выполнения команды параметры, которые могут быть переменными или даже выражениями, причем их тип должен соответствовать типу параметров используемой функции. Отметим, если команда завершается точкой с запятой, то результаты ее выполнения отображаются в области вывода, если команда завершается двоеточием, то она выполняется, но никакого вывода результатов не происходит.

Система обозначений функций в Maple интуитивно проста. Обычно имя функции соответствует действию, которое она выполняет (следует учесть, что все имена заданы на английском языке). Например, ясно, что функция с именем simplify () осуществляет некоторые упрощения над выражением, заданным в качестве ее параметра.

Для некоторых команд существуют активная и пассивная формы. Активная форма команды (в случае ее вызова) немедленно выполняется, а ее имя начинается со строчной буквы. Пассивная форма команды не выполняется немедленно, а просто в области вывода отображается математическая запись того, что она может сделать. Ее имя начинается с прописной буквы. В дальнейшем, если в операторе присваивания для некоторой переменной в правой части задана пассивная форма команды, то командой value () ее можно вычислить. Основное предназначение пассивных форм команд – это использование их как средства документирования производимых действий в обычной математической нотации. Примерами команд с двумя формами являются команда дифференцирования (diff и Diff), интегрирования (int и Int) и др.

Пример 1. Пассивная и активная формы команд.

> k:=Int (cos(x)^3, x);

> k=int (cos(x)^3, x);

> value(k);

Если команды и функции являются частью ядра системы Maple, то они всегда доступны пользователю. А для вызова других команд и функций необходимо подключить библиотеку или пакет, в которых они расположены. Для этого служат команды readlib () и with (). Первая подключает библиотеку, вторая – пакет. Параметром этих команд является имя библиотеки или пакета, функции которых пользователь желает использовать.

Команды и функции Maple, наиболее часто используемые при аналитических преобразованиях, располагаются в его системном ядре – части программного обеспечения системы аналитических вычислений, постоянно находящейся в памяти компьютера. К ним относятся команды, выполняющие разнообразные преобразования выражений, получающие решение уравнений и систем уравнений, дифференцирующие функции и т.д. В данной работе вводятся команды, наиболее часто используемые при выполнении аналитических вычислений.

2. Упрощение выражения: simplify ()

Команда simplify () предназначена для упрощения разнообразных выражений, составленных из чисел, переменных и элементарных функций. Заметим, что Maple может его упростить, а может и не упростить, так как он использует свои внутренние алгоритмы упрощения, результат выполнения которых может не совсем соответствовать взглядам пользователя на то, как он хотел бы упростить выражение и в каком виде его получить.

Эта команда имеет несколько форм вызова. Ее самый простой синтаксис имеет следующий вид: simplify (выражение).

В скобках указывается выражение, подлежащее упрощению. Команда simplify () ищет в выражении вызовы функций, квадратные корни, радикалы и степени и инициализирует подходящие процедуры упрощения. Реально команда simplify () реализована в виде набора процедур упрощения, хранящихся в основной библиотеке Maple. Перечислим некоторые из них, остальные можно найти в справке по этой команде (например, установив курсор в рабочем листе на ее имя и нажав клавишу <F1>): `simplify/exp` – для упрощения выражений с экспоненциальными функциями, `simрlifу/ln` – для упрощения выражений с логарифмами, `simplifу/sqrt` – для упрощения выражений, содержащих квадратные корни, `simplifу/trig` – для упрощения выражении с тригонометрическими функциями, `simplifу/radical` – для упрощения выражений с радикалами (дробные степени), `simplifу/power` – для упрощения выражений со степенями, экспонентами и логарифмами и т.д. По умолчанию Maple пытается использовать максимальный набор функций упрощения, подходящий к конкретному выражению.

В команде можно задать конкретные процедуры упрощения, и тогда только они будут использоваться для упрощения заданного выражения, а не весь возможный, установленный по умолчанию набор. Это обеспечивается следующим синтаксисом команды: simрlifу (выражение, nl, n2,…);

Здесь nl, n2 и т.д. являются именами процедур упрощения: Ei, GAMМА, RootOf, @, hypergeom, ln, polar, power, radical, sqrt, trig. Полную информацию о формулах упрощения при использовании перечисленных значений параметров можно получить с помощью команды? simplify [имя], где [имя] – одно из значений параметров функции упрощения.

Упрощения выражений можно проводить с различными видами чисел, например, положительными или принадлежащими некоторому отрезку действительных чисел. Это достигается с помощью параметра assume=свойство. Форма вызова команды при этом имеет вид: simplify (выражение, аssumе=свойство); где параметр свойство может принимать одно из следующих значений: complex – комплексная область, real – действительная область, positive – положительные действительные числа, integer – целые числа, RealRange (a, b) – интервал (а, b) действительных чисел.

Примеры использования команды упрощения выражений simplify() представлены ниже:

Пример 2. Упрощение выражений.

> c:=ln (exp(x))+x*ln (exp(x));

> simplify(c);

> simplify (c, assume=real);

> d:=1/sqrt(8)*(((1+sqrt(8))/10)^5+((1 sqrt(8))/10)^5);

> simplify(d);

Как видно из примера 2, использование команды без параметров не упростило выражения ln (exp(x))+x·ln (exp(x)), тогда как второй оператор с предположением о действительной области изменения переменной х упростил заданное выражение. Maple по умолчанию работает с комплексными числами (т.е. при упрощении предполагается, что переменные изменяются в области комплексных чисел). При таком предположении упростить выражение с действительно невозможно.

Пример 3. Упрощение с предположением.

> f:=(sqrt (x^2));

> simplify(f);

> simplify (f, assume=real);

> simplify (f, assume=positive);

Команда simplify() позволяет задать правила упрощения в виде равенств. Эти правила задаются вторым параметром, который должен иметь следующий вид:

{равенствоl, равенство2,…}

Если какое-то выражение при упрощении должно равняться нулю, то такое правило можно задать, просто внеся выражение без знака равенства в список правил:

> k:=a+b^2+c^3+d+5;

> simplify (k, {c^3+d, a+b^2=1});

В этом примере предполагается, что выражение c^3+d равно 0.

Использование собственных правил для упрощения тригонометрических выражений позволяет получить именно тот его вид, который необходим для дальнейшей работы, так как третьим параметром можно определить, в какой последовательности должны отображаться неизвестные в упрощенном выражении. Этот параметр задается в двух формах: в виде множества и в виде списка. (Множество – последовательность выражений через запятую, заключенная в фигурные скобки, а список – это тоже объект Maple, который для данного частного случая можно охарактеризовать как последовательность выражений через запятую, заключенную в квадратные скобки.) Так вот, если параметр задан в виде множества, то алгоритм упрощения сортирует в выражении неизвестные по убыванию их степени в слагаемых выражения, учитывая степени всех неизвестных, а потом начинает упрощения в соответствии с заданными правилами. В случае со списком – сначала выражение сортируется по степеням первой неизвестной в списке, затем упрощается в соответствии с заданными правилами, затем полученное выражение сортируется по степеням второй неизвестной списка и упрощается и т.д.

Пример 4. Упрощение в соответствии с правилами пользователя.

> equ:={sin(x)^2+cos(x)^2=1};

e:=sin(x)^3–11*sin(x)^2*cos(x)+3*cos(x)^3 sin(x)*cos(x)+2;

> simplify (e, equ, [sin(x), cos(x)]);

> simplify (e, equ, [cos(x), sin(x)]);

> simplify (e, equ, {sin(x), cos(x)});

> simplify (e, equ, {cos(x), sin(x)});

3. Раскрытие скобок в выражении: expand ()

Команда expand () представляет произведение в виде суммы, т.е. раскрывает скобки в алгебраическом выражении. Она выполняется для любого полинома. Для частного двух полиномов (рациональная алгебраическая дробь) эта команда раскрывает скобки в числителе и делит каждый член полученного выражения на знаменатель, с которым она не производит никаких преобразований.

Эта команда имеет следующий синтаксис: ехраnd (выр, вырl, выр2,…, вырn); где выр является выражением, в котором необходимо раскрыть скобки, а необязательные параметры вырl, выр2, вырn указывают системе, что в данных выражениях в заданном преобразуемом выражении выр раскрывать скобки не надо.

Пример 5. Представление произведений в виде суммы.

> expand((x+3)*(x+4)^2);

> expand((x+3)^3/(x+4)^2);

> expand (cos(x-y));

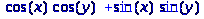
> expand((x+3)*(x+4)^2, x+3);

> expand (x^((a+b)*(k+f)));

4. Разложение полинома на множители: factor ()

Команда factor () разлагает на множители полином от нескольких переменных. Под полиномом в Maple понимается выражение, содержащее неизвестные величины. Каждый член в этом выражении представлен в виде произведения целых неотрицательных степеней неизвестных величин с числовым или алгебраическим коэффициентом, т.е. коэффициент может быть целым, дробным, с плавающей точкой, комплексным числом и даже представлять собой алгебраическое выражение с другими переменными:

> factor (x^3*y 2*x^2*a*y+x*y*a^2 x^3*b^2+2*x^2*b^2*a-x*b^2*a^2+x^2*y^2–2*x*y^2*a+y^2*a^2 y*b^2*x^2+2*y*b^2*x*a-y*b^2*a^2);

Следует помнить правило: команда раскладывает полином на множители над числовым полем, которому принадлежат коэффициенты полинома. Если все коэффициенты целые, то и в получаемых сомножителях будут только целые коэффициенты и не обязательно будут получены линейные сомножители. Второй необязательный параметр этой команды указывает, над каким числовым полем следует осуществлять разложение полинома. Он может иметь значение real, complex, а также один радикал или список / множество радикалов. Пример 6 демонстрирует результаты разложения одного и того же полинома над разными полями.

Пример 6. Разложение полинома над разными полями.

> factor (x^3+2); #над полем целых чисел (целые коэффициенты)

> factor (x^3+2.0); #над полем вещественных чисел

(вещественный коэффициент)

> factor (x^3+2, real); #над полем вещественных чисел

(параметр real)

> factor (x^3+2, complex); #над полем комплексных чисел

(параметр complex)

> factor (x^3+2,2^(1/3)); #над полем целых и радикала 2^(1/3)

(параметр определяет поле с радикалом)

Если применить команду factor () к алгебраической рациональной дроби (отношение двух полиномов), то сначала будет осуществлено приведение дроби к нормальной форме (сокращение общих множителей числителя и знаменателя), а после этого и числитель, и знаменатель раскладываются на множители (с учетом поля коэффициентов):

> d:=(x^11 y^11)/(x^6 y^6);

> factor(d);

5. Сокращение алгебраической дроби: normal ()

Команда normal () приводит выражение, содержащее алгебраические дроби, к общему знаменателю и упрощает полученную алгебраическую дробь, сократив и числитель, и знаменатель на наибольший общий делитель. Команда имеет две формы вызова: normal (f); normal (f, expanded); где f – алгебраическая дробь, а параметр expanded указывает на то, что после сокращения дроби в числителе и знаменателе раскрываются скобки.

Пример 7. Сокращение алгебраических дробей.

> f:=1/x+1/(x+1)^2+1/(x+1);

> normal(f);

Если параметр f задан в виде списка, множества, последовательности, ряда, уравнения, отношения или функции, то команда normal () последовательно применяется к компонентам f. Например, для уравнения это означает, что процедура сокращения применяется и к правой, и к левой части уравнения. В случае ряда, это означает, что упрощаются коэффициенты ряда, а в случае выражения с несколькими функциями, аргументы которых представлены алгебраическими дробями, процедура сокращения применяется к аргументу каждой функции:

> s:=sin (x/(x+1) – x)^2+cos (-x/(x+1)+x);

> normal(s);

> normal (1/x+y=x/y+(3*y)/x);

6. Приведение нескольких членов выражения к одному: combine ()

Назначение команды combine () – привести несколько членов в выражении, представленном суммой, произведением или степенями неизвестных, к одному члену, используя разнообразные правила. Эти правила, по существу, противоположны правилам, применяемым командой expand (). Например, рассмотрим известное тригонометрическое соотношение: sin (а+b) = sin(a) cos(b) +cos(а) sin(b).

Команда expand () использует его слева направо, тогда как команда combine () действует наоборот:

> expand (sin(a+b));

> combine (sin(a)*cos(b)+cos(a)*sin(b));

Однако рассмотрим еще один пример:

> g:=sin (a+b)^2;

> s:=expand(g);

> f:=combine(s);

Как видно из примера, команда combine () преобразовала выражение s не к исходному выражению g, которое мы раскрыли функцией expand (). Это происходит потому, что Марlе осуществляет приведение членов выражения по своим внутренним алгоритмам, которые завершаются, как только получилось (или не получилось) представление в соответствии с идеологией команды combine (). В нашем примере – представление через тригонометрическую функцию с аргументом, являющимся линейной комбинацией аргументов тригонометрических функций преобразуемого выражения. Если мы хотим получить исходный вид выражения g, то следует воспользоваться командой подстановки sub>s (), параметры которой определяют, что на что следует заменить в выражении:

> sub>s (cos(2*a+2*b)=-2*sin (a+b)^2+1, f);

Команда combine () «знакома» с практически всеми правилами преобразования элементарных математических функций. Если вторым ее параметром задать одно из следующих имен:

abs exp piecewise Psi Signum

arctan icombine polylog radical trig

conjugate ln power range

которые соответствуют используемым в Maple функциям, то при преобразовании выражения будут использоваться только правила преобразования соответствующих функций. Для функций, правила преобразования которых зависят от значения их аргументов (arctan) или которые имеют ограничения на значения аргументов (ln, radical), можно задать третий параметр symbolic, который будет предписывать функции combine () не обращать внимания на интервалы изменения аргументов подобных функций, а осуществлять формальные символические преобразования в соответствии с формулами преобразования этих функций.

7. Приведение подобных членов: collect ()

Команда collect () работает с полиномами, в которых в качестве неизвестных могут выступать функции с аргументами, являющимися неизвестными величинами Maple. Команда имеет три формы вызова:

collect (выражение, х);

соllесt (выражение, х, form, func);

соllесt (выражение, x, func);

где параметр х представляет имя неизвестной величины, относительно степеней которой осуществляется приведение коэффициентов. Параметр х может быть также списком или множеством неизвестных в случае полинома нескольких переменных или именем функции с аргументом-неизвестной в выражении, представленном первым параметром выражение.

Команда collect () различает не только целые, но и положительные и отрицательные дробные степени неизвестной, т.е. при всех степенях будут отдельно приведены подобные члены.

Пример 8. Приведение коэффициентов в выражении.

k:=x^3*sin(x)^2+x^3*cos(x)+x^3*exp(x)+x*cos(x)+2*x*exp(x)+7*x*sin(x)+4*x^3;

> collect (k, x);

> collect (k, x^3);

> collect (k, exp(x));

> collect (k, sin(x));

> collect (k, cos(x));

В примере 8 для одного и того же выражения осуществляется приведение коэффициентов относительно разных его неизвестных компонентов.

Параметр form применяется для полиномов от нескольких переменных и определяет алгоритм приведения подобных членов. Заметим, что неизвестные, при степенях которых приводятся подобные члены, должны быть заданы в виде списка или множества. Параметр form два значения: recursive и distributed. В первом случае приводятся подобные члены при степенях первой неизвестной в списке, затем в полученных коэффициентах приводятся подобные члены относительно степеней второй неизвестной в списке и т.д. Если при этом значении параметра form неизвестные полинома, относительно которых приводятся подобные члены, заданы в виде множества, то порядок приведения определяется системой Maple и может меняться от сеанса к сеансу. Значение distributed указывает на приведение коэффициентов при членах, содержащих всевозможные произведения степеней неизвестных в списке или множестве, причем суммарная степень всех переменных возрастает от наименьшей к наибольшей.

Пример 9. Алгоритмы приведения для полиномов нескольких переменных.

> p:=x*y-a^2*x*y+y*x^2 a*y*x^2+x+a*x; #полином двух переменных

> collect (p, [x, y], recursive);

> collect (p, [y, x], recursive);

> collect (p, {x, y}, recursive);

> collect (p, {x, y}, distributed);

> collect (p, [x, y], distributed);

Параметр func определяет имя команды, применяемой к полученным в результате коэффициентам при соответствующих степенях неизвестных. Обычно используют команды simplify () и factor ().

Пример 10. Задание функции, применяемой к полученным коэффициентам.

> d:=a^4*y-y+a^4+a^2;

> collect (d, y);

> collect (d, y, factor); # разложение на множители коэффициентов при y

8. Рационализация дробей: rationalize ()

Рационализация дроби – это избавление от иррациональности в знаменателе этой дроби. Команда rationalize () производит такое преобразование над числовыми и алгебраическими дробями. Причем в случае алгебраической дроби принимается во внимание только знаменатель в виде полинома. Эта команда может рационализировать алгебраическую дробь, знаменатель которой содержит трансцендентные функции типа sin (), ехр (), ln () и т.п. Однако если их аргумент является дробью с иррациональностями в знаменателе, то эти конструкции не участвуют в процессе рационализации.

Пример 11. Рационализация дробных выражений.

> a:=7*(3^(1/3)+4^(1/5))/(3–2^(1/3));

> rationalize(a);

> b:=y/(y+sqrt (2 sqrt(5)));

> rationalize(b);

> c:=1/(3 root (cos(1/(2+sqrt(mu))), 5));

> rationalize(c);

9. Ограничения на неизвестные: assume ()

Часто в математических выводах приходится делать те или иные предположения относительно некоторых величин, фигурирующих в наших исследованиях, т.е. как-то ограничивать эти величины. Одни ограничения логически вытекают из области определения независимых переменных, входящих в выражения, другие мы накладываем сами. В системе Марlе имеются команды для введения и проверки ограничений, наложенных на некоторые неизвестные или даже целые выражения. Введенные ограничения используются командами и функциями Maple, например simplify(), sqrt(), для получения более простого ответа, если введенные ограничения позволяют это.

Назначение команды assume () – накладывать ограничения на неизвестные величины Maple. Команда имеет следующий синтаксис:

assume (x, свойство);

Здесь х – любая неопределенная переменная или выражение с такими переменными, а параметр свойство может принимать значения, равные названиям свойств (специальным символьным именам, зарезервированным Maple для задания различных ограничений на переменную или выражение, определенные первым параметром), имени типа данных и числовому диапазону. Некоторые из наиболее употребительных свойств перечислены в табл. 1.

Таблица 1. Свойства числовых переменных и выражений

Название свойства	Описание
negative	Отрицательные вещественные числа из интервала (, 0) (нуль не включается)
nonnegative	Неотрицательные вещественные числа из интервала (0,) (нуль включается)
positive	Положительные вещественные числа из интервала (0,) (нуль не включается)
natural	Натуральные числа (целые, большие или равные 0)
posint	Целые строго большие 0
odd	Нечетные числа
even	Четные числа
complex	Комплексные числа
NumeralNonZero	Комплексные числа, исключая 0
real	Вещественные числа
rational	Рациональные числа (дроби и целые)
irrational	Иррациональные числа
integer	Целые числа
fraction	Только дробные числа
prime	Простые числа

Некоторые параметры (х, свойство) можно заменить математическим отношением, если, конечно, это возможно. Например, (x, negative) соответствует отношению х<0, а (х, nonnegative) соответствует х>=0 и т.д.

При наложении на переменную каких-либо ограничений в результатах выполнения действий над выражениями, в которые входит эта переменная, сразу же за ее именем по умолчанию отображается символ тильда (~). Эту функциональность по умолчанию можно изменить на следующие:

 либо вообще не информировать пользователя, что на переменную наложены ограничения, и она будет продолжать отображаться как и все переменные без ограничений (команда Options  Assumed Variables  No Annotation);

 либо в области вывода, если отображаются результаты, в которых присутствует переменная с наложенными ограничениями, словесно сообщается, на какие переменные наложены ограничения (команда Options  Assumed Variables  Phrase).

Пример 12. Способы отображения переменных с ограничениями.

> assume (a>0);

> ln (a^2); #Отображение по умолчанию

> ln (a^2); #Режим не информировать пользователя

> ln (a^2); #Словесное сообщение

Вернуться в режим отображения переменных с наложенными ограничениями по умолчанию можно командой Options  Assumed Variables  Trailing Tildes.

В качестве своих параметров команда assume () может получать несколько пар (х, свойство) или несколько математических отношений. В этом случае все заданные ограничения действуют одновременно. Поэтому наложение ограничений в виде

> аssumе (х>3, х<5);

соответствует тому, что переменная х может изменяться только в интервале (3,5).

Новое ограничение, накладываемое новой командой assume () на переменную, отменяет все предыдущие ограничения. Поэтому последовательное задание ограничений двумя командами:

> assume (x>3);

> assume (x<5);

соответствует предположению, что значение переменной х не превосходит числа 5, а не тому, что значение этой переменной должно лежать в интервале (3,5).

Если необходимо еще добавить ограничения на переменную, то можно использовать команду additionally(), параметры которой полностью соответствуют параметрам команды assume (). Тогда ограничения, определенные командой additionally (), добавляются к ограничениям, введенным командой assume () и предыдущими командами additionally ():

> assume (x>3); # В последующих вычислениях предполагается х>3

(какие-то вычисления)

> аdditiоnаllу (х<=5); #Теперь предполагается, что 3<х<=5

Чтобы снять все ранее наложенные на переменную ограничения следует этой переменной просто присвоить ее же символьное имя (имя переменной, заключенное в одинарные кавычки). Для снятия всех ограничений переменной х предыдущих примеров, следует просто выполнить следующую операцию присваивания:

> x:='x';

Если же переменная с наложенными ограничениями использовалась в выражениях, то простое присваивание имени переменной самой переменной не снимает ограничения на переменную в этих выражениях. Подобная ситуация иллюстрируется в примере 13.

Пример 13. Снятие ограничений с переменной.

> assume (b>0);

> d:=surd (b^4,4);

> b:='b':b;

> d;

Как видим, снятие всех наложенных на переменную b ограничений не снимает, однако, этих ограничений с переменной b в выражении d. Чтобы снять ограничения с этой переменной, следует до команды снятия ограничений с переменной воспользоваться командой подстановки sub>s () и первым параметром указать замену переменной b на ее символьное имя 'b'.

Пример 14. Снятие ограничений с переменной в выражении.

> assume (b>0);

> d:=sqrt (b^4);

> d;

> d:=sub>s (b='b', d);

> b:='b';

> d;

Функция is () определяет, удовлетворяет ли некоторая переменная рабочего листа определенному свойству. Эта функция возвращает значение true, если все возможные значения переменной соответствуют заданному свойству. Если хотя бы одно из возможных значений не соответствует заданному свойству, то функция is () возвращает false. Функция is () может возвратить значение FAIL, что говорит о невозможности определить, соответствует или нет заданная переменная заданному свойству. Это бывает или в результате недостаточности информации относительно ограничений на переменную, или невозможности вычислить логические ограничения на переменную.

Пример 15. Удовлетворяет ли переменная заданным ограничениям.

> assume (a>0);

> is (a>0);

> is (a<1);

> additionally (a<1);

> is (a<1);

С помощью функции coulditbe () можно проверить, может ли заданная переменная соответствовать заданному свойству. Она возвращает true, если хотя бы одно из возможных значений переменной может иметь заданное свойство, и fа1sе в противном случае. Смысл значения FAIL соответствует такому же значению для функции is().

Пример 16. Может ли переменная удовлетворять заданным ограничениям.

> assume (a>0);

> is (a>0);

> coulditbe (a=1);

> additionally (a<1);

> coulditbe (a=1);

Команда about () отображает информацию о наложенных ограничениях на неизвестную величину:

> about(a);

Originally a, renamed a~:

is assumed to be: RealRange (Open(0), Open(1))

Как отмечалось ранее, многие функции и команды Maple используют информацию о наложенных на неизвестную величину ограничениях при выполнении символьных вычислений. Например, Марle не может вычислить следующий предел из-за неизвестности знака символьной переменной а:

> int (exp(a*x), x=0..infinity);

Definite integration: Can't determine if the integral is convergent.

Need to know the sign of –> – a

Will now try indefinite integration and then take limits.

Стоит предположить, что a>0, и Maple тут же вычислит данный интеграл, который он свел к вычислению предела, зависящего от параметра:

> assume (a>0);

> int (exp(a*x), x=0..infinity);

Литература

1. Говорухин В.Н., Цибулин В.Г. Введение в Maple. Математический пакет для всех. – М.: Мир, 1997. – 208 с.

2. Дьяконов В.П. Математическая система Maple V. – М.: Издательство «Солон», 1998.

3. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 176 с.

4. Матросов А.В. Maple 6. Решение задач высшей математики и механики. – СПб.:БХВ – Петербург, 2001. – 528 с.

5. Манзон Б.М. Maple V Power Edition – М.: Информационно-издательский дом «Филинъ», 1998 г.