Информатика. Текстовый редактор

РЕФЕРАТ

Основными задачами учебной практики по информатике являлись:

- освоение способов ускоренного набора текста на примере десятипальцевого метода;

- закрепление навыков самостоятельного оформления технической документации по специальности в соответствии с ГОСТом и иными требованиями, предъявляемыми к ним законодательством,

- формирование умений и закрепление навыков работы в текстовом редакторе MS Word в задачах оформления технической документации;

- формирование умений и закрепление навыков работы с электронными таблицами MS Excel в задачах обработки, анализа и визуализации статистического и графического материала технической документации;

- закрепление умений автоматизировать рутинные процессы формирования технической документации с использованием макроязыка VBA и формул электронных таблиц.

Соло на клавиатуре, MS Word, MS Exсel, Visual Basic

Д.091400.01.1.01.05/147.УП

Фамилия Подпись Дата

Разработал

Рук.практики

Н.контр.

СОДЕРЖАНИЕ

1. Введение.

2. Общая часть.

2.1. Метод десятипальцевого набора текста

2.1.1. Тема, задание, цель

2.1.2. Отчет о выполнении

2.1.3. Вывод

2.2. Средство обработки информации MS Word

2.2.1. Тема, задание, цель

2.2.2. Исходные данные и индивидуальное задание

2.2.3. Отчет о выполнении

2.2.4. Вывод

2.3. Средство обработки информации MS Excel

2.3.1. Тема, задание, цель

2.3.2. Исходные данные и индивидуальное задание

2.3.3. Отчет о выполнении

2.3.4. Листинг модуля

2.3.4. Вывод

2.4. Средство обработки информации VBA

2.4.1. Тема, задание, цель

2.4.2. Исходные данные и индивидуальное задание

2.4.3. Алгоритм

2.4.4. Листинг работы макроса

2.4.5. Отчет о выполнении

2.4.6. Вывод

3. Заключение

4. Список использованной литературы

1. ВВЕДЕНИЕ

Учебная практика призвана дать первичные сведения и познакомить со спецификой практической деятельности по избранной специальности.

Основной целью учебной практики является подготовка к осознанному и углубленному изучению общепрофессиональных и специальных дисциплин и привитие им практических профессиональных умений и навыков по избранной специальности.

В период учебной практики должно сформироваться представление о культуре труда, культуре и этике межличностных отношений, потребность бережного отношения к рабочему времени, качественного выполнения заданий.

2. ОБЩАЯ ЧАСТЬ

Общая часть включает в себя отчеты индивидуальных заданий, выданные руководителем практики.

2.1 Метод десятипальцевого набора текста

Соло на клавиатуре – программа, которая обучает основным навыкам набора слепым десятипальцевым методом. Программа реализована для начинающих пользователей, а также для улучшения набора. Она состоит из 100 заданий, которые оцениваются 5-ой системой.

2.1.1 Тема, задание, цель

Тема - основные навыки успешного специалиста.

Задание - пройти 10 уроков «Соло на клавиатуре».

Цель - получить мотивацию обучения умению и получения навыкам

слепого набора.

2.1.2 Отчет о выполнении

Отчетом о выполнении 10 уроков является ниже приведенный рисунок статистики прохождения программы.

Рисунок 2.1 Статистика прохождения программы «Соло на клавиатуре»

Рисунок 2.1 подтверждающий факт прохождения программы. На нем изображена общая статистка.

2.1.3 Вывод

Выполнив задание данной программы, я получил мотивацию обучения умению и получения навыкам слепого набора.

2.2 Средство обработки информации MS Word

Microsoft Word – мощное средство обработки информации корпорации Майкрософт, которая имеет множество утилит необходимых для набора и обработки информации.

2.2.1 Тема, задание, цель

Тема - набор и форматирование документов в Word.

Задание - безошибочно набрать около 14 страниц сложного текста, получить основные умения по форматированию.

Цель - получить основные умения по набору текстового и графического материала, привести материал в соответствии с ГОСТ.

2.2.2 Исходные данные и индивидуальное задание

Исходными данными и индивидуальным заданием является электронная книга, выданная руководителем практики и номер задание из списка журнала (6. Ахо.pdf 104-116).

2.2.3 Отчет о выполнении

Отчетом о выполнении данного задания будет набранный и отформатированный текст, приведенный ниже.

ТЕСТ ПО ИНДИВИДУАЛЬНОМУ ЗАДАНИЮ

Уровень 3 1 (1,2)

Уровень 2 1 (0,0,0) 2 (0,1,1)


Уровень1 0 0 0 1 (0,0) 0 1 (0,0)


Уровень 0 0 0 0 0

Рисунок 3.4. а) Числа, приписанные алгоритмом распознавания изоморфизма деревьев.

Уровень 3 1 (1,2)

Уровень 2 1 (0,0,0) 2 (0,1,1)


Уровень 1 1(0,0) 0 1 (0,0) 0 0 0


Уровень 0 0 0 0

Дерево Т2

Рисунок 3.4. б) Числа, приписанные алгоритмом распознавания изоморфизма деревьев.

Тогда изоморфизм двух помеченных деревьев можно распо­знать за линейное время, если включить метку каждого узла в ка­честве первой компоненты кортежа, приписываемого этому узлу из­ложенным выше алгоритмом. Таким образом, справедливо

Следствие. Распознавание изоморфизма двух помеченных деревь­ев с п узлами, метками которых служат целые числа между 1 и п, занимает время 0(п).

3.3. СОРТИРОВКА С ПОМОЩЬЮ СРАВНЕНИЙ

Здесь мы изучим задачу упорядочения последовательности из п элементов, взятых из линейно упорядоченного множества 5, о структуре которых ничего не известно. Информацию об этой после­довательности можно получить только с помощью операции сравне­ния двух элементов. Сначала мы покажем, что любой алгоритм, упорядочивающий с помощью сравнений, должен делать по крайней мере О (n log n) сравнений на некоторой последовательности дли­ны n. Пусть надо упорядочить последовательность, состоящую из n различных элементов а>г>, а>2>, . . . , а>n>.

Алгоритм, упорядочивающий с помощью сравнений, можно представить в виде дерева решений так, как описано в разделе 1.5. На рис. 1.18 изображено дерево реше­ний, упорядочивающее последовательность a, b, c. Далее мы пред­полагаем, что если элемент a сравнивается с элементом b в некотором узле v дерева решений, то надо перейти к левому сыну узла v при a < b и к правому — при a b.

Как правило, алгоритмы сортировки, в которых для разветвле­ния используются сравнения, ограничиваются сравнением за один раз двух входных элементов. В самом деле, алгоритм, который ра­ботает на произвольном линейно упорядоченном множестве, не мо­жет никак преобразовать входные данные, поскольку при самой об­щей постановке задачи операции над данными "не имеют смысла". Так или иначе, мы докажем сильный результат о высоте любого де­рева решений, упорядочивающего последовательность из п эле­ментов.

Лемма 3.1. Двоичное дерево высоты Н содержит не более 1п ли­стьев.

Доказательство. Элементарная индукция по h. Нужно лишь заметить, что двоичное дерево высоты h составлено из корня и самое большее двух поддеревьев, каждое высоты не более h - 1 .

Теорема 3.4. Высота любого дерева решений, упорядочивающего последовательность из п различных элементов, не меньше log n!.

Доказательство. Так как результатом упорядочения последовательности из п! элементов может быть любая из п\ переста­новок входа, то в дереве решений должно быть по крайней мере n! листьев. По лемме 3.1 высота такого дерева должна быть не меньше log n!.

Следствие. В любом алгоритме, упорядочивающем с помощью сравнений, на упорядочение последовательности из п элементов тра­тится не меньше сп log п сравнений при некотором с>0 и достаточ­но большом п.

Доказательство. Заметим, что при n >1

n!n(n-1)(n-2)…()() ,

так что log n!(n/2)log(n/2)(n/4)log n при n 4

По формуле Стирлинга точнее приближает n!функция (п/е)п, так что n(log п — log е)=п log п — 1,44n служит хорошим приближе­нием нижней границы числа сравнений, необходимых для упорядо­чения последовательности из п элементов.

3.4. СОРТ ДЕРЕВОМ — УПОРЯДОЧЕНИЕ С ПОМОЩЬЮ О(n log n) СРАВНЕНИЙ

Так как любой сортирующий алгоритм, упорядочивающий с помощью сравнений, затрачивает по необходимости п log п срав­нений для упорядочения хотя бы одной последовательности длины n, естественно спросить, существуют ли сортирующие алгоритмы, затрачивающие не более О (п log п) сравнений для упорядочения любой последовательности длины п. Один такой алгоритм мы уже видели — это сортировка слиянием из разд. 2.7. Другой алгоритм — Сортдеревом. Помимо того, что это полезный алгоритм упорядо­чения, в нем используется интересная структура данных, которая находит и другие приложения.

Сортдеревом лучше всего понять в терминах двоичного дерева вроде изображенного на рис. 3.5, у которого каждый лист имеет глубину d. или d-1. Узлы дерева помечаются элементами последова­тельности, которую хотят упорядочить. Затем Сортдеревом меняет размещение этих элементов на дереве до тех пор, пока элемент, соответствующий произвольному узлу, станет не меньше элементов, соответствующих его сыновьям. Такое помеченное дерево мы будем называть сортирующим.

Пример 3.3. На рис. 3.5 изображено сортирующее дерево. За­метим, что последовательность элементов, лежащих на пути из любого листа в корень, линейно упорядочена и наибольший эле­мент в поддереве всегда соответствует его корню.

На следующем шаге алгоритма Сортдеревом из сортирующего дерева удаляется наибольший элемент — он соответствует корню дерева. Метка некоторого листа переносится в корень, а сам лист уда­ляется. Затем полученное дерево переделывается в сортирующее, и процесс повторяется. Последовательность элементов, удаленных из сортирующего дерева, упорядочена по невозрастанию.

Удобной структурой данных для сортирующего дерева служит такой массив А, что А[1] — элемент в корне, а А[2i] и A[2i+1] – элементы в левом и правом сыновьях (если они существуют) того узла, в котором хранится А[i].


Рисунок 3.5 Сортирующее дерево.

Например, сортирующее дерево на рис. 3.5 можно представить массивом

4

11

9

10

5

6

8

1

2

16

Заметим, что узлы наименьшей глубины стоят в этом массиве первыми, а узлы равной глубины стоят в порядке слева направо.

Не каждое сортирующее дерево можно представить таким спо­собом. На языке представления деревьев можно сказать, что для образования такого массива требуется, чтобы листья самого низ­кого уровня стояли как можно левее (как, например, на рис. 3.5).

Если сортирующее дерево представляется описанным массивом, то некоторые операции из алгоритма Сортдеревом легко выполнить. Например, согласно алгоритму, нужно удалить элемент из корня, где-то запомнить его, переделать оставшееся дерево в сортирующее и удалить непомеченный лист. Можно удалить наибольший эле­мент из сортирующего дерева и запомнить его, поменяв местами A[1] и A[n], и затем не считать более ячейку п нашего массива частью сортирующего дерева. Ячейка п рассматривается как лист, удаленный из этого дерева. Для того чтобы переделать дерево, хра­нящееся в ячейках 1,2, ... , n—1, в сортирующее, надо взять новый элемент A[1] и провести его вдоль подходящего пути в дереве. Затем можно повторить процесс, меняя местами A[1] и A[п—1] и считая, что дерево занимает ячейки 1,2 … п—2 и т. д.

Пример 3.4. Рассмотрим на примере сортирующего дерева рис. 3.5, что происходит, когда мы поменяем местами первый и по­следний элементы массива, представляющего это дерево. Новый массив

16

11

9

10

5

6

8

1

2

4

соответствует помеченному дереву на рис. 3.6,а. Элемент 16 ис­ключается из дальнейшего рассмотрения. Чтобы превратить полу­ченное дерево в сортирующее, надо поменять местами элемент 4 с большим из его сыновей, т. е. с элементом 11.

В своем новом положении элемент 4 обладает сыновьями 10 и 5. Так как они больше 4, то 4 переставляется с 10, большим сыном. После этого сыновьями элемента 4 в новом положении становятся 1 и 2. Поскольку 4 превосходит их обоих, дальнейшие перестановки не нужны.







Рисунок 3.6. а — результат перестановки элементов 4 и 16 в сортирующем дерев








Рисунок 3.6; б — результат перестройки сортирующего дерева и удаления элемента 16.

Полученное в результате сортирующее дерево показано на рис. 3.6,6. Заметим, что хотя элемент 16 был удален из сортирующе­го дерева, он все же присутствует в конце массива А .

Теперь перейдем к формальному описанию алгоритма Сорт-деревом.

Пусть а>г>, а>2>, . . ., а>п> — последовательность сортируемых эле­ментов. Предположим, что вначале они помещаются в массив А именно в этом порядке, т. е. A[i] = a,1in. Первый шаг состоит в построении сортирующего дерева, т. е. элементы в А перераспре­деляются так, чтобы удовлетворялось свойство сортирующего де­рева: A[i]A[2i] при 1 i n/2 и A[i]A[2i+1] при 1in/2. Это делают, строя, начиная с листьев, все большие и большие сор­тирующие деревья. Всякое поддерево, состоящее из листа, уже яв­ляется сортирующим. Чтобы сделать поддерево высоты h сортирую­щим, надо переставить элемент в корне с наибольшим из элементов, соответствующих его сыновьям, если, конечно, он меньше какого-то из них. Такое действие может испортить сортирующее дерево высоты h — 1, и тогда его надо снова перестроить в сортирующее. Приведем точное описание этого алгоритма.

Алгоритм 3.3. Построение сортирующего дерева

Вход. Массив элементов A[i], 1i n

Выход. Элементы массива А, организованные в виде сортирую­щего дерева, т. е.A[i]A[] для 1<in.

Метод. В основе алгоритма лежит рекурсивная процедура пересыпка. Ее параметры i и j задают область ячеек массива А, обладающую свойством сортирующего дерева; корень строящегося дерева помещается в i.

procedure ПЕРЕСЫПКА ((i,j):

1. if i — не лист и какой-то его сын содержит элемент, пре­восходящий элемент в i then begin

2. пусть k— тот сын узла i, в котором хранится

наибольший элемент;

    переставить А[i] и А[k];

    ПЕРЕСЫПКА (k,j)

    end

Параметр j используется, чтобы определить, является ли i листом и имеет он одного или двух сыновей. Если i > j/2, то i — лист, и процедуре ПЕРЕСЫПКА(i,j) ничего не нужно делать, поскольку А[i] — уже сортирующее дерево.

Алгоритм, превращающий весь массив А в сортирующее дерево, выглядит просто:

procedure ПОСТРСОРТДЕРЕВА:

for i п1) stер —1 until 1 do ПЕРЕСЫПКА (i,n)

Покажем, что алгоритм 3.3 преобразует А в сортирующее дере­во за линейное время.

Лемма 3.2. Если узлы i+1, i+2, . . ., n являются корнями сор­тирующих деревьев, то после вызова процедуры ПЕРЕСЫПКА (i, п) все узлы i, i+1, . . ., п будут корнями сортирующих деревьев.

Доказательство. Доказательство проводится возврат­ной индукцией по I.

Базис, т. е. случай i=п, тривиален, так как узел п должен быть листом и условие, проверяемое в строке 1, гарантирует, что ПЕ­РЕСЫПКА (п, п) ничего не делает.

Для шага индукции заметим, что если i — лист или у него нет сына с большим элементом, то доказывать нечего (как и при обо­сновании базиса). Но если у узла i есть один сын (т. е. если 2i=n) и A[i]<A[2i], то строка 3 процедуры ПЕРЕСЫПКА переставляет А[i] и А[2i]. В строке 4 вызывается ПЕРЕСЫПКА (2i, n); поэто­му из предположения индукции вытекает, что дерево с корнем 2i будет переделано в сортирующее. Что касается узлов i+1, i+2, . . . . . ., 2i — 1, то они и не переставали быть корнями сортирующих деревьев. Так как после этой новой перестановки в массиве А вы­полняется неравенство A[i]>A[2i], то дерево с корнем i также оказывается сортирующим.

Аналогично, если узел i имеет двух сыновей (т. е. если 2i+1n) и наибольший из элементов в А [2i] и в А [2i+1] больше элемента в A [i], то, рассуждая, как и выше, можно показать, что после вызова процедуры ПЕРЕСЫПКА(i,n) все узлы i, i+1,..., n будут кор­нями сортирующих деревьев.

Теорема 3.5. Алгоритм 3.3 преобразует А в сортирующее дере­во за линейное время.

Доказательство. Применяя лемму 3.2, можно с по­мощью простой возвратной индукции по i показать, что узел i становится корнем какого-нибудь сортирующего дерева для всех i, 1in

Пусть Т (h) — время выполнения процедуры ПЕРЕСЫПКА на узле высоты h. Тогда Т (h)Т (h — 1)+с для некоторой постоянной с. Отсюда вытекает, что Т (h) есть О (h).

Алгоритм 3.3 вызывает процедуру ПЕРЕСЫПКА, если не счи­тать рекурсивных вызовов, один раз для каждого узла. Поэтому время, затрачиваемое на ПОСТРСОРТДЕРЕВА, имеет тот же поря­док, что и сумма высот всех узлов. Но узлов высоты i не больше, чем . Следовательно, общее время, затрачиваемое процедурой ПОСТРСОРТДЕРЕВА, имеет порядок in/2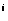, т.е O(n)

Теперь можно завершить детальное описание алгоритма СОРТДЕРЕВОМ. Коль скоро элементы массива А преобразованы в сор­тирующее дерево, некоторые элементы удаляются из корня по од­ному за раз. Это делается перестановкой А[1] и А[n] и последую­щим преобразованием A[1], А[2], ..., А[n - 1] в сортирующее дерево. Затем переставляются А[1] и А[n - 1], а A[1], А[2], ..., А [п - 2] преобразуется в сортирующее дерево. Процесс продол­жается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда А[1], А[2], ..., А[n] — упорядоченная последова­тельность.

Алгоритм 3.4. Сортдеревом

Вход. Массив элементов А[i], 1in.

Выход. Элементы массива А, расположенные в порядке неубы­вания.

Метод. Применяется процедура ПОСТРСОРТДЕРЕВА, т. е. алгоритм 3.3. Наш алгоритм выглядит так:

begin

ПОСТРСОРТДЕРЕВА;

For in step -1 until 2 do

Begin

переставить А[1] и А[i];

ПЕРЕСЫПКА(i,i - 1)

End end

Теорема 3.6. Алгоритм 3.4 упорядочивает последовательность из п элементов за время 0(n log п).

Доказательство. Корректность алгоритма доказывает­ся индукцией по числу выполнений основного цикла, которое обозначим через m. Предположение индукции состоит в том, что по­сле m итераций список A[n-m+1], ..., А [n] содержит m наи­больших элементов, расположенных в порядке неубывания, а спи­сок A[1], ..., А[n-m] образует сортирующее дерево. Детали до­казательства оставляем в качестве упражнения. Время выполнения процедуры ПЕРЕСЫПКА(1, i) есть 0(log i)- Следовательно, ал­горитм 3.4 имеет сложность О (n log i ).

Следствие. Алгоритм Сортдеревом имеет временную сложность O(nlog n)

3.5. БЫСТРСОРТ — УПОРЯДОЧЕНИЕ ЗА СРЕДНЕЕ ВРЕМЯ О(n log n)

До сих пор мы рассматривали поведение сортирующих алгорит­мов только в худшем случае. Для многих приложений более реа­листичной мерой временной сложности является усредненное вре­мя работы. В случае сортировки с помощью деревьев решений мы видим, что никакой сортирующий алгоритм не может иметь сред­нюю временную сложность, существенно меньшую n 1оg n. Однако известны алгоритмы сортировки, которые работают в худшем слу­чае сn2 времени, где с — некоторая постоянная, но среднее время работы, которых относит их к лучшим алгоритмам сортировки. При­мером такого алгоритма служит алгоритм Быстрсорт, рассматривае­мый в этом разделе.

Чтобы можно было рассуждать о среднем времени работы алгоритма, мы должны договориться о вероятностном распределе­нии входов. Для сортировки естественно допустить, что мы и сде­лаем, что любая перестановка упорядочиваемой последовательности равновероятна в качестве входа. При таком допущении уже можно оценить снизу среднее число сравнений, необходимых для упорядо­чения последовательности из n элементов.

Общий метод состоит в том, чтобы поставить в соответствие каж­дому листу v дерева решений вероятность быть достигнутым при данном входе. Зная распределение вероятностей на входах, можно найти вероятности, поставленные в соответствие листьям. Таким образом, можно определить среднее число сравнений, производи­мых данным алгоритмом сортировки, если вычислить сумму взятую по всем листьям дерева решений данного алгоритма, в ко­торой р>i> — вероятность достижения i-го листа, а d, - его глубина. Это число называется средней глубиной дерева решений. Итак, мы пришли к следующему обобщению теоремы 3.4.

Теорема 3.7. В предположении, что все перестановки п-элементной последовательности появляются на входе с равными вероят­ностями, любое дерево решений, упорядочивающее последователь­ность из п элементов, имеет среднюю глубину не менее log n!.

Доказательство. Обозначим через D (Т) сумму глубин листьев двоичного дерева Т. Пусть D (Т) — ее наименьшее значение, взятое по всем двоичным деревьям Т с m листьями. Покажем индук­цией по m, что D(m)m log m.

Базис, т. е. случай /п=1, тривиален. Допустим, что предположе­ние индукции верно для всех значений m, меньших k. Рассмотрим дерево решений Т с и листьями. Оно состоит из корня с левым подде­ревом Т с k листьями и правым поддеревом T с k – 1 листьями при некотором i, 1ik. Ясно, что

D(T)=i+D(T)+(k-i)+D(T)

Поэтому наименьшее значение D (Т) дается равенством

D(k)= [k+D(i)+D(k-1)]. (3.1)

Учитывая предположение индукции, получаем отсюда

D(k)k+[i log i+(k-i)log(k-i)] (3.2)

Легко показать, что этот минимум достигается при i=k/2. Сле­довательно, D(k)k+k log =k log k

Таким образом, D (m)m log m для всех m1.

Теперь мы утверждаем, что дерево решений Т, упорядочивающее n случайных элементов, имеет не меньше /г! листьев. Более того, в точности п\ листьев появляются с вероятностью 1/n! каждый, а остальные — с вероятностью 0. Не изменяя средней глубины дерева Т можно удалить из него все узлы, которые являются предками только листьев вероятности 0. Тогда останется дерево Т' с n! листь­ями, каждый из которых достигается с вероятностью 1/п!. Так как D(Т')n! log n!, то средняя глубина дерева Т' (а значит, и Т) не меньше (1/n!) n! log n! = log n!.

Следствие. Любая сортировка с помощью сравнений выполняет в среднем не менее сп log n сравнений для некоторой постоянной с>0.

Заслуживает упоминания эффективный алгоритм, называемый Быстрсорт, поскольку среднее время его работы, хотя и ограничено снизу функцией сn lоg n для некоторой постоянной с (как и у вся­кой сортировки с помощью сравнений), но составляет лишь часть времени работы других известных алгоритмов при их реализации на большинстве существующих машин. В худшем случае Быстрсорт имеет квадратичное время работы, но для многих приложений это не существенно.

Procedure БЫСТРСОРТ(S):

    if S содержит не больше одного элемента then return S

else

begin выбрать произвольный элемент a из S;

    пустьS1, S2 и S3 — последовательности элементов из S,

соответственно меньших, равных и больших а;

    return (БЫСТРСОРТ(S1), затем S2, затем БЫСТРСОРТ (S3))

end

Рисунок 3.7. Программа Быстрсорт.

Алгоритм 3.5. Быстрсорт

Вход. Последовательность S из n элементов a>ь> a>2>, ... , a>п>.

Выход. Элементы последовательности S, расположенные по порядку.

Метод. Рекурсивная процедура БЫСТРСОРТ определяется на рис. 3.7. Алгоритм состоит в вызове БЫСТРСОРТ(S).

Теорема 3.8. Алгоритм 3.5. упорядочивает последовательность из п элементов за среднее время О (п log п).

Доказательство. Корректность алгоритма 3.5 доказы­вается прямой индукцией по длине последовательности S. Чтобы проще было анализировать время работы, допустим, что все элементы в S различны. Это допущение максимизирует размеры последова­тельностей S1 и S3, которые строятся в строке 3, и тем самым мак­симизирует среднее время, затрачиваемое в рекурсивных вызовах в строке 4. Пусть Т (n) — среднее время, затрачиваемое алгоритмом БЫСТРСОРТ на упорядочение последовательности из n элементов. Ясно, что Т(0)=Т(1)=b для некоторой постоянной b.

Допустим, что элемент а, выбираемый в строке 2, является 1-м наименьшим элементом среди n элементов последовательности S. Тогда на два рекурсивных вызова БЫСТРСОРТ в строке 4 тратится среднее время Т(i - 1) и Т (n - i) соответственно. Так как i равно­вероятно принимает любое значение между 1 и n, а итоговое по­строение последовательности БЫСТРООРТ(S) очевидно занимает время cn для некоторой постоянной с, то

T(n)cn+[T(i-1)+T(n-1)] для n2 (3.3)

Алгебраические преобразования в (3.3) приводят к неравенству

T(n)cn+T(i) (3.4)

Покажем, что при n2 справедливо неравенство Т (n)<kn 1n n, где k=2с+2b и b=Т(0)=T(1). Для базиса (n=2) неравенство Т(2)2с+2b непосредственно вытекает из (3.4). Для проведения шага индукции запишем (3.4) в виде

T(n)cn + + ki ln i (3.5)

Так как функция i ln i вогнута, легко показать, что

i ln i x ln x dx (3.6)

Подставляя (3.6) в (3.5), получаем

T(n)cn + + kn ln n -

Поскольку n2 и k=2с+2b, то сn+4 b/nkn/2. Таким образом, неравенство Т (n)kn 1n n следует из (3.7).

Рассмотрим две детали, важные для практической реализации алгоритма. Первая — способ "произвольного" выбора элемента а в строке 2 процедуры БЫСТРСОРТ. При реализации этого опера­тора может возникнуть искушение встать на простой путь, а именно всегда выбирать, скажем, первый элемент последовательности S. Подобный выбор мог бы оказаться причиной значительно худшей работы алгоритма БЫСТРСОРТ, чем это вытекает из (3.3). После­довательность, к которой применяется подпрограмма сортировки, часто бывает уже "как-то" рассортирована, так что первый элемент мал с вероятностью выше средней. Читатель может проверить, что в крайнем случае, когда БЫСТРСОРТ начинает работу на уже упо­рядоченной последовательности без повторений, а в качестве эле­мента а всегда выбирается первый элемент из S, в последователь­ности S всегда будет на один элемент меньше, чем в той, из которой она строится. В этом случае БЫСТРСОРТ требует квадратичного числа шагов.

Лучшей техникой для выбора разбивающего элемента в строке 2 было бы использование генератора случайных чисел для порожде­ния целого числа i, 1<i<|S| 1), и выбора затем i-го элемента из S в качестве а. Более простой подход — произвести выборку элемен­тов из S, а затем взять ее медиану в качестве разбивающего элемен­та. Например, в качестве разбивающего элемента можно было бы взять медиану выборки, состоящей из первого, среднего и послед­него элементов последовательности S.

Вторая деталь — как эффективно разбить S на три последова­тельности S1, S2 и S3? Можно (и желательно) иметь в массиве А все n исходных элементов. Так как процедура БЫСТРСОРТ вызы­вает себя рекурсивно, ее аргумент S всегда будет находиться в по­следовательных компонентах массива, скажем A[f], A[f+1], ..., A[l] для некоторых f и l, 1<f<n. Выбрав "произвольный" элемент а, можно устроить разбиение последовательности S на этом же месте. Иными словами, можно расположить S1 в компонентах A[f], A[f+1], ... A[k], а S2S3— в A[k+1], A[k+2], ..., A[l] при некотором k, fklЗатем можно, если нужно, расщепить S2S3, но обычно эффективнее просто рекурсивно вызвать БЫСТР­СОРТ на S1 и S2S3, если оба этих множества не пусты.

По-видимому, самый легкий способ разбить S на том же месте — это использовать два указателя на массив, назовем их i и j. Вначале

    begin

    i f;

    while ij do

begin

    while A[i]>а и j>f do jj - 1;

    while A[j]<а и il do ii + 1;

    if < j then

begin

    переставить А[i] и A[j];

    ii + 1;

    ij -1

end

еnd

еnd

Рис. 3.8. Разбиение S на S1 и S2S3 на месте их расположения.

i=f, и все время в A [f], ..., А [i-1] будут находиться элементы из S1. Аналогично вначале i=f, а в A[j+1], ..., A[l] все время будут находиться элементы из S2S3. Это разбиение производит подпрограмма на рис. 3.8.

Затем можно вызвать БЫСТРСОРТ для массива A[f], ... A[i—1], т.е. S1 и для массива A[j+1], ..., А[1], т.е. S2S3. Но если i=f то надо сначала удалить из S2S3> >хотя бы один элемент, равный а. Удобно удалять тот элемент, по которому производилось разбиение. Следует также заметить, что если это представление в виде массива применяется для последова­тельностей, то можно подать аргументы для БЫСТРСОРТ, просто поставив указатели на первую и последнюю ячейку используемого куска массива.

Пример 3.5. Разобьем массив А

1

2

3

4

5

6

7

8

9

6

9

3

1

2

7

1

8

3

по элементу а=3. while-оператор (строка 4) уменьшает j с 9 до 7, поскольку числа A[9]=3 и A[8]=8 оба не меньше а, но A[7]=1<а. Строка 5 не увеличивает i с его начального значения 1, поскольку A[1]=6а. Поэтому мы переставляем A[1] и A [7], полагаем i=2, j=6 и получаем массив на рис. 3.9, а. Результаты, получаемые после следующих двух срабатываний цикла в строках 3—9, пока­заны на рис. 3.9, б и в. В этот момент i>j, и выполнение while-опе­ратора, стоящего в строке 3, заканчивается.

a)

1

9

3

1

2

7

6

8

3

i j

б)

1

2

1

3

9

7

6

8

3

j i

Рис. 3.9. Разбиение массива.

2.2.4 Вывод

Проделав индивидуальное задание, были получены основные умения по набору текстового и графического материала, приведя материал в соответствии с ГОСТ.

2.3 Средство обработки информации MS Excel

MS Exсel - мощное средство обработки информации корпорации Майкрософт, которая имеет множество утилит необходимых для набора и обработки информации.

2.3.1 Тема, задание, цель

Тема - работа с электронными таблицами MS Excel.

Цель - получить основные умения по работе с электронными таблицами.

Задания индивидуальные в рабочем порядке.

2.3.2 Исходные данные и индивидуальное задание

Дан файл Excel, содержащий данные о студентах группы с указанием номера зачетки, ФИО студента, размера стипендии, года рождения и пола. На другом листе вывести список, упорядоченный по увеличению стипендии. Форматирование и заполнение итоговых ячеек выполнить в модуле.

2.3.3 Отчет о выполнении

Отчетом о выполнении данного задания будет электронный вид листа excel, предоставленный руководителю практики. В данном отчете будет предоставлен рисунок работы exel файла, а также следующий пункт содержит листинг модуля.

ФИО

Номер зачетной книжки

Стипендия

Год рождения

Пол

Азаров Игорь

87934

150.5

16.10.1988

м

Анцибор Наталья

87967

151.0

13.05.1988

ж

Бандорчук Алексей

65477

143.5

03.07.1987

м

Булавин Александр

77685

155.5

04.05.1988

м

Гуляева Мария

67545

120.5

12.07.1989

ж

Давыдова Екатерина

45654

160.0

01.07.1988

ж

Дандыкин Александр

65465

130.0

23.12.1988

м

Звада Инна

56765

110.0

25.11.1987

ж

Калашников Максим

86985

123.5

19.10.1988

м

Морчук Станислав

65365

143.0

25.10.1988

м

Полярова Ксения

35676

150.0

13.05.1989

ж

Солодовник Михаил

35686

147.0

18.08.1988

м

Усенко Тарас

45676

159.5

23.11.1987

м

Рисунок 2.3.1 Лист Excel, содержащий данные о студентах группы с указанием номера зачетки, ФИО студента, размера стипендии, года рождения и пола.

ФИО

Номер зачетной книжки

Стипендия

Год рождения

Пол

Звада Инна

56765

110.0

25.11.1987

ж

Гуляева Мария

67545

120.5

12.07.1989

ж

Калашников Максим

86985

123.5

19.10.1988

м

Дандыкин Александр

65465

130.0

23.12.1988

м

Морчук Станислав

65365

143.0

25.10.1988

м

Бандорчук Алексей

65477

143.5

03.07.1987

м

Солодовник Михаил

35686

147.0

18.08.1988

м

Полярова Ксения

35676

150.0

13.05.1989

ж

Азаров Игорь

87934

150.5

16.10.1988

м

Анцибор Наталья

87967

151.0

13.05.1988

ж

Булавин Александр

77685

155.5

04.05.1988

м

Усенко Тарас

45676

159.5

23.11.1987

м

Давыдова Екатерина

45654

160.0

01.07.1988

ж

Рисунок 2.3.2 Лист excel выводящий список, упорядоченный по увеличению стипендии.

Рисунок 2.3.1 и рисунок 2.3.2 – предоставляют отчет о выполнении индивидуального задания, предоставленный в пункте 2.3.2.

2.3.4 Листинг модуля

sub> практика()

'

'Сочетание клавиш : Ctrl+w

'

Sheets("Лист2").Select

Range("A1:E14").Sort Key1:=Range("C2"), Order1:=xlAscending, Header:= _

xlGuess, OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, _

DataOption1:=xlSortNormal

End sub>

Данный листинг модуля показывает, что при нажатии сочетании клавиш Ctrl + w происходит переход на другой лист, где происходит сортировка личностей по возрастанию стипендий.

2.3.4 Вывод

Проделав индивидуальное задание, были получены основные умения по работе с электронными таблицами.

2.4 Средство обработки информации VISUAL BАSIC

Visual Basic - средство программирования информации корпорации Майкрософт в Microsoft Worde. Данный программный продукт является мощным дополнения Microsoft Word, который служит для составления программ и макросов в Microsoft Worde.

2.4.1 Тема, задание, цель

Тема - работа с макросам VBA.

Задание – индивидуальное задание.

Цель – получить навыки работа с макросам VBA.

2.4.2 Исходные данные и индивидуальное задание

Дан текст. Сформировать файл report.txt со словами данного текста (каждое слово с новой строки), исходный текст отформатировать по ширине, шрифт Arial 14 .

2.4.3 Алгоритм

Макрос записывается на поиске и замене пробелов в тексте. В случае, если существует пробелы они заменяются на enter, что переводит каждое слово на новую строку.

Затем происходит форматирование текста по заданному индивидуальному заданию, которое осуществляется просто записью макроса.

2.4.4 Листинг работы макроса

sub> практика()

'

' практика Макрос

'

'

Selection.Find.ClearFormatting

Selection.Find.Replacement.ClearFormatting

With Selection.Find

.Text = " "

.Replacement.Text = _

" "

.Forward = True

.Wrap = wdFindContinue

.Format = False

.MatchCase = False

.MatchWholeWord = False

.MatchWildcards = False

.MatchSoundsLike = False

.MatchAllWordForms = False

End With

Selection.Find.Execute Replace:=wdReplaceAll

Selection.WholeStory

With Selection.Font

.Name = "Arial"

.Size = 14

.Bold = False

.Italic = False

.Underline = wdUnderlineNone

.UnderlineColor = wdColorAutomatic

.StrikeThrough = False

.DoubleStrikeThrough = False

.Outline = False

.Emboss = False

.Shadow = False

.Hidden = False

.SmallCaps = False

.AllCaps = False

.Color = wdColorAutomatic

.Engrave = False

.Superscript = False

.sub>script = False

.Spacing = 0

.Scaling = 100

.Position = 0

.Kerning = 0

.Animation = wdAnimationNone

End With

Selection.ParagraphFormat.Alignment = wdAlignParagraphJustify

End sub>

2.4.5 Отчет о выполнении

Рисунок 2.4 а) Запись до выполнения макроса

Рисунок 2.4 б) Запись после выполнения макроса

На рисунках 2.4 а) и б) наглядно изображено работа макроса.

2.4.6 ВЫВОД

Проделав индивидуальное задание, были получены основные умения по работе с макросам VBA.

ЗАКЛЮЧЕНИЕ

Пройдя учебную практику :

- освоены способы ускоренного набора текста на примере десятипальцевого метода;

- закреплены навыки самостоятельного оформления технической документации по специальности в соответствии с ГОСТом и иными требованиями, предъявляемыми к ним законодательством,

- сформированы умения и закреплены навыки работы в текстовом редакторе MS Word в задачах оформления технической документации;

- сформированы умения и закреплены навыки работы с электронными таблицами MS Excel в задачах обработки, анализа и визуализации статистического и графического материала технической документации;

- закреплены умения автоматизировать рутинные процессы формирования технической документации с использованием макроязыка VBA и формул электронных таблиц.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

    Шахиджанян В.В. Соло на пишущей машинке. - М.: СП Вся Москва, 1992. - 172 с.

    Егоренков А.А. Изучаем Microsoft Office XP: Word XP для начинающих. - М.: Лист Нью, 2004 - 288 с.

    Шпак Ю.А. Microsoft Office 2003. Русская версия / Под ред. Ковтанюка Ю.С. - К.: Юниор, 2005 - 768 с.

    Мюррей К. Microsoft Office System 2003 / Пер. c англ. Рожевского В. - СПб.: Питер, 2005 - 368 с.

    Кронан Д. Microsoft Office Excel 2003 / Пер. c англ. Вереиной О.Б. - М.: НТ Пресс; Мн.: Харвест, 2005 – 224 с.