Арифметические устройства

Арифметические устройства

Двоичное сложение

К арифметическим устройствам относятся логические схемы, которые способны реализовывать сложение и вычитание. Сумматоры и вычитатели можно получить, соединяя друг с другом обычные логические элементы.

Рассмотрим сложение двух чисел (рис. 15.1)

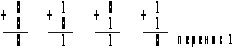
Рис. 15.1. Правила двоичного сложения

Первые три результата очевидны. Поскольку они соответствуют сложению десятичных чисел. В последнем суммировании (1+1), при сложении десятичных чисел результат будет 2. В двоичной системе 2 записывается как 10. Из рис. 15.1 видно, что происходит перенос 1 в соседний, старший двоичный разряд.

Рассмотрим пример на сложение двоичных чисел (рис 15.2)

Рис. 15.2. Пример двоичного сложения

Рис. 15.3. Правила двоичного сложения

Пример решается просто, пока не доходим до разряда двоек, где нужно найти двоичную сумму 1+1+1. В десятичной системе счисления эта сумма равна 3, что соответствует двоичному числу 11. При этом следует заметить, что сумма 1+1+1 может возникать в любом разряде, исключая разряд единиц. Таким образом к рис 15.1 нужно добавить еще одну комбинацию (рис. 15.3), которая справедлива для всех разрядов двоичных чисел (двоек, четверок, восьмерок и т. д.), за исключением разряда единиц.

Полусумматоры

Рассмотрим таблицу истинности для двоичных чисел (табл. 15.1). входные столбцы таблицы заполнены значениями слагаемых. В качестве выходных используется столбец для суммы и столбец для переноса.

Таблица 15.1. Таблица истинности полусумматора

Для построения схемы полусумматора, определим из табл. 15.1 булево выражение, которым можно описать состояние выходов и : , т. е. для обеспечения требуемого логического уровня на выходе входные сигналы нужно подать на входы логического элемента И;

, для реализации такой логической функции можно использовать два логических элемента И и один логический элемент ИЛИ. Кроме этого, такая логическая функция может быть реализована логическим элементом исключающее ИЛИ. Состояние этого выхода запишем в более простой булевой форме: .

Построим логическую схему полусумматора, который состоит из двух логических элементов: 2-входового логического элемента И и 2-входового логического элемента исключающее ИЛИ (рис. 15.4). Полусумматор имеет два входа (А,В) и два выхода (У,С0).

Рис. 15.4. Логическая схема полусумматора

Полусумматор осуществляет сложение только в разряде единиц. Для двоичного сложения в разрядах двоек, четверок, восьмерок и т. д. Необходимо пользоваться полным сумматором.

Полный сумматор

Рассмотрим таблицу истинности, в которой представлены все возможные комбинации двоичный одноразрядных слагаемых А и В и сигнала переноса Cin (табл. 15.2).

Таблица 15.2 Таблица истинности сумматора

Таблица 15.2 - таблица истинности для полного сумматора. Полные сумматоры используются для сложения во всех двоичных разрядах, кроме разряда единиц. Полные сумматоры имеют три входа: А, В и дополнительный вход переноса.

Один из способов построения логической структуры полного сумматора показан на рис. 15.5. В данном способе используется два полусумматора и логический элемент ИЛИ. Соответствующие булево выражение для этой логической структуры имеют вид , .

Рис. 15.5. Структурная схема полного сумматора

Используя схему полусумматора (рис. 15.4), структурную схему изображенную на рис. 15.5 можно развернуть (рис. 15.6).

Рис. 15.6. Логическая схема полного сумматора

Полусумматоры, сумматоры обычно используются вместе. Так, для решения примера, показанного на (рис. 15.3), нужно иметь один полусумматор (для сложения в разделе единиц) и два полных сумматора (для сложения в разрядах двоек и четверок). Для сложения много разрядных двоичных чисел требуется довольно много полусумматоров и полных сумматоров. Микропроцессорные арифметико-логические устройства (АЛУ) используются для сложения 8-разрядных, 16- или 32-разрядных двоичных чисел в микропроцессорных системах, и в их состав входит большое количество схем, аналогичных полусумматорам и сумматорам.

Параллельный сумматор

Определенным образом, соединяя полусумматоры и полные сумматоры, друг с другом, получают устройства, одновременно выполняющие сложение нескольких двоичных разрядов. На рис. 15.7 показана схема 3-разрядного сумматора. Слагаемые обозначены A2A1A0 и B2B1B0.

Рис. 15.7. Структура 3-разрядного сумматора

Сигналы, соответствующие значениям разряда единиц в слагаемых, поступают на входы полусумматора. Входными сигналами для полного сумматора разряда двоек является сигнал переноса с выхода полусумматора на вход и значения разряда двоек в слагаемых. Сумматор четверок складывает и сигнал переноса с выхода сумматора двоек. Полученный результат отображается на выходах полусумматора и двух полных сумматоров. В результате сложения двух полных сумматоров. В результате сложения двух 3-разрядных двоичных чисел может получиться 4-разрядное число, поэтому на индикаторе суммы имеется дополнительный разряд восьмерок. Этот разряд связан с выходом сумматора четверок.

3-разрядный сумматор, изображенный на (рис. 15.7) является параллельным сумматором. В данной схеме информационных биты всех разрядов поступают на входы одновременно. Результат сложения появится на выходе практически мгновенно. Параллельный сумматор относится к классу комбинационных логических схем. Для фиксации данных на входах и выходах сумматоров обычно используется различные дополнительные регистры.

Двоичное вычитание

Рассмотрим вычитание двоичных чисел (рис. 15.8).

Рис. 15.8. Правила двоичного вычитания

На основании этих правил вычитания двоичных чисел, составим таблицу истинности (табл. 15.3).

Таблица 15.3. Таблица истинности для полувычитателя

Из табл. 15.3 видно, что если В больше А, то нужно занять 1 в соседнем старшем разряде. Сигнал заема указан в столбце .

С помощью табл. 15.3 можно найти логические функции, реализуемые полувычитанием. Для выхода получим: . Для выхода . На основании этих функций построим логическую схему полувычитателя (рис.15.9).

Рис. 15.9. Логическая схема полувычитателя

При вычитании многоразрядных двоичных чисел нужно принимать во внимание заем 1 в более старших разрядах.

Рассмотрим пример на вычитание двоичных чисел (рис. 15.10).

Рис. 15.10. Пример на двоичное вычитание

Составим таблицу истинности, которая содержит все возможные комбинации при вычитании двоичных чисел (табл. 15.4).

Таблица 15.4. Таблица истинности для полного вычитателя

Например, строка 5 (табл. 15.4) описывает ситуацию, возникающего при вычитании в разрядах единиц для вышерассмотренного примера (рис. 15.10).

Вычитанию в разряде двоек соответствует строка 3, в разряде четверок – строка 6, в разряде восьмерок – строка 3, в разряде с весом 16 – строка 2 и в разряде с весом 32 – строка 6 (табл. 15.4).

Полный вычитатель, по аналогии с полным сумматором, можно собрать из двух полувычитателей и логического элемента ИЛИ (рис. 15.11).

Рис. 15.11. Структурная схема полного вычитателя

Полный сумматор имеет три входа и два выхода . Используя схему полувычитателя (рис. 15.9) можно построить развернутую логическую схему полного вычитателя, которая работает в соответствии с табл. 15.4 (рис. 15.12).

Рис. 15.12. Логическая схема полного вычитателя

Параллельный вычитатель

Чтобы построить параллельный вычитатель, нужно соединить друг с другом полувычитатели, по аналогии с построением параллельного сумматора (рис. 15.7). Рассмотрим схему 3-разрядного параллельного вычитателя, который обеспечивает вычитание двоичного числа из двоичного числа (рис. 15.13).

Рис. 15.13. Структурная схема 3-разрядного параллельного вычитателя

Из рис. 15.13 видно, что выход полувычитателя связан с вычитанием разряда двоек. В данной схеме выходы заема каждого вычитателя связаны со входами заема вычитателя старшего разряда.

Использование сумматоров для вычитания

В этом разделе рассмотрим возможность использования сумматоров для вычитания двоичных чисел. Решим пример на вычитание двоичного числа 0110 из числа 1010. Вычитание произведем по следующей схеме: сначала запишем вычитаемое в форме поразрядного дополнения до 1, а затем сложим с уменьшаемым. Дополнение до 1 означает замену 1 на 0 и 0 на 1 во всех разрядах вычитаемого. В результате сложения получим промежуточный результат. Далее осуществляем циклический перенос старшего разряда в разряд единиц и складываем с полученным остатком промежуточной суммы. В результате получается разность исходных двоичных чисел. Эта схема вычисления проиллюстрировала на (рис. 15.14).

Рис. 15.14. Пример вычитания двоичных чисел

В результате решения предложенного примера получим двоичное число 100.

Рассмотренный способ вычитания используется в сумматорах для вычитания. Рассмотрим схему 3-разрядного параллельного вычитателя, который построен на трех полных сумматорах и трех инверторах (рис. 15.15).

Рис. 15.15. Структурная схема вычитателя с использованием полных сумматоров

Инверторы обеспечивают преобразования двоичного числа в форму дополнения до 1. Сумматоры складывают двоичные числа и . Циклический перенос осуществляется с выхода сумматора старшего разряда на вход сумматора единиц. Разность двоичных чисел отображается на выходном индикаторе.

Рассмотрим схему, которая позволяет производить операции и сложения и вычитания двоичных чисел (рис. 15.16).

Рис. 15.16. Структурная схема 3-разрядного сумматора вычитателя

В схеме используются 3 логических элемента исключающее ИЛИ. При подаче логического 0 на вход элемента исключающее ИЛИ информационные биты каждого разряда двоичного числа проходом через этот элемент без инверсии и происходит сложение двух чисел : и . Логический 0, кроме этого блокирует цепь циклического переноса, т. к. 0 поступает на один из входов элемента И (рис. 15.16). В данном случае схема работает как 3-разрядный двоичный сумматор.

Для того, чтобы схема работала как 3-разрядный вычитатель нужно на управляющий вход подать логическую 1. В этом случае элементы исключающее ИЛИ работают как инверторы и на входах сумматоров получим . Кроме этого, логическая 1 открывает логический элемент И, в результате чего, сигнал с выхода последнего сумматора поступает по цепи циклического переноса на вход сумматора единиц. На выходном индикаторе отобразится разность двух двоичных чисел.

Суммирующее устройство последовательного действия

В параллельном сумматоре для каждого двоичного разряда нужен отдельный полный сумматор. При другом способе сложения последовательном, требуется только один полный сумматор. На рис. 15.17 показан принцип работы сумматора последовательного действия, которая помимо полного сумматора включает два регистра сдвига (А и В) и регистр суммы. Регистры сдвига А и В связаны со входами А и В полного сумматора.

Рис. 15.17. Принцип работы суммирующего устройства последовательного действия

Процесс последовательного суммирования состоит из нескольких шагов, которые отображены на рис. 15.17. На первом шаге регистры А и В загружаются двоичными числами и . С приходом первого тактового импульса складываются значения разряда единиц ( и ) и сумма заносится в выходной регистр, который связан с выходом У полного сумматора. С приходом второго тактового импульса складываются

значения разряда двоек ( и ) и перенос, который поступает на вход сумматора от триггера–задержки. Результат заносится в выходной регистр, при этом предыдущая сумма сдвигается вправо. С приходом третьего тактового импульса происходит сложение и переноса . Результат помещается в выходной регистр. Таким образом после трех тактовых импульсов в регистре суммы находится результат – двоичное число . Следует заметить, что в данной схеме тактовые входы всех регистров (двух входных и выходного) и триггера с задержкой связаны между собой. Кроме этого, в каждый момент времени складываются только два бита информации. Для сложения двух 3-разрядных чисел следует использовать только три тактовых импульса, поскольку большее число импульсов приведет к сдвигу двоичного числа в регистре суммы и на индикаторе будет неверный результат.

Двоичное умножение

В двоичной системе счисления правила умножения очень просты. Они показаны на рис. 15.18.

Рис. 15.18. Правила двоичного умножения

Рассмотрим пример на умножение двоичных чисел 111 и 101 (рис. 15.19).

Рис. 15.19. Пример на двоичное сложение

Сначала множимое (111) умножается на значения разряда единиц множителя. В результате получается первое частичное произведение, равное 111. Затем множимое умножается на значение разряда двоек множителя, при этом младший разряд второго частичного произведения отбрасывается. На третьем этапе множимое умножается на значение разряда четверок множителя. В результате получается третье частичное произведение 11100, но записывается это число как 111. В конце, первое, второе и третье частичные произведения складываются.

На рис. 15.20 показан еще один пример на двоичное умножение.

Рис. 15.20. Пример на двоичное умножение

Рассмотрим способы, которыми можно реализовать умножение двоичных чисел. Первый способ умножения – это многократно повторяемая операция сложения. Рассмотрим пример. Допустим необходимо найти произведение десятичных чисел 6 и 4. Произведением этих чисел является число 24. Этот же результат можно получить, используя операцию сложения: 6+6+6+6=24. Таким образом, операцию умножения можно заменить многократным сложением.

Рассмотрим схему устройства, которое позволяет реализовать такой способ умножения (рис. 15.21).

Рис. 15.21. Структурная схема операции умножения с использованием многократно повторяемого сложения

Рассмотрим процесс умножения двоичного числа 110 (десятичное 6) на двоичное число 100 (десятичное 4). Число 110 загружается в регистр множимого. Множитель (100) содержится в вычитающем счетчике. Произведение накапливается в регистре произведения.

В табл. 15.5 показан пошаговый процесс умножения двоичных чисел.

Таблица 15.5. Пошаговый процесс умножения двоичных чисел путем многократного сложения

Сначала множимое и множитель загружаются в регистр множимого и вычитающий счетчик множителя соответственно, а регистр произведения обнуляется. После первого шага в регистре произведения появляется число 00110, а множитель уменьшается на 1. После второго шага в регистре произведения оказывается сумма множимого (110) и числа 00110, множитель уменьшается на 1. Таким образом процесс завершается после четырех шагов, когда счетчик множителя содержит 000, а регистр произведения 11000 (десятичное число 24). Но этот способ не всегда удобен. Например, для нахождения произведения 56*12 нужно определить сумму 12 слагаемых, каждое из которых равно 56. Такой процесс вычисления занимает слишком много времени.

Вторым способом умножения двоичных чисел является способ сложения со сдвигами.

Вернемся к примеру, показанному на рис. 15.19. В этом примере двоичное число 111 умножается на двоичное число 101. При рассмотрении данного примера можно сделать следующие выводы:

1) Частичное произведение всегда равно 000, если множитель равен 0, и равно множимому, если множитель равен 1.

2) Число разделов в регистре произведения должно быть в два раза больше числа разделов в регистре множимого.

3) При сложении первое частичное произведение сдвигается на одну позицию (разряд) вправо (по отношению ко второму произведению).

На основе сделанных выводов можно построить схему для умножения двоичных чисел (рис. 15.22).

Рис. 15.22. Структурная схема умножителя с использованием операций сложения и сдвига

В исходном состоянии множимое (111) загружается в регистр, регистр-накопитель очищен (установлен в состояние 0000) и множитель (101) загружен в регистр. При этом регистр-накопитель и регистр-множителя составляют единый регистр (рис. 15.22.). Рассмотрим пошаговый процесс умножения двоичных чисел.

1) Загрузка исходных данных в регистры.

2) Сложение содержимого регистра-накопителя и регистра-множимого, инициируемое логической 1 младшего разряда на управляющую шину.

3) Сдвиг содержимого регистра-накопителя и регистра-множителя на одну позицию вправо. При этом младший разряд регистра-множителя теряется.

4) Регистр-множитель подает логический 0 на управляющую шину. Этот сигнал блокирует сумматор и сложение не производится.

5) Сдвиг содержимого регистра – накопителя и регистра – множителя на одну позицию вправо.

6) Сложение содержимого регистра – накопителя и регистра – множимого, инициируемое логической 1 младшего разряда регистра – множителя на управляемую шину.

7) Сдвиг содержимого регистра – накопителя и регистра – множителя на одну позицию вправо.

В результате этих шагов произведение (100011) находится сразу в двух регистрах (табл. 15.6).

Таблица 15.6. Пошаговый процесс умножения с использованием операций сложения и сдвига

В таблицах 15.5 – 15.6 показаны принципы умножения двумя способами: путем многократного сложения и путем сложений со сдвигами. При этом микропроцессоры могут и не содержать в своих АЛУ умножителей. Конкретный способ умножения можно запрограммировать. Таким образом задавая процессору программу, он выполнит последовательность операций, которая обеспечит умножение двоичных чисел. Благодаря этому существенно уменьшается число электронных схем в центральном процессоре.

15.10. Сложение и вычитание чисел, представленных в дополнительном коде

До сих пор сложение и вычитание производилось над положительными числами. Однако микропроцессоры должны обрабатывать не только положительные, но и отрицательные числа. Используя дополнительный код числа, можно задать как знак числа, так и его абсолютную величину.

Рассмотрим 4 – разрядный дополнительный код. Старший разряд отводится под знак числа: 0 – соответствует положительному числу, 1 – отрицательному. Три разряда отводятся абсолютной величине числа. В табл. 15.7 приведен 4 – разрядный дополнительный код чисел от +7 до –8.

Таблица 15.7. Представление двоичных чисел со знаком.

Из табл. 15.7 видно, что дополнительный код положительных чисел совпадает с обычным представлением двоичного числа. Для получения дополнительного кода отрицательного числа нужно сначала сформировать дополнение этого числа до 1, а затем прибавить 1. На рис. 15.23 показана процедура получения дополнительного кода отрицательного числа.

Рис. 15.23. Пример преобразования числа со знаком в дополнительный код

Эта процедура состоит из трех шагов:

1) десятичное число преобразуется к его двоичному эквиваленту соответствующего положительного числа;

2) находится дополнение полученного двоичного числа до 1, путем замены всех единиц на нули и всех нулей на единицы;

3) к полученному дополнению до 1 прибавляется 1. В результате сложения получаем дополнительный код числа.

Процедура перехода от дополнительного кода к двоичному числу, по которому затем определяется десятичное число, показано на рис. 15.24. Обратное преобразование выполняется следующим образом:

1) находим дополнение до 1 для исходного дополнительного кода, путем замены всех единиц на нули и всех нулей на единицы;

к полученному дополнению до 1 прибавляется 1 путем двоичного сложения. В результате получаем искомое двоичное число, но поскольку в старшем разряде дополнительного кода стоит 1, соответствующее десятичное число является отрицательным.

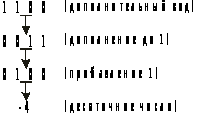
Рис. 15.24. Пример преобразования дополнительного кода в двоичное число

Рассмотрим примеры на сложение и вычитание чисел, представленных в дополнительном коде (рис. 15.25).

Рис. 15.25. Примеры сложения и вычитания чисел в дополнительном коде

Из рис. 15.25 можно сделать выводы, что сложение чисел, представленных в дополнительном коде, осуществляется обычным способом, за исключением случая, когда в результате получается 5 – разрядная комбинация. В этом случае самый старший разряд отбрасывается и остается дополнительный код суммы.

При вычитании, вычитаемое представляется в дополнительном коде. Далее образуется дополнение до 2 полученного дополнительного кода. При получении 5 – разрядной комбинации самый старший разряд отбрасывается.

Сложение и вычитание чисел, представленных в дополнительном коде, можно осуществить с использованием сумматоров.

Рассмотрим схему 3-разрядного сумматора – вычитателя, работающего с числами, представленными в дополнительном коде (рис. 15.26).

Рис. 15.26. Структурная схема 3-разрядного сумматора – вычитателя чисел в дополнительном коде

Для сложения и вычитания двух чисел, представленных в 3-разрядном дополнительном коде, используется три полных сумматора. Для задания режима работы устройства на входе В каждого сумматора введем элемент исключающее ИЛИ. При подаче логического 0 устройство складывает двоичные комбинации и . На выходе отображается дополнительный код сумы. При этом уровень логического 0 поступает на вход полного сумматора разряда единиц, т. е. этот сумматор работает как обычный двоичный сумматор.

Для выполнения операции вычитания чисел, представленных в дополнительном коде, на управляющем входе задания режима устанавливается уровень логической 1. В этом случае элементы исключающее ИЛИ инвертируют информационные сигналы, поступающие на входы В. На входе полного сумматора разряда единиц устанавливается высокий уровень сигнала. Инвертирование информационных сигналов элементами исключающее ИЛИ с прибавлением 1 на входе сумматора единиц соответствует дополнению до 1 дополнительного кода вычитаемого и последующему сложению с 1 младшего разряда. Это эквивалентно дополнению до 2 дополнительного кода вычитаемого . В результате этих действий на выходе отображается дополнительный код разности.