Анализ и моделирование цифровых и аналоговых схем
Министерство образования республики Беларусь
Учреждение образования "Полоцкий государственный университет"
Кафедра конструирования и технологии РЭС
Контрольная работа
По курсу " Теоретические основы САПР "
Выполнил
Номер зачетной книжки
Проверил
Новополоцк 2008
Задача №1. Оценка статического риска сбоя
Задание: для заданной схемы оценить риск статического сбоя по всем выходным переменным для заданного варианта изменения вектора входных переменных.
Исходные данные:
Схема:

Заданный вариант изменения вектора входных переменных:
X=(a,b,c) c (0,0,1) на (1,1,1)
Решение:
Для оценки риска статического сбоя необходимо разработать синхронную модель цифровой схемы в трехзначной логике. Математическая модель заданной схемы имеет вид:
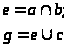
При анализе трехзначных моделей значения всех переменных – входных и выходных вычисляются трижды:
Исходное значение вектора входных переменных X=(a,b,c) задано заданием; исходное значение вектора выходных переменных Y=(e,g) вычисляется по правилам двоичной логики;
Окончательное значение вектора входных переменных X=(a,b,c) задано заданием; окончательное значение вектора выходных переменных Y=(e,g) вычисляется по правилам двоичной логики;
Промежуточные значения входных переменных X=(a,b,c) определяются по следующему правилу: если исходное значение входной переменной совпадает с окончательным, то промежуточное равно исходному и окончательному. Если исходное значение входной переменной не совпадает с окончательным, т.е. имеет место переключение входного сигнала в течение такта модельного времени, то промежуточное равно 2 (неопределенное состояние переключения). Промежуточные значения выходных переменных Y=(e,g) рассчитываются по правилам трехзначной логики. Статический риск сбоя по выходной переменной имеет место в случае, если сочетание значений этой переменной в исходном, промежуточном и окончательном состоянии имеют вид 0-2-0 или 1-2-1.
Правила выполнения основных логических операций И, ИЛИ, НЕ в двоичной и трехзначной логике для произвольных переменных а и b приведены в таблице 1:
Таблица 1
|
a |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
|
b |
0 |
0 |
0 |
1 |
1 |
1 |
2 |
2 |
2 |
|
|
0 |
0 |
0 |
0 |
1 |
2 |
0 |
2 |
2 |
|
|
0 |
1 |
2 |
1 |
1 |
1 |
2 |
1 |
2 |
|
|
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
Результат анализа трехзначной модели заданной схемы приведен в таблице 2.
Таблица 2
|
Значения переменных |
входные |
выходные |
|||
|
a |
b |
c |
e |
g |
|
|
Исходное |
0 |
0 |
1 |
1 |
1 |
|
Промежуточное |
2 |
2 |
0 |
2 |
2 |
|
Окончательное |
1 |
1 |
1 |
0 |
1 |
Таким образом, результат расчета по выходным переменным e и g показывает наличие статистического риска сбоя.
Задача №2. Анализ цифровых схем по методу простой итерации и событийному методу
Задание: выполнить анализ заданной схемы по методу простой итерации и событийному методу для заданного изменения вектора входных переменных.
Исходные данные:
Схема:

Заданный вариант изменения вектора входных переменных:
X=(a,b,c,d,e) меняет свое значение с 00100 на 11101
Решение:
Для выполнения анализа схемы необходимо разработать ее синхронную модель в двоичной логике. Математическая модель заданной схемы имеет вид:

Для реализации анализа по методу простой итерации необходимо задать начальное приближение для вектора выходных переменных Y>0>=(f,g,h,p,q). Для расчета начальных приближений вектора выходных переменных воспользуемся начальным значением вектора входных переменных X=(a,b,c,d,e)=(00100), предварительно расположив уравнения в порядке прохождения сигналов по схеме:

Y>0>=(f,g,h,p,q)=( 1,0,1,1,1).
Метод простой итерации состоит в выполнении итераций по формуле:
Y>i>= (Y>i-1>, X),
где Y>i> - значение вектора Y на i-й итерации, т.е. при вычислении Y>1> в правые части уравнений модели поставляются значения выходных переменных из начального приближения Y>0>, при вычислении Y>2 >– значения из результата первой итерации Y>1 >и так далее. Если Y>i>=Y>i-1>, то решение найдено; если
Y>i>Y>i-1>, то выполняется новая итерация; если итерационный процесс не сходится, то это свидетельствует об ошибках проектирования схемы устройства, вызывающих неустойчивость его состояния.
Результат анализа заданной схемы по методу простой итерации приведен в таблице 3.
Таблица 3
-
№
итерации
Начальное приближение Y0
g
p
f
h
q
0
1
1
1
1
1
2
0
0
1
1
0
0
1
1
1
1
Из таблицы 3 видно, что потребовалось два раза обращаться к каждому из пети уравнений модели, прежде чем результат второй итерации, совпадающий с результатом первой итерации, показал, что решение найдено.
Таким образом, искомое значение вектора выходных переменных при изменении X=(a,b,c,d,е) с 00100 на 11101 для заданной схемы равно:
Y=(e,g,p,f,h,q)=(0,1,0,1,1).
При использовании событийного метода вычисления на каждой итерации выполняются только по уравнениям активизированных элементов, т.е. элементов, у которых хотя бы на одном входе произошло событие (изменилась входная переменная). В алгоритме событийного метода на каждом шаге вычислительного процесса имеется своя группа активизированных элементов.
В заданном варианте изменения вектора входных переменных изменяются только значения переменных а, b и е, следовательно, на первой итерации при реализации событийного алгоритма анализа должны быть пересчитаны только выходные переменные f и h, в правые части уравнений которых входят аргументами b и d. Если по результатам вычисления значения f и h совпадут с начальным приближением, то решение будет найдено, если хотя бы одна из этих переменных изменится, то на второй итерации должны быть пересчитаны те выходные переменных, в правые части уравнений которых входят изменившиеся в результате первой итерации переменные. Процесс продолжается до тех пор, пока в результате очередной итерации значения рассчитываемых переменных не совпадут с их предыдущими значениями, т.е. до выполнения условия Y>i>=Y>i-1>.
Результат анализа заданной схемы по методу простой итерации приведен в таблице 4.
Таблица 4
|
№ итерации |
Начальное приближение Y0 |
Изменяющиеся переменные |
Активизированные уравнения |
|||||
|
e |
g |
p |
f |
h |
q |
|||
|
0 |
0 |
1 |
1 |
1 |
0 |
|||
|
0 1 2 3 4 5 6 |
|
0
|
1 1
|
1
|
1 1 0
|
0 1 1 |
b, d f g h q p - |
4 и 5 2 5 6 3 6 - |
|
Результат |
0 |
1 |
0 |
0 |
0 |
1 |
Как видно из таблицы 4, на 6-ой итерации результат расчета переменной q совпал с ее предыдущим значением, следовательно решение найдено.
Таким образом, искомое значение вектора выходных переменных при изменении X=(a,b,c,d) с 0110 на 0011 при расчете по событийному методу для заданной схемы совпадает с результатом анализа по методу простой итерации и равно:
Y=(e,g,p,f,h,q)=(0,1,0,0,0,1).
Однако, при вычислении по методу простой итерации, потребовалось на каждой итерации вычислять все выходные переменные, т.е. объем вычислений составил 66=36 операций. Тот же результат при использовании событийного метода потребовал значительно меньшего объема вычислений, а именно выполнения 8 операций. Таким образом, трудоемкость событийного метода значительно меньше.
Задача №3. Анализ цифровых схем по методам Зейделя
Задание: выполнить анализ заданной схемы по методам Зейделя для заданного изменения вектора входных переменных.
Исходные данные:
Схема:

Заданный вариант изменения вектора входных переменных:
X=(a,b,c,d,e) меняет свое значение с 00100 на 11101
Математическая модель заданной схемы имеет вид:

При реализации анализа по методу Зейделя при вычислении очередного из элементов вектора Y>i> в правую часть уравнений системы там, где это возможно, подставляются не элементы вектора Y>i-1>, а те элементы вектора Y>i>, которые уже вычислены к данному моменту, т.е. итерации выполняются по формуле: Y>i>= (Y>i>,Y>i-1>, X).
Результат вычислений по методу Зейделя без ранжирования, для исходного произвольного порядка уравнений модели представлен в таблице 5. Для организации вычислений использовалось значение начального приближения вектора выходных переменных Y>0>, полученное в задаче 2.
Таблица 5
-
№
итерации
Начальное приближение Y0
g
p
f
h
q
0
1
1
1
1
1
2
0
0
1
1
0
0
1
1
1
1

Задача №4. Моделирование аналоговых схем (метод узловых потенциалов)
Цель: освоение метода узловых потенциалов моделирования аналоговых схем.
Задание: для заданного варианта схемы задачи №6 разработать модель топологии с использованием метода узловых потенциалов: построить матрицу «узел-ветвь», записать топологические уравнения в общем виде; в развернутой матричной форме; в виде системы уравнений по законам Кирхгофа.
Решение:
В методе узловых потенциалов в вектор базисных координат включаются потенциалы всех узлов схемы, за исключением одного узла, принимаемого за опорный. Топологические уравнения – это уравнения закона токов Кирхгофа, записанные для узлов схемы, и уравнения связи вектора напряжений ветвей U с вектором узловых потенциалов:
AI=0;
AT+U=0,
где А – матрица «узел-ветвь»; AT - транспонированная матрица «узел-ветвь»; I – вектор токов ветвей. Строки матрицы соответствуют узлам, а столбцы - ветвям схемы. В столбце i-той ветви записываются единицы на пересечении со строками узлов, при чем +1 соответствует узлу, в который ток i-той ветви втекает, а -1 соответствует узлу, из которого этот ток вытекает. Матрица «узел-ветвь» для схемы с введенными обозначениями узлов, полученной в задаче 6 и показанной на рисунке 10, имеет вид, представленный на рисунке 14 (узел 8 принят в качестве опорного).
-
С1
С2
С3
С4
С5
С6
R1
R2
R3
R4
R5
E1
1
0
0
0
0
0
0
-1
0
0
0
0
+1
2
-1
-1
0
0
0
0
+1
0
0
0
0
0
3
0
+1
0
0
0
0
0
-1
-1
0
0
0
4
0
0
-1
0
0
0
0
+1
0
0
0
0
5
0
0
0
-1
0
0
0
0
+1
-1
0
0
6
0
0
0
0
-1
0
0
0
0
+1
0
0
7
0
0
0
+1
+1
-1
0
0
0
0
-1
0
Рисунок 14
Запишем топологические уравнения по закону токов Кирхгофа
в общем виде:
AI=0;
в развернутой матричной форм

в виде системы уравнений, которая получена из матричной формы умножением вектора-столбца токов ветвей схемы на матрицу «узел-ветвь»:

Запишем топологические уравнения по закону напряжений через узловые потенциалы:
в общем виде:
AT+U=0;
в развернутой матричной форме (в транспонированной матрице столбцы соответствуют строкам исходной матрицы «узел-ветвь»):

в виде системы уравнений, которая получена из матричной формы умножением вектора-столбца узловых потенциалов на матрицу «узел-ветвь» после приведения ее к виду U=-AT :

Таким образом, модель топологии заданной схемы получена с использованием метода узловых потенциалов в виде двух систем уравнений - по закону токов Кирхгофа и по закону напряжений через узловые потенциалы.
Задача №5. Моделирование аналоговых схем (метод переменных состояния)
Цель: освоение метода узловых потенциалов моделирования аналоговых схем.
Теория, методы и примеры решения: раздел 3.3.2.3 курса лекций.
Задание: для заданного варианта схемы задачи №6 разработать модель топологии с использованием метода переменных состояния: построить граф, нормальное фундаментальное дерево и матрицу контуров и сечений. Записать топологические уравнения в общем виде; в развернутой матричной форме; в виде системы уравнений по законам Кирхгофа. Записать окончательную математическую модель схемы в виде системы уравнений, в которой ёмкостные токи и индуктивные напряжения выражены явно и заменены производными переменных состояния.
Решение:
Базисными координатами в этом методе являются переменные состояния, т.е. фазовые переменные, непосредственно характеризующие запасы энергии в элементах электрической схемы. К таким переменным относятся независимые друг от друга емкостные напряжения и индуктивные токи. Исходными топологическими уравнениями являются те же уравнения, что и в табличном методе:
U>x>+MU>вд>=0; I>вд>=MТI>x>=0.
Матрицу М контуров и сечений в методе переменных состояния формируют на основе построения нормального дерева графа схемы. Нормальным деревом называют фундаментальное дерево, в которое включение ветвей производится не произвольно, а в следующем порядке: ветви источников напряжения, емкостные, резистивные, индуктивные, источников тока. Использование нормального дерева облегчает дальнейшее преобразование исходных уравнений с целью получения нормальной формы Коши.
В графе схемы, приведенной на рисунке 12, построенное фундаментальное дерево является нормальным. Топологические уравнения в общем виде и в развернутой матричной форме были получены при решении задачи 6. Топологические уравнения в виде системы уравнений по законам Кирхгофа, полученные с использованием матрицы контуров и сечений, построенной в задаче №6, имеют вид:

Для получения окончательной ММС используют компонентные уравнения. При их преобразовании стремятся получить уравнения, выражающие емкостные токи I>С> и индуктивные напряжения U>L> через переменные состояния. Далее, заменяя I>C> и U>L> производными переменных состояния, получают окончательную ММС.
Запишем компонентные уравнения (уравнения сопротивления, емкости и индуктивности) в общем виде:



В заданной схеме нет индуктивных ветвей, поэтому уравнение индуктивности нам не понадобится.
В левых частях уравнений второй системы необходимо заменить I>Cj> на С>j>dU>Cj>/dt, а в правые части вместо I>Ri> подставить величины U>Ri>, выраженные из уравнений первой системы путем деления на R>i>. Окончательная форма ММС по методу переменных состояния имеет вид:

Таким образом, с использованием метода переменных состояния получена окончательная полная ММС заданной схемы, объединяющая в себе компонентные и топологические уравнения схемы.



 0
0 1
1 0
0 0
0