Алгоритмы поиска подстроки в строке (работа 2)

Введение

Цель курсовой работы: Изучить и проанализировать алгоритмы поиска подстроки в строке, и рассмотреть ряд практических задач на данную тематику.

Задачи курсовой работы: изучить задачи связанные с проблемой поиска подстроки в строке, дать основные определения; рассмотреть применение различных алгоритмов поиска подстроки в строке на практике; написать программный код, реализующий один из алгоритмов поиска подстроки в строке.

Тема моей курсовой работы является актуальной и на сегодняшний день, те, кому приходиться часто работать с текстовыми редакторами, знают цену функции нахождения нужных слов в тексте, существенно облегчающей редактирование документов и поиск нужной информации. Действительно, современные программы обработки текста приучили нас к такой удобной возможности, как поиск и замена фрагментов, и если разрабатывать подобную программу, пользователь вправе ожидать, что в его распоряжении будут соответствующие команды.

Конечно, сейчас функции поиска инкапсулированы во многие языки программирования высокого уровня, поэтому чтобы найти строчку в небольшом тексте используется встроенная функция. Но если такого рода поиск является ключевой задачей программы, знать принципы организации функций поиска будет полезным. В готовых подпрограммах далеко не всегда все написано лучшим образом. Во-первых, в стандартных функциях не всегда используются самые эффективные алгоритмы, а во-вторых, вполне возможно, что понадобится изменить стандартное поведение этих функций (например, предусмотреть возможность поиска по шаблону). Наконец, область применения функции поиска не ограничивается одними лишь текстовыми редакторами. Следует отметить использование алгоритмов поиска при индексации страниц поисковым роботом, где актуальность информации напрямую зависит от скорости нахождения ключевых слов в тексте html. Работа простейшего спам–фильтра, заключается в нахождении в тексте письма фраз таких, как «Миллион за час» или «Раскрутка сайта». Это всё говорит об актуальности проблемы поиска.

Работа содержит три основных главы. В первой будут рассмотрены алгоритмы, их теоретическое обоснование, алгоритмическая модель, будет проведена попытка их классификации. Во второй главе будет рассмотрена практическая часть курсовой работы. Реализован программный код поиска подстроки в строке при помощи алгоритма последовательного поиска. В третьей главе работы будут приведены данные о практическом применении алгоритмов. В заключении будет сделан вывод о наиболее эффективном (с временной точки зрения) алгоритме.

Глава 1. Теоретические сведения об алгоритмах поиска подстроки в строке

1.1. Основные понятия

Определение. Строка (слово) - это последовательность знаков (называемых буквами) из некоторого конечного множества, называемого алфавитом.

Определение . Длина строки – количество знаков в строке.

Слова обозначаются буквами латинского алфавита, напр. X=x[1]x[2]…x[n] – слово длинной n, где x[i] (i-ая буква слова) принадлежит алфавиту. Lentgh(X)==n – обозначение длины строки.

Определение . Слово не содержащее ни одной буквы называется пустым.

Пустое слово обычно обозначается буквой L. Length(L)=0.

Определение . Слово X называется префиксом слова Y, если есть такое слово Z, что Y=XZ. Причем само слово является префиксом для самого себя (т.к. найдется нулевое слово L, что X=LX.

Пример: слово ab является префиксом слова abcfa.

Определение . Слово X называется суффиксом слова Y, если есть такое слово Z, что Y=ZX. Аналогично, слово является суффиксом самого себя.

Пример: слово bfg является суффиксом слова vsenfbfg.

Определение . Слово X называется подстрокой строки Y, если найдутся такие строки Z_>1> и Z_>2>, что Y=Z_>1>XZ_>2>. При этом Z_>1> называется левым, а Z_>2> - правым крылом подстроки. Подстрокой может быть и само слово. Иногда при этом слово X называют вхождением в слово Y. Среди всех вхождений слова X в слово Y, вхождение с наименьшей длиной своего левого крыла называют первым или главным вхождением. Для обозначения вхождения используют обозначение XY.

Пример: слова hrf и fhr является подстроками слова abhrfhr, gfsfdgfro.

В программировании понятие сложности алгоритма связано с использованием ресурсов компьютера: насколько много процессорного

времени требует программа для своего выполнения, насколько много при этом расходуется память машины? Учет памяти обычно ведется по объему данных и не принимается во внимание память, расходуемая для записи команд программы. Время рассчитывается в относительных единицах так, чтобы эта оценка, по возможности, была одинаковой для машин с разной тактовой частотой.

Существует две характеристики сложности алгоритмов - временная и емкостная.

Временная сложность будет подсчитываться в исполняемых командах: количество арифметических операций, количество сравнений, пересылок (в зависимости от алгоритма). Емкостная сложность будет определяться количеством переменных, элементов массивов, элементов записей или просто количеством байт.

Эффективность алгоритма также будет оцениваться с помощью подсчета времени выполнения алгоритмом конкретно поставленной задачи, т.е. с помощью эксперимента, подробнее об этом в главе 2 данной работы.

1.2. Алгоритм последовательного (прямого) поиска

Самый очевидный алгоритм. Обозначеное S - слово, в котором ищется образец X. Пусть m и n - длины слов S и X соответственно. Можно сравнить со словом X все подслова S, которые начинаются с позиций 1,2,...,m-n+1 в слове S; в случае равенства выводится соответствующая позиция. Реализация этого алгоритма представлена в приложении 1.

Это не эффективный алгоритм т.к. максимальное, количество сравнений будет равно O((m-n+1)*n+1), хотя большинство из них на самом деле лишние. Оценим скорость работы этого программного кода. В ней присутствуют два цикла (один вложенный), время работы внешнего большей степенью зависит от n, а внутренний в худшем случае делает m операций. Таким образом, время работы всего алгоритма есть O((n-m+1)m). Для маленьких строк поиск проработает быстро, но если в каком-то многомегабайтном файле будет искаться последовательность длинной 100 Кб, то придется ждать ну очень долго. Впрочем многим хватает и этого. Например, найдя строку aabc и обнаружив несоответствие в четвертом символе (совпало только aab), алгоритм будет продолжать сравнивать строку, начиная со следующего символа, хотя это однозначно не приведет к результату.

1.3. Алгоритм Рабина

Алгоритм Рабина представляет собой модификацию линейного алгоритма.

В слове A, длина которого равна m, ищется образец X длины n. Вырежем "окошечко" размером n оно двигается по входному слову. Совпадает ли слово в "окошечке" с заданным образцом? Фиксируется некоторая числовая функция на словах длины n, тогда задача сводится к сравнению чисел, что, несомненно, быстрее. Если значения этой функции на слове в "окошечке" и на образце различны, то совпадения нет. Только если значения одинаковы, необходимо проверять последовательно совпадение по буквам.

Этот алгоритм выполняет линейный проход по строке (n шагов) и линейный проход по всему тексту (m шагов), стало быть, общее время работы есть O(n+m). При этом не учитывается временная сложность вычисления хеш-функции, так как, суть алгоритма в том и заключается, чтобы данная функция была настолько легко вычисляемой, что ее работа не влияла на общую работу алгоритма. Тогда, время работы алгоритма линейно зависит от размера строки и текста, стало быть программа работает быстро. Ведь вместо того, чтобы проверять каждую позицию на предмет соответствия с образцом, можно проверять только те, которые «напоминают» образец. Итак, для того, чтобы легко устанавливать явное несоответствие, будет использоваться функция, которая должна:

1. Легко вычисляться.

2. Как можно лучше различать несовпадающие строки.

3. hash( y[ i+1 , i+m ] ) должна легко вычисляться по hash( y[ i , i+m-1 ].

Во время поиска х будет сравниваться hash( x ) с hash( y[ i, i+m-1 ] ) для i от 0 до n-m включительно. Если обнаруживается совпадение, то проверяется посимвольно. Реализация этого алгоритма представлена в приложении 2.

Пример (удобной для вычисления функции). Заменяются все буквы в слове и образце их номерами, представляющими собой целые числа. Тогда удобной функцией является сумма цифр. (При сдвиге "окошечка" нужно добавить новое число и вычесть "пропавшее".)

Однако, проблема в том, что искомая строка может быть длинной, строк в тексте тоже хватает. А так как каждой строке нужно сопоставить уникальное число, то и чисел должно быть много, а стало быть, числа будут большими (порядка D*n, где D - количество различных символов), и работать с ними будет так же неудобно. Но какой интерес работать только с короткими строками и цифрами? Выше рассмотренный алгоритм можно улучшить.

Пример (семейства удобных функций). Выбирается некоторое число p (желательно простое) и некоторый вычет x по модулю p. Каждое слово длины n будет рассматриваться как последовательность целых чисел (заменив буквы их кодами). Эти числа будут рассматриваться как коэффициенты многочлена степени n-1 и вычисляется значение этого многочлена по модулю p в точке x. Это и будет одна из функций семейства (для каждой пары p и x получается своя функция). Сдвиг "окошечка" на 1 соответствует вычитанию старшего члена, умножению на x и добавлению свободного члена. Следующее соображение говорит в пользу того, что совпадения не слишком вероятны. Пусть число p фиксировано и к тому же оно является простым, а X и Y - два различных слова длины n. Тогда им соответствуют различные многочлены (мы предполагаем, что коды всех букв различны - это возможно при p, большем числа букв алфавита). Совпадение значений функции означает, что в точке x эти два различных многочлена совпадают, т.е. их разность обращается в 0. Разность есть многочлен степени n-1 и имеет не более n-1 корней. Таким образом, если n много меньше p, то случайному значению x мало шансов попасть в "неудачную" точку.

Строго говоря, время работы всего алгоритма в целом, есть O(m+n+mn/P), mn/P достаточно невелико, так что сложность работы почти линейная. Понятно, что простое число следует выбирать большим, чем больше это число, тем быстрее будет работать программа.

Алгоритм Рабина и алгоритм последовательного поиска являются алгоритмами с наименьшими трудозатратами, поэтому они годятся для использования при решении некоторого класса задач. Однако эти алгоритмы не являются наиболее оптимальными (хотя бы потому, что иногда выполняют явно бесполезную работу, о чем было сказано выше), поэтому будет рассматриваться следующий класс алгоритмов. Эти алгоритмы появились в результате тщательного исследования алгоритма последовательного поиска. Исследователи хотели найти способы более полно использовать информацию, полученную во время сканирования (алгоритм прямого поиска ее просто выбрасывает).

1.4.Алгоритм Кнута - Морриса - Пратта (КМП)

Метод использует предобработку искомой строки, а именно: на ее основе создается так называемая префикс-функция. Суть этой функции в нахождении для каждой подстроки S[1..i] строки S наибольшей подстроки S[1..j] (j<i), присутствующей одновременно и в начале, и в конце подстроки (как префикс и как суффикс). Например, для подстроки abcHelloabc такой подстрокой является abc (одновременно и префиксом, и суффиксом). Смысл префикс-функции в том, что можно отбросить заведомо неверные варианты, т.е. если при поиске совпала подстрока abcHelloabc (следующий символ не совпал), то имеет смысл продолжать проверку продолжить поиск уже с четвертого символа (первые три и так совпадут). Вначале рассматриваются некоторые вспомогательные утверждения. Для произвольного слова X рассматриваются все его начала, одновременно являющиеся его концами, и выбираются из них самое длинное (не считая, конечно, самого слова X). Оно обозначается n(X). Такая функция носит название префикс – функции [13].

Примеры.

n(aba)=a, n(n(aba))=n(a)=L;

n(abab)=ab, n(n(abab))=n(ab)=L;

n(ababa)=aba, n(n(ababa))=n(aba)=a, n(n(n(ababa)))=n(a)=L; n(abc)=L.

Справедливо следующее предложение:

(1) Последовательность слов n(X),n(n(X)),n(n(n(X))),... "обрывается" (на пустом слове L).

(2) Все слова n(X),n(n(X)),n(n(n(X))),...,L являются началами слова X.

(3) Любое слово, одновременно являющееся началом и концом слова X (кроме самого X), входит в последовательность n(X),n(n(X)),....,L.

Метод КМП использует предобработку искомой строки, а именно: на ее основе создается префикс-функция. При этом используется следующая идея: если префикс (он же суффикс) строки длинной i длиннее одного символа, то он одновременно и префикс подстроки длинной i-1. Таким образом, проверяется префикс предыдущей подстроки, если же тот не подходит, то префикс ее префикса, и т.д. Действуя так, находится наибольший искомый префикс. (см. приложение 3).

Следующий вопрос, на который стоит ответить: почему время работы процедуры линейно, ведь в ней присутствует вложенный цикл? Ну, во-первых, присвоение префикс-функции происходит четко m раз, остальное время меняется переменная k. Так как в цикле while она уменьшается (P[k]<k), но не становится меньше 0, то уменьшаться она может не чаще, чем возрастать. Переменная k возрастает на 1 не более m раз. Значит, переменная k меняется всего не более 2m раз. Выходит, что время работы всей процедуры есть O(m).

Алгоритм последовательного поиска и алгоритм КМП помимо нахождения самих строк считают, сколько символов совпало в процессе работы. Реализация этого алгоритма представлена в приложении 4.

1.5. Алгоритм Бойера – Мура

Алгоритм Бойера-Мура, разработанный двумя учеными – Бойером и Муром, считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке.

Простейший вариант алгоритма Бойера-Мура состоит из следующих шагов. На первом шаге строится таблица смещений для искомого образца. Процесс построения таблицы будет описан ниже. Далее совмещается начало строки и образца и начинается проверка с последнего символа образца. Если последний символ образца и соответствующий ему при наложении символ строки не совпадают, образец сдвигается относительно строки на величину, полученную из таблицы смещений, и снова проводится сравнение, начиная с последнего символа образца. Если же символы совпадают, производится сравнение предпоследнего символа образца и т. д. Если все символы образца совпали с наложенными символами строки, значит нашлась подстрока и поиск окончен. Если же какой-то (не последний) символ образца не совпадает с соответствующим символом строки, сдвигается образец на один символ вправо и снова начинается проверку с последнего символа. Весь алгоритм выполняется до тех пор, пока либо не будет найдено вхождение искомого образца, либо не будет достигнут конец строки.

Величина сдвига в случае несовпадения последнего символа вычисляется исходя из следующих соображений: сдвиг образца должен быть минимальным, таким, чтобы не пропустить вхождение образца в строке. Если данный символ строки встречается в образце, смещается образец таким образом, чтобы символ строки совпал с самым правым вхождением этого символа в образце. Если же образец вообще не содержит этого символа, сдвигается образец на величину, равную его длине, так что первый символ образца накладывается на следующий за проверявшимся символ строки.

Величина смещения для каждого символа образца зависит только от порядка символов в образце, поэтому смещения удобно вычислить заранее и хранить в виде одномерного массива, где каждому символу алфавита соответствует смещение относительно последнего символа образца.

Пример. Пусть есть алфавит из пяти символов: a, b, c, d, e и надо найти вхождение образца “abbad” в строке “abeccacbadbabbad”. Следующие схемы иллюстрируют все этапы выполнения алгоритма. Таблица смещений будет выглядеть так.

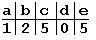
Начало поиска.

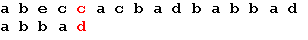
Последний символ образца не совпадает с наложенным символом строки. Сдвигается образец вправо на 5 позиций:

Три символа образца совпали, а четвертый – нет. Сдвигается образец вправо на одну позицию:

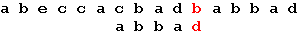
Последний символ снова не совпадает с символом строки. В соответствии с таблицей смещений сдвигается образец на 2 позиции:

Еще раз сдвигается образец на 2 позиции:

Теперь, в соответствии с таблицей, сдвигается образец на одну позицию, и получается искомое вхождение образца:

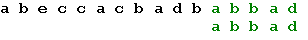
Прежде всего следует определить тип данных «таблица смещений». Для кодовой таблицы, состоящей из 256 символов, определение этого типа будет выглядеть так:

Type

TBMTable = Array [0..255] of Integer;

Реализация процедуры, вычисляющая таблицу смещений для образца p, представлена в приложении 5.

Теперь пишется функция, осуществляющая поиск (см. Приложение 6).

Параметр StartPos позволяет указать позицию в строке s, с которой следует начинать поиск. Это может быть полезно в том случае, если надо найти все вхождения p в s. Для поиска с самого начала строки следует задать StartPos равным 1. Если результат поиска не равен нулю, то для того, чтобы найти следующее вхождение p в s, нужно задать StartPos равным значению «предыдущий результат плюс длина образца».

Глава 2. Практическая часть.

Дан некоторый текст, в котором следует найти фрагмент этого текста.

Данную задачу можно интерпретировать как поиск подстроки в строке.

Эту задачу я реализовал при помощи алгоритма последовательного (прямого) поиска. Программный код задачи реализовал на языке программирования Turbo Pascal 7.1 и он представлен в приложении 7.

Описание работы программы.

После запуска программа запрашивает ввод текста:

Например, введём следующий текст: ”алгоритм рабина представляет собой модификацию линейного алгоритма.”

Далее программа запрашивает ввод строки(подстроки) для поиска:

Например, вводим фрагмент текста: ”алгоритм”

После ввода, программа ищет строку в тексте, если строка существует то программа выводит текст на экран, выделяет строку красным цветом и выдает с какого символа начинается строка:

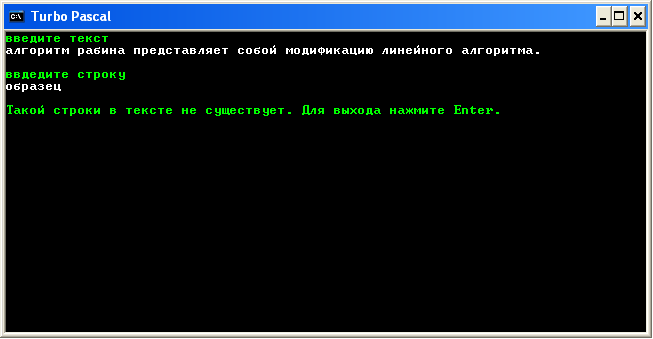
Если фрагмента нет в тексте, то программа выдаст сообщение о том, что данной строки в тексте не существует:

Глава 3. Анализ алгоритмов

В курсовой работе я рассмотрел несколько алгоритмов. Была проведена оценка их временной и емкостной сложности. Экспериментальный анализ состоял в измерении времени, за которое алгоритм выполняет конкретно поставленную задачу.

Задача: Имеется несколько текстовых файлов, содержащих 10000 записей вида:

строка

подстрока (имеющаяся в данной строке)

место вхождения

длина подстроки,

причем с разными максимальными длинами строк и подстрок.

Алфавит кириллицы содержит 32 буквы, поэтому длина строки будет не более 10, 100, 250 символов.

Проводится поиск подстрок в строках для каждого из алгоритмов и измеряется время работы программы. При этом будет учитываться следующее:

строки предварительно загружаем в оперативную память (в виде массива), причем время считывания в массив не учитывается. Предобработка (создание таблиц перехода) входит в общее время.

каждый алгоритм запускается 5 раз, время выбирается наименьшее.

Эксперимент проходил на ПК:

Процессор Intel Pentium IV 2,66Ггц

1024 Мб ОЗУ

Компилятор Turbo Pascal 7.1

Фрагмент кода тестируемой программы приводится в Приложении 8.

Такой замер времени даст приблизительные результаты, так как напрямую зависит от характеристик и загрузки процессора. Поэтому во время проведения эксперимента, отключались все сторонние и фоновые приложения, которые не влияют на работу программы. При запуске одной и той же задачи можно получить разное время, поэтому совершается несколько запусков, из которых выбирается наилучший результат.

Эксперимент проводился для четырех алгоритмов – представителей классов алгоритмов. Так как все алгоритмы ставились в одинаковые условия, то можно провести их сравнительный анализ. Заметим, что данный анализ применим только для данных параметров поиска, и при иных условиях может отличаться.

Таблица 1

езультаты эксперимента занесены в таблицу 1.

Алгоритм	Время выполнения (мс)
Длина ≤10	Длина ≤100	Длина ≤250
Послед. Поиск	15	93	234
Алгоритм Рабина	15	63	93
КМП	5	30	50
БМ	31	31	32

Из таблицы видно, что алгоритм Бойера – Мура справился с экспериментальной задачей быстрее остальных. Следует, однако, заметить, что его эффективность растет лишь с увеличением длины строки и, соответственно, длины образца. Так при длине строки меньшей или равной 10 символов, он показал себя хуже, чем последовательный поиск. Аналогичные результаты показывает и алгоритм КМП, как для коротких, так и для длинных слов. Его можно использовать как универсальный, когда неизвестны длины строки и образца.

Алгоритм Рабина, при его схожести с последовательным работает быстрее, а его простота и малые трудозатраты на реализацию, делают его привлекательным для использования в неспециальных программах.

Наихудший результат показал алгоритм последовательного поиска. Как предполагалось лишь при небольшом увеличении длины строки, он работает существенно медленнее остальных алгоритмов.

Заключение

В процессе выполнения курсовой работы были рассмотрены различные алгоритмы поиска подстроки в строке и проведен их сравнительный анализ, результаты которого представлены в таблице 2 (см. приложение 9).

Изучив полученные результаты легко можно сделать вывод, что алгоритм Бойера – Мура является ведущим по всем параметрам. Но, как показывает эксперимент, алгоритм Кнута – Мориса - Пратта, превосходит алгоритм БМ на небольших длинах образца. Поэтому нельзя сделать вывод, что какой-то из алгоритмов является самым оптимальным. Каждый алгоритм эффективно работает в определенных классах задач, об этом еще говорят различные узконаправленные улучшения каждого из алгоритмов. Таким образом, тип алгоритмов поиска подстроки в строке следует выбирать только после точной постановки задачи, определение её целей и функциональности, которая она должна реализовать.

Только после этого этапа необходимо переходить к реализации программного кода.

В связи с глобализацией информации в сети internet был разработан интеллектуальный поиск. Который позволяет найти документ по смыслу содержащейся в нем информации, то есть документы по заданной теме. В системе реализован алгоритм с использованием компьютерной обработки документа. Согласно гипотезе Ципфа смысл документа зависит от частоты терминов, встречающихся в документе. Однако гораздо важнее не сама частота слова, а то, насколько часто в текущем документе это слово встречается относительно других слов.

Список используемой литературы:

1) Альсведе Р., Вегенер И. "Задачи поиска" , 1982г, Издательство "Мир"

2). Ахо, Альфред Структура данных и алгоритмы [Текст]. – М.: Издательский дом «Вильямс», 2000. - 384 с.

3). Белоусов А. Дискретная математика [Текст]. – М.: Издательство МГТУ им. Н.Э. Баумана, 2001. – 744 с.

4). Брайан, К. Практика программирования [Текст].- СПб:. Невский диалект, 2001. - 381 с.

5). Вирт, Н. Алгоритмы и структуры данных [Текст].– М:. Мир, 1989. – 360 с.

6) Кнут, Д. Искусство программирования на ЭВМ [Текст]: Том 3. – М:. Мир, 1978. – 356 с.

7). Кормен, Т. Алгоритмы: построение и анализ [Текст]/ Т. Кормен, Ч. Лейзерсон, Р. Ривест - М.: МЦНМО, 2002. М.: МЦНМО, 2002.

8). Успенский В. Теория алгоритмов: основные открытия и приложения [Текст]. – М.: Наука, 1987. – 288 с.

9). Шень, А. Программирование: теоремы и задачи [Текст]. – М.: Московский центр непрерывного математического образования, 1995.

Электронные источники.

1) http://www.ipkro.isu.ru/informat/methods/findsort/

2) http://www.delphikingdom.com/asp/viewitem.asp?catalogid=65

3) http://revolution./programming/00013926_0.html

4) http://ric.uni-altai.ru/fundamental/pascal1/lab15/l15-teor.htm

5) http://www.rsdn.ru/article/alg/textsearch.xml

Приложение 1

Реализация алгоритма последовательного поиска

Function Search (S: String; X: String; var Place: Byte): Boolean;

{ Функция возвращает результат поиска в слове S }

{ подслова X. Place - место первого вхождения }

var Res: Boolean; i : Integer;

Begin

Res:=FALSE;

i:=1;

While (i<=Length(S)-Length(X)+1) And Not(Res) do

If Copy(S,i,Length(X))=X then

begin

Res:=TRUE;

Place:=i

end

else i:=i+1;

Search:=Res

End;

Приложение 2

Реализация алгоритма Рабина

Function Search (S: String; X: String; var Place: Byte): Boolean;

{ Функция возвращает результат поиска в слове S }

{ подслова X. Place - место первого вхождения }

Var Res: Boolean; i: Byte; h,NowH,LenX:Integer; HowMany:Integer;

Begin

Res:=FALSE;

i:=1;

h:=Hash(x); {Вычисление хеш-функции для искомого слова}

NowH:=Hash(Copy(S,1,Length(x)));

HowMany:=Length(S)-Length(X)+1;

LenX:=Length(X);

While (i<=HowMany) And Not(Res) do

If (h=NowH) and (Copy(S,i,Length(X))=X) then

Begin

Res:=TRUE;

Place:=i

End

else

Begin

i:=i+1;

NextHash(s,i,NowH,LenX); {Вычисление следующего значения хеш-функции}

End;

Search:=Res

End;

Приложение 3

Алгоритм Кнута-Морриса-Пратта

Нахождение наибольшего искомого префикса.

Procedure PrefFunc(P:String; Var Fl:TMas);

Var n,i,j:Integer;

Begin

n:=Length(P);

Fl[1]:=0;

For i:=2 To n Do

Begin

j:=Fl[i-1];

While (j<>0) And (P[j]<>P[i-1]) Do j:= Fl[j];

Fl[i]:=j+1;

End;

Приложение 4

Реализация алгоритма Кнута-Морриса-Пратта

Function KMPSearch(S,P:String):Integer;

{ Алгоpитм Кнута-Моpиса-Пpатта, устанавливающий }

{ вхождение непустой стpоки P в стpоку S }

Var Fl:TMas;

i,j,n,m:Integer;

Begin

n:=Length(S);

m:=Length(P);

PrefFunc(P,Fl);

j:=1;

For i:=1 To n Do

begin

While (j<>0) And (P[j]<>S[i]) do j:=Fl[j];

If j=m Then Break;

j:=j+1

end;

If (j=m) then Result:=i-j+1 Else Result:=0;

End;

Приложение 5

Алгоритм Бойера-Мура

Реализация процедуры, вычисляющая таблицу смещений для образца p.

Procedure MakeMBTable( var Bmt : TBMTable; Const p : string);

Var i : Integer;

Begin

For i := 0 to 255 do Bmt[i] := Length(p);

For i := Length(p) Downto 1 Do

If Bmt[Byte(p[i])] = Length(p) Then

Bmt[Byte(p[i])] := Length(p) – i;

End;

Приложение 6

Алгоритм Бойера-Мура

Функция, осуществляющая поиск.

function bmsearch( startpos : integer; const s, p : string;

const bmt : tbmtable : integer;)

var

pos, lp, i : integer;

begin

lp := length(p);

pos := startpos + lp –1;

while pos < length(s) do

if p[lp] <> s[pos] then pos := pos + bmt[s[pos]]

else for i := lp - 1 downto 1 do

if p[i] <> s[pos – lp + i] then

begin

inc(pos);

break;

end

else if i = 1 then

begin

result := pos – lp + 1;

exit;

end;

result := 0;

end;

Приложение 7

Реализация программного кода

program Poisk;

uses crt;

var

t,s,tex,t2:string; p,i,d1,d2,d3,x:integer; text:array [1..100] of string;

begin

clrscr; { }

textcolor(10);

writeln('Введите текст');

textcolor(15);

readln(t);

writeln;

textcolor(10);

writeln(‘Введите строку’);

textcolor(15);

readln(s);

writeln;

d3:=0;

repeat

textcolor(10);

p:=pos(s,t);

if p=0 then

if x>1 then

begin

writeln;

writeln('Конец поиска. Для выхода нажмите Enter.')

end

else

writeln('Такой строки в тексте не существует. Для выхода нажмите Enter.')

else

begin

tex:=tex+text[x];

d3:=length(tex);

writeln;

writeln('Образец входит в текст с ',p+d3,'-ого символа ');

writeln;

d1:=length(s);

textcolor(15);

write(tex);

for i:=1 to p-1 do

write(t[i]);

for i:=1 to d1 do

begin

textcolor(12);

write(s[i]);

end;

d2:=length(t);

for i:= d1+p to d2 do

begin

textcolor(15);

write(t[i]);

end;

readln;

x:=x+1;

text[x]:=copy(t,1,p+d1-1);

delete(t,1,p+d1-1);

end;

until p=0;

readln;

end.

Приложение 8

Фрагмент кода тестируемой программы

LoadFromFile('C:\String_250.txt');

{Происходит загрузка в массив}

Tick:=GetTickCount;

{Запоминаем текцщее значение переменной Tick}

Poisk;

{Процедура в которой происходит поиск 10000 раз}

Tick:=GetTickCount-Tick;

{Получаем разницу – время в миллисекундах}

WriteLn('Za vremja ',Tick, ' ms');

Приложение 9

Общие результаты с анализов рассмотренных алгоритмов

Таблица 2

Примечания	Алгоритмы, основанные на алгоритме последовательного поиска	Малые трудозатраты на программу, малая эффективность	Алгоритм Кнута-Морриса-Пратта	Универсальный алгоритм, если неизвестна длина образца	Алгоритм Бойера-Мура	Алгоритмы этой группы наиболее эффективны в обычных ситуациях. Быстродействие повышается при увеличении образца или алфавита.
Время работы (мс) при длине строки ≤250	234	93	31	32
Затраты памяти	нет	нет	O(m)	O(m+s)
Худшее время поиска	O((m-n+1)*n+1)	O((m-n+1)*n+1)	O(n+m)	O(n*m)
Среднее время поиска	O((m-n+1)*n+1)/2	O(n+m)	O(n+m)	O(n+m)
Время на пред. обработку	нет	нет	O(m)	O(m+s)
Алгоритм	Алгоритм прямого поиска	Алгоритм Рабина	КМП	БМ

Алгоритмы поиска подстроки в строке (работа 2)

Введение

Глава 1. Теоретические сведения об алгоритмах поиска подстроки в строке

1.1. Основные понятия

1.2. Алгоритм последовательного (прямого) поиска

1.3. Алгоритм Рабина

1.4.Алгоритм Кнута - Морриса - Пратта (КМП)

1.5. Алгоритм Бойера – Мура

Глава 2. Практическая часть.

Дан некоторый текст, в котором следует найти фрагмент этого текста.

Глава 3. Анализ алгоритмов

Список используемой литературы:

Приложение 3

Алгоритм Кнута-Морриса-Пратта

Реализация алгоритма Кнута-Морриса-Пратта

Алгоритм Бойера-Мура

Реализация процедуры, вычисляющая таблицу смещений для образца p.

Алгоритм Бойера-Мура

Реализация программного кода

d2:=length(t); for i:= d1+p to d2 do begin textcolor(15); write(t[i]); end; readln; x:=x+1; text[x]:=copy(t,1,p+d1-1); delete(t,1,p+d1-1); end; until p=0; readln; end.

Приложение 8

d2:=length(t);

for i:= d1+p to d2 do

begin

textcolor(15);

write(t[i]);

end;

readln;

x:=x+1;

text[x]:=copy(t,1,p+d1-1);

delete(t,1,p+d1-1);

end;

until p=0;

readln;

end.