Разработка математической модели и ПО для задач составления расписания (работа 2)

То, что вы здесь прочтете в большинстве своем чушь. Тем не менее в некоторых местах по моему мнению присутствуют здравые мысли, к сожалению таких мест получилось не так уж и много  Не вздумайте сдавать это там, где проблемами теории расписаний занимаются серьезно. Тем, кто захочет написать что-либо лучше этого, настоятельно рекомендую почитать книгу Ху. Т. “Целочисленное программирование и потоки в сетях ”, кроме этого пожалуй стоит почитать лекции ВМиК по теории оптимизации Н.М. Новиковой (где это в инете лежит, не помню). Сейчас активно занимаюсь проблемами теории оптимизации, так что кому тоже интересна эта тема, то всегда рад пообщаться. Пишите leb@metacom.ru.

Содержание

Введение 8

1. ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОЙ ОБЛАСТИ 10

1.1. Формулировка задачи составления расписания 10

1.1.1. Общая формулировка задачи составления расписаний 10

1.1.2. Формулировка задачи составления раписания в применении к расписанию учебных занятий. 11

1.2. Анализ существующего ПО 12

1.3. Постановка задачи. 15

2. Разработка математической модели и практическая реализация системы автоматического составления расписания 16

2.1. Математическая модель расписания в вузе 16

2.1.1. Обозначения 16

2.1.2. Переменные 18

2.1.3. Ограничения 18

2.1.4. Целевая функция 21

2.2. МЕТОДЫ РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ 22

2.2.1. ПОЛНОСТЬЮ ЦЕЛОЧИСЛЕННЫЙ АЛГОРИТМ 23

2.2.2 Прямой алгоритм целочисленного программирования 28

2.2.3. ТЕХНИКА ПОЛУЧЕНИЯ НАЧАЛЬНОГО ДОПУСТИМОГО БАЗИСА 32

2.3. ОСОБЕННОСТИ ПРАКТИЧЕСКОЙ РЕАЛИЗАЦИИ СИСТЕМЫ 36

2.3.1. ВЫБОР МОДЕЛИ 36

2.3.2. ОПИСАНИЕ ВХОДНОЙ ИНФОРМАЦИИ 39

Наименование реквизитов 40

Характеристика реквизитов 40

Тип 40

Макс. длина 40

Точность 40

2.3.3. РАЗРАБОТКА ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ЗАДАЧИ 41

2.3.4. ОСОБЕННОСТИ ФОРМИРОВАНИЯ ОГРАНИЧЕНИЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ СОСТАВЛЕНИЯ РАСПИСАНИЯ 43

Рис.2. Линейно пересекающиеся множества 44

A Xa B Xb C Xc D Xd E 44

Рис.3. Произвольно пересекающиеся множества 45

2.4. Результаты работы программы 45

Рис.3. Форма занесения исходных данных 46

2.5. Анализ полученных результатов 49

Выводы 51

В ходе работы была построена математическая модель расписания в вузе для случая вечерней формы обучения без переходов между корпусами, выбраны методы решения поставленной задачи и разработана модель хранения исходных данных задачи. Модель хранения исходных данных, алгоритм математической формализации модели и методы решения были реализованы в виде программных модулей. Скорость работы алгоритмов была протестирована на разнородных наборах исходных данных, в результате чего были определены возможности и области применения алгоритмов. 51

ЛИТЕРАТУРА 52

Приложение 1. Возможности программных продуктов систем составления расписаний. 53

Приложение 2. Листинг программного модуля методов решения задачи автоматического составления расписания 62

Введение

Качество подготовки специалистов в вузах и особенно эффективность использования научно-педагогического потенциала зависят в определенной степени от уровня организации учебного процесса.

Одна из основных составляющих этого процесса - расписание занятий - регламентирует трудовой ритм, влияет на творческую отдачу преподавателей, поэтому его можно рассматривать как фактор оптимизации использования ограниченных трудовых ресурсов - преподавательского состава. Технологию же разработки расписания следует воспринимать не только как трудоемкий технический процесс, объект механизации и автоматизации с использованием ЭВМ, но и как акцию оптимального управления. Таким образом, это - проблема разработки оптимальных расписаний занятий в вузах с очевидным экономическим эффектом. Поскольку интересы участников учебного процесса многообразны, задача составления расписания - многокритериальная.

Задачу составления расписания не стоит рассматривать только как некую программу, реализующую функцию механического распределения занятий в начале семестра, на которой ее (программы) использование и заканчивается. Экономический эффект от более эффективного использования трудовых ресурсов может быть достигнут только в результате кропотливой работы по управлению этими трудовыми ресурсами. Расписание здесь является лишь инструментом такого управления, и для наиболее полного его использования необходимо, чтобы программа сочетала в себе не только средства для составления оптимального расписания, но и средства для поддержания его оптимальности в случае изменения некоторых входных данных, которые на момент составления расписания считались постоянными. Кроме этого оптимальное управление такой сложной системой невозможно без накопления некоей статистической информации о процессах, происходящих в системе. Потому сама задача составления оптимального расписания является лишь частью сложной системы управления учебным процессом.

Многокритериальность этой задачи и сложность объекта, для которого сроится математическая модель, обуславливает необходимость серьезного математического исследования объекта для увеличения функциональных возможностей алгоритмов составления расписаний без значительного усложнения модели и, как следствие, увеличения объемов используемой памяти и времени решения задачи.

1. ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОЙ ОБЛАСТИ

1.1. Формулировка задачи составления расписания

Задача теории расписаний в общей ее постановке считается весьма привлекательной, хотя достижение даже небольшого прогресса на пути к решению связано, как правило, с огромными трудностями. Несмотря на то, что задачами теории расписаний занимались многие весьма квалифицированные специалисты, до сих пор никому не удалось получить сколько-нибудь существенных результатов. Безуспешные попытки получения таких результатов, как правило, не публикуются и это отчасти обуславливает тот факт, что задача продолжает привлекать внимание многих исследователей кажущейся простотой постановки.

1.1.1. Общая формулировка задачи составления расписаний

В наиболее общей формулировке задача составления расписания состоит в следующем. С помощью некоторого множества ресурсов или обслуживающих устройств должна быть выполнена некоторая фиксированная система заданий. Цель заключается в том, чтобы при заданных свойствах заданий и ресурсов и наложенных на них ограничениях найти эффективный алгоритм упорядочивания заданий, оптимизирующих или стремящийся оптимизировать требуемую меру эффективности. В качестве основных мер эффективности изучаются длина расписания и среднее время пребывания заданий в системе. Модели этих задач являются детерминированными в том плане, что вся информация, на основе которой принимаются решения об упорядочивании, известны заранее.

1.1.2. Формулировка задачи составления раписания в применении к расписанию учебных занятий.

Общая теория расписаний предполагает, что все обслуживающие устройства (или процессоры) не могут выполнять в данный момент времени более одного задания, что для расписания учебных занятий не является достаточным, если в качестве процессора при распределении заданий принять учебную аудиторию. Так в некоторых случаях в одной аудитории могут проводиться занятия с более чем одной группой одновременно, например общие лекции для нескольких потоков.

Поэтому при переносе общей теории расписаний на расписание учебных занятий были сделаны следующие допущения:

все процессоры (т.е. в случае учебного расписания - аудитории) имеют вместимость - некоторое число C ≥ 1. Вместимость процессора определяет количество заданий, которые он может одновременно "обрабатывать" в данный момент времени (в отношении неединичности процессоров было бы интересным рассмотреть вариант, когда в качестве процессора выступает не аудитория, а преподаватель, а в качестве задания - поток из одной или более учебных групп, с которыми он работает);

в качестве множества заданий для распределения выступают учебные занятия преподавателя с учебными группами;

модель времени в системе является дискретной; все распределение предполагается периодически повторяющимся на протяжении некоторого временного интервала;

все задания выполняются за одинаковое время, которое принимается за единицу дискретизации временного интервала;

задания имеют принадлежность к объектам, в качестве которых выступают учебные группы и преподаватели.

В итоге, формулировка задачи составления расписания учебных занятий звучит следующим образом: "Для заданного набора учебных аудиторий (в данном случае под учебной аудиторией понимается широкий круг помещений, в которых проводятся учебные занятия (от компьютерной аудитории до спортивного зала)) и заданного набора временных интервалов (т.е. по сути, уроков или учебных пар) построить такое распределение учебных занятий для всех объектов (учителя и учебные группы), для которого выбранный критерий оптимальности является наилучшим".

1.2. Анализ существующего ПО

На данный момент времени сектор рынка ПО систем составления расписания занятий представлен большим количеством различных программных продуктов. В таблице 1. представлены лишь некоторые из известных мне.

В силу объективных причин система составления расписания в вузе (имеется в виду крупный государственный вуз) обязательно должна реализовывать ряд основных функций:

- учет пожеланий преподавателей;

- закрепление обязательных аудиторий;

- указание желательных аудиторий;

- учет перехода между корпусами;

- объединение групп в потоки по любой совокупности дисциплин;

- разбиение на подгруппы;

- после составления расписания при необходимости осуществлять замену преподавателей или изменять время проведения занятия.

Кроме этого существуют еще и специфические для каждого вуза требования к функциональным возможностям программного продукта.

Возможности на мой взгляд наиболее популярных на российском рынке программных продуктов приведены в приложении 1.

Из приведенного списка пожалуй только программа "Методист" более или менее соответствует требуемой функциональности программного продукта составления расписания в вузе. Такое положение вещей легко объясняется тем, что школьное образование на сегодняшний день более "стандартизовано" (в смысле организации учебного процесса), чем вузовское. Такая стандартизация ведет к большому объему потенциального рынка продаж программного обеспечения и окупаемости разработки путем продажи большого числа копий продукта по сравнительно низкой цене.

В случае вузов спрос на системы составления расписаний пожалуй даже больше, чем для школ, но дело осложняется большой спецификой организации учебного процесса в каждом отдельно взятом вузе. Создать унифицированное программное обеспечение не представляется возможным, а стоимость создания специализированного продукта у сторонних разработчиков оказывается неоправданно велика. Кроме того, обязательным условием является наличие "устоявшегося" расписания, что предполагает наличие возможности осуществлять замену преподавателей или время проведения занятий. Пока ни один программный продукт не позволяет достаточно просто этого делать (хотя некоторые возможности и есть в "Методисте").

1.3. Постановка задачи.

Целью данной работы было создание такой математической модели расписания в вузе, которая позволяла бы эффективно (в заданные сроки и с заданной степенью оптимальности) решать задачу автоматического составления расписания и обладала бы гибкостью (незначительных изменений в случае изменений входной информации) для адаптации системы в рамках конкретной практической задачи. Для некоторого упрощения задачи на начальном этапе проектирования были сделаны некоторые допущения:

расписание составляется из расчета не более двух пар в день (что вполне подходит для случая вечерней формы обучения);

все пары проводятся в одном корпусе;

задача ставится в терминах линейного программирования;

дальнейшая декомпозиция модели не производится;

все коэффициенты модели и искомые переменные целочисленны;

Поставленная задача должна решаться одним из универсальных (не зависящих от целочисленных значений коэффициентов) методов целочисленного линейного программирования.

2. Разработка математической модели и практическая реализация системы автоматического составления расписания

2.1. Математическая модель расписания в вузе

Построим математическую модель расписания в вузе в терминах линейного программирования. Введем обозначения и определим переменные и ограничения.

2.1.1. Обозначения

ГРУППЫ

В вузе имеется N учебных групп, объединенных в R потоков; r – номер потока, r = 1, ..., R, k_>r> – номер учебной группы в потоке r, k_>r> = 1, …, G_>r>.

Разбиение на групп на потоки осуществляется исходя из принципов:

Использование двумя группами одного и того же аудиторного фонда для своих лекций автоматически предполагает помещение их в 1 поток (предполагается, что все лекции учебных групп проходят вместе).

Группа(или ее часть), как единица учебного процесса в вузе, может входить в разные потоки, но только по одному раз в каждый из них.

Количество потоков не лимитируется.

ЗАНЯТИЯ

Занятия проводятся в рабочие дни в полуторочасовые интервалы, которые будем называть парами.

Обозначим:

t – номер рабочего дня недели, t Є T_>kr>, где

T_>kr>_>>–_>>множество номеров рабочих дней для группы k_>r>;

j – номер пары, j = 1 ,…, J;

J – общее количество пар.

С каждой учебной группой k_>r> потока r в течение недели, согласно учебному плану, проводится W_>kr> занятий, из которых S_>r> лекционных и Q_>kr> практических. Обозначим:

s_>r> – номер дисциплины в списке лекционных занятий для потока r, s_>r> = 1 ,…,S_>r>;

q_>kr> – номер дисциплины в списке практических занятий для группы k_>r>, q_>kr> = 1 ,…, Q_>kr>.

Предполагается, что лекции проводятся у всех групп потока одновременно и в одной аудитории. Тогда, если по какой-то дисциплине в течение недели проводится более одного занятия, эта дисциплина упоминается в списке лекций или практических занятий столько раз, сколько их предусматривается учебным планом для каждого потока или группы.

ПРЕПОДАВАТЕЛИ

Пусть p – номер (имя) преподавателя, p = 1 ,…, P. Введем в рассмотрение булевы значения и :

_>>

1, если на потоке r лекцию s_>r> читает преподаватель p;

0 – в противном случае;

1, если в группе k_>r> практическое занятие q_>kr> проводит преподаватель p;

0 – в противном случае;

Учебная нагрузка преподавателей планируется до составления расписания занятий, вследствие чего на данном этапе величины _>>и _>>можно считать заданными. Для каждого преподавателя p, p = 1 ,…,P, задана также его аудиторная нагрузка - N_>p> часов в неделю.

АУДИТОРНЫЙ ФОНД

Занятия каждого потока могут проводиться только в определенных аудиториях (например, практические занятия по информатике могут проводится только в дисплейных классах). Пусть:

{A_>1>_>r>} – множество аудиторий для лекций на потоке r;

{A_>2>_>r>} – множество аудиторий для практических занятий на потоке r;

A_>1>_>r>_>> – число элементов множества {A_>1>_>r>};

A_>2>_>r>_>> – число элементов множества {A_>2>_>r>};

A_>1>_>r>_>> + A_>2>_>r> – число аудиторий объединения множеств {A_>1>_>r>}∩{A_>2>_>r>}.

Аудиторный фонд определяется до начала составления расписания, поэтому множества можно считать заданными.

2.1.2. Переменные

Задача составления расписания заключается в определении для каждой лекции (на потоке) и практического занятия (в группе) дня недели и пары в этот день с учетом выполнения конструируемых ниже ограничений и минимизации некоторой целевой функции.

Введем следующие искомые булевы переменные:

1, если на потоке r в день t на паре j читается лекция s_>r>;

0 – в противном случае;

1, если на потоке r в день t на паре j у группы k_>r> проводится практическое занятие q_>kr>;

0 – в противном случае;

_>>=

В случае составления расписания для групп вечерней формы обучения J=2. Обобщение модели на все формы обучения см. [1], стр. 669.

2.1.3. Ограничения

Для каждой группы k_>r> должны выполняться все виды аудиторной работы в течение недели:

_>>

(1)

В любой день t на каждой паре j для каждой группы k_>r> может проводиться не более одного занятия:

(2)

Каждые лекция s_>r> и практическое занятие q_>kr> соответственно для всех потоков r и всех групп k_>r> могут проводиться не более одного раза в любой день t:

(3)

Если переменные и увязывают все виды занятий с временем их проведения, то произведения _>>и _>>связывают время проведения с именем преподавателя.

В каждый день t и в каждой паре j преподаватель p может вести не более одного занятия по одной дисциплине на одном потоке или в одной группе:

(4)

Каждый преподаватель p в течение недели должен провести аудиторные занятия:

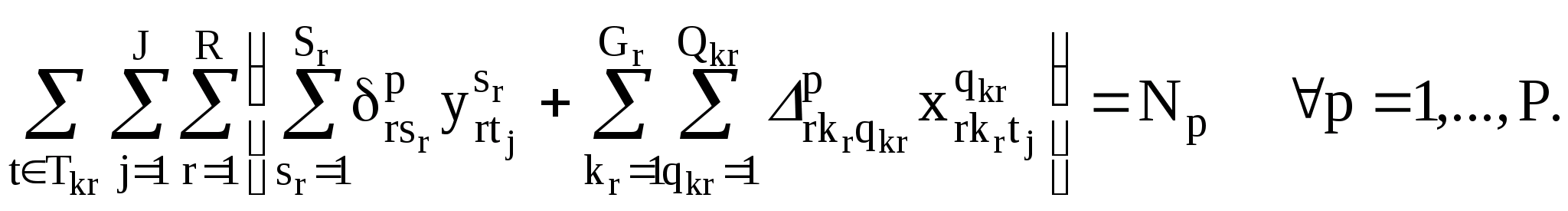
(5)

Наконец, в каждый день на каждой паре число лекций и практических занятий не должно превышать имеющийся в вузе аудиторный фонд:

(6)

(7)

Кроме того, для всех совокупностей пересекающихся множеств {A_>1>_>r>} и {A_>2>_>r>} должны выполняться условия:

(8)

Представленными соотношениями исчерпываются безусловные ограничения, с которыми всегда считаются при составлении расписания. Могут, однако быть и специфические условия, прежде всего проведение отдельных видов работы по “верхней” или по “нижней” неделе (т.е. один академический час в неделю). Не исключены и другие специальные условия, но для упрощения модели они не рассматривались.

2.1.4. Целевая функция

Чтобы полноценно вести научную, учебно-методическую работу, готовиться к занятиям, преподаватель вуза должен иметь свободное время. Это условие недостаточное, но необходимое. Очевидно, что свободным временем он должен располагать не в “рваном” режиме, каковым, например, являются “окна” между занятиями со студентами, а по возможности в полностью свободные рабочие дни. Этому эквивалентна максимизация аудиторной нагрузки преподавателей в те дни, когда они ее имеют (см. (5)). Однако при этом претензии на свободное время у преподавателей неравны, так как у них разный творческий потенциал. Поэтому необходимо ввести весовые коэффициенты, посредством которых должен учитываться соответствующий статус преподавателя – его ученые степени и звание, занимаемая должность, научно-общественная активность и т.п. В некоторых случаях можно на основании экспертных оценок использовать индивидуальные весовые коэффициенты, учитывающие другие факторы.

Итак, выберем критерий качества составления расписания занятий в виде максимизации взвешенного числа свободных от аудиторной работы дней для всех преподавателей, что при условии фиксированной длины рабочей недели эквивалентно максимальному совокупному уплотнению аудиторной нагрузки.

Рассмотрим выражение для величины аудиторной нагрузки в день t преподавателя p:

(9)

Вводятся ограничения вида:

(10)

где M – произвольное положительное достаточно большое число; - искомая булева переменная.

Из (10) вытекает, что если , то = 1, и если , то = 0.

С учетом указанного выше содержательного смысла критерия оптимизации в дополнительных ограничениях (10), а также вводя весовые коэффициенты статуса преподавателя , получаем искомый критерий оптимальности:

(11)

Введенная целевая функция не является единственно возможной. Введение других целевых функций не меняет ограничений математической модели и методов решения задачи, но может существенно повлиять на результаты вычислений.

2.2. МЕТОДЫ РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ

Поставленная в предыдущем пункте задача максимизации линейной целевой функции при заданной системе ограничений является задачей линейного целочисленного булева программирования, поскольку все коэффициенты ограничений целочисленны в силу дискретности исходных данных задачи; кроме этого искомые переменные математической модели могут принимать только два значения. На данный момент времени существует несколько возможных методов решения такого рода задач.

В [3] – [8] описаны методы упорядоченной индексации и модифицированных пометок, основанные на лагранжевой декомпозиции исходной модели на ряд однострочных задач, решаемых соответственно методами упорядочивающей индексации или модифицированных пометок. К сожалению количество операций каждого из методов не допускает полиномиальной оценки; кроме того, размерность таблицы наборов (промежуточных значений) методов резко возрастает при увеличении размерности решаемой задачи, что недопустимо в нашем случае. Возможно, изменение алгоритма декомпозиции под конкретную математическую модель позволит уменьшить размерность таблиц, но пока такого алгоритма не существует.

В связи с этим в качестве методов решения были выбраны описанные в [2] модификации симплекс-метода для случая задачи целочисленного линейного программирования. В общем случае количество операций симплекс-метода не допускает полиномиальной оценки (был даже показан класс задач, для которых количество операций составляет O(eⁿ)), но для случая нашей задачи среднее число операций допускает полиномиальную оценку: O(n³m^1/(ⁿ^-1)) (n – количество переменных; m – количество ограничений).

2.2.1. ПОЛНОСТЬЮ ЦЕЛОЧИСЛЕННЫЙ АЛГОРИТМ

Этот алгоритм назван полностью целочисленным, потому что если исходная таблица состоит из целочисленных элементов, то все таблицы, получающиеся в процессе работы алгоритма, содержат только целочисленные элементы. Подобно двойственному симплекс-методу, алгоритм начинает работать с двойственно допустимой таблицы. Если a_>i>_>0> (i = 1 ,…, n+m; a_>i>_>0> – коэффициенты целевой функции) – неотрицательные целые, то задача решена. Если для какой-нибудь строки a_>i>_>0><0, то составляется новое уравнение и записывается внизу таблицы. После этого используется двойственный симплекс-метод. Все элементы дополнительной строки должны быть целыми числами, а ведущий элемент равен –1. Введенная таким образом ведущая строка сохранит таблицу целочисленной.

Пусть задана задача целочисленного линейного программирования:

максимизировать

при условиях

(12)

Условия (12) могут быть записаны как

(13)

Предположим, что для t=0 (т.е. для исходной таблицы) все a_>ij> – целые и столбцы (j = 1 ,…, n) – лексикографически положительны. Тогда все столбцы на протяжении вычислений остаются лексикографически положительными.

Прежде чем изложить способ получения дополнительного ограничения из производящей строки, введем новое представление чисел. Пусть [x] обозначает наибольшее целое число, не превосходящее x. Для любого числа y (положительного или отрицательного) и положительного можно записать:

(14)

где (r_>y> – неотрицательный остаток от деления нацело y на ). В частности, . Поэтому если , то и r = 1. Если , то и r = 0.

Вводимое дополнительное неравенство должно выполняться при любом целом решении задачи (12). Рассмотрим некоторое уравнение в t – таблице (опуская индекс строки) с a_>0><0:

(15)

где x – соответствующая компонента вектора , а - текущие небазисные переменные. Можно выразить x, a_>0
и> a_>j>, используя введенное выше представление (14):

(16)

(17)

Подставив выражения (16) и (17) в (15) и переставив члены, получим:

(18)

Поскольку , и на переменные x и наложено требование неотрицательности, левая часть уравнения (18) всегда неотрицательна. Рассмотрим выражение в правой части, заключенное в фигурные скобки. Коэффициенты в этом выражении представляют собой целые числа, а переменные подчинены требованию целочисленности. Поэтому все выражение в скобках должно быть целым. Обозначим его через s, т.е.:

(19)

Целочисленная слабая переменная s является неотрицательной. Действительно, если бы s было отрицательным, т.е. принимало бы значения -1, -2, …, то умножение на сделало бы всю правую часть уравнения (18) отрицательной, в то время как левая часть неотрицательна.

Рассмотрим два случая и . Для и . Подставляя в уравнение (19) выражение для x из (15), получим:

(20)

Полученное уравнение есть не что иное как отсечение Гомори. Для имеем и уравнение (19) приобретает вид:

(21)

Уравнение (21) должно выполняться для любого целочисленного решения задачи (12). Заметим, что если a_>0><0, то в уравнении (21). Потому уравнение (21) может использоваться в качестве ведущей строки в симплекс-методе. В частности, всегда можно выбрать достаточно большим, так чтобы ведущий элемент в строке (21) стал равным –1, что позволит сохранить целочисленность таблицы. Выбор соответствующего будет влиять на скорость сходимости алгоритма. Прежде всего опишем сам алгоритм. В качестве начального необходимо взять двойственно допустимое решение, которое можно получить добавлением ограничения x_>n>_>+>_>m>_>+1>=M – x_>1> - - … - x_>n> 0, где M – достаточно большая константа, и проведением одной итерации с добавленной строкой и с лексикографически минимальным столбцом, взятыми в качестве ведущих. Алгоритм состоит из следующих шагов:

Шаг 0. Начать с двойственно допустимой матрицы A⁰ в уравнении (13), элементы которой – целые числа (матрица A⁰ может содержать и нецелые элементы, об этом см. [2], стр. 306).

Шаг 1. Среди строк с a_>i>_>0><0 (i=1, …, n+m) выбрать строку с наименьшим значением i; эта строка станет производящей. (Если a_>i>_>0>0 (i=1, …, n+m), то задача решена.)

Шаг 2. Выбрать (правило выбора будет описано дальше) и написать внизу таблицы дополнительную строку

Эта строка выбирается в качестве ведущей.

Шаг 3. Провести шаг двойственного симплекс-метода, вычеркнуть дополнительную строку и вернуться к шагу 1.

Доказательство конечности алгоритма см. [2], стр. 303-304.

Правило выбора формулируется следующим образом.

Шаг 0. Пусть строка с номером v является производящей.

Шаг 1. Пусть - лексикографически минимальный столбец среди столбцов с a_>vj><0.

Шаг 2. Для каждого a_>vj><0 пусть - наибольшее целое, такое, что (лексикографически меньше).

Шаг 3. Пусть , а (строка v - производящая). Тогда

Шаг 4. Положить для a_>vj><0.

Правило выбора , описанное выше, позволяет сделать ведущий элемент равным –1, при этом сохраняется двойственная допустимость таблицы и в то же время нулевой столбец будет максимально лексикографически уменьшаться.

Подробнее об алгоритме можно прочитать в [2], стр. 300.

2.2.2 Прямой алгоритм целочисленного программирования

Термин “прямой”, примененный к алгоритму целочисленного программирования, обозначает метод, который приводит к оптимальному решению посредством получения последовательно “улучшаемых” решений. Каждой из этих решений допустимо в том смысле, что оно удовлетворяет как линейным ограничениям, так и условию целочисленности. Одним из вероятных достоинств алгоритма является возможность прервать вычисления, до того как получено оптимальное решение, и использовать наилучшее из полученных решений как приближенное. Кроме того, можно использовать прямой алгоритм в соединении с двойственными алгоритмами, чтобы получать различные составные алгоритмы, которые могут переходить от фазы, дающей двойственно допустимые решения, к фазе, дающей прямо допустимые решения.

Естественным прецедентом для прямого алгоритма является полностью целочисленный алгоритм Гомори, поскольку в процессе этого алгоритма получается последовательность двойственно допустимых целочисленных решений. Следует напомнить, что полностью целочисленный алгоритм Гомори представляет собой модификацию двойственного симплекс-метода. Основное отличие этого алгоритма состоит в том, что в качестве ведущей строки используется отсечение Гомори с ведущим элементом, равным –1. Это отсечение получается из производящей строки, которая определяется как одна из возможных ведущих строк в двойственном симплекс-методе. Использование такого отсечения в качестве ведущей строки сохранит после итерации двойственную допустимость и целочисленность таблицы.

Оказывается, можно аналогично модифицировать симплекс-метод таким образом, чтобы получить алгоритм, который сохраняет прямую допустимость и целочисленность таблиц. Для описания вычислительной процедуры рассмотрим следующую задачу целочисленного программирования:

максимизировать

(22)

при условиях

(целые) (k=1,…,n),

где a_>0>_>j>, a_>ij> и a_>i>_>0> – целые числа и a_>i>_>0>0.

(23)

редположим, что столбец

выбран в качестве ведущего и строка v – ведущая строка в итерации симплекс-метода, т.е.

для всех строк I, в которых a_>is>>0. Прежде чем провести процедуру исключения Гаусса в симплекс-методе, добавим к таблице отсечение Гомори, полученное из строки v:

где J – множество индексов небазисных переменных в (22), s_>k> – новая (базисная) слабая переменная и - неопределенная (временно) положительная константа.

Заметим, что если положить = a_>vs>, отсечение (23) будет обладать двумя важными свойствами. Во-первых,

Это означает, что прямая допустимость таблицы сохраниться, если использовать отсечение (23) в качестве ведущей строки. Во-вторых, , т.е. ведущий элемент равен 1 (если отсечение используется как ведущая строка). Легко удостовериться (путем исследования формул изменения базисных переменных), что преобразование симплексной таблицы с единичным ведущим элементом сохраняет целочисленность элементов симплексной таблицы.

Эти идеи послужили основанием прямого алгоритма в целочисленном программировании:

Шаг 0. Начать со столбцовой таблицы, в которой a_>i>_>0>0 (i1) и все элементы a_>0>_>j>, a_>ij> и a_>i>_>0> – целые.

Шаг 1. Проверить выполнение условий a_>0>_>j>0 (j1); если они выполнены, то конец, текущее базисное решение оптимально; если нет – перейти к шагу 2.

Шаг 2. Выбрать ведущий столбец s с a_>0>_>s>< 0. Выбрать строку v по правилу проверки отношения a_>i>_>0>/a_>is> среди строк с a_>is>> 0. Эта строка служит производящей для отсечения Гомори.

Шаг 3. Получить отсечение Гомори из производящей строки и дописать ее внизу таблицы, т.е. добавить к ограничениям задачи уравнение (23), где .

Шаг 4. Произвести преобразование таблицы, используя отсечение (23) как ведущую строку. Слабая переменная s_>k> в (23) станет небазисной. Вернуться к шагу 1.

Доказательство конечности алгоритма см. [2], стр. 346-353.

Поскольку выбор производящей строки является задачей нетривиальной, по-видимому, должно существовать несколько строк, которые могут служить в качестве производящих. В предварительных рассуждениях в качестве производящей строки использовалась ведущая строка симплекс-метода. Эта строка всегда дает отсечение, которое является ведущей строкой с ведущим элементом, равным единице. По-видимому, в таблице существуют и другие строки, из которых могут быть получены отсечения с такими же свойствами. Допустим, что отсечение получается по формуле:

(24)

Строка v может стать производящей тогда и только тогда, когда

(25)

где определяется из условия

Определим множество V(s) как совокупность строк, удовлетворяющих условию (25).

Следующие два правила представляют собой примеры допустимых правил выбора производящей строки:

Правило 1.

Составить последовательный конечный список индексов строк таким образом, чтобы индекс каждой строки вошел в него по меньшей мере один раз. Перейти к 2.

Если список пуст или не содержит ни одного индекса из V(s), вернуться к 1.; в противном случае найти в списке первый индекс vV(s). Выбрать строку v как производящую. Вывести из списка индекс v и все предшествующие ему индексы. Перейти к 3.

Последовательно выбирать строку v, взятую в 2., как производящую, до тех пор, пока vV(s). Как только vV(s), вернуться к 2.

Правило 2.

Пусть V_>t>(s) – множество V(s), соответствующее t-й таблице. Если V_>t>(s) содержит более одного элемента: V_>t>(s) = {v_>1>, v_>2>, …, v_>k>_>+2>}, то в качестве производящей выбрать такую строку , что в последовательности множеств V_>1>(s_>1>), V_>2>(s_>2>), …, V_>t>(s) строка появилась раньше (не позднее) остальных и затем сохранялась вплоть до V_>t>(s); перейти к 2.

Последовательно выбирать строку v, взятую в 1., до тех пор, пока . Как только , вернуться к 1.

Подробнее об алгоритме можно прочитать в [2], стр. 344.

2.2.3. ТЕХНИКА ПОЛУЧЕНИЯ НАЧАЛЬНОГО ДОПУСТИМОГО БАЗИСА

Решение каждым из приведенных выше методов может производиться только в том случае, если задача линейного программирования является или прямо, или двойственно допустимой. Такая допустимость означает наличие начального допустимого базиса в исходной задаче. Если задача допустима и прямо, и двойственно, то полученное решение – оптимально. В большинстве случаев после постановки задачи оказывается, что она не допустима ни прямо, ни двойственно. Поэтому приведем алгоритм получения начального допустимого базиса.

Пусть задача линейного программирования записана в канонической форме:

минимизировать

при условиях

Все b_>i> можно сделать неотрицательными, умножив, если надо, соответствующее уравнение на –1. Тогда можно добавить в каждое уравнение искусственную переменную (искусственные переменные должны быть неотрицательными) таким образом, чтобы из искусственных переменных образовать начальный базис:

Искусственные переменные можно получить из слабых переменных, используемых для превращения неравенств в уравнения. Действительно, если исходные ограничения задачи линейного программирования заданы в виде неравенств:

то, добавив слабую переменную в каждое неравенство, получим:

Если b_>i>0, то s_>i> можно использовать в качестве начальных базисных переменных.

Различие между искусственными переменными и слабыми переменными s_>i> состоит в следующем. В оптимальном решении задачи все искусственные переменные должны быть равными нулю, поскольку в исходной задаче таких переменных нет. С другой стороны, вполне возможно, что в оптимальном решении слабые переменные будут иметь положительные значения. Для того, чтобы искусственные переменные стали равными нулю, можно представить целевую функцию следующим образом:

где M_>i> – достаточно большие положительные числа. Идея метода соответствует тому, что искусственным переменным придаются заведомо большие цены. Такой способ приводит к нулевым значениям искусственных переменных в оптимальном решении.

Существует и другой способ получения начального допустимого базиса. В этом способе, как и в первом, в качестве начальных базисных переменных используются искусственные переменные. Рассматривается новая целевая функция , представляющая собой сумму искусственных переменных. Требуется минимизировать , используя z – уравнение как одно из ограничений. Если исходная система уравнений имеет допустимое решение, то все искусственные переменные должны стать равными нулю. Следовательно, минимальное значение должно стать равным нулю. Если , то исходная система уравнений не имеет допустимых решений. Если , то можно опустить целевую функцию и использовать оптимальный базис -формы в качестве начального допустимого базиса для минимизации z. В литературе такой способ называется двухфазовым симплекс-методом. На первой фазе метода находится допустимый базис путем минимизации , на второй – минимизируется z и получается оптимальный базис.

Рассмотри в качестве примера следующую задачу линейного программирования:

минимизировать

при условиях

где все b_>i> неотрицательны.

Если ввести искусственные переменные и новую целевую функцию , то получим задачу:

минимизировать

при условиях

-z

Если вычесть все уравнения, содержащие b_>i>, из -формы, получим:

(26)

-z

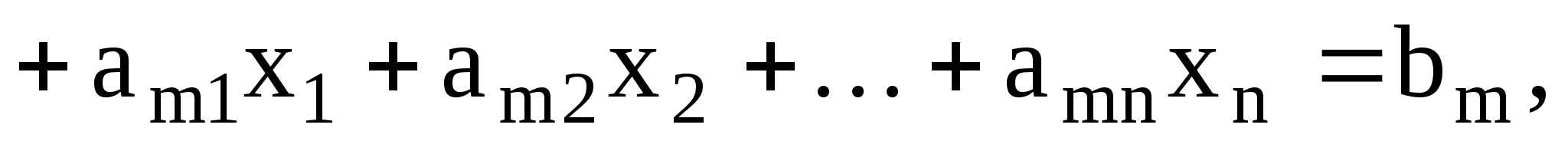
где Система (26) является диагональной относительно Первая фаза симплекс-метода состоит в минимизации при условиях (26). На знак z ограничений не накладывается. В процессе вычислений, как только искусственная переменная становится небазисной и ее коэффициент в -форме положителен, сама переменная и соответствующий ей вектор-столбец из дальнейших вычислений исключаются.

Подробнее об алгоритме можно прочитать в [2], стр. 53.

2.3. ОСОБЕННОСТИ ПРАКТИЧЕСКОЙ РЕАЛИЗАЦИИ СИСТЕМЫ

На практике не очень удобно работать с информацией в том виде, в котором она определяется в математической модели. Поэтому прежде всего определимся со способом организации данных или моделью данных.

2.3.1. ВЫБОР МОДЕЛИ

Модель данных – это совокупность соглашений о способах и средствах формализованного описания объектов и их связей, имеющих отношение к автоматизации процессов системы. Вид модели и используемые в ней типы структур данных отражают концепцию организации и обработки данных, используемую в СУБД, поддерживающей модель, или в языке системы программирования, на котором создается прикладная программа обработки данных.

В рамках решения поставленной задачи необходимо создание такой модели данных, при которой объем вспомогательной информации был бы минимальным, существовала принципиальная возможность многопользовательского доступа к данным и был бы обеспечен высокий уровень защиты данных.

В настоящее время существовует три основных подхода к формированию модели данных: иерархический, сетевой и реляционный.

ИЕРАРХИЧЕСКИЙ СПОСОБ ОРГАНИЗАЦИИ

Иерархическая БД состоит из упорядоченного набора деревьев; более точно, из упорядоченного набора нескольких экземпляров одного типа дерева. Тип дерева состоит из одного "корневого" типа записи и упорядоченного набора из нуля или более типов поддеревьев (каждое из которых является некоторым типом дерева). Тип дерева в целом представляет собой иерархически организованный набор типов записи.

Автоматически поддерживается целостность ссылок между предками и потомками. Основное правило: никакой потомок не может существовать без своего родителя. Заметим, что аналогичное поддержание целостности по ссылкам между записями, не входящими в одну иерархию, не поддерживается.

СЕТЕВОЙ СПОСОБ ОРГАНИЗАЦИИ

Сетевой подход к организации данных является расширением иерархического. В иерархических структурах запись-потомок должна иметь в точности одного предка; в сетевой структуре данных потомок может иметь любое число предков.

Сетевая БД состоит из набора записей и набора связей между этими записями, а если говорить более точно, из набора экземпляров каждого типа из заданного в схеме БД набора типов записи и набора экземпляров каждого типа из заданного набора типов связи.

Тип связи определяется для двух типов записи: предка и потомка. Экземпляр типа связи состоит из одного экземпляра типа записи предка и упорядоченного набора экземпляров типа записи потомка. Для данного типа связи L с типом записи предка P и типом записи потомка C должны выполняться следующие два условия:

Каждый экземпляр типа P является предком только в одном экземпляре L;

Каждый экземпляр C является потомком не более, чем в одном экземпляре L.

РЕЛЯЦИОННЫЙ СПОСОБ ОРГАНИЗАЦИИ

Основными недостатками иерархичекого и сетевого типов моделей данных являются:

Слишком сложно пользоваться;

Фактически необходимы знания о физической организации;

Прикладные системы зависят от этой организации;

Их логика перегружена деталями организации доступа к БД.

Наиболее распространенная трактовка реляционной модели данных, по-видимому, принадлежит Дейту, который воспроизводит ее (с различными уточнениями) практически во всех своих книгах. Согласно Дейту реляционная модель состоит из трех частей, описывающих разные аспекты реляционного подхода: структурной части, манипуляционной части и целостной части.

В структурной части модели фиксируется, что единственной структурой данных, используемой в реляционных БД, является нормализованное n-арное отношение.

В манипуляционной части модели утверждаются два фундаментальных механизма манипулирования реляционными БД - реляционная алгебра и реляционное исчисление. Первый механизм базируется в основном на классической теории множеств (с некоторыми уточнениями), а второй - на классическом логическом аппарате исчисления предикатов первого порядка. Основной функцией манипуляционной части реляционной модели является обеспечение меры реляционности любого конкретного языка реляционных БД: язык называется реляционным, если он обладает не меньшей выразительностью и мощностью, чем реляционная алгебра или реляционное исчисление.

Наконец, в целостной части реляционной модели данных фиксируются два базовых требования целостности, которые должны поддерживаться в любой реляционной СУБД. Первое требование называется требованием целостности сущностей. Второе требование называется требованием целостности по ссылкам.

После предварительного анализа математической модели системы и способов организации данных, а также имеющегося на рынке ПО (иерархический и сетевые способы организации предполагают объектно - орентированный подход к организации данных и на сегодняшний день имеются такие СУБД (например, Jasmin или Informix Dynamic Server), но на момент разработки возможности их использования не было, в то же время существуют очень “мощные” реляционные СУБД (к примеру Oracle 8i)) выбор был сделан в пользу реляционного способа организации хранения данных.

2.3.2. ОПИСАНИЕ ВХОДНОЙ ИНФОРМАЦИИ

Вся необходимая для решения поставленной задачи информация задается до начала итераций методов решения задачи составления расписания. Для упрощения считается, что заданная информация является постоянной на всем протяжении периода, для которого составляется расписание.

Не теряя определенной степени общности поставленной задачи, можно определить некую совокупность входных данных, необходимых для формирования ограничений и решения задачи, и в то же время общих для всех разновидностей практических реализаций системы. В силу специфики поставленной задачи (возможность сравнительно легкой адаптации математической модели для случая практической реализации в рамках конкретного вуза) формы документов входной информации не разрабатывались. Реквизиты входной информации описаны в табл.2.

Таблица 2. Описание реквизитов входной информации

Наименование реквизитов

Характеристика реквизитов

входных документов

Тип

Макс. длина

Точность

Фамилия, имя, отчество преподавателя;

Контактный телефон преподавателя;

Ученая степень;

Ученое звание;

Кафедра;

Название группы;

Численный состав группы;

Название читаемого курса;

Количество аудиторных часов;

Номера аудиторий;

Информация об аудиториях;

Название предмета, читаемого преподавателем;

Номер группы, где читается предмет;

Информация об аудиториях, где читается предмет.

текстов.

числов.

текстов.

числов.

текстов.

числов.

текстов.

100

Кроме этих данных для математической модели необходимо наличие еще некоторых дополнительных данных, которые могут быть получены после анализа входной информации программным путем.

2.3.3. РАЗРАБОТКА ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ЗАДАЧИ

Произведем анализ исходной информации с целью определения состава и структуры информации для последующей формализации и построения информационно-логической модели данных (ИЛМ). Приведенная выше математическая модель, а также дополнительные сведения из описания предметной области позволяют определить роль реквизитов во взаимосвязанной информации, содержащейся в документе. На основе такого анализа установим функциональные зависимости реквизитов в соответствии с рекомендациями и требованиями нормализации данных, после чего проведем саму нормализацию. Цель нормализации состоит в том, чтобы уменьшить (но необязательно устранить) избыточность данных. Однако иногда некоторая избыточность данных создается намеренно, чтобы повысить эффективность работы программы. Дадим определение трех форм нормализации базы данных.

Таблица находится в первой нормальной форме (1NF), если она имеет первичный ключ, все атрибуты представляют собой простые типы данных и отсутствуют повторяющиеся атрибуты. Чтобы соответствовать 1NF, домены атрибутов должны быть атомарными значениями и не должно быть повторяющихся групп атрибутов. Все повторяющиеся группы атрибутов должны быть перенесены в новую таблицу.

Таблица находится во второй нормальной форме (2NF) тогда, когда она находится в первой нормальной форме и каждый неключевой атрибут полностью функционально зависит от первичного ключа (т.е. в 2NF каждый неключевой атрибут должен полностью зависеть от полей первичного ключа).

Таблица находится в третьей нормальной форме (3NF), если она находится в 2NF и не содержит транзитивных зависимостей. Транзитивные зависимости – это функциональные зависимости между неключевыми атрибутами. Любой неключевой атрибут, который функционально зависит от другого неключевого атрибута той же таблицы, создает транзитивную зависимость и должен быть перемещен в другую таблицу.

Получающиеся функциональные зависимости довольно тривиальны и очевидно вытекают из математической модели, поэтому в дальнейшем описании они не приводятся. Также в дальнейшем изложении опускаются промежуточные степени нормализации. Поэтому приведем лишь окончательную инфологическую модель базы данных (см. рис. 1.).

Рис.1. Инфологическая модель базы данных задачи составления расписания занятий

Н_пр-ля (pk)

Имя

Фамилия

Отчество

Адрес

Телефон

Н_записи (pk)

Уч. степень

Н_потока(pk)

Уч. звание

Описание

Н_пр-ля (fk)

Кафедра

Н_потока (fk)

Н_пр-та (fk)

Н_группы(pk)

Н_потока(pk,fk)

Н_группы(pk,fk)

Н_об-ия (fk)

Название

Пара

Количество

Нач_неделя

Кон_неделя

Н_ауд-ии(pk)

Н_пр-та(pk)

Название

Описание

Число часов

Н_об-ия (pk)

Н_ауд-ии(pk,fk)

Н_об-ия (pk,fk)

Описание

2.3.4. ОСОБЕННОСТИ ФОРМИРОВАНИЯ ОГРАНИЧЕНИЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ СОСТАВЛЕНИЯ РАСПИСАНИЯ

Составление ограничений (1) – (7) математической модели задачи составления расписания является достаточно тривиальной задачей, решаемой с помощью несложных SQL – запросов и не требующей предварительного анализа входной информации. Поэтому подробнее лишь остановимся на ограничениях вида (8).

Заметим, что в математической модели системы читаемый предмет “привязывается” не к определенной аудитории проведения, а к некоторому множеству аудиторий. Расстановка конкретных номеров аудиторий производится уже после решения поставленной задачи. Ограничения вида (8) имеют смысл только тогда, когда множества аудиторий пересекаются. В математической модели системы предлагается учитывать все уникальные пересекающиеся пары в виде ограничений. Количество этих пересечений может быть велико, что может привести к большому числу дополнительных ограничений, отрицательно влияющих на скорость работы алгоритмов оптимизации. Однако можно существенно уменьшить количество дополнительных ограничений.

Рассмотрим случай линейного расположения пересекающихся множеств (см. рис. 2.).

Рис.2. Линейно пересекающиеся множества

A X_>a>B X_>b> C X_>c> D X_>d> E

В случае такого расположения множеств аудиторий для проведения занятий общее число ограничений вида (8) будет n-1, где n – количество множеств. Описанное выше расположение пересекающихся множеств может быть названо линейным, так как при этом n пересекающихся множеств расположены как бы в линию. Можно рассмотреть случай, когда множества пересекают друг друга произвольным образом (см . рис. 3.).

Рис.3. Произвольно пересекающиеся множества

Число ограничений вида (8) в этом случае можно уменьшить, проведя формирование этих ограничений по аналогии со случаем линейного расположения множеств. Для этого необходимо предположить, что, например, множества B и D, пересекающиеся с A, являются одним множеством, определить область пересечения такого множества с множеством A, после чего провести те же самые действия с получившейся областью пересечения.

Подробнее об этом см. [2], стр. 210.

2.4. Результаты работы программы

При практической реализации системы особое внимание было уделено задаче написания “ядра” системы – методам решения задачи и процедурам формирования ограничений. Поскольку не ставилось задачи написать полнофункциональный коммерческий продукт, интерфейсная часть была написана для целей тестирования ядра и определения границ применимости алгоритмов, поэтому включает в себя минимум функциональных возможностей и не содержит модулей предобработки входных данных.

Ядро системы и интерфейсная часть были написаны на Delphi 6.0. Методы решения и алгоритмы формирования ограничений написаны с использованием объектно-ориентированнных технологий, что позволит в будущем легко инкапсулировать их в дальнейшие модификации системы, не нарушая целостности взаимодействия различных алгоритмов. Текст объектов методов решения задачи приведен в приложении 2. База данных была реализована на СУБД Oracle 8i, запросы к ней осуществляются на языке PL/SQL.

Исходные данные задачи заносятся в таблицы базы данных с помощью запросных форм. Одна из таких форм приведена на рис. 3.

Рис.3. Форма занесения исходных данных

Данных, получаемых в результате решения задачи, недостаточно для вывода расписания занятий непосредственно после решения задачи, поэтому был написан модуль постобработки данных. Конечное расписание занятий выводится в виде таблицы, пример которой см .рис. 4.

Рис. 4. Пример расписания занятий

Алгоритмы решения задачи были протестированы на различных выборках исходных данных. Тестирование производилось на ЭВМ с процессором Intel Pentium 350 Мгц, СУБД Oracle 8i был установлен на двухпроцессорном сервере: 2 CPU Intel Pentium II 350 Мгц, ОЗУ 384 Мб; в качестве канала связи использовалась LAN с пропускной способностью до 100 Мбит/с. В качестве тестовых исходных данных были использованы как реальные данные о группах, преподавателях и читаемых предметах вечерней формы обучения ЧГУ на 1999/2000 учебные годы, так и случайно формируемые исходные данные (читаемым предметам случайным образом определяли аудитории для проведения занятий). В среднем производилось от 5 до 10 тестов для каждой тестируемой размерности исходных данных. В результате получили данные, приведенные в таблице 2. На рисунке 5. приведен график зависимости среднего времени решения задачи от количества читаемых предметов и количества групп.

2.5. Анализ полученных результатов

Анализируя полученные данные можно сделать некоторые выводы о функциональных возможностях алгоритмов решения и математической модели, их недостатках и областях применения.

Во-первых, использованная математическая модель содержит в себе “лишние” ограничения, существование которых обусловлено линейной целочисленной моделью, кроме этого каждому читаемому на потоке (поток может состоять и из одной группы) предмету ставится в соответствие 12 (для случая вечерников) переменных, каждая из которых представляет из себя булеву переменную. Во-вторых, резко возрастает время решения задачи при увеличении входных данных. Это происходит из-за резкого увеличения количества переменных и ограничений в модели, в результате чего возрастает размерность массивов и соответственно время решения задачи. В-третьих, формализованная математически задача охватывает только задачу составления расписания для студентов вечерней формы обучения без учета переходов между корпусами. Учет дополнительных требований увеличит количество ограничений задачи, что отрицательно повлияет на скорость работы алгоритмов решения.

Обратим внимание на возрастающую разницу между минимальным и средним значением времени решения задачи по мере увеличения размерности задачи. Эта разница соответствует тому, насколько “удачно” (наиболее близко к оптимальному) было найдено начальное допустимое базисное решение задачи. Поэтому время решения задачи можно значительно уменьшить, “удачно” найдя начальное базисное допустимое решение. Для поиска такого решения лучше всего использовать эвристические и декомпозиционные алгоритмы.

Выводы

В ходе работы была построена математическая модель расписания в вузе для случая вечерней формы обучения без переходов между корпусами, выбраны методы решения поставленной задачи и разработана модель хранения исходных данных задачи. Модель хранения исходных данных, алгоритм математической формализации модели и методы решения были реализованы в виде программных модулей. Скорость работы алгоритмов была протестирована на разнородных наборах исходных данных, в результате чего были определены возможности и области применения алгоритмов.

На основе результатов тестирования было установлено, что по скорости работы алгоритмы решения задачи сильно зависят от объема входной информации и начального допустимого базисного решения, и поэтому значительно уступают эвристическим и декмпозиционным. Но в случае эвристического решения его (решения) оптимальность (или достижение глобального максимума) может быть доказана только полным перебором всех возможных вариантов (ясно, что в этом случае время работы алгоритма будет очень большим), поэтому итерации эвристических алгоритмов прекращаются по достижении некоего максимального (нельзя сказать, локального или глобального) значения. Решение такого алгоритма может быть близким к оптимальному, но не оптимальным. В этом случае для достижения глобального максимума можно использовать рассмотренный в работе способ решения, поскольку оптимум может быть достигнут за несколько итераций описанных методов решения.

ЛИТЕРАТУРА

Лагоша Б.А., Петропавловская А.В. Комплекс моделей и методов оптимизации расписания занятий в вузе // Экономика и мат. методы. 1993. Т. 29. Вып. 4.

Ху Т. Целочисленное программирование и потоки в сетях. М.: Мир, 1979.

Лебедев С.С. Модификация метода Бендерса частично целочисленного линейного программирования // Экономика и мат. методы. 1994. Т. 30. Вып. 2.

Лебедев С.С., Заславский А.А. Использование специального метода ветвей и границ для решения целочисленной обобщенной транспортной задачи // Экономика и мат. методы. 1995. Т. 31. Вып. 2.

Заславский А.А. Использование стратегии расслоения переменных в общих задачах целочисленного линейного программирования // Экономика и мат. методы. 1997. Т. 33. Вып. 2.

Лебедев С.С. О методе упорядочивающей индексации целочисленного линейного программирования // Экономика и мат. методы. 1997. Т. 33. Вып. 2.

Лебедев С.С., Заславский А.А. Модифицированный метод пометок для задач булева программирования // Экономика и мат. методы. 1998. Т. 34. Вып. 4.

Заславский А.А. Комбинированный метод решения задач о рюкзаке // Экономика и мат. методы. 1999. Т. 35. Вып. 1.

Приложение 1. Возможности программных продуктов систем составления расписаний.

1. Система АВТОР-2+

Система АВТОР-2+ предназначена для быстpого и удобного составления расписаний занятий и сопровождения их в течение всего учебного года.
АВТОР-2+ - универсальная система. Есть несколько версий программы, рассчитанные на любые учебные заведения:

сpедние и специализиpованные (математические, языковые и т.п.) школы, лицеи, гимназии;

техникумы, училища и колледжи;

ВУЗы с одним учебным корпусом;

ВУЗы с несколькими учебными корпусами (с учетом переездов между корпусами).

АВТОР-2+ позволяет максимально облегчить и автоматизиpовать сложный тpуд составителей расписания. Система помогает легко стpоить, коppектиpовать и pаспечатывать в виде удобных и наглядных документов:

pасписания занятий классов (учебных групп);

расписания пpеподавателей;

расписание аудиторий (кабинетов);

учебные планы;

тарификацию.

АВТОР-2+ имеет пpиятный дизайн и дpужеcтвенный сеpвис. Программа достаточно проста в освоении. Имеется подробное руководство, в котором описаны все возможности и способы работы с программой.
Программа работает на любых IBM-совместимых компьютерах, начиная с 486DX с оперативной памятью 4Mb (и выше), занимает около 1 Mb на жестком диске. Операционная система: MS DOS, либо WINDOWS 95/98.
Время работы зависит от размерности учебного заведения и мощности компьютера. Полный расчет и оптимизация расписания школы среднего размера (30 классов, 60 преподавателей, две смены) идет около 15 минут на компьютере типа Celeron-400.

Программа отличается уникальным и очень мощным алгоритмом построения и оптимизации расписания. Полученное автоматическое расписание практически не требует ручной доработки, то есть даже при очень сложных и жестких ограничениях автоматически размещаются все возможные занятия. Если в исходных данных имеются неразрешимые противоречия, то их можно обнаружить и устранить, используя специальный блок анализа.

АВТОР-2+ позволяет:

оптимизировать "окна" в расписании;

учитывать требуемый диапазон дней/часов как для классов, так и для преподавателей;

оптимально pазмещать занятия по кабинетам (аудиториям) с учетом особенностей классов, предметов, пpеподавателей и вместимости кабинетов;

учитывать хаpактеp pаботы и пожелания как штатных сотpудников, так и совместителей-почасовиков;

легко соединять ("спаpивать") несколько классов (учебных групп) в потоки пpи пpоведении любых занятий;

pазделять классы пpи пpоведении занятий по иностранному языку, физической культуре, тpуду, информатике (и любым другим предметам) на любое количество подгрупп (до десяти!);

вводить (помимо основных пpедметов) спецкуpсы и факультативы;

оптимизировать равномерность и трудоемкость расписания.

По желанию заказчика АВТОР-2+ модифициpуется под условия конкретного учебного заведения.

2. Система “Расписание” ver 4.0 Москва – ЛинТех

Необходимо сразу же отметить, что программа “Расписание” ориентирована на составление школьного расписания, использование в ВУЗ`ах и колледжах возможно лишь с некоторыми оговорками. Составление расписания производится в рамках комплекса условий, которые определяются на шагах ввода исходных данных. Полный перечень возможных условий приведен ниже:

Ограничен максимальный номер урока – т.е. количество уроков, максимально допустимое в день;

Равномерность распределения нагрузки преподавателей между днями расписания;

Равномерность распределения нагрузки классов между днями расписания;

Контроль окон в расписании преподавателей;

Программа учитывает то обстоятельство, что классы могут произвольно объединяться и дробиться (классы могут объединяться в потоки или же дробиться на более мелкие подгруппы, причем эти подгруппы, в свою очередь, могут служить основой для объединения в более крупные группы. Пример: в школе №1859 есть 2 старших класса, но в каждом из этих классов есть две подгруппы по специализации, занятия по общеобразовательным предметам проводятся сразу для всего класса, а предметы по специализации – отдельно. Но поскольку подгруппы по специализации слишком малы, а преподавателей не хватает, по некоторым предметам подгруппы 11а и 11б также могут объединяться (например, на ин.яз.) – это усложняет обеспечении непрерывности расписания для классов (необходимо обеспечивать непрерывность расписания для каждой из подгрупп);

Наличие нескольких смен – в этом случае отдельные классы должны приходить позже, чем группы первой смены, кроме этого, усложняется контроль окон в расписании преподавателей, если есть преподаватели, работающие в обе смены – в этом случае в расписании этих преподавателей их занятия необходимо “стягивать” вокруг пересечения смен;

Условие привязки преподавателей к аудитории – отдельные преподаватели имеют “свою” аудиторию, в которой проводят все свои занятия;

Наличие “плавающей” смены – когда время начала первого урока точно не определено, т.к. оно формируется динамически, в зависимости от освобождения связанных с соответствующим классов, преподавателей, аудиторий;

Контроль вхождения расписания объекта (класс, преподаватель, аудитория) в допустимый рабочий диапазон (в карту временных ограничений). Например, для преподавателя в карте временных ограничений обычно указываются методические дни, иногда, отдельные номера уроков – словом, указываются те позиции, на которые установка занятий с участием данного объекта невозможна;

Наличие комбинированных предметов – типа “ин.яз./информатика” “информатика/труд” и т.п. - когда класс разбивается на подгруппы;

Условие привязки предметов к аудиториям – проведения занятий по отдельным предметам возможно лишь в строго определенной аудитории или списке аудиторий (физкультура, труд и т.п.);

Составление расписания с учетом того обстоятельства, что по некоторым предметам на занятия приходит не целый класс, а его подгруппа. Чтобы другая подгруппа в это время не гуляла по школе, такие занятия могут ставиться строго только первыми или последними занятиями в расписании класса;

“Выдержать параллели” – для некоторых преподавателей необходимо учитывать то обстоятельство, что для проведения занятий требуется длительная подготовка (например, занятия по химии), в этом случае занятия в дневном расписании преподавателя стараются поставить блоками параллелей, например, сначала 5-ые классы, затем 7-ые и т.п., или же при распределении между днями разнести занятия в разных параллелях на разные дни;

Иногда при составлении расписания требуется учитывать тот нюанс, что по некоторым предметам расписание известно заранее –в этом случае такие занятия вводятся как неперемещаемые (фиксированные);

Контроль запрещенных комбинаций предметов, приходящихся на один день расписания класса – например, нежелательно, чтобы “физическая культура” и “труд” проводились в один и тот же день;

Выполнение условия требуемых последовательностей предметов – когда необходимо обеспечивать установку групп занятий, в которых занятия должны идти в определенной последовательности, например, физика-астрономия и т.п.;

Наличие классов, привязанных к аудиториям – основная масса занятий для таких классов проводится именно в этой аудитории, за исключением тех занятий, для которых требуется специализированная аудитория;

Необходимость расстановки занятий по отдельным предметам по два занятия подряд (“парами”, “спарками”), причем это условие может быть жестким (ни в коем случае не разрывать “спарки” занятий), а может носить предпочтительный характер (если не получается перемещать по два занятия, “спарку” можно разрывать);

Учитывается то обстоятельство, когда по некоторым предметам расстановка допустима лишь одиночными занятиями.

3. Система “Методист”

Выпускается в двух версиях.

Версия virtual.

Выпускается без модуля автоматического составления расписания. Возможности версии virtual:

быстрый поиск в списках преподавателей, аудиторий, классов (групп), дисциплин, корпусов;

получение справочной информации по каждому найденному элементу списка (вместимость аудитории, все ауд. корпуса Х, адрес и тел. преподавателя, список кафедры, кол-во часов по дисциплине, учебная нагрузка преподавателя и мн. др.);

контроль и возможность перераспределения часов между неделями по любой дисциплине уч. группы;

автоматическая проверка возможных ошибок ввода данных (соответствие общей суммы часов и по видам занятий, неназначение преподавателей по подгруппам, бюджет времени уч. группы и преподавателя, несоответствие часов в группах потока и мн. др.);

возможность систематизированного хранения (и быстрого поиска) дополнительной (не обязательной для составления расписания) информации: фото преподавателей, кураторы учебных групп (классные руководители), данные о представителях родительских комитетов, должности, ученые степени и звания, ответственные за аудиторию, ...

быстрое получение полной информации по сочетанию факторов (все группы потока, все дисциплины преподавателя Х с указанием нагрузки по неделям и видам занятий, какие дисциплины разрешено проводить в компьютерном классе, личные пожелания к проведению занятий любого преподавателя, перечень праздничных дат в сирийской группе и мн. др.);

возможность просмотра, печати и редактирования готового расписания с проверкой корректности изменений (занятость ауд., преп., групп/подгрупп, ...);

в любой момент можно заказать модуль формирования расписания для подготовленных данных;

расписание формируется на вашем компьютере с возможностью изменения настроек, контроля, правки и т.п. (без возможности изменения часов, дисциплин, преподавателей, ...);

если обнаружена необходимость незначительного (до 10%) изменения исходных данных (обнаружены ошибки, внезапные дополнения), возможен повторный заказ модуля формирования расписания за незначительную плату;

в любой момент можно перейти на версию стандарт;

Методист – стандарт.

Помимо возможностей версии virtual включает в себя:

Модуль автоматического составления расписания;

Распределение и контроль учебной нагрузки ;

Учет методических рекомендаций и личных пожеланий преподавателей ("окна", метод. дни, теннис по четвергам, день рождения сына, ...);

Cтрогое выдерживание последовательности прохождения дисциплины (лекции - 2 час., практические - 4 час., лабораторные ...);

Составление расписания для любого типа учебного заведения: недельное или семестровое (от 1 до 23 недель);

Учет объединения групп (классов) в потоки и/или разбиение их на подгруппы;

Закрепление специальных аудиторий (компьютерные классы, лингафонные кабинеты, бассейн, ...);

Учет занятости преподавателей и аудиторий (совместительство, использование общей учебной базы);

Учет времени переходов между корпусами;

Выходные и праздничные дни - общие и для отдельных учебных групп (национальные, религиозные, государственные праздники);

Указание причин "неудачного назначения" занятий (занята аудитория, преподаватель назначен в нежелательный для него день недели) с возможностью их "ручного" исправления;

Возможность многократного автоматического "улучшения" расписания;

Возможность изменения значимости учитываемых при составлении расписания факторов;

Возможность введения приоритетов преподавателей - степени учета их индивидуальных пожеланий;

Ограничения функциональности “Методиста”:

многосменные расписания ограничены максимальным кол-вом уроков в день – 7;

занятия всегда начинаются с первого урока / пары (при необходимости возможно назначение на первую пару "свободного занятия" );

не учитывется время перемен (например для проверки возможности перехода между корпусами);

не учитывается "уровень сложности" занятий для их рационального распределения по неделе (хотя имеется возможность делать это косвенным образом) ;

продолжительность занятий постоянна (невозможно составление расписания для 30 мин. урока в младших и 45 мин. - в старших классах).

Приложение 2. Листинг программного модуля методов решения задачи автоматического составления расписания

uses

SysUtils;

type MyArray= array of array of real;

MyArray_X = array of longint;

procedure Step_Dual_simplex(var a:MyArray; m,n,i1,j1:integer);

{производит один шаг двойственного симплекс-метода,

ведущий элемент - a[i1,j1]}

var i,j:integer;

b,b1:array of real;

begin

SetLength(b,m);Setlength(b1,n);

for i:=0 to m-1 do b[i]:=a[i,j1];

for i:=0 to n-1 do b1[i]:=a[i1,i];

for i:=0 to m-1 do

for j:=0 to n-1 do begin

if (i=i1) and (j=j1) then a[i,j]:=1/b[i1]

else

if (i=i1) then a[i,j]:=b1[j]/b[i1]

else

if (j=j1) then a[i,j]:=-b[i]/b[i1]

else a[i,j]:=a[i,j]-b[i]*b1[j]/b[i1];

end;

for i:=0 to n-1 do a[i1,i]:=0;a[i1,j1]:=-1;

Finalize(b);Finalize(b1);

end;

function Lexikogr_few(a:MyArray; m,n:integer;i,i1:integer):boolean;

{первый столбец лексикографически меньше второго}

var j:integer;

begin

Lexikogr_few:=false;

j:=0;

while (a[j,i]=a[j,i1]) and (j<m-1) do Inc(j);

if (j<m-1) and (a[j,i]<a[j,i1]) then Lexikogr_few:=true;

end;

function Find_nu(a:MyArray;m,n:integer; i,i1:integer):longint;

{i - индекс лексикографически минимального столбца}

var j:integer;

begin

Find_nu:=1;

j:=0;

while (a[j,i]=a[j,i1]) and (j<m-1) do Inc(j);

if (j<m-1) and (a[j,i]<>0) then Find_nu:=Round(Int(a[j,i1]/a[j,i]));

end;

procedure Full_Integer_Simplex(var x:MyArray_X; a:MyArray; m,n:integer);

{Полностью целочисленный алгоритм задачи линейного целочисленного

программирования,

см. Ху Т. "Целочисленное программирование и потоки в сетях", стр. 300-309,

a - матрица размером m+n+2*n+1, по аналогии:

Требуется найти максимум

z= - 10x1 - 14x2 - 21x3

2x1 + 2x2 + 7x3 >= 14

8x1 + 11x2 + 9x3 >= 12

9x1 + 6x2 + 3x3 >=10,

тогда матрица а будет выглядеть:

1 10 14 21

0 -1 0 0

0 0 -1 0

0 0 0 -1

-14 -2 -2 -7

-12 -8 -11 -9

-10 -9 -6 -3

0 0 0 0,

процедура возвращает вектор X, первые m компонент которого - искомое решение,

если последняя компонента вектора = 1, то решения не существует или оно = бесконечности}

var i,i1:integer;

j,j1:integer;

alfa:real;

begin

repeat

i:=1;

while (i<m-1) and (a[i,0]>=0) do Inc(i); {производящая строка}

if i<m-1 then begin

j:=1;

while (j<n) and (a[i,j]>=0) do Inc(j);

if j<n then

for i1:=1 to n-1 do if (a[i,i1]<0) and Lexikogr_few(a,m,n,i1,j) then j:=i1; {лексикографически

минимальный столбец}

{выбор альфа}

if j<n then begin

{Writeln(i,' ',j);readln;}

alfa:=0;

for i1:=1 to n-1 do if a[i,i1]<0 then

begin

j1:=Find_nu(a,m,n,j,i1);

if (j1>0) and (-a[i,i1]/j1>alfa) then alfa:=-a[i,i1]/j1;

end;

{writeln(alfa,' ',i,' ',j);readln;}

{получение отсечения Гомори}

for i1:=0 to n-1 do if a[i,i1]>0 then a[m-1,i1]:=round(Int(a[i,i1]/alfa))

else begin

a[m-1,i1]:=round(Int(a[i,i1]/alfa));

if Frac(a[i,i1]/alfa)<>0 then a[m-1,i1]:=a[m-1,i1]-1;

end;

Step_Dual_simplex(a,m,n,m-1,j);

end;

until (i>=m-1) or (j>=n);

for i:=0 to m-1 do x[i]:=round(a[i,0]);

if j>=n then x[m-1]:=1 else x[m-1]:=0;

end;

procedure Step_One_Simplex(var a:MyArray; m,n,i:integer);

var i1,i2:integer;

{Один шаг прямого целочисленного метода (производящая строка - последняя

i - производящий столбец)}

begin

for i1:=0 to m-2 do a[i1,i]:=a[i1,i]/(-a[m-1,i]);

for i2:=0 to n-1 do

for i1:=0 to m-2 do

if i2<>i then a[i1,i2]:=a[i1,i2]+a[i1,i]*a[m-1,i2];

end;

procedure Direct_Integer_Simplex(var x:MyArray_X; a:MyArray; m,n:integer);

{Прямой целочисленный алгоритм задачи целочисленного линейного программирования,

см. Ху Т. "Целочисленное программирование и потоки в сетях", стр. 344-370,

a - матрица размером m+n+3*n+1 по аналогии:

требуется максимизировать

z = x1 + x2 + x3

-4x1 + 5x2 + 2x3 <= 4

-2x1 + 5x2 <= 5

3x1 - 2x2 + 2x3 <= 6

2x1 - 5x2 <= 1

тогда матрица а будет выглядеть:

0 -1 -1 -1

4 -4 5 2

5 -2 5 0

6 3 -2 2

1 2 -5 0

0 -1 0 0

0 0 -1 0

0 0 0 -1

10 1 1 1 - в этой строке первое число - грубая max суммы небазисных переменных

0 0 0 0 - строка для отсечения Гомори,

алгоритм работает только при a[i,0]>=0

возвращает вектор X - на месте единичной матрицы искомое решение,

если в последней компоненте единица - ошибка при расчетах}

var i,j,i1,j1:integer;

bool:boolean;

b,b1,b2:array of byte;

r:real;

begin

SetLength(b,m);SetLength(b1,m);

for i:=0 to m-1 do b1[i]:=0;

{проверка условия оптимальности}

bool:=false;

for j:=1 to n-1 do if a[0,j]<0 then bool:=true;

while bool do begin

{поиск производящего столбца}

bool:=false;j1:=0;

for j:=1 to n-1 do begin

if a[m-2,j]>0 then

begin

for i:=0 to m-3 do a[i,j]:=a[i,j]/a[m-2,j];

if not bool then begin j1:=j;bool:=true;end else if Lexikogr_few(a,m,n,j,j1)

then j1:=j;

end;

{поиск производящей строки}

for j:=1 to n-1 do

if a[m-2,j]>0 then

for i:=0 to m-3 do a[i,j]:=a[i,j]*a[m-2,j];

for i:=0 to m-1 do b[i]:=0;

i:=1; while (i<m-1) and (a[i,j1]<=0) do Inc(i);

i1:=i;

while (i<m-1) do begin

if (a[i,j1]>0) and (a[i,0]/a[i,j1]<a[i1,0]/a[i1,j1]) then begin i1:=i;end;

Inc(i);

end;

if i1<m-1 then begin

if a[i1,0]/a[i1,j1]<1 then begin

b[i1]:=1;

for i:=1 to m-2 do

if (a[i,j1]>0) and (a[i,0]/a[i,j1]<1) then b[i]:=1;

for i:=1 to m-2 do if (b[i]=1) and (b1[i]=1) then i1:=i;

end;

{формирование отсечения Гомори}

for i:=0 to n-1 do if a[i1,i]>0 then a[m-1,i]:=round(Int(a[i1,i]/a[i1,j1]))

else begin

a[m-1,i]:=round(Int(a[i1,i]/a[i1,j1]));

if Frac(a[i1,i]/a[i1,j1])<>0 then a[m-1,i]:=a[m-1,i]-1;

end;

Step_One_Simplex(a,m,n,j1);

end;

bool:=false;

if i1<m-1 then begin

b2:=b1;b1:=b;b:=b2;

for j:=1 to n do if a[0,j]<0 then bool:=true;

end;

{for j1:=0 to n-1 do Write(a[0,j1]:1:0,' ');Writeln;readln;}

end;

for i:=0 to m-2 do x[i]:=round(a[i,0]);

if i1>=m-1 then x[m-1]:=1 else x[m-1]:=0;

Finalize(b);Finalize(b1);

end;

Доклад.

Бакалаврская работа на тему “Разработка математической модели и ПО для задач составления расписания”

Уважаемые члены комиссии, вам представляется доклад бакалаврской работы на тему “Разработка математической модели и ПО для задач составления расписания”.

Технологию разработки расписания следует воспринимать не только как трудоемкий технический процесс, объект механизации и автоматизации с использованием ЭВМ, но и как акцию оптимального управления. Таким образом, это - проблема разработки оптимальных расписаний занятий в вузах с очевидным экономическим эффектом. Поскольку интересы участников учебного процесса многообразны, задача составления расписания - многокритериальная.

В ходе работы на начальном этапе были проанализированы и протестированы существующие на сегодняшний момент программные продукты. Тестирование осуществлялось на основе данных о ЧГУ за 1999/2000 учебный год. Из проанализированных программ только 3 оказались в состоянии составить расписание, удовлетворяющие почти всем требованиям, причем окончательных результатов работы одной программы дождаться так и не удалось, а 2 остальные работали около 3-4 часов.

Поэтому была поставлена задача: создание такой математической модели расписания в вузе, которая позволяла бы эффективно (в заданные сроки и с заданной степенью оптимальности) решать задачу автоматического составления расписания и обладала бы гибкостью (незначительных изменений в случае изменений входной информации) для адаптации системы в рамках конкретной практической задачи. Для некоторого упрощения задачи на начальном этапе проектирования были сделаны некоторые допущения:

все пары проводятся в одном корпусе;

задача ставится в терминах линейного программирования;

дальнейшая декомпозиция модели не производится;

все коэффициенты модели и искомые переменные целочисленны;

В ходе работы была построена математическая модель расписания в вузе для случая вечерней формы обучения без переходов между корпусами, выбраны методы решения поставленной задачи и разработана модель хранения исходных данных задачи.

Математическая формализация задачи составления расписания выполнялась исходя из принципов (см. плакат 1.):

Вводились целочисленные константы, соответствующие группам, проводимым занятиям, преподавателям, аудиторной нагрузке преподавателей и аудиторному фонду, причем часть из них может принимать только булевы значения.

Вводились булевы переменные, соответствующие паре, на которой проводится то или иное занятие. Для сохранения линейной целочисленности полученной модели потребовалось вводить по 12 переменных на каждое проводимое занятие.

На основе введенных констант и априорной информации о задаче составлялись ограничения на значения булевых переменных.

Целевая функция составлялась таким образом, чтобы максимизировать взвешенное число свободных от аудиторной работы дней для всех преподавателей, что при условии фиксированной длины рабочей недели эквивалентно максимальному совокупному уплотнению аудиторной нагрузки. Все переменные, входящие в целевую функцию, первой степени, и все коэффициенты при переменных постоянны.

Поставленная таким образом задача максимизации линейной целевой функции при заданной системе ограничений является задачей линейного целочисленного булева программирования, поскольку все коэффициенты ограничений целочисленны в силу дискретности исходных данных задачи; кроме этого искомые переменные математической модели могут принимать только два значения. На данный момент времени существует несколько возможных методов решения такого рода задач.

Алгоритмы математической формализации модели и методы решения были реализованы в виде программных модулей. Скорость работы алгоритмов была протестирована на разнородных наборах исходных данных, в результате чего были определены возможности и области применения алгоритмов.

Ядро системы и интерфейсная часть были написаны на Delphi 6.0. База данных была реализована на СУБД Oracle 8i, запросы к ней осуществляются на языке PL/SQL.

Отметим, что эвристические и декомпозиционные алгоритмы нельзя использовать в “чистом” виде, поскольку в случае эвристического решения его (решения) оптимальность (или достижение глобального максимума) может быть доказана только полным перебором всех возможных вариантов (ясно, что в этом случае время работы алгоритма будет очень большим), поэтому итерации эвристических алгоритмов прекращаются по достижении некоего максимального (нельзя сказать, локального или глобального) значения. Решение такого алгоритма может быть близким к оптимальному, но не оптимальным. В этом случае для достижения глобального максимума можно использовать рассмотренный в работе способ решения, поскольку оптимум может быть достигнут за несколько итераций представленных на плакате 2. методов решения.

Математическая модель расписания в вузе

Константы:

r – номер потока, r = 1, ..., R;

k_>r> – номер учебной группы в потоке r, k_>r> =1,…,G_>r>;

t – номер рабочего дня недели, t Є T_>kr>;

s_>r> – номер дисциплины в списке лекций для потока r, s_>r> = 1 ,…,S_>r>;

q_>kr> – номер дисциплины в списке практик для группы k_>r>, q_>kr> = 1 ,…, Q_>kr>;

1, если на потоке r лекцию s_>r> читает

преподаватель p;

0 – в противном случае;

1, если в группе k_>r> практическое занятие q_>kr>

проводит преподаватель p;

0 – в противном случае;

{A_>1>_>r>} – множество аудиторий для лекций на потоке r;

{A_>2>_>r>} – множество аудиторий для практических занятий на потоке r.

Переменные:

1, если на потоке r в день t на паре j читается

лекция s_>r>;

0 – в противном случае;

1, если на потоке r в день t на паре j у группы k_>r> проводится практическое занятие q_>kr>;

0 – в противном случае;

Ограничения:

Таблица 1. Продолжение.
Название	Краткая характеристика	Цена
Разработка стран СНГ
"Schedule" (Гутман, Роньшин) г.Киев	DOS, одна неделя, только школы	?
"Методист"	Windows, школы, ВУЗы	$100
"ABTOP-2+ ver 9.9" (Губенко И.О.) г.Ростов	DOS (без ограничений размерности) школы, ВУЗы	от $100 до $750
"РАСПИСАНИЕ+" ИнфоЦентр г. Абакан	DOS одна неделя школы, ВУЗы	$150 - $190
Без названия "АСИКУРАЦИОНЕ ИНТЕРНАЦИОНАЛЕ" (Кокотов С. П.) г.Благовещенск	Windows, школы, ВУЗы	$500
"Расписание 2000" (Николай Цигуро)	Windows, DOS: школы, лицеи, техникумы, без ограничения размерности	$ 50
"Ника" (НикаСофт)	Windows: школы, лицеи, гимназии, одна неделя	4000 - 7000 руб.
Программа редактирования учебного расписания ХроноГраф 2.0 (Хронобус-Москва)	Windows, для средних уч. заведений	8400 руб
Разработка зарубежных стран (все Windows)
"CELCAT" ver 5.0; Англия	колледжи, ВУЗы, минимальная конфигурация	$1600
"Tabulex 99"; Дания	школы (Basic - до 11 классов, Pro - более 11 классов)	Basic $1700
"Schedule Builder" США	колледжи, ВУЗы	$4750
"Time Tabler 4" Англия	школы	$1015 ( 645 фунтов+ VAT)

Системы составления расписания занятий Таблица 1.
Название	Краткая характеристика	Цена
Разработка стран СНГ
"Расписание" ver 4.0 Москва - ЛИнТех	DOS; только школы и колледжи; до 3 недель без дат; до 100 классов.	$230
"Пенал" ИКФ ТPИССТАP	DOS, одна неделя, только школы	$40
"Мечта" г.С-Петербург	Windows, одна неделя, только школы	390 руб
"Расписание 1.1" г. Уфа (Кожинов Д. Г., "Моделедром Сату")	Windows, одна неделя, только школы, без ограничения размерности	1740 руб

ВРЕМЯ РЕШЕНИЯ ЗАДАЧИ СОСТАВЛЕНИЯ РАСПИСАНИЯ

Размер задачи (количество читаемых предметов * количество групп)	Время решения (мин)
max	min	среднее
1	0,01	0,01	0,01
12	0,8	0,05	0,24
24	3,2	0,9	1,96
36	5,4	2,1	3,5
48	12	3,1	5,8
60	14	5,2	7,6
72	25	10	14,05
84	39	14,5	18,1
96	46	19	26,5
108	51	25	32
120	*	30	39
132	*	37	47,5
* - задача не решена из-за превышения заданного периода времени (60 мин)
ЗАВИСИМОСТЬ ВРЕМЕНИ РЕШЕНИЯ ОТ РАЗМЕРНОСТИ ЗАДАЧИ

Разработка математической модели и ПО для задач составления расписания (работа 2)

Содержание

Введение

1. ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОЙ ОБЛАСТИ

1.1. Формулировка задачи составления расписания

1.1.1. Общая формулировка задачи составления расписаний

1.1.2. Формулировка задачи составления раписания в применении к расписанию учебных занятий.

1.2. Анализ существующего ПО

1.3. Постановка задачи.

2. Разработка математической модели и практическая реализация системы автоматического составления расписания

2.1. Математическая модель расписания в вузе

2.1.1. Обозначения

2.1.2. Переменные

2.1.3. Ограничения

2.1.4. Целевая функция

2.2. МЕТОДЫ РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ

2.2.1. ПОЛНОСТЬЮ ЦЕЛОЧИСЛЕННЫЙ АЛГОРИТМ

2.2.2 Прямой алгоритм целочисленного программирования

2.2.3. ТЕХНИКА ПОЛУЧЕНИЯ НАЧАЛЬНОГО ДОПУСТИМОГО БАЗИСА

2.3. ОСОБЕННОСТИ ПРАКТИЧЕСКОЙ РЕАЛИЗАЦИИ СИСТЕМЫ

2.3.1. ВЫБОР МОДЕЛИ

ИЕРАРХИЧЕСКИЙ СПОСОБ ОРГАНИЗАЦИИ

2.3.2. ОПИСАНИЕ ВХОДНОЙ ИНФОРМАЦИИ

Наименование реквизитов

Характеристика реквизитов

Тип

Макс. длина

Точность

2.3.3. РАЗРАБОТКА ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ЗАДАЧИ

2.3.4. ОСОБЕННОСТИ ФОРМИРОВАНИЯ ОГРАНИЧЕНИЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ СОСТАВЛЕНИЯ РАСПИСАНИЯ

Рис.2. Линейно пересекающиеся множества

A X>a >B X>b> C X>c> D X>d> E

Рис.3. Произвольно пересекающиеся множества

2.4. Результаты работы программы

Рис.3. Форма занесения исходных данных

2.5. Анализ полученных результатов

Выводы

ЛИТЕРАТУРА

Приложение 1. Возможности программных продуктов систем составления расписаний.

Приложение 2. Листинг программного модуля методов решения задачи автоматического составления расписания

Математическая формализация задачи составления расписания выполнялась исходя из принципов (см. плакат 1.):

Математическая модель расписания в вузе

A X_>a>B X_>b> C X_>c> D X_>d> E