Методы приобретения знаний в интеллектуальных системах

Введение.

Инженерия знаний – это область информационной технологий, цель которой – накапливать и применять знания, не как объект обработки их человеком, но как объект для обработки их на компьютере. Для этого необходимо проанализировать знания и особенности их обработки человеком и компьютером, а также разработать их машинное представление. К сожалению точного и неоспоримого определения, что собой представляют знания, до сих пор не дано. Но тем не менее цель инженерии знаний – обеспечить использование знаний в компьютерных системах на более высоком уровне, чем до сих пор – актуальна. Но следует заметить, что возможность использования знаний осуществима только тогда, когда эти знания существуют, что вполне объяснимо. Технология накопления и суммирования знаний идет бок о бок с технологией использования знаний, они взаимно дополняют друг друга и ведут к созданию одной технологии, технологии обработки знаний.

В данной работе я постарался описать методы решения одной из проблем данного комплекса – это проблемы приобретения знаний, или говоря другими словами – обучения.

Методы приобретения знаний.

Приобретение знаний реализуется с помощью двух функций: получения информации извне и ее система­тизации. При этом в зависимости от способности си­стемы обучения к логическим выводам возможны различные формы приобретения знаний, а также раз­личные формы получаемой информации. Форма пред­ставления знаний для их использования определяется внутри системы, поэтому форма информации, которую она может принимать, зависит от того, какие спо­собности имеет система для формализации информа­ции до уровня знаний. Если обучающаяся система со­всем лишена такой способности, то человек должен заранее подготовить все, вплоть до формализации информации, т. е. чем выше способности машины к логическим выводам, тем меньше нагрузка на че­ловека.

Функции, необходимые обучающейся системе для приобретения знаний, различаются в зависимости от конфигурации системы. В дальнейшем при рассмот­рении систем инженерии знаний предполагается, что Существует система с конфигурацией, показанной на рис, 1.1, которая включает базу знаний и механизм логических выводов, использующий эти знания при решении задач. Если база знаний пополняется зна­ниями о стандартной форме их представления, то этими знаниями также можно воспользоваться. Сле­довательно, от функций обучения требуется преобра­зование полученной извне информации в знания и пополнение ими базы знаний.

Рис.1 Базовая структура систем обработки знаний

Можно предложить следующую классификацию систем приобретения знаний, которая будет опираться на способность системы к восприятию знаний в разных форматах, качественно различающихся между собой и способностью к формализации (рис 2).

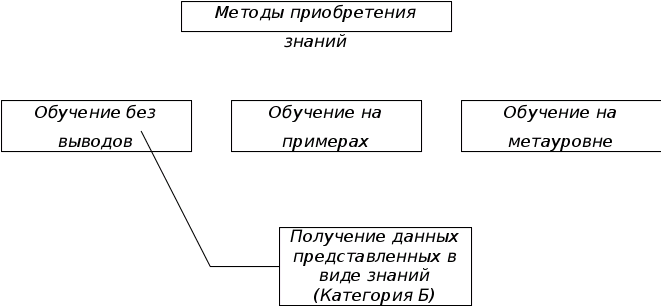
Рис 2.Классификация методов приобретения знаний.

Обучение без выводов.

Категорию А можно назвать обучением без выводов или механическим запоминанием, это простой процесс получения информации, при котором необяза­тельны функции выводов, а полученная информация в виде программ или данных используется для реше­ния задач в неизменном виде. Другими словами, это способ получения информации, характерный для су­ществующих компьютеров.

Категория Б—это получение информации извне, представленной в форме знаний, т. е. В форме, кото­рую можно использовать для выводов. Обучающейся Системе необходимо иметь функцию преобразования входной информации в формат, удобный для даль­нейшего использования и включения в базу знании.

Приобретение знаний на этом этапе происходит в наиболее простой форме: это знания, предварительно подготовленные человеком во внутреннем формате, какими являются большинство специальных знании, изначально заданных в экспертных системах. В слу­чае прикладных систем инженерии знаний необходи­мо преобразовать специальные знания из какой-либо области в машинный формат, но для этого нужен посредник, хорошо знающий как проблемную об­ласть, так и инженерию знаний. Таких посредников называют инженерами по знаниям. В общем случае для замены функции посредника можно использовать и специальные подпрограммы. Т.е. необходимо иметь функции выводов достаточно высокого уровня, но можно ограничиться и выводами на сравнительно низком уровне, а остальное доверить человеку — в этом и состоит приобретение знаний в диалоге. При­мером служит хорошо известная система TEIRESIAS. Это система-консультант в области медицины, разра­ботанная на базе системы MYCIN. Специалисты в проблемной области являются преподавателями обучающейся системы, а ученик — система инженерии знаний — изучает ответы на поставленные задачи и корректирует те правила в базе знаний, которые ра­нее приводили к ошибкам. Для подготовки знаний в экспертной системе необходимы вспомогательные средства типа редактора знаний, причем в процессе приобретения знаний в диалоге не только редактируются отдельные правила и факты, но и воспол­няются недостатки существующих правил, т. е. ведется редактирование базы знаний.

Если знания заданы во внешнем формате, например на естественном языке, то следует преобразовать их во внутренний формат. Для этого необходимо по­нимать внешнее представление, т. е. естественный язык, графические данные и т. п. Фактически приобретение знаний и их понимание тесно связаны. Проб­лема понимания сводится не только к преобразованию структуры предложений — необходимо получить фор­мат, удобный для применения.

Аналогичная проблема — преобразование во внутренний формат советов, подсказок по решению задач, что называется «операционализацией» знаний В этом заключается центральная проблема искус­ственного интеллекта; она, в частности, изучает пре­образование советов, подсказок, представленных в терминах проблемной области, в процедуры. Напри­мер, система UNDERSTAND выполняет операционализацию представления задачи о ханойской башне на английском языке путем построения соответствующих состояний и операций, приводящих к этим состоя* киям.

Приобретение знаний на метауровне

Выше было рассмотрено обучение на объектном уровне, а еще более сложная проблема - приобре­тение знаний на метауровне, т. е. знаний, основой которых является информация по управлению реше­нием задач с использованием знаний на объектном уровне. Для знаний на метауровне пока не установ­лены ни формы представления и использования, ни связь со знаниями на объектном уровне, ни другая техника их систематизации. Поскольку не определена форма их представления с точки зрения ис­пользования, то трудно говорить о приобретении знаний на метауровне. Тем не менее с этой пробле­мой связаны многие надежды в инженерии знаний,

Приобретение знаний из примеров

Метод приобретение знаний из примеров отличается от предыдущего метода, тем , что здесь выполняется сбор отдельных фактов, их преобразование и обобщение, а только затем они будут использованы в качестве знаний. И соответственно от уровня сложности системы вывода в системе будут возникать разные по степени общности и сложности знания. Необходимо также упомянуть о том, что этот метод приобретения знаний почти не нашёл практического применения, это может быть связано с тем, что входная информация представляет собой не систематизированный набор данных и для их обработки требуется наличие в системе обширных знаний по конкретной области.

По сравнению с предыдущим методом приобретения знаний, этот метод имеет большую степень свободы и соответственно необходимо описать общие положения этого принципа.

1. Языки представления. Обучение по примерам — это процесс сбора отдельных фактов, их обобщение и систематизация, поэтому необходим унифицирован­ный язык представления примеров и общих правил. Эти правила, будучи результатом обучения, должны стать объектами для использования знаний, поэтому и образуют язык представления знаний. И наоборот, язык представления знаний должен учитывать и определять указанные выше условия приобретения знаний.

2. Способы описания объектов. В случае обучения .по примерам из описаний отдельных объектов созда­ются еще более общие описания объектов некоторого класса, при этом возникает важная проблема: как описать данный класс объектов. В полном классе некоторых объектов следует определить меньший класс объектов, обладающих общим свойством (объ­екты только в этом классе обладают заданным свойством), но в действительности проще опреде­лить список объектов и убедиться, что все объекты в нем обладают общим свойством. Для некоторо­го типа задач можно эффективно использовать лож­ные примеры или контрпримеры, убедительно пока­зывающие, что данные объекты не входят в этот класс.. Иллюстрацией применения контр­примеров может служить понятие «почти то».

3. Правила обобщения. Для сбора отдельных приме­ров и создания общих правил необходимы правила обобщения. Предложено несколько способов их опи­сания: замена постоянных атрибутов языка на пере­менные, исключение описаний с ограниченным при­менением и т. п. Очевидно, что эти способы тесно свя­заны с языком представления знаний.

4. Управление обучением. В процессе обучения по примерам можно применять различные стратегии структуризации информации и необходимо управлять этим процессом в ответ на входные данные. Сущест­вуют два классических метода: метод «снизу-вверх», при .котором, последовательно выбираются и структу­рируются отдельные сообщения, и метод «сверху-вниз», при котором сначала выдвигается гипотеза, а затем она корректируется по мере поступления инфор­мации. На практике эти методы комбинируются, хотя управление обучением с максимальным эффектом не такая уж простая проблема.

При изучении метода приобретения знаний по примерам можно выделить следующий ряд методов:

Параметрическое обучение

Обучение по аналогии

Обучение по индукции.

Параметрическое обучение.

Наиболее простая фор­ма обучения по примерам или наблюдениям состоит в определении общего вида правила, которое должно стать результатом вывода, и последующей корректи­ровки входящих в это правило параметров в зависи­мости от данных. При этом используют психологи­ческие модели обучения, системы управления обуче­нием и другие методы.

Примером обучающейся системы этой категории в области искусственного интеллекта является си­стема Meta-Dentral. Эта система выводит новые пра­вила путем коррекции правил продукций в процессе обучения или на основе исходных массспектральных данных параметрическое обучение в ней представ­лено в несколько специфичном виде, но все же она относятся к указанной выше категории, поскольку в системе задана основная структура знаний, кото­рая корректируется последовательно по отдельным данным.

Ярким примером применения этого метода приобретения знаний могут также служить системы распознавания образов (обсуждавшиеся ранее в другом докладе). В них ясно просматривается основной принцип этого метода - в ходе обучения нейронная сеть автоматически по определенным заранее законам корректирует веса связей между элементами и значения самих элементов.

Метод обучения по индукции.

Среди всех форм обучения необходимо особо выделить обучение на основе выводов по индукции - это обучение с использованием выводов высокого уровня, как и при обучении по аналогии. В процессе этого обучения путем обобщения совокупности имею­щихся данных выводятся общие правила. Возможно обучение с преподавателем, когда входные данные задает человек, наблюдающий за состоянием обу­чающейся системы, и обучение без преподавателя, когда данные поступают в систему случайно. И в том и в другом случае выводы могут быть различными, они имеют и различную степень сложности в зави­симости от того, задаются ли только корректные данные или в том числе и некорректные данные и т. п. Так или иначе, обучение этой категории включает открытие новых правил, построение теорий, создание структур и другие действия, причем модель теории или структуры, которые следует создать, за­ранее не задаются, поэтому их необходимо разра­ботать так, чтобы можно было объяснить все пра­вильные данные и контрпримеры.

Индуктивные выводы возможны в случае, когда представление результата вывода частично опреде­ляется из представления входной информации. В по­следнее время обращают на себя внимание про­граммы генерации программ по образцу с исполь­зованием индуктивных выводов.

Как уже было сказано, индуктивный вывод — это вы­вод из заданных данных объясняющего их общего правила. Например, пусть известно, что есть некото­рый многочлен от одной переменной. Давайте посмот­рим, как выводится f(х), если последовательно за­даются в качестве данных пары значений (0, f(0)), (1, f(1)), .... Вначале задается (0, 1), и естественно, что есть смысл вывести постоянную функцию f(х)=1. Затем задается (1, 1), эта пара удовлетворяет предложенной функции f{х)= 1. Следовательно в этот момент нет необходимости менять вывод. Наконец, задается (2, 3), что плохо согласуется с нашим выводом, поэтому откажемся от пего и после несколь­ких проб и ошибок выведем новую функцию f(х)==х²—х+1, которая удовлетворяет всем задан­ным до сих пор фактам (0, 1), (1, 1), (2,3). Далее мы убедимся, что эта же функция удовлетворяет фактам (3, 7), (4, 13), (5, 21) ..., поэтому нет необ­ходимости менять этот вывод. Таким образом, из последовательности пар переменная-функция можно вывести многочлен второй степени. Грубо говоря, такой метод вывода можно назвать индуктивным.

Как видно из этого примера, при выводе в каждый момент времени объясняются все данные, полученные до этого момента. Разумеется, данные, полученные позже, уже могут и не удовлетворять этому выводу. В таких случаях приходится менять вывод. Следова­тельно, в общем случае индуктивный вывод—это не­ограниченно долгий процесс. И это не удивительно, если вспомнить процесс освоения человеком языков, процесс совершенствования программного обеспече­ния и т. п.

Для точного определения индуктивного вывода необходимо уточнить:

множество правил—объ­ектов вывода,

метод представления правил,

способ показа примеров,

метод вывода и

критерий правильности вывода.

В качестве правил—объектов вывода—можно рассматривать главным образом индуктивные функ­ции, формальные языки, программы и т. п. Кроме того, эти правила могут быть представлены в виде машины Тьюринга для вычисления функций, грам­матики языков, операторов Пролога и другим спо­собом. Машина Тьюринга—это математическая модель компьютера, ее в принципе можно считать про­граммой. В случае когда объектом вывода является формальный язык, он сам определяет правила, а его грамматика — метод представления правил, поэтому говорят о грамматическом выводе.

Для показа примеров функции f можно использо­вать последовательность пар (х,f(х)) входных и вы­ходных значений так, как указано выше, последовательность действий машины Тьюринга, вычисляющей и другие данные. Задание машине выводов пары входных и выходных значений (х, f(х)) функции f соответствует заданию системе автоматического син­теза программ входных значений х и выходных зна­чений f(х), которые должны быть получены програм­мой вычисления f в ответ на х. В этом смысле авто­матический синтез программ по примерам также можно считать индуктивным выводом функции f. Формальные языки — это множество слов; поэтому, например, для языка L можно рассматривать TYPE=RANDOM FORMAT=ARABIC>11ва типа слов, принадлежащих и не принадлежащих этому языку. Первые назовем положительными, а вторые — отрицательными данными. Другими слова­ми, есть два способа показа примеров формального языка: с помощью положительных и отрицательных данных. Когда объектом служат сами программы, тогда то же самое можно говорить о функциях языка Лисп, но для Пролога показ примеров осуществляется в виде фактов. Например, (3>4, истина), (2<=1, ложь). В этом случае положительным данным соот­ветствуют данные с атрибутом «истина», а отрица­тельным — данные с атрибутом «ложь».

Вывод реализуется благодаря неограниченному повторению основного процесса

запрос входных данных -> предположение -> выходные данные.

Другими словами, при выводе последовательно по­лучают примеры как входные данные, вычисляют предположение па данный момент и выдают резуль­тат вычислений. Предположение в каждый момент времени основано на ограниченном числе примеров, полученных до сих пор, поэтому обычно в качестве метода вывода используют машину Тьюринга, вычис­ляющую предположение по ограниченному числу при­меров. Такую машину назовем машиной выводов.

Учитывая, что индуктивный вывод, как уже было отмечено, это неограниченно продолжающийся про­цесс, критерием правильности вывода, как правило, считают понятие идентификации в пределе. Это поня­тие введено Голдом, оно используется почти всегда в теории индуктивных выводов. Говорят, что машина вывода М идентифицирует в пределе правило R, если при показе примеров К последовательность выходных данных, генерируемых М, сходится к некоторому представлению т, а именно: все выходные данные, на­чиная с некоторого момента времени, совпадают с т, при этом т называют правильным представлением К.. Кроме того, говорят, что множество правил Г позво­ляет сделать индуктивный вывод, если существует некоторая машина выводов М, которая идентифици­рует в пределе любое правило К из множества Г. Обратите внимание на то, что слова «позволяет сде­лать индуктивный вывод» не имеют смысла для един­ственного правила, а относятся только к множеству правил.

Обучение по аналогии.

Приобре­тение новых понятий возможно путем преобразова­ния существующих знаний, похожих на те, которые собираются получить. Это важная функция, которую называют обучением на основе выводов по аналогии или просто обучением по аналогии. В нашей жизни много примеров, когда новые понятия или техни­ческие приемы приобретаются с помощью аналогии

Выводы по аналогии - один из важных объектов исследования искусственного интеллекта, наиболее интересные результаты здесь получены П. Уинстоном. Он использует выводы по аналогии, основываясь на следующей гипотезе: «Если две ситуации подобны по нескольким признакам, то они подобны и еще По одному признаку». Подобие двух ситуаций распознается путем обнаружения наилучших совпадений по наиболее важным признакам.

Аналогия—это метод выводов, при которых обнару­живается подобие между несколькими заданными объектами; благодаря переносу фактов и знаний, справедливых для одних объектов, на основе этого подобия на совсем другие объекты либо определяется. способ решения задач, либо предсказываются неиз­вестные факты и знания. Следовательно, когда чело­век сталкивается с неизвестной задачей, он на первых порах использует этот естественный метод вывода.

Направления исследования аналогии

Одна из важнейших проблем инженерии знаний— приобретение знаний. Под приобретением здесь по­нимается получение знаний в виде, пригодном для их использования компьютерами, поэтому многие исследователи указывают, что ключом к знаниям является теория и методология машинного обучения. В общем случае машинное обучение включает приобретение новых декларативных знаний, систематизацию и хра­нение новых знаний, а также обнаружение новых фактов. Среди указанных форм обучения аналогия, о которой будет идти далее речь, связана, и частности, с проблемой машинного обнаружения новых фактов.

Под новыми фактами мы будем понимать факты, которые дедуктивно не выводятся из некоторых существующих знаний. Получение новых знаний также рассматривалось выше в отношении к индуктивному выводу . В общем случае при индук­тивных выводах по заданным данным создается ги­потеза, их объясняющая, а с помощью дедукции из этой гипотезы можно вывести новые факты. С дру­гой стороны, при аналогии новые факты предсказы­ваются путем использования некоторых преобразова­ний уже известных знаний.

Индукция и аналогия крайне необходимы при об­работке интеллектуальной информации, и поэтому желательно изложить основы их совместного приме­нения. Шапиро ввел стро­гую формализацию индуктивных выводов в части вы­вода моделей с использованием логики предикатов первого порядка; в теории индуктивных выводов есть заметные успехи.

С целью обзора исследований аналогии, проведен­ных до настоящего времени, выделим два типа ана­логии: для решения задач и для предсказаний. Ана­логия первого типа применяется главным образом для повышения эффективности решения задач, кото­рые, вообще говоря, можно решить и без аналогии. Например, благодаря использованию решений ана­логичных задач в областях программирования и до­казательства теорем можно прийти к выводам о про­граммах или доказательствах. С другой стороны, используя аналогию для предсказаний, благодаря преобразованию знаний на основе подобия между объектами можно сделать заключение о том, что, возможно, справедливы новые факты. Например, если объектами аналогии является некая система аксиом, то знаниями могут быть теоремы, справедливые в этой системе. При этом, используя схожесть между системами аксиом, можно преобразовать теорему в одной из систем в логическую формулу для другой системы и сделать вывод о том, что эта формула есть теорема. Другими словами, аналогия используется и для решения некоторых строго сформулированных задач и для предсказаний, а также для приобретения не заданной ранее информации.

Примером использования метода приобретений знаний по аналогии может служить система доказательства теорем. При этом общая схема вывода выглядит следующим образом.

Рис. 3 Стратегия абстрагирования.