Задачи по схемотехнике
Задачи по схемотехнике
Перевести следующие числа из десятичной системы счисления в двоичную и из двоичной в шестнадцатеричную: 127,184,356,200,427.
127=128-1 = 1111111;
0111|1111= 7FH;
184=128+32+16+8=10111000;
1011|1000=B8H;
356=256+64+32+4=101100100;
1|0110|0100=164H;
200=128+64+8=11001000;
1100|1000=C8H;
427=256+128+32+8+2+1=110101011;
1|1010|1011=1ABH;
1.2. Перевести следующие числа из шестнадцатеричной системы в двоичную и из двоичной в десятичную, а также непосредственно из шестнадцатеричной в десятеричную: BD5H; 8E1H; CABH; 91DH; AF1H;
BD5H=1011|1101|0101=1+4+16+64+128+256+512+2048=3029;
162*11+162*13+160+5=3029;
8E1H=1000|1110|0001=1+32+64+128+2048=2273;
8E1H=8*162+4*161+1*160=2273;
CABH=110010101011=1+2+8+32+128+1024+2048=3243;
CABH=12*162+10*161+11=3243;
91DH=100100011101=1+4+8+16+256+2048=2333;
91DH=9*162+1*16+13=2333;
AF1H=101011110001=1+16+32+64+128+512+2048=2801;
AF1H=162*10+16*15+1=2801;
1.4. На вход узла равнозначности подается серия импульсов, приведенная на рис.1.2. Построить временную диаграмму выходного сигнала без учета задержек и фронтов, создаваемых логическими элементами устройства.

X>1>








t










X>2>


t







X>вых>










t






1.6. Синтезировать шифратор на пять входов
а) на элементах ИЛИ-НЕ;
б) на элементах И-НЕ;
a
1


Q>1>
b




c
1


d



Q>2>
e


1




Q>3>


&
&
&
















 a
a





Q>1>





 b
b


Q>2>



 c
c







Q>3>
d




 e
e
1.8. Синтезировать полный сумматор на элементах И-ИЛИ-НЕ.
A
&
&
1












&








&



B





&







Cn


&

1





Cn+1

&





&


1.11. На рисунке приведена схема суммирующего 3 – разрядного счетчика на D – триггерах 155ТМ2:

Рис. 3 – разрядного двоичного счетчика на D – триггерах.
а) пояснить принцип работы счетчика;
б) составить таблицу переключений счетчика. Определить коэффициент пересчета (модуль счета) k;
в) построить временные диаграммы сигналов на выходах Q1,Q2, и Q3;
г) определить максимальную задержку, создаваемую счетчиком. Задержка создаваемая одним триггером, tзтр=55нс;
а) Принцип работы счетчика: асинхронные входы установлены в положение синхронной загрузки с входов D,C. На входе D установлено значение инвертированного выхода Q, поэтому при появлении на тактовом входе С положительного перепада в триггер записывается значение входа D, а на выходе устанавливается инвертированное значение входа. В случае счетчика типа делителя на два на выходе устанавливается сигнал того – же уровня после подачи на вход С двух импульсов. Для переключения следующего счетчика из одного уровня в тот же самый необходимо подать четыре импульса и т. д., счет составляет 2 n где n – количество триггеров, в данном случае 23=8 импульсам на входе. У данного счетчика есть одна особенность, при включении выходы Q кроме первого принимают значения 1, поэтому после включения счетчик необходимо обнулить, подав на вход R импульс.
б)
Таблица переключений счетчика.
-
Счет
Выход
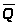 1
1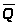 2
2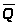 3
3С
0
Н
В
В
1
В
Н
В
2
Н
Н
В
3
В
В
Н
4
Н
В
Н
5
В
Н
Н
6
Н
Н
Н
7
В
В
В
Таблица составлена после обнуления всех триггеров.
Коэффициент пересчета или модуль счета k= 23.
в) Временные диаграммы составлены для не инвертированных выходов Q1, Q2, Q3 после обнуления счетчика.







































 С
С










































 Q1
Q1

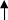













 Q2
Q2








 Q3
Q3
г) максимальное время задержки создаваемое счетчиком происходит при переключении третьего триггера, поэтому максимальное время задержки счетчика есть сумма времени задержки на каждом триггере с момента поступления положительного перепада на вход С, tмзc=tтр1+tтр2+tтр3; tмзс=3*tтр;
tмзс=3*55; tмзс=165нс.
1.13. Суммирующий счетчик находится в нулевом состоянии. В каком состоянии он будет находиться после подачи 64 и 67 входных импульсов?
Так как счетчик считает до 23 , при 64 импульсах мы будем иметь состояния входов в состоянии Q1= H, Q2= H, Q3= H, так как 64 кратно 23 .
При 67 импульсах состояния входов будет Q1= B, Q2= B, Q3= H, так как 67- 64=3, третий импульс соответствует счету 2.
2.2. Разработать схему не инвертирующего усилителя сумматора на 3 входа со следующими коэффициентами суммирования по каждому из входов: 2; 5; 7. Рассчитать значение Uвых при Uвх1=1 В, Uвх2=0.2 В, Uвх3=0.05 В. Сопротивление обратной связи Rос=10 кОм.








R>1>
R>oc>






R’>1>




R’>2>

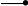
R’>3>
R’>oc>









Uвых=U1+U2+...Un;
R’o.c=10 KOm;
Ro.c/R1=R’o.c/R’1+R’o.c/R’2+...+R’o.c/R’n;
Uвых=2U1+5U2+7U3;
R’1=R’o.c/2=5 KOm;
R’2=R’o.c/5=2 KOm;
R’3=R’o.c/7=1.42 KOm;
Ro.c/R1=10KOm/5KOm+10KOm/2KOm+10KOm/1.42KOm;
R1=10KOm/2+5+7=10KOm/14=714 Om;
Uвых=2*1+5*0.2+7*0.05=3.35B;
2.3. Разработать схему трехвходового суммирующего интегратора со следующими постоянными интегрирования: =7 мс. Рассчитать и начертить значение Uвых при постоянных значениях Uвх1=0.1 В, Uвх2=0.2 В, Uвх3=0.05 В на участке изменения выходного напряжения от 0 до напряжения насыщения Uнас=10 В. Конденсатор в цепи отрицательной обратной связи Сос= 100нФ.





U>1>














R>1>
R>2>
R>3>
C>1>
U>2>
U>3>
U>вых>






Uвых=-1/R1*C1(U1+U2+...+Un)d;
если R1=R2=...Rn;
ic=iR1+iR2+...+iRn так что,
-C(dUвых/dt)=(U1/R1)+(U2/R2)+...+(Un/Rn);
При R1=R2=...=Rn имеем dUвых=-(U1+U2+...+Un)/C1R1.
Проинтегрировав это равенство
Uвых=-1/RC (U1+U2+...+Un)dt;
(U1+U2+...+Un)dt;
=R*C;
7*10-3=R*100*10-9;
R1=7*10-3/100*10-9;
R1=70 kOм;
так как для всех входов равно одному времени интегрирования следует, что R1=R2=R3.
max Uвых =10 B – напряжению насыщения ;
min Uвых = 0B ;
10B=(-1/(70*103Om*100*10-9F))*0.35B*t;
10/(-1/70000*100*10-9)*0.35=0.2c;
2.4. Докажите, что дифференциальный усилитель может выполнять математическую операцию вычитания двух чисел.
R>ос>
U>1>


















R>1>
R>2>
U>2>
U>вых>


R>ос>

U>3>









R’>1>
R’>2>
U>4>


Uвых=U3(R’oc/R’1)+U4(R’oc/R’2)-U1(Roc/R1)-U2(Roc/R2);
если Roc/R1+Roc/R2=R’oc/R’1+R’oc/R’2;
2.7. Начертить гистерезисную схему сравнения двух напряжений. Объяснить принцип ее работы.











U>вх>
U>вых>





R1
R2





В качестве гистерезисной схемы сравнения примем триггер Шмитта с двумя источниками питания, уровни включения и выключения и выключения которого не совпадают, как у обычного компаратора, а различаются на величину, называемую гистерезисом переключения Ue. Когда Uвх<Uвто, то Uвых велико, напряжение верхней точки опрокидывания получается с помощью деления на сопротивлениях напряжения выхода Uвых. Когда Uвх>Uвто, то выходное напряжение становится отрицательным и стремится к –Uнас, т.е. к максимальному отрицательному выходному напряжению компаратора. Отрицательное выходное напряжение вызывает падение напряжения на не инвертирующем входе до напряжения нижней точки опрокидывания. Компаратор не изменит своего состояния, пока Uвх>Uнто.
2.8. Начертить временные диаграммы выходных напряжений Uвых одно-пороговой и гистерезисной схем сравнения для заданных входных напряжений Uвх1, Uвх2.
3.1. Начертить структурную схему АЦП «напряжение – код» параллельного типа. Объяснить принцип его работы.
U>оп>
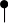


























=
K>3>
K>2>
ПК
a>2>
a>1>
a>0>
U>вх>
R>1>
R>2>
R>3>
R>4>
=
=
K>1>
АЦП параллельного типа состоит из резисторного делителя на резисторах, линейки компараторов и преобразователя кода. На вход Uвх поступает оцифровываемый аналоговый сигнал, а на вход Uоп подается опорное напряжение, которое через резисторный делитель распределяется на входы компараторов. Так как Uвх подаётся на не инвертирующий вход, то выходное напряжение будет велико, когда Uвх>Uоп, и мало, когда Uвх<Uоп. Входное напряжение может принимать значения от 0 до n-1/n. При выполнении условия Uвх>Uоп на выходе компаратора Kn устанавливается высокий логический уровень, далее берется наибольший разряд Kn, на котором устанавливается высокий логический уровень в линейке компараторов, код подаётся на шифратор и преобразуется в соответствующий двоичный код.
Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа