Усложнение решающего правила при управлении в задачах распознавания образов

Усложнение решающего правила при управлении в задачах распознавания образов

Бекмуратов К.А.

Рассматривается один из возможных принципов усложнения решающего правила непрерывного пространства признаков, порождаемого опорными объектами конкретного образа. Предложена процедура нахождения предельного значения размерности признакового пространства, в котором возможно кусочно-линейное разделение образов и гарантированы требуемые качество и надежность распознавания, необходимые в системах управления.

В работе [1] описан метод формирования пространства непрерывных признаков, приводящий к безошибочному разделению образов. Введено понятие непрерывного признака и показано, что если набирать пространство только из определенных в [1] признаков, то можно достичь безошибочного разделения образов.

В данной работе так же, как и в [2], рассмотрим случай, когда в пространстве непрерывных признаков размерности n безошибочное разделение обучающей последовательности невозможно.

Пусть на некотором множестве мощности объектов определены подмножества при , представляющие собой образы на обучающей выборке

Допустим, что - подмножество на , соответствующее конкретному образу , а - подмножество на , соответствующее остальным образом

Требуется с использованием обучающую выборки найти решающее правило , указывающее принадлежность любого объекта из одному

из заданных образов или с вероятностью ошибки, не превышающей , достигаемой с надежностью (1-), и определить целесообразности усложнения решающих правил при синтезе непрерывных признаковых пространств.

Если обучающая последовательность не может быть безошибочно разделима выбранным решающим правилом, то в общем случае справедлива теорема Вапника - Червоненкиса [3], смысл которой состоит в том, что если в n-мерном пространстве признаков решающее правило совершает ошибок при классификации обучающей последовательности длины , то с вероятностью можно утверждать, что вероятность ошибочной классификации составит величину, меньшую ,

,

где N- число всевозможных правил заданного класса, которое можно построить в пространстве заданной размерности.

Предположим, что в процессе обучения из последовательно поступивших непрерывных свойств относительно опорных объектов синтезирована подсистема непрерывных признаков. В зависимости от состава случайной и независимой выборки процесс обучения может остановиться при любом значении n, но если разделение конкретной обучающей выборки наступило в n-мерном пространстве, то число N всевозможных решающих правил в классе не должно превышать числа всех подмножеств множества, состоящего из элементов, т.е.

,

где

.

Логарифмируя получим

(1)

Если учесть , то (1) принимает вид

, (2)

где 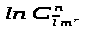можно оценить в виде

(3)

Подставляя (3) в (2), получаем

(4)

Используя теорему Вапника-Червоненкиса [3], можно вычислить предельную размерность пространства

, (5)

которая при заданных гарантирует требуемые  и .

Пусть вычислено максимально допустимое значение размерности пространства в виде (5) и в этом пространстве фиксирована линейная решающая функция

(6)

Далее, для того чтобы в процессе обучения синтезировать пространство, в котором линейное решающее правило (6) безошибочно разделило бы обучающую выборку длины , и при этом размерность пространства не превышала бы , необходимо на признаки наложить дополнительные требования. Зная предельную размерность простанства (8), можно оценить минимально допустимую разделяющую силу каждого выбираемого признака в виде

Минимально допустимая разделяющая сила признака позволяет при синтезе непрерывного пространства использовать не все признаки, а выбирать только те, разделяющая сила которых удовлетворяет неравенству

Допустим, что в синтезированном пространстве непрерывных признаков размерности n линейная решающая функция (9) совершает ошибки с частотой . Тогда рассмотрим соотношение

, (7)

где N* - соответствует решающему правилу, работающему с частотой ошибки , N**- безошибочно разделяющая обучающая последовательность длины .

С использованием этого соотношения, можно установить целесообразность усложнения решающего правила в случае, если в пространстве размерности n ещё не достигнуто безошибочное разделение обучающей выборки.

Известно [3], что если вместо линейного правила используется кусочно-линейное и оно безошибочно разделяет обучающую выборку длины l, то в соответствии (7) вместо n следует выбирать величину

n=nk+k , (8)

где k - число линейных решающих правил, составляющих искомое кусочно - линейное правило. Используя соотношения (7) и (8), ответим на вопрос: стоит ли усложнять решение, если линейное правило в пространстве размерности n не обеспечивает безошибочного разделения обучающей выборки. Для этого нужно сделать подстановку:

, (9)

В этом случае усложнение решающего правила, определяемое числом k, не приведёт к снижению вероятности ошибки, если будет выполнено соотношение (7) после подстановки (8). Из этого условия можно найти такое значение k, выше которого теряет всякий смысл усложнение решающего правила, действующего в пространстве непрерывных признаков размерности n:

. (10)

Таким образом, если выбирать n и k согласно (5) и (10), то процедура позволяет, при синтезе пространства, использовать не все признаки, а выбирать только те, разделяющая сила которых позволяет при заданных обеспечить требуемые значения ε и η.

Список литературы

1. Бекмуратов. К.А. Процедура формирования непрерывных признаковых пространств при последовательном обучении. Узб. Журнал // «Проблемы информатики и энергетики».- 1994.-№4.-С.17-20.

2. К.А. Бекмуратов. Пошаговая проверка целесообразности усложнения решающего правила при последовательном обучении задаче распознавания. Узб. Журнал // «Проблемы информатики и энергетики». -2000. -№1. – С. 16-19.

3. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов.(Статистические проблемы обучения). – М.: Наука, 1974. –С. 415.