Synchronization and effect of Zommerfelda as typical resonant samples

Synchronization and Sommerfeld as Typical Resonant Patterns

Part I. Single Driver Example

Kovriguine D.A.

Abstract We analyze a classical problem of oscillations arising in an elastic base caused by rotor vibrations of an asynchronous driver near the critical angular velocity. The nonlinear coupling between oscillations of the elastic base and rotor takes place naturally due to unbalanced masses. This provides typical frequency-amplitude patterns, even let the elastic properties of the beam be linear one. As the measure of energy dissipation increases the effect of bifurcated oscillations can disappear. The latter circumstance indicates the efficiency of using vibration absorbers to eliminate or stabilize the dynamics of the electromechanical system.

Key Words Sommerfeld effect, asynchronous device; Lyapunov criterion, Routh-Hurwitz criterion, stability.

stationary oscillation resonance synchronization

Introduction

The phenomenon of bifurcated oscillations of an elastic base, while scanning the angular velocity of an asynchronous driver, is referred to the well-known Sommerfeld effect [1-9]. Nowadays, this plays the role of one of classical representative examples of unstable oscillations in electromechanical systems, even being the sub>ject of student laboratory work in many mechanical faculties. This effect is manifested in the fact that the descending branch of resonant curve can not be experienced in practice. A physical interpretation is quite simple. The driver of limited power cannot maintain given amplitude of stationary vibrations of the elastic base. Any detailed measurements can reveal that the oscillation frequency of the base is always somewhat higher than that predicted by linear theory. This implies a very reasonable physical argument. With an increase of base vibrations, for example, the geometric nonlinearity of the elastic base should brightly manifest itself, so that this assuredly may lead to the so-called phenomenon of “pulling” oscillations. However, a more detailed mathematical study can demonstrate that the dynamic phenomena associated with the Sommerfeld effect are of more sub>tle nature. If one interprets this effect as a typical case of resonance in nonlinear systems, then one should come to a very transparent conclusion. The appearance of the frequency-amplitude characteristic naturally encountered in nonlinear systems, say, when regarding the Düffing-type equations, does not necessarily have place due to the geometric nonlinearity of the elastic base. This dependence appears as a result of nonlinear resonant coupling between oscillations of the elastic base and rotor vibrations, even when the elastic properties being absolutely linear one. The latter circumstance may attract an interest in such a remarkable phenomenon, as the effect of Sommerfeld, which is focused in the present paper.

The equations of motion

The equations describing a rotor rolling on an elastic base read [1-6]

;(1)

,

where is the mass of a base with one degree of freedom, characterized by the linear displacement , is the elasticity coefficient of the base, is the damping coefficient, stands for the mass of an eccentric, denotes the radius of inertia of this eccentric, is the moment of inertia of the rotor in the absence of imbalance, is the driving moment, 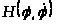describes the torque resistance of the rotor. The single device (unbalanced rotor) set on the platform, while the rotation axis is perpendicular to the direction of oscillation. The angle of rotation of the rotor is measured counter-clockwise. Assume that the moment characteristics and the engine drag torque are modeled by the simple functions and , where is the starting point, is the coefficient characterizing the angular velocity of the rotor, i.e. , is the resistance coefficient. Then the equations of motion are rewritten as

After introducing the dimensionless variables the basic equations hold true:

where is the-small parameter, , , . Here stands for the oscillation frequency of the base, is the new dimensionless linear coordinate measured in fractions of the radius of inertia of the eccentric, is the dimensionless coefficient of energy dissipation, .is the new dimensionless time.

The set (3) is now normalized at the linear part approaching a standard form. First, the equations can be written as a system of four first-order equations

Then we introduce the polar coordinates, and . So that the equations take the following form

Now the set (5) experiences the transform on the angular variable . Then the equations obtain the form close to a standard form

Here denotes the partial angular velocity of the rotor. The system of equations (6) is completely equivalent to the original equations. It is not a standard form, allowed for the higher derivatives [10], but such form is most suitable for the qualitative study of stationary regimes of motion, due to the explicit presence of generalized velocities in the right-hand side terms.

Resonance

We study the resonance phenomenon in the dynamical system (6). Let, then eqs. (6) are reduced to the following set: , , , , which has a simple solution

where , , , 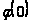are the integration constants. Now the solution (7) is sub>stituted into the right-hand terms of eqs. (6). Then one discards all the terms in order and higher, as well, to perform the averaging over the period of fast rotating phases. In the problem (6) the fast variables are the angles and , accordingly, the slow variables are and . The average of an arbitrary function is calculated as

.

Now the average is examined for the presence of jumps along a smooth change of system parameters. One of which represents the partial angular velocity . It is easy to see that the jump of the average takes place at the value .

The equations of slow motions

In the case when the system is far from resonance, i.e. , eqs. (6) can easily be solved using the Poincaré perturbation method applied to the small non-resonant terms in order. However, in the resonant case, as, the first-order nonlinear approximation solution should contain the so-called secular terms appearing due to the known problems of small denominators. To overcome such a problem one usually applies the following trick. As soon as and the quantities and are changing rapidly, with approximately the same rate, it is natural to introduce a new generalized slow phase , where is a small variation of the angular velocity. Then after the averaging over the fast variable, one obtains the equations for the slow variables only, which are free of secularity. Such equations are called the evolution equations or truncated ones. In the case of set (6) the truncated equations hold true:

where is the small frequency detuning, is the new generalized phase. Note that for the problem of averaging over the fast variable is enough to write .

Stationary oscillations in the absence of energy dissipation

Now the usual condition of a steady motion, i.e. , is applied. We are looking now for the stationary oscillatory regimes in vacuo, i.e. . The solution corresponding to these regimes reads

This solution describes a typical resonant curve at . The plus sign in front of the unit is selected when , otherwise .

The next stage of the study is to test the stability properties of stationary solutions. To solve this problem, one should obtain the equations in perturbations. The procedure for deriving these equations is that, firstly, one performs the following change of variables

where is the steady-state amplitude of oscillations, then after replacing the variables the perturbation equations get the following form

To solve the stability problem evoking the Lyapunov criterion we formulate the eigenvalue problem defined by the following cubic polynomial, implicitly presented by determinant of the third order

Now we can apply one of the most widely known criteria, for example, the Hurwitz criterion, for the study the stability properties in the space of system parameters. The result is that the descending branch of the resonant curve, when, cannot be practically observed because of the volatility associated with the fact that the driver is of limited power. This cannot maintain the given stationary oscillation of the elastic base near the resonance. This result corresponds to the well-known paradigm associated with the so-called Sommerfeld effect.

Formally, there are stable stationary regains, when . However, this range of angular velocity is far beyond the accuracy of the first-order nonlinear approximation.

Damped stationary oscillations

A small surprise is that the response of the electromechanical system (2) has a significant change in the presence of even very small energy dissipation. Depending on the parameters of the set (2) the small damping can lead to typical hysteretic oscillatory patterns when scanning the detuning parameter. While let the dissipation be sufficiently large, then a very simple stable steady-state motions, inherent in almost linear systems, holds true.

From the stationary condition, one looks for the stationary oscillation regimes , and , as . The equations corresponding to these regimes are the following ones

;

;

.

For a small damping the solution of these equations describes a typical non-unique dependence between the frequency and amplitude, i.e. , defined parametrically upon the phase . Near the resonance (), at some given specific parameters of the problem, say, , , and , the picture of this curve is shown in Fig. 1. Accordingly, the dependence of the angular velocity is presented in Fig. 2.

Fig. 1. The frequency-amplitude dependence near the resonance at (arbitrary units).

Fig. 2. The angular velocity changes (arbitrary units).

To study the stability problem of stationary solutions to the perturbed equations we should formulate the eigenvalue problem. This leads to the following characteristic cubic polynomial

with the coefficients¹

;

;

;

.

Now one traces the stability properties by finding the areas of system parameters by applying the Routh-Hurwitz criterion, which states the necessary and sufficient conditions of positivity of the following numbers , , , . These conditions are violated along the frequency-amplitude curve when scanning the parameter between the points A and C. The characteristic points A and B originate from the traditional condition that the derivative of function approaches infinity. The point C appears due to the multiple and zero valued roots of the characteristic equation , as the determinants in the Routh-Hurwitz criterion approach zero, more precisely, . At the direct scanning of the parameter together with increasing the angular velocity of the driver, one can observe a “tightening” of oscillations up to the point A. Then, the upper branch of the resonant curve becomes unstable and the stationary oscillations jump at the lower stable branch. At the reverse scan the angular velocity of the driver at the point C, in turn, there is a loss of stability of stationary oscillations at the lower branch and the jumping to stable oscillations with the greater amplitude at the upper branch of the resonance curve. The point B, apparently, is physically unrealizable mode of oscillations.

However, with the growth of the dissipation the instability zone shrinks. Then the frequency-amplitude curve becomes unambiguous, and the instability zone is completely degenerated. In this case the Sommerfeld effect also disappears.

Conclusions

Near the resonance the rotor is sub>stantially influenced by the pair of forces acting from the vibrating base. The average value of this moment is a definite value proportional to quadrate of the amplitude of vibrations of the base. Therefore, near the resonance some increase in the angular velocity of the engine is experienced. This leads to the phenomenon of ‘pulling’ hesitation, despite the fact that the elastic properties of the base are linear. Together with the growth of dissipation the zone of the Sommerfeld instability narrows down to its complete disappearance. This leads to the idea of efficiency of utilizing vibration absorbers to stabilize the motion of electromechanical systems.

Acknowledgments

The work was supported in part by the RFBR grant (project 09-02-97053-р поволжье).

References

Vibrations in Engineering, v. 2, Moscow. Mechanical Engineering, 1979: 351 (in Russian).

Frolov K.V. Vibrations of machines with limited capacity power source and the variable parameters (Proc. K.V. Frolov ed.), Nonlinear oscillations and transient processes in machines, Moscow: Nauka, 1972: 5-16 (in Russian).

Kononenko V.O. Nonlinear vibrations of mechanical systems. Kiev: Nauk. Dumka, 1980: 382 (in Russian).

Nagaev R.F. Quasiconservative systems. St. Petersburg: Nauka, 1996: 252 (in Russian).

Blekhman I.I. Synchronization in Nature and Technology. Moscow: Nauka, 1977: 345 (in Russian).

Blekhman I.I., Landa P.S., Rosenblum M.G. Synchronization and chaotization in interacting dynamical systems (J) Appl. Mech. Rev., 1995, 11(1): 733-752.

Samantaray A.K., Dasguptaa S.S.and R. Bhattacharyyaa. Sommerfeld effect in rotationally symmetric planar dynamical systems (J), Int. J. Eng. Sci., 2010, 48(1): 21-36.

Masayoshi Tsuchidaa, Karen de Lolo Guilhermeb and Jose Manoel Balthazarb. On chaotic vibrations of a non-ideal system with two degrees of freedom: Resonance and Sommerfeld effect (J), J. Sound and Vibration, 2005, 282(3-5): 1201-1207.

Leonov G.A., Ponomarenko D.V. and Smirnova V.B. Frequency-domain methods for nonlinear analysis. Theory and applications. Singapore: World Sci., 1996: 498.

Zhuravlev V.F., Klimov D.M. Applied methods in oscillation theory, Moscow: Nauka, 1988: 328 (in Russian).

1 It should be noted that the characteristic polynomial coefficients are calculated with a somewhat inflated for the first-order approximation accuracy. In fact, it is easy to prove by series expansion in the small parameter. However, the coefficients in the truncated form are such that again lead to a transcendental equation. Therefore, the value of such asymptotics is small.