Наближене обчислення визначених інтегралів, що не беруться через елементарні функції /Укр./

Наближене обчислення визначених інтегралів, що не беруться через елементарні функції

Зміст

Вступ.

Формули прямокутників і трапеції.

Параболічне інтерполювання.

Дроблення проміжку.

Залишковий член формули прямокутників.

Залишковий член формули трапеції.

Залишковий член формули Сімпсона.

Додаток 1.

Додаток 2.

Висновки.

Література.

Вступ.

Багато задач науки і техніки приводять до проблеми обчислення інтегралів, але не всі інтеграли піддаються обчисленню. В даній роботі разглядається питання наближеного обчислення визначених інтегралів, що не беруться через елементарні функції. Зокрема, виводяться формули наближеного обчислення прямокутників, формула трапецій а також формула Сімпсона.

Формули прямокутників і трапеції.

Нехай треба обчислити значення визначеного інтегралу , де є деяка заданая на проміжку неперервна функція. Існує багато прикладів обчислення подібних інтегралів, або за допомогою первістної, якщо вона виражається в скінченному вигляді, або ж – минуя первістну – за допомогою різних прийомів, як правило, штучних. Потрібно відмітити, однак, що всім цим вичерпується вузький клас интегралів; за його межами зазвичай вдаються до різних методів наближеного обчислення.

В даній роботі можно ознайомитися з основними із цих методів, в яких наближені формули для інтегралів складаються по деякому числу значень підінтегральної функції, обчислених для ряду (зазвичай рівновіддалених) значень незалежної змінної.

Перші формули, які сюди відносяться, простіші всього отримуються із геометричних міркувань. Витлумачуючи визначений інтеграл як площу деякої фігури, яка обмежена кривою , ми і ставимо перед собою задачу знаходження цієї площі.

Перш за все, вдруге використовуючі ту думку, яка привела нас до самого поняття о визначеном інтегралі, можно розбити усю фігуру (мал. 1) на смуги, скажемо однієї і той же ширини , а потім кожну смугу наближено замінити прямокутником, за висоту якого прийнята будь-яка із його ординат. Це приводе нас до формули

,

де . Тут шукана площа криволінійної фігури замінюється площею деякої ступенчатої фігури, яка складається із прямокутників (або ж, можно сказати, що визначений інтеграл замінюється інтегральною сумою). Ця наближена формула і називається формулою прямокутників.

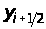На практиці зазвичай беруть _> > якщо відповідну середню ординату _> > позначити через , то формула перепишеться у вигляді

_>>. (1)

Надалі, кажучи про формулу прямокутників, ми будемо мати на увазі якраз цю формулу.

Геометричні міркування природньо приводять і до другої, часто використовуваємій наближеній формулі. Замінивши дану криву вписаною в неї ламаною, з вершинами у точках , где 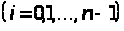. Тоді наша криволінійна фігура заміниться іншою, яка складається із ряду трапецій (рис2.). Якщо, як і раніш рахувати, що
проміжок разбитий на рівні частини, то площі цих трапецій будуть

_>>.

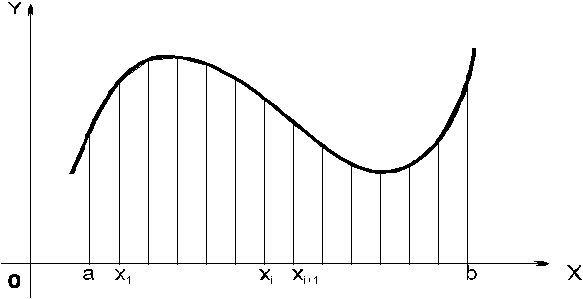
Мал. 2

Додаючи, прийдемо до нової наближеної формули

_>>. (2)

Це так звана формула трапецій.

Можно показати, що при зростанні до нескінченності похибка формули прямокутників і формули трапецій нескінченно зменьшується. Таким чином, при достатньо великому обидві ці формули відтворюють шукане значення з довільним рівнем точності.

Параболічне інтерполювання.

Для наближеного обчислення інтеграла можно спробувати замінити функцію «близьким» до неї многочленом

(3)

і покласти

Можно сказати, що тут – при обрахуванні площі – дана «крива» замінюється на «параболу - го порядку» (3), в зв'язку з чим цем процес отримав назву параболічного интерполювання.

Сам вибір інтерполюючуго многочлена частіше всього виконують наступним чином. У проміжку беруть значень незалежної змінної і підбирають многочлен так, щоб при усіх взятих значеннях його значення співпадало зі значенням функції . Цією умовою, як ми знаємо, многочлен визначається однозначно, і його вираз даеться інтерполяціонною формулою Лагранжа:

При інтерполюванні виходить лінійний, відносно значень вираз, коефіцієнти якого вже не залежать від цих значень. Вирахувавши коефіціенти раз і назавжди, можно їх використовувати для будь-якої функції в даному проміжку .

В найпростішому випадку, при , функція просто замінюється сталою , де – будь-яка точка у проміжку , скажемо, середня: . Тоді наближено

(4)

Геометрично – площа криволінійної фігури замінюється тут площадью прямокутника з висотою, яка рівна середній її ординаті.

При функція замінюється лінійною функцією , яка має однакові з нею значення при и . Якщо взяти , , то

(5)

і, як легко обчислити,

_>>

Таким чином, тут ми наближено вважаємо

На цей раз площа криволінійної фігури замінюється площею трапеції: замість кривої береться хорда, яка зполучає її кінці.

Менш тривіальний результат отримаємо взявши . Якщо покласти , , , то інтерполяційний многочлен буде мати вигляд

(7)

За допомогою легкого обчислення вираховуємо

і, аналогічно

,

.

Таким чином, приходимо до наближеної формули

.

Тут площа фігури під даною кривою замінюється площею фігури, яка обмежена звичайною параболою (з вертикальною віссю), що проходить через крайні і середню точки кривої.

Збільшуя степінь інтерполяційного многочлена, тобто проводя параболу (3) через все більше число даної кривої, можно розраховувати отримати більшу точність. Но більш практичним виявляється інший шлях, якій грунтується на поєднанні ідеї параболічного інтерполювання із ідеєю дроблення.

Дроблення проміжку.

При обчисленні інтегралу можно зроботи так. Розіб'ємо спочатку проміжок на деяке число, , рівних проміжків

,

в зв'язку з чим, шуканий інтеграл постане у вигляді суми

(9)

Тепер же до кожного із цих проміжків застосуємо параболічне інтерполювання, тобто станемо обчислювати інтеграли (9) по одній із наближених формул – (4), (6), (8).

Легко збагнути, що виходячи із формул (4) або (6), ми таким шляхом знов отримаємо вже відомі нам формули прямокутників і трапецій, (1) и (2).

Застосуємо тепер до інтегралів (9) формулу (8), при цьому для стислості положимо, як і вище,

, , .

Ми отримаємо

,

,

. . . . . . . . . . . . . . . . . . . . . . . . . .

.

Зрештою, додаючи почленно ці равенства, прийдемо до формули

_>> (10)

Вона носит назву формули Сімпсона (Th. Simpson); цією формулою користуються для наближенного обчислення інтегралів частіші, аніж формулами прямокутников і трапецій, бо она – при тих же затратах – дає зазвичай більш точний результат.

Залишковий член формули прямокутників.

Почнемо з формули (4). Припустимо, що у проміжку функція має неперервні похідні перших двох порядків. Тогді, розкладая (по формулі Тейлора) за степенями двочлена аж до його квадрату, будемо мати для всіх значень в

,

де міститься між та і залежить від .

Якщо проінтегрувати цю рівність у проміжку від до , то другий член зправа зникне, бо

(11)

Таким чином, отримаємо

,

так, що залишковий член формули (4), який поновлює її точність має вигляд

.

Позначив через і , відповідно найменьше та найбільше значення неперервної функції у проміжку і коростуючись тим, що другий множник підінтегрального виразу на змінює знака, за узагальненою теоремою про середне можемо написати

,

де міститься між точками и . По відомій властивості неперервної функції, знайдеться в така точка , що , і остаточно

. (12)

Якщо зараз розділити проміжок на рівних частин, то для кожного часткового проміжку будемо мати точную формулу

.

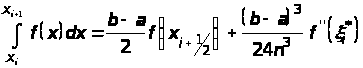
Додавнши ці равенства (при ) почленно отримаємо при звичайних скорочених позначеннях

,

де вираз

і є залишковий член формули прямокутників (1). Так як вираз

також знаходиться між і , то і він представляє одне із значень функції .

Тому остаточно маємо

(13).

При зростанні цей додатковий член спадає приблизно як .¹

Залишковий член формули трапеції.

Займемось тепер формулою (6) при попередніх здогатках відносно функції . Скориставшись інтерполяційною формулою Лагранжа із залишковим членом можемо написати

.

Інтегруя цю формули від до , знайдемо

,

так що залишковий член формули (6) буде

.

Розмірковуючи, як і вище, і користуючись тим, що другий множник підінтегральної функції і тут не змінює знака, знайдемо

.

Нарешті, для випадку ділення проміжку на рівних частин

(14).

Таким є залишковий член формули трапецій (2). При зростанні він також зменьшуеться приблизно як . Ми бачемо, що застосування формули трапецій приводить до похибки того ж порядку, що і для формули прямокутників.

Залишковий член формули Сімпсона.

Звернемося, нарешті до формули (8). Можно було б, аналогічно тому, як це було зроблено тількі що, знов скористатись формулою Лагранжа з залишковим членом і покласти

(15).

Но ми стикаємося тут з таким станом речей, а саме, проінтегрувавши рівність (15), ми не змогли б спростити інтегральний вираз для додаткового члену за допомогою теореми про середне, бо вираз в підінтегральній функції вже змінює знак на проміжку . Тому ми зробимо інакше.

Вираз

,

яким би не було число , в точках , , приймає одні і тіж значення, що і функція . Легко підібрати число так, щоб і похідна цього виразу при співпадала з похідною . Таким чином, при цьому значенні ми маємо не що інше, як інтерполяційний многчлен Эрміта, який відповідаї простим вузлам , і двукратному вузлу . Скориставшись формулою Эрміта з залишковим членом – в пропушенні існування для функції похідних до четвертого порядку включно – отримаємо:

.

Тепер проінтегрувавши цю равність від до ; ми знайдемо, що

так як

.

Якщо припустити похідну неперервною, то, як і в попередніх випадках, залишковий член формули (8)

,

користуючись тим, що другий множник в підінтергальному виразі не змінює знака, можно підставити в такому вигляді²:

_>>.

Якщо проміжок розділити на рівних частин, то – для формули Сімпсона (10) – отримаємо залишковий член у вигляді

(16).

При зростанні цей вираз зменьшується приблизно як ; таким чином, формула Симпсона дійсно більш вигідна, ніж попередні дві формули.

Додаток 1.

Текст программи для автоматичного обчислення інтегралів на мові програмування QBASIC:

'Тут описуються сталі

e = 2.718281828459045#

pi = 3.141592653589793#

'Тут задається від під інтегральної функції

DEF fny# (x#) = e^x# ^2

DEF fncoef# (i#) = (i# MOD 2) * 2 + 2

DEF fnxi# (i#) = a# + i# * h#

DEF fnxis# (i#) = a# + i# * h# / 2

DEF fnxic# (i#) = a# + i# * h# + h# / 2

DEF fnxir# (i#) = a# + i# * h# + h# / 2

CLS

'Тут вводяться межі інтегрування та

'кількість проміжків

INPUT “Введіть нижню межу інтегрування ” a#

INPUT “Введіть верхню межу інтегрування ” b#

INPUT “Введіть кількість проміжків ” n#

'Тут обчислюється крок

h# = (b# - a#) / n#

'Тут обчислюється наближене значення

'інтеграла за методом Сімпсона

integ# = 0

FOR i# = 1 TO ((2 * n#) - 1)

integ# = integ# + fncoef#(i#) * fny#(fnxis#(i#))

NEXT

integ# = integ# + fny#(a#) + fny#(b#)

integ# = integ# * (h# / 6)

PRINT "Simpson = "; integ#

'Тут обчислюється наближене значення

'інтеграла за методом трапецій

integ# = 0

FOR i# = 1 TO (n# - 1)

integ# = integ# + fny#(fnxi#(i#))

NEXT

integ# = integ# + (fny#(a#) + fny#(b#)) / 2

integ# = integ# * h#

PRINT "Trapeze = "; integ#

'Тут обчислюється наближене значення

'інтеграла за методом лівих прямокутників

integ# = 0

FOR i# = 0 TO (n# - 1)

integ# = integ# + fny#(fnxi#(i#))

NEXT

integ# = integ# * h#

PRINT "L Rectangle = "; integ#

'Тут обчислюється наближене значення

'інтеграла за методом центральних прямокутників

integ# = 0

FOR i# = 0 TO n#

integ# = integ# + fny#(fnxic#(i#))

NEXT

integ# = integ# * h#

PRINT "C Rectangle = "; integ#

'Тут обчислюється наближене значення

'інтеграла за методом правих прямокутників

integ# = 0

FOR i# = 1 TO n#

integ# = integ# + fny#(fnxir#(i#))

NEXT

integ# = integ# * h#

PRINT "R Rectangle = "; integ#

Додаток 2.

Далі подані результати роботи програми, яка викладена в додатку 1.

1) в межах від 0 до

n=1000

Метод Сімпсона -8.742278155181581D-08

Метод трапецій -8.742270585611512D-08

Метод лівих прямокутників 3.141505318306509D-03

Метод центральних прямокутників -3.14167628761223D-03

Метод правих прямокутників -6.283265152840917D-03

2) в межах від 0 до

n=1000

Метод Сімпсона 2.000000000000067

Метод трапецій 1.999998355065565

Метод лівих прямокутників 1.999998355202888

Метод центральних прямокутників 1.999995887392223

Метод правих прямокутників 1.999990952591778

3) в межах від 0 до 1

	n=1	n=10	n=100	n=1000	n=10000
М-д Сімпсона	,33333333333	,3333333333333	,3333333333333	,3333333333	,3333333333333
М-д трапецій	,5	,335	,33335	,3333334999999	,3333333349999
М-д лів. прямокутників	0	,2850000000000001	,32835	,3328334999999	,3332833349999
М-д центр. прямокутників	2,5	,44275	,34342525	,33433425025	,3334333425002
М-д правих прсмокутників	2,25	,4425000000000001	,3434249999999	,33433425	,3334333424999

4) в межах від 0 до 1

n=1000

Метод Сімпсона .7468241385662959

Метод трапецій .7468240772530558

Метод лівих прямокутників .7471401375268841

Метод центральних прямокутників .7471916808878213

Метод правих прямокутників .7461916811378212

5) в межах від 0 до

n=1000

Метод Сімпсона .8323745796964475

Метод трапецій .8323723082182791

Метод лівих прямокутників .8325874590746988

Метод центральних прямокутників .8319367429487694

Метод правих прямокутників .8319318081462942

Висновки.

У данній роботі було розглянуто методи наближених обчислень визначених інтегралів, були виведині формули обчислень, формули додаткових членів. Результати, які наведені в додатку 2 наочно показують, що найбільш вигідним є використання формули Сімпсона.

Література.

Пискунов Н. С. Дифференциальное и интегральное исчисление для ВТУЗов. Т. 1 М.: 1968.

Воробьева Г. Н., Данилова А. Н. Практикум по численным методам.
М.: 1979.

Математический практикум. М.: 1960.

1

2