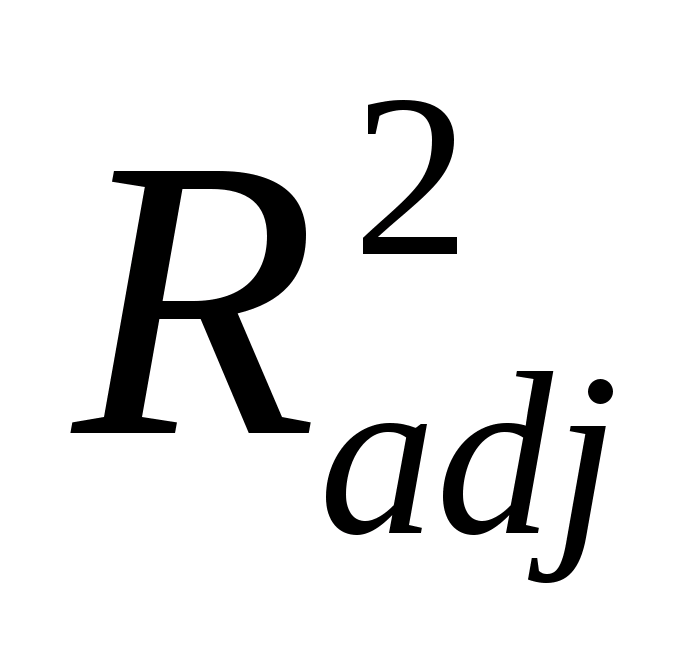Факторы, влияющие на уровень разводов в Российской Федерации
ФАКТОРЫ, ВЛИЯЮЩИЕ НА УРОВЕНЬ РАЗВОДОВ В РОССИЙСКОЙ ФЕДЕРАЦИИ
Оглавление
Введение 3
1.Сбор данных и отбор факторов 4
2.Исследование влияние каждого фактора в отдельности 5
2.1 Исследование влияния величины прожиточного минимума на уровень разводов 5
2.2 Исследование влияния величины среднедушевого денежного дохода на уровень разводов 10
2.3 Исследование влияния числа психических расстройств на уровень разводов 13
2.4 Исследование влияния алкоголизма на уровень разводов 17
2.5 Исследование влияния наркомании на уровень разводов 22
2.6 Исследование влияния числа инвалидов на уровень разводов 25
3.Исследование влияния всех факторов в совокупности 29
Заключение 31
Список использованной литературы: 33
Приложение А 34
Приложение Б 38
Приложение В 41
Приложение Г 43
Приложение Д 45
Приложение Е 47
Приложение Ж 49
Приложение З 51
Введение
развод уровень величина
Тема разводов является достаточно актуальной сегодня с точки зрения Российского законодательства и международного частного права. Возрастающее количество распавшихся семей привлекает внимание различных специалистов. Поэтому изучение зависимости уровня разводов важно для людей, чтобы понять, стоит ли заключать брак. В настоящее время для студентов изучение данной темы представляется более значимым, так как в ближайшее время они столкнутся с выбором места работы, местом их проживания. Следовательно, им важно знать, какие факторы могут повлиять на их будущую жизнь с выбранной ими второй половинкой.
Цель данного исследования – выявление факторов, которые могут повлиять на уровень разводов в Российской Федерации, выбрать из них наиболее значимые и установить вид зависимости уровня разводов от этих факторов.
Сбор данных и отбор факторов
Для проведения исследования были отобраны следующие факторы, которые влияют на уровень разводов:
 величина
прожиточного минимума (руб.);
величина
прожиточного минимума (руб.);
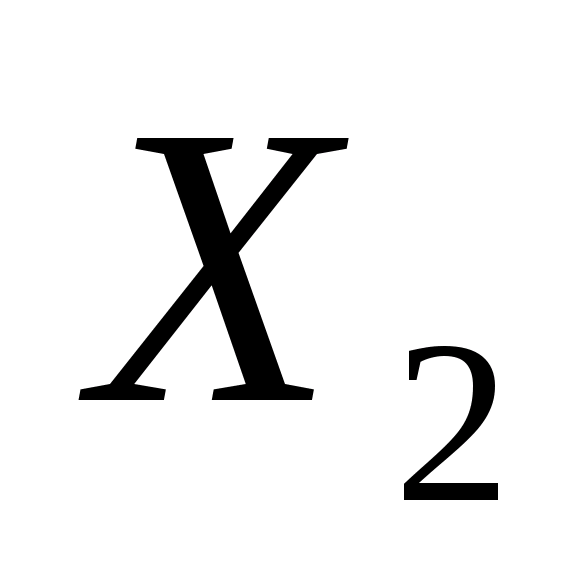 среднедушевой
денежный доход (руб.);
среднедушевой
денежный доход (руб.);
 психические
расстройства (чел.);
психические
расстройства (чел.);
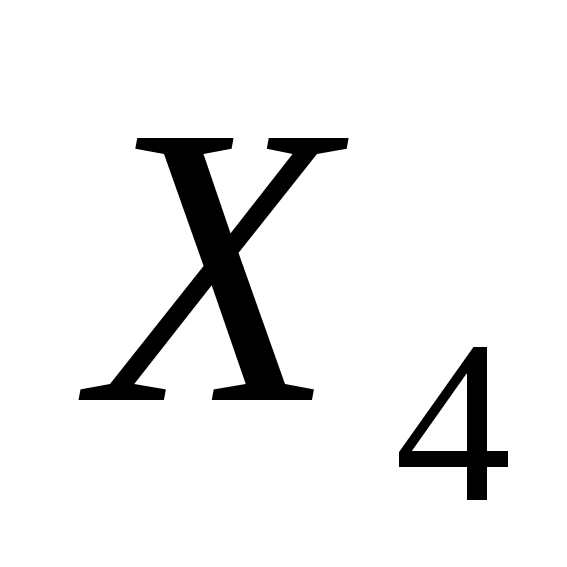 алкоголизм
(чел.);
алкоголизм
(чел.);
 наркомания
(чел.);
наркомания
(чел.);
 инвалидность
(тыс.чел.).
инвалидность
(тыс.чел.).
В качестве результирующего признака (уровня разводов) были использованы данные по количеству разводов за 2009 год по субъектам РФ. Для исследования использовались данные, отражающие вариацию факторов и результирующего признака в региональном разрезе. В данном исследовании не задействованы данные по двум городам федерального значения: Москва и Санкт-Петербург. Это объясняется серьезным различием в экономическом и социальном развитии.
В исследовании использовались данные Федеральной службы государственной статистики (Росстат) за 2009 год по субъектам РФ1. Далее будет рассмотрено влияние каждого из приведенных выше факторов на уровень разводов в отдельности и влияние всех этих факторов в совокупности.
Исследование влияние каждого фактора в отдельности
2.1 Исследование влияния величины прожиточного минимума на уровень разводов
Представим исходные данные об уровне разводов и величине прожиточного минимума по субъектам РФ на 2009 год в виде статистической таблицы, которая достаточно удобна для анализа (табл. 1).
Табл.1. Уровень разводов и величина прожиточного минимума
|
Субъекты РФ |
Число разводов за год (У) |
Величина прожиточного минимума (Х1) |
|
Белгородская область |
6641 |
4037 |
|
Брянская область |
7056 |
4155,5 |
|
Владимирская область |
7133 |
4815,25 |
|
Воронежская область |
12048 |
4343,75 |
|
Ивановская область |
5152 |
4534 |
|
Калужская область |
5304 |
4406,25 |
|
Костромская область |
3330 |
4506,25 |
|
Курская область |
6039 |
4174,25 |
|
Липецкая область |
6035 |
4226 |
|
Московская область |
37069 |
5704,25 |
|
Орловская область |
3954 |
3949,25 |
|
Рязанская область |
5651 |
4649,5 |
|
Смоленская область |
5406 |
4653,75 |
|
Тамбовская область |
5102 |
3715,5 |
|
Тверская область |
7243 |
4791,5 |
|
Тульская область |
7760 |
4647,25 |
|
Ярославская область |
6484 |
5034,75 |
|
Республика Карелия |
3543 |
5743 |
|
Республика Коми |
5259 |
6486,5 |
|
Архангельская область |
6527 |
5915,75 |
|
Ненецкий авт.округ |
220 |
8762,5 |
|
Вологодская область |
6587 |
5141,75 |
|
Калининградская область |
5097 |
5129 |
|
Ленинградская область |
8478 |
4414 |
|
Мурманская область |
5838 |
6978,5 |
|
Новгородская область |
3226 |
4931,5 |
|
Псковская область |
3295 |
4487,25 |
|
Республика Адыгея |
1757 |
4276,75 |
|
Республика Калмыкия |
1168 |
3872,25 |
|
Краснодарский край |
24756 |
4633 |
|
Астраханская область |
5346 |
4514 |
|
Волгоградская область |
12798 |
4539,75 |
|
Ростовская область |
21961 |
4551,75 |
|
Республика Дагестан |
4144 |
3700,25 |
|
Республика Ингушетия |
378 |
4150 |
|
Кабардино-Балкарская Республика |
2342 |
3661,5 |
|
Карачаево-Черкесская Республика |
1394 |
3839,5 |
|
Республика Северная Осетия-Алания |
1982 |
3729,5 |
|
Ставропольский край |
12121 |
4503 |
|
Республика Башкортостан |
17453 |
4140,5 |
|
Республика Марий Эл |
2926 |
4083 |
|
Республика Мордовия |
3462 |
4039,75 |
|
Республика Татарстан |
15671 |
4186 |
|
Удмуртская Республика |
6100 |
4297,75 |
|
Чувашская Республика |
4786 |
4178 |
|
Пермский край |
12295 |
5295,75 |
|
Кировская область |
6465 |
4621,25 |
|
Нижегородская область |
17275 |
4964 |
|
Оренбургская область |
10412 |
4238,25 |
|
Пензенская область |
7279 |
4320,75 |
|
Самарская область |
16555 |
5412,75 |
|
Саратовская область |
12110 |
4523 |
|
Ульяновская область |
7037 |
4343,25 |
|
Курганская область |
5441 |
4584 |
|
Свердловская область |
22765 |
4918,5 |
|
Тюменская область |
21202 |
4870,5 |
|
Ханты-Мансийский авт.округ-Югра |
10732 |
7684,5 |
|
Ямало-Ненецкий авт.округ |
3610 |
7972 |
|
Челябинская область |
21686 |
4607,5 |
|
Республика Алтай |
1076 |
5852,25 |
|
Республика Бурятия |
4140 |
4938,25 |
|
Республика Тыва |
632 |
4912,75 |
|
Республика Хакасия |
2808 |
4647,5 |
|
Алтайский край |
13313 |
4530,5 |
|
Красноярский край |
16401 |
5600,5 |
|
Иркутская область |
12330 |
4900,75 |
|
Кемеровская область |
15577 |
4278,5 |
|
Новосибирская область |
15769 |
5217 |
|
Омская область |
10524 |
4751,5 |
|
Томская область |
5602 |
5075 |
|
Республика Саха (Якутия) |
4529 |
7908,75 |
|
Камчатский край |
2351 |
9871,5 |
|
Приморский край |
10530 |
6283,25 |
|
Хабаровский край |
8118 |
7202 |
|
Амурская область |
5062 |
5959,25 |
|
Магаданская область |
1304 |
7579,75 |
|
Сахалинская область |
3446 |
7645,75 |
|
Еврейская автономная область |
985 |
5734,75 |
|
Чукотский авт.округ |
406 |
10005,5 |
Для
изучения фактора
 на результирующий признак
на результирующий признак
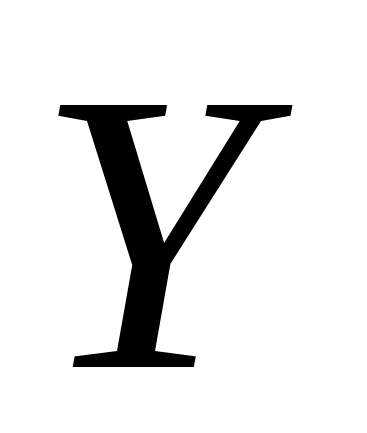 необходимо сначала построить поле
корреляции (рис. 1).
необходимо сначала построить поле
корреляции (рис. 1).
При его рассмотрении трудно точно выявить вид зависимости, но можно сделать предположение о существовании нескольких возможных видов зависимостей:
линейная зависимость;
гиперболическая зависимость;
логарифмическая зависимость;
квадратичная зависимость;
степенная зависимость.
Была изучена возможность существования каждой из этих видов зависимостей. Получены следующие уравнения парных регрессий:
линейная
зависимость
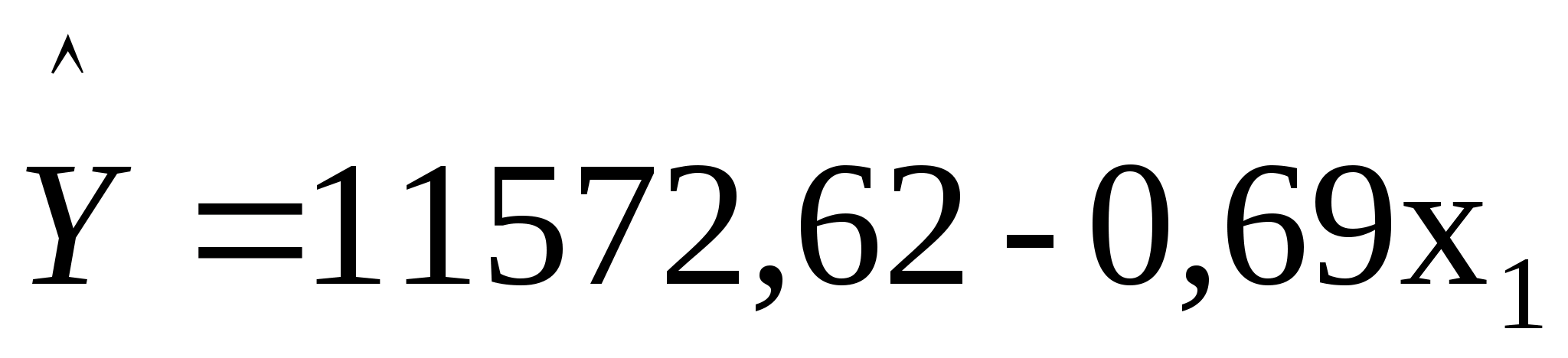 ;
;
гиперболическая
зависимость
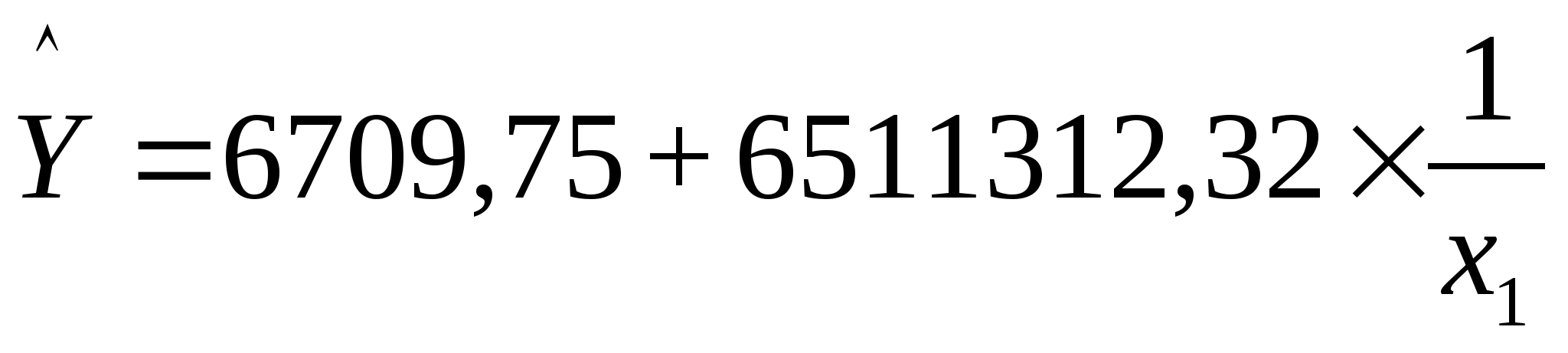 ;
;
логарифмическая
зависимость
 ;
;
квадратичная
зависимость
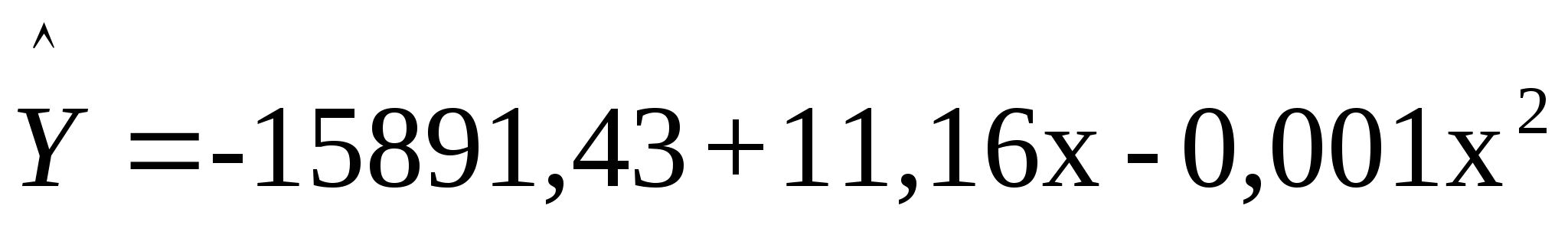 ;
;
степенная
зависимость
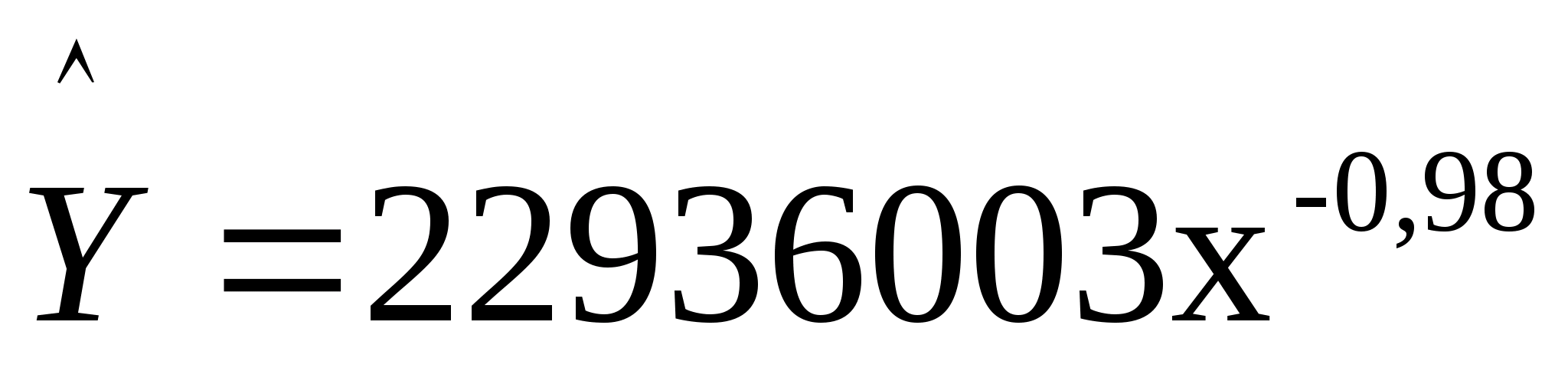 .
.

Рис.1.
Корреляционное поле
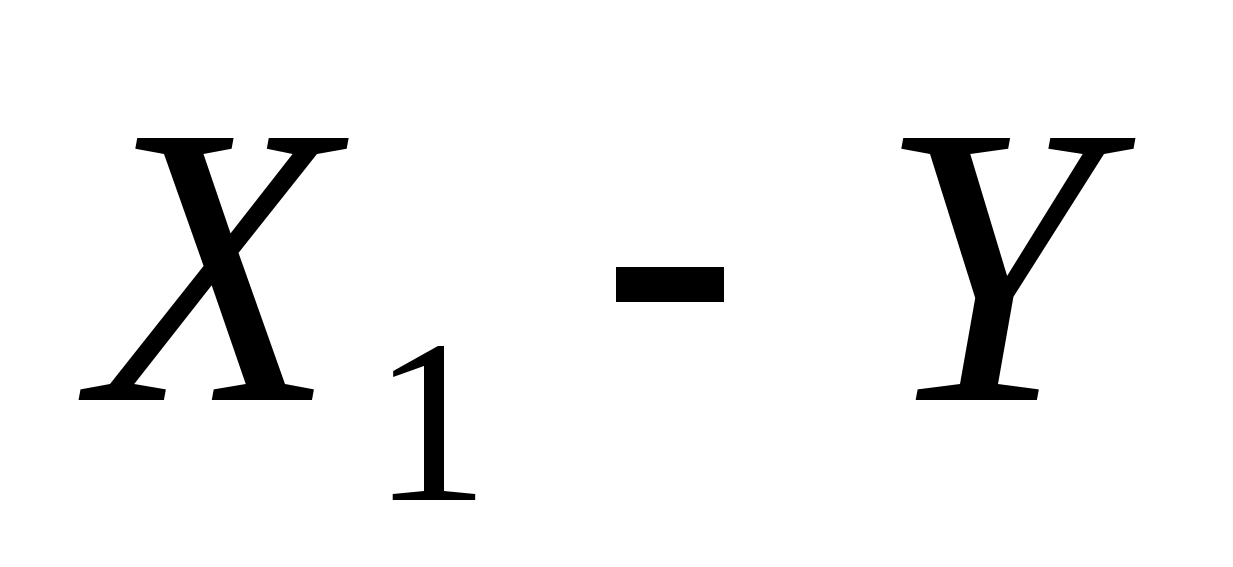
Для того чтобы осуществить выбор в пользу какой-либо из них, необходимо использовать следующие критерии:
метод абсолютных отклонений. Лучшей из нескольких моделей является та, у которой этот показатель наименьший;
средняя ошибка аппроксимации. Чем меньше эта ошибка, тем лучше построенная модель аппроксимирует наблюдаемые данные;
коэффициент детерминации. Изменяется от нуля до единицы. Чем ближе к единице, тем лучше регрессия аппроксимирует данные;
оценка стандартного отклонения остатков. Является несмещенной оценкой дисперсии.
Табл. 2. Значения критериев отбора модели.
|
Тип модели |
R^2 |
Ā |
MAD |
Sост |
|
линейная |
0,02 |
185,90% |
65,366702 |
6716,85 |
|
квадратичная |
0,10 |
170,74% |
61,464397 |
6475,26 |
|
гипербол(обратная) |
0,00 |
204,05% |
64,375875 |
6776,72 |
|
степенная |
0,05 |
123,19% |
59,348639 |
0,97 |
|
показательная |
0,08 |
8,87% |
0,0090476 |
0,96 |
|
логарифмическая |
0,01 |
99,70% |
101,76518 |
6753,78 |
На основе сравнения полученных результатов выбор был сделан в пользу показательной модели.
По
критерию Фишера модель является значимой,
т.к.
 ,
где
,
где
 и
и
 .
.
Оценим
тесноту связи с помощью коэффициента
детерминации, который равен
 .
Это говорит о том, что лишь
8% вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 92% вариации объясняются
неучтенными в модели факторами.
.
Это говорит о том, что лишь
8% вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 92% вариации объясняются
неучтенными в модели факторами.
Отсюда можно сделать вывод, что математическая модель, выражающая данную зависимость объясняющей переменной, не подходит для описания зависимой переменной. Поэтому включение данного фактора в модель множественной регрессии нецелесообразно.
2.2 Исследование влияния величины среднедушевого денежного дохода на уровень разводов
Представим исходные данные об уровне разводов и величине среднедушевого денежного дохода по субъектам РФ на 2009 год в виде статистической таблицы, которая достаточно удобна для анализа (табл. 3).
Табл.3. Уровень разводов и величина среднедушевого денежного дохода
|
Субъекты РФ |
Число разводов за год (Y) |
Среднедушевой денежный доход (X2) |
|
Белгородская область |
6641 |
12757,9 |
|
Брянская область |
7056 |
10042,6 |
|
Владимирская область |
7133 |
9596,2 |
|
Воронежская область |
12048 |
10304,8 |
|
Ивановская область |
5152 |
8353,8 |
|
Калужская область |
5304 |
11755,9 |
|
Костромская область |
3330 |
9413,2 |
|
Курская область |
6039 |
11411 |
|
Липецкая область |
6035 |
12274,4 |
|
Московская область |
37069 |
19776 |
|
Орловская область |
3954 |
9814,5 |
|
Рязанская область |
5651 |
11311,3 |
|
Смоленская область |
5406 |
11522,7 |
|
Тамбовская область |
5102 |
11252,8 |
|
Тверская область |
7243 |
10856 |
|
Тульская область |
7760 |
11388,5 |
|
Ярославская область |
6484 |
12587,2 |
|
Республика Карелия |
3543 |
12228,6 |
|
Республика Коми |
5259 |
18636,4 |
|
Архангельская область |
6527 |
14823,6 |
|
Ненецкий авт.округ |
220 |
48764,9 |
|
Вологодская область |
6587 |
12193,5 |
|
Калининградская область |
5097 |
12922,3 |
|
Ленинградская область |
8478 |
12014,4 |
|
Мурманская область |
5838 |
18773,2 |
|
Новгородская область |
3226 |
11645,6 |
|
Псковская область |
3295 |
10290,9 |
|
Республика Адыгея |
1757 |
7986,3 |
|
Республика Калмыкия |
1168 |
5651,2 |
|
Краснодарский край |
24756 |
12023,9 |
|
Астраханская область |
5346 |
11120,4 |
|
Волгоградская область |
12798 |
10866,4 |
|
Ростовская область |
21961 |
12160,5 |
|
Республика Дагестан |
4144 |
10962 |
|
Республика Ингушетия |
378 |
5512,9 |
|
Кабардино-Балкарская Республика |
2342 |
8589,3 |
|
Карачаево-Черкесская Республика |
1394 |
8676,1 |
|
Республика Северная Осетия-Алания |
1982 |
9837,7 |
|
Ставропольский край |
12121 |
9952,5 |
|
Республика Башкортостан |
17453 |
14252,7 |
|
Республика Марий Эл |
2926 |
7843,4 |
|
Республика Мордовия |
3462 |
8384,2 |
|
Республика Татарстан |
15671 |
14180,5 |
|
Удмуртская Республика |
6100 |
9581,1 |
|
Чувашская Республика |
4786 |
8593,6 |
|
Пермский край |
12295 |
16119 |
|
Кировская область |
6465 |
10112,2 |
|
Нижегородская область |
17275 |
13090 |
|
Оренбургская область |
10412 |
10184 |
|
Пензенская область |
7279 |
10172,9 |
|
Самарская область |
16555 |
15805,2 |
|
Саратовская область |
12110 |
9061,5 |
|
Ульяновская область |
7037 |
9756,4 |
|
Курганская область |
5441 |
11160,8 |
|
Свердловская область |
22765 |
17171,3 |
|
Тюменская область |
21202 |
27612,2 |
|
Ханты-Мансийский авт.округ-Югра |
10732 |
32871,9 |
|
Ямало-Ненецкий авт.округ |
3610 |
38133,4 |
|
Челябинская область |
21686 |
14161,2 |
|
Республика Алтай |
1076 |
10172,5 |
|
Республика Бурятия |
4140 |
11298,5 |
|
Республика Тыва |
632 |
7871,2 |
|
Республика Хакасия |
2808 |
10763,9 |
|
Алтайский край |
13313 |
9748,6 |
|
Красноярский край |
16401 |
15604,5 |
|
Иркутская область |
12330 |
12881,6 |
|
Кемеровская область |
15577 |
14439,3 |
|
Новосибирская область |
15769 |
12838,1 |
|
Омская область |
10524 |
13626,5 |
|
Томская область |
5602 |
13481,7 |
|
Республика Саха (Якутия) |
4529 |
18740,8 |
|
Камчатский край |
2351 |
19063 |
|
Приморский край |
10530 |
12807,8 |
|
Хабаровский край |
8118 |
15705,1 |
|
Амурская область |
5062 |
11936,3 |
|
Магаданская область |
1304 |
19703,2 |
|
Сахалинская область |
3446 |
24552,3 |
|
Еврейская автономная область |
985 |
10876,9 |
|
Чукотский авт.округ |
406 |
32140,4 |
Для
выявления влияния фактора
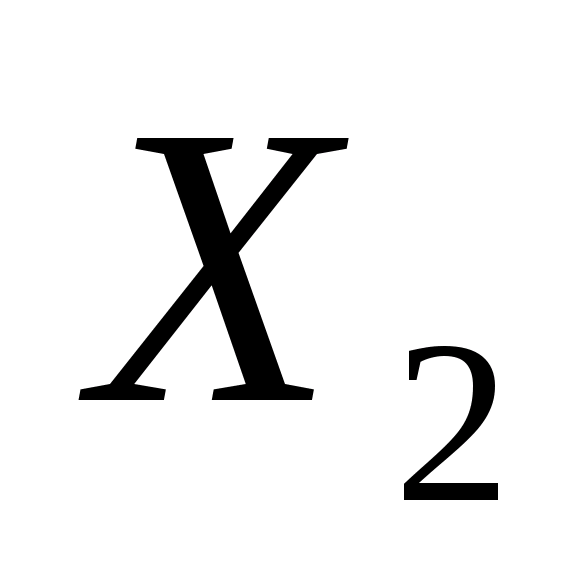 на результирующий признак
на результирующий признак
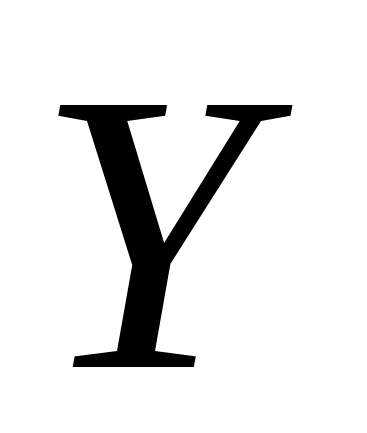 необходимо
сначала построить поле корреляции (рис.
2).
необходимо
сначала построить поле корреляции (рис.
2).
При
его рассмотрении можно заявить, что
наиболее подходящей не будет никакая
модель, т.к. ни одна визуально не отражает
зависимость
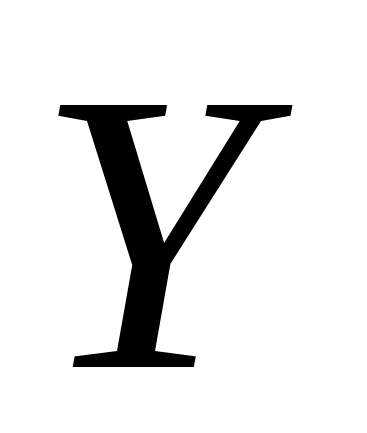 от фактора
от фактора
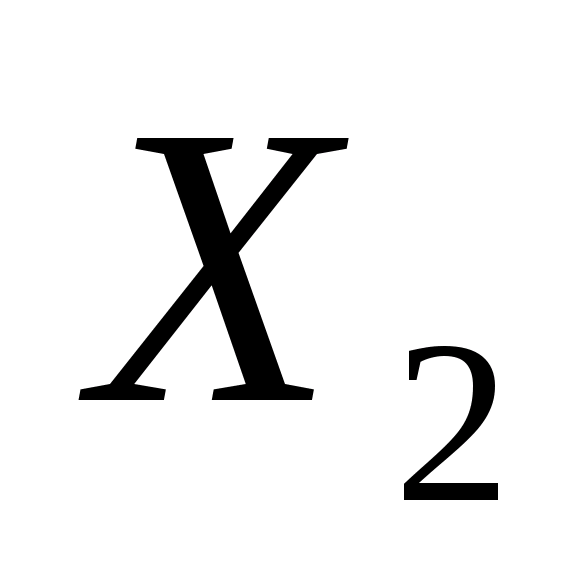 .
Также мы можем увидеть это из данных
приведенных в следующей таблице (табл.
4).
.
Также мы можем увидеть это из данных
приведенных в следующей таблице (табл.
4).

Рис.2.
Корреляционное поле

Табл. 4. Значения критериев отбора модели
|
Тип модели |
R^2 |
Ā |
MAD |
Sост |
|
линейная |
0,01 |
223,06% |
65,393156 |
6761,04 |
|
квадратичная |
0,18 |
165,59% |
57,119903 |
6192,06 |
|
гипербол(обратная) |
0,09 |
204,57% |
59,23613 |
6452,18 |
|
степенная |
0,00 |
145,56% |
58,709741 |
1,00 |
|
показательная |
0,02 |
9,01% |
0,009154 |
0,99 |
|
логарифмическая |
0,04 |
99,67% |
101,7535 |
6629,04 |
Можно сделать вывод, что нет математической модели, выражающей данную зависимость объясняющей переменной, т.е. ни одна модель не подходит для описания зависимой переменной. Поэтому включение данного фактора в модель множественной регрессии нецелесообразно.
2.3 Исследование влияния числа психических расстройств на уровень разводов
Представим исходные данные об уровне разводов и числе психических расстройств по субъектам РФ на 2009 год в виде статистической таблицы, которая достаточно удобна для анализа (табл. 5).
Табл.5. Уровень разводов и число психических расстройств
|
Субъекты РФ |
Число разводов за год (Y) |
Психические расстройства (X3) |
|
Белгородская область |
6641 |
643 |
|
Брянская область |
7056 |
727 |
|
Владимирская область |
7133 |
596 |
|
Воронежская область |
12048 |
1864 |
|
Ивановская область |
5152 |
478 |
|
Калужская область |
5304 |
339 |
|
Костромская область |
3330 |
318 |
|
Курская область |
6039 |
554 |
|
Липецкая область |
6035 |
617 |
|
Московская область |
37069 |
2289 |
|
Орловская область |
3954 |
242 |
|
Рязанская область |
5651 |
525 |
|
Смоленская область |
5406 |
599 |
|
Тамбовская область |
5102 |
501 |
|
Тверская область |
7243 |
718 |
|
Тульская область |
7760 |
588 |
|
Ярославская область |
6484 |
1135 |
|
Республика Карелия |
3543 |
225 |
|
Республика Коми |
5259 |
470 |
|
Архангельская область |
6527 |
330 |
|
Ненецкий авт.округ |
220 |
10 |
|
Вологодская область |
6587 |
570 |
|
Калининградская область |
5097 |
446 |
|
Ленинградская область |
8478 |
454 |
|
Мурманская область |
5838 |
219 |
|
Новгородская область |
3226 |
821 |
|
Псковская область |
3295 |
417 |
|
Республика Адыгея |
1757 |
182 |
|
Республика Калмыкия |
1168 |
195 |
|
Краснодарский край |
24756 |
1208 |
|
Астраханская область |
5346 |
364 |
|
Волгоградская область |
12798 |
468 |
|
Ростовская область |
21961 |
2210 |
|
Республика Дагестан |
4144 |
2623 |
|
Республика Ингушетия |
378 |
234 |
|
Кабардино-Балкарская Республика |
2342 |
530 |
|
Карачаево-Черкесская Республика |
1394 |
221 |
|
Республика Северная Осетия-Алания |
1982 |
386 |
|
Ставропольский край |
12121 |
1035 |
|
Республика Башкортостан |
17453 |
2276 |
|
Республика Марий Эл |
2926 |
499 |
|
Республика Мордовия |
3462 |
397 |
|
Республика Татарстан |
15671 |
2407 |
|
Удмуртская Республика |
6100 |
946 |
|
Чувашская Республика |
4786 |
958 |
|
Пермский край |
12295 |
1658 |
|
Кировская область |
6465 |
622 |
|
Нижегородская область |
17275 |
1334 |
|
Оренбургская область |
10412 |
1632 |
|
Пензенская область |
7279 |
654 |
|
Самарская область |
16555 |
1014 |
|
Саратовская область |
12110 |
2480 |
|
Ульяновская область |
7037 |
484 |
|
Курганская область |
5441 |
125 |
|
Свердловская область |
22765 |
3033 |
|
Тюменская область |
21202 |
1356 |
|
Ханты-Мансийский авт.округ-Югра |
10732 |
546 |
|
Ямало-Ненецкий авт.округ |
3610 |
118 |
|
Челябинская область |
21686 |
2792 |
|
Республика Алтай |
1076 |
221 |
|
Республика Бурятия |
4140 |
692 |
|
Республика Тыва |
632 |
59 |
|
Республика Хакасия |
2808 |
670 |
|
Алтайский край |
13313 |
1782 |
|
Красноярский край |
16401 |
1945 |
|
Иркутская область |
12330 |
2396 |
|
Кемеровская область |
15577 |
2901 |
|
Новосибирская область |
15769 |
1662 |
|
Омская область |
10524 |
1325 |
|
Томская область |
5602 |
722 |
|
Республика Саха (Якутия) |
4529 |
711 |
|
Камчатский край |
2351 |
150 |
|
Приморский край |
10530 |
1037 |
|
Хабаровский край |
8118 |
938 |
|
Амурская область |
5062 |
843 |
|
Магаданская область |
1304 |
240 |
|
Сахалинская область |
3446 |
356 |
|
Еврейская автономная область |
985 |
91 |
|
Чукотский авт.округ |
406 |
39 |
Для
выявления влияния фактора
 на результирующий признак
на результирующий признак
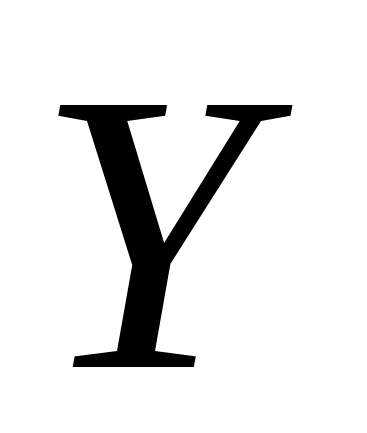 необходимо
сначала построить поле корреляции (рис.
3).
необходимо
сначала построить поле корреляции (рис.
3).

Рис.3.
Корреляционное поле

При
его рассмотрении можно сказать, что
наиболее подходящей будет степенная
модель, т.к. она визуально отражает
зависимость
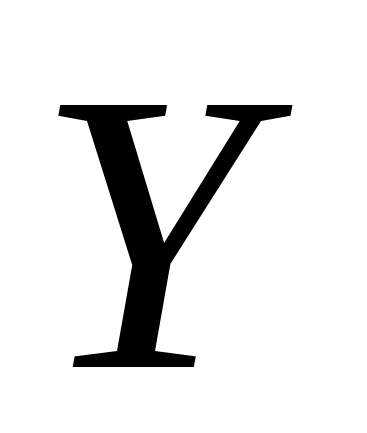 от фактора
от фактора
 .
Также мы можем это увидеть из данных
приведенных в табл. 6.
.
Также мы можем это увидеть из данных
приведенных в табл. 6.
Табл. 6. Значения критериев отбора модели
|
Тип модели |
R^2 |
Ā |
MAD |
Sост |
|
линейная |
0,58 |
78,37% |
35,079544 |
4416,73 |
|
квадратичная |
0,61 |
50,77% |
33,857617 |
4283,81 |
|
гипербол(обратная) |
0,07 |
188,12% |
62,695746 |
6543,16 |
|
степенная |
0,72 |
46,64% |
33,378383 |
0,53 |
|
показательная |
0,48 |
6,70% |
0,0067243 |
0,72 |
|
логарифмическая |
0,49 |
99,83% |
101,79224 |
4841,05 |
Уравнение данной модели выглядит следующим образом:
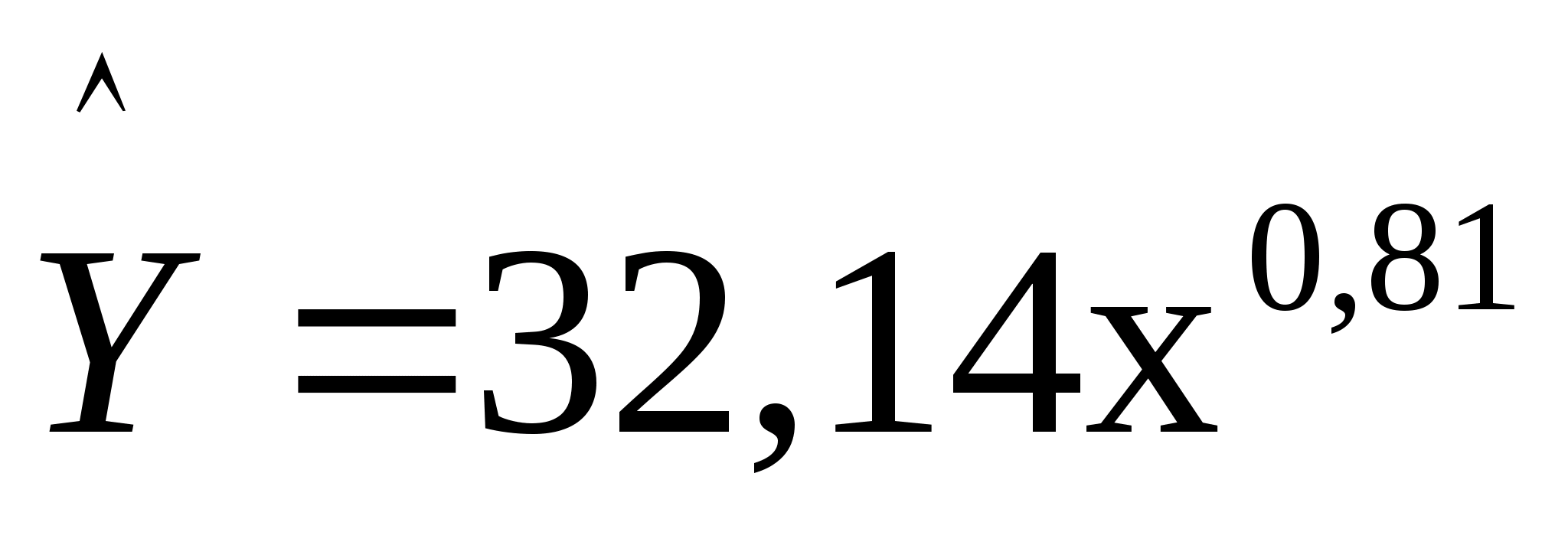 .
.
По
критерию Фишера модель является значимой,
т.к.
 ,
где
,
где
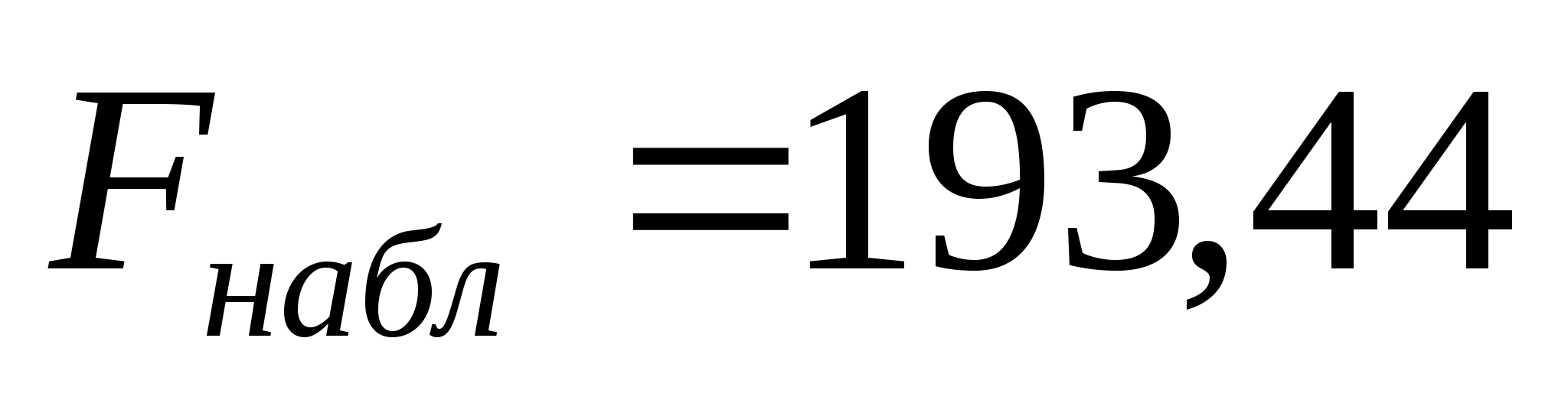 и
и
 .
.
Оценим
тесноту связи с помощью коэффициента
детерминации, который равен
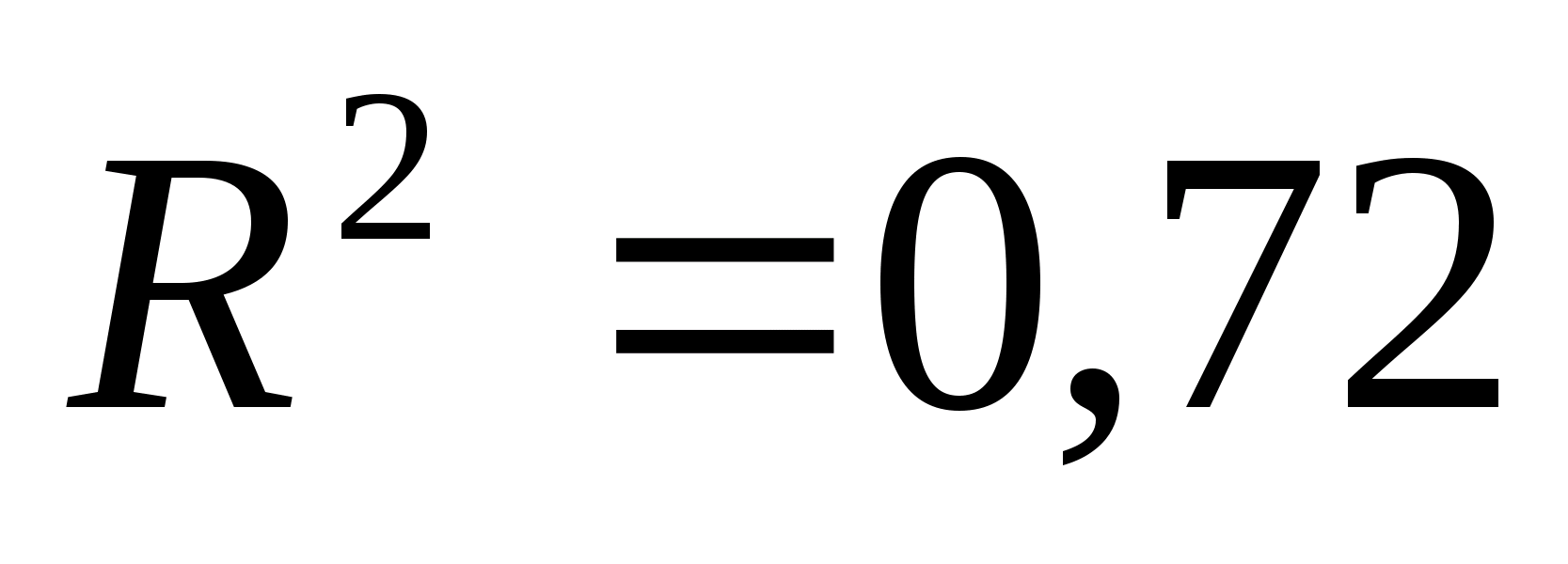 .
Это говорит о том, что 72%
вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 28% вариации объясняются
неучтенными в модели факторами.
.
Это говорит о том, что 72%
вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 28% вариации объясняются
неучтенными в модели факторами.
Итак, математическая модель, выражающая данную зависимость объясняющей переменной, подходит для описания зависимой переменной. Включение этого фактора в модель множественной регрессии целесообразно.
2.4 Исследование влияния алкоголизма на уровень разводов
Представим исходные данные об уровне разводов и числе психических расстройств по субъектам РФ на 2009 год в виде статистической таблицы, которая достаточно удобна для анализа (табл. 7).
Табл.7. Уровень разводов и уровень алкоголизма
|
Субъекты РФ |
Число разводов за год (Y) |
Алкоголизм (X4) |
|
Белгородская область |
6641 |
1405 |
|
Брянская область |
7056 |
2944 |
|
Владимирская область |
7133 |
2095 |
|
Воронежская область |
12048 |
3551 |
|
Ивановская область |
5152 |
1958 |
|
Калужская область |
5304 |
1662 |
|
Костромская область |
3330 |
749 |
|
Курская область |
6039 |
2375 |
|
Липецкая область |
6035 |
2147 |
|
Московская область |
37069 |
7342 |
|
Орловская область |
3954 |
900 |
|
Рязанская область |
5651 |
1476 |
|
Смоленская область |
5406 |
1888 |
|
Тамбовская область |
5102 |
1566 |
|
Тверская область |
7243 |
2052 |
|
Тульская область |
7760 |
2640 |
|
Ярославская область |
6484 |
1892 |
|
Республика Карелия |
3543 |
1277 |
|
Республика Коми |
5259 |
2112 |
|
Архангельская область |
6527 |
1138 |
|
Ненецкий авт.округ |
220 |
128 |
|
Вологодская область |
6587 |
1510 |
|
Калининградская область |
5097 |
947 |
|
Ленинградская область |
8478 |
2088 |
|
Мурманская область |
5838 |
1110 |
|
Новгородская область |
3226 |
1339 |
|
Псковская область |
3295 |
1272 |
|
Республика Адыгея |
1757 |
587 |
|
Республика Калмыкия |
1168 |
317 |
|
Краснодарский край |
24756 |
4963 |
|
Астраханская область |
5346 |
1165 |
|
Волгоградская область |
12798 |
3020 |
|
Ростовская область |
21961 |
3680 |
|
Республика Дагестан |
4144 |
860 |
|
Республика Ингушетия |
378 |
3 |
|
Кабардино-Балкарская Республика |
2342 |
728 |
|
Карачаево-Черкесская Республика |
1394 |
350 |
|
Республика Северная Осетия-Алания |
1982 |
553 |
|
Ставропольский край |
12121 |
1505 |
|
Республика Башкортостан |
17453 |
4599 |
|
Республика Марий Эл |
2926 |
1005 |
|
Республика Мордовия |
3462 |
1394 |
|
Республика Татарстан |
15671 |
2929 |
|
Удмуртская Республика |
6100 |
1778 |
|
Чувашская Республика |
4786 |
2139 |
|
Пермский край |
12295 |
4853 |
|
Кировская область |
6465 |
2094 |
|
Нижегородская область |
17275 |
3734 |
|
Оренбургская область |
10412 |
3128 |
|
Пензенская область |
7279 |
3167 |
|
Самарская область |
16555 |
3773 |
|
Саратовская область |
12110 |
3048 |
|
Ульяновская область |
7037 |
2108 |
|
Курганская область |
5441 |
1466 |
|
Свердловская область |
22765 |
5362 |
|
Тюменская область |
21202 |
5071 |
|
Ханты-Мансийский авт.округ-Югра |
10732 |
2413 |
|
Ямало-Ненецкий авт.округ |
3610 |
863 |
|
Челябинская область |
21686 |
5034 |
|
Республика Алтай |
1076 |
276 |
|
Республика Бурятия |
4140 |
994 |
|
Республика Тыва |
632 |
311 |
|
Республика Хакасия |
2808 |
656 |
|
Алтайский край |
13313 |
5000 |
|
Красноярский край |
16401 |
4775 |
|
Иркутская область |
12330 |
4659 |
|
Кемеровская область |
15577 |
3297 |
|
Новосибирская область |
15769 |
2497 |
|
Омская область |
10524 |
2027 |
|
Томская область |
5602 |
1047 |
|
Республика Саха (Якутия) |
4529 |
2726 |
|
Камчатский край |
2351 |
583 |
|
Приморский край |
10530 |
2227 |
|
Хабаровский край |
8118 |
1877 |
|
Амурская область |
5062 |
982 |
|
Магаданская область |
1304 |
868 |
|
Сахалинская область |
3446 |
1703 |
|
Еврейская автономная область |
985 |
471 |
|
Чукотский авт.округ |
406 |
263 |
Для
выявления влияния фактора
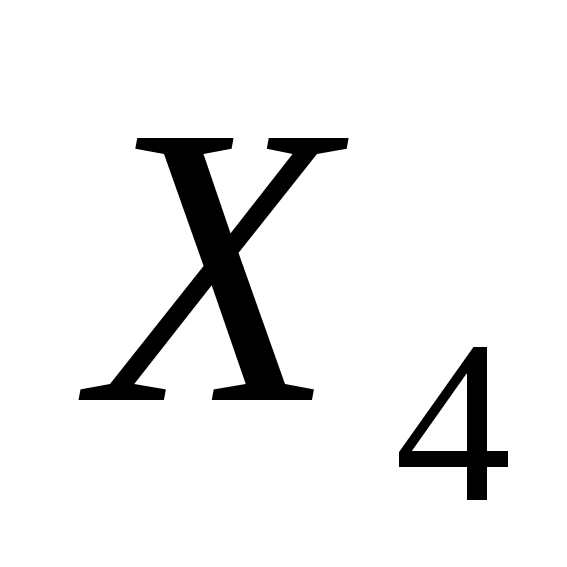 на результирующий признак
на результирующий признак
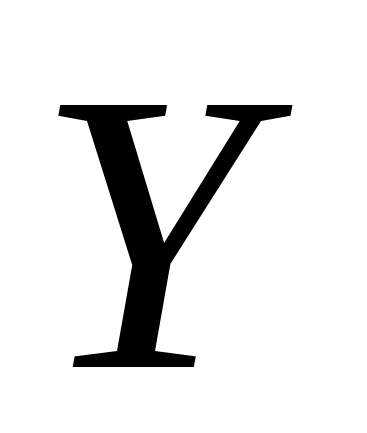 необходимо
сначала построить поле корреляции (рис.
4).
необходимо
сначала построить поле корреляции (рис.
4).

Рис.4.
Корреляционное поле
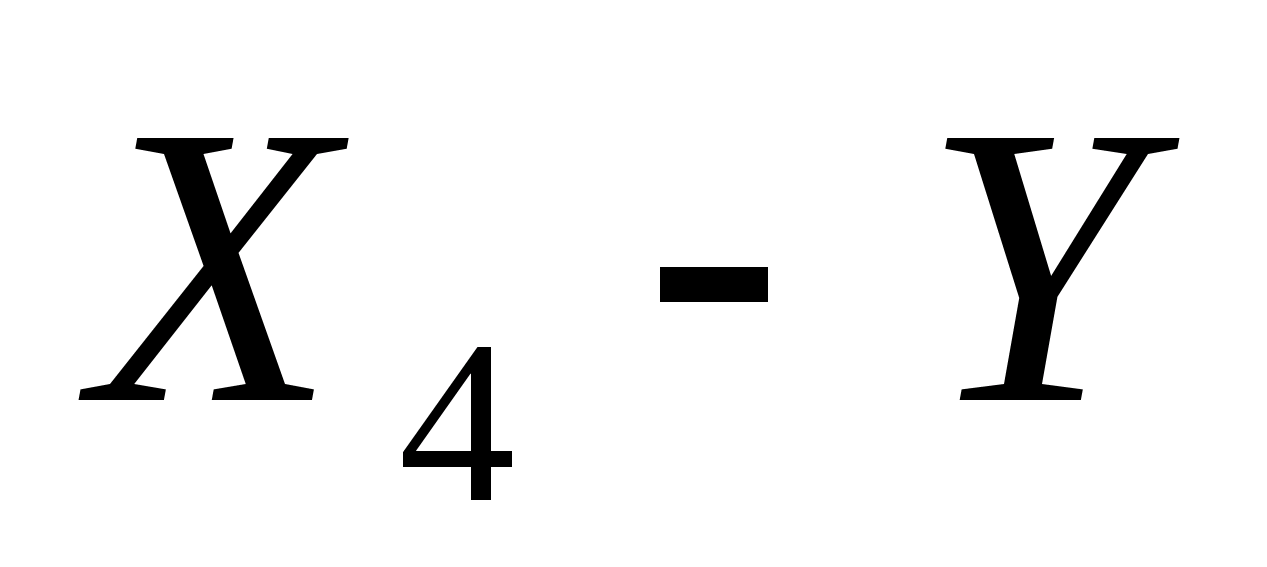
При
его рассмотрении можно сказать, что
наиболее подходящей будет степенная
модель, т.к. она визуально отражает
зависимость
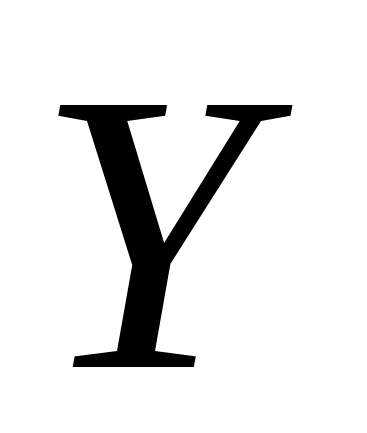 от фактора
от фактора
 .
Также мы можем это увидеть из данных
приведенных в табл. 8.
.
Также мы можем это увидеть из данных
приведенных в табл. 8.
Табл. 8. Значения критериев отбора модели
|
Тип модели |
R^2 |
Ā |
MAD |
Sост |
|
линейная |
0,83 |
32,96% |
25,917639 |
2807,94 |
|
квадратичная |
0,84 |
40,89% |
24,208439 |
2723,75 |
|
гипербол(обратная) |
0,02 |
187,12% |
63,568308 |
6710,86 |
|
степенная |
0,76 |
36,67% |
29,022731 |
0,49 |
|
показательная |
0,68 |
5,24% |
0,0052745 |
0,57 |
|
логарифмическая |
0,46 |
99,80% |
101,78042 |
4991,56 |
Уравнение данной модели выглядит следующим образом:
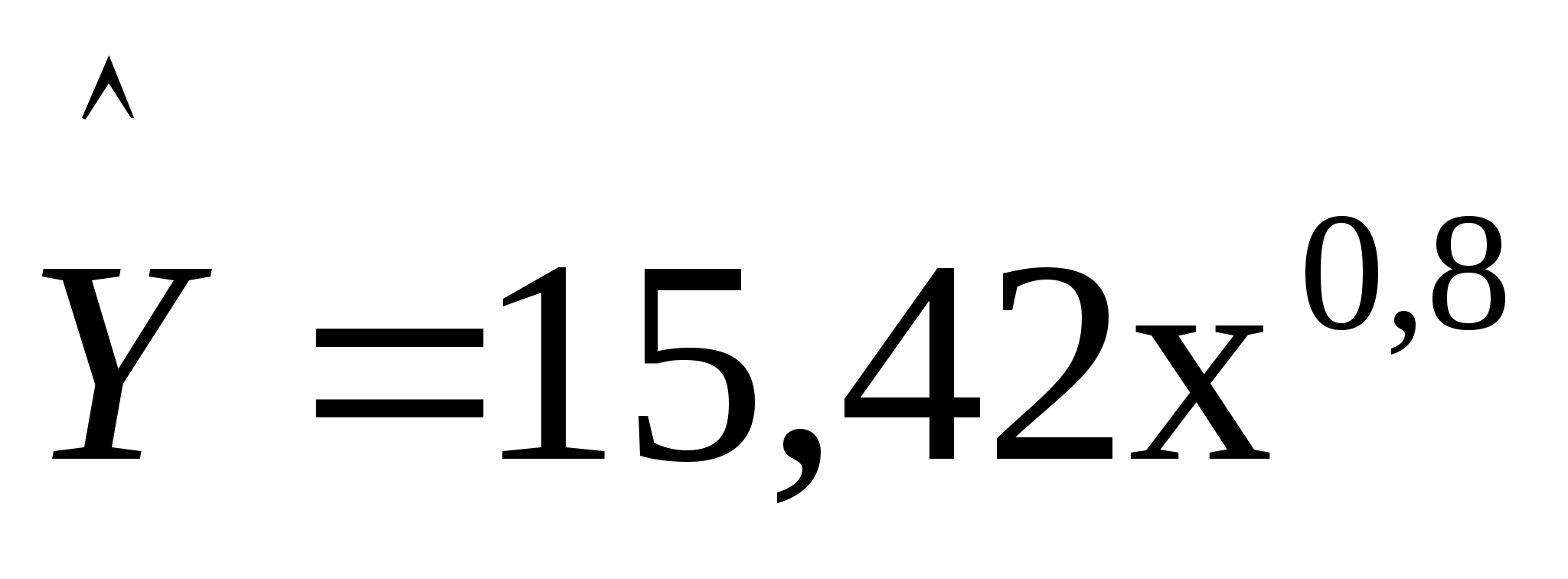 .
.
По
критерию Фишера модель является значимой,
т.к.
 ,
где
,
где
 и
и
 .
.
Оценим
тесноту связи с помощью коэффициента
детерминации, который равен
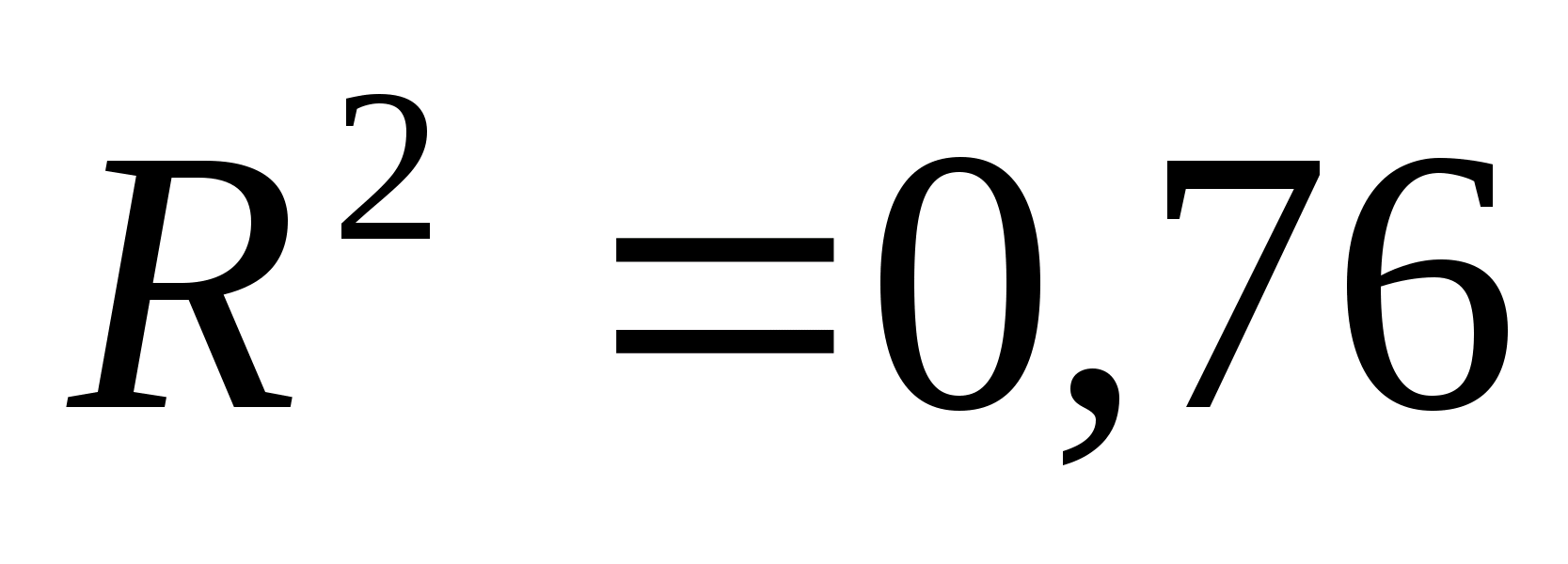 .
Это говорит о том, что 76%
вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 24% вариации объясняются
неучтенными в данной модели факторами.
.
Это говорит о том, что 76%
вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 24% вариации объясняются
неучтенными в данной модели факторами.
Отсюда можно сделать вывод, что математическая модель, выражающая данную зависимость объясняющей переменной, подходит для описания зависимой переменной. Поэтому включение данного фактора в модель множественной регрессии целесообразно.
2.5 Исследование влияния наркомании на уровень разводов
Представим исходные данные об уровне разводов и величине прожиточного минимума по субъектам РФ на 2009 год в виде статистической таблицы, которая достаточно удобна для анализа (табл. 9).
Табл.9. Уровень разводов и величина прожиточного минимума
|
Субъекты РФ |
Число разводов за год (Y) |
Наркомания (X5) |
|
Белгородская область |
6641 |
64 |
|
Брянская область |
7056 |
188 |
|
Владимирская область |
7133 |
98 |
|
Воронежская область |
12048 |
368 |
|
Ивановская область |
5152 |
191 |
|
Калужская область |
5304 |
56 |
|
Костромская область |
3330 |
127 |
|
Курская область |
6039 |
276 |
|
Липецкая область |
6035 |
197 |
|
Московская область |
37069 |
1327 |
|
Орловская область |
3954 |
26 |
|
Рязанская область |
5651 |
114 |
|
Смоленская область |
5406 |
136 |
|
Тамбовская область |
5102 |
37 |
|
Тверская область |
7243 |
141 |
|
Тульская область |
7760 |
100 |
|
Ярославская область |
6484 |
111 |
|
Республика Карелия |
3543 |
32 |
|
Республика Коми |
5259 |
215 |
|
Архангельская область |
6527 |
33 |
|
Ненецкий авт.округ |
220 |
7 |
|
Вологодская область |
6587 |
103 |
|
Калининградская область |
5097 |
48 |
|
Ленинградская область |
8478 |
460 |
|
Мурманская область |
5838 |
320 |
|
Новгородская область |
3226 |
87 |
|
Псковская область |
3295 |
115 |
|
Республика Адыгея |
1757 |
165 |
|
Республика Калмыкия |
1168 |
31 |
|
Краснодарский край |
24756 |
1429 |
|
Астраханская область |
5346 |
68 |
|
Волгоградская область |
12798 |
362 |
|
Ростовская область |
21961 |
313 |
|
Республика Дагестан |
4144 |
462 |
|
Республика Ингушетия |
378 |
24 |
|
Кабардино-Балкарская Республика |
2342 |
188 |
|
Карачаево-Черкесская Республика |
1394 |
67 |
|
Республика Северная Осетия-Алания |
1982 |
36 |
|
Ставропольский край |
12121 |
566 |
|
Республика Башкортостан |
17453 |
379 |
|
Республика Марий Эл |
2926 |
68 |
|
Республика Мордовия |
3462 |
122 |
|
Республика Татарстан |
15671 |
651 |
|
Удмуртская Республика |
6100 |
220 |
|
Чувашская Республика |
4786 |
72 |
|
Пермский край |
12295 |
970 |
|
Кировская область |
6465 |
59 |
|
Нижегородская область |
17275 |
380 |
|
Оренбургская область |
10412 |
177 |
|
Пензенская область |
7279 |
188 |
|
Самарская область |
16555 |
678 |
|
Саратовская область |
12110 |
159 |
|
Ульяновская область |
7037 |
164 |
|
Курганская область |
5441 |
252 |
|
Свердловская область |
22765 |
2235 |
|
Тюменская область |
21202 |
696 |
|
Ханты-Мансийский авт.округ-Югра |
10732 |
405 |
|
Ямало-Ненецкий авт.округ |
3610 |
114 |
|
Челябинская область |
21686 |
833 |
|
Республика Алтай |
1076 |
32 |
|
Республика Бурятия |
4140 |
69 |
|
Республика Тыва |
632 |
24 |
|
Республика Хакасия |
2808 |
60 |
|
Алтайский край |
13313 |
944 |
|
Красноярский край |
16401 |
538 |
|
Иркутская область |
12330 |
987 |
|
Кемеровская область |
15577 |
1466 |
|
Новосибирская область |
15769 |
904 |
|
Омская область |
10524 |
323 |
|
Томская область |
5602 |
160 |
|
Республика Саха (Якутия) |
4529 |
90 |
|
Камчатский край |
2351 |
13 |
|
Приморский край |
10530 |
548 |
|
Хабаровский край |
8118 |
145 |
|
Амурская область |
5062 |
246 |
|
Магаданская область |
1304 |
48 |
|
Сахалинская область |
3446 |
190 |
|
Еврейская автономная область |
985 |
52 |
|
Чукотский авт.округ |
406 |
1 |
Для
выявления влияния фактора
 на результирующий признак
на результирующий признак
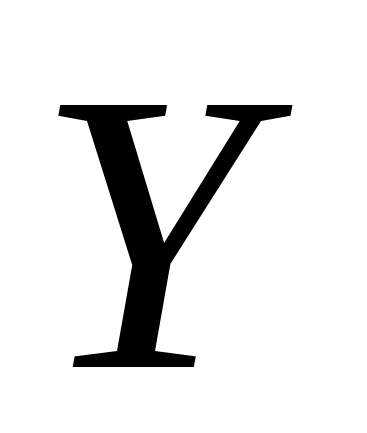 необходимо
сначала построить поле корреляции (рис.
5).
необходимо
сначала построить поле корреляции (рис.
5).

Рис.5.
Корреляционное поле

При
его рассмотрении можно сказать, что
наиболее подходящей будет степенная
модель, т.к. она визуально отражает
зависимость
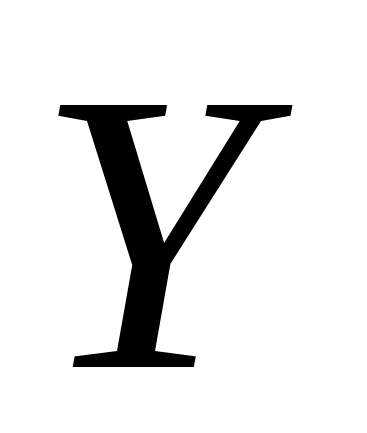 от фактора
от фактора
 .
Также мы можем это увидеть из данных
приведенных в табл. 10.
.
Также мы можем это увидеть из данных
приведенных в табл. 10.
Табл. 10. Значения критериев отбора модели
|
Тип модели |
R^2 |
Ā |
MAD |
Sост |
|
линейная |
0,62 |
105,40% |
38,479737 |
4181,87 |
|
квадратичная |
0,69 |
78,68% |
34,240944 |
3810,32 |
|
гипербол(обратная) |
0,04 |
189,33% |
63,391849 |
6643,38 |
|
степенная |
0,69 |
52,21% |
34,840513 |
0,56 |
|
показательная |
0,39 |
7,22% |
0,0072226 |
0,78 |
|
логарифмическая |
0,56 |
99,88% |
101,80943 |
4496,70 |
Уравнение данной модели выглядит следующим образом:
 .
.
По
критерию Фишера модель является значимой,
т.к.
 ,
где
,
где
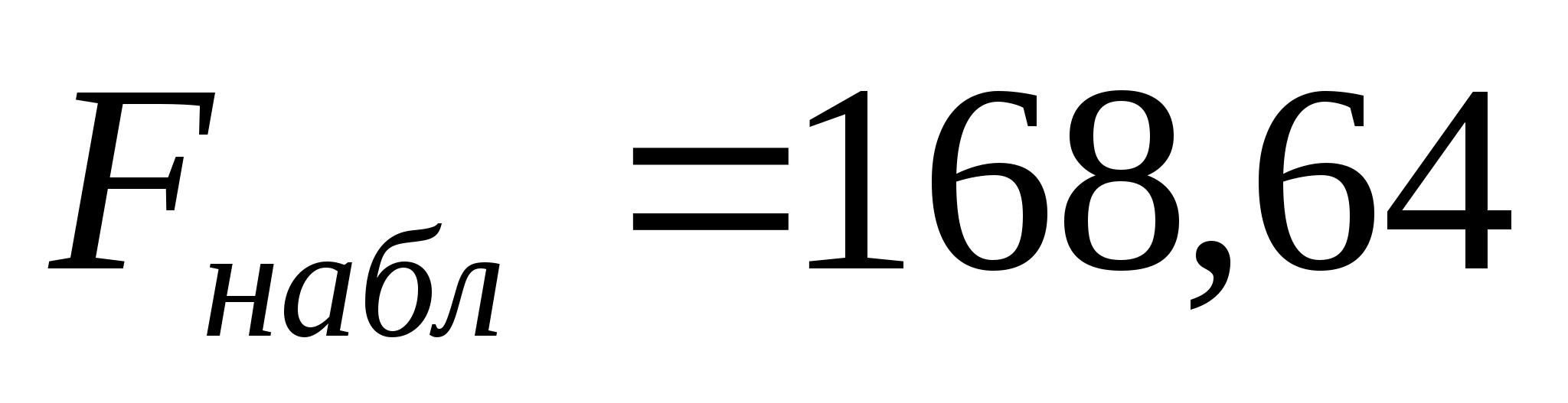 и
и
 .
.
Оценим
тесноту связи с помощью коэффициента
детерминации, который равен
 .
Это говорит о том, что 69%
вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 31% вариации объясняются
неучтенными в данной модели факторами.
.
Это говорит о том, что 69%
вариации уровня разводов объясняется
вариацией уровня прожиточного минимума.
Остальные 31% вариации объясняются
неучтенными в данной модели факторами.
Отсюда можно сделать вывод, что математическая модель, выражающая данную зависимость объясняющей переменной, подходит для описания зависимой переменной. Поэтому включение данного фактора в модель множественной регрессии целесообразно.
2.6 Исследование влияния числа инвалидов на уровень разводов
Представим исходные данные об уровне разводов и величине прожиточного минимума по субъектам РФ на 2009 год в виде статистической таблицы, которая достаточно удобна для анализа (табл. 11).
Табл.11. Уровень разводов и величина прожиточного минимума
|
Субъекты РФ |
Число разводов за год у2 |
Инвалидность х6 |
|
Белгородская область |
6641 |
9 |
|
Брянская область |
7056 |
9,7 |
|
Владимирская область |
7133 |
13,6 |
|
Воронежская область |
12048 |
16,2 |
|
Ивановская область |
5152 |
8,7 |
|
Калужская область |
5304 |
7,1 |
|
Костромская область |
3330 |
4,9 |
|
Курская область |
6039 |
9,5 |
|
Липецкая область |
6035 |
11,6 |
|
Московская область |
37069 |
5,3 |
|
Орловская область |
3954 |
13 |
|
Рязанская область |
5651 |
6 |
|
Смоленская область |
5406 |
6,4 |
|
Тамбовская область |
5102 |
10,1 |
|
Тверская область |
7243 |
13,5 |
|
Тульская область |
7760 |
10,9 |
|
Ярославская область |
6484 |
75,1 |
|
Республика Карелия |
3543 |
4,6 |
|
Республика Коми |
5259 |
5,7 |
|
Архангельская область |
6527 |
8 |
|
Ненецкий авт.округ |
220 |
0,3 |
|
Вологодская область |
6587 |
9,7 |
|
Калининградская область |
5097 |
6,7 |
|
Ленинградская область |
8478 |
14 |
|
Мурманская область |
5838 |
4 |
|
Новгородская область |
3226 |
5,1 |
|
Псковская область |
3295 |
4 |
|
Республика Адыгея |
1757 |
2,4 |
|
Республика Калмыкия |
1168 |
2,3 |
|
Краснодарский край |
24756 |
35,3 |
|
Астраханская область |
5346 |
5,3 |
|
Волгоградская область |
12798 |
15,5 |
|
Ростовская область |
21961 |
17,1 |
|
Республика Дагестан |
4144 |
15 |
|
Республика Ингушетия |
378 |
3,7 |
|
Кабардино-Балкарская Республика |
2342 |
5,5 |
|
Карачаево-Черкесская Республика |
1394 |
3 |
|
Республика Северная Осетия-Алания |
1982 |
4,9 |
|
Ставропольский край |
12121 |
17,1 |
|
Республика Башкортостан |
17453 |
20,8 |
|
Республика Марий Эл |
2926 |
5,2 |
|
Республика Мордовия |
3462 |
5,6 |
|
Республика Татарстан |
15671 |
25 |
|
Удмуртская Республика |
6100 |
9,9 |
|
Чувашская Республика |
4786 |
6 |
|
Пермский край |
12295 |
8,2 |
|
Кировская область |
6465 |
20,7 |
|
Нижегородская область |
17275 |
13,8 |
|
Оренбургская область |
10412 |
21,6 |
|
Пензенская область |
7279 |
20,5 |
|
Самарская область |
16555 |
19 |
|
Саратовская область |
12110 |
13,9 |
|
Ульяновская область |
7037 |
10,1 |
|
Курганская область |
5441 |
6,6 |
|
Свердловская область |
22765 |
24,6 |
|
Тюменская область |
21202 |
6,4 |
|
Ханты-Мансийский авт.округ-Югра |
10732 |
4,3 |
|
Ямало-Ненецкий авт.округ |
3610 |
1,4 |
|
Челябинская область |
21686 |
23,7 |
|
Республика Алтай |
1076 |
1,4 |
|
Республика Бурятия |
4140 |
7,1 |
|
Республика Тыва |
632 |
1,9 |
|
Республика Хакасия |
2808 |
2,9 |
|
Алтайский край |
13313 |
14,2 |
|
Красноярский край |
16401 |
7,4 |
|
Иркутская область |
12330 |
13,1 |
|
Кемеровская область |
15577 |
18,4 |
|
Новосибирская область |
15769 |
31,9 |
|
Омская область |
10524 |
17,5 |
|
Томская область |
5602 |
9,5 |
|
Республика Саха (Якутия) |
4529 |
4,6 |
|
Камчатский край |
2351 |
7,6 |
|
Приморский край |
10530 |
1,8 |
|
Хабаровский край |
8118 |
10,7 |
|
Амурская область |
5062 |
7,9 |
|
Магаданская область |
1304 |
0,5 |
|
Сахалинская область |
3446 |
2,2 |
|
Еврейская автономная область |
985 |
1,7 |
|
Чукотский авт.округ |
406 |
0,2 |
Для
выявления влияния фактора
 на результирующий признак
на результирующий признак
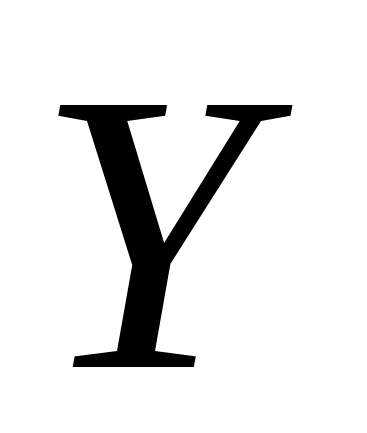 необходимо
сначала построить поле корреляции (рис.
6).
необходимо
сначала построить поле корреляции (рис.
6).

Рис.6.
Корреляционное поле
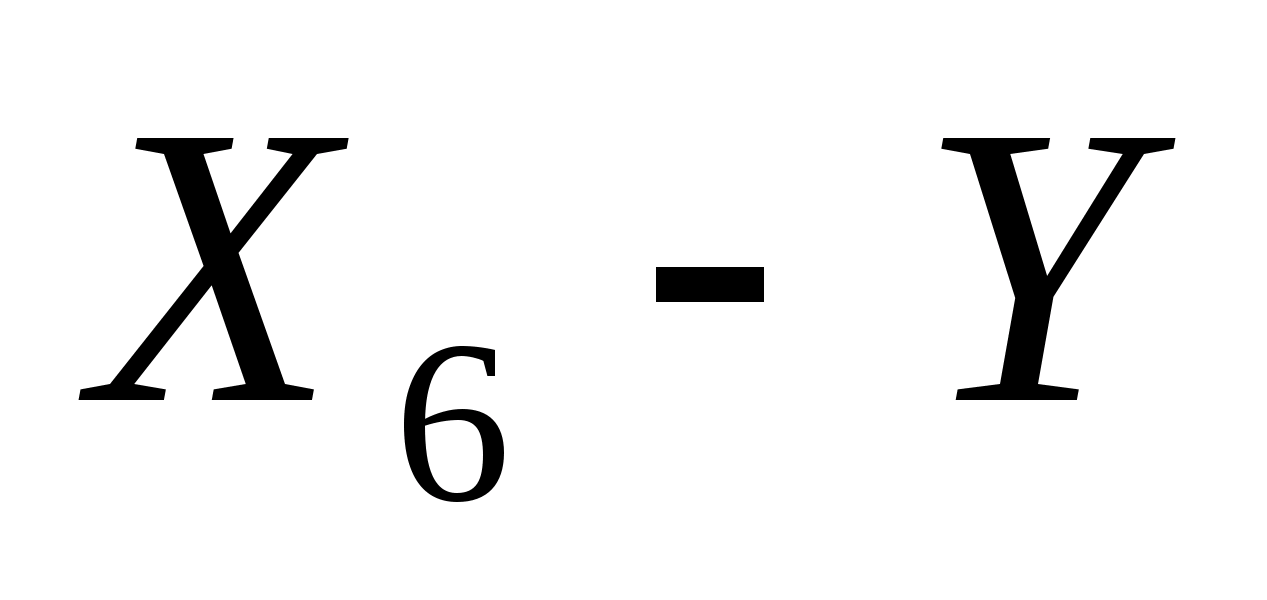
При
его рассмотрении можно сказать, что
наиболее подходящей будет степенная
модель, т.к. она визуально отражает
зависимость
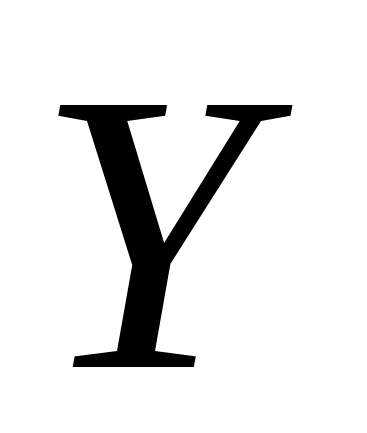 от фактора
от фактора
 .
Также мы можем это увидеть из данных
приведенных в табл. 12.
.
Также мы можем это увидеть из данных
приведенных в табл. 12.
Табл. 12. Значения критериев отбора модели
|
Тип модели |
R^2 |
Ā |
MAD |
Sост |
|
линейная |
0,18 |
145,89% |
53,91433 |
6143,55 |
|
квадратичная |
0,38 |
74,27% |
40,744138 |
5361,10 |
|
гипербол(обратная) |
0,09 |
157,15% |
62,058889 |
6479,29 |
|
степенная |
0,59 |
53,26% |
41,088475 |
0,64 |
|
показательная |
0,24 |
7,47% |
0,0075565 |
0,87 |
|
логарифмическая |
0,28 |
99,97% |
101,84785 |
5741,17 |
Уравнение данной модели выглядит следующим образом:
 .
.
По
критерию Фишера модель является значимой,
т.к.
 ,
где
,
где
 и
и
 .
.
Оценим
тесноту связи с помощью коэффициента
детерминации, который равен
 .
Это значит, что 59% вариации
уровня разводов объясняется вариацией
уровня прожиточного минимума. Остальные
41% вариации объясняются неучтенными в
данной модели факторами.
.
Это значит, что 59% вариации
уровня разводов объясняется вариацией
уровня прожиточного минимума. Остальные
41% вариации объясняются неучтенными в
данной модели факторами.
Значит, математическая модель, выражающая данную зависимость объясняющей переменной, подходит для описания зависимой переменной. Включение этого фактора в модель множественной регрессии целесообразно.
Исследование влияния всех факторов в совокупности
В качестве факторов, оказывающих влияние на уровень доходов, после предварительного исследования, были отобраны следующие факторы:
 психические
расстройства (чел.);
психические
расстройства (чел.);
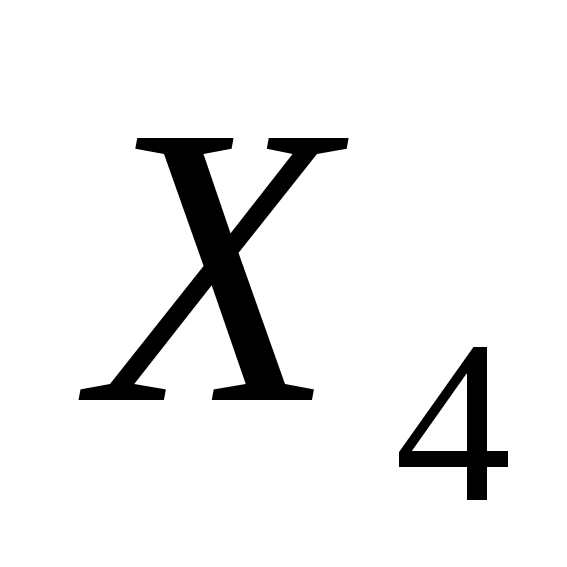 алкоголизм
(чел.);
алкоголизм
(чел.);
 наркомания
(чел.);
наркомания
(чел.);
 инвалидность
(тыс. чел.).
инвалидность
(тыс. чел.).
Рассчитанные парные коэффициенты корреляции представим в виде корреляционной матрицы (табл. 13).
Табл. 13. Корреляционная матрица
|
|
|
|
|
|
|
|
|
1 |
0,76 |
0,91 |
0,79 |
0,42 |
|
|
0,76 |
1 |
0,75 |
0,73 |
0,47 |
|
|
0,91 |
0,75 |
1 |
0,76 |
0,39 |
|
|
0,79 |
0,73 |
0,76 |
1 |
0,36 |
|
|
0,42 |
0,47 |
0,39 |
0,36 |
1 |
Из анализируемых факторов наибольшее влияние на уровень разводов оказывают все факторы, кроме шестого – инвалидность, т.к. значение линейных коэффициентов корреляции выше 0,7.
Построим модель множественной линейной регрессии:

Коэффициент
детерминации
 ,
т.е. 85,7% вариации уровня разводов
объясняется вариацией четырех
рассмотренных факторов.
,
т.е. 85,7% вариации уровня разводов
объясняется вариацией четырех
рассмотренных факторов.
Скорректированный
коэффициент детерминации
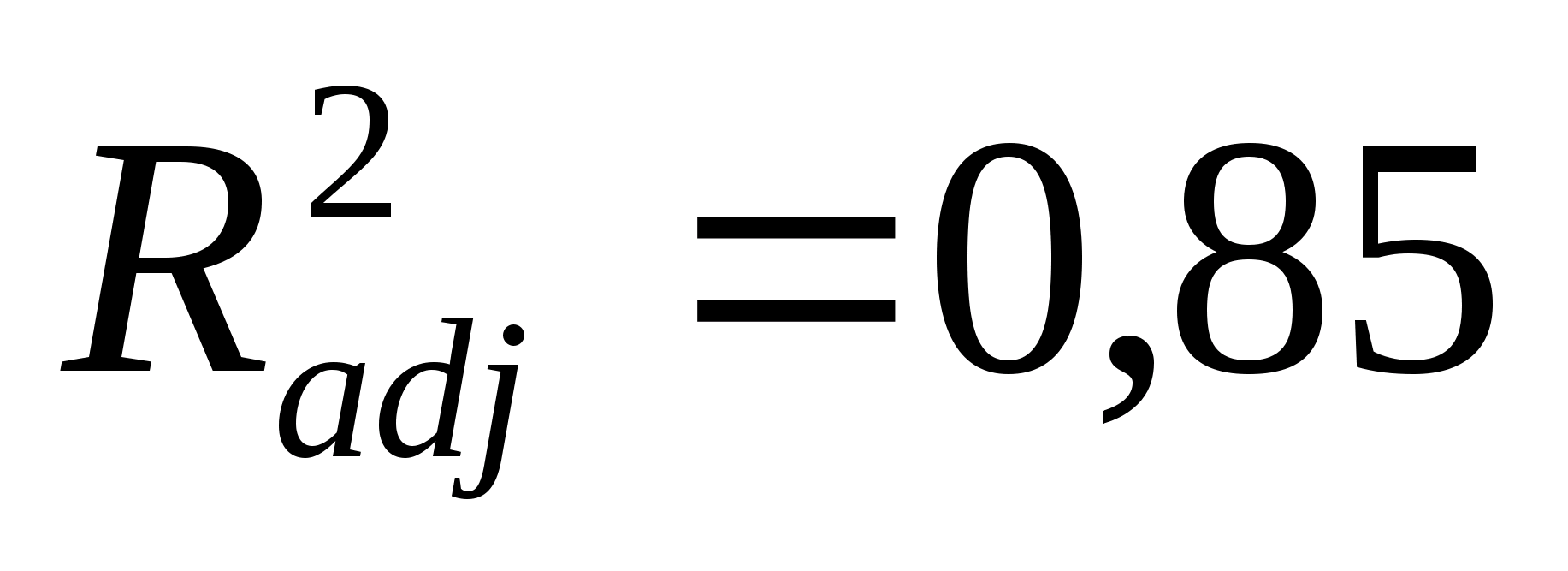 .
.
Данная модель является значимой по критерию Фишера, т.к.
 ,
где
,
где
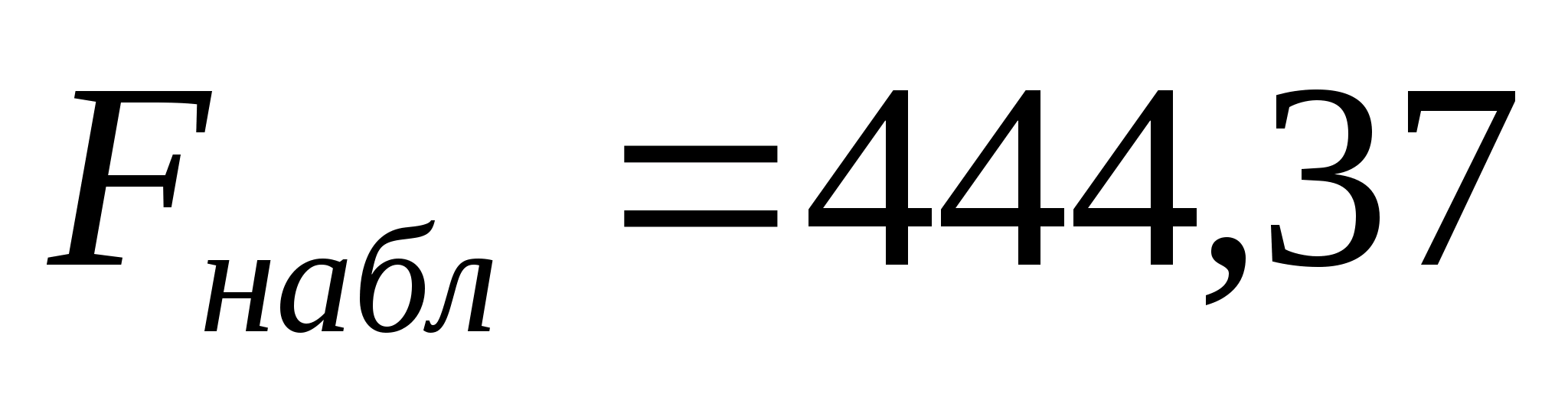 и
и
 .
.
Также
проверим коэффициенты линейной регрессии
на значимость:
 ,
а
,
а
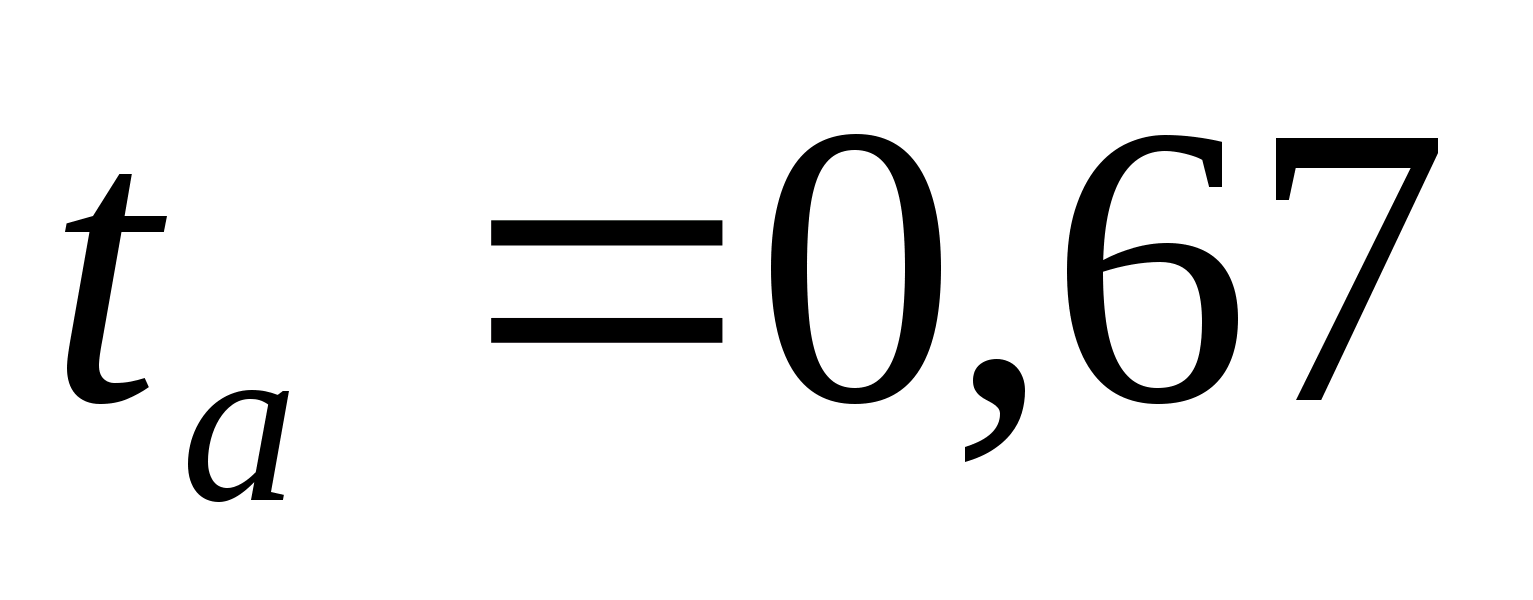 ,
,
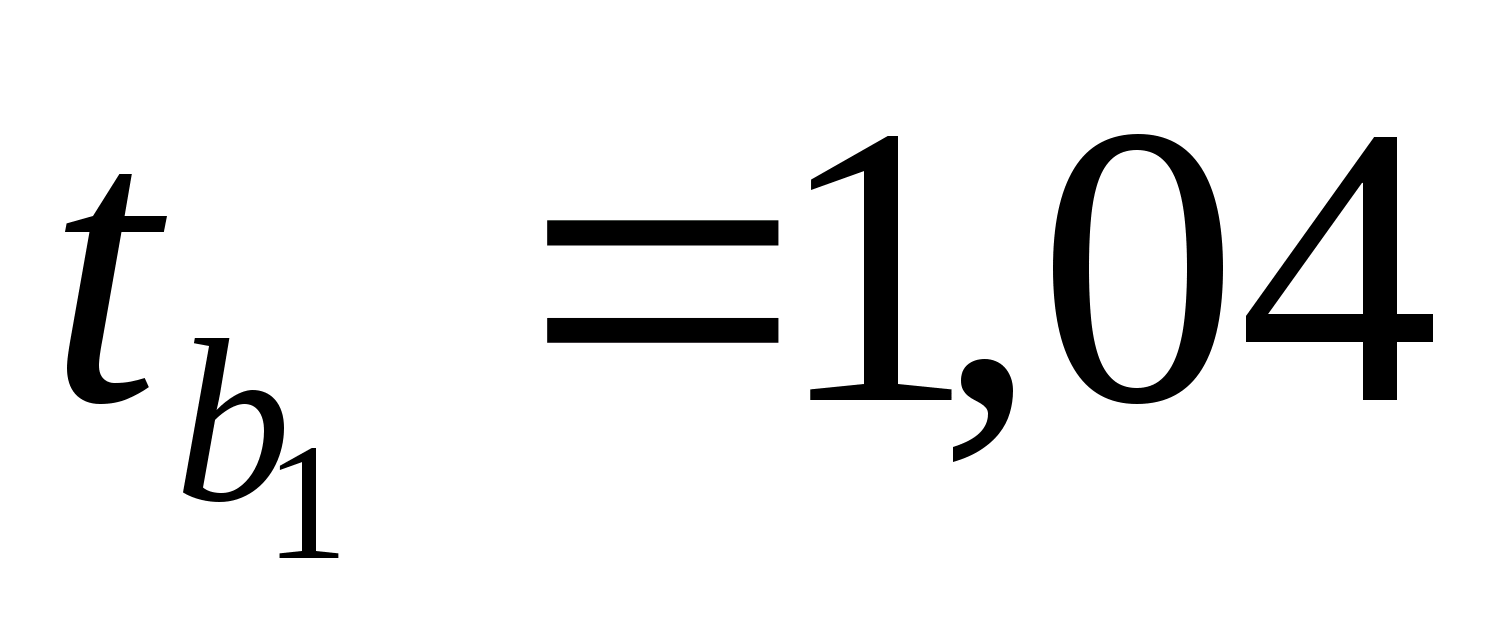 ,
,
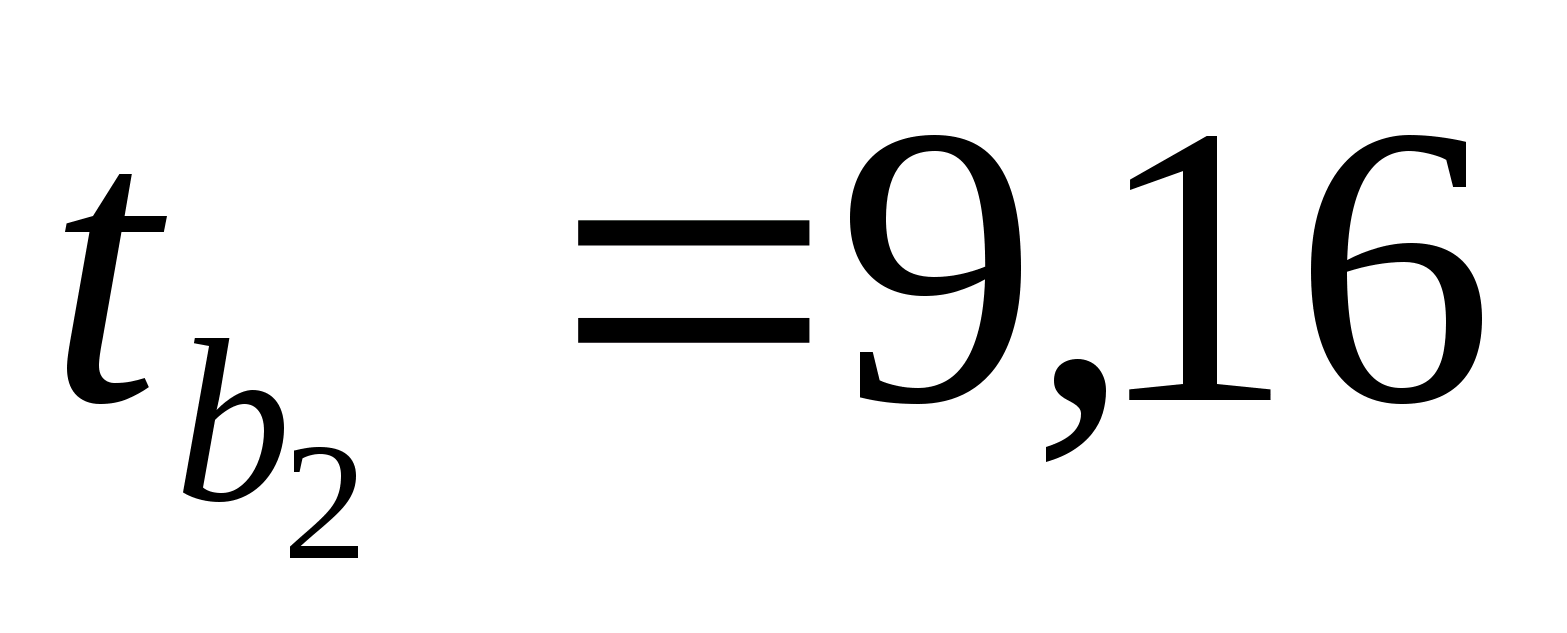 ,
,
 ,
,
 .
Таким образом,
.
Таким образом,
 ,
,
 ,
,
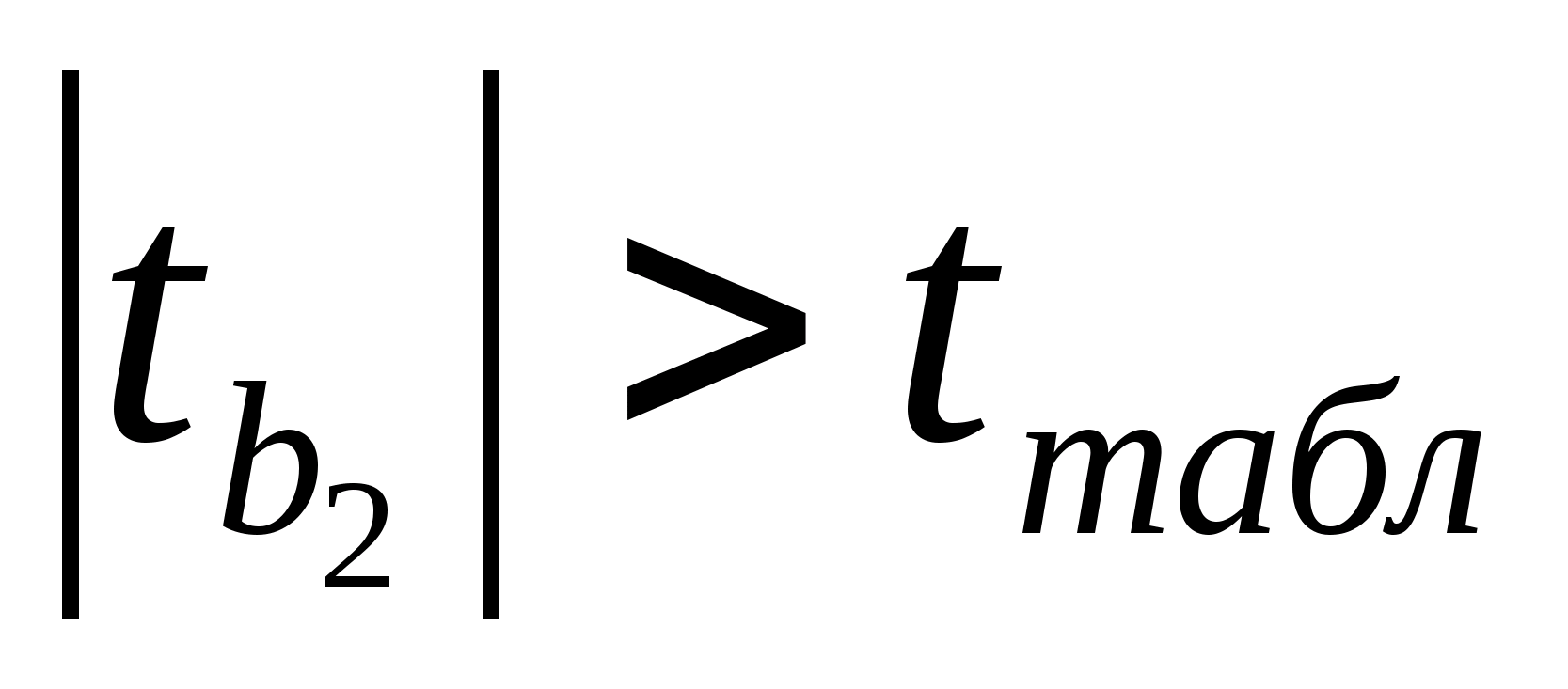 ,
,
 ,
,
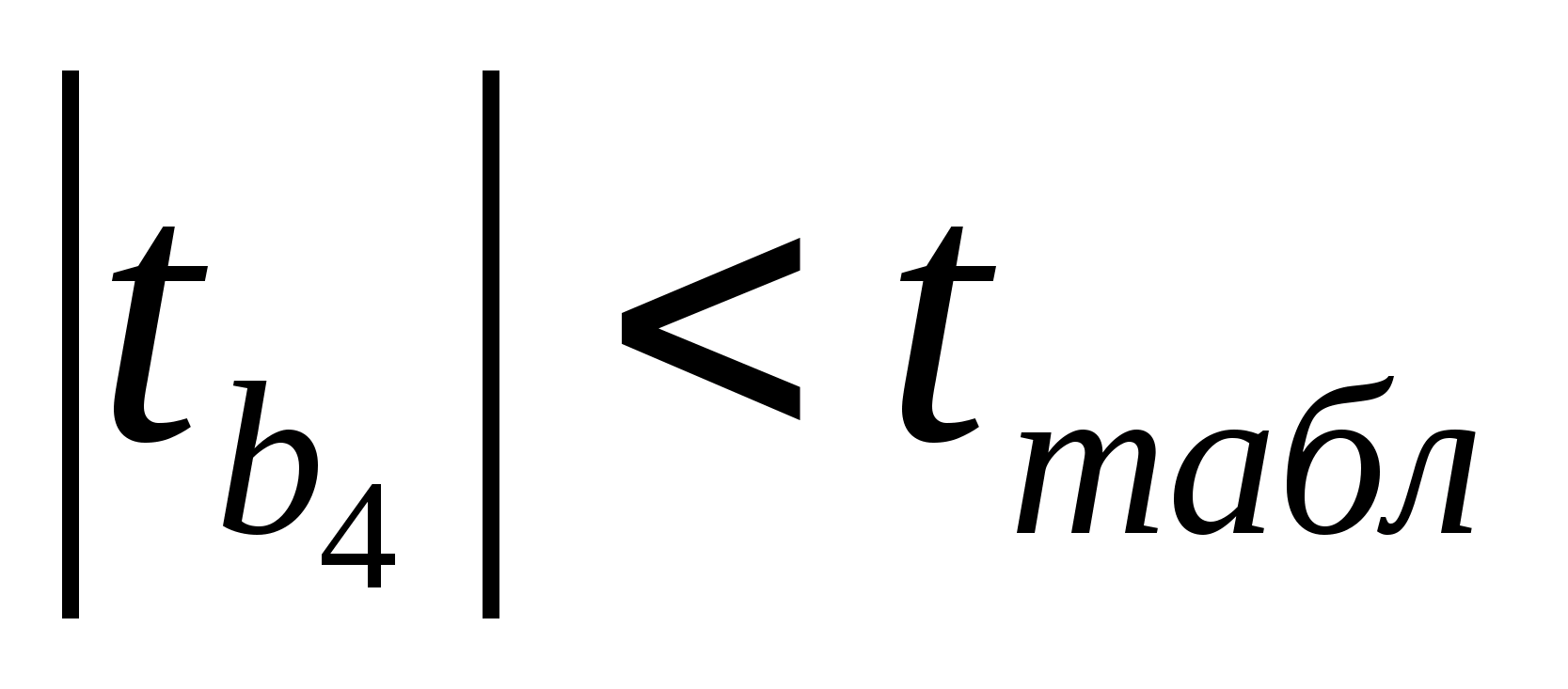 ,
,
значит,
коэффициенты
 и
и
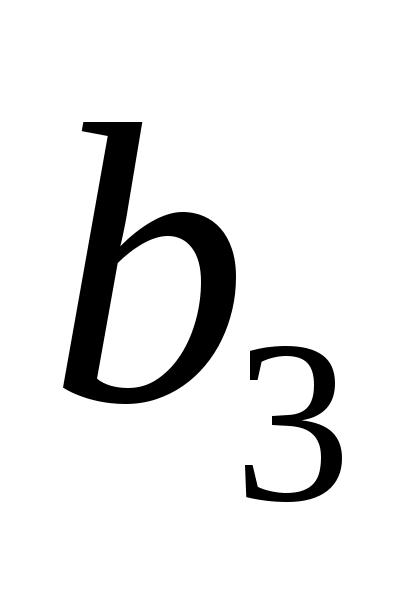 значимы.
значимы.
Теперь
мы получили новую модель, которая
выглядит следующим образом:
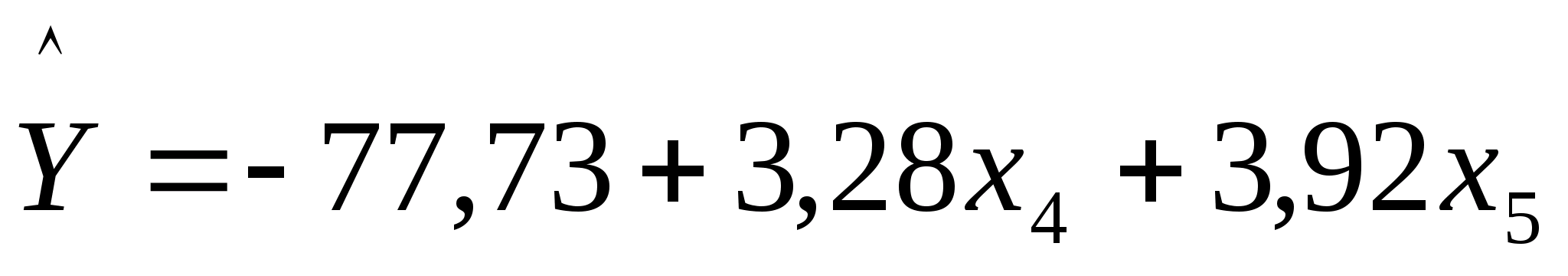 .
.
Оценим
точность прогноза, для этого рассчитаем
среднюю ошибку аппроксимации:

По
данной модели средняя ошибка аппроксимации,
хотя и превышает рекомендуемое значение
8-10%, но не намного, следовательно,
приближение построенной модели к
наблюдаемым статистическим значениям
считается хорошим. Точность прогноза
найдена с помощью критерия
 .
.
Произведем сравнение построенных моделей множественной и парной регрессии зависимости уровня разводов от алкоголизма. Сравнение производится, чтобы сделать выбор между двумя моделями (табл. 13).
Табл. 13. Сравнение моделей
|
Тип модели |
|
|
|
|
|
|
Парная |
0,76 |
0,75 |
0,49 |
29,02 |
36,67 |
|
Множественная |
0,857 |
0,85 |
2613,84 |
1755,825 |
27,93 |
Модель множественной регрессии лучше по каждому из рассмотренных показателей, кроме среднего абсолютного отклонения. Поэтому, не смотря на рост среднего абсолютного отклонения, мы выбираем лучшей моделью множественную регрессию.
Проверив модель по критерию Дарбина-Уотсона, мы получили следующее (табл. 14):
Табл. 14. Тест Дарбина-Уотсона
|
n |
α |
k |
dl |
du |
d |
|
79 |
0,05 |
2 |
1,53 |
1,74 |
1,79 |
В
данном случае – положительную
автокорреляцию,
 .
.
Заключение
Было произведено исследование влияния факторов на уровень разводов, и мы получили следующие результаты.
В ходе исследования была изучена зависимость каждого из приведенных выше факторов на результирующий признак (уровень разводов), как в отдельности, так и в совокупности. Для этого были построены шесть парных моделей степенной регрессии и модель множественной линейной регрессии. Предположение о степенной зависимости признака от факторов было выдвинуто на основе построенных корреляционных полей.
Проведенное исследование показало, что значимыми можно признать все построенные модели. Но во множественной модели было выявлено, что при рассмотрении факторов в совокупности есть незначимые. Ими являются следующие факторы: величина прожиточного минимума, среднедушевой денежный доход, психические расстройства и инвалидность. Также в ходе исследования было установлено, что наиболее подходящей является модель, отражающая зависимость уровня разводов от алкоголизма и наркомании.
Данная
модель имеет следующий вид:
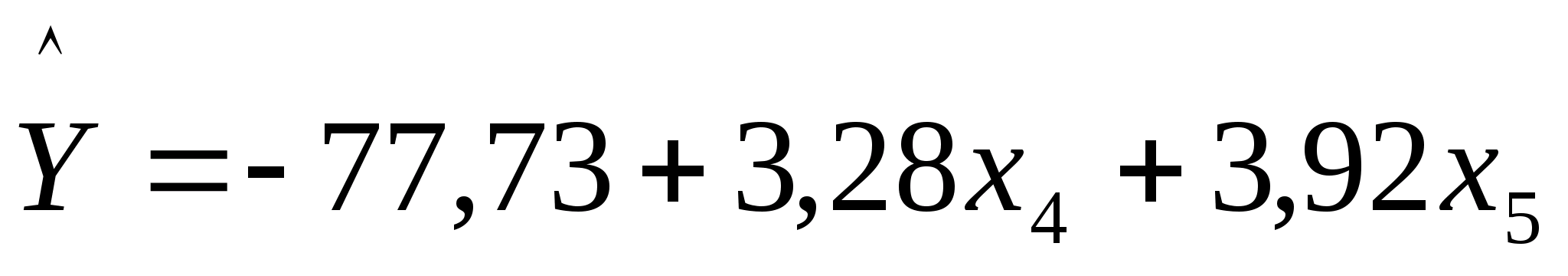 .
.
Полученной модели можно дать следующую экономическую интерпретацию: с увеличением числа алкоголиков на 3,28 и наркоманов на 3,92 на каждые 1000 человек, растет и уровень разводов в РФ.
Изменение уровня разводов на 85% объясняется изменением числа алкоголиков и наркоманов на каждые 1000 человек. А увеличение числа алкоголиков и наркоманов на 1% приводит к увеличению разводов на 317,37% и 265,06% соответственно. Остальные факторы слабо влияют.
Подводя итог, необходимо заметить, что исследование косвенным образом выявило имеющиеся проблемы социального развития РФ. Среди приведенных факторов в большей степени влияют на распадение браков – это алкоголизм и наркомания. Остальные четыре фактора тоже влияют, но в меньшей мере. Скорее всего, эти четыре фактора могут быть только толчками сначала для ссор, обид между супругами. Казалось бы, что деньги в нашей жизни играют немаловажную роль, но в жизни двух людей любящих друг друга – это не самое важное.
Список использованной литературы:
Евсеев Е. А., Буре В. М. Эконометрика. – СПб.: Изд-во МБИ, 2007. –139 с.
Тарашнина С.И., Панкратова Я.Б. Выполнение курсовой работы по эконометрике: учебно-методическое пособие. – СПб.: Изд-во МБИ, 2007. – 97 с.
Официальный сайт Федеральной службы государственной статистики Росстат – www.gks.ru
Приложение А
Исходные данные
|
Субъекты РФ |
Число разводов за год (у) |
Величина прожиточного минимума (х1) |
Среднедушевой денежный доход (х2) |
Психические расстройства (х3) |
Алко-голизм (х4) |
Нарко-мания (х5) |
Инвалид-ность (х6) |
|
Белгородская область |
6641 |
4037 |
12757,9 |
643 |
1405 |
64 |
9 |
|
Брянская область |
7056 |
4155,5 |
10042,6 |
727 |
2944 |
188 |
9,7 |
|
Владимирская область |
7133 |
4815,25 |
9596,2 |
596 |
2095 |
98 |
13,6 |
|
Воронежская область |
12048 |
4343,75 |
10304,8 |
1864 |
3551 |
368 |
16,2 |
|
Ивановская область |
5152 |
4534 |
8353,8 |
478 |
1958 |
191 |
8,7 |
|
Калужская область |
5304 |
4406,25 |
11755,9 |
339 |
1662 |
56 |
7,1 |
|
Костромская область |
3330 |
4506,25 |
9413,2 |
318 |
749 |
127 |
4,9 |
|
Курская область |
6039 |
4174,25 |
11411 |
554 |
2375 |
276 |
9,5 |
|
Липецкая область |
6035 |
4226 |
12274,4 |
617 |
2147 |
197 |
11,6 |
|
Московская область |
37069 |
5704,25 |
19776 |
2289 |
7342 |
1327 |
5,3 |
|
Орловская область |
3954 |
3949,25 |
9814,5 |
242 |
900 |
26 |
13 |
|
Рязанская область |
5651 |
4649,5 |
11311,3 |
525 |
1476 |
114 |
6 |
|
Смоленская область |
5406 |
4653,75 |
11522,7 |
599 |
1888 |
136 |
6,4 |
|
Тамбовская область |
5102 |
3715,5 |
11252,8 |
501 |
1566 |
37 |
10,1 |
|
Тверская область |
7243 |
4791,5 |
10856 |
718 |
2052 |
141 |
13,5 |
|
Тульская область |
7760 |
4647,25 |
11388,5 |
588 |
2640 |
100 |
10,9 |
|
Ярославская область |
6484 |
5034,75 |
12587,2 |
1135 |
1892 |
111 |
75,1 |
|
Республика Карелия |
3543 |
5743 |
12228,6 |
225 |
1277 |
32 |
4,6 |
|
Республика Коми |
5259 |
6486,5 |
18636,4 |
470 |
2112 |
215 |
5,7 |
|
Архангельская область |
6527 |
5915,75 |
14823,6 |
330 |
1138 |
33 |
8 |
|
Ненецкий авт.округ |
220 |
8762,5 |
48764,9 |
10 |
128 |
7 |
0,3 |
|
Вологодская область |
6587 |
5141,75 |
12193,5 |
570 |
1510 |
103 |
9,7 |
|
Калининградская область |
5097 |
5129 |
12922,3 |
446 |
947 |
48 |
6,7 |
|
Ленинградская область |
8478 |
4414 |
12014,4 |
454 |
2088 |
460 |
14 |
|
Мурманская область |
5838 |
6978,5 |
18773,2 |
219 |
1110 |
320 |
4 |
|
Новгородская область |
3226 |
4931,5 |
11645,6 |
821 |
1339 |
87 |
5,1 |
|
Псковская область |
3295 |
4487,25 |
10290,9 |
417 |
1272 |
115 |
4 |
|
Республика Адыгея |
1757 |
4276,75 |
7986,3 |
182 |
587 |
165 |
2,4 |
|
Республика Калмыкия |
1168 |
3872,25 |
5651,2 |
195 |
317 |
31 |
2,3 |
|
Краснодарский край |
24756 |
4633 |
12023,9 |
1208 |
4963 |
1429 |
35,3 |
|
Астраханская область |
5346 |
4514 |
11120,4 |
364 |
1165 |
68 |
5,3 |
|
Волгоградская область |
12798 |
4539,75 |
10866,4 |
468 |
3020 |
362 |
15,5 |
|
Ростовская область |
21961 |
4551,75 |
12160,5 |
2210 |
3680 |
313 |
17,1 |
|
Республика Дагестан |
4144 |
3700,25 |
10962 |
2623 |
860 |
462 |
15 |
|
Республика Ингушетия |
378 |
4150 |
5512,9 |
234 |
3 |
24 |
3,7 |
|
Кабардино-Балкарская Республика |
2342 |
3661,5 |
8589,3 |
530 |
728 |
188 |
5,5 |
|
Карачаево-Черкесская Республика |
1394 |
3839,5 |
8676,1 |
221 |
350 |
67 |
3 |
|
Республика Северная Осетия-Алания |
1982 |
3729,5 |
9837,7 |
386 |
553 |
36 |
4,9 |
|
Ставропольский край |
12121 |
4503 |
9952,5 |
1035 |
1505 |
566 |
17,1 |
|
Республика Башкортостан |
17453 |
4140,5 |
14252,7 |
2276 |
4599 |
379 |
20,8 |
|
Республика Марий Эл |
2926 |
4083 |
7843,4 |
499 |
1005 |
68 |
5,2 |
|
Республика Мордовия |
3462 |
4039,75 |
8384,2 |
397 |
1394 |
122 |
5,6 |
|
Республика Татарстан |
15671 |
4186 |
14180,5 |
2407 |
2929 |
651 |
25 |
|
Удмуртская Республика |
6100 |
4297,75 |
9581,1 |
946 |
1778 |
220 |
9,9 |
|
Чувашская Республика |
4786 |
4178 |
8593,6 |
958 |
2139 |
72 |
6 |
|
Пермский край |
12295 |
5295,75 |
16119 |
1658 |
4853 |
970 |
8,2 |
|
Кировская область |
6465 |
4621,25 |
10112,2 |
622 |
2094 |
59 |
20,7 |
|
Нижегородская область |
17275 |
4964 |
13090 |
1334 |
3734 |
380 |
13,8 |
|
Оренбургская область |
10412 |
4238,25 |
10184 |
1632 |
3128 |
177 |
21,6 |
|
Пензенская область |
7279 |
4320,75 |
10172,9 |
654 |
3167 |
188 |
20,5 |
|
Самарская область |
16555 |
5412,75 |
15805,2 |
1014 |
3773 |
678 |
19 |
|
Саратовская область |
12110 |
4523 |
9061,5 |
2480 |
3048 |
159 |
13,9 |
|
Ульяновская область |
7037 |
4343,25 |
9756,4 |
484 |
2108 |
164 |
10,1 |
|
Курганская область |
5441 |
4584 |
11160,8 |
125 |
1466 |
252 |
6,6 |
|
Свердловская область |
22765 |
4918,5 |
17171,3 |
3033 |
5362 |
2235 |
24,6 |
|
Тюменская область |
21202 |
4870,5 |
27612,2 |
1356 |
5071 |
696 |
6,4 |
|
Ханты-Мансийский авт.округ-Югра |
10732 |
7684,5 |
32871,9 |
546 |
2413 |
405 |
4,3 |
|
Ямало-Ненецкий авт.округ |
3610 |
7972 |
38133,4 |
118 |
863 |
114 |
1,4 |
|
Челябинская область |
21686 |
4607,5 |
14161,2 |
2792 |
5034 |
833 |
23,7 |
|
Республика Алтай |
1076 |
5852,25 |
10172,5 |
221 |
276 |
32 |
1,4 |
|
Республика Бурятия |
4140 |
4938,25 |
11298,5 |
692 |
994 |
69 |
7,1 |
|
Республика Тыва |
632 |
4912,75 |
7871,2 |
59 |
311 |
24 |
1,9 |
|
Республика Хакасия |
2808 |
4647,5 |
10763,9 |
670 |
656 |
60 |
2,9 |
|
Алтайский край |
13313 |
4530,5 |
9748,6 |
1782 |
5000 |
944 |
14,2 |
|
Красноярский край |
16401 |
5600,5 |
15604,5 |
1945 |
4775 |
538 |
7,4 |
|
Иркутская область |
12330 |
4900,75 |
12881,6 |
2396 |
4659 |
987 |
13,1 |
|
Кемеровская область |
15577 |
4278,5 |
14439,3 |
2901 |
3297 |
1466 |
18,4 |
|
Новосибирская область |
15769 |
5217 |
12838,1 |
1662 |
2497 |
904 |
31,9 |
|
Омская область |
10524 |
4751,5 |
13626,5 |
1325 |
2027 |
323 |
17,5 |
|
Томская область |
5602 |
5075 |
13481,7 |
722 |
1047 |
160 |
9,5 |
|
Республика Саха (Якутия) |
4529 |
7908,75 |
18740,8 |
711 |
2726 |
90 |
4,6 |
|
Камчатский край |
2351 |
9871,5 |
19063 |
150 |
583 |
13 |
7,6 |
|
Приморский край |
10530 |
6283,25 |
12807,8 |
1037 |
2227 |
548 |
1,8 |
|
Хабаровский край |
8118 |
7202 |
15705,1 |
938 |
1877 |
145 |
10,7 |
|
Амурская область |
5062 |
5959,25 |
11936,3 |
843 |
982 |
246 |
7,9 |
|
Магаданская область |
1304 |
7579,75 |
19703,2 |
240 |
868 |
48 |
0,5 |
|
Сахалинская область |
3446 |
7645,75 |
24552,3 |
356 |
1703 |
190 |
2,2 |
|
Еврейская автономная область |
985 |
5734,75 |
10876,9 |
91 |
471 |
52 |
1,7 |
|
Чукотский авт.округ |
406 |
10005,5 |
32140,4 |
39 |
263 |
1 |
0,2 |
Приложение Б
Модель
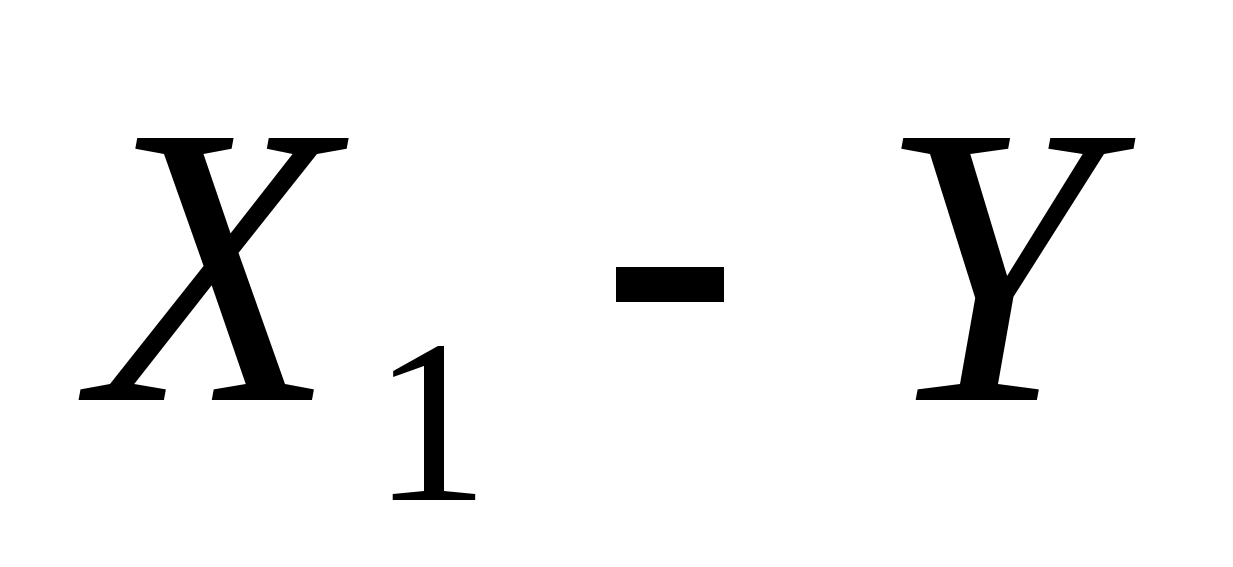 .
Вывод итогов
.
Вывод итогов
|
Регрессионная статистика |
|
|
Множественный R |
0,041337447 |
|
R-квадрат |
0,001708785 |
|
Нормированный R-квадрат |
-0,011256036 |
|
Стандартная ошибка |
10680,12691 |
|
Наблюдения |
79 |
|
Дисперсионный анализ |
||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
67675896,6 |
67675896,6 |
1,500041722 |
0,224398629 |
|
|
Остаток |
77 |
3473932732 |
45116009,51 |
|||
|
Итого |
78 |
3541608629 |
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
Y-пересечение |
12355,3295 |
2656,278566 |
4,651368144 |
1,34462E-05 |
|
Переменная X 1 |
0,063111699 |
0,173839907 |
0,363044944 |
0,717566041 |
|
Приложение В
Модель
 .
Вывод итогов
.
Вывод итогов
|
Регрессионная статистика |
|
|
Множественный R |
0,041337447 |
|
R-квадрат |
0,001708785 |
|
Нормированный R-квадрат |
-0,011256036 |
|
Стандартная ошибка |
10680,12691 |
|
Наблюдения |
79 |
|
Дисперсионный анализ |
||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
15033967,71 |
15033967,71 |
0,131801632 |
0,717566041 |
|
|
Остаток |
77 |
8783013527 |
114065110,7 |
|||
|
Итого |
78 |
8798047494 |
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
Y-пересечение |
12355,3295 |
2656,278566 |
4,651368144 |
1,34462E-05 |
|
Переменная X 1 |
0,063111699 |
0,173839907 |
0,363044944 |
0,717566041 |
|
ВЫВОД ОСТАТКА |
||
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
12970,58021 |
8076,419786 |
|
2 |
13108,64968 |
-5749,649679 |
|
3 |
13290,87209 |
-3256,872088 |
|
4 |
13057,15684 |
-4477,156843 |
|
5 |
13160,50225 |
-785,502251 |
|
6 |
12989,13505 |
-2451,135054 |
|
7 |
12960,96199 |
-1329,961991 |
|
8 |
13041,12647 |
6539,873528 |
|
9 |
13124,88201 |
-3512,882008 |
|
10 |
13005,68294 |
4188,317058 |
|
11 |
13041,78914 |
-11469,78914 |
|
12 |
12882,55202 |
-4635,552016 |
|
13 |
13168,30917 |
7182,690832 |
|
14 |
12897,41482 |
-6262,414821 |
|
15 |
13170,87781 |
-4468,877814 |
|
16 |
13097,26433 |
-4195,264328 |
|
17 |
13558,42783 |
-10277,42783 |
|
18 |
12902,89292 |
-9401,892917 |
|
19 |
13266,61826 |
11796,38174 |
|
20 |
12993,52763 |
-2682,527628 |
|
21 |
12949,41255 |
-6972,41255 |
|
22 |
13114,17826 |
29597,82174 |
|
23 |
13340,15601 |
10839,84399 |
|
24 |
13059,70656 |
-4704,706556 |
|
25 |
13075,4971 |
-3848,497103 |
|
26 |
13113,5787 |
-1426,578703 |
|
27 |
13129,98774 |
-3317,987744 |
|
28 |
13598,83194 |
-11993,83194 |
|
29 |
13603,42647 |
42694,57353 |
|
30 |
13540,13806 |
-6245,138056 |
|
31 |
15432,96521 |
-15080,96521 |
|
32 |
13181,46165 |
13021,53835 |
|
33 |
13090,30311 |
-7527,303108 |
|
34 |
13165,56381 |
12031,43619 |
|
35 |
13215,32107 |
3009,678927 |
|
36 |
12998,05905 |
4244,940952 |
|
37 |
12974,73928 |
-6525,739275 |
|
38 |
12997,35851 |
-2000,358508 |
|
39 |
13372,62698 |
7226,373017 |
|
40 |
13163,65152 |
4089,348475 |
|
41 |
13004,80569 |
-7634,805689 |
|
42 |
12859,35847 |
-9193,358467 |
|
43 |
12997,33326 |
-10890,33326 |
|
44 |
13254,84162 |
19394,15838 |
|
45 |
13068,39704 |
-5132,397037 |
|
46 |
13047,15995 |
10765,84005 |
|
47 |
12703,25799 |
-9397,25799 |
|
48 |
12711,98634 |
-10430,98634 |
|
49 |
13127,09723 |
-7250,097229 |
|
50 |
13531,50438 |
-5828,504375 |
|
51 |
12850,3398 |
-7489,339805 |
|
52 |
12884,47061 |
-6971,470612 |
|
53 |
13538,09324 |
-6129,093237 |
|
54 |
12976,20347 |
-8013,203467 |
|
55 |
13250,28495 |
16246,71505 |
|
56 |
12852,09431 |
-10130,09431 |
|
57 |
13034,65752 |
-8592,657523 |
|
58 |
13122,79932 |
20775,20068 |
|
59 |
13069,20487 |
-3945,204867 |
|
60 |
13352,82253 |
14337,17747 |
|
61 |
12927,21617 |
6835,783834 |
|
62 |
13904,86688 |
-8935,866877 |
|
63 |
13439,03942 |
23018,96058 |
|
64 |
13082,54668 |
-5017,54668 |
|
65 |
12983,44869 |
7238,55131 |
|
66 |
13065,51283 |
-5106,512832 |
|
67 |
13040,47011 |
-1048,47011 |
|
68 |
13206,1825 |
-3687,182499 |
|
69 |
13074,07709 |
-641,07709 |
|
70 |
14097,98237 |
19861,01763 |
|
71 |
12960,009 |
-1167,009005 |
|
72 |
12971,07249 |
-2647,072486 |
|
73 |
13346,50505 |
-866,5050511 |
|
74 |
14429,93097 |
1643,06903 |
|
75 |
13249,0669 |
16014,9331 |
|
76 |
12897,6862 |
-3572,686202 |
|
77 |
14383,76476 |
-13899,76476 |
|
78 |
14761,99318 |
-9960,993176 |
|
79 |
13149,72908 |
-2490,729084 |
Приложение Г
Модель
 .
Вывод итогов
.
Вывод итогов
|
Регрессионная статистика |
|
|
Множественный R |
0,75886525 |
|
R-квадрат |
0,575876467 |
|
Нормированный R-квадрат |
0,57036837 |
|
Стандартная ошибка |
4416,732592 |
|
Наблюдения |
79 |
|
Дисперсионный анализ |
||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
5725005586 |
5725005586 |
143,4492087 |
2,88536E-19 |
|
|
Остаток |
77 |
3073041908 |
39909635,17 |
|||
|
Итого |
78 |
8798047494 |
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
|
Y-пересечение |
3365,498591 |
1086,978184 |
3,096197 |
0,002733837 |
|
|
Переменная X 1 |
11,04339376 |
0,922047892 |
11,97702838 |
2,88536E-19 |
|
ВЫВОД ОСТАТКА |
||
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
23044,82628 |
-1997,826276 |
|
2 |
12675,07953 |
-5316,079533 |
|
3 |
7009,818533 |
3024,181467 |
|
4 |
7385,293921 |
1194,706079 |
|
5 |
10466,40078 |
1908,59922 |
|
6 |
11394,04586 |
-856,0458565 |
|
7 |
9947,361274 |
1683,638726 |
|
8 |
8533,806872 |
11047,19313 |
|
9 |
9660,233036 |
-48,23303574 |
|
10 |
23950,38456 |
-6756,384565 |
|
11 |
4370,447423 |
-2798,447423 |
|
12 |
8644,24081 |
-397,2408096 |
|
13 |
29825,47005 |
-9474,470047 |
|
14 |
9218,497285 |
-2583,497285 |
|
15 |
8290,852209 |
411,1477908 |
|
16 |
7109,209077 |
1792,790923 |
|
17 |
5022,007655 |
-1741,007655 |
|
18 |
5806,088613 |
-2305,088613 |
|
19 |
35402,3839 |
-10339,3839 |
|
20 |
10234,48951 |
76,51048859 |
|
21 |
6877,297808 |
-900,2978075 |
|
22 |
16705,91826 |
26006,08174 |
|
23 |
24844,89946 |
-664,8994596 |
|
24 |
4745,922811 |
3609,077189 |
|
25 |
9483,538736 |
-256,5387355 |
|
26 |
8379,199359 |
3307,800641 |
|
27 |
10179,27254 |
-367,2725426 |
|
28 |
6015,913094 |
-4410,913094 |
|
29 |
28643,82691 |
27654,17309 |
|
30 |
5784,001825 |
1510,998175 |
|
31 |
3475,932529 |
-3123,932529 |
|
32 |
18097,38587 |
8105,614129 |
|
33 |
12432,12487 |
-6869,12487 |
|
34 |
21719,61902 |
3477,380975 |
|
35 |
17997,99533 |
-1772,995327 |
|
36 |
21388,31721 |
-4145,317212 |
|
37 |
6037,999882 |
411,0001185 |
|
38 |
10587,87811 |
409,1218882 |
|
39 |
21675,44545 |
-1076,44545 |
|
40 |
14817,49792 |
2435,502077 |
|
41 |
7970,59379 |
-2600,59379 |
|
42 |
5375,396256 |
-1709,396256 |
|
43 |
5806,088613 |
-3699,088613 |
|
44 |
28500,2628 |
4148,737205 |
|
45 |
11007,52707 |
-3071,527075 |
|
46 |
32332,32043 |
-8519,320431 |
|
47 |
5949,652731 |
-2643,652731 |
|
48 |
5518,960375 |
-3237,960375 |
|
49 |
5850,262188 |
26,73781243 |
|
50 |
8555,893659 |
-852,8936595 |
|
51 |
8876,152079 |
-3515,152079 |
|
52 |
7749,725915 |
-1836,725915 |
|
53 |
11217,35156 |
-3808,351556 |
|
54 |
7628,248583 |
-2665,248583 |
|
55 |
29946,94738 |
-449,9473781 |
|
56 |
4017,058823 |
-1295,058823 |
|
57 |
10764,57241 |
-6322,572412 |
|
58 |
27771,39881 |
6126,601193 |
|
59 |
9163,280316 |
-39,28031642 |
|
60 |
14563,49987 |
13126,50013 |
|
61 |
30753,11512 |
-10990,11512 |
|
62 |
7296,94677 |
-2327,94677 |
|
63 |
36860,11187 |
-402,1118736 |
|
64 |
9980,491455 |
-1915,491455 |
|
65 |
14795,41114 |
5426,588865 |
|
66 |
8898,238866 |
-939,2388661 |
|
67 |
11294,65531 |
697,3446874 |
|
68 |
11338,82889 |
-1819,828888 |
|
69 |
9859,014123 |
2573,985877 |
|
70 |
18340,34053 |
15618,65947 |
|
71 |
13812,54909 |
-2019,549091 |
|
72 |
8710,501172 |
1613,498828 |
|
73 |
13724,20194 |
-1244,20194 |
|
74 |
9395,191585 |
6677,808415 |
|
75 |
34198,65398 |
-4934,653977 |
|
76 |
13945,06982 |
-4620,069816 |
|
77 |
3796,190948 |
-3312,190948 |
|
78 |
4668,619055 |
132,3809451 |
|
79 |
15899,75051 |
-5240,750512 |
Приложение Д
Модель
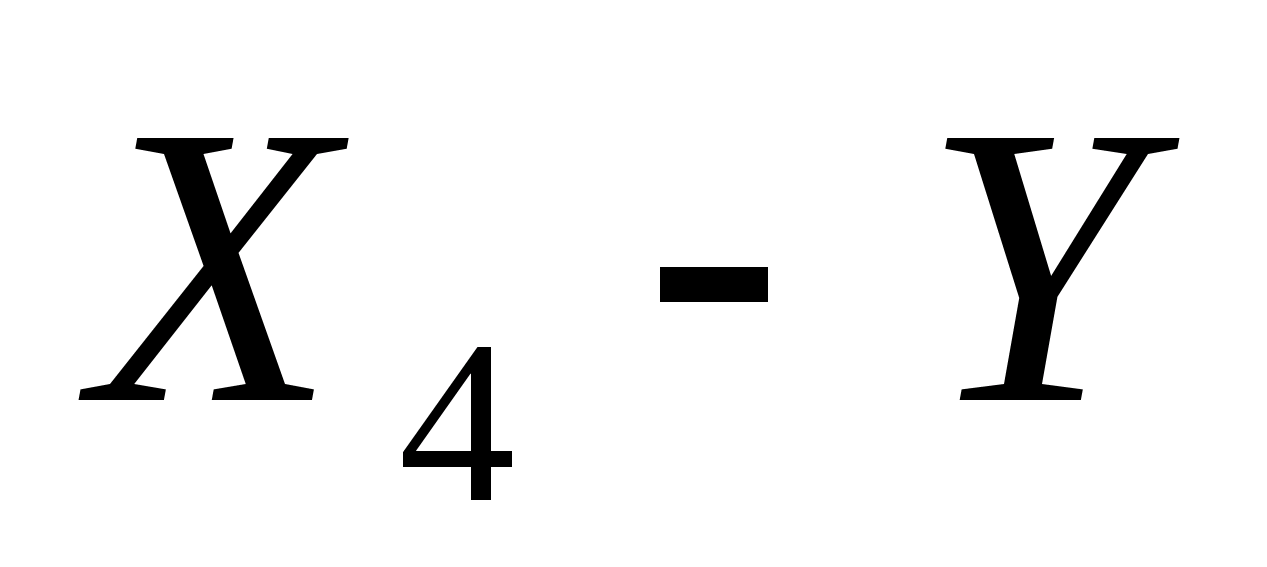 .
Вывод итогов
.
Вывод итогов
|
Регрессионная статистика |
|
|
Множественный R |
0,91026244 |
|
R-квадрат |
0,82857771 |
|
Нормированный R-квадрат |
0,826351447 |
|
Стандартная ошибка |
2807,944807 |
|
Наблюдения |
79 |
|
Дисперсионный анализ |
||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
6774734206 |
6774734206 |
257,8219284 |
2,73503E-26 |
|
|
Остаток |
77 |
2023313289 |
26276795,96 |
|||
|
Итого |
78 |
8798047494 |
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
Y-пересечение |
201,2380967 |
994,7534668 |
0,202299468 |
0,840216171 |
|
Переменная X 1 |
6,175205809 |
0,384584264 |
16,05683432 |
2,73503E-26 |
|
ВЫВОД ОСТАТКА |
||
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
31077,26714 |
-10030,26714 |
|
2 |
6265,290201 |
1093,709799 |
|
3 |
7228,622307 |
2805,377693 |
|
4 |
7395,352864 |
1184,647136 |
|
5 |
8877,402258 |
3497,597742 |
|
6 |
18381,044 |
-7843,043999 |
|
7 |
13138,29427 |
-1507,294267 |
|
8 |
18850,35964 |
730,6403599 |
|
9 |
9525,798868 |
86,20113158 |
|
10 |
22129,39392 |
-4935,393925 |
|
11 |
3109,760033 |
-1537,760033 |
|
12 |
12292,29107 |
-4045,291071 |
|
13 |
28971,52196 |
-8620,521961 |
|
14 |
4696,787926 |
1938,212074 |
|
15 |
6049,157998 |
2652,842002 |
|
16 |
10464,43015 |
-1562,430151 |
|
17 |
3801,383083 |
-520,3830834 |
|
18 |
2362,56013 |
1138,43987 |
|
19 |
20560,89165 |
4502,108351 |
|
20 |
13132,11906 |
-2821,119061 |
|
21 |
4826,467248 |
1150,532752 |
|
22 |
30848,78453 |
11863,21547 |
|
23 |
29687,84584 |
-5507,845835 |
|
24 |
9254,089813 |
-899,0898128 |
|
25 |
14867,35189 |
-5640,351893 |
|
26 |
13095,06783 |
-1408,067826 |
|
27 |
13459,40497 |
-3647,404969 |
|
28 |
5561,316739 |
-3956,316739 |
|
29 |
45539,59915 |
10758,40085 |
|
30 |
7055,716545 |
239,2834552 |
|
31 |
991,6644403 |
-639,6644403 |
|
32 |
23259,45659 |
2943,543412 |
|
33 |
8469,838675 |
-2906,838675 |
|
34 |
15620,727 |
9576,272998 |
|
35 |
12718,38027 |
3506,619728 |
|
36 |
19517,28187 |
-2274,281868 |
|
37 |
5758,923325 |
690,0766751 |
|
38 |
19758,11489 |
-8761,114894 |
|
39 |
30169,51189 |
-9570,511888 |
|
40 |
13953,42143 |
3299,578566 |
|
41 |
8056,099886 |
-2686,099886 |
|
42 |
3826,083907 |
-160,0839066 |
|
43 |
1905,5949 |
201,4051 |
|
44 |
28601,00961 |
4047,990387 |
|
45 |
6339,392671 |
1596,607329 |
|
46 |
5511,915093 |
18301,08491 |
|
47 |
219,7637141 |
3086,236286 |
|
48 |
2158,778338 |
122,2216618 |
|
49 |
8086,975915 |
-2209,975915 |
|
50 |
13243,27277 |
-5540,272765 |
|
51 |
6407,319935 |
-1046,319935 |
|
52 |
8809,474995 |
-2896,474995 |
|
53 |
17034,84913 |
-9625,849132 |
|
54 |
3616,126909 |
1346,873091 |
|
55 |
18288,41591 |
11208,58409 |
|
56 |
2121,727103 |
600,2728967 |
|
57 |
4252,173107 |
189,8268925 |
|
58 |
22925,99547 |
10972,00453 |
|
59 |
9315,841871 |
-191,8418709 |
|
60 |
23500,28961 |
4189,710386 |
|
61 |
19023,2654 |
739,7345972 |
|
62 |
10717,61359 |
-5748,61359 |
|
63 |
33312,69165 |
3145,308355 |
|
64 |
11860,02666 |
-3795,026664 |
|
65 |
9494,922839 |
10727,07716 |
|
66 |
9871,610394 |
-1912,610394 |
|
67 |
12872,76042 |
-880,7604169 |
|
68 |
6666,678579 |
2852,321421 |
|
69 |
16503,78143 |
-4070,781433 |
|
70 |
31515,70675 |
2443,293245 |
|
71 |
11180,75403 |
612,2459747 |
|
72 |
13218,57194 |
-2894,571942 |
|
73 |
11792,0994 |
687,9005996 |
|
74 |
15102,00971 |
970,990286 |
|
75 |
31287,22414 |
-2023,22414 |
|
76 |
13410,00332 |
-4085,003322 |
|
77 |
1825,317224 |
-1341,317224 |
|
78 |
5530,44071 |
-729,4407099 |
|
79 |
11884,72749 |
-1225,727487 |
Приложение Е
Модель
 .
Вывод итогов
.
Вывод итогов
|
Регрессионная статистика |
|
|
Множественный R |
0,787263114 |
|
R-квадрат |
0,61978321 |
|
Нормированный R-квадрат |
0,61484533 |
|
Стандартная ошибка |
4181,87037 |
|
Наблюдения |
79 |
|
Дисперсионный анализ |
||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
5576335357 |
5576335357 |
133,2762842 |
1,80156E-18 |
|
|
Остаток |
77 |
3221712137 |
41840417,37 |
|||
|
Итого |
78 |
8798047494 |
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
|
Y-пересечение |
6672,711455 |
922,3939135 |
7,234123466 |
2,98637E-10 |
|
|
Переменная X 1 |
21,22668563 |
1,838678297 |
11,54453482 |
1,80156E-18 |
|
ВЫВОД ОСТАТКА |
||
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
26710,70269 |
-5663,702688 |
|
2 |
11894,47612 |
-4535,47612 |
|
3 |
7373,192081 |
2660,807919 |
|
4 |
8116,126078 |
463,8739223 |
|
5 |
8031,219335 |
4343,780665 |
|
6 |
10663,32835 |
-125,3283532 |
|
7 |
8752,926647 |
2878,073353 |
|
8 |
14356,77165 |
5224,228347 |
|
9 |
8859,060075 |
752,9399253 |
|
10 |
14484,13177 |
2709,868234 |
|
11 |
7776,499108 |
-6204,499108 |
|
12 |
10727,00841 |
-2480,00841 |
|
13 |
27623,45017 |
-7272,45017 |
|
14 |
10663,32835 |
-4028,328353 |
|
15 |
7691,592365 |
1010,407635 |
|
16 |
7861,40585 |
1040,59415 |
|
17 |
6948,658368 |
-3667,658368 |
|
18 |
8094,899392 |
-4593,899392 |
|
19 |
37791,03259 |
-12728,03259 |
|
20 |
7925,085907 |
2385,914093 |
|
21 |
9368,50053 |
-3391,50053 |
|
22 |
37005,64522 |
5706,354782 |
|
23 |
18092,66832 |
6087,331677 |
|
24 |
12021,83623 |
-3666,836233 |
|
25 |
12531,27669 |
-3304,276688 |
|
26 |
16436,98684 |
-4749,986844 |
|
27 |
10854,36852 |
-1042,368524 |
|
28 |
7691,592365 |
-6086,592365 |
|
29 |
34840,52328 |
21457,47672 |
|
30 |
13465,25086 |
-6170,250856 |
|
31 |
6821,298254 |
-6469,298254 |
|
32 |
14738,85199 |
11464,14801 |
|
33 |
8519,433105 |
-2956,433105 |
|
34 |
25861,63526 |
-664,6352632 |
|
35 |
13528,93091 |
2696,069087 |
|
36 |
10429,83481 |
6813,165189 |
|
37 |
7224,605281 |
-775,6052813 |
|
38 |
10663,32835 |
333,6716468 |
|
39 |
27262,59651 |
-6663,596515 |
|
40 |
18304,93518 |
-1051,935179 |
|
41 |
9113,780302 |
-3743,780302 |
|
42 |
10175,11458 |
-6509,114584 |
|
43 |
7351,965395 |
-5244,965395 |
|
44 |
14717,62531 |
17931,37469 |
|
45 |
8137,352763 |
-201,3527634 |
|
46 |
16479,44022 |
7333,559785 |
|
47 |
7182,15191 |
-3876,15191 |
|
48 |
7330,738709 |
-5049,738709 |
|
49 |
7351,965395 |
-1474,965395 |
|
50 |
11236,44887 |
-3533,448865 |
|
51 |
8116,126078 |
-2755,126078 |
|
52 |
9262,367102 |
-3349,367102 |
|
53 |
8583,113162 |
-1174,113162 |
|
54 |
7436,872138 |
-2473,872138 |
|
55 |
20491,2838 |
9005,716201 |
|
56 |
7182,15191 |
-4460,15191 |
|
57 |
7946,312593 |
-3504,312593 |
|
58 |
13316,66406 |
20581,33594 |
|
59 |
9092,553617 |
31,44638336 |
|
60 |
21064,40431 |
6625,595689 |
|
61 |
10047,75447 |
9715,24553 |
|
62 |
10705,78172 |
-5736,781724 |
|
63 |
54114,35383 |
-17656,35383 |
|
64 |
9559,5407 |
-1494,5407 |
|
65 |
18687,01552 |
1534,984479 |
|
66 |
7458,098823 |
500,9011768 |
|
67 |
9665,674129 |
2326,325871 |
|
68 |
10068,98116 |
-549,9811556 |
|
69 |
8795,380018 |
3637,619982 |
|
70 |
21446,48465 |
12512,51535 |
|
71 |
11342,58229 |
450,4177067 |
|
72 |
10153,8879 |
170,1121019 |
|
73 |
9750,580871 |
2729,419129 |
|
74 |
15269,51913 |
803,4808654 |
|
75 |
24354,54058 |
4909,459416 |
|
76 |
8201,03282 |
1123,96718 |
|
77 |
6693,938141 |
-6209,938141 |
|
78 |
9092,553617 |
-4291,553617 |
|
79 |
9028,87356 |
1630,12644 |
Приложение Ж
Модель
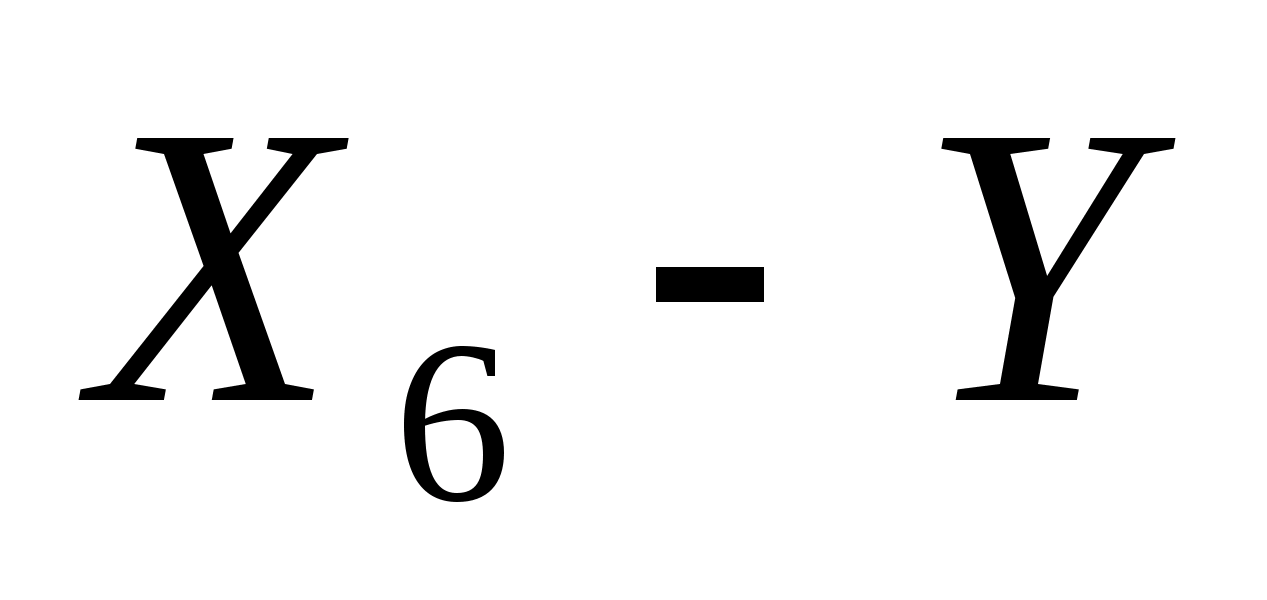 .
Вывод итогов
.
Вывод итогов
|
Регрессионная статистика |
|
|
Множественный R |
0,423561749 |
|
R-квадрат |
0,179404556 |
|
Нормированный R-квадрат |
0,168747472 |
|
Стандартная ошибка |
6143,551055 |
|
Наблюдения |
79 |
|
Дисперсионный анализ |
||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
1754565329 |
1754565329 |
19,18107083 |
3,70252E-05 |
|
|
Остаток |
77 |
7043482166 |
91473794,36 |
|||
|
Итого |
78 |
8798047494 |
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
|
Y-пересечение |
8289,632708 |
1556,545473 |
5,325660479 |
9,65749E-07 |
|
|
Переменная X 1 |
458,0190867 |
104,5796423 |
4,379619941 |
3,70252E-05 |
|
ВЫВОД ОСТАТКА |
||
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
14793,50374 |
6253,496261 |
|
2 |
11907,98349 |
-4548,983493 |
|
3 |
11953,7854 |
-1919,785402 |
|
4 |
10717,13387 |
-2137,133868 |
|
5 |
12411,80449 |
-36,80448843 |
|
6 |
12732,41785 |
-2194,417849 |
|
7 |
14518,69229 |
-2887,692287 |
|
8 |
15388,92855 |
4192,071448 |
|
9 |
12732,41785 |
-3120,417849 |
|
10 |
15709,54191 |
1484,458087 |
|
11 |
9068,265156 |
-7496,265156 |
|
12 |
12274,39876 |
-4027,398762 |
|
13 |
14289,68274 |
6061,317256 |
|
14 |
10808,73769 |
-4173,737685 |
|
15 |
11358,36059 |
-2656,360589 |
|
16 |
11541,56822 |
-2639,568224 |
|
17 |
11770,57777 |
-8489,577767 |
|
18 |
9663,689968 |
-6162,689968 |
|
19 |
16717,1839 |
8345,816097 |
|
20 |
17770,6278 |
-7459,627803 |
|
21 |
10533,92623 |
-4556,926233 |
|
22 |
24457,70647 |
18254,29353 |
|
23 |
11678,97395 |
12501,02605 |
|
24 |
11312,55868 |
-2957,55868 |
|
25 |
12640,81403 |
-3413,814032 |
|
26 |
14701,89992 |
-3014,899922 |
|
27 |
13602,65411 |
-3790,654114 |
|
28 |
8518,642252 |
-6913,642252 |
|
29 |
10717,13387 |
45580,86613 |
|
30 |
10121,70906 |
-2826,709055 |
|
31 |
8427,038434 |
-8075,038434 |
|
32 |
14610,2961 |
11592,7039 |
|
33 |
10625,53005 |
-5062,53005 |
|
34 |
22900,44157 |
2296,558427 |
|
35 |
16304,96673 |
-79,96672521 |
|
36 |
18182,84498 |
-939,8449806 |
|
37 |
14243,88084 |
-7794,880835 |
|
38 |
17679,02399 |
-6682,023985 |
|
39 |
12045,38922 |
8553,610781 |
|
40 |
9114,067064 |
8138,932936 |
|
41 |
10121,70906 |
-4751,709055 |
|
42 |
9388,878516 |
-5722,878516 |
|
43 |
8930,85943 |
-6823,85943 |
|
44 |
17816,42971 |
14832,57029 |
|
45 |
11541,56822 |
-3605,568224 |
|
46 |
15159,91901 |
8653,080991 |
|
47 |
9984,303329 |
-6678,303329 |
|
48 |
9343,076608 |
-7062,076608 |
|
49 |
10396,52051 |
-4519,520507 |
|
50 |
10900,3415 |
-3197,341502 |
|
51 |
10671,33196 |
-5310,331959 |
|
52 |
10854,53959 |
-4941,539594 |
|
53 |
10396,52051 |
-2987,520507 |
|
54 |
10533,92623 |
-5570,926233 |
|
55 |
19740,10988 |
9756,890125 |
|
56 |
9159,868973 |
-6437,868973 |
|
57 |
9617,88806 |
-5175,88806 |
|
58 |
16121,75909 |
17776,24091 |
|
59 |
11037,74723 |
-1913,747228 |
|
60 |
16991,99536 |
10698,00464 |
|
61 |
14656,09801 |
5106,901987 |
|
62 |
9297,274699 |
-4328,274699 |
|
63 |
19556,90224 |
16901,09776 |
|
64 |
11220,95486 |
-3155,954863 |
|
65 |
16121,75909 |
4100,240909 |
|
66 |
12915,62548 |
-4956,625484 |
|
67 |
14472,89038 |
-2480,890378 |
|
68 |
12640,81403 |
-3121,814032 |
|
69 |
13282,04075 |
-849,0407531 |
|
70 |
11220,95486 |
22738,04514 |
|
71 |
12824,02167 |
-1031,021666 |
|
72 |
12915,62548 |
-2591,625484 |
|
73 |
13190,43694 |
-710,4369358 |
|
74 |
10259,11478 |
5813,885219 |
|
75 |
19144,68506 |
10119,31494 |
|
76 |
11037,74723 |
-1712,747228 |
|
77 |
8381,236526 |
-7897,236526 |
|
78 |
8930,85943 |
-4129,85943 |
|
79 |
42686,86612 |
-32027,86612 |
Приложение З
Множественная регрессия
|
Регрессионная статистика |
||
|
Множественный R |
0,926961813 |
|
|
R-квадрат |
0,859258202 |
|
|
Нормированный R-квадрат |
0,847529719 |
|
|
Стандартная ошибка |
2631,149849 |
|
|
Наблюдения |
79 |
|
Дисперсионный анализ |
||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
6 |
3043156263 |
507192710,5 |
73,26251741 |
1,15419E-28 |
|
|
Остаток |
72 |
498452366,2 |
6922949,53 |
|||
|
Итого |
78 |
3541608629 |
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
Y-пересечение |
-280,3190398 |
1530,654787 |
-0,183136682 |
0,855205506 |
|
Переменная X 1 |
-0,18513892 |
0,361191458 |
-0,512578345 |
0,609815267 |
|
Переменная X 2 |
0,066020709 |
0,0690531 |
0,956086105 |
0,342227977 |
|
Переменная X 3 |
0,715876331 |
0,668158791 |
1,071416466 |
0,287560537 |
|
Переменная X 4 |
3,028268331 |
0,338201129 |
8,954045593 |
2,54338E-13 |
|
Переменная X 5 |
3,111989868 |
1,249906253 |
2,489778621 |
0,015092273 |
|
Переменная X 6 |
36,89531368 |
33,19932151 |
1,111327341 |
0,270124795 |
|
ВЫВОД ОСТАТКА |
||
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
19403,18374 |
-6090,183737 |
|
2 |
4038,700576 |
1023,299424 |
|
3 |
3683,376704 |
2843,623296 |
|
4 |
3813,812634 |
1532,187366 |
|
5 |
5060,811406 |
1580,188594 |
|
6 |
9991,95845 |
-2935,95845 |
|
7 |
7039,374426 |
93,62557427 |
|
8 |
10775,42216 |
2022,57784 |
|
9 |
5231,920624 |
1355,079376 |
|
10 |
13426,50466 |
-1378,504659 |
|
11 |
1092,060827 |
-107,0608271 |
|
12 |
6618,70247 |
-1466,70247 |
|
13 |
19041,61822 |
-6711,618219 |
|
14 |
2980,838603 |
-638,838603 |
|
15 |
3206,867918 |
1890,132082 |
|
16 |
5391,937651 |
-87,93765134 |
|
17 |
1344,35703 |
1006,64297 |
|
18 |
1118,934199 |
275,0658009 |
|
19 |
17182,86576 |
-1605,865759 |
|
20 |
7265,531701 |
-800,5317006 |
|
21 |
2578,696245 |
751,3037547 |
|
22 |
21299,27118 |
3456,728821 |
|
23 |
17512,66721 |
-1111,667211 |
|
24 |
5164,504514 |
276,4954862 |
|
25 |
8498,374593 |
-2459,374593 |
|
26 |
8291,758836 |
186,2411638 |
|
27 |
7732,083923 |
-1697,083923 |
|
28 |
2585,36387 |
-1281,36387 |
|
29 |
28166,57055 |
8902,429453 |
|
30 |
4328,681761 |
1509,318239 |
|
31 |
1744,524084 |
-1524,524084 |
|
32 |
13619,1069 |
3655,893102 |
|
33 |
4677,014129 |
-1451,014129 |
|
34 |
12342,96351 |
3426,036487 |
|
35 |
8477,301338 |
2046,698662 |
|
36 |
11595,86533 |
-1183,86533 |
|
37 |
3095,715715 |
858,2842848 |
|
38 |
10991,481 |
-3712,480995 |
|
39 |
19007,70025 |
-6712,700248 |
|
40 |
8660,086222 |
1869,913778 |
|
41 |
4224,266694 |
-929,2666945 |
|
42 |
1965,059358 |
-208,0593577 |
|
43 |
453,0452236 |
622,9547764 |
|
44 |
17397,29389 |
55,70610699 |
|
45 |
3533,522842 |
606,4771584 |
|
46 |
6231,563091 |
-2087,563091 |
|
47 |
-296,8797058 |
674,8797058 |
|
48 |
656,7608622 |
511,2391378 |
|
49 |
3761,241939 |
-218,2419392 |
|
50 |
7360,711401 |
-2101,711401 |
|
51 |
3285,688485 |
-359,6884847 |
|
52 |
4617,182316 |
-1155,182316 |
|
53 |
8706,589507 |
-4177,589507 |
|
54 |
1922,476612 |
59,52338811 |
|
55 |
13422,09662 |
2248,903375 |
|
56 |
458,6189447 |
173,3810553 |
|
57 |
2329,78511 |
478,21489 |
|
58 |
14010,89656 |
7950,103441 |
|
59 |
5027,355457 |
623,6445429 |
|
60 |
14723,53589 |
1831,464113 |
|
61 |
11493,73071 |
616,2692942 |
|
62 |
6009,556027 |
-2563,556027 |
|
63 |
26214,48636 |
-3449,486361 |
|
64 |
6424,368698 |
-1018,368698 |
|
65 |
7233,843482 |
4887,156518 |
|
66 |
5363,423681 |
-261,4236809 |
|
67 |
7214,191771 |
28,80822853 |
|
68 |
4206,055849 |
1395,944151 |
|
69 |
8740,092544 |
-980,0925438 |
|
70 |
19370,09084 |
1831,909157 |
|
71 |
6667,932662 |
-567,9326622 |
|
72 |
7172,783586 |
-135,783586 |
|
73 |
6624,742342 |
1493,257658 |
|
74 |
9584,292783 |
1147,707217 |
|
75 |
20511,32184 |
1174,678157 |
|
76 |
7122,236757 |
-2336,236757 |
|
77 |
824,050297 |
-418,050297 |
|
78 |
3865,63686 |
-255,6368602 |
|
79 |
9276,840905 |
-2792,840905 |
1 Официальный сайт Федеральной службы государственной статистики Росстат – www.gks.ru