Использование статистики в правоведении
Контрольная работа по предмету «Правовая статистика»
Ситуация 1
Народным судом города М в 1995 г. было осуждено П = 600 человек. За этот же год среднее число жителей, в возрасте 14 лет и старше, составило Н =75 000 человек. Определите коэффициент преступности К для этого города.
Коэффициент преступности рассчитывается по формуле:
КП = (П х 100000) : Н,
где П – абсолютное число учтенных преступлений; а Н – абсолютная численность всего населения.
В данной ситуации: КП = (600х100000) : 75000 = 800 преступлений на 100000 чел. населения.
Ситуация 2
Годовая нагрузка п = 15 судей городского суда, специализирующихся на рассмотрении гражданских дел разной направленности, составила: 17, 42. 47, 47, 50. 50. 50, 63. 68, 68, 75. 78, 80, 80, 85 (количество дел) .
Вычислить среднюю годовую нагрузку на одного судью (среднюю арифметическую X ).
Средняя арифметическая рассчитывается по формуле:
В
данной ситуации
Х
= (17+ 42+ 47+ 47+ 50+50+ 50+ 63+ 68+68+75+78+ 80+ 80+ 85) = 60 дел
на одного судью
Ситуация 3
Определите средний срок расследования уголовных дел на основе следующих данных:
|
Срок расследования |
до 1 мес. |
от 1 до 2 мес. |
от 2 до 3 мес. |
от 3 до 4 мес. |
|
Число уголовных дел |
20 |
60 |
30 |
10 |
Для удобства расчетов средней взвешенной заполните следующую таблицу.
|
Срок интервалов расследования |
Центр интервалов (варианты), дни |
Число уголовных дел |
Произведение интервалов на веса |
|
до 1 месяца |
15 |
20 |
300 |
|
от 1 месяца до 2 месяцев |
30 |
60 |
1800 |
|
от 2 месяцев до 3 месяцев |
75 |
30 |
2250 |
|
от 3 месяцев до 4 месяцев |
105 |
10 |
1050 |
|
итого |
120 |
5400 |
средний срок расследования уголовных дел равен 5400:120 =45дней
Ситуация 4
Динамика преступности в России в 1991 -1996 гг. характеризуется следующими данными:
|
Годы |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
|
Темп роста (подвижная база). % |
100,0 |
127,31 |
101,4 |
94.0 |
104,7 |
95,3 |
Вычислите среднегодовые темпы роста преступности, используя формулу средней геометрической (1991 г. -базовый год)
среднегодовой вариация медиана среднеквадратический
Среднегодовой темп роста – это среднее относительное изменение состояния (уровня) явления за рассматриваемый период времени в целом, рассчитываемое по формуле:
где yn – абсолютное значение последнего уровня ряда динамики;
y1 – абсолютное значение первого (базисного) уровня ряда динамики;
n − число уровней ряда динамики в изучаемом периоде, включая базисный.
х
100 = 99%
Ситуация 5
Распределение сроков лишения свободы среди 100 осужденных имеет следующий вид
|
Срок лишения свободы |
1 год |
2 года |
3 года |
5 лет |
8 лет |
|
Число осужденных |
8 |
23 |
38 |
21 |
10 |
Определите моду Мо указанного ряда распределения.
Мода - это наиболее часто встречающаяся в совокупности величина варианта.
Наибольшее число осуждённых (38) со сроком лишения свободы 3года.
Следовательно, Мо =3 года
Ситуация 6
Период времени с 1991 Г. по 1996 г. характеризовался следующим распределением зарегистрированных хищений художественных и исторических ценностей:
|
Годы |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
|
Число хищений |
2147 |
4189 |
4796 |
3493 |
3436 |
3119 |
29944 |
Укажите значение признака (число хищений), являющееся медианой Me в соответствующем ранжированном ряду
Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.
В данной ситуации Me=3493
Ситуация 7
По данным уголовно-правовой статистики раскрываемость преступлений по ряду регионов России в 1996 г составила:
Республика Карелия 58,7%
Красноярский край 61,3%
Свердловская область 64,6%
Сахалинская область 65,1%
Республика Татарстан 78%
Курская область 82.6%
Тамбовская область 87,6%
Чему равен размах вариации R в указанной совокупности?
Размах вариации – разность между максимальной и минимальной вариантами выборки.
В данной ситуации R=87,6% - 58,7% = 28,9%
Ситуации 8
В суде 10 осужденным были назначены следующие сроки лишения свободы: 6, 6, 7, 7, 7, 7, 8, 8, 8, 8 лет.
Рассчитайте среднее квадратическое отклонение σ в этом ряду распределения.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности.
Расчет отклонений
|
Количество осуждённых |
|||
|
Сроки лишения свободы |
Отклонение от среднего |
Квадрат отклонения от среднего |
|
|
1 |
6 |
-1,2 |
1,44 |
|
2 |
6 |
-1,2 |
1,44 |
|
3 |
7 |
-0,2 |
0,04 |
|
4 |
7 |
-0,2 |
0,04 |
|
5 |
7 |
-0,2 |
0,04 |
|
6 |
7 |
-0,2 |
0,04 |
|
7 |
8 |
+1,2 |
1,44 |
|
8 |
8 |
+1,2 |
1,44 |
|
9 |
8 |
+1,2 |
1,44 |
|
10 |
8 |
+1,2 |
1,44 |
|
Итого |
72 |
0 |
8,56 |
Средняя арифметическая составляет 72 : 10 = 7,2.
Квадрат отклонения от среднего = 8,56
Дисперсия σ2 = 8,56 : 10 = 0,856, а среднее квадратическое отклонение:
σ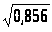
= = 0, 925
Ситуация 9
В порядке случайной выборки обследовано 400 заключенных и установлено, что доля заключенных, совершивших преступления в состоянии алкогольного опьянения, составила Р = 0,8. Определить среднюю ошибку W репрезентативности при определении этой доли заключенных.
W = √ [p(1-p) / n] = √[ 0,8(1-0.8) /400 = √0,0004 = 0,02
Ситуация 10
Данные по числу разбоев, зарегистрированных в Камчатской области, представлены в следующей таблице
|
Годы |
1991 |
1992 |
1993 |
1994 |
1995 |
|
Число разбоев |
48 |
64 |
100 |
111 |
113 |
Определить средний уровень (У) данного ряда динамики.
В данной ситуации мы имеем интервальный ряд и средний уровень такого ряда определяется по формуле простой средней арифметической величины из уровней ряда, т.е.
У = (48+64+100+111+113) : 5 = 87,2