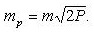Основные сведения по геодезии

Содержание

Задание 1

Задание 2

Задание 3

Задание 4

Список литературы

магнитный азимут нивелирование теодолит угол

Задание 1

магнитный азимут меридиана нивелирование

Ответы на вопросы по темам 2, 3, 5, 7 (вопрос 9) раздела 1, «Основные сведения по геодезии».

1 Что называют магнитным азимутом и как перейти к нему от измеренного на плане или карте дирекционного угла линии?

Магнитным азимутом Am направления называется горизонтальный угол, измеряемый по ходу часовой стрелки (от 0 до 360 градусов) от северного направления магнитного меридиана до определяемого направления, (рис.1). Магнитные азимуты определяются на местности с помощью угломерных приборов, у которых имеется магнитная стрелка (компасов и буссолей). Использование этого простого способа ориентирования направлений невозможно в районах магнитных аномалий и магнитных полюсов.

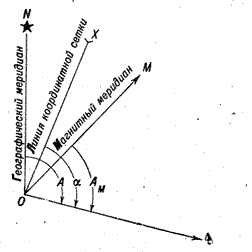
Рис.1

Магнитное склонение. Переход от магнитного азимута к геодезическому азимуту. Свойство магнитной стрелки занимать определенное положение в данной точке пространства обусловлено взаимодействием ее магнитного поля с магнитным полем Земли. Направление установившейся магнитной стрелки в горизонтальной плоскости соответствует направлению магнитного меридиана в данной точке. Магнитный меридиан в общем случае не совпадает с геодезическим меридианом.

Угол между геодезическим меридианом данной точки и ее магнитным меридианом, направленным на север, называется склонением магнитной стрелки или магнитным склонением. Магнитное склонение считается положительным, если северный конец магнитной стрелки отклонен к востоку от геодезического меридиана (восточное склонение), и отрицательным, если он отклонен к западу (западное склонение). Зависимость между геодезическим азимутом, магнитным азимутом и магнитным склонением (рис.2) может быть выражена формулой:

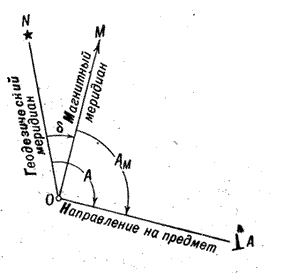
Рис.2

Магнитное склонение изменяется с течением времени и переменой места. Изменения бывают постоянные и случайные. Эту особенность магнитного склонения необходимо учитывать при точном определении магнитных азимутов направлений, например, при наводке орудий и пусковых установок, ориентировании с помощью буссоли технических средств разведки, подготовке данных для работы с навигационной аппаратурой, движении по азимутам. Изменения магнитного склонения обусловлены свойствами . магнитного поля Земли.

Переход от магнитного азимута к дирекционному углу. На местности при помощи компаса (буссоли) измеряют магнитные азимуты направлений, от которых затем переходят к дирекционным углам; На карте, наоборот, измеряют дирекционные углы и от них переходят к магнитным азимутам направлений на местности. Для решения этих задач необходимо знать величину отклонения магнитного меридиана в данной точке от вертикальной линии координатной сетки карты. Угол, образованный вертикальной линией координатной сетки и магнитным меридианом, представляющий собой сумму сближения меридианов и магнитного склонения, называется отклонением магнитной стрелки или поправкой направления (ПН). Он отсчитывается от северного направления вертикальной линии координатной сетки и считается положительным, если северный конец магнитной стрелки отклоняется к востоку от этой линии, и отрицательным при западном отклонении магнитной стрелки: На рис.3 поправка направления равна 2°16' +5*16'= +7°32'. Поправку направления и составляющие ее сближение меридианов и магнитное склонение приводят на карте под южной стороной рамки в виде схемы с пояснительным текстом. Поправку направления в общем случае можно выразить формулой:

Рис.3

Если на карте измерен дирекционный угол направления, то магнитный азимут этого направления на местности:

Измеренный на местности магнитный азимут какого-либо направления переводится в дирекционный угол этого направления по формуле:

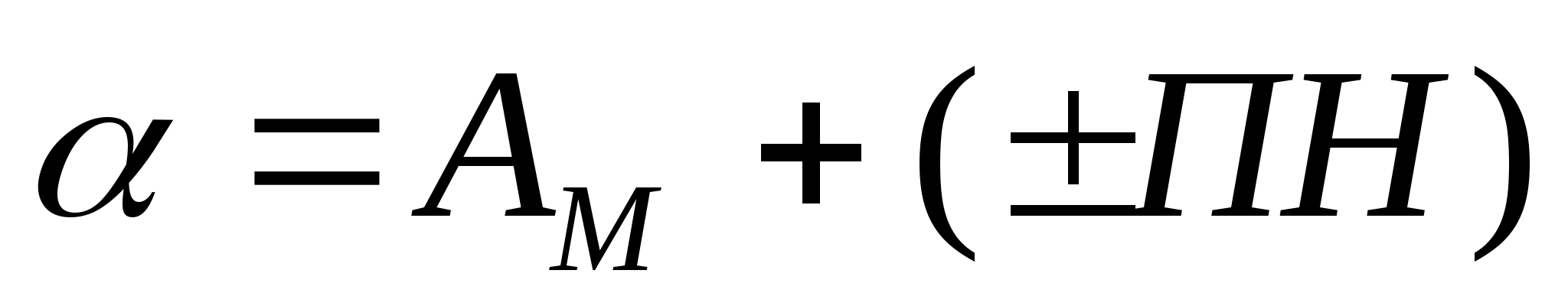
Чтобы избежать ошибок при определении величины и знака поправки направления, нужно пользоваться помещаемой на карте схемой направлений геодезического меридиана, магнитного, меридиана и вертикальной линии координатной, сетки. При точных измерениях переход от дирекционных углов к магнитным азимутам и обратно выполняется с учетом годового изменения магнитного склонения. Сначала определяют склонение магнитной стрелки на данное время (указанное на карте годовое изменение склонения магнитной стрелки умножают на число лет, прошедших после создания карты), затем полученную величину алгебраически суммируют с величиной склонения магнитной стрелки, указанной на карте. После этого переходят от измеренного дирекционного угла к магнитному азимуту по приведенным выше формулам.

2. Какие способы применяют для определения площадей на планах и картах и какова их точность?

(вопрос 9) раздела 1, «Топографические планы и карты».

Для решения многих инженерных задач землеустройства требуется знать площади земельных угодий. Эти площади могут быть рассчитаны аналитически по результатам измерений на местности либо определены по плану или карте графическим и механическим способами либо их комбинациями.

Графический способ определения площадей.

Следует иметь в виду, что по планам (картам) площадь определяется с меньшей точностью, чем по результатам непосредственных измерений на местности; при этом на точность определения площадей оказывают влияние погрешности измерений на местности, построения плана и измерений на них, а также деформация бумаги.

Для определения площадей небольших участков по плану или карте применяется графический способ с разбивкой участка на геометрические фигуры либо с помощью палеток. В первом случае искомую площадь небольшого участка разбивают на простейшие геометрические фигуры: треугольники, прямоугольники, трапеции. При криволинейном контуре участка его разбивка на геометрические фигуры выполняется с таким расчетом, чтобы стороны фигур по возможности ближе совпадали с этим контуром. Затем на плане(карте) измеряют соответствующие элементы фигур и по геометрическим формулам вычисляются площади этих фигур. Площадь всего участка определяется как сумма отдельных фигур.

Точность определения площади во многом зависит от масштаба плана, чем мельче масштаб, тем грубее измеряется площадь. Поскольку графическая погрешность линейных измерений на плане не зависит от длины отрезков, то относительная погрешность короткой линии будет больше, чем длинной. Поэтому заданный участок следует разбивать на фигуры больших размеров с примерно одинаковыми длинами оснований и высот. Для контроля и повышения точности площадь участка определяется дважды, для чего строят новые геометрические фигуры или в треугольниках измеряют другие основания и высоты. Относительное расхождение в результатах двукратных определений общей площади участка не должно превышать 1:200.

Правило: Каждую измеренную сторону (длину) на карте или плане в см необходимо перевести в масштаб заданной карты или плана и только после этого подсчитывать площадь по формуле.

Ошибки определения площадей графическим способом

Графический способ вычисления площадей состоит в том, что участок, изображенный на плане, разбивают на простейшие геометрические фигуры (треугольники, прямоугольники, трапеции). В каждой фигуре на плане измеряют высоту и основание, по которым вычисляют площадь, и сумма площадей фигур дает площадь участка.

Если участок разбит на треугольники, то площадь каждого треугольника равна:

P = 0,5lh (1.1)

Для получения зависимости между относительными средними квадратическими ошибками площади и измерений основания и высоты необходимо прологарифмировать выражение (1.1):

lnP = lnl + lnh - ln2

Дифференцируя по переменам l и h , получаем:

dP/P = dl/l + dh/h

Относительная средняя квадратическая ошибка площади треугольника равна:

(mp/P)2 = (ml/l)2 = (mh/h)2

Такую же зависимость можно получить для прямоугольника, параллелограмма, ромба и трапеции, если их площадь вычисляется по основанию и высоте (площадь трапеции по средней линии и высоте).

Ошибки измерения по плану можно считать одинаковыми независимо от длин линий:

(ml/P) = (mh/l) = m

Основание определяется несколько точнее высоты, потому что на определение высоты, помимо ошибки определения на плане, влияет также ошибка проведения основания между вершинами углов, до которого измеряется высота. Однако влияние этой ошибки на ошибку определения высоты невелико, если треугольник равнобедренный. Если же треугольник близок к прямоугольному, то ошибка высоты в 1,2 раза больше ошибки основания.

Тогда получаем:

Так как для треугольника lh = 2P , а для остальных фигур lh = P , то получим:

1) - для треугольника.

2) - для прямоугольника, параллелограмма и трапеции.

3) если участок разбивается на треугольники, у которых высоты примерно равны основаниям, то ошибка площади участка вычисляется по формуле:

где m - ошибка определения расстояния по плану.

А для прямоугольника (по форме близкого к квадрату), параллелограмма и трапеции:

Таким образом, площадь треугольника графическим способом вычисляется точнее площадей других фигур, следовательно, разбивкой участка на треугольники вычисляется площадь точнее, чем разбивкой на прямоугольники, трапеции и другие фигуры.

Способ определения площадей с помощью палетки

Определение площадей малых участков с резко выраженными криволинейными границами рекомендуется производить с помощью квадратной палетки. Палетка представляет собой лист прозрачной основы, на которую нанесена сетка квадратов со сторонами 1-5 мм. Зная длину сторон и масштаб плана, легко вычислить площадь квадрата палетки s.

Для определения площади участка палетку произвольно накладывают на план и подсчитывают число N1 полных квадратов, расположенных внутри контура участка. Затем оценивают «на глаз» число квадратов N2, составляемых из неполных у границ участка. Тогда общая площадь измеряемого участка

Палетки бывают прямолинейные и криволинейные.

К прямолинейным относятся квадратные и параллельные палетки.

К криволинейным относятся гиперболические палетки, представляющие систему гиперболических кривых и применяющиеся для определения площадей простейших геометрических фигур. Однако гиперболические палетки применяются редко, так как они не пригодны для быстрого определения площадей с криволинейными контурами.

Наиболее удобными для пользования и построения являются квадратная и параллельная палетки.

Квадратная палетка представляет сеть взаимно перпендикулярных линий, проведенных через 1-2мм на прозрачном материале. Площадь фигуры определяется простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитываются на глаз.

Для упрощения подсчетов количества клеток проводят утолщенные линии через 0,5см и 1см, чтобы подсчитать клетки группами – в 25 и 100 кв.мм.

Недостатком квадратной палетки является то, что площади долей квадратиков, рассекаемых контуром, берутся на глаз и то что, подсчет целых квадратиков или их долей сопровождался ошибками.

Площадь параллельной палеткой определяется так: накладывают палетку на контур так, чтобы крайние точки разместились посередине между параллельными линиями палетки. Так, весь контур оказывается рассеченным параллельными линиями на трапеции с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций.

При оценке точности определения площадей палетками принимается во внимание, что ими определяют площади криволинейных контуров, так как площадь участка, ограниченного прямыми линиями, быстрее и точнее можно определить графическим способом.

Палетками определяют площади небольших контуров, не превышающих 10 кв.см (с.к.о. или m = 0,03).

Механический способ определения площадей

В инженерной практике для определения площадей достаточно больших участков по планам или картам наиболее часто применяется механический способ, основанный на использовании специального прибора- планиметра. Конструкция планиметра впервые была предложена в 1856 г. одновременно швейцарцем Амслером и нашим соотечественником механиком А. Н. Зарубиным. Из многочисленных конструкций планиметров в настоящее время наибольшее распространение получили полярные планиметры типа ПП- 2К и его модернизированная модель ПП-М.

Допустимая ошибка при этом методе 1/400. В современных условиях применяют четвертый метод – электронный способ. Он связан с картами в электронном виде, т.е. с использованием ПК.

3. Опишите порядок работы при измерении теодолитом горизонтального угла "от нуля" (отсчет по горизонтальному кругу при визировании на опорную точку 0⁰).

(вопрос 9) раздела 1 «Угловые измерения».

Сначала теодолит устанавливают в рабочее положение, т. е. прибор центрируют над вершиной измеряемого угла, приводят ось вращения теодолита в отвесное положение, устанавливают зрительную трубу «по глазу» и «предмету» и готовят отсчетный микроскоп для наблюдений.

Центрирование выполняют при помощи: нитяного отвеса с точностью 3-5 мм, оптического центрира (Т15, Т5 и др.) или зрительной трубы (Т30), направленной объективом вниз, с точностью до 0,5-1 мм. Приближенное центрирование выполняют перемещением штатива, а точное — перемещением теодолита по горизонтальной платформе штатива при открепленном становом винте.

Установка оси вращения теодолита в отвесное положение выполняют путем приведения в нуль-пункт пузырька цилиндрического уровня подъемными винтами. В результате при вращении алидады пузырек уровня не должен отклоняться от нуль-пункта более чем на одно деление уровня. Установка зрительной трубы «по глазу» и «по предмету» позволяет четко видеть штрихи сетки нитей и наблюдаемый предмет. Штрихи лимба и шкала отсчетного микроскопа также должны иметь четкое изображение.

Затем незакрепленную алидаду отводят влево на 30-40° и обратным вращением наводят на визирную цель первого направления так, чтобы она оказалась справа от биссектора (в поле зрения трубы); алидаду закрепляют. Наводящим винтом алидады, только ввинчиванием, биссектор наводят на визирную цель и берут отсчет по оптическому микрометру (если имеется окулярный микрометр, то трижды наводят его биссектор на визирную цель и берут отсчеты). Открепляют алидаду и наводят на 2-е направление так же, как и на 1-е. На этом заканчивают полуприем. Трубу переводят через зенит, по часовой стрелке наводят на 2-е направление, предварительно отведя алидаду влево на 30-40°; наводящим винтом биссектор наводят на визирную цель и берут отсчет по оптическому микрометру. По часовой стрелке алидаду поворачивают на угол, дополняющий измеряемый до 360°, наводят на визирную цель 1-го направления, берут отсчет. Заканчивается прием.

4. В чем сущность гидростатического нивелирования?

(вопрос 9) раздела 1 «Измерение превышений (нивелирование)».

Гидростатическое нивелирование – определение высот точек земной поверхности относительно исходной точки с помощью сообщающихся сосудов с жидкостью.

Гидростатическое нивелирование основано на том, что свободная поверхность жидкости в сообщающихся сосудах находится на одном уровне. Гидростатический нивелир состоит из двух стеклянных трубок, вставленных в рейки с делениями, соединённых резиновым или металлическим шлангом и заполненных жидкостью (вода, спирт, диметилфталат и т.п.). Разность высот определяют по разности уровней жидкости в стеклянных трубках, причём учитывают различие температуры и давления в различных частях жидкости гидростатического нивелира. Погрешности определения разности высот этим методом составляют 1–2 мм. Гидростатическое нивелирование применяют для непрерывного изучения деформаций инженерных сооружений, высокоточного определения разности высот точек, разделённых широкими водными преградами, и др.

Задание 2

Вычисление исходных дирекционных углов линий; решение прямой геодезической задачи.

Задача 1. Вычислить дирекционные углы линий BC и CD, если известны дирекционный угол _>AB> = 4940,2’ и измеренные правые по ходу углы _>1> = 18959,2’ и _>2> = 15928,0’ (рис. 1).

Рис

Дирекционные углы вычисляют по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180 и минус горизонтальный угол, справа по ходу лежащий. Следовательно,

_>BC> = _>AB> + 180 - _>1>

_>CD> = _>BC> + 180 - _>2>

Вычисляем в столбик,

_>AB> ------ 4940,2’

+ 180

------------

22940,2’

- 18959,2’

------------

_>BC> ------ 3941,0’

+ 180

------------

21941,0’

- 15928,0’

_>CD> ------ 6013,0’

Задача 2. Найти координаты x_>C> и y_>C> точки C (рис. 1), если известны координаты x_>B> = -14,02 м и y_>B> = +627,98 м точки B, длина (горизонтальное проложение) d_>BC> =239,14м линии BC и дирекционный угол _>BC> = 3941,0’этой линии.

Координаты точки C вычисляются по формулам:

x_>C> = x_>B> + x_>BC>

x_>BC> = d_>BC>*cos_>BC>

y_>C> = y_>B> + y_>BC>

y_>BC> = d_>BC>*sin_>BC>

Таблица

x>B> + x>BC>	-14,02 +184,04		y>B> + y>BC>	+627,98 +152,70
x>C>	+170,02		y>C>	+780,68

Задание 3

Составление топографического плана строительной площадки.

По данным полевых измерений составить и вычертить топографический план строительной площадки в масштабе 1:2000 с высотой сечения рельефа 1 м.

Работа состоит из следующих этапов: обработка ведомости вычисления координат вершин теодолитного хода; обработка тахеометрического журнала; построение топографического плана.

ИСХОДНЫЕ ДАННЫЕ

1. Для съемки участка на местности между двумя пунктами полигонометрии ПЗ8 и ПЗ19 был проложен теодолитно-высотный ход. В нем измерены длины всех сторон (рис. 2), а на каждой вершине хода – правый по ходу горизонтальный угол и углы наклона на предыдущую и последующую вершины. Результаты измерений горизонтальных углов и линий сведены в таблицу 1. Результаты тригонометрического нивелирования сведены в таблицы 3 и 4.

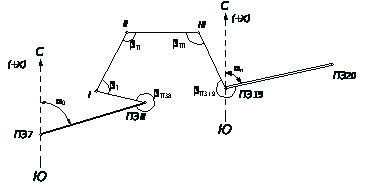
Рис. 2. Схема теодолитно-высотного хода съемочного обоснования

Таблица 1 . Результаты измерений углов и длин сторон хода

Номера вершин хода	Измеренные углы (правые)	Длины сторон (горизонтальные проложения) ,м
	‘
ПЗ 8	330	59,2	263,02
I	50	58,5
239,21
II	161	20,0
269,80
III	79	02,8
192,98
ПЗ 19	267	08,2

Измерение углов производилось оптическим теодолитом 2Т30 с точностью отсчетов по шкаловому микроскопу 0,5’.

2. Координаты полигонометрических знаков ПЗ8 и ПЗ19 (т. е. начальной и конечной точек хода):

x_>ПЗ8> = -14,02;x_>ПЗ19> = +170,02

y_>ПЗ8> = +627,98;y_>ПЗ19> = +780,68

дирекционный угол _>0> направления ПЗ7 – ПЗ8 = 4940,2’

дирекционный угол _>n> стороны ПЗ19 – ПЗ20 = 6013,0’

3. Отметки пунктов ПЗ8 и ПЗ19 принимаем условно согласно варианту

ПЗ8 – 149,149 м,

ПЗ19 – 152,431 м.

4. При съемке участка были составлены абрисы (рис. 3 и рис. 4. методических указаний)

Обработка ведомости вычисления координат вершин теодолитного хода (таблица 2)

Увязка углов хода

Значения измеренных углов записываем в графу 2 ведомости вычисления координат (табл. 2). В графе 4 записываем исходный дирекционный угол _>0 >(на верхней строчке) и конечный дирекционный угол _>n> (на нижней строчке). Вычисляем сумму _>пр> измеренных углов хода. Определяем теоретическую сумму углов:

Σβ_>т >=α_>0>–α_>n>+180°*n

где n – число вершин хода.

Находим угловую невязку

f_>>=_>пр>-_>т>

Допустимая величина

f_>βдоп>=±1√n

Невязка f_>> не превышает допустимой величины, поэтому распределяем ее с обратным знаком поровну на все углы хода с округлением значений поправок до десятых долей минут. Исправленные этими поправками углы записываем в графу 3 ведомости. Сумма исправленных углов должна равняться теоретической.

Вычисление дирекционных углов и румбов сторон хода

По исходному дирекционному углу _>0> и исправленным значениям углов  хода по формуле для правых углов вычисляем дирекционные углы всех остальных сторон: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180 и минус правый (исправленный) угол хода, образованный этими сторонами.

_>П>_>38-I>=_>0>+180-_>П>_>38>=4940,2’+180+360-33058,9’= 25841,3’

_>I-II>=_>П>_>38-I>+180-_>I>=25841,3’+180-360-5058,2’=2743,1’

_>II-III>=_>I-II>+180-_>II>=2743,1’+180-16119,7’=4623,4’

_>III>_>-ПЗ19>=_>II>_>->_>III>+180-_>III>=4623,4’+180-7902,5’=14720,9’

Для контроля вычисления дирекционных углов находим конечный дирекционный угол _>n> по дирекционному углу _>III>_>-ПЗ19> последней стороны и исправленному углу _>П319> при вершине ПЗ 19 (рис. 2). Вычисленный угол _>n> и угол по условию задачи _>n> должны быть равны.

_>n>=_>III>_>-ПЗ19>+180-_>П319>=14720,9’+180-26707,9’=6013,0’

6013,0’=6013,0’

Переход от дирекционных углов к румбам. Согласно таблицы 1 методического пособия имеем:

r_>П>_>38-I>=_>П>_>38-I>-180=25841,3’–180=7841,3’ЮЗ

r_>I-II>=_>I-II>=2743,1’СВ

r_>II-III>=_>II-III>=4623,4’СВ

r_>III->_>ПЗ>_>19>=180-_>III->_>ПЗ>_>19>=180-14720,9’=3239,1’ ЮВ

Значения дирекционных углов записываем в графу 4 ведомости с точностью до десятых долей минут, а румбов – в графу 5; при этом значения румбов округляем до целых минут.

Вычисление приращений координат

Приращения координат вычисляем по формулам

x=d*cos=d*cosr ;y=d*sin=d*sinr

x_>ПЗ>_>8-I>=263,02*cos7841’=51,61 м

y_>ПЗ>_>8-I>=263,02*sin7841’=257,91 м

x_>I-II>=239,21*cos2743’=211,76 м

y_>I-II>=239,21*sin2743’=111,26 м

x_>II-III>=269,80*cos4623’=186,12 м

y_>II-III>=269,80*sin4623’=195,33 м

x_>III->_>ПЗ>_>19>=192,98*cos3239’=162,48 м

y_>III->_>ПЗ>_>19>=192,98*sin3239’=104,11 м

Вычисленные значения приращений x и y выписываем в графы 7 и 8 ведомости с точностью до сотых долей метра. Знаки приращений устанавливаем по названию румба, руководствуясь таблицей 1 методического пособия. В каждой из граф складываем все вычисленные значения x и y, и тем самым находим практические суммы приращений координат x_>пр> и y_>пр> :

x_>пр>=-51,61+211,76+186,12-162,48 = +183,79 м

y_>пр>=-257,91+111,26+195,33+104,11 = +152,79 м

Нахождение абсолютной и относительной линейных невязок хода; увязка приращений координат. Сначала вычисляем невязки f_>x> и f_>y>, в приращениях координат по осям x и y

x_>т>=x_>кон>–x_>нач>=+170,02–(-14,02)=+184,04

y_>т>=y_>кон>–y_>нач>=+780,68–627,98=+152,7

f_>x>=x_>пр->x_>т>=+183,79 –184,04= -0,25

f_>y>=y_>пр->y_>т>=+152,79 –152,7= +0,09

Абсолютную линейную невязку P хода вычисляем по формуле и записываем с точностью до сотых долей метра. м. Относительная линейная невязка хода 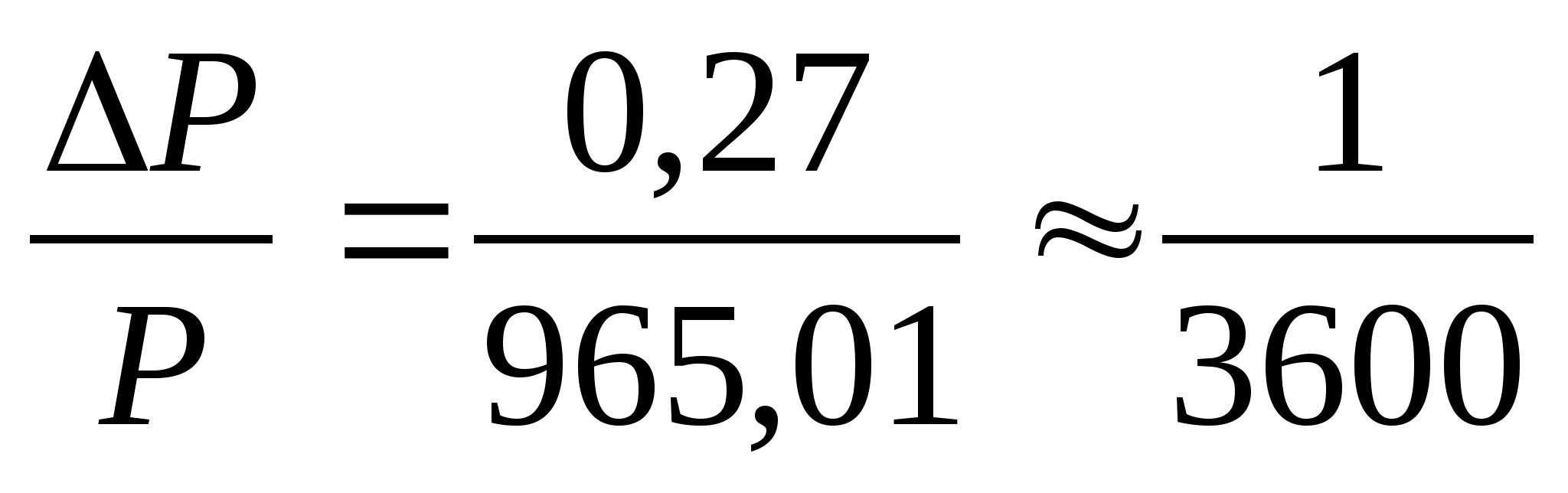. Так как относительная невязка меньше допустимой , то невязки f_>x>_> >и f_>y> распределяем, вводя поправки в вычисленные значения приращений координат. Поправки приращения распределяем прямо пропорционально длинам сторон хода, записанным в графе 6, и видим со знаком, обратным знаку соответствующей невязки. Значения поправок округляем до сотых долей метра и записываем в ведомости над соответствующими приращениями, следя за тем, чтобы суммы поправок в x и y равнялись невязке соответственно f_>x>_> >и f_>y>_> >с противоположным знаком. Исправленные приращения записываем в графы 9 и 10; суммы исправленных приращений координат должны быть равны соответственно x_>т> и y_>т.>.

Вычисление координат вершин хода. Координаты вершин хода получаем путем последовательного алгебраического сложения координат предыдущих вершин хода с соответствующими исправленными приращениями:

x_>I>=x_>ПЗ8>+x_>ПЗ8->_>I>_> >= -14,02–51,54 = -65,56 м x_>II>=x_>I>+x_>I>_>->_>II>_> >= -65,56+211,82 = 146,26 м x_>III>=x_>II>+x_>II>_>->_>III>_> >= 146,26 +186,2 = 332,46 м y_>I>=y_>ПЗ8>+y_>ПЗ8->_>I>_> >= 627,98–257,93 = 370,05 м y_>II>=y_>I>+y_>I>_>->_>II>_> >= 370,05+111,24 = 481,29 м y_>III>=y_>II>+y_>II>_>->_>III>_> >= 481,29+195,31 = 676,6 м

Контролем правильности вычислений являются полученные по формулам известные значения конечной точки ПЗ19.

x_>ПЗ19>=x_>III>+x_>III>_>-ПЗ19 >= 332,46–162,43 = 170,02 м y_>ПЗ19>=y_>III>+y_>III>_>-ПЗ19 >= 676,6+104,09 = 780,68 м

Таблица

ё	Измерен-ные углы	Испр. углы	Дирекцион-ные углы	Румбы, r	Длины (гор.), d	Приращения координат	Координаты	№ вер-шин хода
вычисленные	исправленные
°	'	°	'	°	'	назв.	°	'	±	Δх	±	Δy	±	Δх	±	Δy	±	х	±	y
1	2	3	4	5	6	7	8	9	10	11	12	13
ПЗ 7	-	-	-	-	49	40,2	-	-	-											-		-	ПЗ 7
ПЗ 8	330	-0,3 59,2	330	58,9	-	14,02	+	627,98	ПЗ 8
258	41,3	ЮЗ	78	41	263,02	-	+0,07 51,61	-	-0,02 257,91	-	51,54	-	257,93
I	50	-0,3 58,5	50	58,2	-	65,56	+	370,05	I
27	43,1	СВ	27	43	239,21	+	+0,062211,76	+	-0,02 111,26	+	211,82	+	111,24
II	161	-0,3 20,0	161	19,7	+	146,26	+	481,29	II
46	23,4	СВ	46	23	269,80	+	+0,08 186,12	+	-0,02 195,33	+	186,2	+	195,31
III	79	-0,3 02,8	79	02,5	+	332,46	+	676,6	III
147	20,9	ЮВ	33	21	192,98	-	+0,05 162,48	+	-0,02 104,11	-	162,43	+	104,09
ПЗ 19	267	-0,3 08,2	267	07,9	+	170,02	+	780,68	ПЗ 19
60	13,0	-	-	-
ПЗ 20	-	-	-	-		-		-	ПЗ 20
Σβ>т >= α>0> – α>n> + 180° * n Σβ>т >= 49°40,2' – 60°13,0' + 180° * 5 = 889°27,2' f>β доп >= ± 1√ n = ± 1√ 5=0°02,2' f>> = >пр> - >т> f>> = 88928,7’ - 889°27,2' = 001,5’	Р=965,01	+	397,88	+	410,7	+	398,02	+	410,64
Σ>пр>	889	28,7	889	27,2		-	214,09	-	257,91	-	213,97	-	257,93
Σ>т>	889	27,2	889	27,2	ΣΔ>пр>	+	183,79	+	152,79	+		+
f>>	+0	01,5	0	00,0	ΣΔ>т>	+	184,04	+	152,70	+	184,04	-	152,70
f>>> доп>	±0	02,2			f	-	0,26	+	0,08
P= f2>x>+f2>y>> > 0,27 м

Обработка тахеометрического журнала (таблица 3)

Вычисление места нуля вертикального круга и углов наклона

Из отсчетов по вертикальному кругу при «круге лево» (КЛ) и «круге право» (КП) на предыдущую и последующую станции дважды вычисляют место нуля (М0). Для оптического теодолита 2Т 30, которым была выполнена тахеометрическая съемка

При наведении со станции ПЗ19 на станцию III

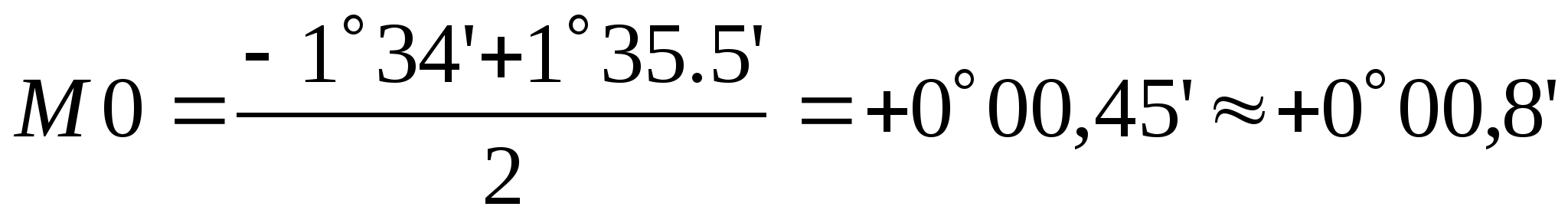
Углы наклона v на предыдущую и последующие точки теодолитно-высотного хода вычисляют с контролем по формуле

и записывают со своим знаком (плюс или минус) в графу 6 таблицы 3.

При наблюдении со станции ПЗ19 на станцию III угол наклона

При наблюдении со станции ПЗ19 на станцию ПЗ20

;

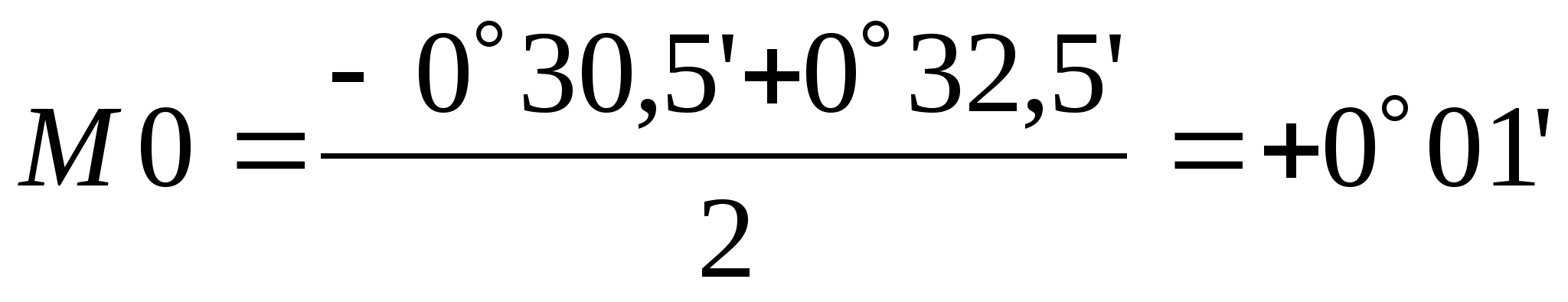Из полученных на станции ПЗ19 двух значений М0 выводим среднее арифметическое (+0,9’), округляем до целых минут (+1’) и используем для вычисления углов наклона на реечные точки.

Вычисление горизонтальных проложений и превышений

Значения горизонтальных расстояний между вершинами теодолитно-высотного хода переписываем в графу 7 табл. 3 из ведомости вычисления координат (табл. 2). Вычисление горизонтальных проложений d от станций до реечных точек производят по значениям расстояний D^' (табл. 3, графа 2), полученных по нитяному дальномеру:

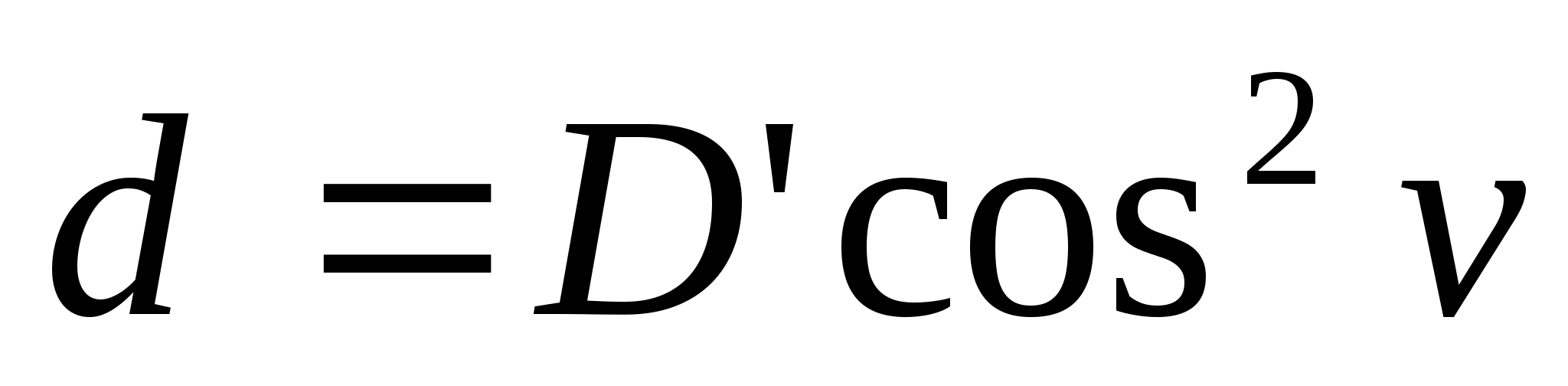
Значения горизонтальных проложений d в графу 7 журнала с округлением до десятых долей метра. Превышения h относительно станции вычисляют по формуле

,

где i – высота инструмента на данной станции; l – высота наводки (таб. 3 графа 9).

Так как расстояния до реечных точек измерялись по нитяному дальномеру, то при определении превышений на реечные точки используем формулу

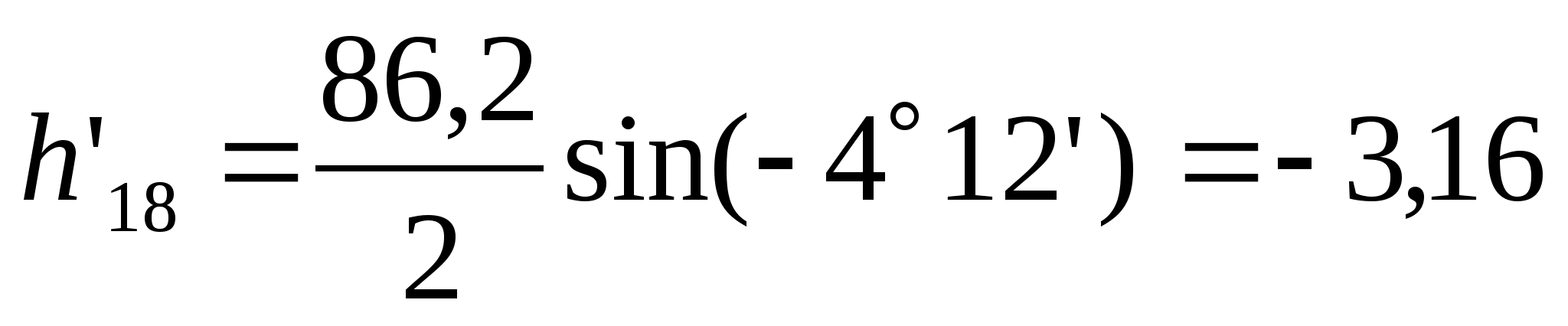
Вычисленные значения h’ записываем в графу 8 с округлением до сотых долей метра. В графу 10 записываем значения превышений h. Если при визировании на точку труба наводилась на высоту, равную высоте инструмента ( l = i ), то h = h’ и значение превышения из графы 8 без изменения переписываем в графу 10.

Вычисление отметок станций

Вычисление отметок станций выполняем в «Ведомости увязки превышений теодолитно-высотного хода и вычисления отметок станций» (табл. 5). Известные отметки (п. 3 исходных данных) округленные до сотых долей метра, записываем в графу 8 на первой и последней строчках ведомости. Из журнала тахеометрической съемки выписываем значения прямых h_>пр> и обратных h_>обр> превышений по сторонам хода (даны в графах 3 и 4 табл. 5 методического пособия – общие для всех вариантов), вычисляем среднее значение h_>ср> этих превышений. Затем определяем сумму h_>ср>=+3,38, вычисляем теоретическое значение суммы превышений, равное разности известных отметок конечной и начальной точек хода: h_>т>=H_>кон>–Н_>нач>=152,43–149,14=+3,28, находим невязку хода f_>h>=h_>ср>-_>h>_>т>=+3,38–3,28 =+0,10 и ее допустимое значение f_>h>_>доп>=0,20мL=0,20м, где L1 - длина хода, км.

В графе 6 ведомости в превышения введены поправки пропорционально длинам сторон хода. Отметки станций вычисляем по известной отметке Н_>ПЗ8> станции ПЗ8 и по исправленным превышениям h_>испр> и записываем в графу 8:

H_>I>=H_>ПЗ>_>8>+h_>ПЗ>_>8-I>=144,96

H_>II>=H_>I>+h_>I-II>=144,66

H_>III>=H_>II>+h_>II>_>->_>III>=145,54

Контроль правильности вычислений:

H_>ПЗ19>=H_>III>+h_>III>_>-ПЗ19>=152,42

Вычисленные отметки станций переписываем в графу 5 табл. 4 на одной строчке с номером той станции, к которой данная отметка относится. Отметки станций аккуратно подчеркиваем.

Вычисление отметок реечных точек

Отметки реечных точек на каждой станции вычисляем путем алгебраического сложения отметки данной станции с соответствующим превышением. Полученные отметки записываем в графу 6 табл. 4.

Таблица 3. Тахеометрический журнал

Номера точек наблюдения	Отсчеты	Место нуля М0	Угол наклона ν	Горизонтальное положение d = D*Cos2ν	h'= D/2 Sin 2ν или h' = d tg ν	Высота наводки l	Превышение h = h'+i – l	Отметки H	Примечания
по дальномеру D=Kn	по гориз. кругу	по вертик. кругу
°	'	°	'	°	'
1	2	3	4	5	6	7	8	9	10	11	12
				Станция ПЗ 19, i = 1,40						Оптический теодолит 2T30 № 45686 с точностью отсчетов по шкаловому микроскопу 0,5'
ПЗ 20	-	-	-	КП 0	32,5
III	-	-	-	1	35,5
ПЗ 20	-	-	-	КЛ	30,5	+01'	-	-	-	-	3,00	-	-
III	-	0	00	-1	34	+0,8'	-1	34,8	192,98	-5,32	3,00	-6,92	-	Коэффициент нитяного дальномера К = 100,0; постоянное слагаемое с  0
						М0
18	86,2	29	31	-2	05	+01'	-2	0,6	86,1	-3,16	l = i	-3,16
19	56,2	69	28	-2	16	+01'	-2	17	56,1	-2,24	l = i	-2,24		Съемка произведена 05.05.2011
20	48,0	165	26	-3	23	+01'	-3	24	47,8	-2,84	l = i	-2,84
21	103,2	288	07	-0	52	+01'	-0	53	103,2	-1,59	3,00	-3,19		Вычислял Коростелев В.И. ПГСзу2в-02 10041035249
22	60,3	340	11	-2	49	+01'	-2	50	60,2	-2,98	l = i	-2,98

Таблица

Номера точек наблюдения	Отсчеты по гориз. кругу	Горизонтальное положение d = D*Cos2ν	Превышения	Отметки H	Примечания
°	'	станций	реечных точек
1	2	3	4	5	6	7
			Станция ПЗ 8
I	0	0	-	-4,17	149,14
1	57	50	111,2	-2,32		146,82
2	140	5	61,8	+0,20		149,34
3	181	10	66	-		-	т.3 – на грунтовой дороге
3а	238	0	13,6	-		-
4	345	0	82,1	+0,05		149,19
			Станция I
II	-	-	-	-0,30	144,96
ПЗ 8	0	0	-	+4,13
5	13	0	149,6	+4,05		149,01
6	52	05	68,0	+2,02		146,98
7	148	30	11,8	-0,80		144,16	т.7, 8 – на линии уреза воды
8	175	58	25,2	-		-
9	327	45	147,8	+2,06		148,03
			Станция II
III	-	-	-	+0,90	144,66
I	0	00	-	+0,26
10	27	08	98,3	-0,23		144,43	т.10 – 13 – на линии уреза воды
11	50	28	24,6	-		-
12	66	48	34,4	-		-
13	182	43	62,1	-0,03		144,63
			Станция III
ПЗ 19	-	-	-	+6,87	145,54
II	0	00	-	-0,92
14	24	41	102,8	-0,76		144,78	т.14 – 17 – на линии уреза воды
15	56	23	44,1	-0,63		144,91
16	128	00	38,0	-		-
17	143	19	25,6	-0,60		144,94

Таблица 5. Ведомость увязки превышений теодолитно-высотного хода и вычисления отметок станций

Номера станций	Горизонтальные проложения d	Превышения	Поправки в превышения	Исправленные превышения h испр	Отметки станций Н	Номера станций
прямые h пр	обратные h обр	средние h ср
1	2	3	4	5	6	7	8	9
ПЗ 8	263,02	-4,17	+4,13	-4,15	-0,03	-4,18	149,14	ПЗ 8
I	144,96	I
239,21	-0,30	+0,26	-0,28	-0,02	-0,30
II	144,66	II
269,80	+0,90	-0,92	+0,91	-0,03	+0,88
III	145,54	III
192,98	+6,87	-6,92	+6,90	-0,02	+6,88
ПЗ 19	152,42	ПЗ 19
Р =	965,01			+7,81 -4,43	-0,10	+7,76 -4,48
			Σh>ср>	+3,38	Σh>испр>	+3,28

h_>т> = H_>ПЗ19> – Н_>ПЗ8> = 152,43 – 149,14 = +3,28

f_>h> = h_>ср> - _>h>_>т> = + 3,38 – 3,28 = +0,10

f_>h>_>доп>_> >= 0,20мL = 0,20м

Построение топографического плана.

Построение координатной сетки. Координатную сетку в виде квадратов со сторонами 10 см вычерчиваем на листе чертежной бумаги размером А3.

Рассчитаем необходимое количество квадратов.

Самая северная и самая южная точки имеют следующие координаты

x_>сев>=332,46 м 333 м;y_>сев>=780,68 м  781м ;

x_>юж>=-65,56 м -66 м;y_>юж>=370,05 м  370м .

В масштабе плана (1:2000) стороне квадрата в 10 см на местности соответствует расстояние в 200 м.

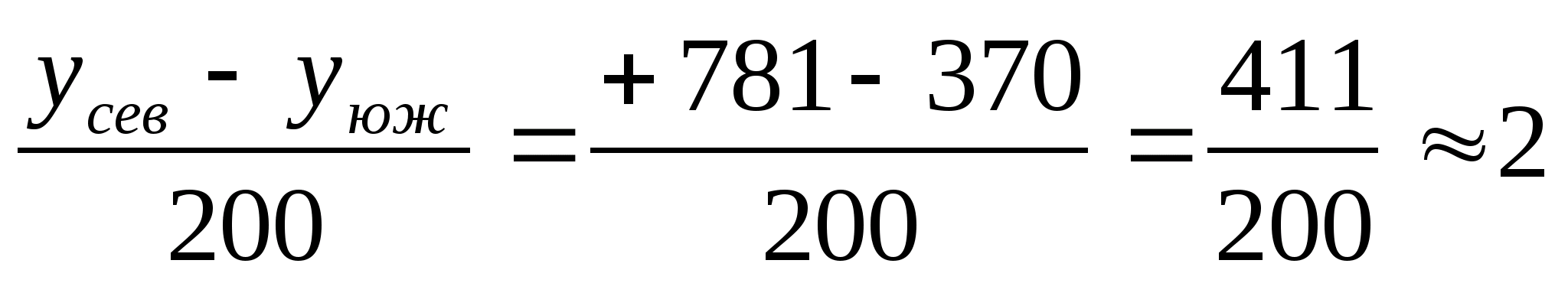
Следовательно, необходимо построить по два ряда горизонтальных и вертикальных квадратов.

Построим теодолитный ход по координатам его вершин

Проконтролируем нанесение точек хода, для этого измерим расстояние между нанесенными вершинами и сравним с длинами сторон хода, записанными в графе 6 ведомости вычислений координат.

Нанесение на план реечных точек

Согласно нашему варианту наносим реечные точки 1, 3а, 4 – 12, изображая ситуацию и рельеф в пределах участка, ограниченного линией ПЗ8 – II, рекой, и шоссейной дорогой.

Изображение ситуации на плане

Накладку ситуации производим в масштабе 1:2000 по абрисам съемки зданий (рис. 3, а методического пособия – согласно варианту «а») и абрисам тахеометрической съемки (рис. 4, а- в, методического пособия – согласно варианту «а»). Вначале наносим здание. Шоссе и грунтовая дорога наносятся по реечным точкам 3u,J и 6; ширина шоссе (22 м) в пределах участка съемки сохраняются постоянными. Линия уреза воды в реке Ик проводится по реечным точкам 7, 10, 11 и 8,12; ширина реки определяется взаимным положением точек 7 и 8, 11 и 12.

Рисовка рельефа на плане

По отметкам станций и реечных точек на плане проводим горизонтали с сечением рельефа через 1 м. Следы горизонталей отыскиваем графической интерполяцией.

Построение графика заложений

В нижней части плана строим график заложений для уклонов. Задаваясь уклонами 0,01; 0.02; 0,03; 0,04; 0,05; 0,06; 0,07 и высотой сечения рельефа 1 м составляемого плана, вычисляем соответствующие им заложения.

d = h / i

d(0,01) = 1/0,01 = 100

d(0,02) = 1/0,02 = 50

d(0,03) = 1/0,03 = 33,3

d(0,04) = 1/0,04 = 25

d(0,05) = 1/0,05 = 20

d(0,06) = 1/0,06 = 16,7

d(0,07) = 1/0,07 = 14,3

Задание 4

Решение задач по топографическому плану строительной площадки.

Задача 1. Найти отметку точки А, взятой между двумя соседними горизонталями. Точку А выбираем между горизонталями с отметками Н_>1>=148 Н_>2>=149.

H_>A>=H_>1>+h/d*a

H_>A> – отметка точки A

H_>1> – отметка нижней горизонтали, Н_>1> = 148

h – высота сечения рельефа горизонталями, h = 1 м

d – расстояние между горизонталями, d = 38.14 м

a – расстояние от горизонтали H_>1> до точки A, a = 16.45 м

H_>A>=148+1/38.14*16.45=148.43

Задача 2. Определит уклон отрезка BC, проведенного между соседними горизонталями. Точки BC выбираем на горизонталях H_>B>_> >= 148 и H_>C>_> >= 149.

i_>BC>=(H_>C>–H_>B>)/d

i_>BC> – уклон

d – длина отрезка BC, ВС = 48,01 м

i_>BC> = (149 – 148)/48,01 = 0,021

Задача 3. От ПЗ19 к точке III, пользуясь графиком заложений, провести кратчайшую ломаную линию так, чтобы ни на одном из ее отрезков уклон не превышал i = 0,02.

d=h/i

h – высота сечения рельефа

i_>BC> – уклон, i_>BC> = 0,02

d – минимальная длина горизонтального проложения

d_>ПЗ19-153>=(153,43–153)/0,02=21,5 м

d_>153-152>=d_>152-151>=d_>151-150>=d_>150-149>=d_>149-148>=d_>148-147>=1/0,02=50 м

d_>147->_>III>=(147-146,55)/0,02=22,5 м

Список литературы

1. Инженерная геодезия. / Г. В. Багратуни, В.Н. Ганьшин, Б. Б. Данилевич и др. М., 1984.

2. Инженерная геодезия. Учеб. для вузов/ Е. Б. Клюшин, М. И. Киселев, Д. Ш. Михелев, В. Д. Фельдман; Под ред. Д. Ш. Михелева. –2-е изд. испр. – М.: Высш. шк., 2001. – 454 с.: ил.

3. Хейфец Б. С., Данилевич Б. Б. Практикум по инженерной геодезии. М., 1979.

4. Условные знаки для топографических планов масштабов 1:5000 1:2000 1:1000 и 1:500. М., 1973.