Оптимизация процессов бурения скважин
ГОСУДАРСТВЕННЫЙ ГЕОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра Бурения
КУРСОВАЯ РАБОТА
по курсу:
Оптимизация процессов бурения скважин
2005г.
Исходные данные
|
|
|
|
|
|
1 |
3,5 |
1 |
4,0 |
|
2 |
4,1 |
2 |
4,2 |
|
3 |
4,0 |
3 |
4,1 |
|
4 |
4,2 |
4 |
0,3 |
|
5 |
3,8 |
5 |
0,5 |
|
6 |
1,0 |
6 |
5,2 |
|
7 |
0,9 |
7 |
5,0 |
|
8 |
3,9 |
8 |
3,9 |
|
9 |
4,2 |
9 |
3,8 |
|
10 |
4,1 |
10 |
4,2 |
|
11 |
4,0 |
11 |
4,3 |
|
12 |
14,3 |
12 |
4,4 |
|
13 |
14,0 |
||
|
14 |
13,7 |
Оптимизация процесса бурения возможна по критериям максимальной механической скорости проходки, максимальной рейсовой скорости бурения и стоимости 1 метра проходки, а также по вопросам оптимальной отработки долота при его сработке по вооружению, опоре или по диаметру. Наша задача при этом сводится к нахождению оптимальной механической скорости проходки для осуществления процесса бурения скважин на оптимальном режиме. В данном решении предполагается, что проведены испытания в идентичных горно-геологических условиях и с одинаковыми режимами.
Выборка №1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
3,5 |
4,1 |
4,0 |
4,2 |
3,8 |
1,0 |
0,9 |
3,9 |
4,2 |
4,1 |
4,0 |
14,3 |
14,0 |
13,7 |
Выборка №2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
4,0 |
4,2 |
4,1 |
0,3 |
0,5 |
5,2 |
5,0 |
3,9 |
3,8 |
4,2 |
4,3 |
4,4 |
Расчёт средней величины.
 ,
,
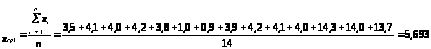

Расчёт дисперсии
 ,
,
Выборка №1.



Выборка №2.
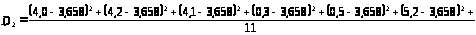


Расчёт среднеквадратичной величины.
 ,
,
Выборка №1

Выборка №2

Расчёт коэффициента вариации
 ,
,
Выборка №1

Выборка №2

Определение размаха варьирования
 ,
,
Выборка №1

Выборка №2

Отбраковка непредставительных результатов измерений.
Метод 3s:


Выборка №1



Значения выборки 1 не выходят за границы критического интервала отбраковки.
|
Выборка №1 |
Выборка №2 |
||||
|
1 |
3,5 |
0,0324 |
1 |
4,0 |
0,01265625 |
|
2 |
4,1 |
0,1764 |
2 |
4,2 |
0,00765625 |
|
3 |
4,0 |
0,1024 |
3 |
4,1 |
0,00015625 |
|
4 |
4,2 |
0,2704 |
4 |
3,9 |
0,04515625 |
|
5 |
3,8 |
0,0144 |
5 |
3,8 |
0,09765625 |
|
6 |
1,0 |
7,1824 |
6 |
4,2 |
0,00765625 |
|
7 |
3,9 |
0,0484 |
7 |
4,3 |
0,03515625 |
|
8 |
4,2 |
0,2704 |
8 |
4,4 |
0,08265625 |
|
9 |
4,1 |
0,1764 |
|||
|
10 |
4,0 |
0,1024 |
|||
|
Среднее значение |
3,68 |
8,376 |
Среднее значение |
4,1125 |
0,28875625 |
|
Дисперсия |
0,93 |
Дисперсия |
0,04 |
Выборка №2


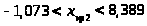
Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
 ,
,
где
 - коэффициент Башинского;
- коэффициент Башинского;
 - размах варьирования.
- размах варьирования.

Выборка №1


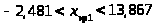
Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу
Башинского значение выборки вышло за
границы критического интервала
отбраковки, поэтому
 и
и
 подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
Расчёт средней величины


Расчёт дисперсии






|
Выборка №1 |
Выборка №2 |
||||
|
1 |
3,5 |
2,343961 |
1 |
4,0 |
0,0016 |
|
2 |
4,1 |
0,866761 |
2 |
4,2 |
0,0576 |
|
3 |
4,0 |
1,062961 |
3 |
4,1 |
0,0196 |
|
4 |
4,2 |
0,690561 |
4 |
0,5 |
11,9716 |
|
5 |
3,8 |
1,515361 |
5 |
5,2 |
1,5376 |
|
6 |
1,0 |
16,248961 |
6 |
5,0 |
1,0816 |
|
7 |
0,9 |
17,065161 |
7 |
3,9 |
0,0036 |
|
8 |
3,9 |
1,279161 |
8 |
3,8 |
0,0256 |
|
9 |
4,2 |
0,690561 |
9 |
4,2 |
0,0576 |
|
10 |
4,1 |
0,866761 |
10 |
4,3 |
0,1156 |
|
11 |
4,0 |
1,062961 |
11 |
4,4 |
0,1936 |
|
12 |
14,0 |
80,442961 |
|||
|
13 |
13,7 |
75,151561 |
|||
|
Среднее значение |
5,031 |
199,287693 |
Среднее значение |
3,96 |
15,0656 |
|
Дисперсия |
16,60730775 |
Дисперсия |
1,50656 |
Расчёт среднеквадратичной величины


Расчёт коэффициента вариации.


Определение размаха варьирования


Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1



Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1



Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу
Башинского значение выборки вышло за
границы критического интервала
отбраковки, поэтому
 и
и
 подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
Расчёт средней величины


|
Выборка №1 |
Выборка №2 |
||||
|
1 |
3,5 |
0,6084 |
1 |
4,0 |
0,0961 |
|
2 |
4,1 |
0,0324 |
2 |
4,2 |
0,0121 |
|
3 |
4,0 |
0,0784 |
3 |
4,1 |
0,0441 |
|
4 |
4,2 |
0,0064 |
4 |
5,2 |
0,7921 |
|
5 |
3,8 |
0,2304 |
5 |
5,0 |
0,4761 |
|
6 |
1,0 |
10,7584 |
6 |
3,9 |
0,1681 |
|
7 |
0,9 |
11,4244 |
7 |
3,8 |
0,2601 |
|
8 |
3,9 |
0,1444 |
8 |
4,2 |
0,0121 |
|
9 |
4,2 |
0,0064 |
9 |
4,3 |
0,0001 |
|
10 |
4,1 |
0,0324 |
10 |
4,4 |
0,0081 |
|
11 |
4,0 |
0,0784 |
|||
|
12 |
13,7 |
88,7364 |
|||
|
Среднее значение |
4,28 |
112,1368 |
Среднее значение |
4,31 |
1,869 |
|
Дисперсия |
10,194 |
Дисперсия |
0,2076 |
Расчёт дисперсии





Расчёт среднеквадратичной величины.


Расчёт коэффициента вариации.


Определение размаха варьирования.


Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1



Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1



Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу
Башинского значение выборки вышло за
границы критического интервала
отбраковки, поэтому
 и
и
 подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
Расчёт средней величины


|
Выборка №1 |
Выборка №2 |
||||
|
1 |
3,5 |
0,005329 |
1 |
4,0 |
0,0441 |
|
2 |
4,1 |
0,452929 |
2 |
4,2 |
0,0001 |
|
3 |
4,0 |
0,328329 |
3 |
4,1 |
0,0121 |
|
4 |
4,2 |
0,597529 |
4 |
5,0 |
0,6241 |
|
5 |
3,8 |
0,139129 |
5 |
3,9 |
0,0961 |
|
6 |
1,0 |
5,890329 |
6 |
3,8 |
0,1681 |
|
7 |
0,9 |
6,385729 |
7 |
4,2 |
0,0001 |
|
8 |
3,9 |
0,223729 |
8 |
4,3 |
0,0081 |
|
9 |
4,2 |
0,597529 |
9 |
4,4 |
0,0361 |
|
10 |
4,1 |
0,452929 |
|||
|
11 |
4,0 |
0,328329 |
|||
|
Среднее значение |
3,427 |
15,401819 |
Среднее значение |
4,21 |
0,9889 |
|
Дисперсия |
1,5401819 |
Дисперсия |
0,1236125 |
расчет дисперсии





Расчёт среднеквадратичной величины
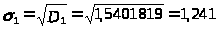

Расчёт коэффициента вариации


Определение размаха варьирования


Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1



Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1



Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу
Башинского значение выборки вышло за
границы критического интервала
отбраковки, поэтому
 и
и
 подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
подлежат отбраковки. Теперь
пересчитаем среднюю величину для обоих
выборок.
Расчёт средней величины


|
Выборка №1 |
Выборка №2 |
||||
|
1 |
3,5 |
0,0324 |
1 |
4,0 |
0,01265625 |
|
2 |
4,1 |
0,1764 |
2 |
4,2 |
0,00765625 |
|
3 |
4,0 |
0,1024 |
3 |
4,1 |
0,00015625 |
|
4 |
4,2 |
0,2704 |
4 |
3,9 |
0,04515625 |
|
5 |
3,8 |
0,0144 |
5 |
3,8 |
0,09765625 |
|
6 |
1,0 |
7,1824 |
6 |
4,2 |
0,00765625 |
|
7 |
3,9 |
0,0484 |
7 |
4,3 |
0,03515625 |
|
8 |
4,2 |
0,2704 |
8 |
4,4 |
0,08265625 |
|
9 |
4,1 |
0,1764 |
|||
|
10 |
4,0 |
0,1024 |
|||
|
Среднее значение |
3,68 |
8,376 |
Среднее значение |
4,1125 |
0,28875625 |
|
Дисперсия |
0,93 |
Дисперсия |
0,04 |
Расчёт дисперсии




Расчёт среднеквадратичной величины.


Расчёт коэффициента вариации


Определение размаха варьирования.


Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1



Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1



Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2



Значения выборки 2 не выходят за границы критического интервала отбраковки.
В выборке №1 по методу Башинского
значение выборки вышло за границы
критического интервала отбраковки,
поэтому
 подлежит отбраковки. Теперь
пересчитаем среднюю величину для выборки
№1.
подлежит отбраковки. Теперь
пересчитаем среднюю величину для выборки
№1.
Расчёт средней величины.

|
Выборка №1 |
Выборка №2 |
||||
|
1 |
3,5 |
0,2282716 |
1 |
4,0 |
0,01265625 |
|
2 |
4,1 |
0,0149382 |
2 |
4,2 |
0,00765625 |
|
3 |
4,0 |
0,0004938 |
3 |
4,1 |
0,00015625 |
|
4 |
4,2 |
0,0493827 |
4 |
3,9 |
0,04515625 |
|
5 |
3,8 |
0,0316049 |
5 |
3,8 |
0,09765625 |
|
6 |
3,9 |
0,0060494 |
6 |
4,2 |
0,00765625 |
|
7 |
4,2 |
0,0493827 |
7 |
4,3 |
0,03515625 |
|
8 |
4,1 |
0,0149382 |
8 |
4,4 |
0,08265625 |
|
9 |
4,0 |
0,0004938 |
|||
|
Среднее значение |
3,97 |
0,395555 |
Среднее значение |
4,1125 |
0,28875625 |
|
Дисперсия |
0,049 |
Дисперсия |
0,04 |
Расчёт дисперсии.


Расчёт среднеквадратичной величины.

Расчёт коэффициента вариации.

Определение размаха варьирования.

Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1



Метод Башинского:
Выборка №1
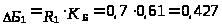
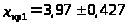

Значения выборки 1 выходят за границы критического интервала отбраковки.
В выборке №1 по методу Башинского
значение выборки вышло за границы
критического интервала отбраковки,
поэтому
 подлежит отбраковки. Теперь
пересчитаем среднюю величину для выборки
№1.
подлежит отбраковки. Теперь
пересчитаем среднюю величину для выборки
№1.
Расчёт средней величины.

|
Выборка №1 |
Выборка №2 |
||||
|
1 |
4,1 |
1 |
4,0 |
0,01265625 |
|
|
2 |
4,0 |
2 |
4,2 |
0,00765625 |
|
|
3 |
4,2 |
3 |
4,1 |
0,00015625 |
|
|
4 |
3,8 |
4 |
3,9 |
0,04515625 |
|
|
5 |
3,9 |
5 |
3,8 |
0,09765625 |
|
|
6 |
4,2 |
6 |
4,2 |
0,00765625 |
|
|
7 |
4,1 |
7 |
4,3 |
0,03515625 |
|
|
8 |
4,0 |
8 |
4,4 |
0,08265625 |
|
|
Среднее значение |
4,0375 |
Среднее значение |
4,1125 |
0,28875625 |
|
|
Дисперсия |
Дисперсия |
0,04 |
Расчёт дисперсии.


Расчёт среднеквадратичной величины.

Расчёт коэффициента вариации.

Определение размаха варьирования.

Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1



Метод Башинского:
Выборка №1



Значения выборки 1 выходят за границы критического интервала отбраковки.
Определение предельной относительной ошибки испытаний.

Выборка №1

Выборка №2

Проверка согласуемости экспериментальных данных с нормальным законом распределения при помощи критерия Пирсона.
|
№ |
Интервал |
Среднее значение |
Частота |
|
1 |
3,8 – 3,9 |
3,85 |
1 |
|
2 |
3,9 – 4,0 |
3,95 |
3 |
|
3 |
4,0 – 4,1 |
4,05 |
2 |
|
4 |
4,1 – 4,2 |
4,15 |
2 |
Выборка №1 Определим количество интервалов:

где
 - размер выборки 1
- размер выборки 1


Сравнение с теоретической кривой.
 - параметр функции
- параметр функции

где
 - среднее значение на
интервале;
- среднее значение на
интервале;




Рассчитываем для каждого интервала

 - функция плотности
вероятности нормально распределения;
- функция плотности
вероятности нормально распределения;




Расчёт теоретической частоты.
 -
теоретическая частота в
i-том
интервале.
-
теоретическая частота в
i-том
интервале.




|
№ |
|
|
|
|
|
|
|
|
1 |
3,85 |
1 |
-1,332 |
0,1647 |
0,9364 |
0,0040 |
0,004 |
|
2 |
3,95 |
3 |
-0,622 |
0,3292 |
1,8717 |
1,2730 |
0,680 |
|
3 |
4,05 |
2 |
0,088 |
0,3977 |
2,2612 |
0,0682 |
0,030 |
|
4 |
4,15 |
2 |
0,799 |
0,2920 |
1,6603 |
0,3397 |
0,204 |

Число
 подчиняется
подчиняется
 -
закону Пирсона
-
закону Пирсона
 - число степеней
свободы;
- число степеней
свободы;
 - порог чувствительности;
- порог чувствительности;
 - вероятность;
- вероятность;

Если
 ,
то данные эксперимента
согласуются с нормальным законом
распределения, где
,
то данные эксперимента
согласуются с нормальным законом
распределения, где
 - табличное значение критерия
Пирсона.
- табличное значение критерия
Пирсона.
Если - данные эксперимента не
согласуются с нормальным законом
распределения, необходимо дальнейшее
проведение опытов. Поскольку вычисленное
значение (
- данные эксперимента не
согласуются с нормальным законом
распределения, необходимо дальнейшее
проведение опытов. Поскольку вычисленное
значение ( )
превосходит табличное
значение критерия Пирсона, то данные
эксперимента не согласуются с нормальным
законом распределения.
)
превосходит табличное
значение критерия Пирсона, то данные
эксперимента не согласуются с нормальным
законом распределения.
Выборка №2
Определим количество интервалов:
 , где
, где
 - размер выборки 2
- размер выборки 2


|
№ |
Интервал |
Среднее значение |
Частота |
|
1 |
3,8 – 3,95 |
3,875 |
2 |
|
2 |
3,95 – 4,10 |
4,025 |
2 |
|
3 |
4,10– 4,25 |
4,175 |
3 |
|
4 |
4,25 – 4,4 |
4,325 |
2 |
Сравнение с теоретической кривой.
 - параметр функции
- параметр функции
 ,
где
,
где
 - среднее значение на
интервале;
- среднее значение на
интервале;




Рассчитываем для каждого интервала

 - функция плотности
вероятности нормально распределения;
- функция плотности
вероятности нормально распределения;




Расчёт теоретической частоты.
 -
теоретическая частота в
i-том
интервале.
-
теоретическая частота в
i-том
интервале.




|
№ |
|
|
|
|
|
|
|
|
1 |
3,88 |
2 |
-1,1694 |
0,2012 |
1,1887 |
0,6582 |
0,5537 |
|
2 |
4,04 |
2 |
-0,4310 |
0,3637 |
2,1489 |
0,0222 |
0,0103 |
|
3 |
4,2 |
3 |
0,3077 |
0,3814 |
2,2535 |
0,5572 |
0,2473 |
|
4 |
4,34 |
2 |
1,0460 |
0,2323 |
1,3725 |
0,3937 |
0,2869 |


 - число степеней
свободы;
- число степеней
свободы;
 - порог чувствительности;
- порог чувствительности;
 - вероятность;
- вероятность;

Если
 ,
то данные эксперимента
согласуются с нормальным законом
распределения, где
,
то данные эксперимента
согласуются с нормальным законом
распределения, где
 - табличное значение критерия
Пирсона.
- табличное значение критерия
Пирсона.
Если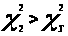 - данные эксперимента не
согласуются с нормальным законом
распределения, необходимо дальнейшее
проведение опытов. Поскольку вычисленное
значение (
- данные эксперимента не
согласуются с нормальным законом
распределения, необходимо дальнейшее
проведение опытов. Поскольку вычисленное
значение ( )
превосходит табличное
значение критерия Пирсона, то данные
эксперимента не согласуются с нормальным
законом распределения.
)
превосходит табличное
значение критерия Пирсона, то данные
эксперимента не согласуются с нормальным
законом распределения.
Определение доверительного интервала
Форма распределения Стьюдента зависит от числа степеней свободы.

где
 коэффициент Стьюдента
коэффициент Стьюдента
Выборка №1

где
 - при вероятности
- при вероятности
 и числе опытов
и числе опытов
 .
.


Выборка №2

где
 - при вероятности
- при вероятности
 и числе опытов
и числе опытов
 .
.


Доверительные интервалы
Выборка №1

Интервал 3,945 - 4,0375 - 4,13.

Дисперсионный анализ
Основной целью дисперсионного
анализа является исследование значимости
различия между средними. В нашем случае
мы просто сравниваем средние в двух
выборках. Дисперсионный анализ даст
тот же результат, что и обычный
 - критерий для зависимых
выборок (сравниваются две переменные
на одном и том же объекте).
- критерий для зависимых
выборок (сравниваются две переменные
на одном и том же объекте).
 - критерий Фишера
- критерий Фишера
 для
для
 и
и

 - различие между
дисперсиями несущественно, необходимо
дополнительное исследование.
- различие между
дисперсиями несущественно, необходимо
дополнительное исследование.
Проверим существенность различия
 и
и
 по
по
 - критерию для зависимых
выборок.
- критерию для зависимых
выборок.

 при
при
 и
и

 - различие между
средними величинами существенно.
- различие между
средними величинами существенно.
Проверим по непараметрическому Т – критерию:
 , где
, где
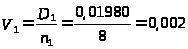 ,
,






Разница между средними величинами несущественна.







