Регулирующий клапан прямого действия

Содержание

Введение

Общие сведения

Регулирующий клапан с мембранным исполнительным механизмом РК-1

Назначение и принцип действия

Определение функциональной зависимости между входом и выходом

Расчет коэффициентов

Определение основных характеристик

Анализ элемента как системы

Список литературы

Введение

В САР для регулирования расхода применяют регуляторы расхода.

Основной деталью всякого гидроаппарата является запорно-регулирующий элемент. Конструктивно он может быть выполнен в виде крана, золотника или клапана.

По назначению всю гидроаппаратуру можно разделить на направляющую и регулирующую. Первая предназначена для изменения направления потока жидкости путем полного перекрытия (открытия) проходного сечения в аппарате, вторая — для изменения давления или расхода (а иногда и направления потока) жидкости путем частичного перекрытия проходного сечения в аппарате.

Регуляторы расхода объединяют устройства, предназначенные для управления расходом рабочей жидкости.

Если, например, к устройству подходит слишком большое количество жидкости, чем было определено при монтаже трубопровода, то под действием давления жидкости и других факторов срабатывает регулятор (регулятор открывается), пропуская только то количество жидкости, необходимое для нормальной работы системы. Если же к устройству подходит малое количество жидкости – давление уменьшается и регулятор закрывается до тех пор пока давление не увеличится и напор жидкости не возрастет.

Следовательно, регулятор обеспечивает контроль над тем количеством жидкости, которое проходит через сечение трубопровода.

К регуляторам прямого действия относят те, у которых перемещение регулирующего элемента осуществляется за счет энергии регулируемого объекта, т. е. применительно к гидроаппарату — за счет энергии рабочей жидкости. Как правило, регуляторы этого типа требуют небольшой мощности для управления регулирующим элементом.

Для исследования и анализа я выбрала регулирующий клапан прямого действия с мембранно-пневматическим исполнительным механизмом. Он прост в конструктивном отношении и является наиболее наглядным объектом для исследования.

Общие сведения

Автоматические регуляторы подразделяются на регуляторы прямого и непрямого действия.

Регуляторами прямою действия называются регуляторы, чувствительные элементы которых непосредственно развивают усилия, необходимые для перемещения регулирующих органов, не используя для своей работы подвода энергии извне. Регуляторы прямого действия применяются для автоматического регулирования температуры, давления, расхода и других параметров жидкостей и газов.

Регуляторы непрямого действия для перемещения своих регулирующих, органов используют энергию извне, и по виду этой энергии подразделяются на гидравлические, пневматические, электрические (включая электронные и комбинированные).

Регулирующий клапан с мембранным исполнительным механизмом РК-1

Назначение и принцип действия

Регулирующие клапаны с мембранным исполнительным механизмом РК-1 предназначены для работы с регулирующими приборами РД-ЗА при автоматизации объектов теплофикации и для регулирования параметром паровых или газовых сред. Они могут также применяться в качестве регуляторов прямого действия. Клапаны состоят из корпуса и мембранного исполнительного механизма.

Клапаны монтируют на горизонтальных участках трубопроводов при вертикальном расположении штока. При этом мембранный исполнительный механизм должен быть над клапаном. Соединительные линии из медных или стальных труб диаметром 8 — 10 мм при монтаже выполняют возможно короткими.

Общий вид клапана представлен на рисунке 1.

Рис. 1. Регулирующий клапан РК-1 (D_>у>= 150 ÷ 250 мм):

1 – корпус; 2 – золотник клапана нормально-открытой сборки; 3 – шток; 4 – сальник; 5 – регулировочная пружина; 6 – чаша гидропривода; 7 – мембрана; 8 – жесткий центр; 9 – золотник клапана нормально-закрытой сборки

Такой регулятор используют для поддержания давления до себя, после себя, а также для поддержания перепада расхода воды на абонентских вводах.

Достоинством регулятора является возможность сборки различных по назначению регуляторов прямого действия из унифицированных деталей. Кроме того, регулятор может быть использован в качестве регулирующего органа в регуляторах непрямого действия. Регулируемое давление устанавливается путем натяжения пружины, а также применения пружин различной жесткости. Разгрузка затвора (золотника) от давления воды до и после него достигается путем применения разгрузочного сильфона, эффективная площадь которого равна эффективной площади золотника.

Рис. 2. Схема вариантов сборки регулятора а – при поддержании давления «до себя»; б – при поддержании давления « после себя»; в – при поддержании перепада давлений

Сила, развиваемая мембраной исполнительного устройства под действием регулируемого давления или перепада давлений, уравновешивается усилием пружины. Регулятор может быть собран по схеме «нормально открыт» и «нормально закрыт».

Схемы вариантов сборки регулятора приведены на рис. 2 /6, c. 83/.

При регулировании давления р_>01> перед регулятором /рис. 2,а/ импульсная линия 6 соединяет точку регулируемого давления с подмембранной зоной. Клапан 1 устанавливается сверху (со стороны сильфона 3). При отсутствии движения воды в трубопроводе регулирующий клапан 1 под действием пружины 4 будет находиться в закрытом состоянии («нормально закрыт»). При движении воды давление р_>01> до регулятора выше давления р_>02> после регулятора. Сильфон 3 разгружает клапан 1 от давления р_>02>. Давление р_>01>, действуя на клапан снизу, создает усилие, поднимающее клапан, этому противодействует усилие растянутой пружины 4. Кроме того, сверху на клапан через шток 7 действует усилие, создаваемое мембраной 5. Если давление до регулятора становится ниже установленной величины, то мембрана 5 опускается вниз, прижимая клапан 1 к седлу 2, уменьшая сток до тех пор, пока не восстановится равновесие сил. При увеличении давления до регулятора мембрана 5 поднимается вверх, усилие, создаваемое мембраной, становится больше силы упругости пружины и клапан с помощью штока 7 поднимается вверх, увеличивая сток воды. Давление р_>01> снижается до заданной величины.

При поддержании давления после регулятора /рис. 2,б/ импульсная трубка 6 соединяет точку регулируемого давления с нижней камерой мембраны 5, а клапан 1 устанавливается снизу (со стороны пружины 4). У собранного таким образом регулятора при отсутствии давления воды в трубопроводе под действием пружины 4 регулирующий клапан 1 находится в открытом положении («нормального открыт»).

Для регулирования перепада давлений (расхода воды) /рис. 2, в/ клапан 1 устанавливается так же, как в предыдущем варианте, снизу; подмембранная зона соединяется с началом регулируемого участка, а надмембранная зона — с концом регулируемого участка импульсными трубками 6. Усилие, развиваемое мембраной 5 под действием перепада давлений, уравновешивается усилием пружины 4. Если регулируемое давление или перепад давлений отклоняется от заданного значения, тогда под действием усилия мембраны 5 клапан 1 открывается или закрывается, что ведет к восстановлению значения регулируемого параметра.

Определение функциональной зависимости между входом и выходом

Входной величиной мембранного пневматического клапана (рис. 3) является давление ∆Р_>вх>, а выходной — перемещение ∆S_>вых> штока клапана (отсчет ведется в малых приращениях от равновесного состояния) /4, с. 44/.

Рис. 3. Мембранный пневматический клапан

Если нельзя пренебречь инерцией подвижной системы клапана и силами трения, то условие равновесия сил, действующих на клапан, запишется как

_>.>

Входное усилие при площади F мембраны равно:

где ∆Р_>вх> - перепад давления на клапане, кПа;

F - площадь мембраны, мм.

Сила инерции f_>и> равна произведению массы m подвижной системы на ускорение a = d²(∆S_>вых>)/dt²:

где m – масса подвижной системы, кг;

∆S_>вых> – перемещение штока клапана, мм;

t – время, с.

Учитывая только силу вязкого трения, которая пропорциональна скорости перемещения подвижной системы, получим:

где b – кинематической вязкостью, м²/с.

Сила противодействия пружины пропорциональна ее сжатию

где с — жесткость пружины.

Подставив значения сил в уравнение равновесия, получим /4, с. 44/:

В настоящее время принято составлять дифференциальные уравнения звеньев в безразмерных (относительных) единицах.

Безразмерной единицей давления будем считать отношение ∆Р_>вх> к максимальной величине давления Р_>макс> на мембрану, при котором клапан полностью закрывается; безразмерной единицей перемещения штока клапана примем отношение ∆S_>вых> к полному ходу S_>макс> /4, с. 45/:

откуда

;

Подставив эти значения в дифференциальное уравнение, получим выражение его в безразмерных единицах:

С учетом того, что сS_>макс> = Р_>макс>F можно записать:

Таким образом, при учете инерции подвижной системы и вязкого трения мембранный пневматический клапан при является колебательным звеном.

Постоянные времени и коэффициент передачи его равны:

Из этого примера следует, что в элементах систем регулирования вязкое трение не всегда является нежелательным /4, с. 45/. В данном случае достаточно высокое вязкое трение обеспечивает устойчивую работу клапана, так как постоянная времени Т_>1> пропорциональна коэффициенту вязкого сопротивления b.

Практически, когда силы вязкого трения в механических элементах, применяют дополнительное демпфирование подвижной системы, т. е. вводят дополнительную силу, противодействующую перемещению подвижной системы и пропорциональную скорости этого перемещения.

Если пневматический клапан применяется в системе с инерционным объектом, в котором переходные процессы протекают медленно, т. е. скорости изменения р_>вх> и s_>вых> небольшие, то величина ускорения d²s_>вых>/dt² с точностью, достаточной для практических расчетов, может быть принята равной нулю. Тогда дифференциальное уравнение клапана примет вид /4, с. 45/:

Следовательно, в этом случае можно пренебречь инерционностью подвижных частей пневматического клапана и представлять его в динамическом отношении как апериодическое звено с передаточной функцией, определяемой формулой.

Расчет коэффициентов

Определим значения коэффициентов: коэффициента вязкости и коэффициента жесткости пружины.

Для этого выбираем клапан.

Будем рассматривать мембранный пневматический клапан – химическая арматура (регулирующий орган). Данные регуляторы в основном применяют для обслуживания тепловых сетей, т. е. для поддержания заданных значений параметров теплоносителя, поступающего в системы отопления, горячего водоснабжения и к техническому оборудованию промышленных предприятий /3, с. 84/. Данный регулятор способен работать с широким температурным диапазоном от –40 до 300˚С.

Марка РК 101.1 – клапан регулирующий. Материал корпуса сталь 12Х18Н9ТЛ.

Предположим, что диаметр заделки мембраны D = 250 мм (F_>э> = 400 см²) и условный ход штока S_>у> = 25 мм. Диаметр условного прохода клапана D_>у> = 150 мм, при этом масса подвижной системы равна 20,5 кг (m = 20,5 кг).

При выполнении технических расчетов в гидравлике обычно пользуются кинематической вязкостью b /1, с. 11/. Единицей кинематической вязкости в системе СИ является метр в квадрате на секунду (м²/с). При необходимости можно пользоваться производной единицей – миллиметр в квадрате на секунду (мм²/с), 1 мм²/с = 10^-6 м²/с.

Для воды кинематическая вязкость находиться по формуле /1, с. 13/:

при температуре жидкости 200˚С кинематическая вязкость будет равна:

Определяем коэффициент сжатия пружины. Данный коэффициент зависит от материала, из которого изготовлена пружина, от диаметра проволоки и от значения индекса пружины.

Материал пружины выбирается в зависимости от его механических свойств по табл. 1 стр. 26 (П_>с> – 4Х13) (П_>с> – пружины цилиндрические сжатия). Определяем ориентировочно индекс с_>пр> пружины по табл. 2 стр. 27 с учетом возможности дальнейшего его уточнения (П_>с> – с_>пр> ≈ 6). Коэффициент с, зависящий от значения индекса, находится по табл. 3 (П_>с> – при с_>пр> ≈ 6 коэффициент с = 1,24).

Зная данные коэффициенты можно определить постоянные времени:

Таким образом, я определила все необходимые коэффициенты, которые понадобятся при анализе и определении основных характеристик.

Определение основных характеристик

_>.>

Определяем передаточную функцию элемента W(р).

Для этого воспользуемся исходным дифференциальным уравнением:

Учитывая, что постоянные времени и коэффициент передачи его равны:

дифференциальное уравнение примет вид:

(1)

Перейдем от дифференциального уравнения к операторной форме. Рассмотрим оператор дифференцирования: и подставим его в уравнение (1) получим.

Запишем передаточную функцию для нашего элемента:

Получили передаточную функцию регулирующего клапана.

Определяем частотную функцию элемента W(jω).

Пусть р – число мнимое, т. е. σ = 0, а р = jω, подставляем р в уравнение для передаточной функции, получим:

Где U(ω) = Re W(jω), а V(ω) = Im W(jω).

Также частотную форму передаточной функции можно представить в виде:

Определяем амплитудно-частотную функцию А(ω).

Построим график амплитудно-частотной функции А(ω):

Определяем фазо-частотную функцию φ(ω).

Построим график фазо-частотной функции φ(ω):

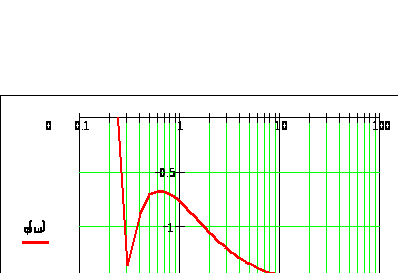
Определяем переходную функцию h(t).

Построим график переходной функции h(t):

Учитывая, что с = 1,24, b = 1,068 мм²/с,

Определяем импульсную функцию ω(t).

Построим график импульсной функции ω (t):

Определяем передаточную функцию элемента W(р).

Запишем передаточную функцию для нашего элемента:

Определяем частотную функцию элемента W(jω).

Пусть р – число мнимое, т. е. σ = 0, а р = jω, подставляем р в уравнение для передаточной функции, получим:

Где U(ω) = Re W(jω), а V(ω) = Im W(jω).

3. Определяем амплитудно-частотную функцию А(ω).

Построим график амплитудно-частотной функции А(ω):

4. Определяем фазо-частотную функцию φ(ω).

Построим график фазо-частотной функции φ(ω):

5. Определяем переходную функцию h(t).

Построим график переходной функции h(t):

Определяем импульсную функцию ω(t).

Построим график импульсной функции ω (t):

Анализ элемента как системы

Исследуем систему с уравнением

на устойчивость.

Для этого перейдем от дифференциального уравнения к операторной форме.

- оператор дифференцирования, подставим его в данное уравнение.

Получаем характеристическое уравнение:

Находим корни квадратного уравнения:

D = b² – 4ac = T_>1>² – 4T_>2> = 0,7396 – 16,264 = –15,52;

α = –0,106.

Получили устойчивое состояние, т. к. α_>i> < 0, т. е. все корни характеристического уравнения находятся в левой полуплоскости.

Проведем оценку качества системы.

а) Прямая оценка качества:

Находим передаточную функцию W(p):

Запишем переходную функцию.

Построим график переходной функции h(t):

Учитывая, что с = 1,24, b = 1,068 мм²/с,

Находим время переходного процесса:

h_>уст> = 1,

тогда Δ = 5%(h_>уст>) = 0,05.

Определим перерегулирование – максимальное отклонение регулируемой величины от установившегося значения:

Находим колебательность системы, которое характеризуется числом колебаний регулируемой величины за время переходного процесса.

h = 3 (т. к. Четвертая волна не до конца).

Время нарастания регулируемой величины:

t_>н>(t_>мах>) = 13 с.

Время первого согласования, т.е. время, когда регулируемая величина первый раз достигает своего установившегося значения:

t_>1> = 7 с.

б) Косвенная оценка качества:

Рассмотрим амплитудно-частотную характеристику процесса.

Построим график амплитудно-частотной функции А(ω):

По графику проводим анализ:

Находим показатель колебательности – М.

, где A_>max> = 4,7545, A(0) = 1.

Следовательно М = 4,7545.

Резонансная частота ω_>р> = 0,243, при A_>max> = 4,7545.

Частота среза при которой амплитудно-частотная характеристика достигает величины равной 1.

ω_>ср> = ± 0,3438.

Время переходного процесса и частота среза связаны соотношением:

t_>П> ≈ (1÷2) 2π/ ω_>ср> ≈ (1÷2) 18,27 (с).

Полоса пропускания частот определяется:

Откладываем получившееся значение от A_>max>.

Получаем полосу пропускания:

ω_>1> = 0,2154 и ω_>1> = 0,2682.

Исследуем систему с уравнением

на устойчивость.

Для этого перейдем от дифференциального уравнения к операторной форме.

- оператор дифференцирования, подставим его в данное уравнение.

Получаем характеристическое уравнение:

Находим корни квадратного уравнения:

р = -1/Т_>1> = -1,163.

Проведем оценку качества системы.

а) Прямая оценка качества:

Находим передаточную функцию W(p):

Запишем переходную функцию.

Построим график переходной функции h(t):

Так как система является устойчивой и график переходной функции не имеет колебаний, то можно определить только максимальное значение регулируемой величины, которое будет равно установившемуся:

h_>мах> = h_>уст> = 1.

Определим перерегулирование:

б) Косвенная оценка качества:

Рассмотрим амплитудно-частотную характеристику процесса.

Для этого находим частотную форму передаточной функции.

Построим график амплитудно-частотной функции А(ω):

По графику проводим анализ:

Находим показатель колебательности – М.

, где A_>max> = 1, A(0) = 1.

Следовательно М = 1.

Резонансная частота ω_>р> = 0, при A_>max> = 1.

Частота среза при которой амплитудно-частотная характеристика достигает величины равной 1.

ω_>ср> = ± 0.

Полоса пропускания частот определяется:

Откладываем получившееся значение от A_>max>.

Получаем полосу пропускания:

ω = 1,155.

Вывод: после выбора и анализа элемента получили, что данный клапан можно применять как регулирующий клапан прямого действия (без дополнительных устройств) и как клапан непрямого действия (вводя дополнительные устройства управления). В первом случае на систему действуют инерционные силы, процесс регулирования становится более длительным и может быть неточным. При анализе элемента получили устойчивую систему, но процесс перерегулирования длится дольше, чем допустимое значение. Колебательность системы также выше приемлемого числа колебаний. Это говорит о том, что в процессе регулирования могут происходить сбои в работе, процесс становится нестабильным. Регуляторы прямого действия просты в конструктивном отношении и надежны в эксплуатации, что объясняет их широкое применение для поддержания постоянного давления или перепада давлений воды на тепловых пунктах небольшой и средней мощности. Однако регуляторы прямого действия имеют меньшую чувствительность, поэтому рекомендуется применять при автоматизации объектов со сложными динамическими характеристиками регуляторы непрямого действия, так как они обеспечивают более широкий диапазон регулирования, возможность введения обратной связи и осуществление многоимпульсного регулирования. В нашем случае пневматический клапан применяется в системе с инерционным объектом, т. е. мы можем применять клапан, например с регулятором давления. Это позволяет получить устойчивую систему, как во втором случае.

Таблица 1 Характеристики материалов, применяемых для пружин

Марка материала или класса проволоки	Диаметр d в мм	Механические свойства	Пределы температур, при которых могут работать пружины, в ˚С	Отличительные свойства материала
проволоки	прутка	Допускаемое напряжение при кручении τ_>кр> в кгс/мм²	Модуль сдвига G в кгс/мм²
П	0,2 – 0,8	–	0,6 σ_>в>	8000	от –40 до +120	Высокие механические свойства
В	0,2 – 0,8	–	0,6 σ_>в>	» –40 » +120	То же и устойчивая деформация
65Г	–	Свыше 5,0	50	» –40 » +120	Повышенная чувствитель-ность к перегревам и к образованию закалочных трещин
60С2	–	» 5,0	75	» –40 » +250	Повышенная склонность к обезуглероживанию пове-рхности при термооб-работке
50ХФА	0,5 – 14,0	» 5,0	75	» –40 » +400	Устойчивая деформация
4Х13	1,0 – 6,0	» 5,0	45	» –40 » +400	Высокая коррозионная стойкость
60С2Н2А	–	» 5,0	100	» –40 » +250	Повышенная склонность к обезуглероживанию пове-рхности при термооб-работке
Бр. КМц 3-1	0,3 – 10,0	–	45	400	» –40 » +200	Высокая коррозионная стойкость и антимаг-нитность
Бр. ОЦ 4-3	0,3 – 10,0	–	40	» –40 » +200	То же

Таблица 2. Значение индекса пружины с_>пр> (отношение среднего диаметра пружины к диаметру проволоки D : d) в зависимости от диаметра проволоки d

d в мм	0,2 – 0,4	0,45 – 1,0	1,1 – 2,2	2,5 – 6,0	7 – 16	18 – 40
с_>пр> = D/d	8 – 14	6 – 12	5 – 10	4 – 10	4 – 8	4 – 6

Таблица 3. Значение коэффициента с в зависимости от определенного значения индекса пружины с_>пр>

с_>пр> = D/d	4	5	6	8	10	12	14
с	1,37	1,29	1,24	1,17	1,14	1,11	1,10

Список литературы

Гейер В.Г., Дулин В.С., Боруменский А.Г., Заря А.Н. Гидравлика и гидропривод. – М.: Недра, 1981. – 295 с.

Емельянов А.И., Емельянов В.А., Калинина С.А. Практические расчеты в автоматике. – М.: Машиностроение, 1967. – 316.

Ионин А.А., Хлыбов Б.М., Братенков В.Н., Терлецкая Е.Н. Теплоснабжение. – М.: Стройиздат, 1982. – 336 с.

Клюев А.С. Автоматическое регулирование. – М.: Энергия, 1973. – 392 с.

Смолянов Л.С. Инженерное оборудование коммунально-бытовых предприятий. – Киев: Будiвельник, 1978. – 256с.

Хакимов А.З., Абросимов В.Ф. Системы автоматизации технологических процессов. Расчет пневматических мембранно-пружинных исполнительных механизмов при проектировании. Руководящий материал. РМ4-179-80. Проектмонтажавтоматика, 1981. – 60 с.

Родов А.Б., Бунин А.Б., Бейгул Е.А., Курдыбал Б.М. Государственная система промышленных приборов и средств автоматизации. Номенклатурный каталог. Часть 2. – М.: Центральный научно-исследовательский институт информации и технико-экономических исследований приборостроения, средств автоматизации и систем управления, 1984. – 151с.

Устинова Е.И., Иванова О.И., Пайкин И.Х. Промышленная трубопроводная арматура. Каталог, часть III. – М.: Цинтихимнефтемаш, 1978. – 136 с.

ГОСТ 13373-67. Механизмы исполнительные пневматические мембранно-пружинные ГСП. Типы. Основные параметры и размеры. – Введ. 07.01.68. – М.: Издательство стандартов, 1967. – 12 с.