Основы геодезических измерений

Содержание

Введение

1. Устройство геодезических сетей при съемке больших территорий.

1.1 Государственные геодезические сети.

1.2 Геодезические сети сгущения.

1.3 Сети специального назначения (ОМС).

1.4 Съёмочные сети.

1.5 Системы координат WGS-84 и СК-95.

2. Измерения в геодезических сетях.

2.1 Устройство и измерение углов теодолитом 3Т2КП, (3Т5КП).

2.2 Устройство светодальномера СТ-5 («Блеск») и измерение и расстояний.

2.3Устройство электронного тахеометра. Измерение им горизонтальных и вертикальных углов, расстояний, координат Х, У, Н точек местности.

2.4. Определение положения точек земной поверхности с помощью геодезических спутниковых систем.

3. Погрешности геодезических измерений (теория и решение задач).

3.1 Геодезическое измерение, результат измерения, методы и условия измерений. Равноточные и неравноточные измерения.

3.2 Классификация погрешностей геодезических измерений. Средняя квадратическая погрешность. Формы Гаусса и Бесселя для её вычисления.

3.3 Веса измерений

3.4 Функции по результатам измерений и оценка их точности.

3.5 Оценка точности по разностям двойных измерений и по невязкам в полигонах и ходах.

4. Определение дополнительных пунктов.

4.1 Цель и методы определения дополнительных пунктов.

4.2 Передача координат с вершины знака на землю. (Решение примера).

4.3 Решение прямой и обратной засечки (по варианту задания).

5. Уравнивание системы ходов съемочной сети.

5.1 Общее понятие о системах ходов и их уравнивании.

5.2 Упрощенное уравнение системы теодолитных ходов по варианту задания.

6. Тахеометрическая съёмка.

6.1 Плановое и высотное обоснование тахеометрической съёмки.

6.2 Нанесение съёмочных и реечных точек.

6.3 Интерполирование отметок пикетов и вычерчивание горизонталей.

6.4 Нанесение ситуации в условных знаках.

6.5 Оформление плана тахеометрической съёмки (по варианту задания).

Список использованной литературы

Введение

Геодезия – наука об измерениях на земной поверхности. В геодезии применяются преимущественно линейные и угловые измерения. Такие измерения необходимы для определения формы и размеров нашей планеты – Земли и её частей, для определения координат пунктов, создания карт, планов и профилей и для строительства различных сооружений. Геодезические измерения производятся также под земной поверхностью (в связи с горными работами, сооружением тоннелей и т.п.), под водой (при съёмках дна морей, океанов, озёр) и в околоземном пространстве.

Геодезия при решении поставленных перед нею задач пользуется достижениями ряда других наук и прежде всего математики и физики.

Материалы геодезических работ в виде планов, карт и числовых величин (координат и высот) точек земной поверхности имеют большое применение в различных отраслях народного хозяйства. Всякое сооружение проектируют с учетом имеющихся на местности контуров сооружений, дорог, водных источников, почвы, грунта. Поэтому для проектирования необходим план местности с подробным отображением всех деталей. Проектирование и строительство сел, городов, железных и шоссейных дорог нельзя выполнять без геодезических материалов.

В теоретических исследованиях и практике геодезических работ особое внимание уделяется определению взаимного положения точек, как в плановом отношении, так и по высоте. Многолетний опыт выполнения такого рода работ позволил выработать основные принципиальные положения, которые следует неукоснительно соблюдать при организации геодезических измерений. Это позволяет свести к минимуму неизбежные ошибки, не допустить накопления погрешностей при переходе от точки к точке, полностью избавиться от грубых промахов.

Цель данной курсовой работы по геодезии на тему: «Геодезические сети» - научиться создавать качественное геодезическое обеспечение работ по проведению земельного кадастра, мониторинга, планирования и осуществления строительства, а также других научных и хозяйственных работ.

Задача: освоить современные технологии геодезических работ по тахеометрической съёмке, уравниванию системы теодолитных и нивелирных ходов, определению дополнительных пунктов при сгущении геодезической сети, оценке точности выполненных работ.

1. Устройство геодезических сетей при съемке больших территорий

1.1 Государственная геодезическая сеть (ГГС)

Государственная геодезическая сеть (ГГС) – система закрепленных на местности пунктов, положение которых определено в единой системе координат и высот.

ГГС предназначена для решения следующих основных задач, имеющих хозяйственное, научное и оборонное значение:

– установление и распространение единой государственной системы геодезических координат на всей территории страны и поддержание ее на уровне современных и перспективных требований;

– геодезическое обеспечение картографирования территории России и акваторий окружающих ее морей;

– геодезическое обеспечение изучения земельных ресурсов и землепользования, кадастра, строительства, разведки и освоения природных ресурсов;

– обеспечение исходными геодезическими данными средств наземной, морской и аэрокосмической навигации, аэрокосмического мониторинга природной и техногенной сред;

– изучение поверхности и гравитационного поля Земли и их изменений во времени;

– изучение геодинамических явлений;

– метрологическое обеспечение высокоточных технических средств определения местоположения и ориентирования.

Геодезические высоты пунктов ГГС определяют как сумму нормальной высоты и высоты квазигеоида над отсчетным эллипсоидом или непосредственно методами космической геодезии, или путем привязки к пунктам с известными геоцентрическими координатами. Нормальные высоты пунктов ГГС определяются в Балтийской системе высот 1977 года, исходным началом которой является нуль Кронштадтского футштока. Карты высот квазигеоида над общим земным эллипсоидом и референц-эллипсоидом Красовского на территории Российской Федерации издаются Федеральной службой геодезии и картографии России и Топографической службой ВС РФ.

Масштаб ГГС задается Единым государственным эталоном времени-частоты-длины.

В работах по развитию ГГС используются шкалы атомного ТA (SU) и координированного UTC (SU) времени, задаваемые существующей эталонной базой Российской Федерации, а также параметры вращения Земли и поправки для перехода к международным шкалам времени, периодически публикуемые Госстандартом России в специальных бюллетенях Государственной службы времени и частоты (ГСВЧ).

Астрономические широты и долготы, астрономические и геодезические азимуты, определяемые по наблюдениям звезд, приводятся к системе фундаментального звездного каталога, к системе среднего полюса и к системе астрономических долгот, принятых на эпоху уравнивания ГГС.

Метрологическое обеспечение геодезических работ осуществляется в соответствии с требованиями государственной системы обеспечения единства измерений.

Все геодезические сети можно разделить по следующим признакам:

По территориальному признаку:

1) глобальная

2) национальные (ГГС)

3) сети специального назначения (ГССН)

4) съемочные сети

по геометрической сущности:

1) плановые

2) высотные

3) пространственные

Глобальные сети создаются на всю поверхность Земли спутниковыми методами, являясь пространственными с началом координат в центре масс Земли и определяемые в системе координат ПЗ-90.

Национальные сети делятся на: Государственную геодезическую сеть (ГГС) с определением координат в СК-95 в проекции Гаусса-Крюгера на плоскости и на Государственную нивелирную сеть (ГНС) с определением нормальных высот в Балтийской системе, т.е. от нуля Кронштадтского футштока.

Геодезические сети специального назначения (ГССН) создаются в тех случаях, когда дальнейшее сгущение пунктов ГГС экономически нецелесообразно или когда требуется особо высокая точность геодезической сети. В зависимости от назначения эти сети могут быть плановыми, высотными, планово-высотными и даже пространственными и создаваться в любой системе координат.

Съемочные сети являются обоснованием для выполнения топосъемок и создаются обычно планово-высотными.

ГГС, созданная по состоянию на 1995 год, объединяет в одно целое:

астрономо-геодезические пункты космической геодезической сети (АГП КГС),

доплеровскую геодезическую сеть (ДГС),

астрономо-геодезическую сеть (АГС) 1 и 2 классов,

геодезические сети сгущения (ГСС) 3 и 4 классов,

Пункты указанных построений совмещены или имеют между собой надежные геодезические связи.

ГГС структурно формируется по принципу перехода от общего к частному и включает в себя геодезические построения различных классов точности:

фундаментальную астрономо-геодезическую сеть (ФАГС)

высокоточную геодезическую сеть (ВГС),

спутниковую геодезическую сеть 1 класса (СГС-1)

В указанную систему построений вписываются также существующие сети триангуляции и полигонометрии 1-4 классов. На основе новых высокоточных пунктов спутниковой сети создаются постоянно действующие дифференциальные станции с целью обеспечения возможностей определения координат потребителями в режиме близком к реальному времени.

По мере развития сетей ФАГС, ВГС и СГС-1 выполняется уравнивание ГГС и уточняются параметры взаимного ориентирования геоцентрической системы координат и системы геодезических координат СК-95.

1.2 Геодезические сети сгущения

В настоящее время наиболее эффективным методом создания геодезической сети, включая и геодезические сети сгущения, является метод, связанный со спутниковыми технологиями (ГЛ0НАСС, GPS). Однако этот метод требует наличия приемной аппаратуры, высокая стоимость которой препятствует широкому ее использованию. Поэтому наряду с высокоэффективными спутниковыми технологиями используют и традиционные методы. Следует заметить, что при выполнении геодезических работ в закрытых помещениях и в стесненных условиях, когда наблюдение созвездия спутников невозможно или затруднительно, традиционные методы являются единственно возможными для решения многих задач.

Геодезические сети сгущения строят методами триангуляции и полигонометрии для сгущения государственной геодезической сети до плотности, необходимой для создания съемочного обоснования съемок крупного масштаба. Триангуляцию 1 и 2-го разрядов развивают в открытой и горной местности. Там, где триангуляцию 1 и 2-го разрядов выполнить по условиям местности невозможно или нецелесообразно, развивают полигонометрическую сеть 4-го класса, 1 и 2-го разрядов. Необходимо отметить, что полигонометрия 4-го класса для крупномасштабных съемок по сравнению с государственной выполняется с пониженной точностью.

При создании полигонометрии выполняют весь комплекс основных геодезических работ: угловые и линейные измерения, нивелирование. Углы на пунктах полигонометрии измеряют способом отдельного угла или круговых приемов оптическими теодолитами типа. Т1, Т2, Т5 с точностью центрирования 1 мм. Высоты на все пункты полигонометрии передаются нивелированием IV класса или техническим. Линии измеряют непосредственно: светодальномерами, подвесными мерными приборами или косвенно — длины сторон хода вычисляют по вспомогательным величинам.

При проведении различных народнохозяйственных, в том числе и землеустроительных, мероприятий на большой территории необходимы топографические карты и планы, составленные на основе сети геодезических пунктов, плановое положение которых на земной поверхности определено в единой системе координат, а высотное — в единой системе высот. При этом геодезические пункты могут быть только плановыми или только высотными или одновременно — плановыми и высотными.

Сеть геодезических пунктов располагается на местности согласно составленному для нее проекту. Пункты сети закрепляются на местности особыми знаками.

Построенная на большой территории в единой системе координат и высот геодезическая сеть дает возможность правильно организовать работу по съемке местности. При наличии такой сети съемка может производиться независимо в разных местах, что не вызовет затруднения при составлении общего плана или карты. Кроме того, использование сети геодезических пунктов приводит к более равномерному распределению по территории влияния погрешностей измерений и обеспечивает контроль выполняемых геодезических работ.

Геодезические сети строятся по принципу перехода от общего к частному, т. е. вначале на большой территории строится редкая сеть пунктов с очень высокой точностью, а затем эта сеть сгущается последовательно по ступеням пунктами, построение которых производится на каждой ступени с меньшей точностью. Таких ступеней сгущения бывает несколько. Сгущение геодезической сети производится с таким расчетом, чтобы в результате получилась сеть пунктов такой плотности (густоты) и точности, чтобы эти пункты могли служить непосредственной опорой для предстоящей съемки.

Плановые геодезические сети строятся в основном методами триангуляции, полигонометрии и трилатерации.

Метод триангуляции состоит в том, что строят сеть треугольников, в которой измеряют все углы треугольников и как минимум две стороны на разных концах сети (вторую сторону измеряют для контроля измерения первой стороны и установления качества всей сети). По длине одной из сторон и углам треугольников определяются стороны всех Треугольников сети. Зная дирекционный угол одной из сторон сети и координаты одного из пунктов, можно затем вычислить координаты всех пунктов.

Метод полигонометрии заключается в построении сети ходов, в которых измеряют все углы и стороны. Полигонометрические ходы отличаются от теодолитных более высокой точностью измерения углов и линий. Этот метод применяется обычно в закрытой местности. Внедрение в производство электромагнитных дальномеров делает целесообразным применение полигонометрии и в открытой местности.

Метод трилатерации состоит в построении сети треугольников с измерением всех сторон треугольников. В некоторых случаях создаются линейно-угловые сети, представляющие собою сети треугольников, в которых измерены стороны и углы (все или в необходимом их сочетании).

Плановые геодезические сети делятся на государственную геодезическую сеть; сети сгущения 1 и 2 разрядов; съемочное обоснование — съемочную сеть и отдельные пункты.

1.3 Сети специального назначения (ОМС)

Опорная межевая сеть (ОМС) – геодезическая сеть специального назначения (ГССН), которая создается для геодезического обеспечения государственного земельного кадастра, мониторинга земель, землеустройства и других мероприятий по управлению земельным фондом страны.

Межевые сети создают в случаях, когда точность и плотность существующих геодезических сетей не соответствуют требованиям, предъявляемым при их построении.

Опорная межевая сеть подразделяется на два класса: ОМС1 и ОМС2. Точность их построения характеризуется средними квадратическими погрешностями взаимного положения смежных пунктов соответственно не более 0,05 и 0,10 м. Расположение и плотность пунктов ОМС (опорных межевых знаков – ОМЗ) должны обеспечивать быстрое и надежное восстановление на местности всех межевых знаков. Плотность пунктов ОМС на 1 кв. км должна быть не менее 4 пунктов в черте города и 2 пунктов – в черте других поселений, в небольших поселениях – не менее 4 пунктов на один населенный пункт. На землях сельскохозяйственного назначения и других землях необходимая плотность пунктов ОМС обосновывается расчетами исходя из требований, предъявляемых к планово-картографическим материалам.

Пункты ОМС по возможности размещают на землях, находящихся в государственной или муниципальной собственности, с учетом их доступности. Пункты ОМС могут не совпадать с межевыми знаками границ земельного участка.

Опорная межевая сеть должна быть привязана не менее чем к двум пунктам государственной геодезической сети. Плановое и высотное положение пунктов ОМС рекомендуется определять с использованием геодезических спутниковых систем (GPS или ГЛОНАСС) в режиме статических наблюдений. При отсутствии такой возможности плановое положение пунктов может определяться методами триангуляции и полигонометрии, геодезическими засечками, лучевыми системами, а также фотограмметрическим методом (для ОМС2); высоты опорных межевых знаков определяются геометрическим или тригонометрическим нивелированием.

Плановое положение пунктов ОМС определяют обычно в местных системах координат. При этом должна быть обеспечена связь местных систем координат с общегосударственной системой координат. Высоты пунктов определяют в Балтийской системе высот.

Для обозначения границ земельного участка на местности на поворотных точках границ закрепляют межевые знаки, положение которых определяют относительно ближайших пунктов исходной геодезической основы. Границы участков, проходящие по «живым урочищам», закрепляют межевыми знаками только на стыках с суходольными границами.

1.4 Съёмочные сети

Съемочная сеть – это совокупность точек, определяемых на местности дополнительно к пунктам государственной геодезической сети для непосредственного обеспечения топографических съемом.

Точки съемочной сети определяются аналитическим способом – триангуляцией, теодолитными ходами, засечками и графическим способом – при помощи мензулы и кипрегеля. Исходной основой для развития съемочных сетей служат пункты государственной геодезической сети.

При составлении проекта съемочной сети рекогностировки местности с целью определения мест установки ее пунктов нужно руководствоваться следующим:

1 между пунктами съемочной сети должны быть обеспечены взаимная видимость и благоприятные условия для измерения линии;

2 в застроенной территории ходы должны прокладываться так, чтобы обеспечить благоприятные условия для съемки зданий и сооружений;

3 местоположение пунктов съемочной сети должно обеспечивать удобную установку геодезических приборов при построении съемочного обоснованиям съемочных работ;

4 пункты съемочной сети нужно помещать на непахотные земли в таких местах, которые обеспечивают их сохранность;

5 на застроенных территориях пункты съемочной сети следует помещать так, чтобы их местоположение в случае утраты можно было восстановить по линейным разметкам от опорных контуров местности.

6 в проект съемочной сети рекомендуется также включать ориентированные местные предметы.

7 при положении теодолитных ходов в застроенной территории следует предусматривать установку и определение створных точек.

Плановые съемочные сети создаются построением триангуляции, проложением теодолитных ходов, прямыми, обратными и комбинированными засечками, методами спутниковой геодезии и проложением электронных тахеометрических ходов. Съемочной сетью могут служить теодолитные, тахеометрические ходы с привязкой их к исходной сети.

При развитии съемочного обоснования определяют, как правило, расположение точек в плане и по высоте. Высоты точек съемочного обоснования определяют геометрическим и тригонометрическим нивелированием.

Техническое нивелирование применяется для высотного обоснования съёмок с сечением рельефа в 1 метр и менее Предельно допустимые длины ходов при сечении рельефа: h = 0,25 м – L = 2 км

h = 0,25 м – L = 2 км

h = 0,25 м – L = 2 км

Чем меньше сечение, тем меньше ход.

Пункты съёмочной сети закрепляются на местности деревянными кольями с окопкой вокруг них.

Межевые точки закрепляются столбами с окопкой их кургана.

В целях большей сохранности геодезических знаков выбирают по возможности такие места для геодезических пунктов, которые обеспечивали бы сохранность знаков: перекрёсток дорог, опушки леса и другие участки мало подверженные изменениям.

Средние ошибки положения пунктов плановой съемочной сети относительно ближайших пунктов геодезических сетей не должны превышать в открытых районах 0,1мм в масштабе плана, и в лесных районах 0,15мм.

Средние ошибки высот пунктов съемочной сети относительно ближайших пунктов геодезической сети не должны превышать в равнинной местности 1/10, а в горной и предгорной 1/6 высоты сечения рельефа, принятой для съемки данного масштаба.

Количество закрепляемых на местности точек, тип центров и знаков съемочной основы на каждом плане определяются проектом в соответствии с требованием технических инструкций, и съемочная основа строится в виде сетей теодолитных ходов или геометрических сетей.

1.5 Системы координат WGS-84 и СК-95

Система координат 1995 г. (СК-95) установлена Постановлением Правительства РФ от 28.07.2002 г № 586 «Об установлении единых государственных систем координат». Используется при осуществлении геодезических и картографических работ, начиная с 1 июля 2002 года.

До завершения перехода к использованию СК правительство РФ постановило использовать единую систему геодезических координат 1942 года, введённую Постановлением Совета министров СССР от 07.04.1996 г № 760.

Целесообразность введения СК-95 состоит в повышении точности, оперативности и экономической эффективности решения задач геодезического обеспечения, отвечающего современным требованиям экономики, науки и обороны страны. Полученные в результате совместного уравнивания координат пунктов космической государственной сети (КГС), доплеровской геодезической сети (ДГС) и астрономо-геодезической сети (АГС) на эпоху 1995 г, Система координат 1995 г закреплена пунктами государственной геодезической сети.

СК-95 строго согласована с единой государственной геоцентрической системой координат, которая называется «Параметры Земли 1990г.» (ПЗ-90). СК-95 установлена под условием параллельности её осей пространственным осям СК ПЗ-90.

За отсчётную поверхность в СК-95 принят референц эллипсоид.

Точность СК-95 характеризуется следующими средними квадратическими ошибками взаимного положения пунктов по каждой из плановых координат: 2-4 см. для смежных пунктов АГС, 30-80 см. при расстояниях от 1 до 9 тыс. км между пунктами.

Точность определения нормальных высот в зависимости от метода их определения характеризуется следующими средними квадратическими ошибками:

• 6-10 см. в среднем по стране из уровня нивелирных сетей 1 и 2 классов;

• 20-30 см из астрономо-геодезических определений при создании АГС.

Точность определения превышений высот квазигеоида астрономогравиметрическим методом характеризуется следующими средними квадратическими ошибками:

• от 6 до 9 см. при расстоянии 10-20 км;

• 30-50 см при расстоянии 1000км.

СК-95 отличается от СК-42

1) повышением точности передачи координат на расстояние свыше 1000 км в 10-15 раз и точностью взаимного положения смежных пунктов в государственной геодезической сети в среднем в 2-3 раза;

2) одинаковой точностью расстояния системы координат для всей территории РФ;

3) отсутствием региональных деформаций государственной геодезической сети, достигающих в СК-42 нескольких метров;

4) возможностью создания высокоэффективной системы геодезического обеспечения на основе использования глобальных навигационных спутниковых систем: Глонасс, GPS, Навстар.

Развитие астрономо-геодезической сети для всей территории СССР было завершено к началу 80х годов. К этому времени стала очевидность выполнения общего уравнивания АГС без разделения на ряды триангуляции 1 класса и сплошные сети 2 класса, т. к. отдельное уравнивание приводило к значительной деформациям АГС.

В мае 1991 года общее уравнивание АГС было завершено. По результатам уравнивания были установлены следующие характеристики точности АГС:

1) средняя квадратическая ошибка направлений 0,7 секунды;

2) средняя квадратическая ошибка измеренного азимута 1,3 сек.;

3) относительная средняя квадратическая ошибка измерения базисных сторон 1/200000;

4) средняя квадратическая ошибка смежных пунктов 2-4 см.;

5) средняя квадратическая ошибка передачи координат исходного пункта на пункты на краях сети по каждой координате 1 м.

Уравненная сеть включала в себя:

• 164306 пунктов 1 и 2 класса;

• 3,6 тысяч геодезических азимутов, определенных из астромомических наблюдений;

• 2,8 тысяч базисных сторон через 170-200км.

Совместному уравниванию подвергались астрономо-геодезическая сеть доплеровская и КГС.

Объём астрономо-геодезической информации обработанной при совместном уравнивании для установления СК-95 превышает на порядок объём измерительной информации.

В 1999 году Федеративная служба геодезии и картографии (ФСГиК) ГГС качественно нового уровня на основе спутниковых навигационных систем: Глонасс, GPS, Навстар. Новая ГГС включает в себя геодезические построения различных классов точности:

1) ФАГС (фундаментальные)

2) Высокоточные ВГС

3) Спутниковая геодезическая сеть 1 класса (СГС 1)

4) Астрономогеодезическая сеть и геодезические сети сгущения.

WGS-84 сейчас стала международной системой навигации. Все аэропорты мира, согласно требованиям ICAO, определяют свои аэронавигационные ориентиры в WGS-84. Россия не является исключением. С 1999 г. издаются распоряжения о ее использовании в системе нашей гражданской авиации (Последние распоряжения Минтранса № НА-165-р от 20.05.02 г. «О выполнении работ по геодезической съемке аэронавигационных ориентиров гражданских аэродромов и воздушных трасс России» и № НА-21-р от 04.02.03 г. «О введении в действие рекомендаций по подготовке … к полетам в системе точной зональной навигации …», см. www.szrcai.ru), но до сих пор нет ясности в главном — станет ли эта информация открытой (иначе она теряет смысл), а это зависит от совсем других ведомств, к открытости не склонных. Для сравнения: координаты концов взлетно-посадочной полосы аэродрома с разрешением 0,01” (0,3 м) сегодня выдают Казахстан, Молдова и страны бывшей Прибалтики; 0,1” (3 м) — Украина и страны Закавказья; и только Россия, Белоруссия и вся Средняя Азия открывают эти важнейшие для навигации данные с точностью 0,1’ (180 м).

У нас есть и своя общеземная система координат, альтернатива WGS-84, которая используется в ГЛОНАСС. Она называется ПЗ-90, разработана нашими военными, и кроме них, по большому счету, никому не интересна, хотя и возведена в ранг государственной.

Наша государственная система координат - «Система координат 1942 г.», или СК-42, (как и пришедшая ей недавно на смену СК-95) отличается тем, что, во-первых, основана на эллипсоиде Красовского, несколько большем по размерам, чем эллипсоид WGS-84, и во-вторых, «наш» эллипсоид сдвинут (примерно на 150 м) и слегка развернут относительно общеземного. Всё потому, что наша геодезическая сеть покрыла шестую часть суши еще до появления всяких спутников. Эти отличия приводят к погрешности GPS на наших картах порядка 0,2 км. После учета параметров перехода (они имеются в любом Garmin’e) эти погрешности устраняются для навигационной точности. Но, увы, не для геодезической: точных единых параметров связи координат не существует, и виной тому локальные рассогласования внутри государственной сети. Геодезистам приходится для каждого отдельного района самим искать параметры трансформирования в местную систему.

2. Измерения в геодезических сетях

2.1 Устройство и измерение углов теодолитом 3Т2КП, (3Т5КП)

Теодолит 3Т2КП предназначен для измерения горизонтальных и вертикальных углов и относится к классу точных приборов. Имеет микрометр с ценой деления 1 сек.

Области применения:

построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса),

в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде).

Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра.

Области применения:

• создание планово- высотного обоснования при проведении топографических съёмок, выполнение тахеометрических съёмок, при проведении изыскательских работ, маркшейдерских работах.

Теодолиты серии 3Т удобны и надежны в работе. Наличие компенсатора при вертикальном круге позволяет производить измерения вертикальных углов быстро и точно. Прибор можно использовать для геометрического нивелирования (горизонтальным лучом).

Теодолиты могут быть использованы для измерения расстояний нитяным дальномером и для определения магнитных азимутов с помощью буссоли. В отличие от зарубежных аналогов теодолиты позволяют выполнить работы при более низких температурах.

Прибор может комплектоваться геодезическим штативом типа ШР-160.

Технические характеристики: 3Т2КП 3T5КП

Средняя квадратическая

погрешность измерения

одним приемом:

горизонтального угла 2" 5″

вертикального угла или

зенитного расстояния 2,4" 5″

Увеличение, крат 30х 30x

Наружный диаметр оправы

объектива, мм 48 48

Поле зрения 1˚35' 1˚35'

Наименьшее расстояние

визирования, м 1,5 1,5

Диапазон работы компенсатора

при вертикальном круге ±3' ±4'

Цена деления шкалы отсчетного

микроскопа 1" 1"

Погрешность отсчитывания 0,1" 0,1"

Масса теодолита с подставкой, кг 4,7 4,4

Масса штатива, кг 5,6 5,5

Диапазон рабочих температур, …-400С…+500С

2.2 Устройство светодальномера СТ-5 («Блеск») и измерение и расстояний

Светодальномер «Блеск» СТ5 является основным топографическим светодальномером, выпускаемым отечественной промышленностью. Он предназначен для измерения расстояния до 5 км.

В шифре светодальномера буква Т означает, что светодальномер - топографический, предназначенный для измерения paсстояний в геодезических сетях сгущения и топографических съемках, а цифра 5 указывает на предел измерения расстояний в км.

Светодальномер можно применять как самостоятельный прибор, и как насадку на теодолиты серии 2Т и ЗТ для одновременного измерения углов и расстояний. Масса светодальномера с основан» составляет 4,5 кг (без основания 3,8 кг). В состав комплект, светодальномера входят отражатели, источник питания, разрядно-зарядное устройство и друг принадлежности. (Для измерения расстояний более 3 км число призм отражателя должно составлять 12 или 18 для максимальных расстояний соответственно 4 и 5 км).

В светодальномере использован импульсный метод измерения расстояния с преобразованием временного интервала. Измерение осуществляется с применением двух частот следования излучаемых импульсов: f1 = 14985,5 кГц и f2 = 149,855 кГц. Источником излучения является полупроводниковый лазерный диод с длиной волны излучения 0,86 мкм, приемником - фотоэлектронный умножитель (ФЭУ).

Перед началом работы необходимо провести внешний осмотр прибора и выполнить его поверки. При внешнем осмотре следует убедиться в отсутствии механических повреждений, сохранности ампул уровней и деталей, крепления органов управления, плавности их действия и четкости фиксации; четкости изображения штрихов сетки и штрихов шкал; работоспособности всех узлов: источников питания, стрелочных приборов, цифровых табло, зуммеров и пр., а также термометров, барометров и других приборов.

Подключение светодальномера (приемопередатчика) СТ5 к аккумулятору производят, когда переключатель 4 установлен в режиме «Выкл». О подключении СТ5 к аккумулятору можно судить по свечению запятой в третьем знаке на цифровом табло.

Порядок измерения линии снетодальпомером СТ5:

1. В начальной точке линии устанавливают на штативах приемопередатчик, а на конечной точке - отражатель, приводят их в рабочее положение над центрами пунктов (центрируют и нивелируют) и взаимно ориентируют (наводят зрительную трубу на отражатель, а отражатель на приемопередатчик).

2. Включают и прогревают приемопередатчик.

3. Проверяют напряжение источника питания и выполняют другие контролирующие действия в соответствии с техническими требованиями инструкции по эксплуатации прибора (см. поверки светодальномера).

4. Включают светодальномер в режим «Наведение», для чего переключатель 7 устанавливают в положение «Точно», а 4 - «Навед». Поворачивают ручку 8 «Сигнал» по часовой стрелке до ограничения, а при большом уровне фоновых шумов в солнечную погоду и при высокой окружающей температуре воздуха -показаний стрелочного прибора не более 20 мкА. Изменяя ориентирование светодальномера в вертикальной и горизонтальных плоскостях с помощью винтов наводящих устройств, добиваются получения сигнала. Наличие сигнала индифицируется звуком и отклонением стрелки прибора 1 вправо по шкале.

Светодальномер наводят по максимуму сигнала, одновременно устанавливая ручкой 8 уровень сигнала в середине рабочей зоны.

5. Устанавливают переключатель 4 в положение «Счет», оценивают свечение индикатора табло (при необходимости ручкой о «Сигнал» подстраивают уровень сигнала), берут три отсчета измеряемого расстояния в режиме «Точно» и записывают их в журнал. В журнал записывают также метеоданные: температуру воздуха и атмосферное давление в месте установки приемопередатчика.

При измерении больших расстояний или значительном перепаде высот концов линии метеоданные определяют как на точке стояния светодальномера, и на точке стояния отражателя.

После этих действий еще два раза производят наведение на отражатель и каждый раз производят три отсчета в режиме «Точно». При измерении расстояний до 400 м на объектив светодальномера надевают аттенюатор.

По окончании измерений переключатель 7 переводят в положение «Контр.» и по табло берут отсчет для определения поправочного коэффициента.

2.3 Устройство электронного тахеометра. Измерение им горизонтальных и вертикальных углов, расстояний, координат Х, У, Н точек местности

Тахеометр – геодезический прибор для измерения расстояний, горизонтальных и вертикальных углов, превышений, решения инженерных задач.

По сути тахеометр представляет собой комплекс состоящий из теодолита, светодальномера и ЭВМ.

С 90-х годов 20 века электронный тахеометр – самый распространенный геодезический прибор. Это связано впервую очередь с его универсальностью. Тахеометр используется для вычисления координат и высот точек местности при топографической съемке местности, при разбивочных работах, выносе в натуру проектных решений и т. п.

В электронных тахеометрах расстояния измеряются по времени прохождения луча лазера до отражателя и обратно, а так же, в некоторых моделях, уточняется по сдвигу фаз. Дальность измерения зависит от технических возможностей модели тахеометра, а также от многих внешних параметров: температура, давление, влажность и т.п. Диапазон измерения расстояний зависит так же от режима работы тахеометра: отражательный или безотражательный. Для режима с отражателем (призмой) – до 5 километров (при нескольких призмах еще дальше); для безотражательного режима – до 1,5 километров. Модели тахеометров, которые имеют безотражательный режим могут измерять расстояния практически до любой поверхности. Однако, следует с осторожностью относиться к результатам измерений, проводимым сквозь ветки, листья, потому как неизвестно, от чего отразится луч, и, соответственно, расстояние до чего он промеряет. Точность угловых измерений современным тахеометром достигает одной угловой секунды (0°00'01), расстояний – до 1 миллиметра.

Тахеометр электронный 4Та5 предназначен для измерения наклонных расстояний, горизонтальных и вертикальных углов и превышений при выполнении топографо-геодезических работ, тахеометрических съемках, а также для решения прикладных геодезических задач. Результаты измерений могут быть занесены во внутреннюю память и переданы в персональный компьютер через интерфейс RS-232C.

Технические характеристики:

Среднеквадратическая погрешность измерения одним приемом: - горизонтального угла - вертикального угла - наклонного расстояния	5" (1,5 мгон) 5" (1,5 мгон) (3+3х10-6D) мм
Диапазон измерения: - зенитного расстояния - вертикального угла	от 45° до 135° (+50…150 гон) от +45° до -45° (+50…-50 гон)
Зрительная труба: - увеличение - предел разрешения - угол поля зрения - диапазон визирования	30х 3,7" 1°30" от 1,5 м до 8
Источник питания: - напряжение - емкость - время заряда	от 6,5 до 8,5 В 1,6 Ач 1,5 ч
Диапазон рабочих температур	от- 20°С до +50°С
Масса (включая источник питания)	5,5 кг

2.4 Определение положения точек земной поверхности с помощью геодезических спутниковых систем

Разработанные Федеральной службой геодезии и картографии России концепция и программа перехода топографо-геодезического производства на автономные методы спутниковых координатных определений изложены в работе Е. А. Жалковского, Г. В. Демьянова, В. И. Зубинского, П. Л. Макаренко, Г. А. Пьянкова «О концепции и программе перехода топографо-геодезического производства на автономные методы спутниковых координатных определений» (Геодезия и картография, 1998, № 5). Традиционные геодезические методы основаны на последовательном развитии геодезических сетей путем угловых и линейных измерений, требующих для обеспечения прямой видимости между смежными пунктами постройки геодезических знаков, сооружение которых потребовало около 80% средств, затраченных на создание существующих опорных сетей.

По сравнению с традиционными спутниковые методы ГЛОНАСС/GPS имеют следующие преимущества:

• передача с высокой оперативностью и точностью координат практически на любые расстояния;

• геодезические пункты можно располагать в благоприятных для их сохранности местах, так как не нужно обеспечивать взаимную видимость между пунктами и, следовательно, строить дорогостоящие геодезические знаки;

• простота и высокий уровень автоматизации работ;

• понижение требований к плотности исходной геодезической основы.

Реализация спутниковых технологий предусматривает построение следующих геодезических сетей:

• фундаментальная астрономо-геодезическая сеть (ФАГС) — высшее звено координатного обеспечения; она должна обеспечивать оперативное воспроизведение общеземной геоцентрической системы координат, стабильность системы координат во времени, метрологическое, обеспечение высокоточных космических средств измерений;

• высокоточная геодезическая сеть (ВГС), обеспечивающая распростра- нение на всю территорию страны общеземной геоцентрической системы координат и определение точных параметров взаимного ориентирования общеземной и референцной систем координат;

• спутниковые геодезические сети 1-го класса (СГС-1).

Эти три класса сетей строго связаны между собой: ФАГС является опорой для ВГС, а ВГС — для СГС-1.

При построении ФАГС, ВГС и СГС-1 предусматривается привязка существующей ГГС к высшему классу спутниковых сетей, т. е. существующая ГГС будет сетью сгущения.

Пункты ФАГС располагаются на расстоянии 800-1000 км, их число — 50+70,10-15 пунктов должны быть постоянно действующими, а остальные — переопределяться группами через промежутки времени, зависящие от геодинамической активности региона.

Пространственное положение пунктов ФАГС определяется в общеземной системе координат с ошибкой положения пунктов относительно центра масс не более (2-3)10^-8 R, где R — радиус Земли, ошибка взаимного положения пунктов ФАГС не более 2 см в плане и 3 см по высоте. Для обеспечения этой точности необходимо использовать весь комплекс существующих космических измерений (лазерных, радиоинтерферометрических и других).

ВГС является системой пунктов с расстоянием D = 150-300 км между ними, которые определяются относительными методами космической геодезии со средней квадратической ошибкой не более 3 мм + 5 • 10^-8 D для плановых координат и 5 мм + 7 • 10^-8 D — для геодезических высот.

СГС-1 состоят из системы легкодоступных пунктов с плотностью, достаточной для использования потребителями всевозможных спутниковых определений. СГС-1 определяются относительными методами космической геодезии со средними квадратическими ошибками: 3 мм + 10^-7 D в плане и 5 мм + + 2 • 10^-8 D по геодезической высоте для геодинамически активных регионов и 5 мм + 2 • 10^-7. D в плане и 7мм + 3 • 10^-7 D по высоте для остальных регионов. Среднее расстояние между пунктами СГС-1 равно 25-35 км. В экономически развитых районах пункты СГС-1 в зависимости от требований потребителей могут иметь большую плотность.

Постоянно действующие пункты ФАГС в основном создаются на базе действующих пунктов спутниковых (космических) наблюдений, астрономических обсерваторий, пунктов службы вращения Земли, радиоинтерферометрических комплексов со сверхдальними базами «Квазар», программы «Дельта» и др. На пунктах ФАГС предусматривают две программы наблюдений: постоянные наблюдения спутниковых систем ГЛОНАСС и GPS (включая и международные программы) и наблюдения других специализированных спутников и космических объектов согласно межведомственным программам построения ФАГС.

Следует заметить, что спутниковые технологии не всегда можно использовать при решении традиционных геодезических задач, например, недостаточна относительная точность определений на коротких расстояниях, ограничено использование GPS-методов в точной инженерной геодезии, процесс привязки ориентирных пунктов, легко решаемый в традиционной технологии, становится довольно сложным и дорогим, особенно в закрытой местности, в спутниковой технологии, так как объем спутниковых определений в этом случае возрастает более чем в два раза.

3. Погрешности геодезических измерений (теория и решение задач)

3.1 Геодезическое измерение, результат измерения, методы и условия измерений. Равноточные и неравноточные измерения

Измерением называется процесс сравнения некоторой физической величины с другой одноименной величиной, принятой за единицу меры.

Единица меры – значение физической величины, принятой для количественной оценки величины того же рода.

Результат измерений – это число, равное отношению измеряемой величины единицы меры.

Различают следующие виды геодезических измерений:

1. Линейные, в результате, которых получают наклонные иррациональные расстояния между заданными точками. Для этой цели применяют ленты, рулетки, проволоки, оптические свето- и радиодальномеры.

2. Угловые, определяющие величины горизонтальных углов. Для выполнения таких измерений применяют теодолит, буссоли, эклиметры.

3. Высотные, в результате, которых получают разности высот отдельных точек. Для этой цели применяют нивелиры, теодолиты-тахеометры, барометры.

Различают два метода геодезических измерений: непосредственные и посредственные (косвенные).

Непосредственные – измерения, при которых определяемые величины получают в результате непосредственного сравнения с единицей измерения.

Косвенные – измерения, при которых определяемые величины получаются как функции других непосредственно измеренных величин.

Процесс измерения включает:

• Объект – свойства которого, например, размер характеризуют результат измерения.

• Техническое средство – получать результат в заданных единицах.

• Метод измерений – обусловлен теорией практических действий и приёмов технических средств.

• Исполнитель измерений – регистрирующее устройство

• Внешняя среда, в которой происходит процесс измерений.

Измерения различают равноточные и неравноточные. Равноточные – это результаты измерений однородных величин, выполняемые с помощью приборов одного класса, одним и тем же методом, одним исполнителем при одних и тех же условиях. Если хотя бы один из элементов, составляющий совокупность, меняется, то результат измерений неравноточный.

3.2 Классификация погрешностей геодезических измерений. Средняя квадратическая погрешность. Формы Гаусса и Бесселя для её вычисления

Геодезические измерения, выполняемые даже в очень хороших условиях, сопровождаются погрешностями, т.е. отклонение результата измерений L от истинного значения Х нумеруемой величины:

∆ = L-X

Истинное – такое значение измеряемой величины, которое идеальным образом отражало бы количественные свойства объекта. Недостижимое условие – истинное значение – понятие гипотетическое. Это величина, к которой можно приближаться бесконечно близко, оно не достижимо.

Точность измерений – степень приближения его результата к истинному значению. Чем ниже погрешность, тем выше точность.

Абсолютная погрешность выражается разностью значения, полученного в результате измерения и истинного измерения величины. Например, истинное значение l = 100 м, однако, при измерении этой же линии получен результат 100,05 м, тогда абсолютная погрешность:

E = X_>изм> – X

E = 100,05 – 100 = 0,05 (м)

Чтобы получить значение достаточно произвести одно измерение. Его называют необходимым, но чаще одним измерением не ограничиваются, а повторяют не менее двух раз. Измерения, которые делают сверх необходимого, называют избыточными (добавочными), они являются весьма важным средством контроля результата измерения.

Абсолютная погрешность не даёт представления о точности полученного результата. Например, погрешность в 0,06 м может быть получена при измерении l = 100 м или l = 1000 м. Поэтому вычисляют относительную погрешность:

C = E_>ср> / X

C = 0,06 / 100 = 1/1667, т.е на 1667 м измеряемой l допущена погрешность в 1 метр.

Относительная погрешность – отношение абсолютной погрешности к истинному или измеренному значению. Выражают дробью. По инструкции линия местности должна быть измерена не грубее 1/1000.

Погрешности, происходящие от отдельных факторов, называются элементарными. Погрешность обобщенная – это сумма элементарных.

Возникают:

• грубые (Q),

• систематические (O),

• случайные (∆).

Грубые погрешности измерений возникают в результате грубых промахов, просчётов исполнителя, его невнимательности, незамеченных неисправностях технических средств. Грубые погрешности совершенно недопустимы и должны быть полностью исключены из результатов измерений путем проведения повторных, дополнительных измерений.

Систематические погрешности измерений – постоянная составляющая, связанная с дефектами: зрение, неисправность технических средств, температура. Систематические погрешности могут быть как одностороннего действия, так и переменного (периодические погрешности). Их стремятся по возможности учесть или исключить из результатов измерений при организации и проведении работ.

Случайные погрешности измерений неизбежно сопутствуют всем измерениям. Погрешности случайные исключить нельзя, но можно ослабить их влияние на искомый результат за счет проведения дополнительных измерений. Это самые коварные погрешности, сопутствующие всем измерениям. Могут быть разные как по величине, так и по знаку.

E = Q + O +∆

Если грубые и систематические погрешности могут быть изучены и исключены из результата измерений, то случайные могут быть учтены на основе глубокого измерения. Изучение на основе теории вероятностей.

На практике сложность заключается в том, что измерения проводятся какое-то ограниченное количество раз и поэтому для оценки точности измерений используют приближённую оценку среднего квадратического отклонения, которую называют среднеквадратической погрешностью (СКП).

Гауссом была предложена формула среднеквадратической погрешности:

∆²_>ср> = (∆²_>1> + ∆²_>2> +… +∆²_>n>) / n,

∆² = m² = (∆²_>1> + ∆²_>2> +… +∆²_>n>) / n,

∆ = m,

∆_>ср> = m = √(∑∆²_>i> / n)

Формула применяется, когда погрешности вычислены по истинным значениям.

Формула Бесселя:

m = √(∑V²_>i> / (n-1))

Средняя квадратическая погрешность арифметической середины в n раз меньше средней квадратической погрешности отдельного измерения

М=m/n

При оценке в качестве единицы меры точности используют среднеквадратическую погрешность с весом равным единице. Её называют средней квадратической погрешностью единицы веса.

µ² = P×m² – µ = m√P, m = µ / √P, т.е. средняя квадратическая погрешность любого результата измерения равна погрешности измерения с весом 1 (µ) и делённая на корень квадратный из веса этого результата (P).

При достаточно большом числе измерений можно записать ∑m²P=∑∆²P (так как ∆ = m):

µ = √(∑(∆²×P)/n), т.е. средняя квадратическая погрешность измерения с весом, равным 1 равна корню квадратному из дроби в числителе которого сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.

Средняя квадратическая погрешность общей арифметической середины по формуле:

M_>0> = µ / √∑P

Подставив вместо µ её значение получим :

M_>0> = √(∑∆²×P/n) / (√∑P) = √[(∑∆²×P) / n×(∑P)]

M_>0> = √[ (∆_>1>²P_>1> + ∆_>2>²P_>2> +… + ∆_>n>²P_>n>) / n×(P_>1> + P_>2> + … + P_>n>) ] – формула Гаусса, средняя квадратическая погрешность общей арифметической середины равна корню квадратному из дроби, в числителе которой сумма произведений квадратов погрешностей неравноточных измерений на их веса, а знаменатель – произведение количества измерений на сумму их весов.

µ = √ [∑( V²×P ) / (n-1)] Это формула Бесселя для вычисления средней арифметической погрешности с измерением веса, равным 1 для ряда неравноточных измерений по их вероятнейшим погрешностям. Она справедлива для большого ряда измерений, а для ограниченного (часто на практике) содержит погрешности: m_>µ> = µ / [2×(n-1)] – это надёжность оценки µ.

Контрольная задача 1

Для исследования теодолита им был многократно измерен один и тот же угол. Результаты оказались следующими: 39˚17.4'; 39˚16.8'; 39˚16.6'; 39˚16.2'; 39˚15.5'; 39˚15.8'; 39˚16.3'; 39˚16.2'. Тот же угол был измерен высокоточным угломерным прибором, что дало результат 39˚16'42". Приняв это значение за точное, вычислить среднюю квадратическую погрешность, определить надёжность СКП, найти предельную погрешность.

Решение:

№ измерения	Результаты измерений, l	Погрешности ∆ = l-X	∆2
1	39˚17.4'	+0.7'	0.49
2	16.8	+0.1	0.01
3	16.6	-0.1	0.01
4	16.2	-0.5	0.25
5	15.5	-1.2	1.44
6	15.8	-0.9	0.81
7	16.3	-0.4	0.16
8	16.2	-0.5	0.25
Сумма			3.42

39˚16'42" = 39˚16.7'

Средняя квадратическая погрешность: m = √([∆²]/n),

m = √(3.42/8) = 0.65'.

Оценка надёжности СКП: m_>m> = m / √2n,

m_>m> = 0.65 / √16=0.1625≈0.16'.

Предельная погрешность: ∆_>пр> = 3×m,

∆_>пр> = 3×0.65' = 1.96'

Контрольная задача 2

Дана совокупность невязок треугольников триангуляции объёмом 50 единиц. Считая невязки истинными погрешностями, вычислить среднюю квадратическую погрешность и произвести надёжность СКП, вычислить предельную погрешность. На данной совокупности проверить свойство случайных погрешностей:

Lim[∆] / n =0, для чего вычислить W = [W] / n.

N	W	N	W	N	W	N	W	N	W
1	+1,02	11	-1,72	21	-0,90	31	+2,80	41	-0,44
2	+0,41	12	+1,29	22	+1,22	32	-0,81	42	-0,28
3	+0,02	13	-1,81	23	-1,84	33	+1,04	43	-0,75
4	-1,88	14	-0,08	24	-0,44	34	+0,42	44	-0,80
5	-1,44	15	-0,50	25	+0,18	35	+0,68	45	-0,95
6	-0,25	16	-1,89	26	-0,08	36	+0,55	46	-0,58
7	+0,12	17	+0,72	27	-1,11	37	+0,22	47	+1,60
8	+0,22	18	+0,24	28	+2,51	38	+1,67	48	+1,85
9	-1,05	19	-0,13	29	-1,16	39	+0,11	49	+2,22
10	+0,56	20	+0,59	30	+1,65	40	+2,08	50	-2,59

Решение:

W = [W] / n, W = +2,51 / 50 = 0,05

Среднюю квадратическую погрешность в данном случае целесообразно вычислять по формуле: m = √( [W²] – [W]²/n ) ÷ (n-1),

m = √( 76,5703 – (2,51²)/50) ÷ 49 = 1,249

Оценку надёжности СКП по формуле: m_>m> = m / √2(n-1),

m_>m> = 1,249/ √(2×49) = 0,13.

Предельная погрешность по формуле: ∆_>пр> = 3×m,

∆_>пр> = 3×1,249= 3,747.

Контрольная задача 5

Определить СКП расстояния вычисленного по формуле

S = √(x_>2 >– x_>1>)² + (y_{>2 –} >y_>1>)²

если x_>2 >= 6 068 740 м; y_>2 >= 431 295 м;

x_>1 >= 6 068 500 м; y_>2 >= 431 248 м;

m_>х >= m_>y>_> >= 0,1 м.

Решение:

S =√(6 068 740 - 6 068 500 )² + (431 295 - 431 248)² =235,36

m_>m> = 0,1/ √4 = 0,05

Контрольная задача 6

Один и тот же угол измерен 5 раз с результатами: 60˚41'; 60˚40'; 60˚40'; 60˚42'; 60˚41'. Произвести математическую обработку этого ряда результатов измерений.

Решение:

Nп/п	l, ˚	ε, '	v, '	v2, '
1	60˚41'	1	-0,2	0,04
2	60˚40'	0	+0,8	0,64
3	60˚40'	0	+0,8	0,64
4	60˚42'	2	-1,2	1,44
5	60˚41'	1	-0,2	0,04
Сумма		4	0	2,8

l_>0 >– минимальное значение измеряемой величины, l_>0 >= 60˚40' ; ε – остаток, полученный как ε = l_>1> - l_>0> ; L – наилучшее значение измеряемой величины,

L = [l]/n; m = √([ v²]/(n – 1), где v-уклонение от арифметического среднего. М – оценка точности среднего арифметического значения, М = m/√n.

L = 60˚40' + 4/5 = 60˚40,8'

m = √2,8 / 4 = 0,7'

М = 0,7'/√5 = 0,313'

Контрольная задача 7

Произвести математическую обработку результатов измерения планиметром площади одного и того же контура: 26,31; 26,28; 26,32; 26,26; 26,31 га.

Решение:

Nп/п	l, га	ε, га	v, га	v2, га
1	26,31	0,05	-0,014	0,000196
2	26,28	0,02	+0,016	0,000256
3	26,32	0,06	-0,024	0,000576
4	26,26	0	0,036	0,001296
5	26,31	0,05	-0,014	0,000576
Сумма		0,18	0	0,0029

l_>0 >= 26,26

L = 26,26 + 0,18/5 = 26,296 га

m = √0,0029/ 4 = 0,0269 га

М = 0,0269/√5 = 0,01204 га

Контрольная задача 8

При исследовании сантиметровых делений нивелирной рейки с помощью женевской линейки определялась температура в момент взятия отчета. Для пяти сантиметровых отрезков получены значения: 20,3˚; 19,9˚; 20,1˚; 20,2˚; 20,3˚. Провести математическую обработку результатов измерения.

Решение:

Nп/п	l, ˚	ε, ˚	v, ˚	v2, ˚
1	20,3	0,4	-0,14	0,0196
2	19,9	0	-0,26	0,0676
3	20,1	0,2	-0,06	0,0036
4	20,2	0,3	0,04	0,0024
5	20,3	0,4	0,14	0,0196
Сумма		1,3	0	0,1128

l_>0 >= 19,9

L = 19,9 + 1,3/5 = 20,16˚

m = √0,1128/ 4 = 0,168˚

М = 0,168/√5 = 0,075˚

3.3 Веса измерений

Вес измерения – это отвлеченное число, обратно пропорциональное квадрату СКП результата измерения.

Формула веса:

P = К / m²,

где P – вес результата измерения,

К – произвольное постоянное число для данного ряда измерений,

m – СКП результата измерения.

Из формулы видно, что чем меньше СКП измерения, тем оно точнее и его вес больше.

Отношение весов двух измерений обратнопропорционально квадратам СКП этих измерений, т.е.:

P_>1> / P_>2> = m_>2>² / m_>1>²

Если имеется ряд измерений l_>1>, l_>2>, …, l_>n>, то очевидно, что вес одного измерения будет меньше веса среднего арифметического этих значений, т.е.:

P_>m> < P_>M>,

где m – погрешность одного измерения,

M – погрешность среднего арифметического значения.

Тогда отношение весов обратнопропорционально отношению квадратов СКП:

P_>M>/P_>m> = m²/M²;M = m/√n;

P_>M>/P_>m> = m²/ (m/√n) ² = m²/ (m²/n) = m²×n/m² = n.

Таким образом, вес среднего арифметического значения больше отдельно взятого значения в n раз. Следовательно, вес арифметической середины равен числу измерений, из которых она составлена.

Общая арифметическая середина из неравноточных измерений равна дроби, в числителе которой – сумма произведений средних арифметических значений из результатов измерений на их веса, а знаменатель – сумма всех весов измерений. Следовательно, вес общей арифметической середины равен сумме весов неравноточных измерений:

A_>0> = (a_>1>P_>1> + a_>2>P_>2> + … + a_>n>P_>n>) / (P_>1> + P_>2> + … +P_>n>),

где A_>0> – общая арифметическая середина,

a_>i> – результат отдельно взятого измерения,

P_>i> – вес отдельно взятого измерения.

СКП любого результата измерения равна погрешности измерения с весом 1, делимой на корень квадратный из веса этого результата, т.е.:

m = M/√P,

где m – СКП любого результата измерения;

M – погрешность измерения с весом 1;

P – вес данного результата измерения.

СКП измерения с весом 1 равна корню квадратному из дроби, в числителе которой – сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.

M = √ (∑∆²P/n),

где ∆ - абсолютная погрешность неравноточного измерения;

P –его вес;

n – число измерений.

Контрольная задача 9

Результатам измерения углов соответствуют m_>1> = 0,5; m_>2> = 0,7; m_>3> = 1,0. Вычислить веса результатов измерений.

Решение:

P = К / m²;

P_>1> = 1 / (0,5)² = 4;

P_>1> = 1 / (0,7)² = 2,04;

P_>1> = 1 / (1,0)² = 1.

Ответ: 4; 2,04; 1.

Контрольная задача 11

Найти вес невязки в сумме углов треугольника, если все углы измерены равноточно.

Решение:

m = √[V²] / (n-1), n = 3

P = К / m²

m = √[ V²_>1> + V²_>2>+ V²_>3>]/(3 – 1) = √[ V²_>1> + V²_>2>+ V²_>3>]/2

P = К / √[ V²_>1> + V²_>2>+ V²_>3>]/2 = 2 К / √[ V²_>1> + V²_>2>+ V²_>3>] = 2/ ∑ V²_>i>

3.4 Функции по результатам измерений и оценка их точности

В практике геодезических работ искомые величины часто получают в результате вычислений, как функцию измеренных величин. Полученные при этом величины (результаты) будут содержать погрешности, которые зависят от вида функции и от погрешности аргументов по которым их вычисляют.

При многократном измерении одной и той же величины получим ряд аналогичных соотношений:

∆U_>1> = k∆l_>1>

∆U_>2> = k∆l_>2>

…………..

∆U_>n> = k∆l_>n>

Возведём в квадрат обе части всех равенств и сумму разделим на n:

(∆U_>1>² + ∆U_>2>² + … + ∆U_>n>²) / n = k²×(∆l_>1>² + ∆l_>2>² + ... + ∆l_>n>²) / n;

∑∆U² / n = k²×(∑∆l² / n);

m = √(∑∆U² / n);

m² = k² × m_>l>²,

где m_>l> – СКП дальномерного отсчёта.

m = k × m_>l>.

СКП функции произведения постоянной величины на аргумент равна произведению постоянной величины на СКП аргумента.

Функция вида U = l_>1> + l_>2>

Определить СКП U, где l_>1> и l_>2> – независимые слагаемые со случайными погрешностями ∆l_>1> и ∆l_>2>. Тогда сумма U будет содержать погрешность:

∆U = ∆l_>1> + ∆l_>2>.

Если каждую величину слагаемого измерить n раз, то можно представить:

∆U_>1> = ∆l_>1>' + ∆l_>2>' – 1-е измерение,

∆U_>2> = ∆l_>1>" + ∆l_>2>" – 2-е измерение,

…………………

∆U_>n> = ∆l_>1>⁽ⁿ⁾ + ∆l_>2>⁽ⁿ⁾ – n-е измерение.

После возведения в квадрат обеих частей каждого равенства почленно их сложим и разделим на n:

∑∆U² / n = (∑∆l_>1>²)/n + 2×(∑∆l_>1>×∆l_>2>)/n + (∑∆l_>2>²)/n.

Так как в удвоенном произведении ∆l_>1> и ∆l_>2> имеют разные знаки, они компенсируются и делим на бесконечно большое число n, то можно пренебречь удвоенным произведением.

m_>U>² = m_>l1>² + m_>l2>²;

m_>U> = √( m_>l1>² + m_>l2>² ).

СКП суммы двух измеренных величин равна корню квадратному из суммы квадратов СКП слагаемых.

Если слагаемые имеют одинаковую СКП, то:

m_>l>_>1> = m_>l>_>2> = m;

m_>U> = √(m² + m²) = √2m² = m√2.

В общем случае:

m_>U> = m√n,

где n – количество аргументов l.

Функция вида U = l_>1> - l_>2>

m_>U> = m√n;

m_>U> = √( m_>l>_>1>² + m_>l>_>2>²).

СКП разности двух измерений величин равна корню квадратному из суммы квадратов СКП уменьшаемого и вычитаемого.

Функция вида U = l_>1> - l_>2> + l_>3>

m_>U> = √( m_>l>_>1>² + m_>l>_>2>² + m_>l>_>3>²…)

СКП суммы n измеренных величин равна корню квадратному из суммы квадратов СКП всех слагаемых.

Линейная функция вида U = k_>1>l_>1> + k_>2>l_>2> + … + k_>n>l_>n>

m_>U> = √[ (k_>1>m_>l1>)² + (k_>2>m_>l2>)² + … + (k_>n>m_>ln>)²],

т.е. СКП алгебраической суммы произведений постоянной величины на аргумент равна корню квадратному из суммы квадратов произведений постоянной величины на СКП соответствующего аргумента.

Функция общего вида U = ƒ( l_>1>, l_>2>, …, l_>n>)

Это наиболее общий случай математической зависимости, включающий все рассматриваемые выше функции, являющиеся частным случаем. Это значит, что аргументы l_>1>, l_>2>, …, l_>n> могут быть заданы любыми уравнениями. Для определения СКП такой сложной функции необходимо проделать следующее:

1. Найти полный дифференциал функции:

dU = (dƒ/dl_>1>)×dl_>1> + (dƒ/dl_>2>)×dl_>2> + … + (dƒ/dl_>n>)×dl_>n>,

где (dƒ/dl_>1>), (dƒ/dl_>2>), …,(dƒ/dl_>n>) – частные производные функции по каждому из аргументов.

2. Заменить дифференциалы квадратами соответствующих СКП, вводя в квадрат коэффициенты при этих дифференциалах:

m_>U>² = (dƒ/dl_>1>)²×m_>l1>² + (dƒ/dl_>2>)²×m_>l2>² + … +(dƒ/dl_>n>)²×m_>ln>².

3. Вычислить значения частных производных по значениям аргументов:

(dƒ/dl_>1>), (dƒ/dl_>2>), …,(dƒ/dl_>n>).

И тогда m_>U> = √[ (dƒ/dl_>1>)²× m_>l>_>1>² + (dƒ/dl_>2>)²×m_>l>_>2>² + … +(dƒ/dl_>n>)²×m_>ln>²].

СКП функции общего вида равна корню квадратному из суммы квадратов произведений частных производных по каждому аргументу на СКП соответствующего аргумента.

3.5 Оценка точности по разностям двойных измерений и по невязкам в полигонах и ходах.

В практике геодезических работ часто одну и ту же величину измеряют дважды. Например, стороны теодолитного хода в прямом и обратном направлении, углы двумя полуприемами, превышения – по черной и красной стороне вех. Чем точнее произведены измерения, тем лучше сходимость результатов в каждой паре.

m_>l>_>ср.> = ½ √∑d²/n

где d – разности в каждой паре; n – количество разностей.

Формула Бесселя:

m_>l>_>ср >= ½ √∑d²/n-1

Если измерения должны удовлетворять какому-либо геометрическому условию, например, сумма внутренних углов треугольника должна быть 180˚, то точность измерений можно определить по невязкам получающимся в результате погрешностей измерений.

μ=√∑ [f² /n]/N,

где - СКП одного угла;

f – невязка в полигоне;

N – количество полигонов;

n – количество углов в полигоне.

4. Определение дополнительных пунктов

4.1 Цель и методы определения дополнительных пунктов

Дополнительные пункты определяются наряду со съемочной сетью в основном для сгущения существующей геодезической сети пунктами съемочного обоснования. Они строятся прямыми, обратными, комбинированными, а при наличии электронных дальномеров – линейными засечками и лучевым методом.

В некоторых случаях дополнительный пункт определяется передачей (снесением) координат с вершины знака на землю.

4.2 Передача координат с вершины знака на землю. (Решение примера)

При производстве топографо-геодезических работ в городских условиях невозможно бывает установить теодолит на пункте геодезической сети (пунктом является церковь, антенна и т.п.). Тогда и возникает задача по снесению координат пункта триангуляции на землю для обеспечения производства геодезических работ на данной территории.

Исходные данные: пункт A с координатами X_>A>, Y_>A>; пункты геодезической сети B (X_>B>, Y_>B>) и C (X_>C>, Y_>C>).

Полевые измерения: линейные измерения выбранных базисов b_>1> и b'_>1>; измерения горизонтальных углов ß_>1 >, ß'_>1 >, ß_>2 >, ß'_>2> ; б , б'.

Требуется найти координаты точки P – X_>P>, Y_>P>.

Решение задачи разделяется на следующие этапы:

Решение числового примера

Исходные данные

Обозначе- ния	А ХА, YА	B ХB, YB	C ХC, YC	β1 β2	β2 β2`	β1 β1`	б б‘
Численные значения	6327,46	8961,24	5604,18	266,12	38o26'00"	70o08'54"	138o33'49"
27351,48	25777,06	22125,76	198,38	42˚26'36"	87˚28'00"	71˚55'02"

Вычисление расстояния D_>АР>

Обозначе- ния	B1 B2	sinβ2 sinβ‘2	sin(β1+β2 ) sin(β‘1+β‘2)	B1 sinβ2 B2 sinβ‘2	D1 D2	D1 -D2 2D/T	Dср
Численные значения	266,12	0,62160	0,94788	165,420	174,52	0,00	174,52
198,38	0,67482	0,76705	133,871	174,52

Решение обратных задач

Обозначения	YB YА	ХB ХА	YC YА	ХC ХА	tgαAB αAB	tgαAC αAC	sinα AB sinα AC cos αAB cosαAC	S AB S AC
Численные значения	10777,06	8961,24	7125,76	5605,08	-0,5977	7,23421	-0,51309 -0,99058 0,85833 -0,13693	3068,48
12351,48	6327,46	12351,48	6327,46	329˚07'55"	262o07'51"	5275,51

Вычисление дирекционных углов α_{>АР =} >α_>D>

Обозна- чения	D	sinб sinб'	S AB S AC	sin ψ sin ψ'	ψ ψ'	φ φ'	αAB αAC	αD α'D	αD-α'D õmß
Численные значения	174,52	0,66179	3068,48	0,03950	2o15'50"	39o10'41"	329o07'55"	8o18'36"	∆α=1'30"
0,95061	5275,51	0,03292	1o53'13"	106o11'46"	262o07'51"	8o18'37"

sin ψ = D×sinб/ S_{> AB}>; sin =174,52×0,66179/3068,48=0,03950;

sin ψ' = D×sinб'/ S_{> A}>_>С>; sin `=174,52×0,95061/5275,51=0,03292;

ψ = arcsin 0,03950 =2 ^o15` 50``;

ψ'= arcsin 0,03292=1 ^o53` 13``;

φ = 180 ^o – (б+ ψ) = 180 ^o – (138^o33` 49``+2 <sup>o</sup>15` 50``) = 39<sup>o</sup>10` 41``

φ`= 180 <sup>o</sup> – (б`+ ψ` ) = 180 <sup>o</sup> – (71<sup>o</sup>55` 02``+1 <sup>o</sup>53` 13``) = 106 ^o11` 46``

α_>D >=_> >α_>AB >± φ =329^o07` 55``+ 39<sup>o</sup>10` 41``= 8<sup>o</sup>18` 36``

α_>D>`=<sub>></sub> >α<sub>>AC</sub>> ± φ`=262^o07` 51``+ 106 <sup>o</sup>11` 46``= 8<sup>o</sup>18` 37``

Контроль:

(α_>D>_> >–_> >α'_>D>) õm_>β>;

где m_>β> –СКП измерения горизонтальных углов.

Знак «+» или «-» в формулах вычисления дирекционного угла берется в зависимости от взаимного расположения пунктов А, Р, В и С.

(8^o18` 36``-8<sup>o</sup>18` 37``) ≤ 30``

0^o00` 01`` ≤ 30``

Решение прямых задач (вычисление координат т.Р)

Обозначения	αD αD'	sinαD sinαD'	cosαD cosαD'	DcosαD DcosαD'	DsinαD Dsinα'D	∆Х - ∆Х' ∆Y - ∆Y'	ХА YА	Хp = ХА+ ∆Х Х'p = ХА+ ∆Х' Yp = YА+ ∆Y Y'p = YА+ ∆Y'
Численные значения	8o18'36"	0,14453	0,98950	172,69	25,22	∆=00,00 ∆=00,00 ∆доп=25см	6327,46	6500,15
8o18'37"	0,14454	0,98950	172,69	25,22	12351,48	12376,70

Х_>p> = Х_>А>+_> >∆Х,Y_>p> = Y_>А>+_> >∆Y,

Х'_>p> = Х_>А>+_> >∆Х',Y'_>p> = Y_>А>+_> >∆Y'.

∆Х= Dcosα_>D>,∆Y= Dsinα_>D>,

∆Х'= Dcosα'_>D>,∆Y'=Dsinα'_>D>.

Расхождение координат не должно превышать величины õm_>ß>×p, где p=206265", m_>ß> – средняя квадратическая погрешность измерения угла.

Оценка точности определения положения пункта P.

Средняя квадратическая погрешность определения отдельного пункта вычисляется по формуле:

M²_>p> = m²_>X> +m²_>Y>,M²_>p> = m²_>D> +(D×m_>α> / P)²

где m_>D>- определяется точностью линейных измерений, а m_> >_>α> – точностью угловых измерений.

Пример: m_>D> =2см, m_>α>= 5``, тогда

M_>p> =√ [(0,02) ²+(170×5/2×10⁵)²] ≈ 2×10^-2 = 0,02м.

4.3 Решение прямой и обратной засечки (по варианту задания)

Определение координат пункта прямой засечкой (формулы Юнга).

Для однократной засечки необходимо иметь два твёрдых пункта. Контроль определения осуществляется вторичной засечкой с третьего твёрдого пункта.

Исходные данные: твердые пункты А(Х_>А>Y_>А>); B(Х_>B>Y_>B>); С(Х_>С>Y_>С>).

Полевые измерения: горизонтальные углы β1, β_{> 2}>, β`<sub>>1</sub>>, β`_>2.>

Определяется пункт P.

Формулы для решения задачи:

Х_>p> -Х_>А>=((Х_>B>-Х_>А>) ctg β_{> 1}>+(Y_>B>-Y_>А>))/ (ctg β_{> 1}>+ ctg β_{> 2}>);

Х_>p>= Х_>А>+∆Х_>А>;

Y_>p> -Y_>А>=((Y_>B>-Y_>А>) ctg β_{> 1}>+(Х_>B>-Х_>А>))/ (ctg β_{> 1}>+ ctg β_{> 2}>); Y_>p>= Y_>А>+∆Y_>А>;

Оценка точности определения пункта P.

Вычисление СКП из 1-го и 2-го определения:

M_>1> =(m_>β>×√(S_>1>²+ S_>2>²))/p×sinγ_>1>;

M_>2> =(m_>β>×√(S_>1>²+ S_>2>²))/p×sinγ_>2>;

Значения величин, входящих в приведённые формулы следующие:

m_>β> =5``, p=206265``; γ=73˚15,9`; γ=62˚55,7`; S_>1>=1686,77 м; S_>2>=1639,80 м; S_>3>=2096,62 м.

Стороны засечки найдены из решения обратных задач.

M_>1> = (5``×√2,86+2,69)/(2×10⁵×0,958)=0,06м.

M_>2> = (5``×√2,69+4,41)/(2×10⁵×0,890)=0,07м.

M_>r >= √ (M_>1>² +M_>2>²); M_>r >=√ [(0,06) ²+(0,07) ²]=0,09м.

Расхождение между координатами из двух определений

r = √ [( Х_>p>- Х`<sub>>p</sub>>) <sup>2</sup>+( Y<sub>>p</sub>>- Y`_>p>) ²] не должно превышать величины 3 M_>r>;

r =√ [(2833,82-2833,82) ²+(2116,38-2116,32) ²]=√0,0036=0,06м.

На основании неравенства r =0,06м 3×0,09м логично сделать вывод о качественном определении пункта P.

За окончательные значения координат принимают среднее из двух определений.

Решение числового примера

β1 β2	XB XA	ctg β1 ctg β2 (XB- XA)ctg β1	YB YA	∆ XA XP = XA+∆XA	(YB-YA)ctgβ1	∆ YA YP=YA+∆YA
XB- XA	YB-YA
ctg β1 + ctg β2
52˚16.7' 52˚27.4'	1630.16 1380.25	0.77349 0.71443 193.30 1.48792	3230.00 1260.50	1453.57 2833.82	1523.39	855.88 2116.38
+249.91	+1969.50
β'1 β'2	XC XB	ctg β'1 ctg β'2 (XC- XB)ctg β'1	YC YB	∆ XB XP = XA+∆XA	(YC-YB)ctgβ'1	∆ YB YP=YA+∆YA
XC- XB	YC-YB
ctg β'1 + ctg β'2
69˚48.5' 52˚27.4'	3401.04 1630.16	0.36777 0.92402 651.28 1.29175	4133.41 3230.00	1203.56 2833.82	332.24	-1113.68 2116.32
+1770.88	+903.41

2833.82 2116.35

Определение координат пункта методом обратной засечки (аналитическое решение задачи Потенота).

Необходимо иметь три твёрдых пункта, для решения задачи с контролем используют четвёртый твердый пункт.

Исходные данные: А(Х_>А>Y_>А>); B(Х_>B>Y_>B>); С(Х_>С>Y_>С>), D(X_>D>Y_>D>).

Полевые измерения: горизонтальные углы γ_>1>, γ_>2>, γ_>3>.

Определяемый пункт P.

Формулы для вычисления:

1.ctgγ_>1>=а; ctgγ_>2>=b

2.k_>1> =a(Y_>B>- Y_>A>)-( Х_>B>- Х_>A>);

3.k_>2> =a( Х_>B>- Х_>A>)+(Y_>B>- Y_>A>);

4.k_>3> =b(Y_>С>- Y_>A>)-( Х_>C>- Х_>A>);

5.k_>4> =b( Х_>C>- Х_>A>)-(Y_>C>- Y_>A>);

6.c=( k_>2> - k_>4>)/( k_>1> - k_>3>)=ctga_>AP>;

7.контроль: k_>2> - с k_>1>= k_>1>- с k_>3>;

8.∆Y=( k_>2> - с k_>1>)/( 1 - с²);

9.∆Х= с _>A>Y;

10.Х_>p> = Х_>А>+_> >∆Х, Y_>p> = Y_>А>+∆Y.

Решение численного примера

1	γ1 γ2 a=ctg γ1 b=ctg γ2	109˚48'42" 224˚15'21" -0.360252 +1.026320
2	XB XC XA	5653.41 8143.61 6393.71
	X'B = XB- XA X'C = XC- XA	-740.30 1749.90
	X'C- X'B = XC- XB	2490.20
	YB YC YA	1264.09 1277.59 3624.69
	Y'B = YB- YA Y'C = YC- YA	-2360.60 -2347.16
	Y'C- Y'B = YC- YB	13.5
3	k1 k3	+1590.71 -4158.78
	k1- k3	+5749.49
	k2 k4	-2093.91 -551.14
	k2- k4	-1542.77
	c = ctg α c2 + 1 k2-ck1 k4-ck3	-0.268332 1.072002 -1667.07 -1667.07
4	∆Y YA Y ∆X XA X	-1555.0 3624.65 +2069.56 +417.28 6393.71 +6810.99

Координаты из первого определения получились Х_>p>=6810,99м, Y_>p> =2069,56 м.

Для контроля задача решается вторично с твердым пунктом D, т.е. пунктом А, B, C.

Исходными данными являются: γ_>1>=109^o48`42``; γ<sub>>3</sub>>=151<sup>o</sup>26`24``; Х_>d>=6524,81м, Y_>d>=893,64м.

Контроль осуществляется следующим образом: определить

ctgα_>PD> =( Х_>D>-_> >Х_>P>)/( Y_>D>-_> >Y_>P>), α_>PD>=256 ^o27`38``;

Из схемы первого решения имеем: С=ctgα_> >_>PA>=-0,26833;

α_>PD>=105^o01`13``.

Контроль определяется пунктом P:

r=√ [( Х_>P> - Х`<sub>>P</sub>>) <sup>2</sup>+( Y<sub>>P</sub>> - Y`_>P>) ²] ≤ 3 M_>r>;

где r, как и в случае прямой засечки,

M_>r>=1/2×√ [M_>1>² +M_>2>²]

5. Уравнивание системы ходов съемочной сети

5.1 Общее понятие о системах ходов и их уравнивании

Координаты пунктов могут быть определены положением через них теодолитных ходов, опирающихся в начале и в конце хода на пункты с известными координатами и стороны с известными дирекционными углами. При математической обработке результатов таких измерений координаты определяемых пунктов получают однозначно, а их точность зависит от точности полевых измерений, точности исходных данных и принятого метода обработки измерений.

На практике возможно появление ситуаций, когда в геодезических построениях возникает неоднозначность получения определяемых величин, например координат пунктов.

С этой точки зрения рассмотрим геодезическое построение в виде системы трех теодолитных ходов с одной узловой точкой. Практическая необходимость построения такой системы обусловлена невозможностью определения положения пунктов путем проложения через них одного теодолитного хода (например, из-за отсутствия на местности необходимых видимостей). Ограничивающим фактором может быть превышение допустимой длины одиночного теодолитного хода или нарушением каких-либо других нормативных требований.

В системе теодолитных ходов положение пунктов определено от трех исходных – В, D, F, тогда как для этой цели достаточно было двух из них, следовательно, в сети имеются избыточные измерения (избыточные в смысле их необходимого числа при бесконтрольном определении координат пунктов). Так, например, координаты любого определяемого пункта сети, могут быть получены, как минимум, дважды. В таком случае говорят о необходимости уравнения.

Способы уравнения разделяются на строгие, когда уравнение производится под условием минимума суммы произведение квадратов поправок в измерение величины, и нестрогие (раздельные), когда сначала уравниваются углы, а затем раздельно между собой приращения координат.

При выборе способа уравнения исходят, прежде всего, из необходимой точности получения координат пунктов. Если раздельное уравнение обеспечивает указанное требование, то его применение в настоящее время предпочтительно, т. к. упрощает процесс вычислений. Последний может быть выполнен как посредством традиционных средств, так и с помощью микрокалькуляторов или ЭВМ.

При раздельном уравнении системы теодолитных ходов с одной узловой точкой уравнивают сначала измеренные углы, а затем по полученным вероятнейшим значениям дирекционных углов и измеренным горизонтальным положениям линий вычисляю приращение координат, которые уравнивают отдельно, приращения по оси абсцисс и приращения по оси ординат.

Уравнивание системы проводят раздельно, т.е. вначале уравнивают горизонтальные углы, а затем – приращения координат.

Вычисление координат пунктов теодолитных ходов производят в ведомости координат, куда вписывают измеренные углы, горизонтальные проложения, координаты исходных геодезических пунктов.

5.2 Упрощенное уравнение системы теодолитных ходов по варианту задания

Вычислим координаты пунктов системы теодолитных ходов с одним узловым пунктом.

Исходные данные

Координаты и дирекционные углы

№№ пунктов	Координаты, м
Х	У
D В F	4740,84 3687,80 3263,23	6451,27 5761,83 6767,63
Дирекционные углы линий
CD EF AB	188˚58.7' 245˚04.1' 80˚35.4'

Вычисление дирекционного угла

Номер хода	Дирекчионный угол Узловой линии
1	99˚35,9'
2	99˚36,1'
3	99˚36,2'

Ведомость вычисления координат

№	ß измер	α	d	∆Х d×cosα	∆У d×sinα	∆Х исп.	∆У исп.	Х	У
1 ход
А
		80˚35,4'
В	155˚17,5'							3687,80	5761,83
		55˚52,9'	200,02	112,19	165,59	112,25	165,67
2	223˚43,0'							3800,05	5927,5
		99˚35,9'	322,34	-53,75	317,83	-53,65	317,96
3	238˚53,5'							3746,4	6245,46
		158˚29,4'	508,76	-473,33	186,54	-473,18	186,74
7	113˚14,0'							3273,22	6432,2
		91˚43,4'	335,45	-10,09	335,30	-9,99	335,43
F	153˚20,5'							3263,23	6767,63
		65˚03,9'
Е
2 ход
Е
		245˚04,1'
F	153˚20,5'							3263,23	6767,63
		271˚43,6'	335,45	10,11	-335,30	10,11	-335,38
7	113˚14,0'							3273,34	6432,25
		338˚29,6'	508,76	473,34	-186,52	473,33	-186,65
3	118˚11,0'							3746,67	6245,6
		40˚18,6'	345,76	263,66	223,68	263,66	223,6
4	226˚15,0'							4010,33	6469,20
		354˚03,6'	292,82	291,25	-30,30	291,25	-30,37
5	172˚25,5'							4301,58	6438,83
		1˚38,1'	439,44	439,26	12,54	439,26	12,44
D	172˚39,5'							4740,84	6451,27
		8˚58,6'
C
3 ход
С
		188˚58,7'
D	187˚20,5'							4740,84	6451,27
		181˚38,2'	439,44	-439,26	-12,55	-439,39	-12,57
5	187˚34,5'							4301,45	6438,7
		174˚03,7'	292,82	-291,25	30,29	-291,34	30,28
4	133˚45,0'							4010,11	6468,98
		220˚18,7'	345,76	-263,65	-223,69	-263,75	-223,71
3	120˚42,5'							3746,36	6245,27
		279˚36,2'	322,34	53,77	-317,82	53,68	-317,83
2	223˚43,0'							3800,04	5927,44
		235˚53,2'	200,02	-112,18	-165,60	-112,24	-165,61
B	155˚17,5'							3687,80	5761,83
		260˚35,7'
A

Вычисление координат пункта

Координаты	Номер хода
1	2	3
X3	3746,4	3746,67	3746,36
Y3	6245,46	6245,6	6245,27

Для проверки доброкачественности линейных измерений вычисляют по двум наиболее коротким ходам, например:

f X_>1+2> = X_>1,3> – X_>2,3>

f Y_>1+2> = Y_>1,3> – Y_>2,3>

f X_>2+3> = X_>2,3> – X_>3,3>

f Y_>2+3> = Y_>2,3> – Y_>3,3>

f X_>1+2> = 3746,4 - 3746,67 = -0,27;

f Y_>1+2 >= 6245,46 – 6245,6 = -0,14;

f X_>2+3 >= 3746,67 – 3746,36 = 0,31;

f Y_>2+3 >= 6245,6 – 6245,27 = 0,33.

Затем вычисляют значения:

fS_>1+2> = √ [f² X_>1+2> + f² Y_>1+2>]

fS_>2+3> = √ [f² X_>2+3> + f² Y_>2+3>]

fS_>1+2 >= √ [(-0,27)² + (-0,14)²] = 0,3;

fS_>2+3 >= √ [(0,31)² + (0,33)²] = 0,45.

и выразив их в относительной мере:

(fS_>1+2>) / (S_>1+2>);

(fS_>2+3>) / (S_>2+3>),

сравнивают с допустимым значением относительной невязки хода (1:2000).

(fS_>1+2>) / (S_>1+2>) = 0,3 / 1366,57; 1: 4555

(fS_>2+3>) / (S_>2+3>) = 0,45 / 1922,23; 1: 4272

Обе невязки допустимы.

Среднее весовое значение X_>3>^ОК, Y_>3>^ОК координат узловой линии определяется выражениями:

X_>3>^ОК = (p_>1> X_>1,3> + p_>2> X_>2,3> + p_>3> X_>3,3>) / (p_>1> + p_>2> + p_>3>),

Y_>3>^ОК = (p_>1> Y_>1,3> + p_>2> Y_>2,3> + p_>3> Y_>3,3>) / (p_>1> + p_>2> + p_>3>).

P_>i>_> >= K /[S]_>i>,

где K-любое положительное число(К=1, [S]_>I>-выражают в километрах.)

P_>1 >= 1/1,36657 = 0,73

P_>2 >= 1/1,92223 = 0,52

P_>3 >= 1/1,60038 = 0,62

X_>3>^ОК = (0,73×3746,4 + 0,52 ×3746,67 + 0,62×3746,36) / (0,73 + 0,52 + 0,62) = 3746,5

Y_>3>^ОК = (0,73×6245,46 + 0,52 ×6245,6 + 0,62×6245,27) / (0,73 + 0,52 + 0,62) = 6245,4

6. Тахеометрическая съёмка

6.1 Плановое и высотное обоснование тахеометрической съёмки

Съёмка местности при тахеометрической съёмке заключается в определении наиболее характерных точек, отображающих контуры предметов и рельеф местности. На каждую снимаемую точку ставится рейка по которой определяются полярные координаты, направление, угол наклона. Снимаемые реечные точки могут быть контурными, рельефными, контурно-рельефными. Во всех случаях каждый раз берутся отсчёты по дальномерным нитям, горизонтальному и вертикальному кругу.

При тахеометрической съёмке работа на станции выполняется в следующей последовательности:

• устанавливают теодолит над точкой съёмочного обоснования и приводят его в рабочее положение, т.е. центрируют и нивелируют. Затем измеряют высоту инструмента, отмечают её на рейке и записывают в тахеометрический журнал

• наводят теодолит на соседнюю точку съёмочного обоснования, средней горизонтальной нитью на отмеченную высоту инструмента и берут отсчёт по КЛ. Переводят трубу через зенит и снова при КП наводят на высоту инструмента и берут отсчёт. Вычисляют место нуля.

• при КЛ совмещают нуль алидады с нулём лимба, т.е. ставят отсчёт 0-0 и закрепляют защёлкой.

• наводят на точки съёмочного обоснования по которым брали вертикальные углы

• открепляют защёлку и наводят на все реечные точки, берут отсчёты и отсчитывают по рейке дальномерное расстояние

• составляются кроки, на которых изображаются все реечные точки, зарисовывается ситуация и показывается рельеф

Далее выполняются камеральные работы в следующей последовательности:

1. поверка записей в тахеометрическом журнале

2. вычисление горизонтальных превышений и проложений

3. вычисление отметок реечных точек

4. построение координатной сетки

5. нанесение по координатам точек съёмочного обоснования

6. нанесение реечных точек по полярным координатам

7. построение контуров по данным тахеометрического журнала и крок

8. зарисовка рельефа по высотам реечных точек и заметкам в кроках

9. вычерчивание контуров и рельефа по условным знакам заданного масштаба

10. зарамочное оформление составленного плана

Главными особенностями тахеометрической съёмки является то, что на местности измеряются углы и расстояния, рисуется рельеф, составляются кроки, план составляется в камеральных условиях.

Для построения съёмочного обоснования применялся метод полигонов (замкнутых ходов). На участке работ было закреплено 5 точек на расстоянии 100 метров. На местности точки были закреплены колышками длиной 25 см. и сторожками длиной 50 см., на которых была сделана надпись порядкового номера точки и номера бригады. Вокруг точки была сделана канавка шириной и глубиной 10 см.

1. Плановое обоснование.

Исходным пунктом при создании планового обоснования была точка опорной геодезической сети. По точкам съёмочного обоснования был проложен ход, с числом сторон 5. В результате измерений было установлено, что наибольшая длина сторон ходе между точками 3-4 составляет 101,8 м., а

наименьшая между точками 4-5 равна 49,6 м. Было вычислено, что средняя длина сторон в ходе 89,68 м.; наименьший угол в треугольнике это угол 4-5-1 равный 20°22'58''. Для выполнения работ были необходимы следующие инструменты и оборудование: теодолит 2Т30М, штатив, лента стальная (20 м), шпильки к ленте (5 шт), отвес, винт.

Были выполнены следующие поверки теодолита:

1. ось цилиндрического уровня на алидаде должна быть перпендикулярна к оси вращения инструмента

Инструмент устанавливается на штатив, прикрепляется становым винтом и плоскость лимба приблизительно приводится в горизонтальное положение. После этого поворотом алидады ставят ось уровня по направлению двух подъемных винтов и, действуя этими подъёмными винтами, выводят пузырёк уровня на середину. Потом поворачивают алидаду на 90° и третьим подъёмным винтом выводят пузырёк в нуль пункт. Затем алидаду поворачивают на 180°. Если пузырёк уровня остановился на середине (в нуль пункте), то условие перпендикулярности осей уровня и инструмента выполнено. Если условие не выполнено, то пользуясь исправительными винтами уровня, перемещают пузырёк к нуль пункту на половину его отклонения от середины.

2. визирная ось трубы должна быть перпендикулярна к оси вращения трубы

Угол отклонения визирной оси от перпендикуляра к оси вращения трубы называется коллимационной ошибкой. Для выявления этой ошибки крест сетки нитей трубы наводят на хорошо видимую точку, удалённую на 50–100 м. и берут по обоим верньерам отсчёты. Записывают градусы по первому верньеру, а минуты и секунды по обоим верньерам и из них подсчитывают среднее. Берут отсчёт по КП по горизонтальному кругу. Затем открепляют алидаду и, повернув трубу через зенит, снова наводят её на эту же точку и снова берут отсчёты при другом положении круга – КЛ.

Коллимационная ошибка подсчитывается по формуле:

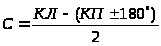
Если С≤2t (t-точность верньера), то можно считать условие выполненным.

Б. Высотное обоснование

Исходными данными высотного обоснования является отметка первой точки .

При высотном обосновании нивелирные ходы прокладываются по точкам теодолитного хода. Геометрическое нивелирование выполняется по методу "из середины". Инструмент устанавливается между нивелируемыми точками на середине. Нивелирные рейки ставятся на теодолитные точки. В случае, когда превышение между теодолитными точками нельзя определить с одной постановки инструмента, применяется сложное нивелирование, при котором разность высот определяется как сумма отдельных превышений. На данном участке нивелирная сеть состоит из 5 станций.

6.2 Нанесение съёмочных и реечных точек

Станции, с которых ведется тахеометрическая съемка, служат точки съемочного обоснования

Порядок работы на станции:

Устанавливают теодолит над точкой съемочного обоснования, центрируют, приводят в рабочее положение;

Наводят трубу на веху, устанавливаемую на точку съемочного обоснования или тахеометрического хода, и совмещают нуль лимба горизонтального круга с нулем алидады;

Определяют место нуля вертикального круга по трем точкам;

При определении пикетных точек измерения ведут при одном положении круга: для определения превышения трубу наводят на высоту прибора.

На рейке при помощи резиновой тесьмы фиксируют высоту прибора, а при использовании реек в выдвижным кольцом нуль рейки устанавливают на высоту прибора.

Съемка предметов местности и контуров угодий производится поерным способом определением по дальномеру кипрегеля расстояний от приборов до пикетов. При съемке контура рейку ставят на всех поворотах границы контура, съемку замкнутого контура необходимо закончить на той же точке, с которой начиналась съемка. Кроме высот пикетов необходимых для проведения горизонталей, следует определять отметки каменных, бетонных и земляных плотин, дам, шлюзов, мостов, углов кварталов. Реечные точки (пикеты) должны быть набраны такой густоты, чтобы расстояния между ними были не более 20 м. для масштаба 1:500. При высоте сечения рельефа менее 1 м. отметки вычисляют и выписывают с точностью до 1 см. Съемку рельефа в застроенной части города производят на планшетах после нанесения контура застройки, если он снимался другим методом.

После построения съемочного обоснования по координатам на план наносят, пользуясь способом полярных координат, реечные точки. При этом пользуются круговым транспортиром (тахеографом) или простым транспортиром и масштабной линейкой. Центр транспортира совмещают с точкой съемочного обоснования (например, вершиной I). Нулевое деление транспортира нужно совместить со стороной хода, по которой ориентирован лимб прибора в процессе съемки (например, I–II), в соответствии с записью в тахеометрическом журнале. Помня, что отсчеты на лимбе возрастают по часовой стрелке, горизонтальные углы (отсчеты по горизонтальному кругу – из соответствующей графы тахеометрического журнала) надо откладывать по часовой стрелке. Отложив с помощью транспортира отсчет по горизонтальному кругу, получаем направление на реечную точку, которое временно закрепляем на бумаге тонкой чертой мягким карандашом. На полученном направлении в масштабе плана откладывают горизонтальное расстояние (графа 9 тахеометрического журнала). Нанесенная точка отмечается условным знаком (черной точкой диаметром 0,6 мм).

6.3 Интерполирование отметок пикетов и вычерчивание горизонталей

По высотам съёмочных пикетов производиться интерполяция горизонталей «на глаз» по направлениям, указанным на абрисах стрелками и провести горизонтали через 1м по высоте. Следует иметь в виду, что интерполяцию можно производить только между пикетами соединёнными стрелками.

Если между двумя пикетами проходит несколько горизонталей, то они должны находиться на одинаковом расстоянии друг от друга.

Подписав на плане высоту уреза воды в озере как среднее арифметической из всех значений высот уреза с округлением до 0,01 м, вычертить план в соответствии с условными знаками.

6.4 Нанесение ситуации в условных знаках

Местные предметы и характерные точки контуров наносят на план, руководствуясь абрисом. Подавляющее большинство предметов и контуров при тахеометрической съемке снимались полярным способом и поэтому, по мере нанесения реечных точек на план, соответствующие точки соединяются линиями, чем и образуют границы соответствующих угодий, которые обозначаются условными знаками. Отдельные предметы или контуры могут быть сняты и другими способами (например: прямоугольных координат, угловых засечек и т.п.). Для накладки точек, снятых на местности способом координат, пользуются линейками и треугольниками, при этом соответствующие отрезки откладывают циркулем-измерителем в масштабе плана. Например, при производстве съемки был заснят правый берег и в абрисе записана ширина реки. Чтобы нанести на план левый берег, от построенного по точкам контура правого берега по перпендикулярам к нему откладывают в масштабе ширину реки в нескольких характерных местах. Последовательно соединив полученные таким образом точки, проводят линию левого берега.

Контуры, снятые угловыми засечками, наносят на план с помощью транспортира и линейки. Углы откладывают от тех же опорных линий, от которых они измерялись при съемке. Например, способом угловых засечек заснято отдельно стоящее дерево (точка а) от линии АВ.

6.5 Оформление плана тахеометрической съёмки (по варианту задания)

При составлении плана тахеометрической съёмки работу производят от «общего к частному». На чертёжной бумаге размером 30*40 см построить сетку квадратов со сторонами 10 см. Значение подписей координат сторон сетки для масштаба 1:2000 должны быть кратны 200м. Далее наносят на план главные опорные пункты, а затем точки съёмочного обоснования. После этого накладывают съёмочные ходы, затем ситуационные и орографические точки по данным полевого журнала и кроки. Точки, снятые при тахеометрической съёмке полярным способом, удобно накладывать на план, пользуясь круглым транспортиром.

Перед нанесением горизонталей необходимо, сообразуясь с зарисовками кроки, предварительно пунктирными линиями нанести скелет рельефа – его характерные и главные линии. После этого приступают к интерполированию и нанесению горизонталей.

План, составленный по результатам тахеометрической съёмки, подвергается полевой поверке.

Тахеометрическая съёмка. Ведомость вычисления координат.

№ точки	Углы, β	Дир. углы,α	Гор. прол.	Приращения координат	Координаты
Вычисл.	Исправл.
Изм.	Испр.	∆X	∆Y	∆X	∆Y	X	Y
Усово
222˚36'
216	122˚14,5'	122˚14'	4255,70	-2009,00
280˚22'	118,25	21,3	-116,3	21,36	-116,39
1	222˚59,5'	222˚59'	4277,06	-2125,39
237˚23'	157,5	-84,9	-132,6	-84,83	-132,7
2	134˚03'	134˚02'30″	4192,23	-2258,09
283˚20'30″	127	29,3	-123,6	29,36	-123,7
225	108˚15'	108˚14'30″	4221,59	-2381,79
355˚06'	∑402,75
226
∑	пр. 287˚32'
теор. 287˚30'

Ведомость вычисления высот съёмочных точек

№ точек	Расстояние S, м	Превышения	Высота точек, Н
прямые	обратные	средние	поправки	исправл.
216 1 2 225 ∑ S							229,66
118,25	-2,77	2,82	-2,8	-0,02	-2,82
						210,63
157,5	-0,74	0,77	-0,75	-0,02	-0,77
						209,86
127	0,36	-0,34	0,35	-0,02	0,33
402,75						226,47

Вычисление высот съёмочных пикетов

I. Вычислить последовательно углы наклона на съёмочные пикеты на каждой съёмочной точке хода по формуле:

ν =Л – МО,

1. ν =359˚12' - 359˚50' = - 0˚38'

II. Вычислить превышения на съёмочные пикеты. Если наведение средней нити производилось на точку рейки, соответствующую высоте прибора, то превышение до пикета вычисляется по формуле:

h =1/2 D' sin2ν; D' = S

1. h = - 0,46

III. Вычислить высоты съёмочных пикетов и записать их в соответствующую строку тахеометрического журнала.

Нi =Hст + hi, i – номер пикета.

Ст.216 Н1=229,66+(-0,46)=229,2

Список использованной литературы

1. Маслов А.В., Гордеев А. В., Батраков Ю.Г. Геодезия . – М.:КолосС, 2006.

2. Кузнецов П. Н. Геодезия. – М.: Недра, 2003.

3. Маслов А. В., Юнусов А. Г., Горохов Г. И. Геодезические работы при землеустройстве. – М.: Недра, 1990.

4. Лысов А.В., Павлов А. П., Шиганов А. С. Геодезия. Методические указания по изучению дисциплины: Саратов, ФГОУ ВПО «Саратовский ГАУ им. Н. И. Вавилова». 2007.

5. Селиханович В.Г., Козлов В.П., Логинова Г.П. Практикум по геодезии. – М.: Недра, 1978.

1